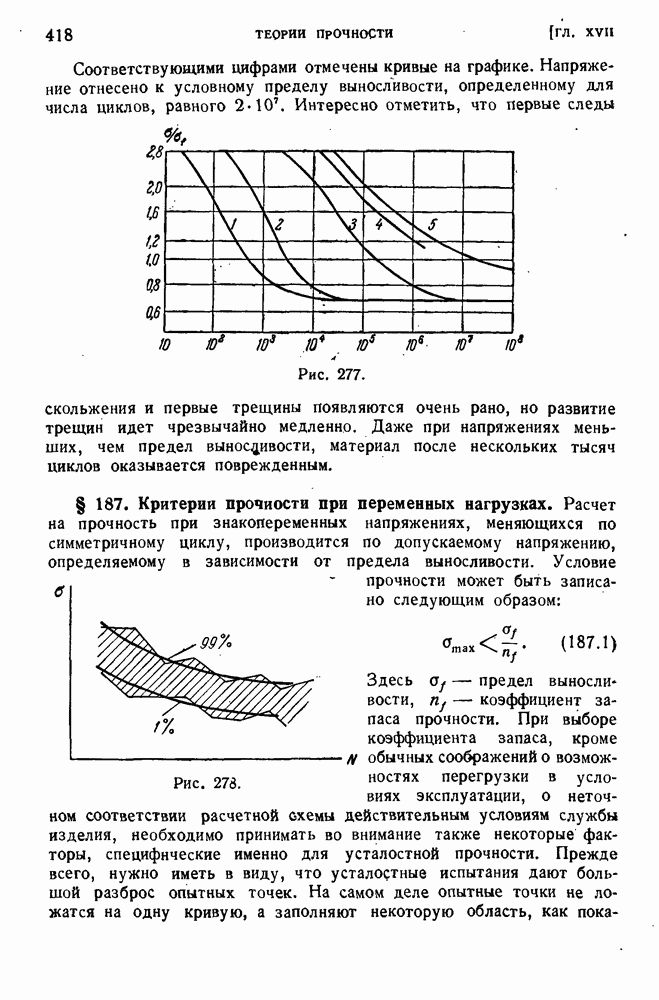
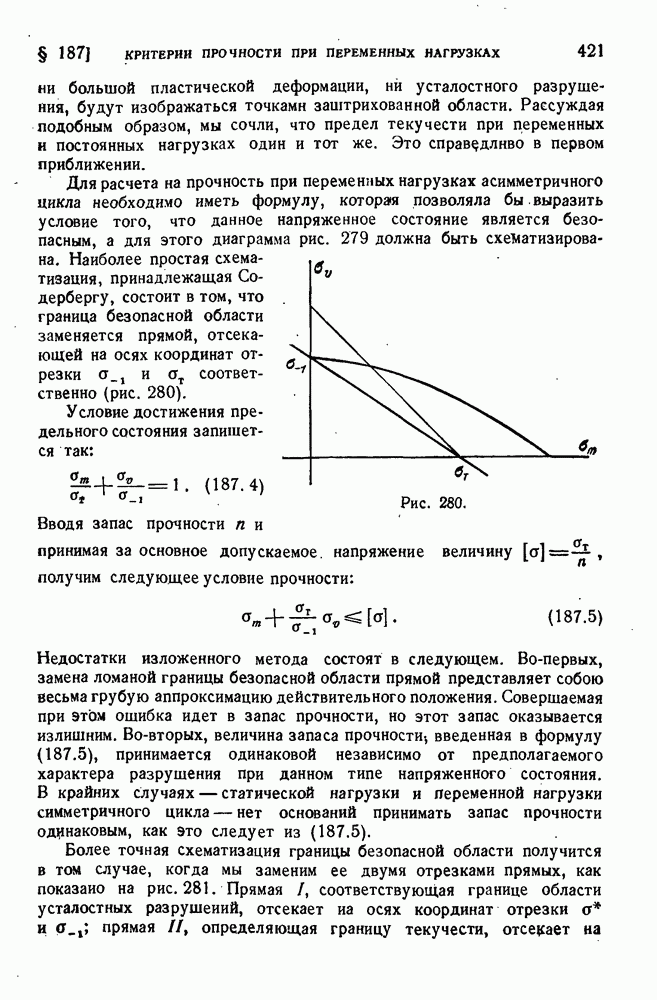
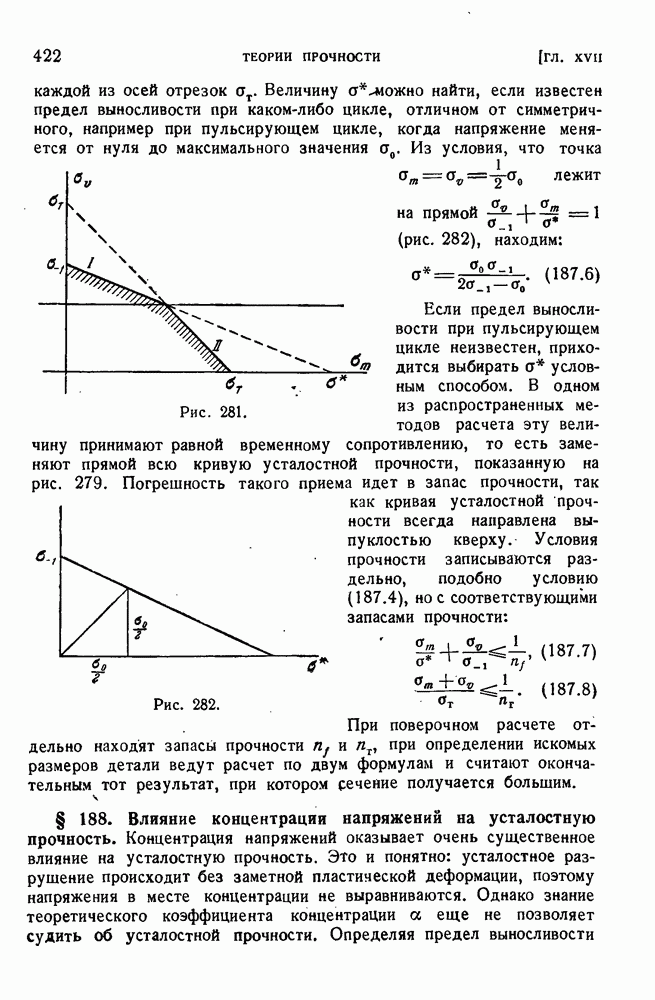
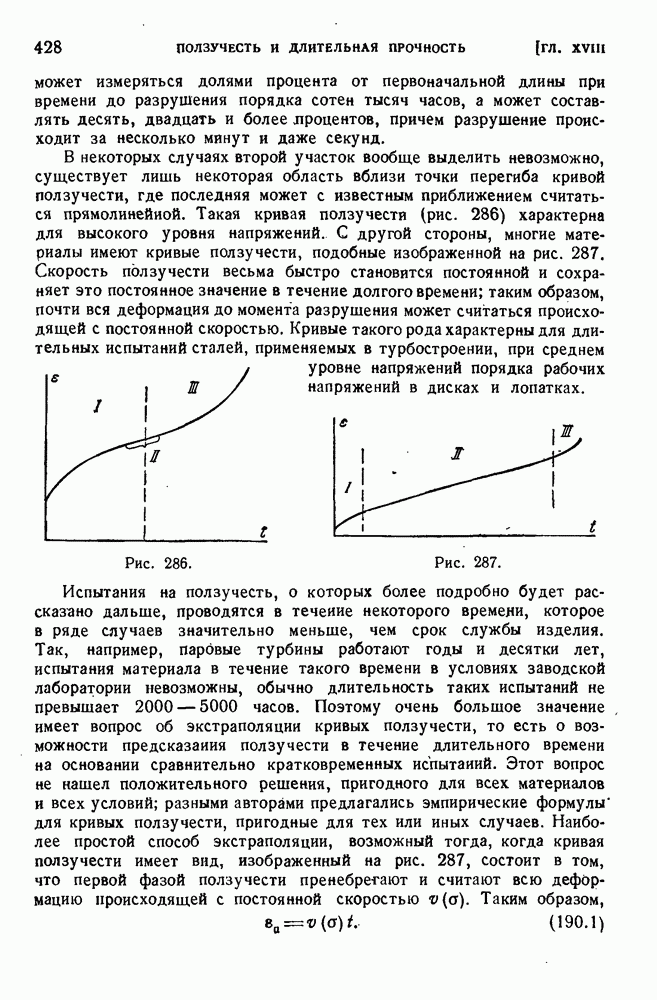
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
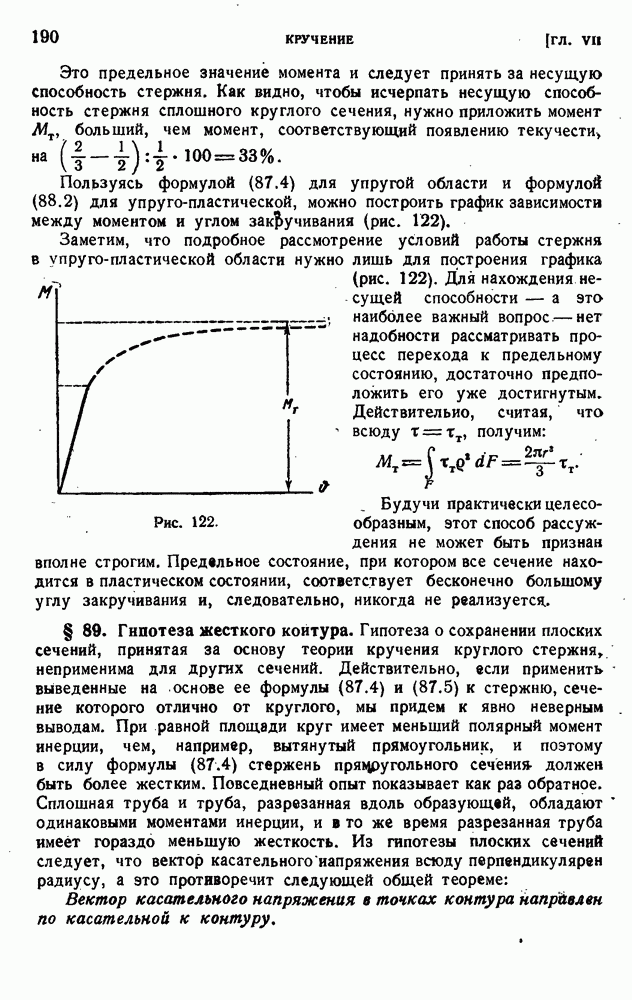
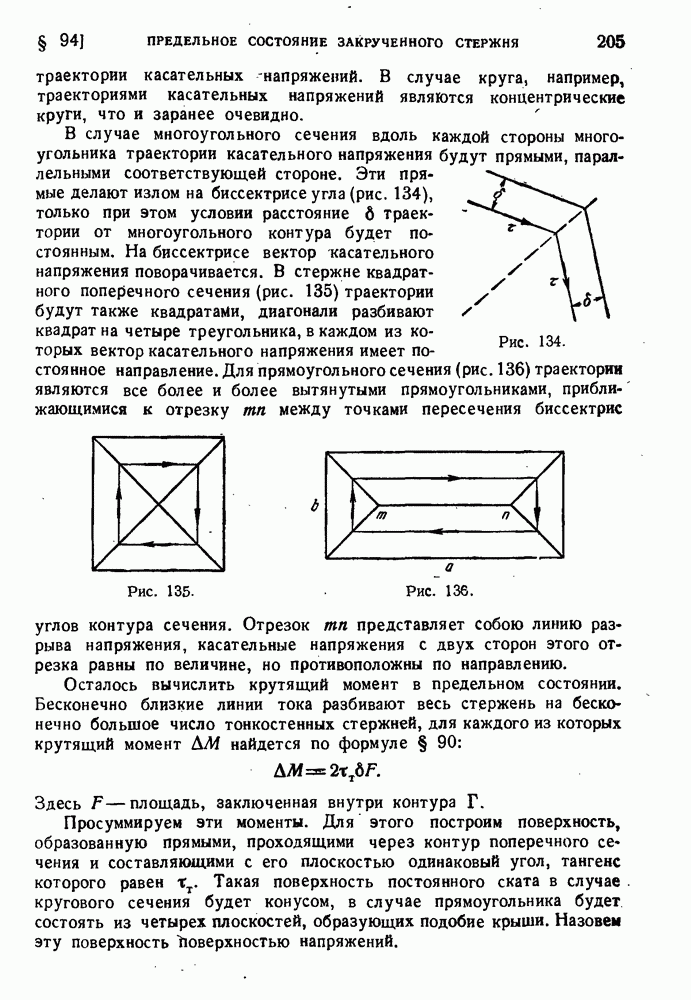
§ 129. Дополнительные напряжения при кручении.
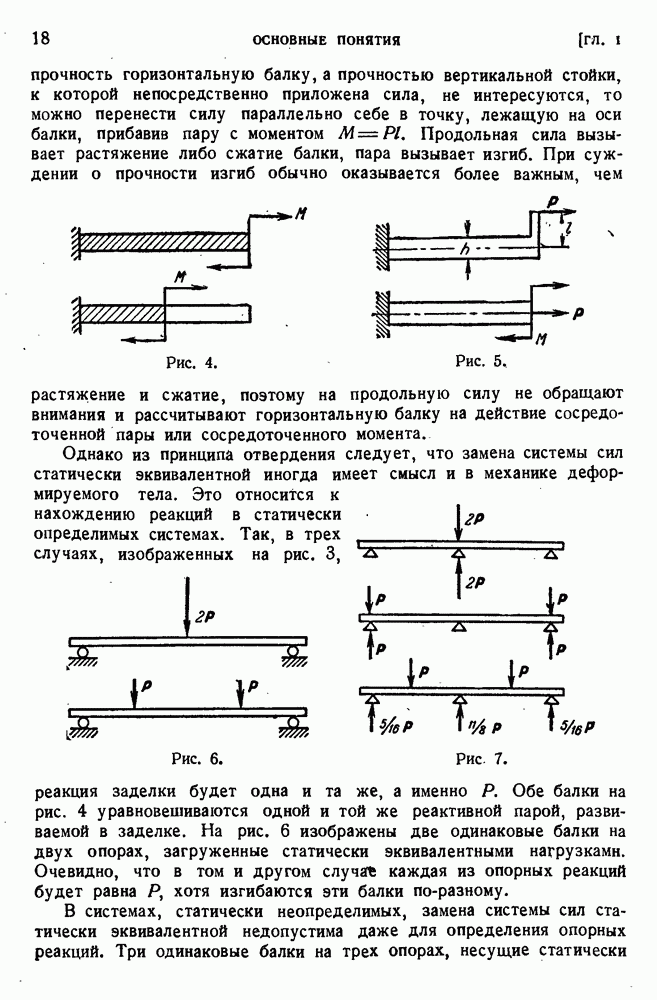
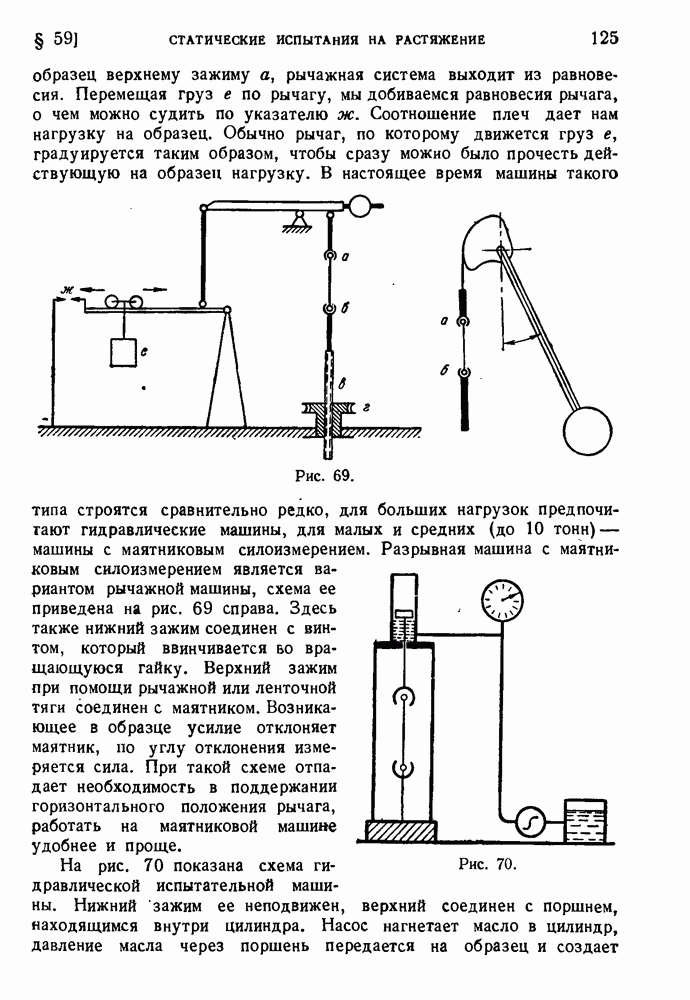
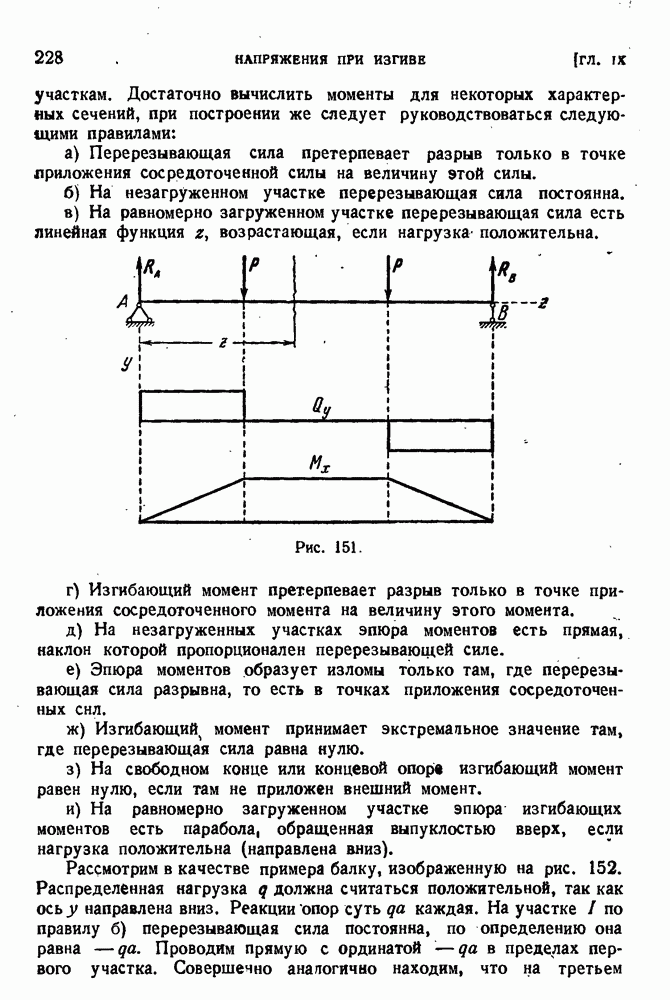
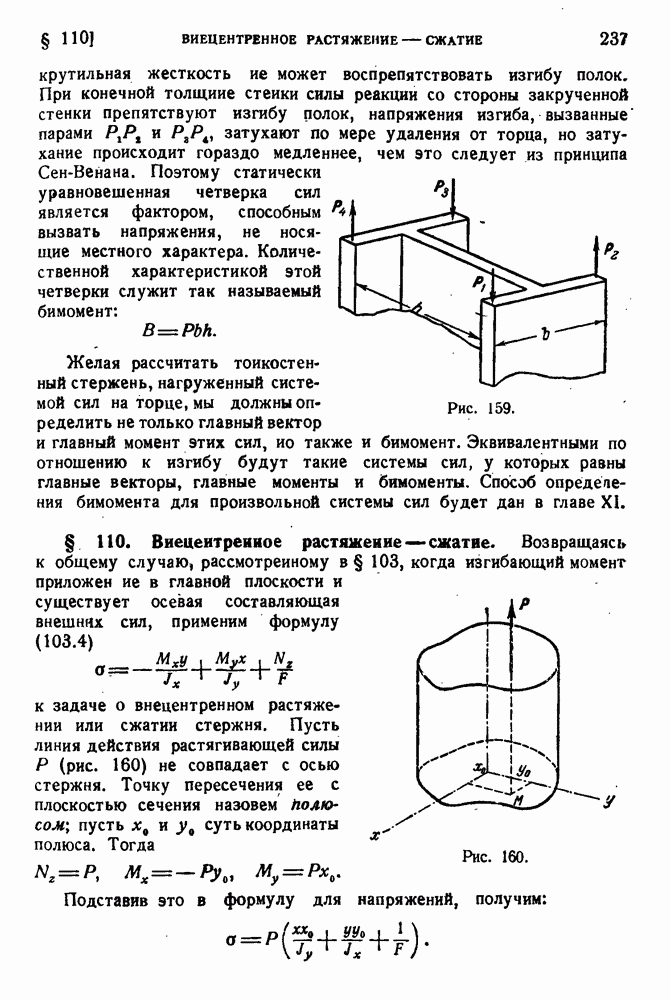
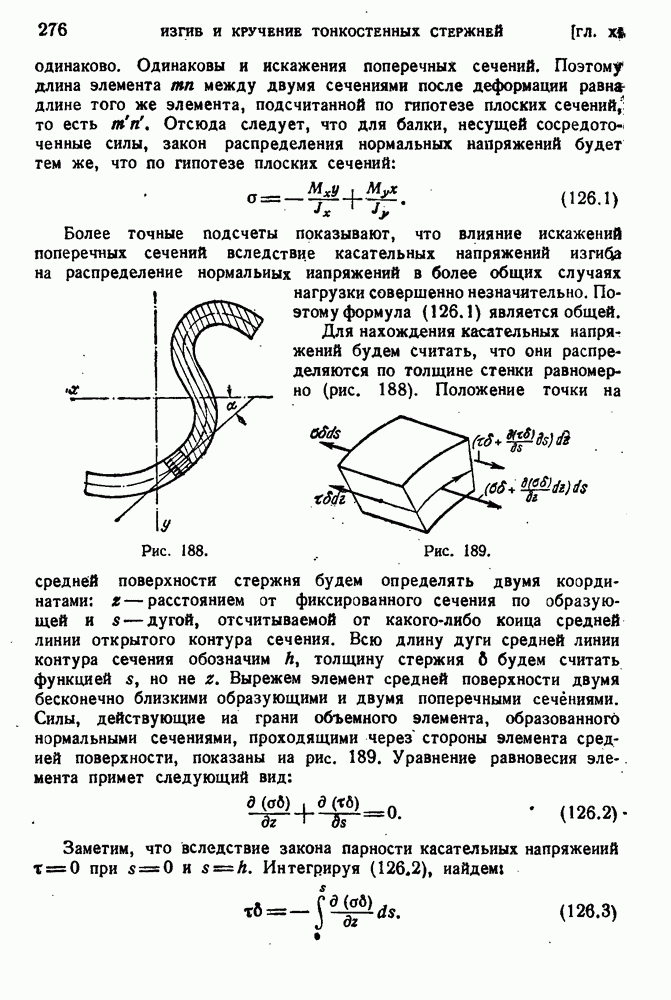
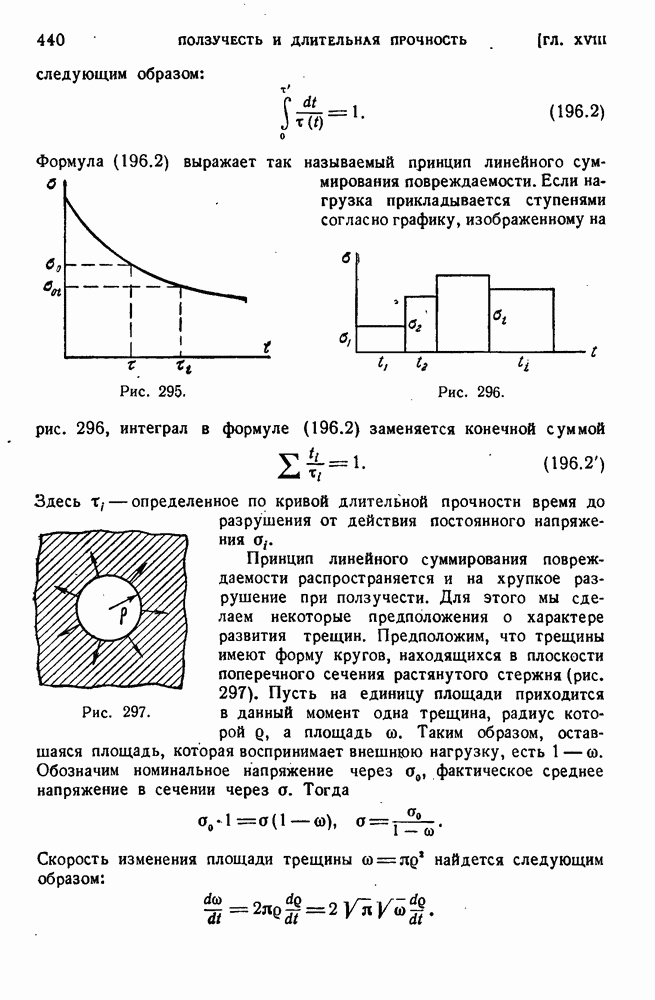
Если внешние силы лежат в плоскости, не проходящей через линию центров изгиба, то в стержне возникают напряжения кручения. Теорией кручения тонкостенных стержней открытого профиля мы занимались в § 90 главы VII. Более подробный анализ показывает, что по отношению к тонкостенным стержням задачи об изгибе и кручении нельзя рассматривать по отдельности, независимо одну от другой. Специфика работы тонкостенных стержней в реальных конструкциях ставит их обычно в такие условия, когда непосредственное применение результатов § 90 невозможно. Все дело в том, что поперечные сечения тонкостенных стержней открытого профиля при кручении значительно искажаются. Возможность свободного искажения поперечного сечения и объясняет малую жесткость таких стержней. Рассмотрим в качестве примера тонкостенную трубу с разрезом. Под действием крутящего момента она деформируется так, как показано на рис. 196, а. Если сварить края разреза (рис. 196, б), то возможность искажения поперечного сечения будет исключена и жесткость трубы значительно возрастет. В случае а жесткость нужно рассчитывать по формуле для стержня открытого профиля:


Рис. 196.
В случае  жесткость по формуле для тонкостенной трубы равна
жесткость по формуле для тонкостенной трубы равна

Предположим теперь, что левый конец разрезанной трубы заделан, а к правому приложен крутящий момент (рис. 196, в). Левое течение при этом не искажается, искажение правого сечения гораздо меньше, чем в случае а, потому что оно связано с продольной деформацией. Действительно, изображенное на рисунке искажение течений стержня при сохранении одного из них плоским возможно лишь при том условии, что образующая  укорачивается, а
укорачивается, а  удлиняется. Продольные деформации неизбежно связаны с появлением нормальных напряжений в поперечных сечениях.
удлиняется. Продольные деформации неизбежно связаны с появлением нормальных напряжений в поперечных сечениях.
Эти напряжения самоуравновешиваются, так как равнодействующая продольных сил в сечении должна быть равна нулю. Жесткость такого стержня, находящегося в условиях стесненного кручения, будет промежуточной между  .
.
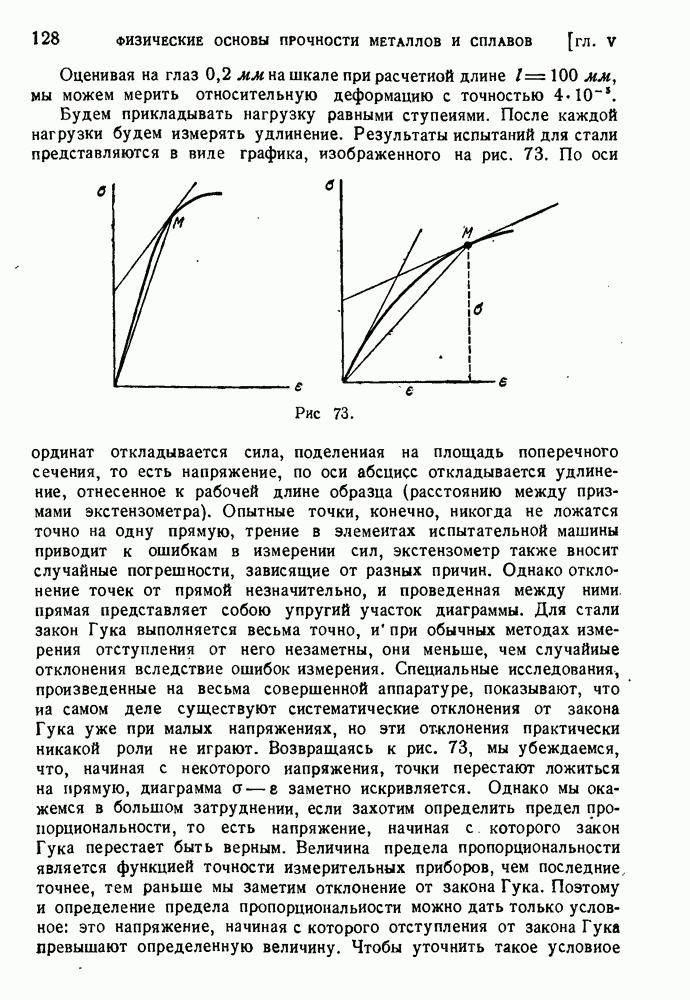
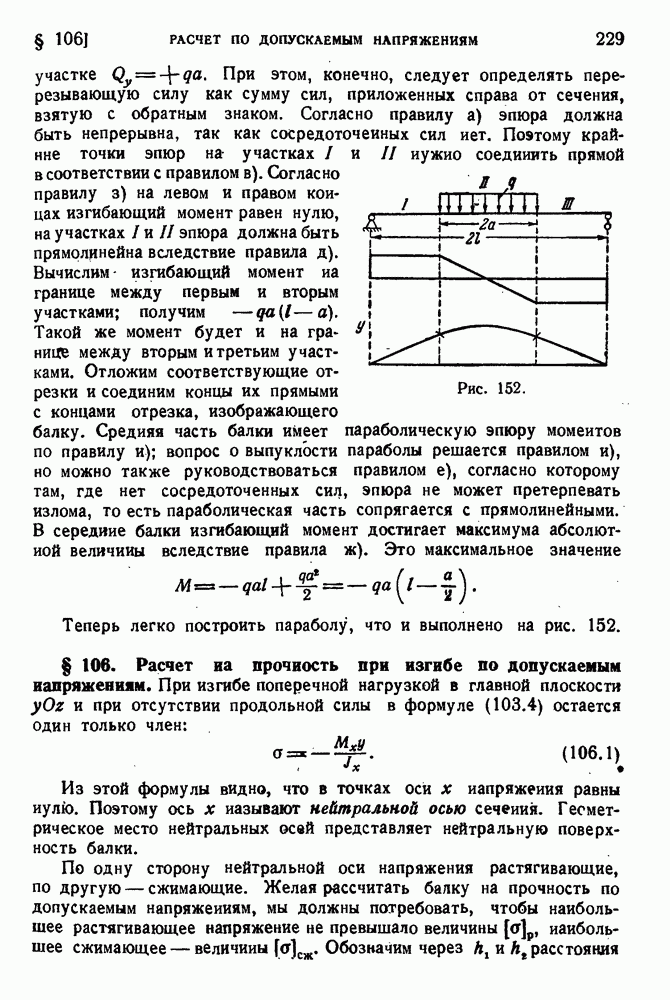
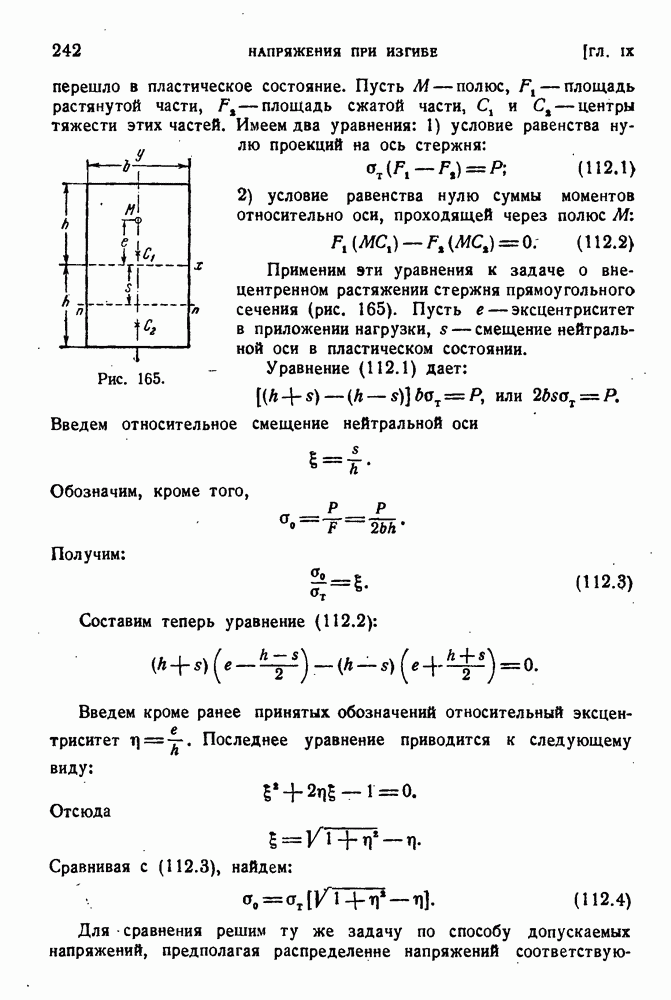
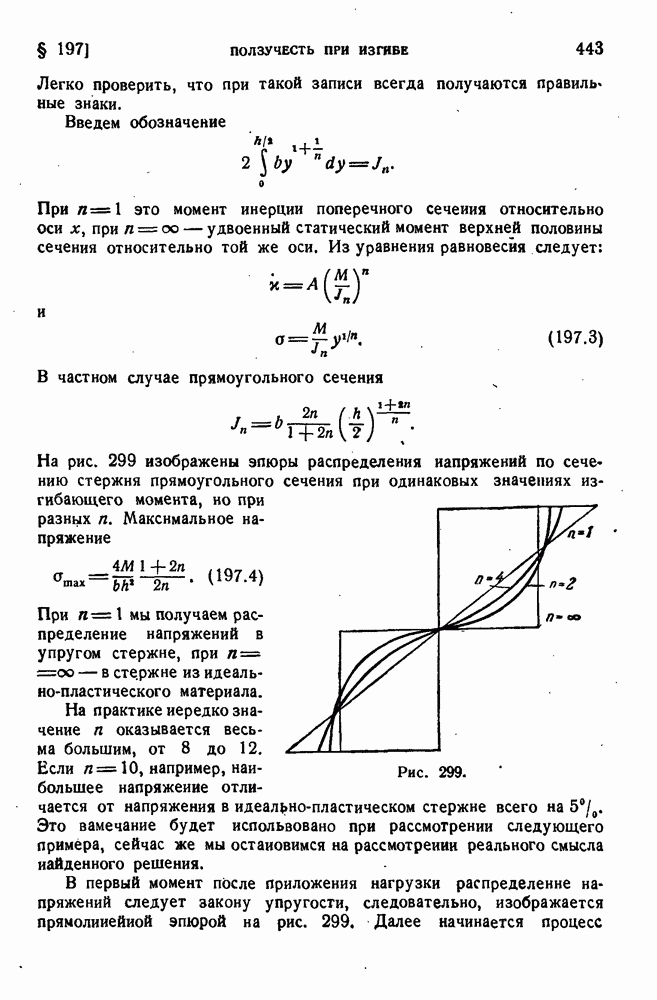
Дополнительные нормальные напряжения при кручении возникают и в других случаях. Предположим, например, что в промежуточном сечении тонкостенного стержня приложен сосредоточенный закручивающий момент. На двух смежных участках стержня крутящие моменты оказываются различными, под действием этих крутящих моментов сечения стержня на смежных участках стремятся исказиться в различной степени. На рис. 197 показаны две части стержня.

Рис. 197.
разрезанного по плоскости приложения момента. Чтобы выполнить условие неразрывности, необходимо приложить показанные на чертеже продольные силы. Вообще нормальные напряжения получатся во всех тех случаях, когда крутящий момент меняется по длине стержня. Разница в искажениях различных поперечных сечений неминуемо влечет за собой появление этих напряжений.
Обращаясь к примерам разрезанной и неразрезанной трубы, можно понять, какие напряжения в сечении уравновешивают крутящий момент, С одной стороны, это система касательных напряжений, распределенных линейно по толщине и возникающих при обычном кручении тонкостенного стержня открытого профиля. С другой, существование нормальных напряжений, как показано в § 126, связано с существованием касательных напряжений, распределенных по толщине стенки равномерно. Эти касательные напряжения (будем называть их изгибно-крутильными) участвуют в уравновешивании крутящего момента.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Задачи и содержание сопротивления материалов.
- § 2. Сопротивление материалов и теоретическая механика.
- § 3. Статически неопределенные задачи.
- § 4. Внешние силы.
- § 5. Принцип отвердения.
- § 6. Недопустимость замены системы сил статически эквивалентной.
- § 7. Однородное тело.
- § 8. Внутренние силы.
- § 9. Напряжение.
- § 10. Простейшие типы напряженного состояния.
- § 11. Простейшие виды деформации.
- § 12. Упругость и пластичность.
- § 13. Закон Гука.
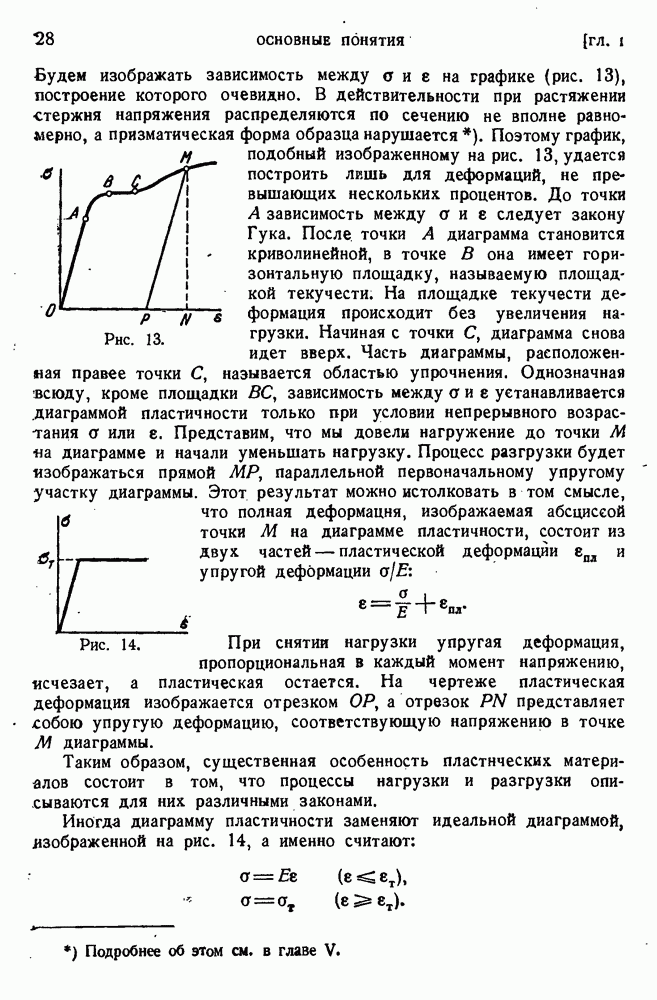
- § 14. Диаграмма пластичности.
- § 15. Тела изотропные и анизотропные.
- ГЛАВА II. РАСТЯЖЕНИЕ СЖАТИЕ
- § 16. Стержни и стержневые системы.
- § 17. Принцип Сен-Венана и гипотеза плоских сечений.
- § 18. Напряжения и деформации при растяжении.
- § 19. Расчеты на прочность при растижении и сжатии.
- § 20. Собственный вес и силы инерции.
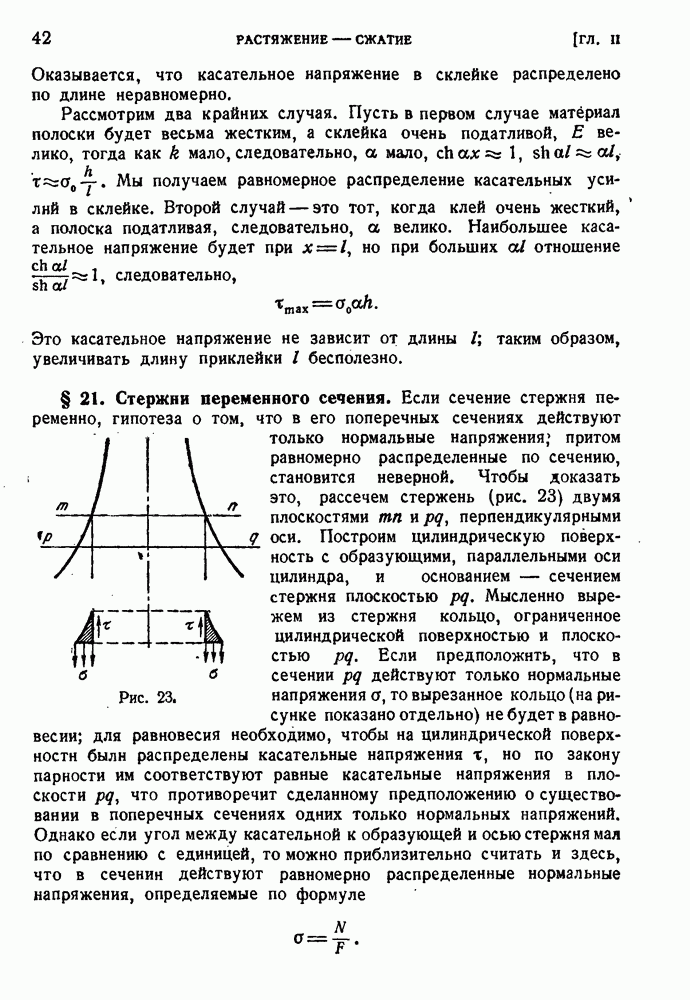
- § 21. Стержни переменного сечения.
- § 22. Перемещения узлов стержневых систем.
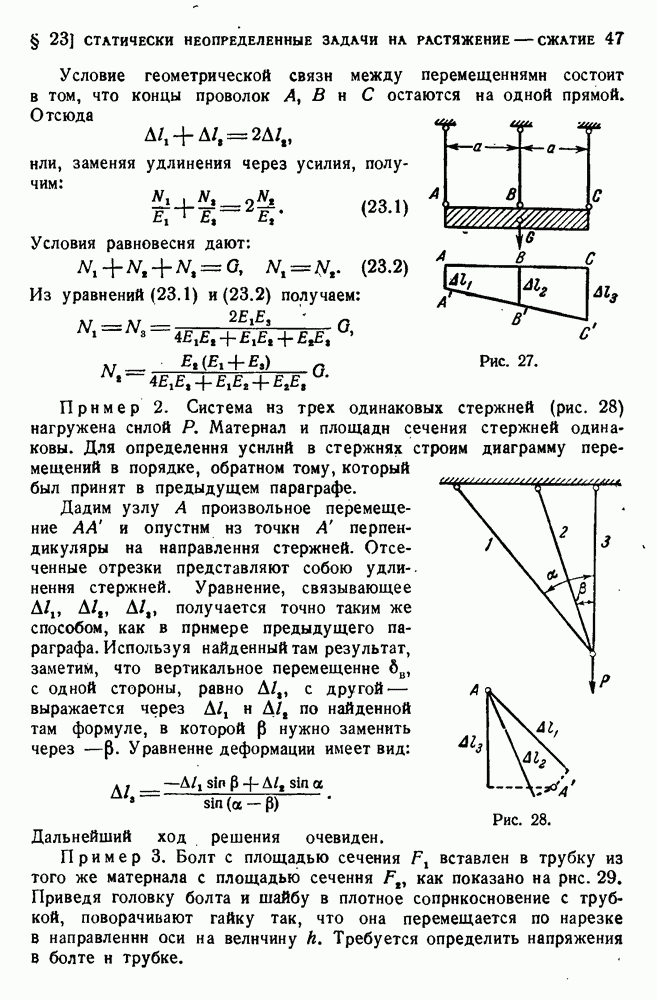
- § 23. Статически неопределенные задачи на растяжение — сжатие.
- § 24. Температурные и монтажные напряжения.
- § 25. Общие соображения о расчете стержневых систем.
- § 26. Расчет статически неопределимых систем по допускаемым нагрузкам.
- § 27. Остаточные напряжения после пластической деформации.
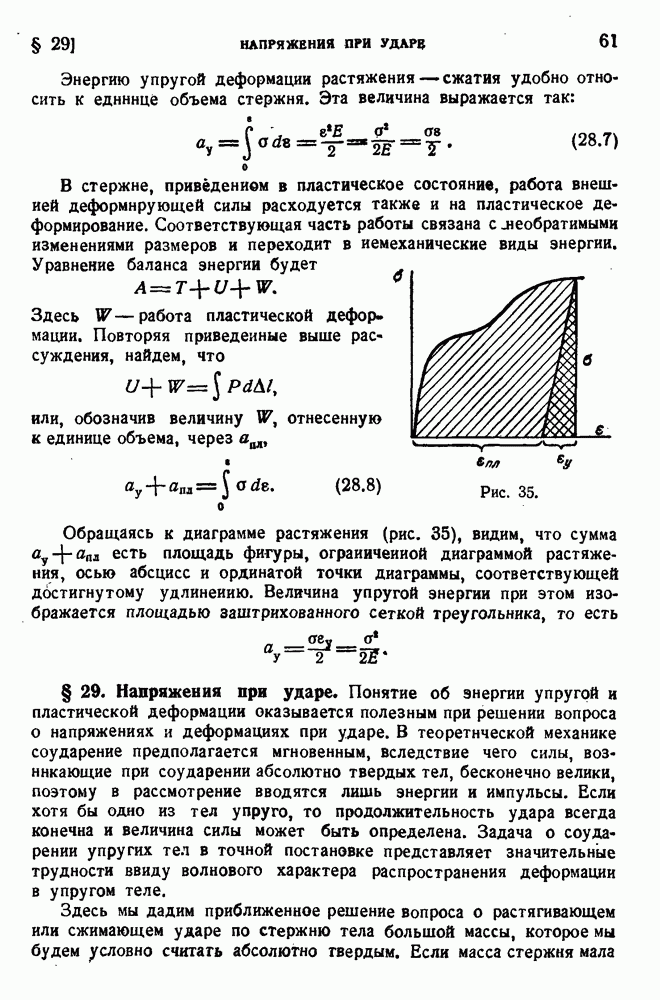
- § 28. Потенциальная энергия растяжении.
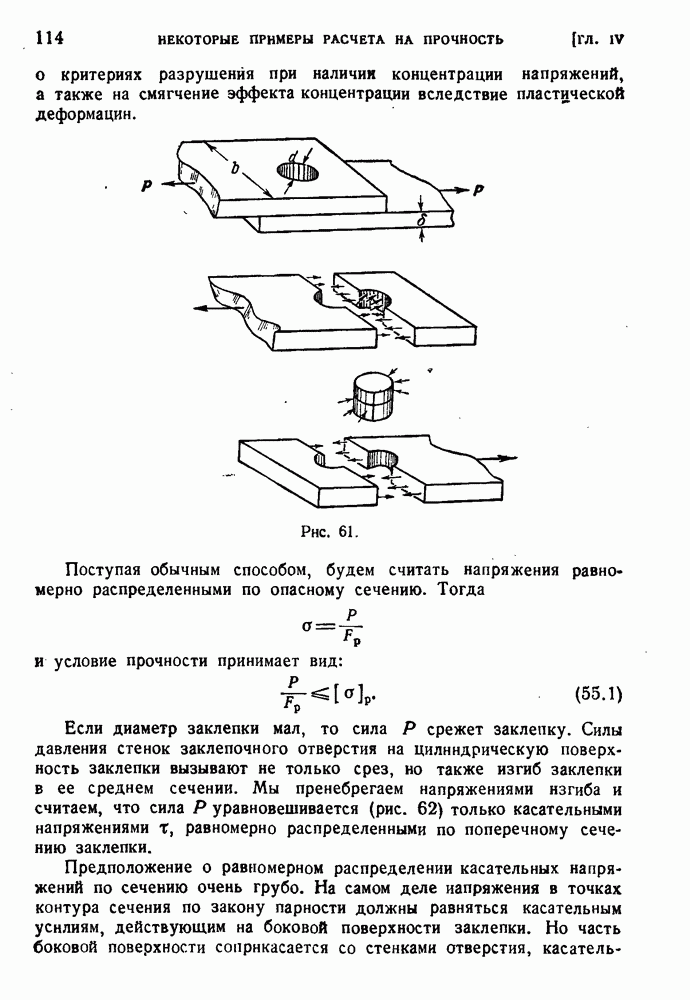
- § 29. Напряжения при ударе.
- § 30. Распространение упругих волн в стержнях.
- § 31. Концентрации напряжений.
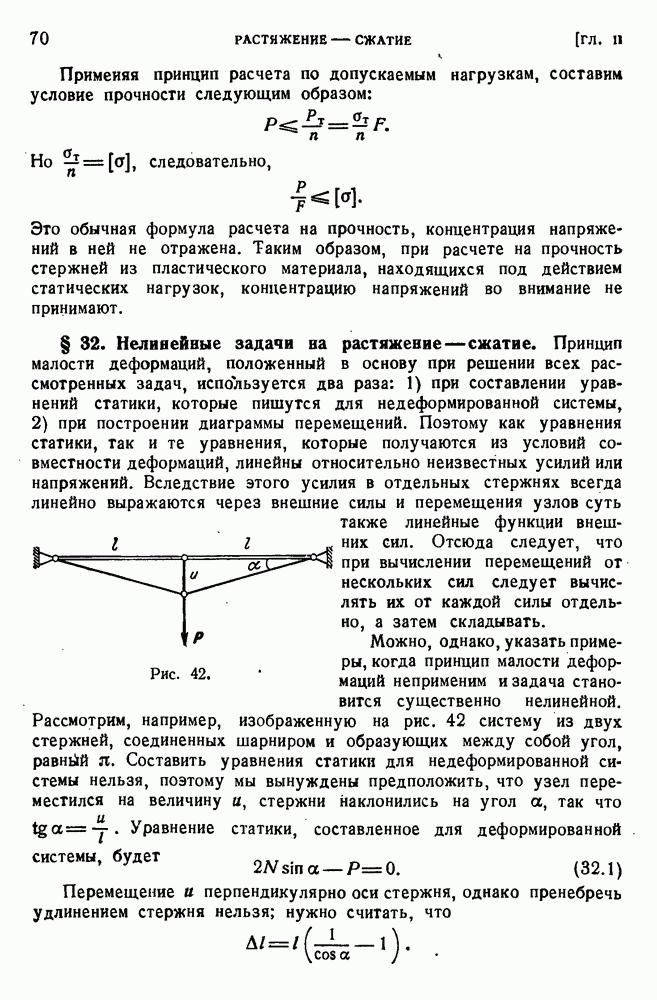
- § 32. Нелинейные задачи на растяжение — сжатие.
- ГЛАВА III. СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
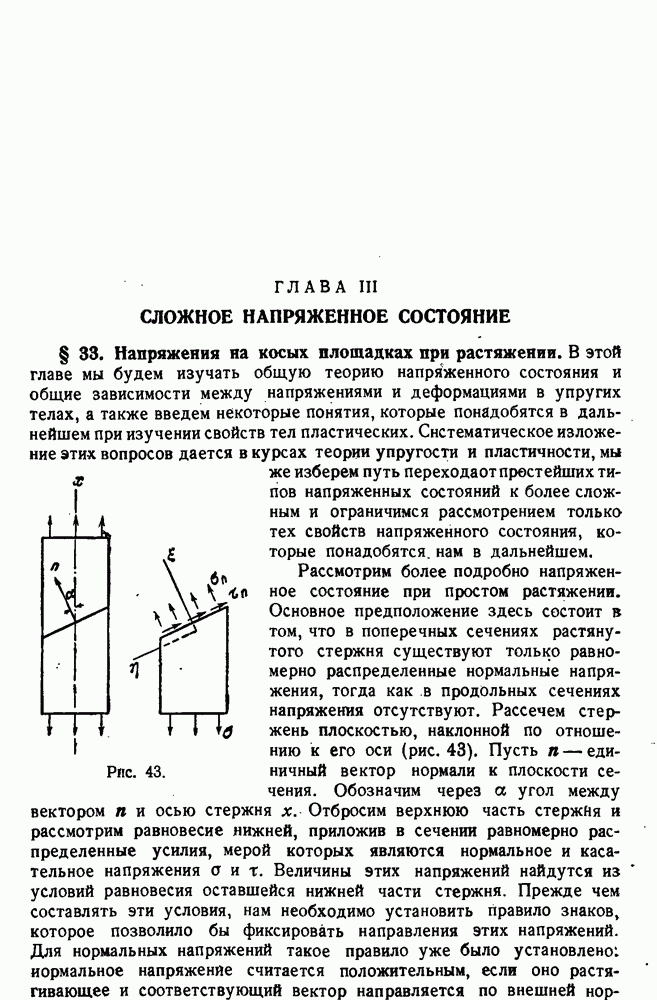
- § 33. Напряжения на косых площадках при растяжении.
- § 34. Напряжения при двухосном растяжении.
- § 35. Круговая диаграмма Мора.
- § 36. Общий случай плоского напряженного состояния.
- § 37. Определение напряжений на произвольной площадке.
- § 38. Пространственное напряженное состояние.
- § 39. Главные напряжения.
- § 40. Главные касательные напряжения.
- § 41. Октаэдрическое напряжение.
- § 42. Закон Гука для главных осей.
- § 43. Изменение объема при упругой деформации.
- § 44. Чистый сдвиг.
- § 45. Деформация элемента объема в общем случае.
- § 46. Условие пластичности Треска — Сен-Венана.
- § 47. Условие пластичности Мизеса.
- § 48. Условия пластичности для плоского напряженного состояния.
- § 49. Потенциальная энергия упругой деформации.
- § 50. Энергия изменения формы.
- ГЛАВА IV. НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
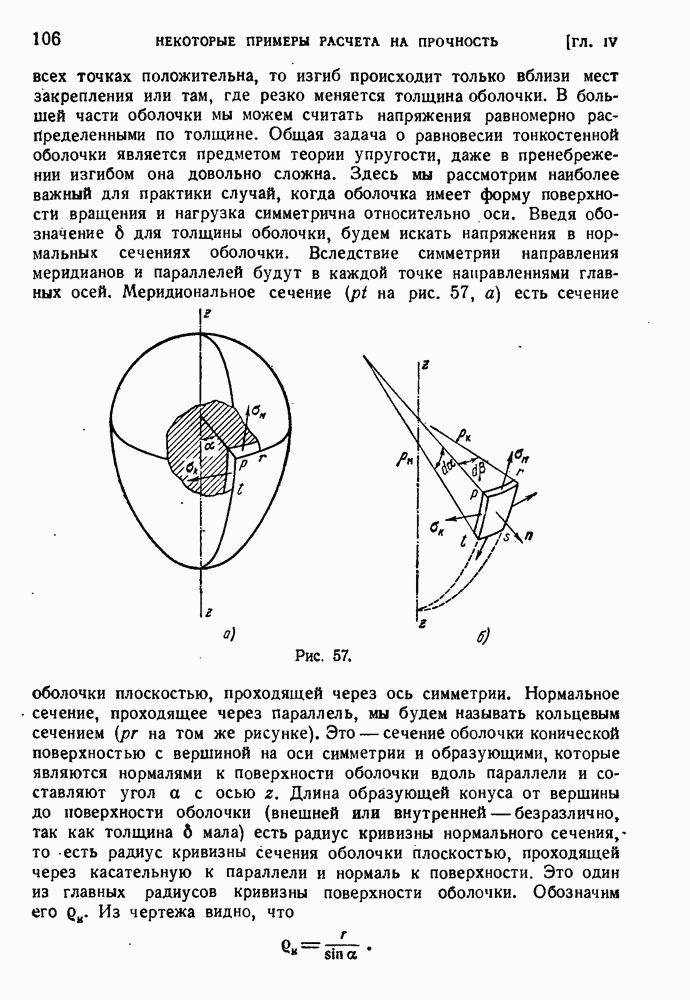
- § 51. Расчеты на прочность изделий сложной формы.
- § 52. Безмоментные оболочки вращении.
- § 53. Местные напряжения в безмоментных оболочках.
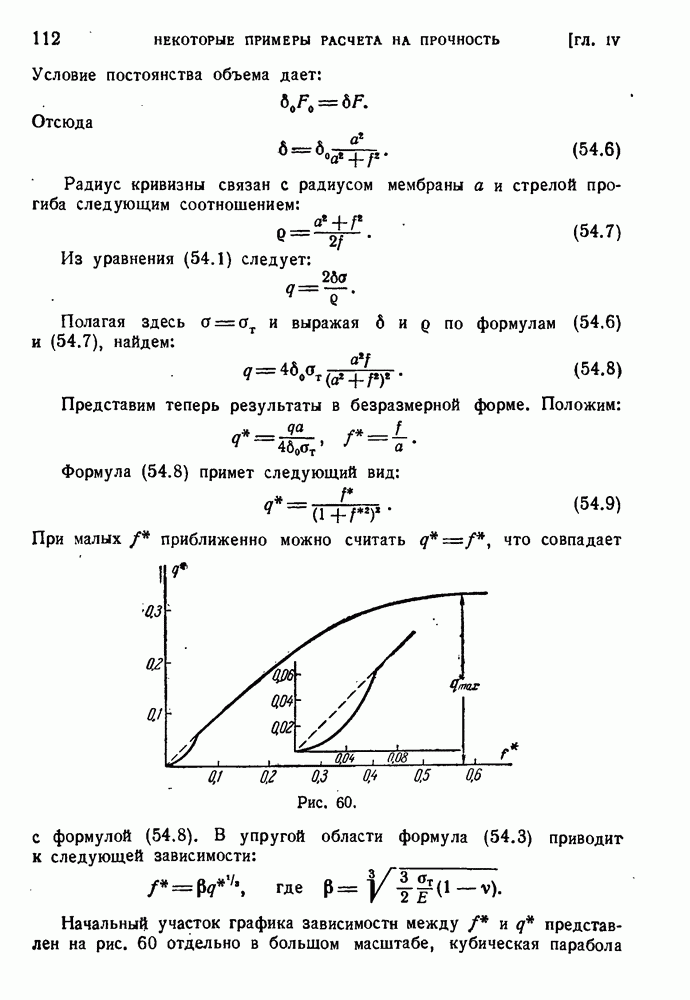
- § 54. Большие прогибы мембраны.
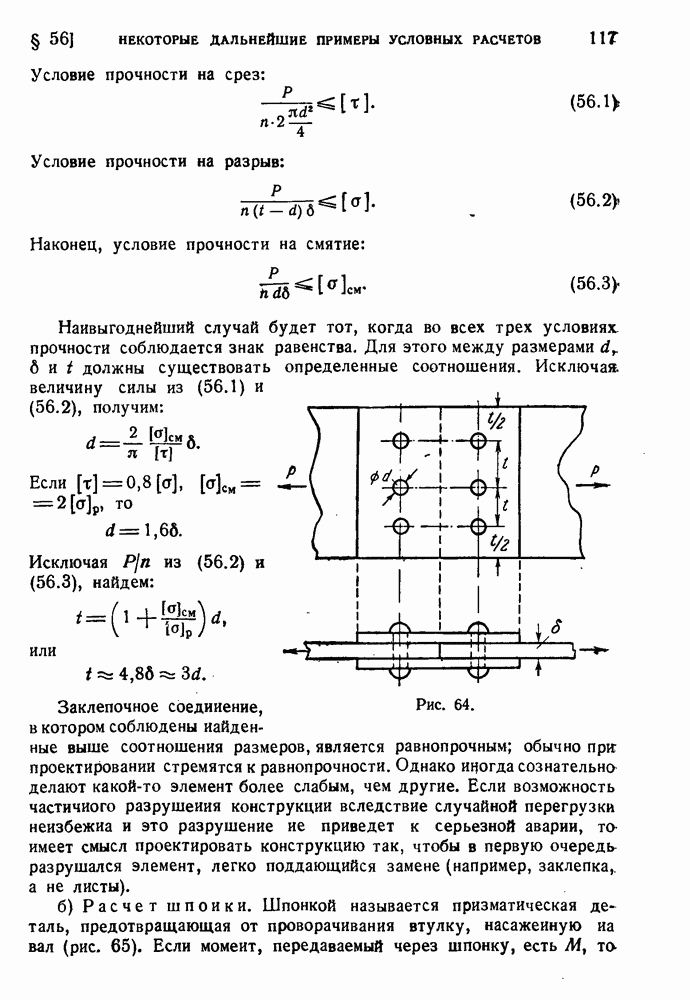
- § 55. Условные расчеты.
- § 56. Некоторые дальнейшие примеры условных расчетов.
- § 57. Расчет сварных соединений.
- ГЛАВА V. ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
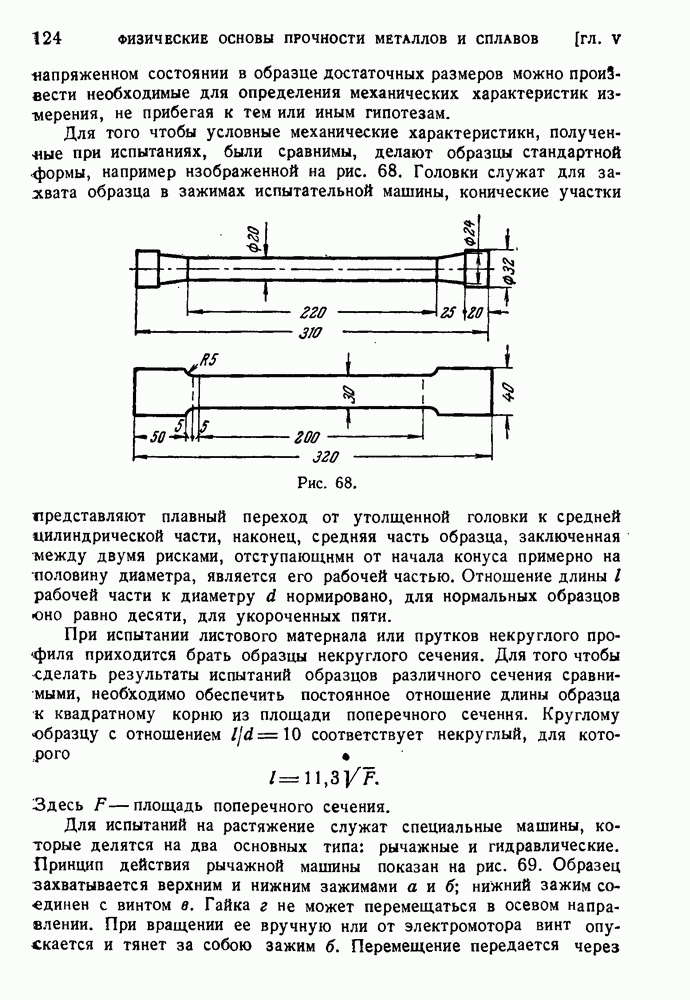
- § 58. Задачи испытания материалов.
- § 59. Статические испытания на растяжение.
- § 60. Исследование металлов в области малых деформаций.
- § 61. Диаграмма растяжения мягкой стали.
- § 62. Опыты на сжатие.
- § 63. Строение и упругая деформация металлических кристаллов.
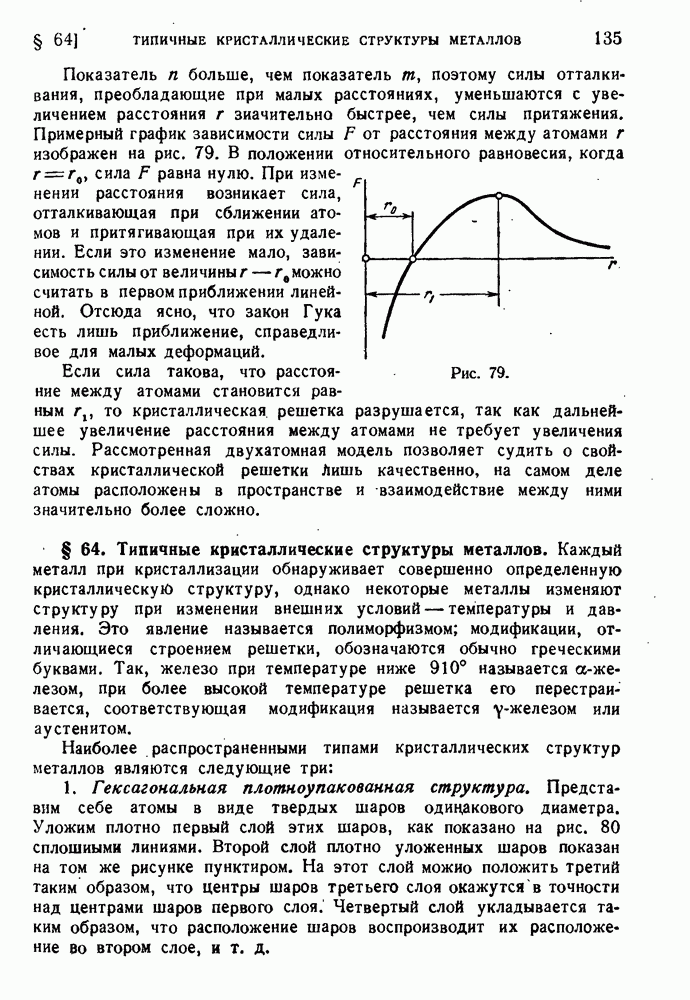
- § 64. Типичные кристаллические структуры металлов.
- § 65. Пластическая деформация монокристаллов.
- § 66. Прочность кристаллов и сопротивление пластическому деформированию.
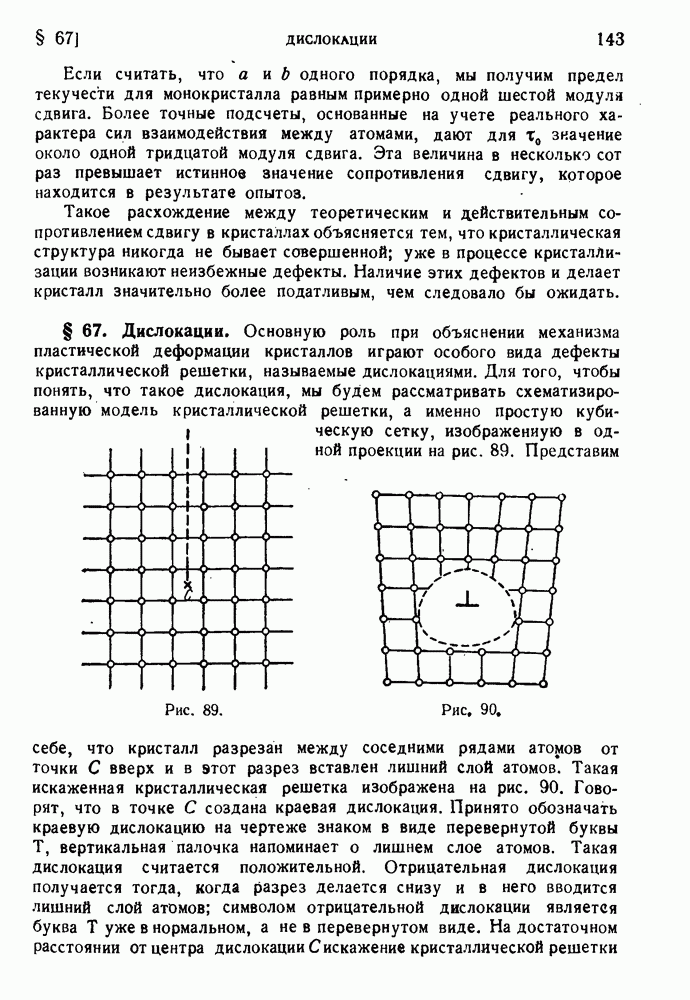
- § 67. Дислокации.
- § 68. Движение и равновесие дислокаций.
- § 69. Источники дислокаций.
- § 70. Границы блоков.
- § 71. Деформация поликристаллических металлов и сплавов.
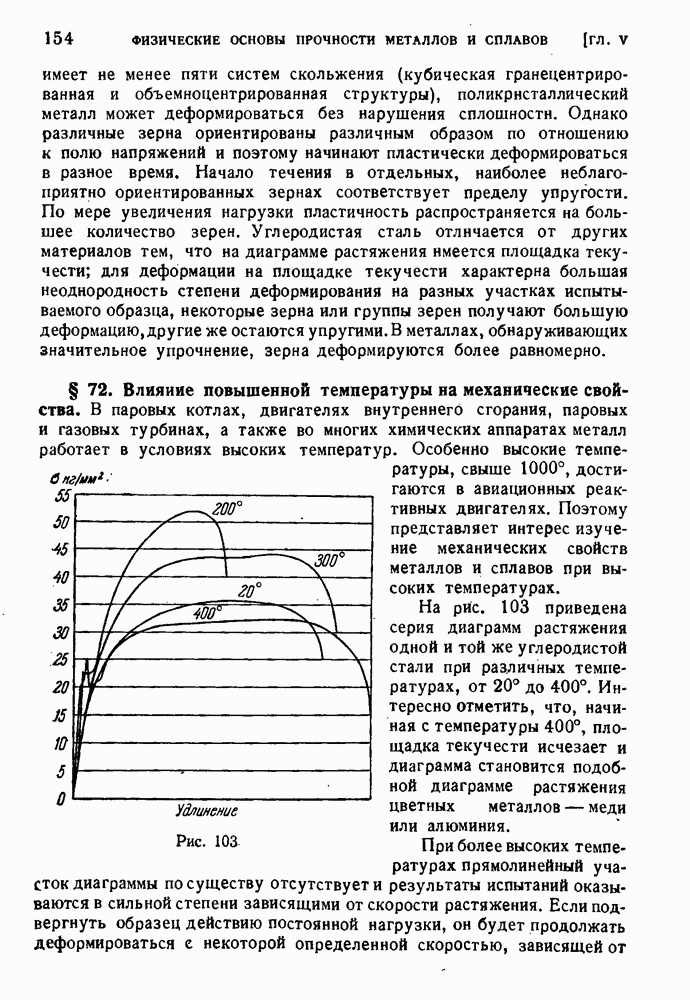
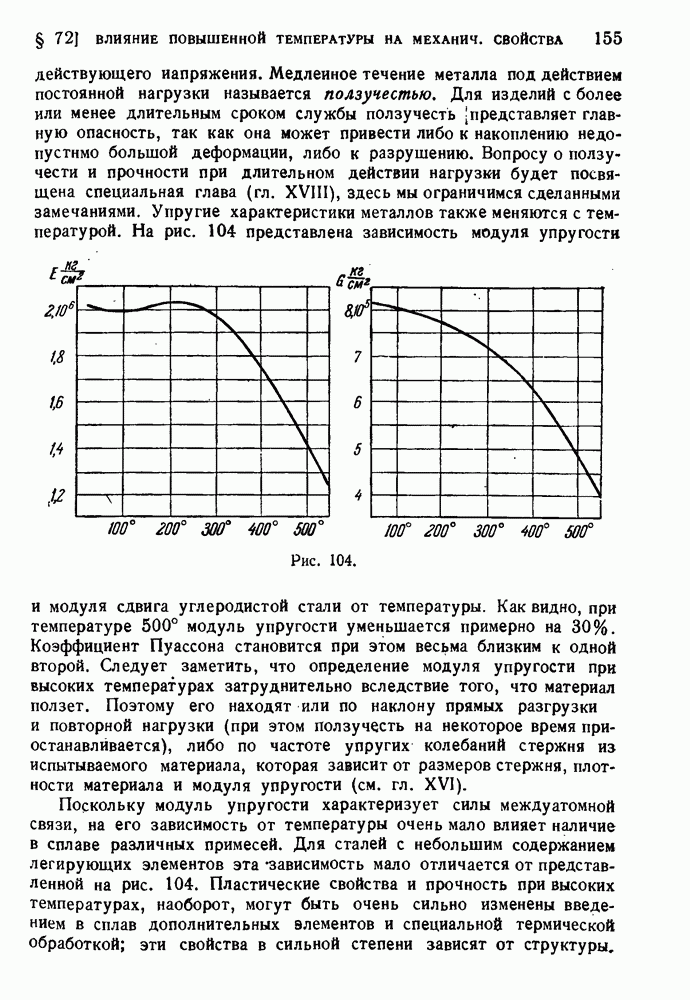
- § 72. Влияние повышенной температуры на механические свойства.
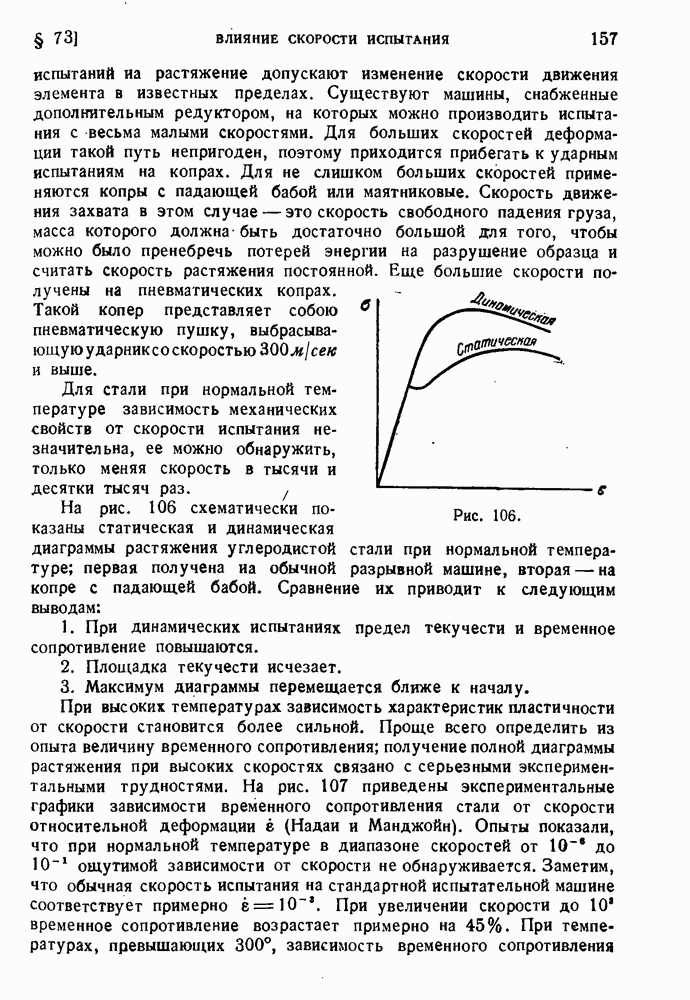
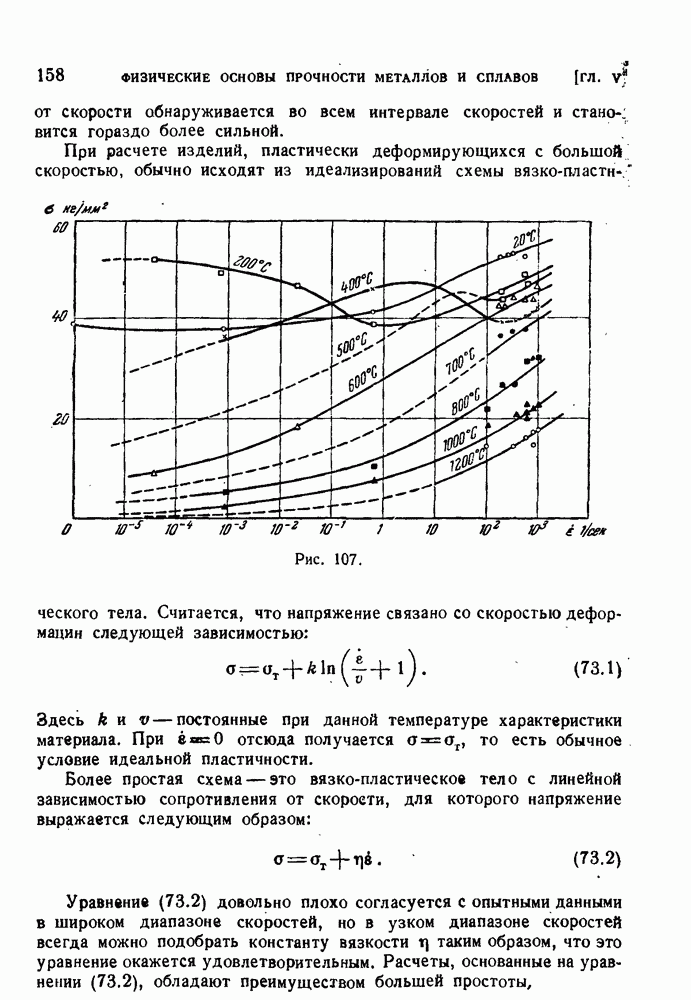
- § 73. Влияние скорости испытания.
- § 74. Испытании на твердость.
- ГЛАВА VI. ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ
- § 75. Основные принципы построения теории пластичности.
- § 76. Ассоциированный закон течения.
- § 77. Течение при условии пластичности Сен-Венана и Мизеса.
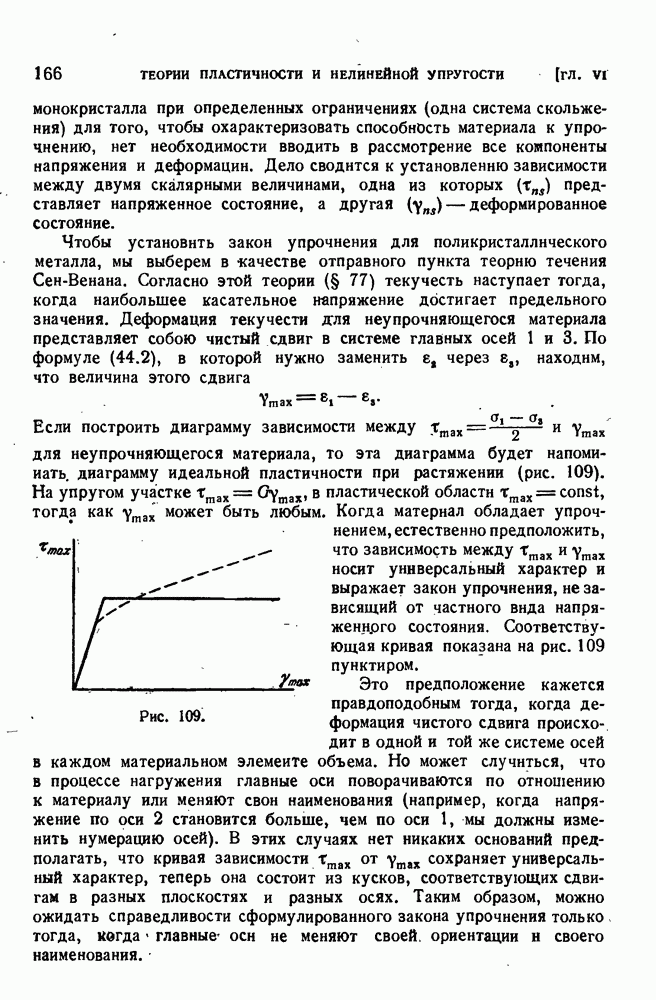
- § 78. Закон упрочнения.
- § 79. Деформационная теория пластичности.
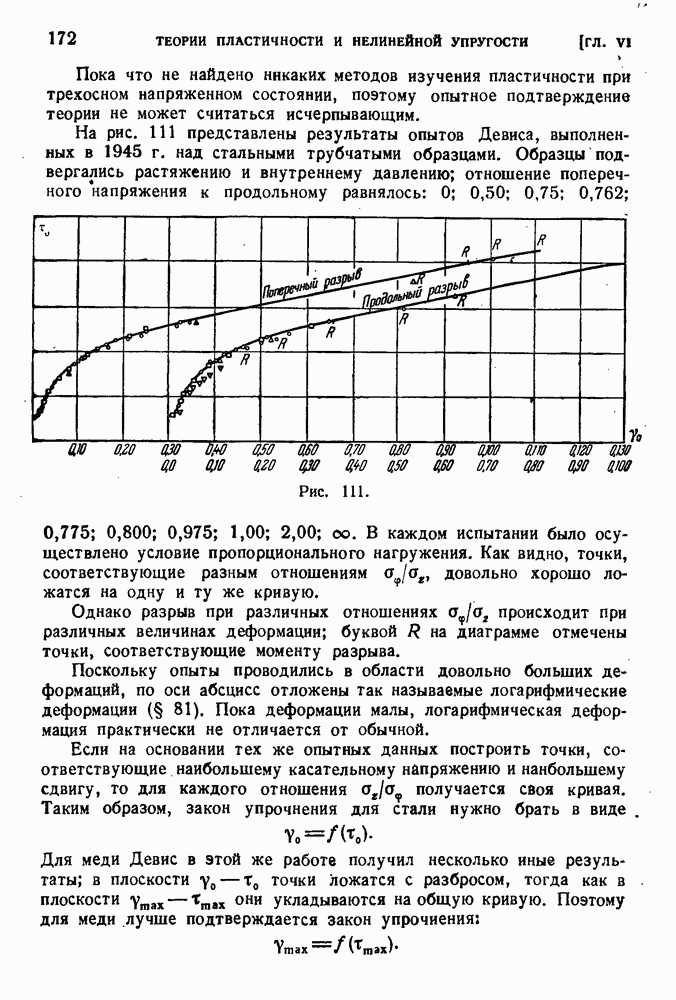
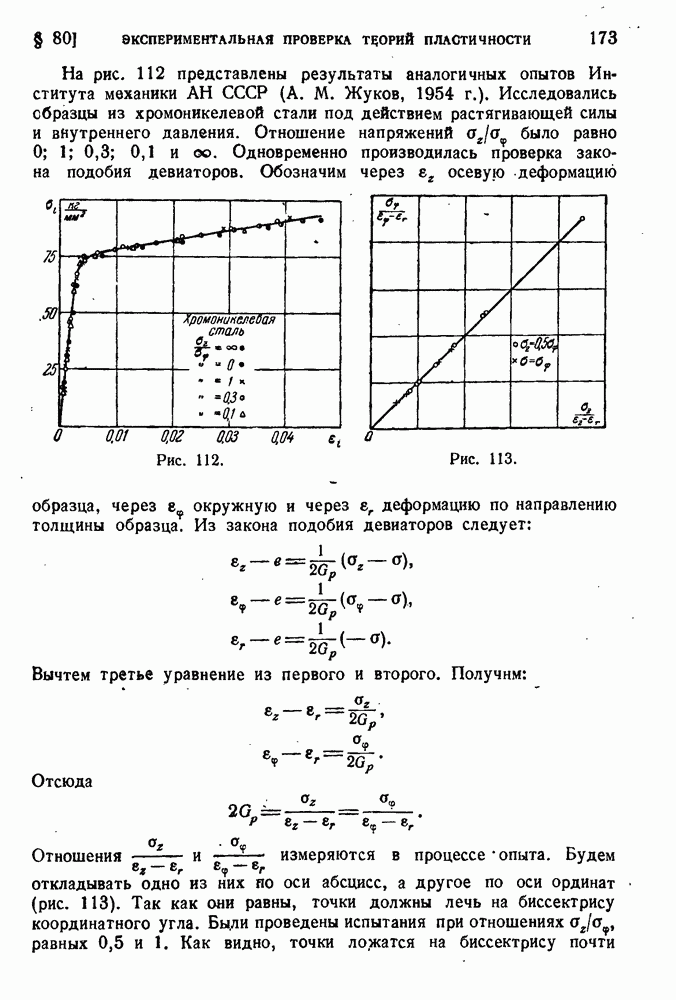
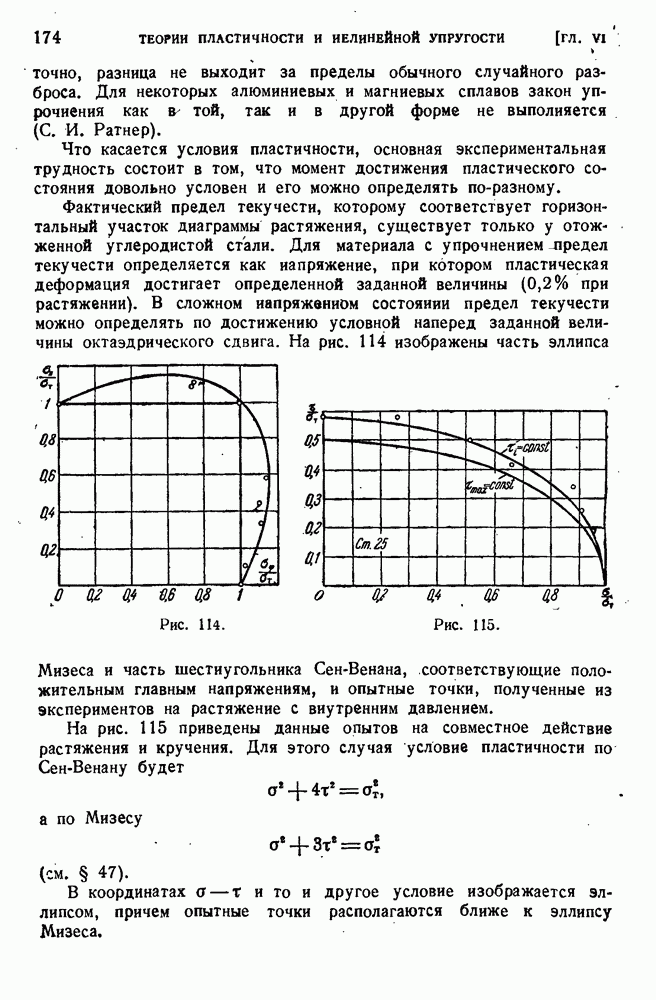
- § 80. Экспериментальная проверка теорий пластичности.
- § 81. Конечная деформация.
- § 82. Нелинейно упругое тело.
- § 83. Высокоэластические деформации.
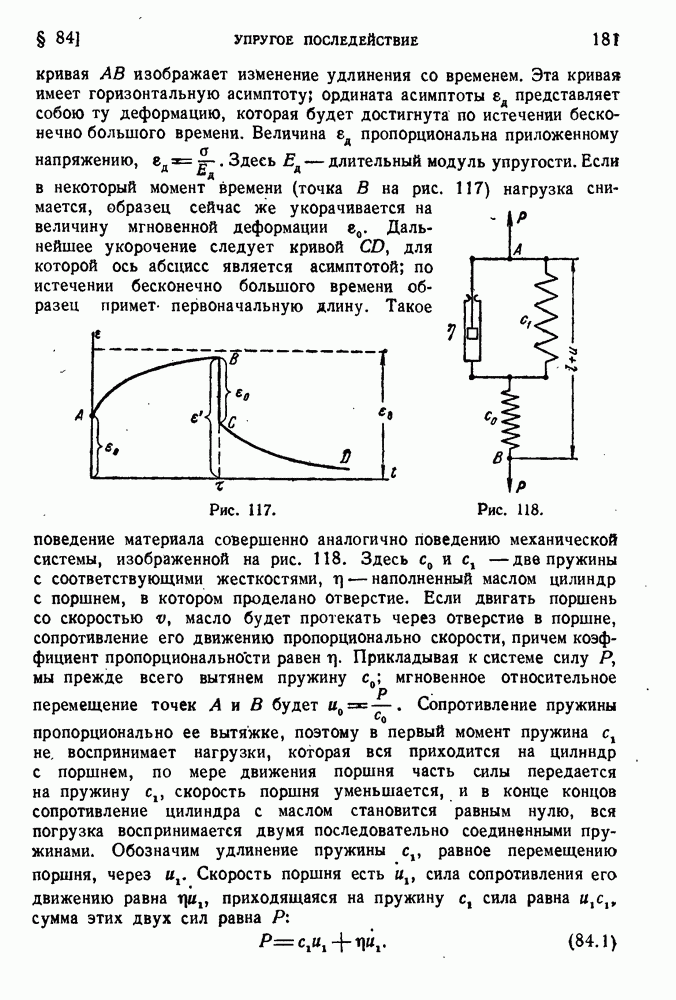
- § 84. Упругое последействие.
- § 85. Некоторые свойства вязко-упругого тела.
- § 86. Принцип суммирования Больцмана—Вольтерра.
- ГЛАВА VII. КРУЧЕНИЕ
- § 87. Кручение стержней круглого сечеиия.
- § 88. Упруго-пластическое кручение стержня круглого сечения.
- § 89. Гипотеза жесткого контура.
- § 90. Кручение тонкостенных стержней замкнутого профиля.
- § 91. Кручение тонкостенных стержней открытого профиля.
- § 92. Кручение упругих стержией сплошного профиля.
- § 93. Опытное исследование кручения.
- § 94. Предельное состояние закрученного стержня из идеально-пластического материала.
- ГЛАВА VIII. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- § 96. Общие теоремы о моментах.
- § 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей.
- § 98. Вычисление моментов инерции.
- § 99. Преобразование моментов инерции при повороте осей.
- § 100. Главные оси и главные моменты инерции.
- ГЛАВА IX. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
- § 101. Действие поперечных сил на балку.
- § 102. Гипотеза плоских сечений и принцип Сен-Венана.
- § 103. Нормальные напряжения при изгибе.
- § 104. Изгибающие моменты и перерезывающие силы.
- § 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры.
- § 106. Расчет на прочность при изгибе по допускаемым напряжениям.
- § 107. Упруго-пластический изгиб.
- § 108. Несущая способность стержня при изгибе.
- § 109. Принцип Сен-Венана.
- § 110. Внецентренное растяжение — сжатие.
- § 111. Ядро сечения.
- § 112. Несущая способность внецентренно сжатого стержня.
- § 113. Расчет составных балок.
- § 114. Изгиб кривого бруса.
- § 115. Нахождение нейтральной осн в кривом стержне.
- ГЛАВА X. ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- § 116. Дифференциальное уравнение изогнутой оси.
- § 117. Пределы применимости приближенной теории.
- § 118. Интегрирование уравнения изгиба.
- § 119. Примеры определения прогибов.
- § 120. Простейшие статически неопределенные задачи.
- § 121. Расчет статически неопределимых балок по способу допускаемых нагрузок.
- § 122. Изгиб стержней переменного сечения.
- § 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами.
- § 124. Продольно-поперечный изгиб.
- § 125. Изгиб балки на упругом основании.
- ГЛАВА XI. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
- § 126. Нормальные и касательные напряжения при изгибе.
- § 127. Касательные напряжении при изгибе в плоскости симметрии.
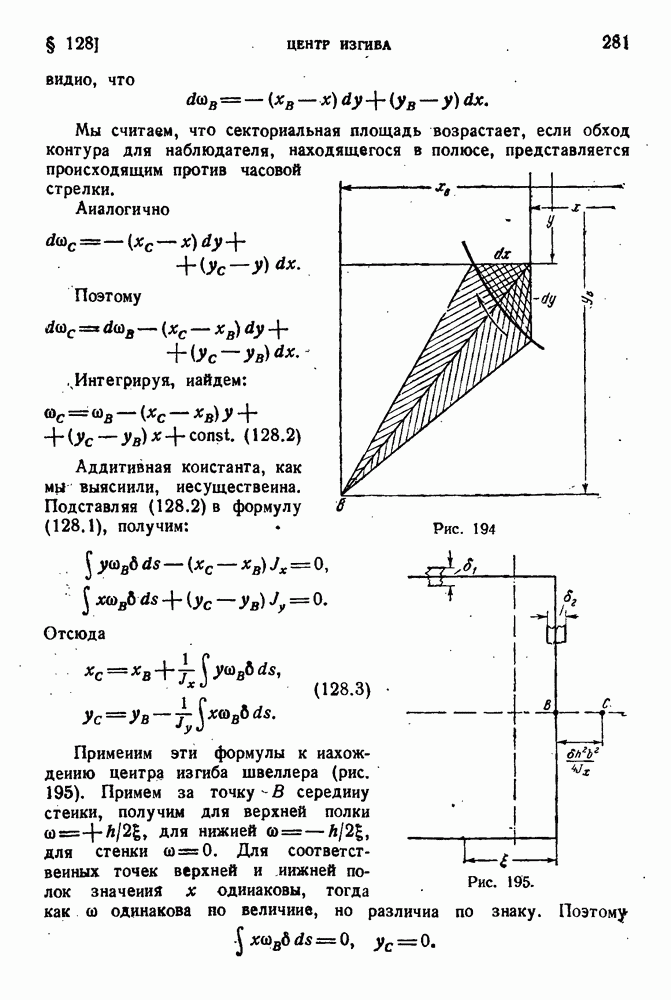
- § 128. Центр изгиба.
- § 129. Дополнительные напряжения при кручении.
- § 130. Закон секториальных площадей.
- § 131. Уравнение стесненного кручения.
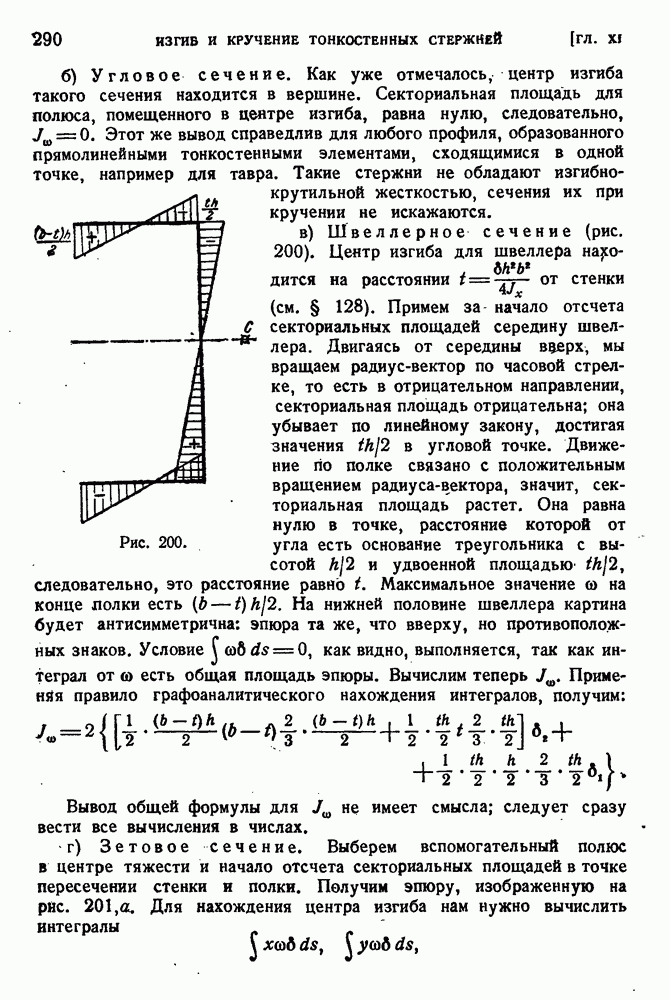
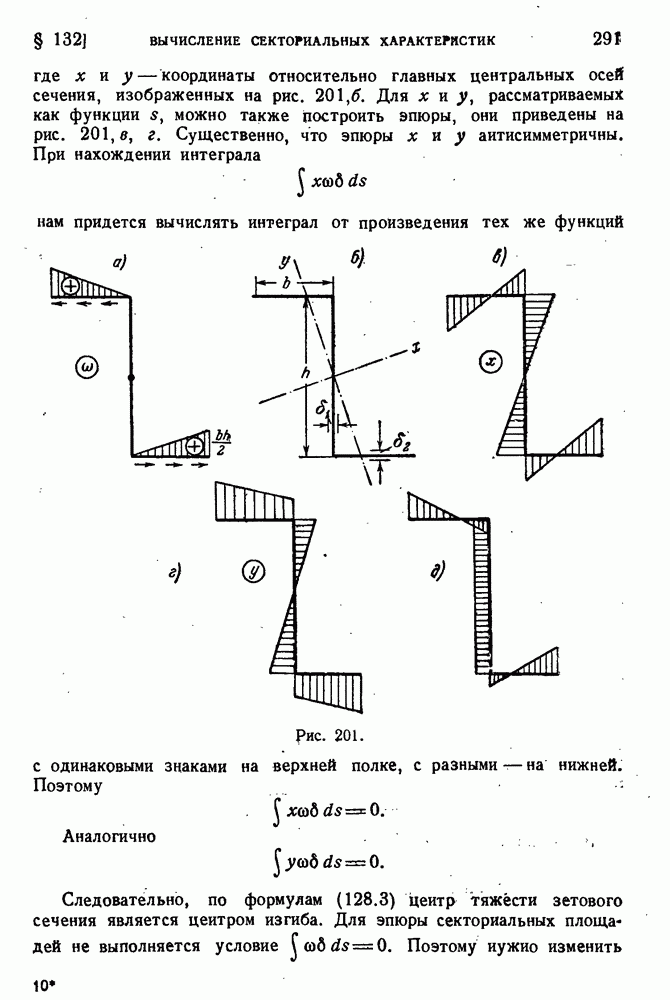
- § 132. Вычисление секториальных характеристик.
- § 133. Стержень, нагруженный бимоментом.
- § 134. Некоторые примеры стесненного кручения.
- ГЛАВА XII. УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ
- § 135. Постановка вопроса об устойчивости.
- § 136. Устойчивость сжатого упругого стержня.
- § 137. Эластика Эйлера.
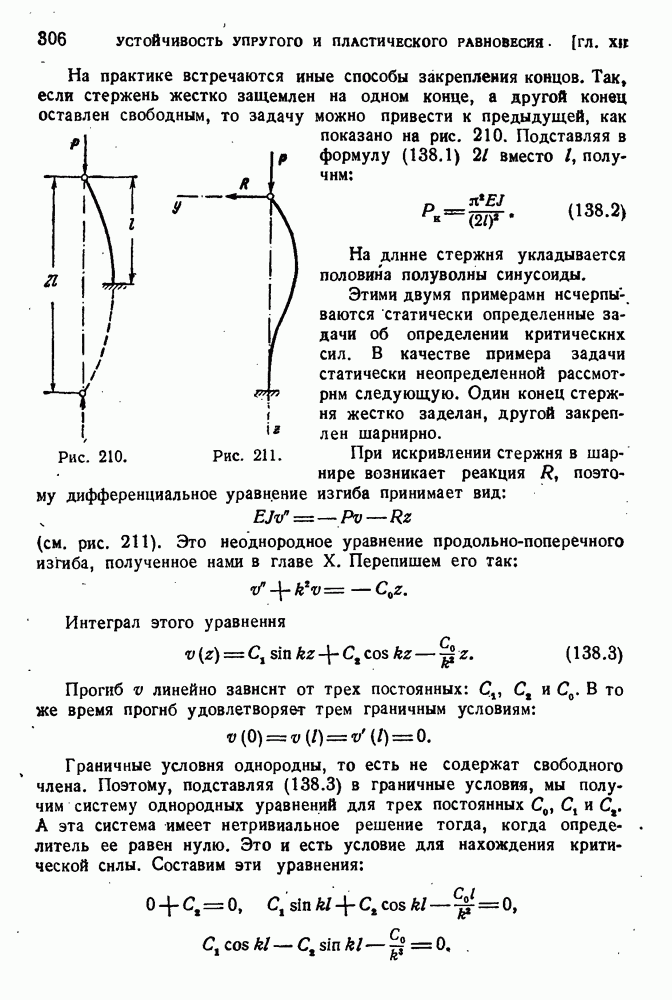
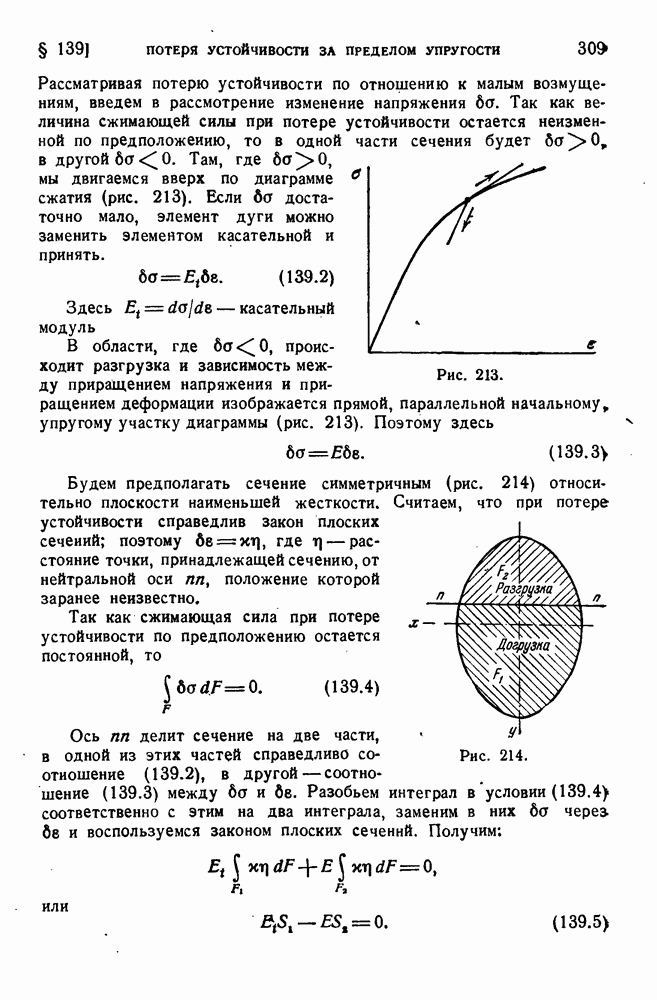
- § 138. Критические силы при иных видах закрепления стержня.
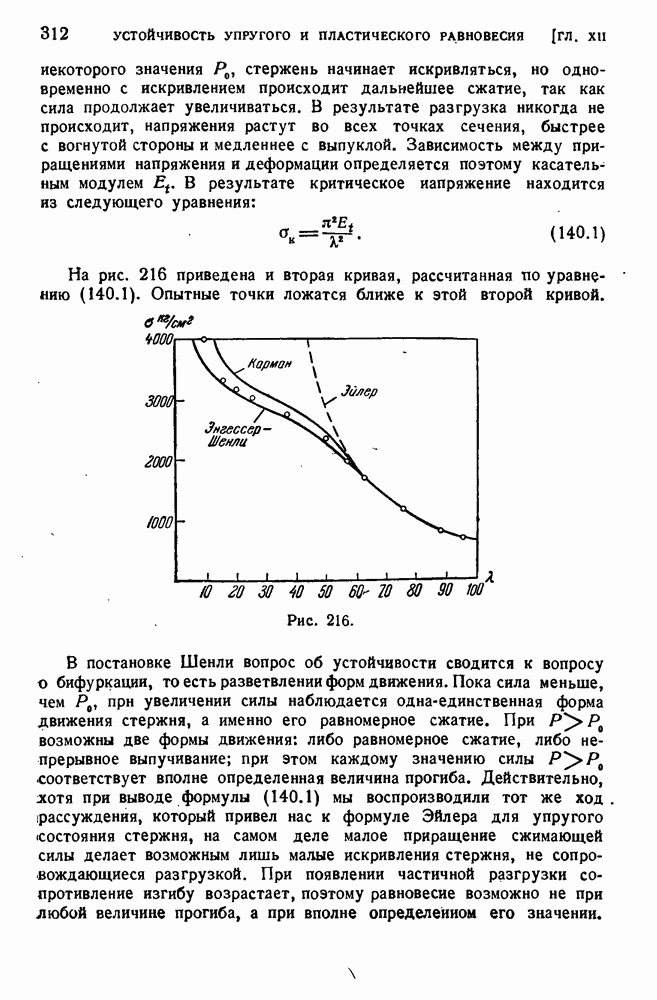
- § 139. Потеря устойчивости за пределом упругости.
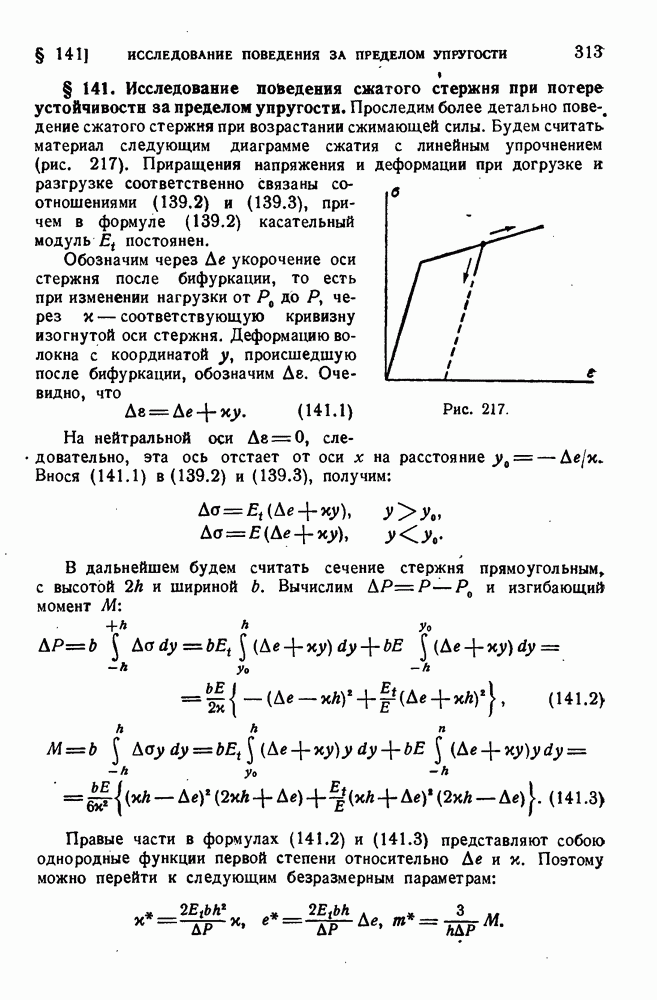
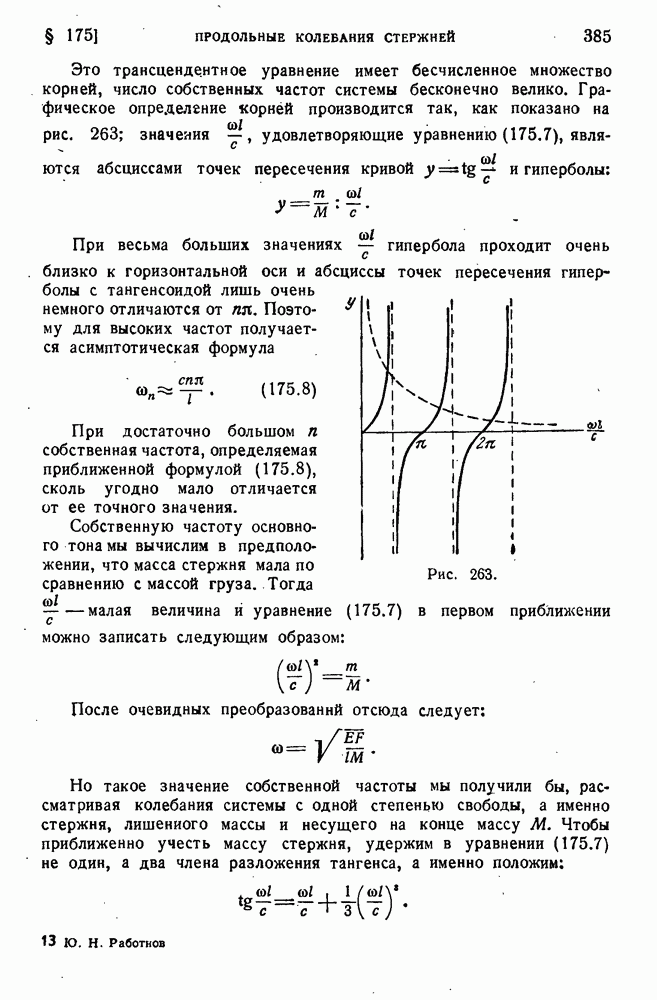
- § 140. Потеря устойчивости за пределом упругости (продолжение).
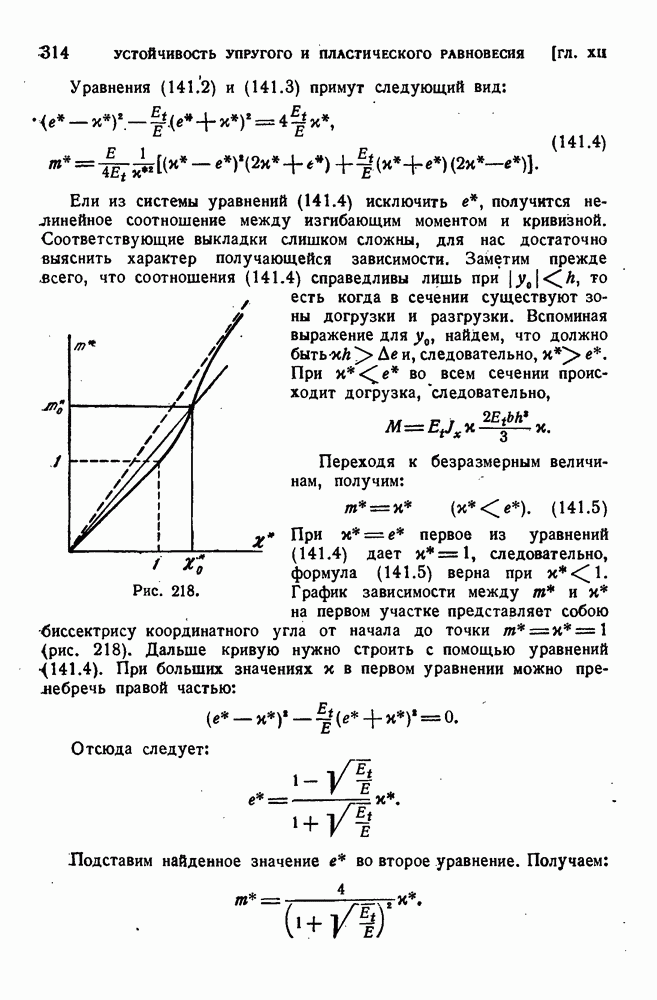
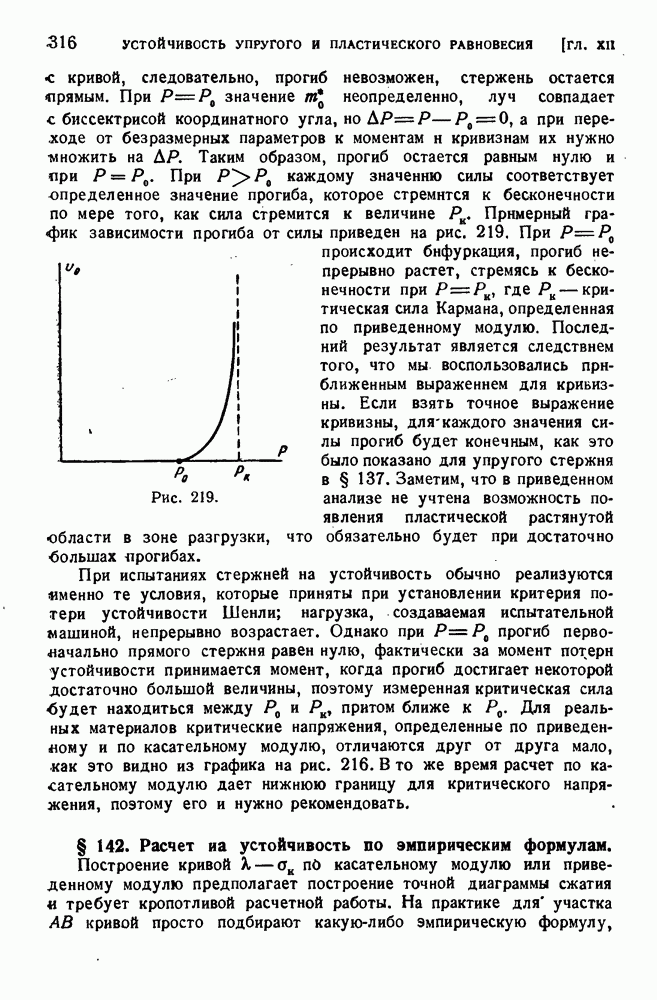
- § 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости.
- § 142. Расчет на устойчивость по эмпирическим формулам.
- ГЛАВА XIII. ТРУБЫ И ДИСКИ
- § 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности.
- § 144. Упругое состояние трубы. Формулы Ламе.
- § 145. Пластическое состояние трубы.
- § 146. Вращающиеся диски. Упругое состояние.
- § 147. Диск равного сопротивления.
- § 148. Предельное равновесие вращающегося диска.
- ГЛАВА XIV. ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 149. Обобщенные силы и обобщенные перемещения.
- § 150. Начало возможных перемещений для деформируемого тела.
- § 151. Теоремы Лагранжа и Кастильяно.
- § 152. Лииейиые упругие системы.
- § 153. Теорема о взаимности работ.
- § 154. Теорема Кастильяно для линейных упругих систем.
- § 155. Расчет винтовых пружин.
- § 156. Теорема о минимуме энергии.
- § 157. Интеграл перемещений.
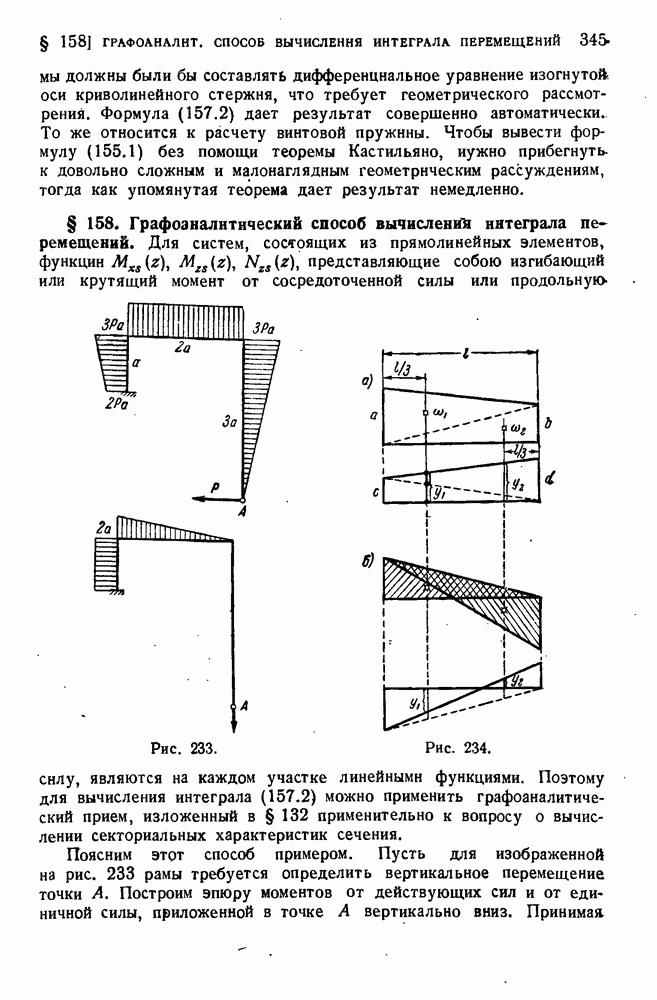
- § 158. Графоаналитический способ вычислений интеграла перемещений.
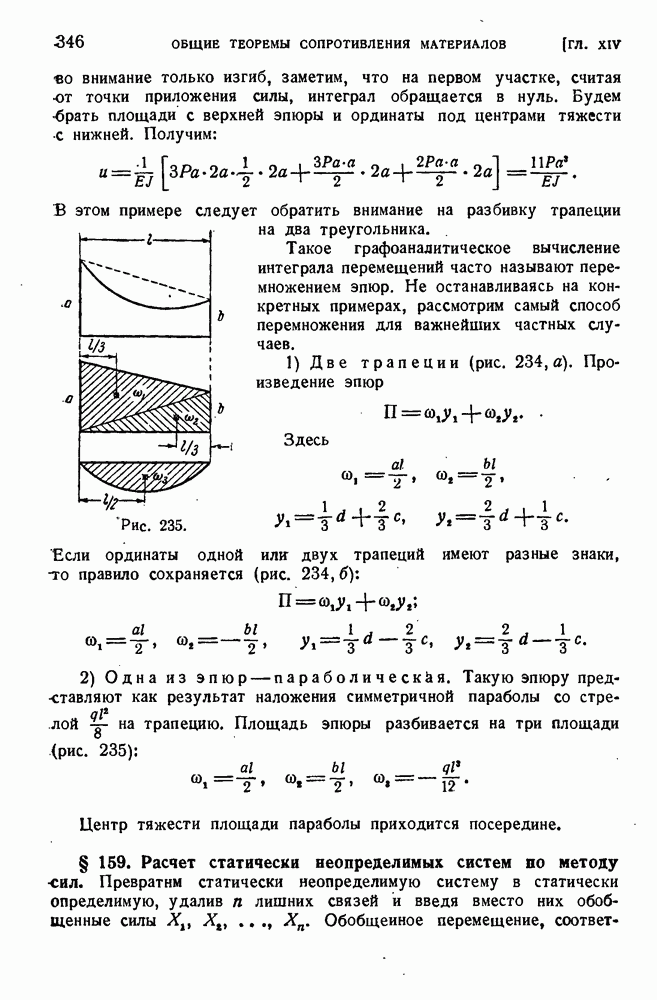
- § 159. Расчет статически неопределимых систем по методу сил.
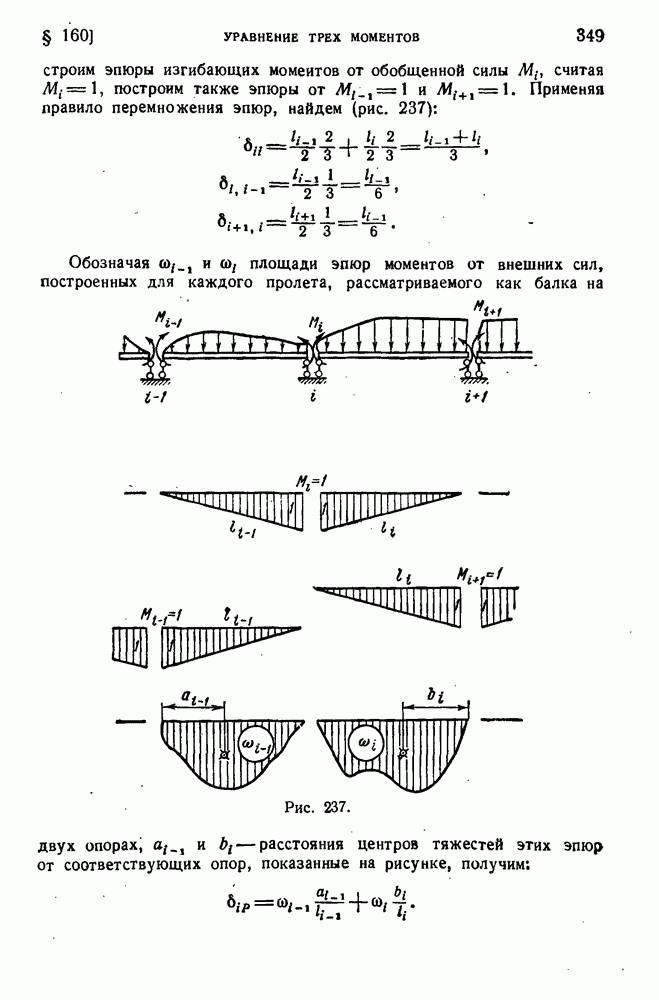
- § 160. Уравнение трех моментов.
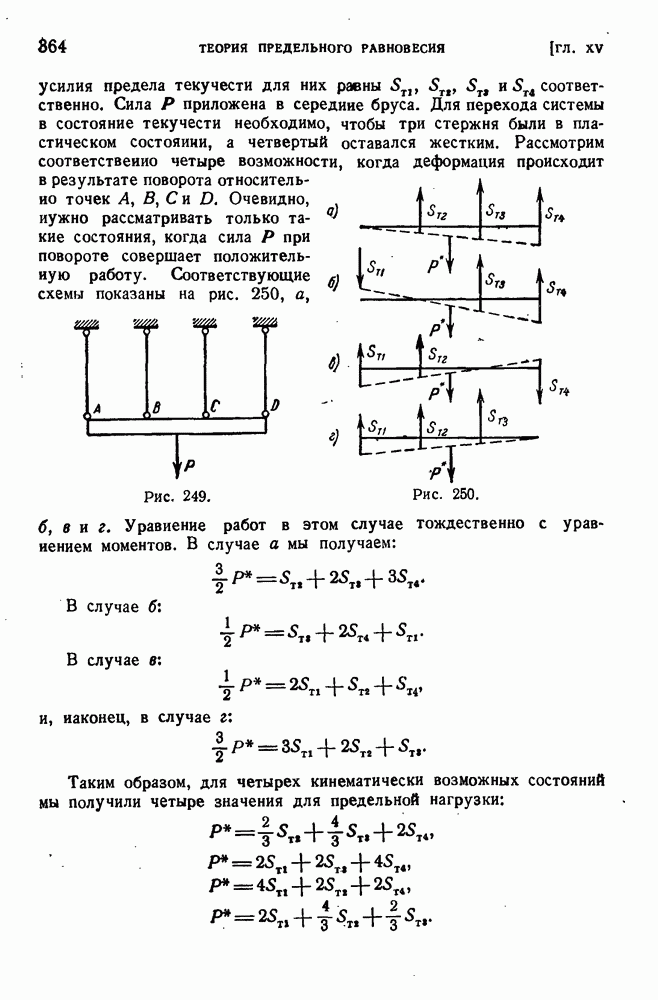
- ГЛАВА XV. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
- § 161. Жестко-пластическое тело.
- § 162. Поверхности нагружения.
- § 163. Истинное и допустимые состояния элемента.
- § 164. Статический метод определения предельной нагрузки.
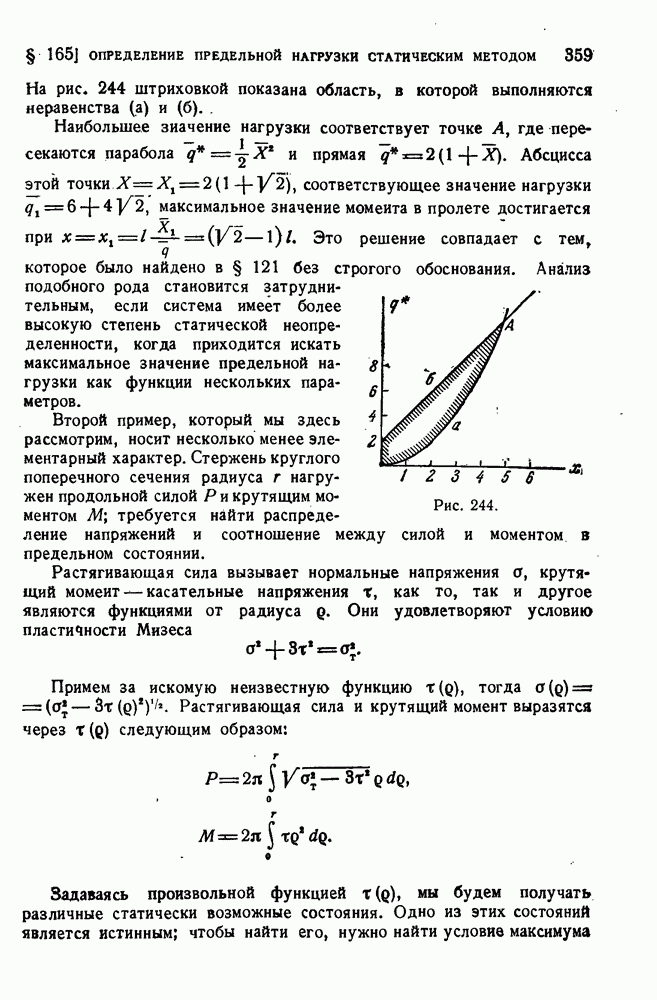
- § 165. Примеры определения предельной нагрузки статическим методом.
- § 166. Кинематически возможные состояния.
- § 167. Кинематический метод определения предельной нагрузки.
- § 168. Примеры определения предельной нагрузки кинематическим методом.
- § 169. Предельное равновесие пластинок.
- ГЛАВА XVI. ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 170. Колебания систем с конечным числом степеней свободы.
- § 171. Собственные частоты и главные формы колебаний.
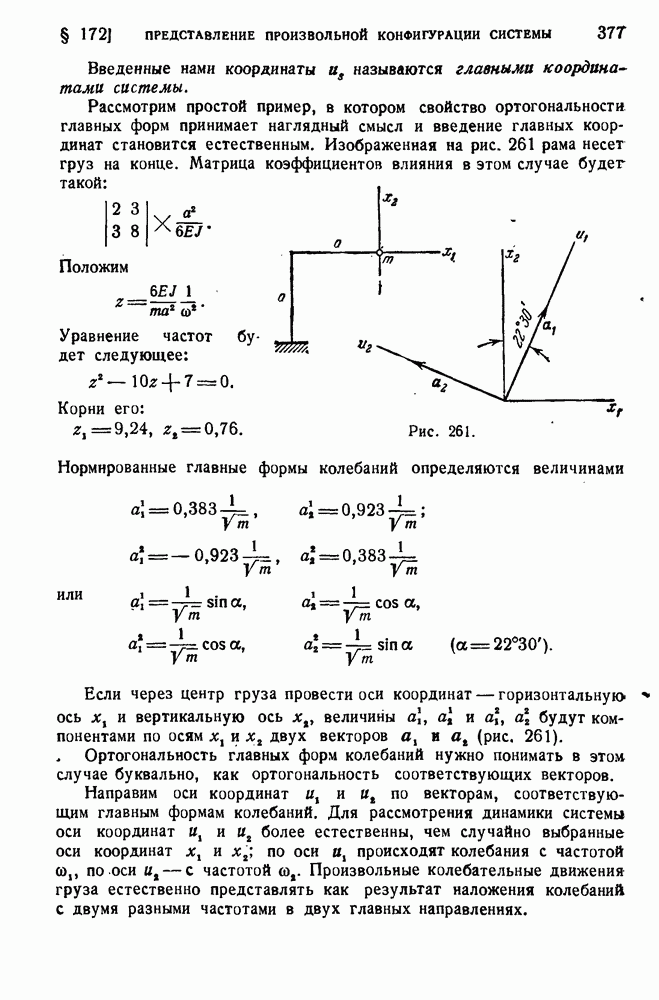
- § 172. Представление произвольной конфигурации системы через главные формы. Главные координаты.
- § 173. Формула и способ Релея.
- § 174. Нижние оценки для частоты основного тона.
- § 175. Продольные колебания стержней.
- § 176. Поперечные колебания стержней.
- § 177. Колебания балок постоянного сечения.
- § 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня.
- § 179. Действие ударных и импульсивных нагрузок на упругие системы.
- ГЛАВА XVII. ТЕОРИИ ПРОЧНОСТИ
- § 180. Постановка вопроса о прочности.
- § 181. Хрупкое и пластическое разрушение.
- § 182. Теория прочности Мора.
- § 183. Механизм хрупкого разрушения.
- § 184. Прочность при низких температурах.
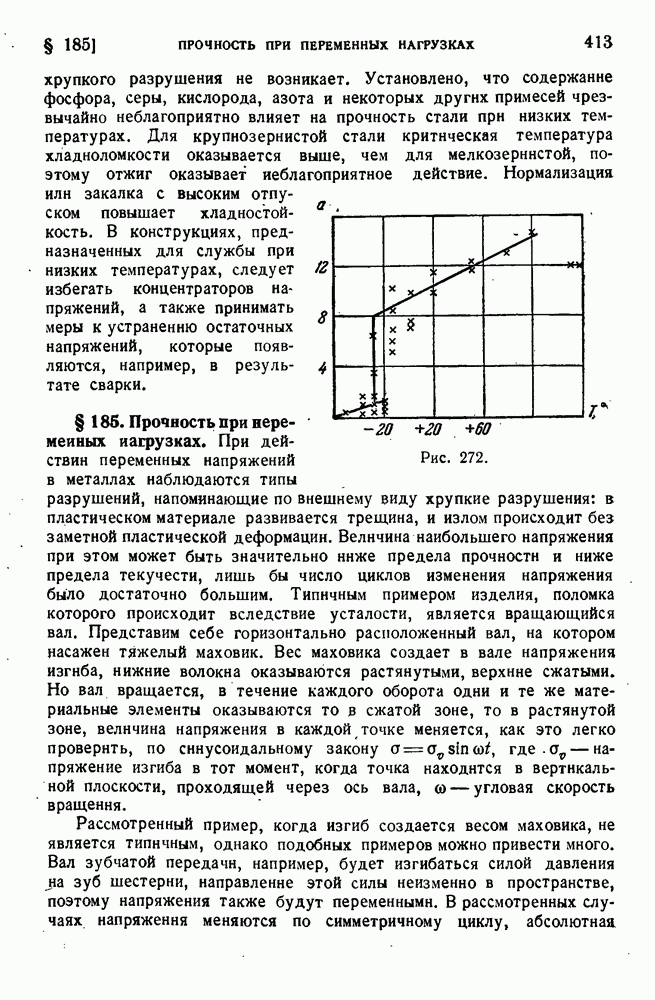
- § 185. Прочность при переменных нагрузках.
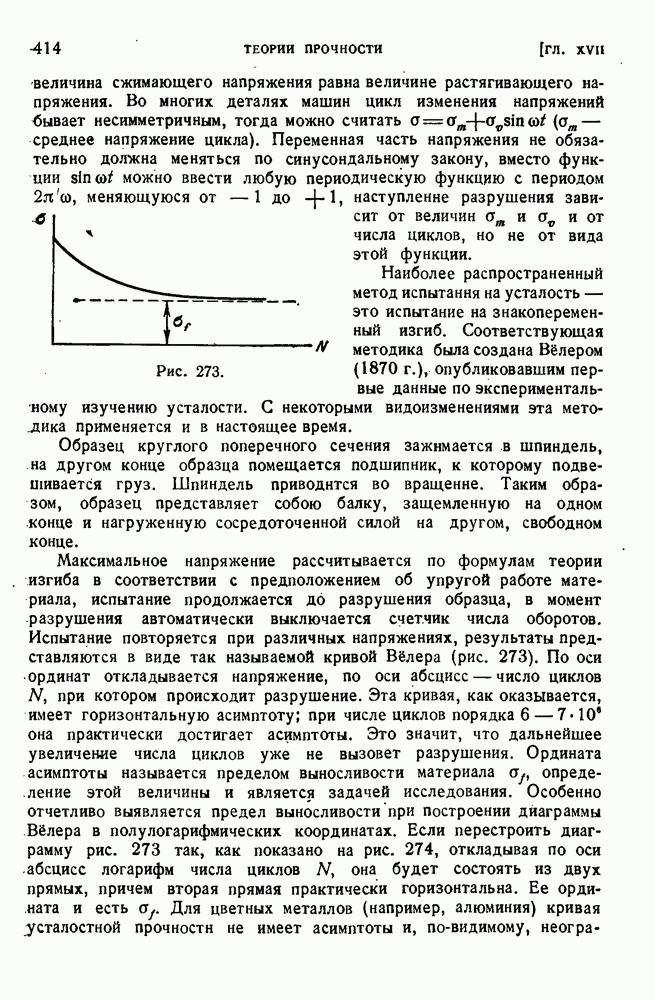
- § 186. Природа усталостного разрушения.
- § 187. Критерии прочности при переменных нагрузках.
- § 188. Влияние концентрации напряжений на усталостную прочность.
- § 189. Усталостная прочность при сложном напряженном состоянии.
- ГЛАВА XVIII. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
- § 190. Ползучесть металлов.
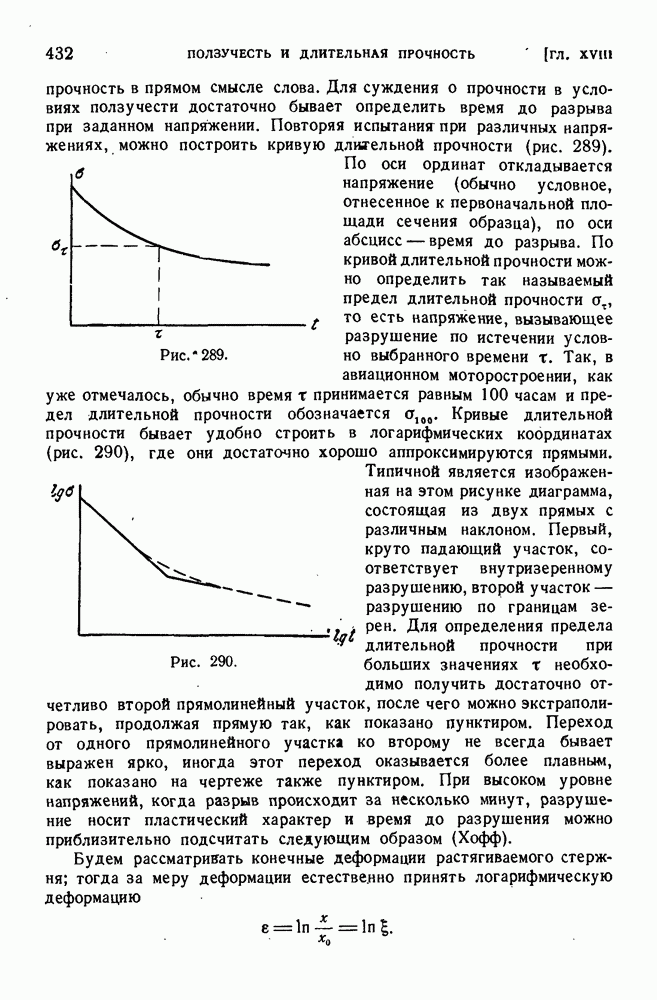
- § 191. Процесс ползучести.
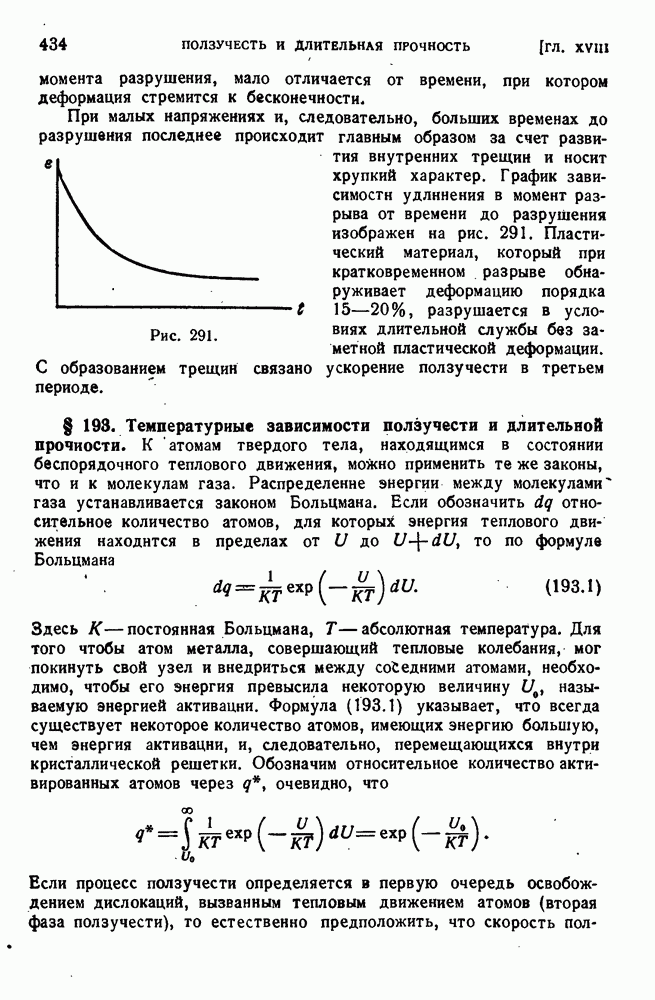
- § 192. Длительное разрушение.
- § 193. Температурные зависимости ползучести и длительной прочности.
- § 194. Феноменологические теории одномерной ползучести.
- § 195. Релаксация напряжений.
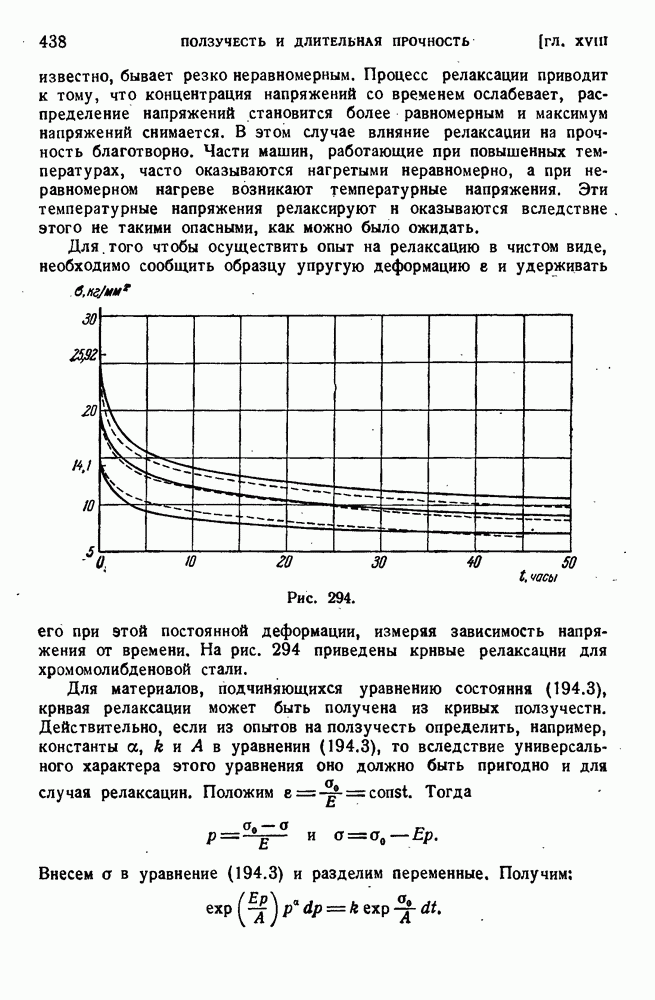
- § 196. Длительная прочность при переменных нагрузках.
- § 197. Ползучесть при изгибе.
- § 198. Критическое время сжатого стержня.
- § 199. Ползучесть и длительная прочность при сложном напряженном состоянии.
- § 200. Вращающиеся диски в условиях ползучести.
- § 201. Расчеты на ползучесть по теории старении.