| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
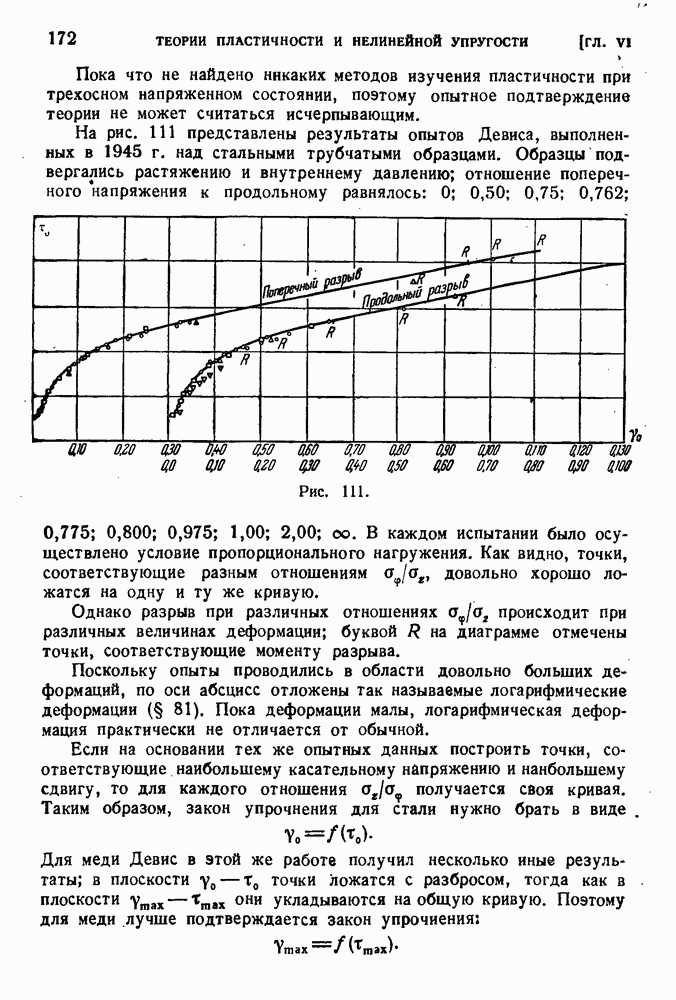
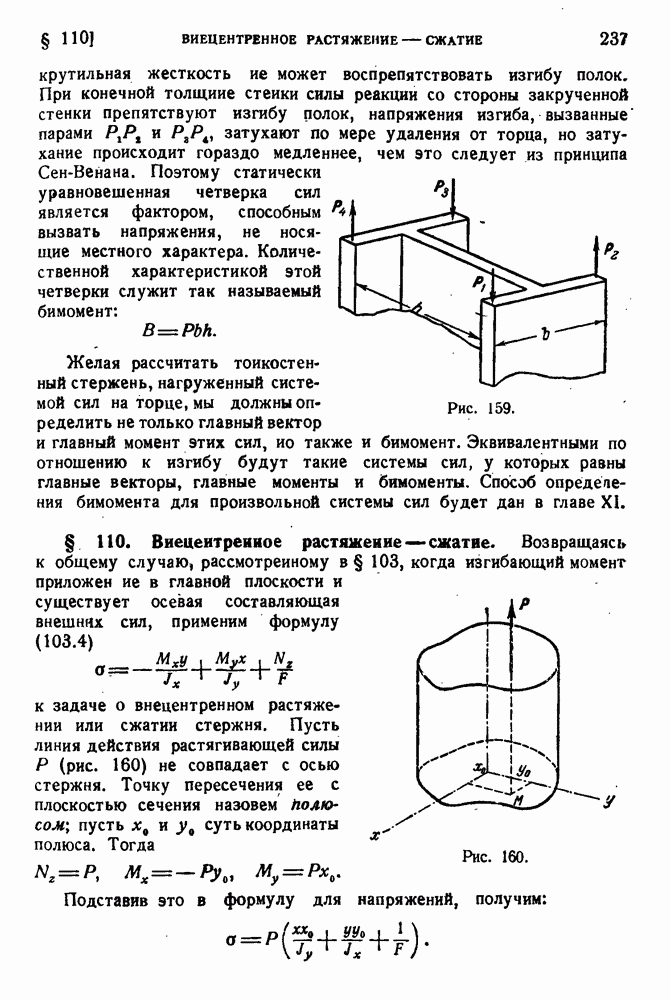
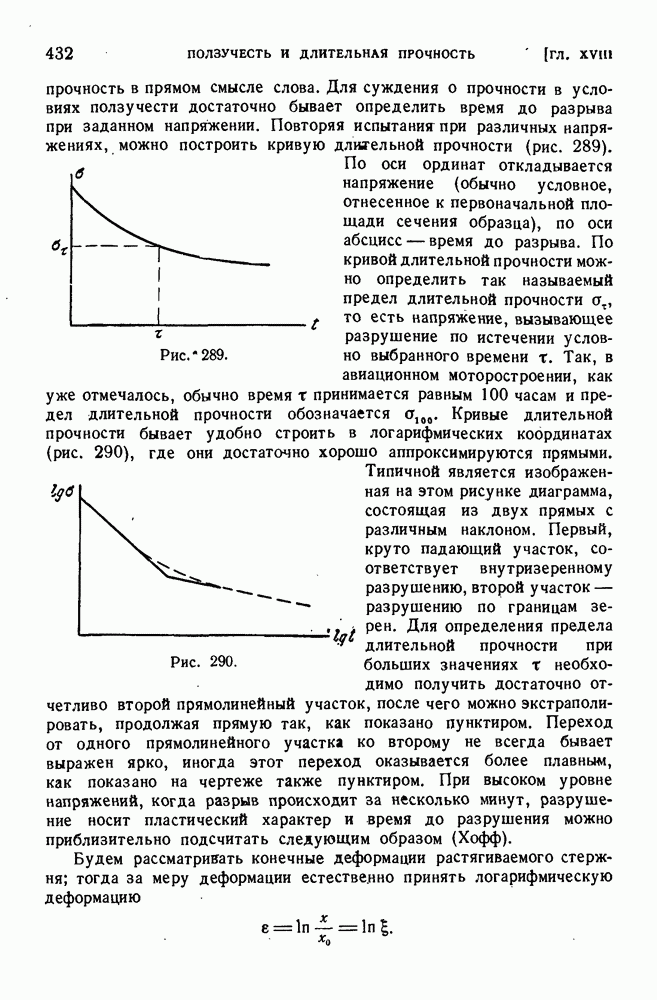
§ 6. Недопустимость замены системы сил статически эквивалентной.
Мы уже отметили, что статически эквивалентные системы сил производят на деформируемое тело различное действие. Поэтому в сопротивлении материалов не имеют места теоремы статики твердого тела, относящиеся к эквивалентности различных систем сил. Так, силу нельзя переносить вдоль линии ее действия и при задании силы необходимо учитывать точку ее приложения. Рассмотрим, например, три одинаковых стержня, нагруженных осевыми силами, как показано на рис. 3.

Рис. 3.
В первом случае сила приложена на конце и растягивает весь стержень. Во втором — сила приложена посередине и растягивает только верхнюю, заштрихованную часть стержня. В третьем случае сила действует непосредственно на заделку и совершенно не растягивает стержня.
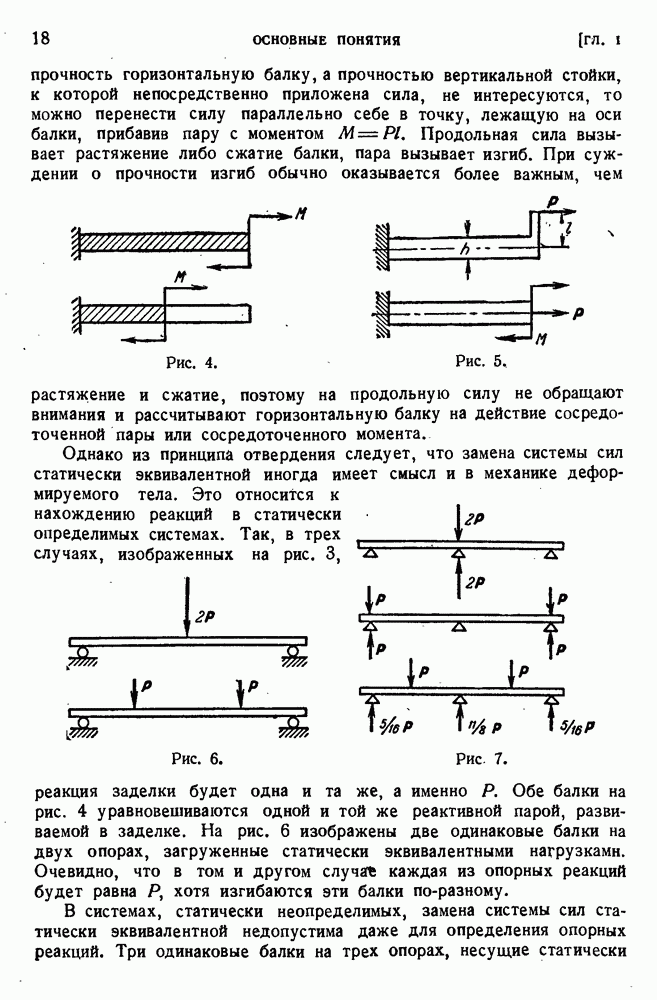
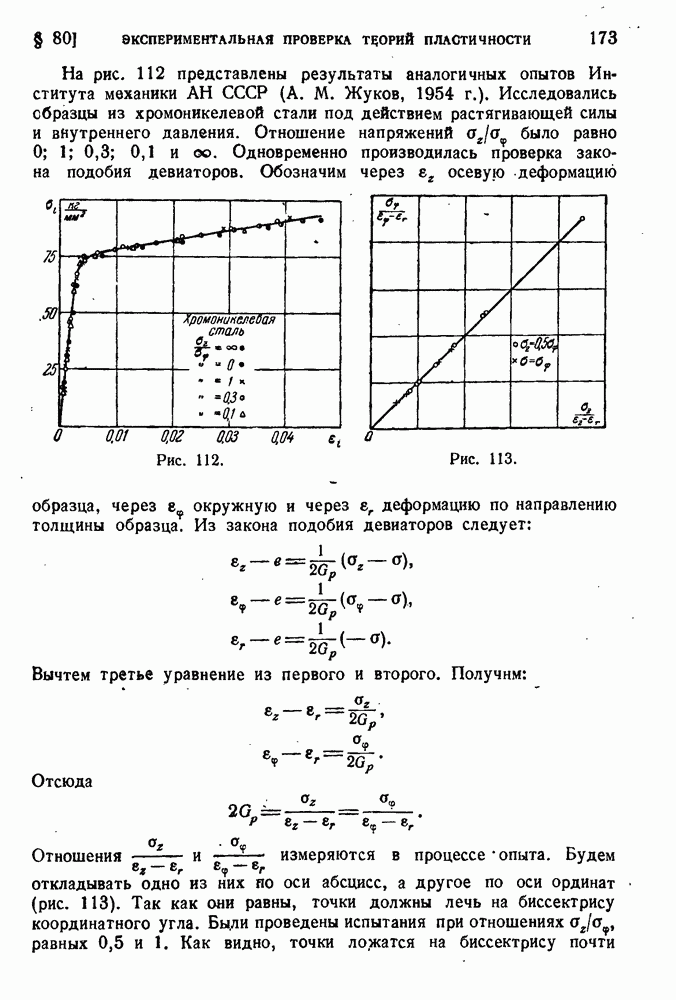
В сопротивлении материалов пару сил нельзя переносить в ее плоскости, и мы говорим о точке приложения пары, о сосредоточенной паре или сосредоточенном моменте. Это ясно из рис. 4, на котором изображены две балки, защемленные на одном конце (замурованные в стену) и нагруженные парами сил. В первом, случае изгибается вся балка, во втором — только заштрихованная половина.
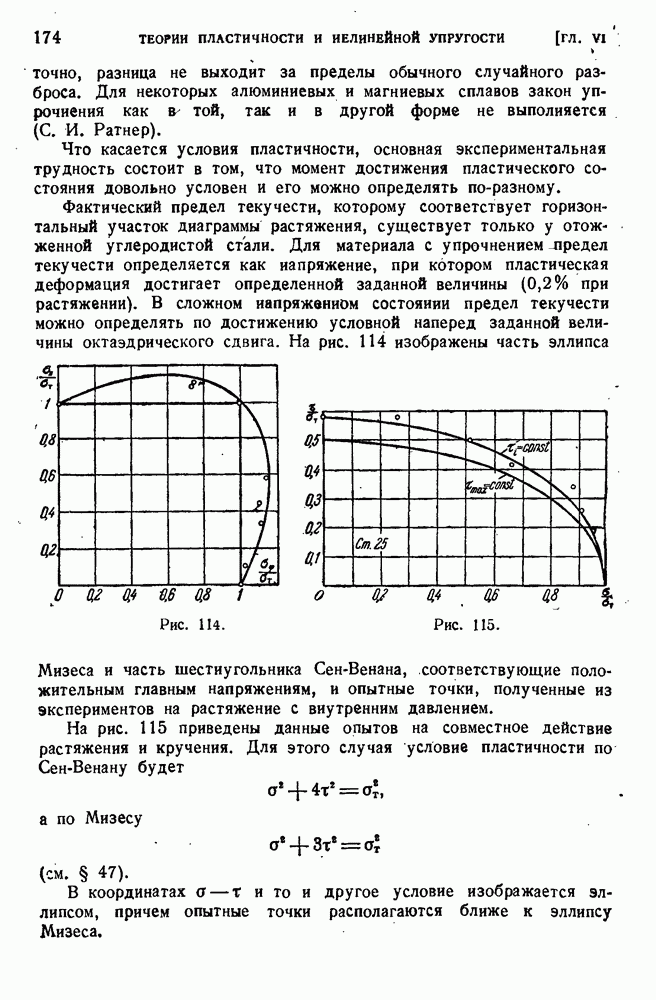
Понятие сосредоточенного момента, или сосредоточенной пары, нуждается в пояснении. Реальная задача обычно соответствует схеме, изображенной на рис. 5.
Ясно, что если требуется рассчитать на прочность горизонтальную балку, а прочностью вертикальной стойки, к которой непосредственно приложена сила, не интересуются, то можно перенести силу параллельно себе в точку, лежащую на оси балки, прибавив пару с моментом  Продольная сила вызывает растяжение либо сжатие балки, пара вызывает изгиб.
Продольная сила вызывает растяжение либо сжатие балки, пара вызывает изгиб.

Рис. 4.

Рис. 5.
При суждении о прочности изгиб обычно оказывается более важным, чем растяжение и сжатие, поэтому на продольную силу не обращают внимания и рассчитывают горизонтальную балку на действие сосредоточенной пары или сосредоточенного момента.
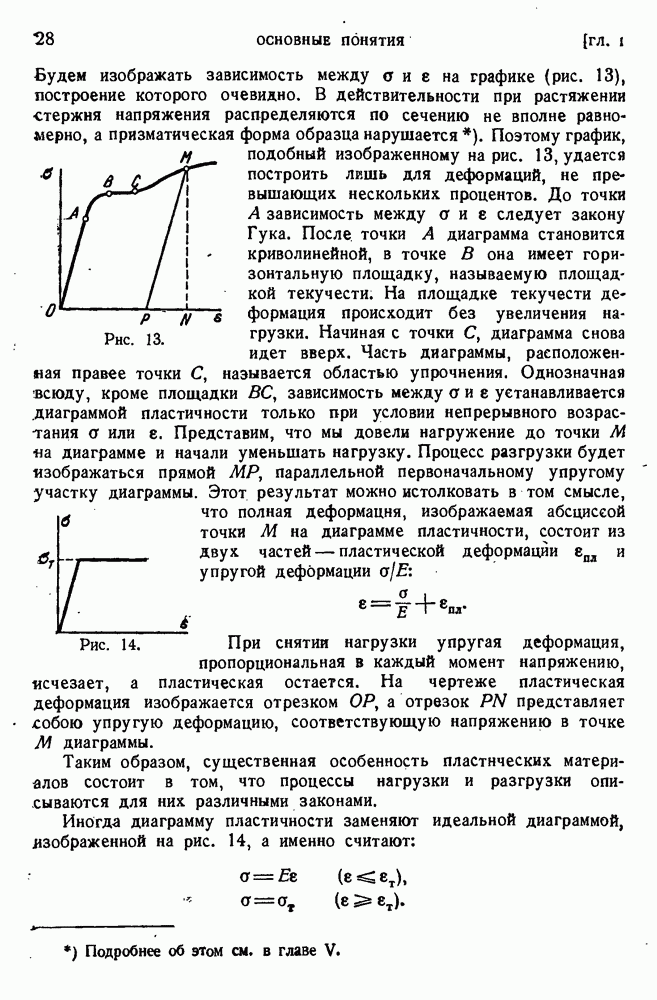
Однако из принципа отвердения следует, что замена системы сил статически эквивалентной иногда имеет смысл и в механике деформируемого тела. Это относится к нахождению реакций в статически определимых системах. Так, в трех случаях, изображенных на рис. 3, реакция заделки будет одна и та же, а именно Р.

Рис. 6.

Рис. 7.
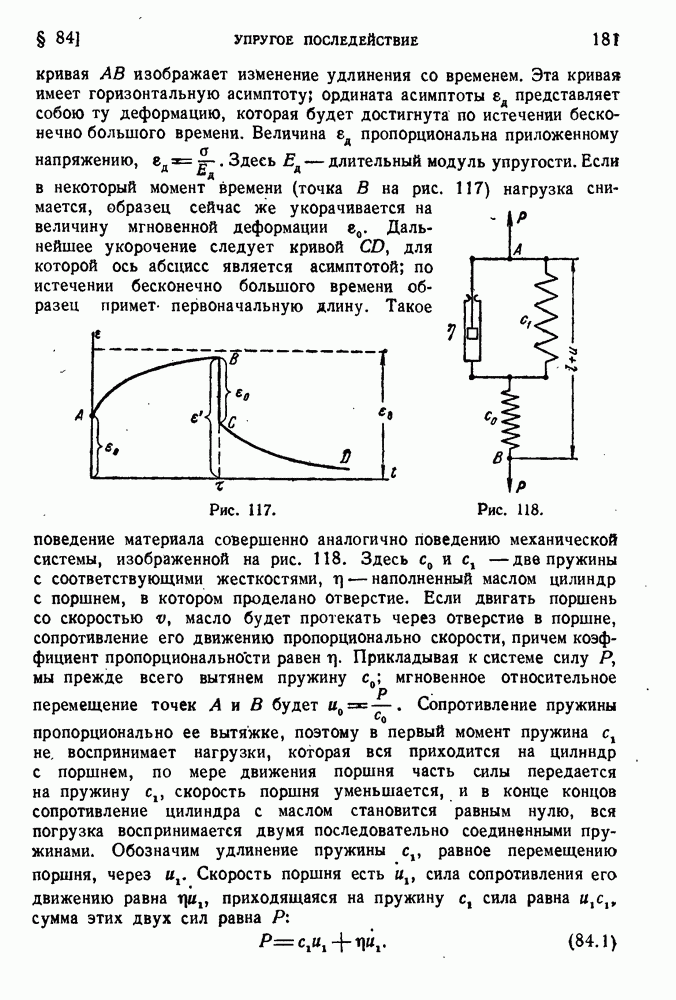
Обе балки на рис. 4 уравновешиваются одной и той же реактивной парой, развиваемой в заделке. На рис. 6 изображены две одинаковые балки на двух опорах, загруженные статически эквивалентными нагрузками. Очевидно, что в том и другом случай каждая из опорных реакций будет равна Р, хотя изгибаются эти балки по-разному.
В системах, статически неопределимых, замена системы сил статически эквивалентной недопустима даже для определения опорных реакций. Три одинаковые балки на трех опорах, несущие статически эквивалентные нагрузки, будут испытывать со стороны опор разные реакции.
Пример этого приведен на рис. 7. В первом случае вся сила воспринимается средней опорой и реакции крайних опор равны нулю; во втором — на средней опоре не возникает реакции, реакция каждой из крайних опор есть Р. Для рассмотрения третьего случая нужно воспользоваться теорией изгиба. Метод решения такого рода задач будет изложен в дальнейшем; на чертеже приведены найденные в результате решения величины этих реакций, по  на крайних опорах и
на крайних опорах и  на средней опоре.
на средней опоре.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Задачи и содержание сопротивления материалов.
- § 2. Сопротивление материалов и теоретическая механика.
- § 3. Статически неопределенные задачи.
- § 4. Внешние силы.
- § 5. Принцип отвердения.
- § 6. Недопустимость замены системы сил статически эквивалентной.
- § 7. Однородное тело.
- § 8. Внутренние силы.
- § 9. Напряжение.
- § 10. Простейшие типы напряженного состояния.
- § 11. Простейшие виды деформации.
- § 12. Упругость и пластичность.
- § 13. Закон Гука.
- § 14. Диаграмма пластичности.
- § 15. Тела изотропные и анизотропные.
- ГЛАВА II. РАСТЯЖЕНИЕ СЖАТИЕ
- § 16. Стержни и стержневые системы.
- § 17. Принцип Сен-Венана и гипотеза плоских сечений.
- § 18. Напряжения и деформации при растяжении.
- § 19. Расчеты на прочность при растижении и сжатии.
- § 20. Собственный вес и силы инерции.
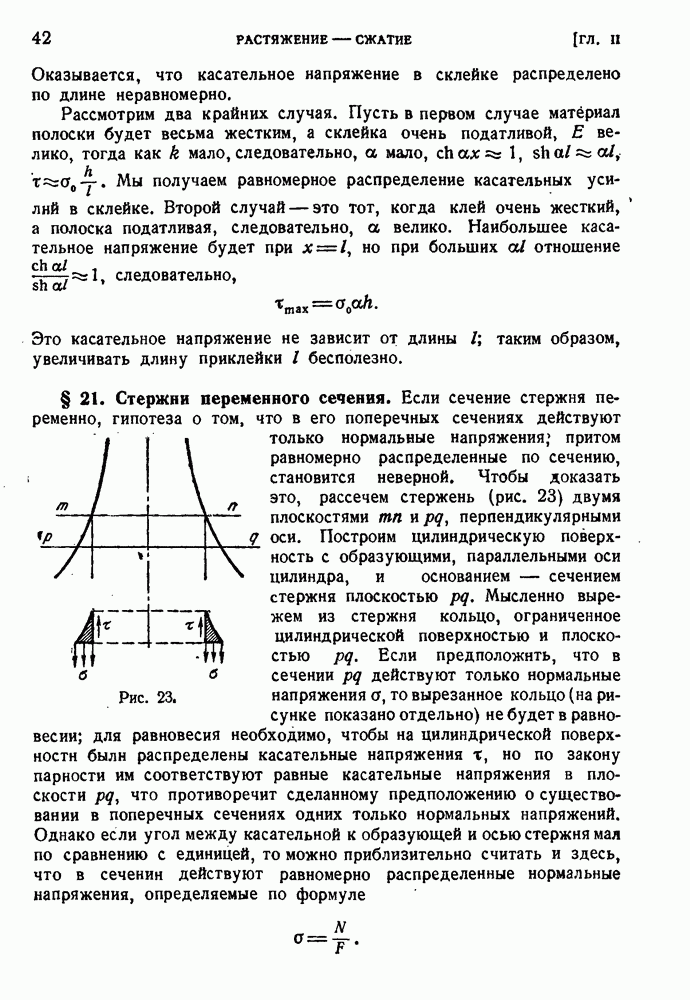
- § 21. Стержни переменного сечения.
- § 22. Перемещения узлов стержневых систем.
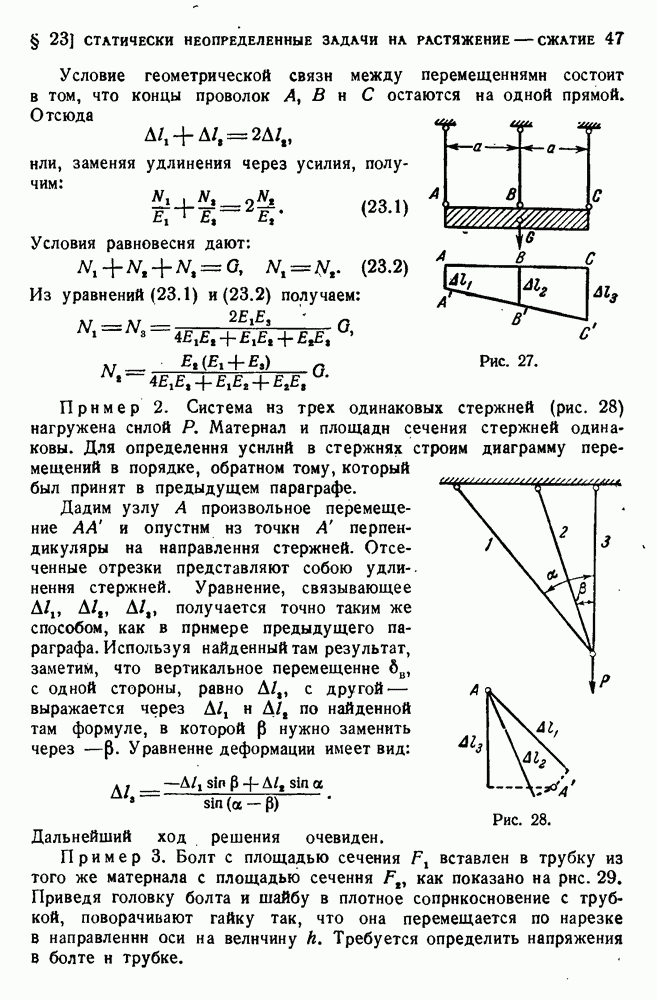
- § 23. Статически неопределенные задачи на растяжение — сжатие.
- § 24. Температурные и монтажные напряжения.
- § 25. Общие соображения о расчете стержневых систем.
- § 26. Расчет статически неопределимых систем по допускаемым нагрузкам.
- § 27. Остаточные напряжения после пластической деформации.
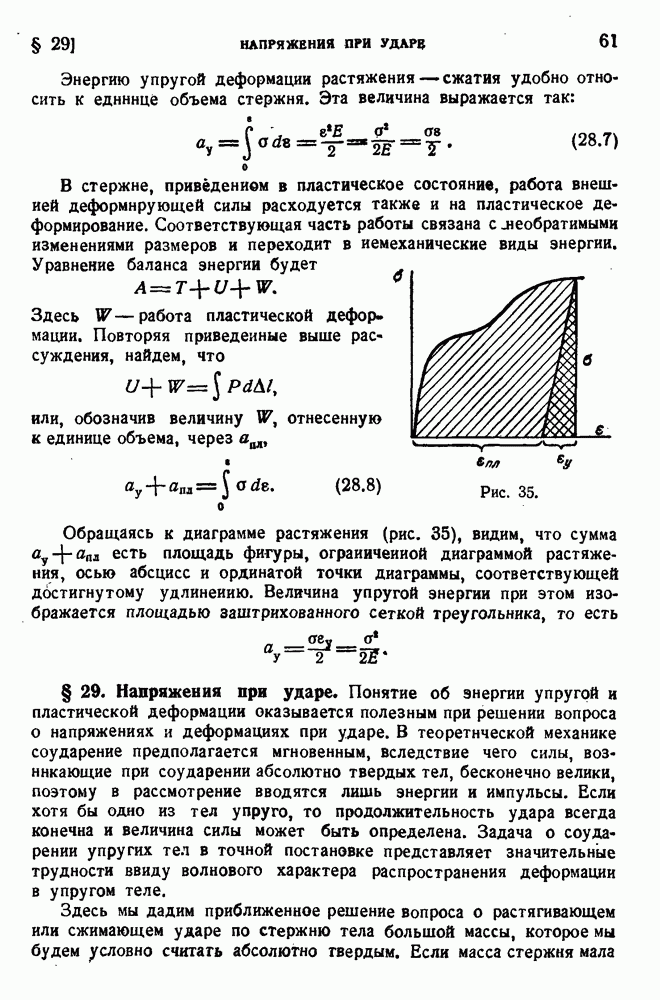
- § 28. Потенциальная энергия растяжении.
- § 29. Напряжения при ударе.
- § 30. Распространение упругих волн в стержнях.
- § 31. Концентрации напряжений.
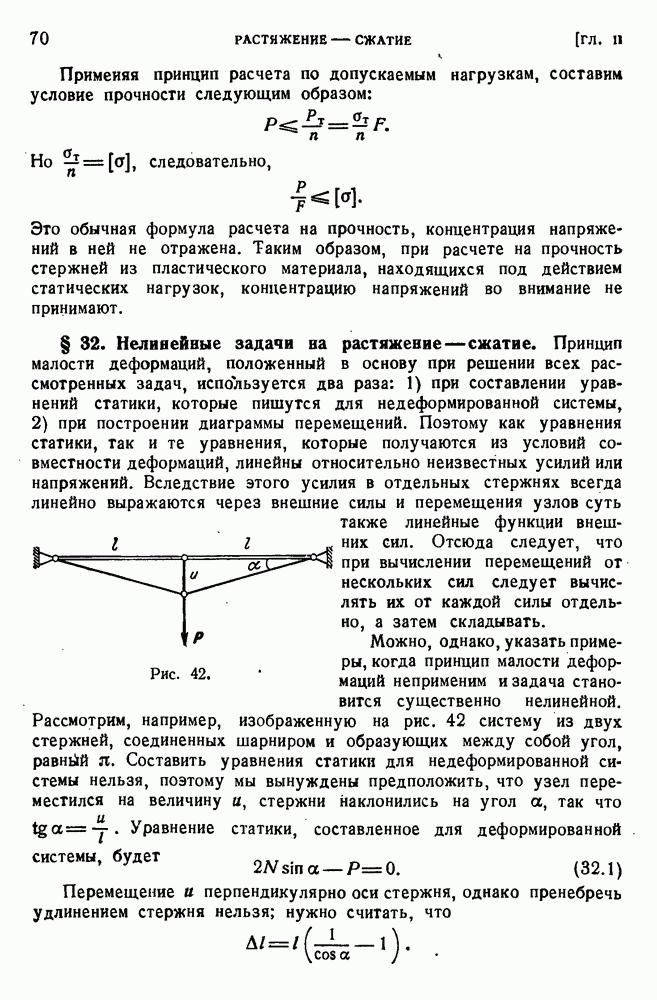
- § 32. Нелинейные задачи на растяжение — сжатие.
- ГЛАВА III. СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
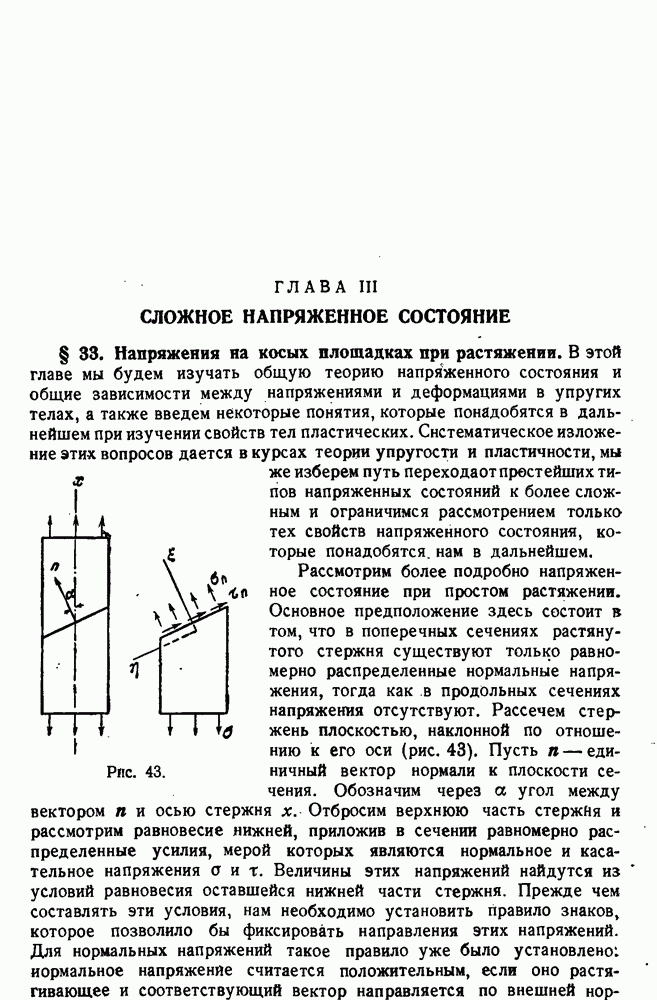
- § 33. Напряжения на косых площадках при растяжении.
- § 34. Напряжения при двухосном растяжении.
- § 35. Круговая диаграмма Мора.
- § 36. Общий случай плоского напряженного состояния.
- § 37. Определение напряжений на произвольной площадке.
- § 38. Пространственное напряженное состояние.
- § 39. Главные напряжения.
- § 40. Главные касательные напряжения.
- § 41. Октаэдрическое напряжение.
- § 42. Закон Гука для главных осей.
- § 43. Изменение объема при упругой деформации.
- § 44. Чистый сдвиг.
- § 45. Деформация элемента объема в общем случае.
- § 46. Условие пластичности Треска — Сен-Венана.
- § 47. Условие пластичности Мизеса.
- § 48. Условия пластичности для плоского напряженного состояния.
- § 49. Потенциальная энергия упругой деформации.
- § 50. Энергия изменения формы.
- ГЛАВА IV. НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
- § 51. Расчеты на прочность изделий сложной формы.
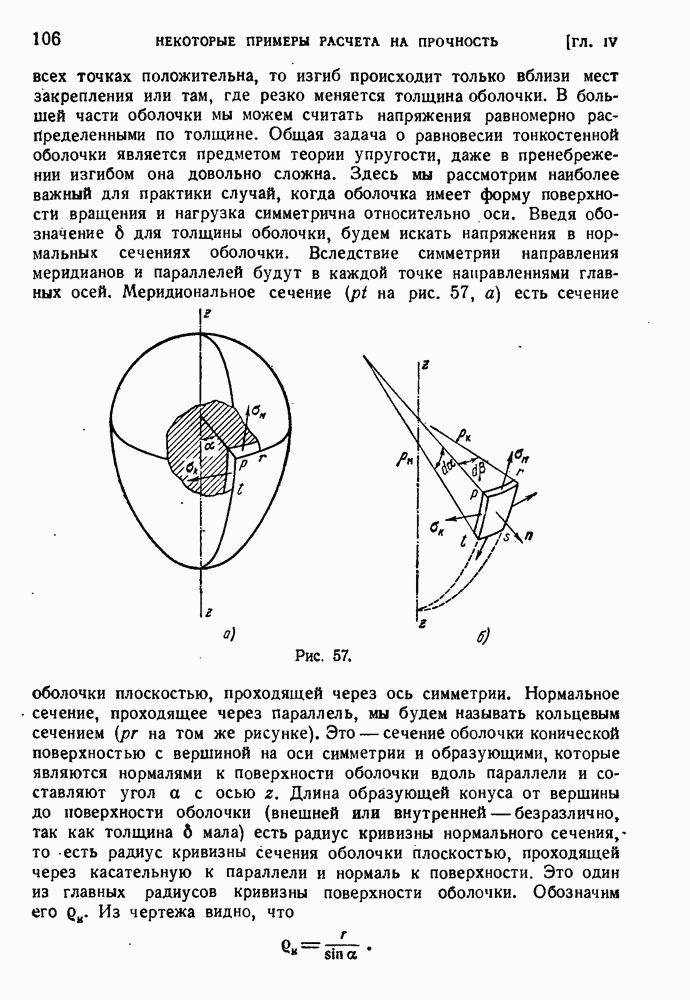
- § 52. Безмоментные оболочки вращении.
- § 53. Местные напряжения в безмоментных оболочках.
- § 54. Большие прогибы мембраны.
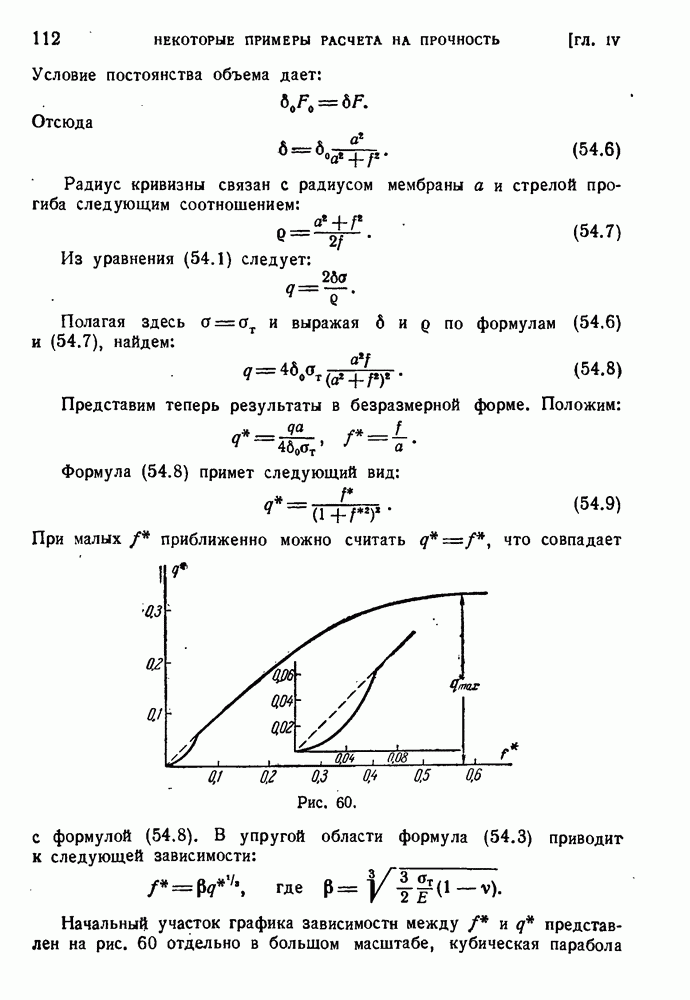
- § 55. Условные расчеты.
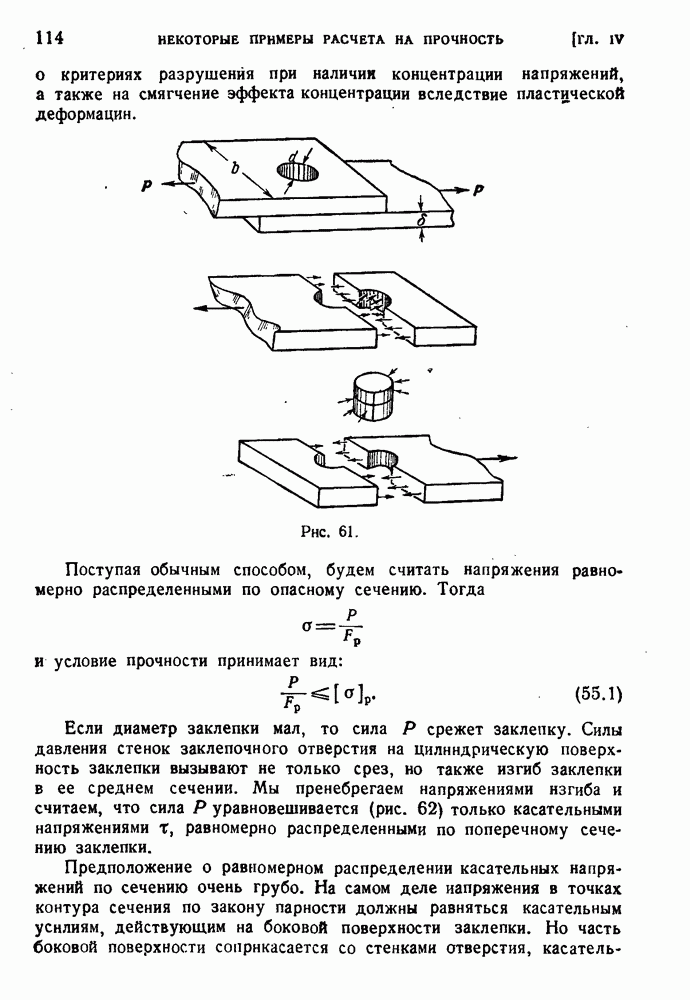
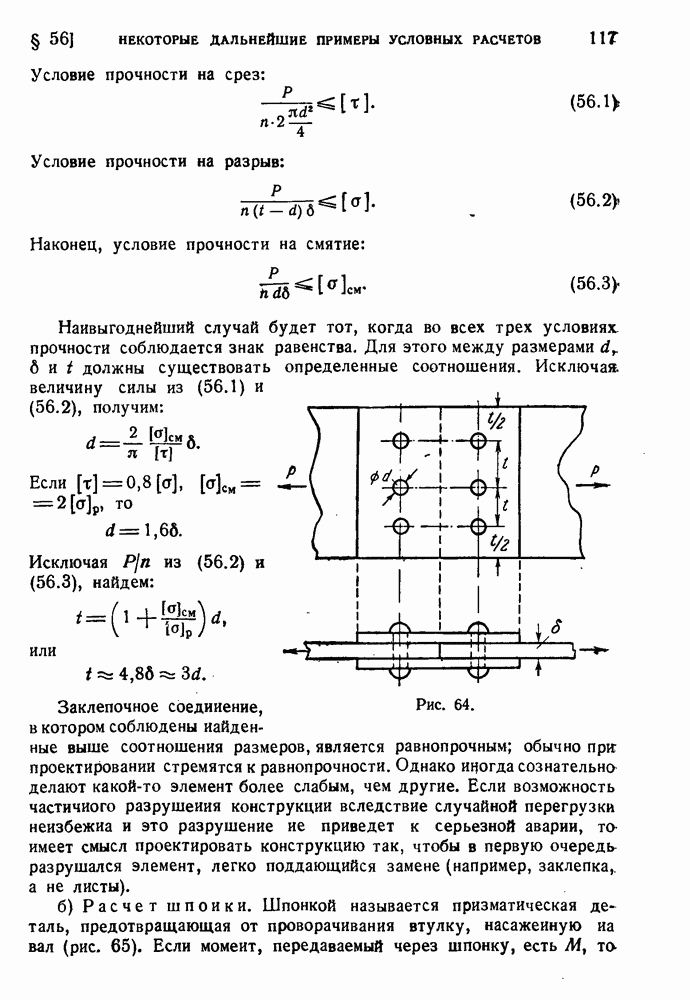
- § 56. Некоторые дальнейшие примеры условных расчетов.
- § 57. Расчет сварных соединений.
- ГЛАВА V. ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
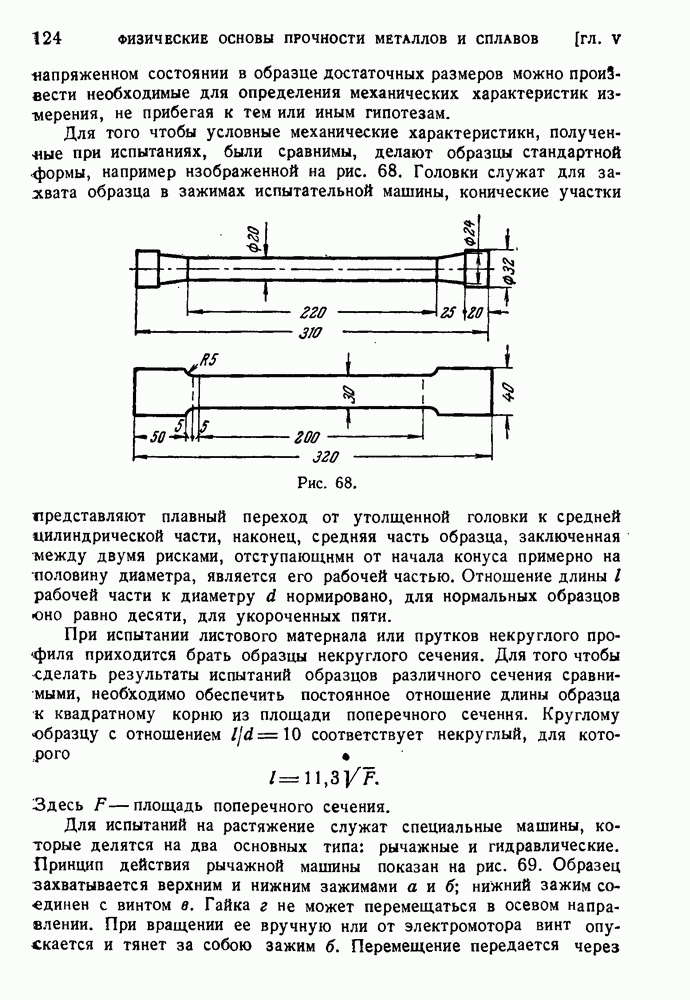
- § 58. Задачи испытания материалов.
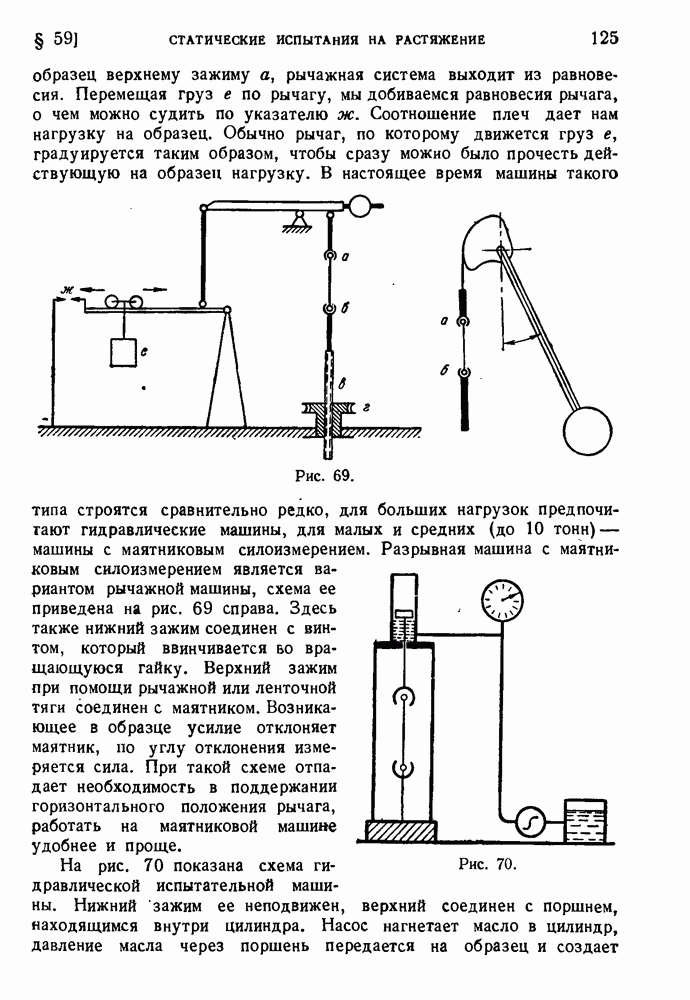
- § 59. Статические испытания на растяжение.
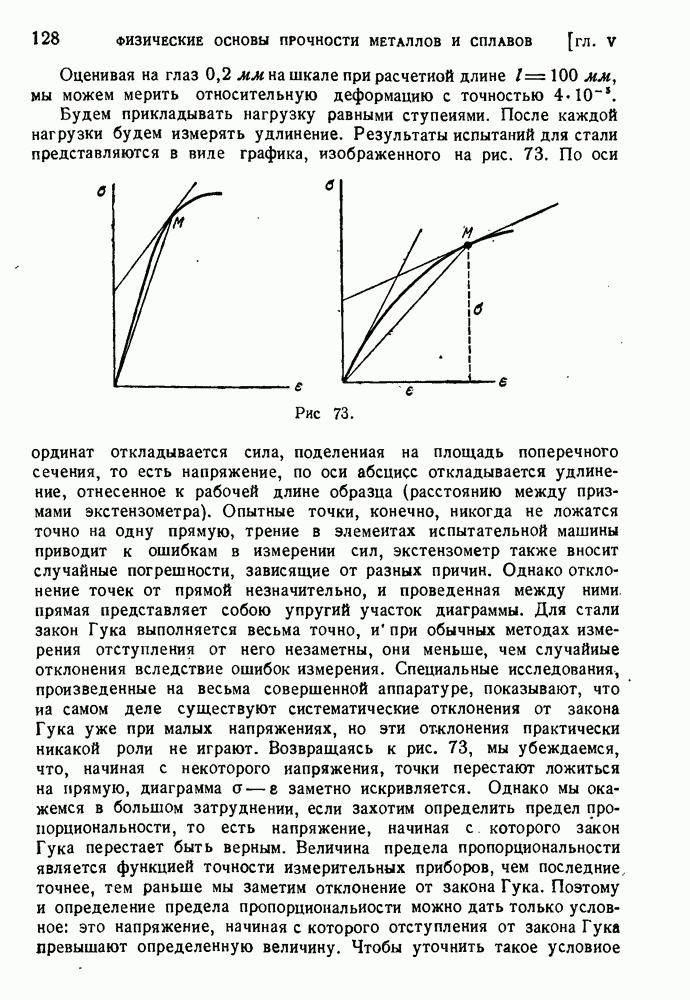
- § 60. Исследование металлов в области малых деформаций.
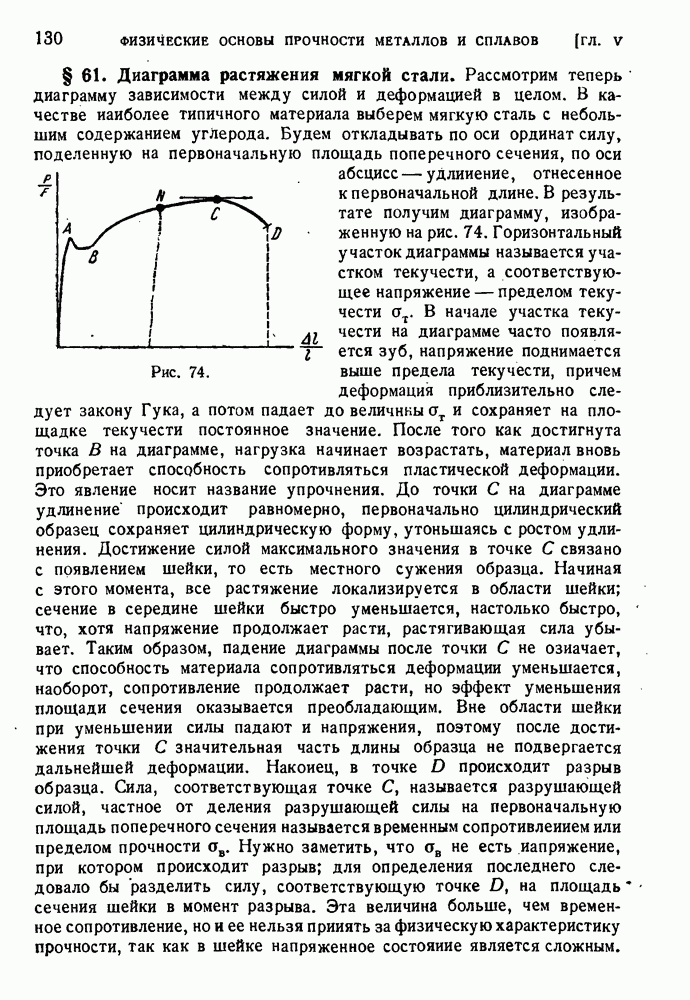
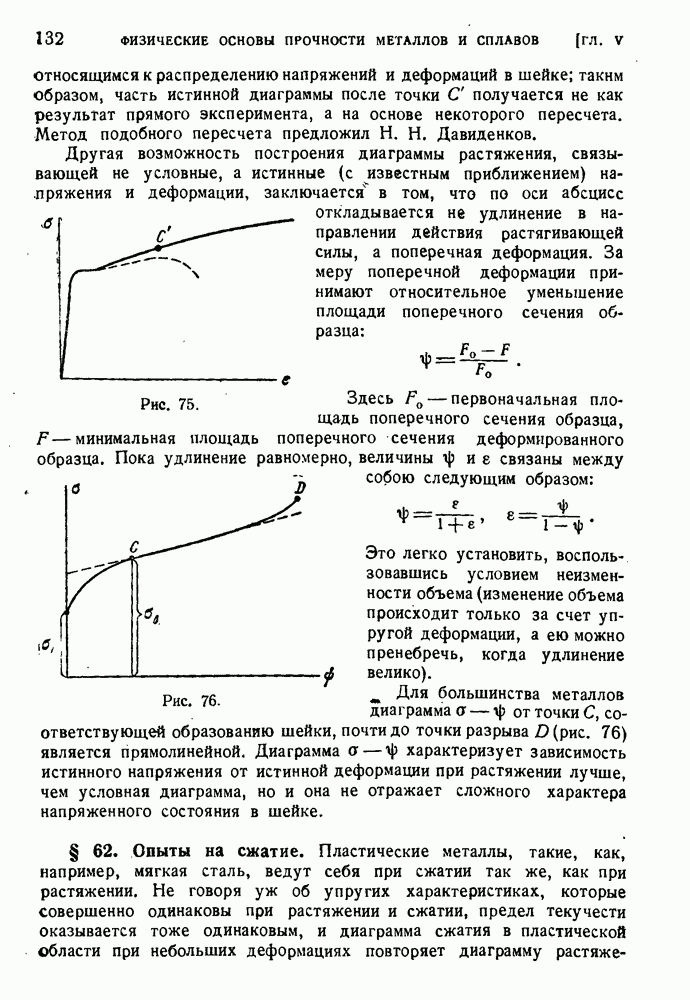
- § 61. Диаграмма растяжения мягкой стали.
- § 62. Опыты на сжатие.
- § 63. Строение и упругая деформация металлических кристаллов.
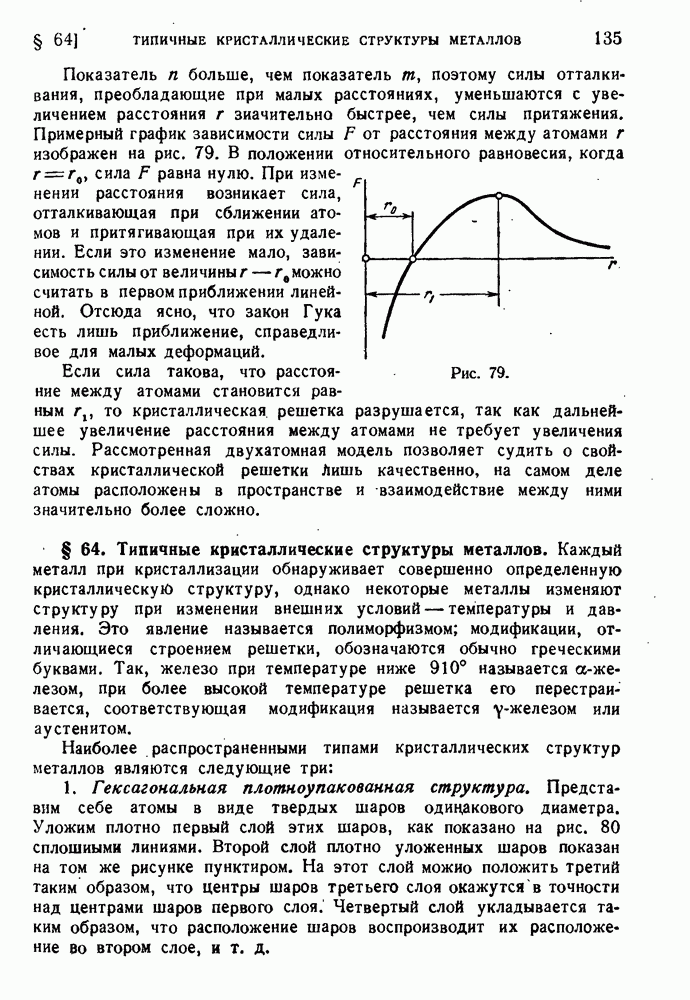
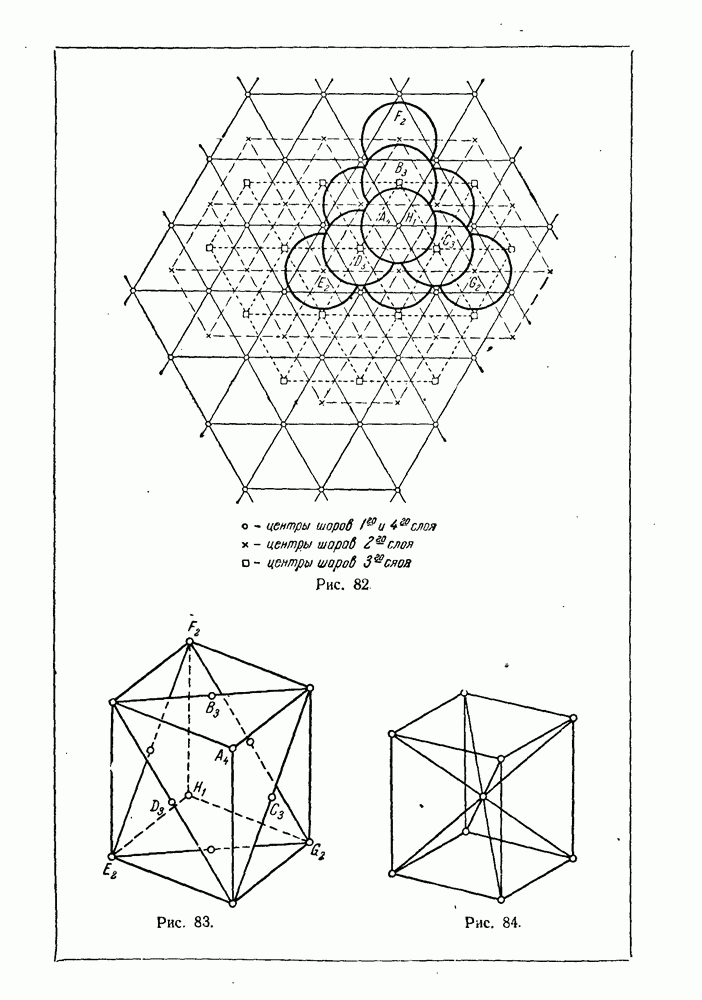
- § 64. Типичные кристаллические структуры металлов.
- § 65. Пластическая деформация монокристаллов.
- § 66. Прочность кристаллов и сопротивление пластическому деформированию.
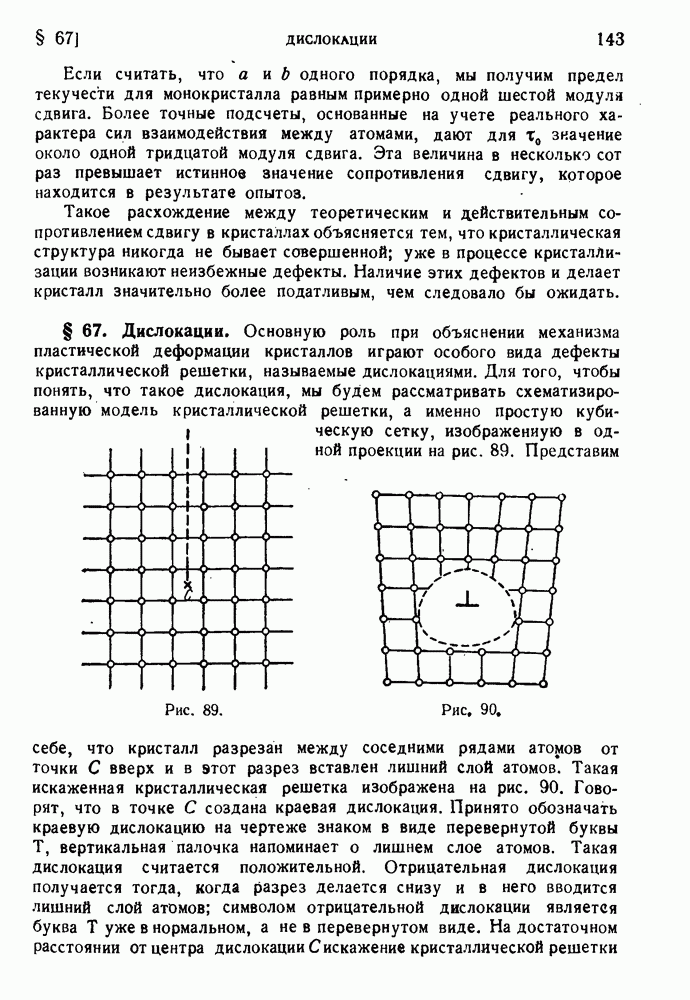
- § 67. Дислокации.
- § 68. Движение и равновесие дислокаций.
- § 69. Источники дислокаций.
- § 70. Границы блоков.
- § 71. Деформация поликристаллических металлов и сплавов.
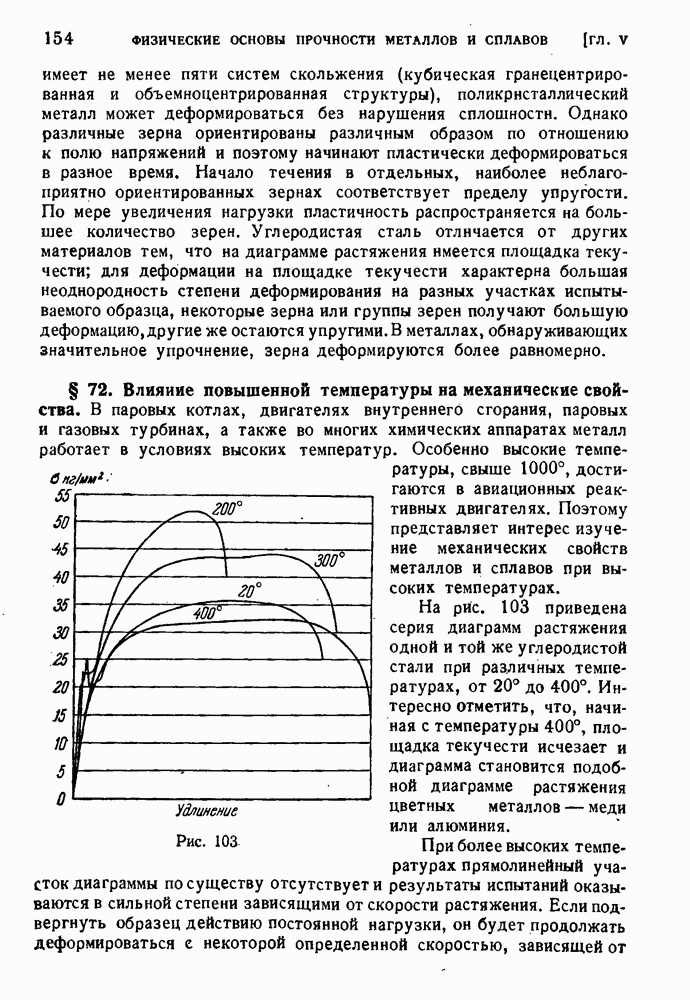
- § 72. Влияние повышенной температуры на механические свойства.
- § 73. Влияние скорости испытания.
- § 74. Испытании на твердость.
- ГЛАВА VI. ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ
- § 75. Основные принципы построения теории пластичности.
- § 76. Ассоциированный закон течения.
- § 77. Течение при условии пластичности Сен-Венана и Мизеса.
- § 78. Закон упрочнения.
- § 79. Деформационная теория пластичности.
- § 80. Экспериментальная проверка теорий пластичности.
- § 81. Конечная деформация.
- § 82. Нелинейно упругое тело.
- § 83. Высокоэластические деформации.
- § 84. Упругое последействие.
- § 85. Некоторые свойства вязко-упругого тела.
- § 86. Принцип суммирования Больцмана—Вольтерра.
- ГЛАВА VII. КРУЧЕНИЕ
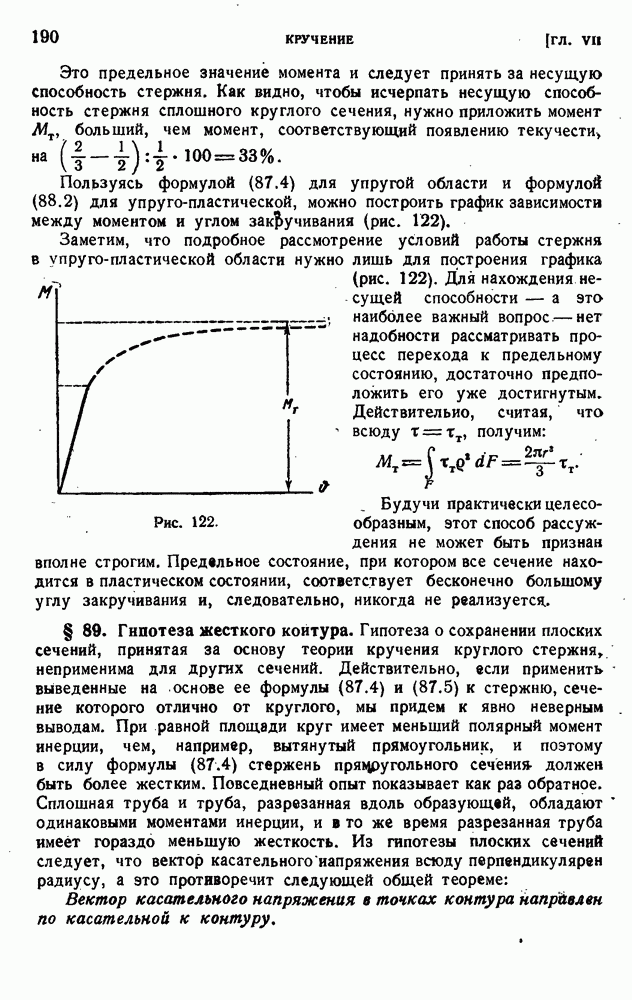
- § 87. Кручение стержней круглого сечеиия.
- § 88. Упруго-пластическое кручение стержня круглого сечения.
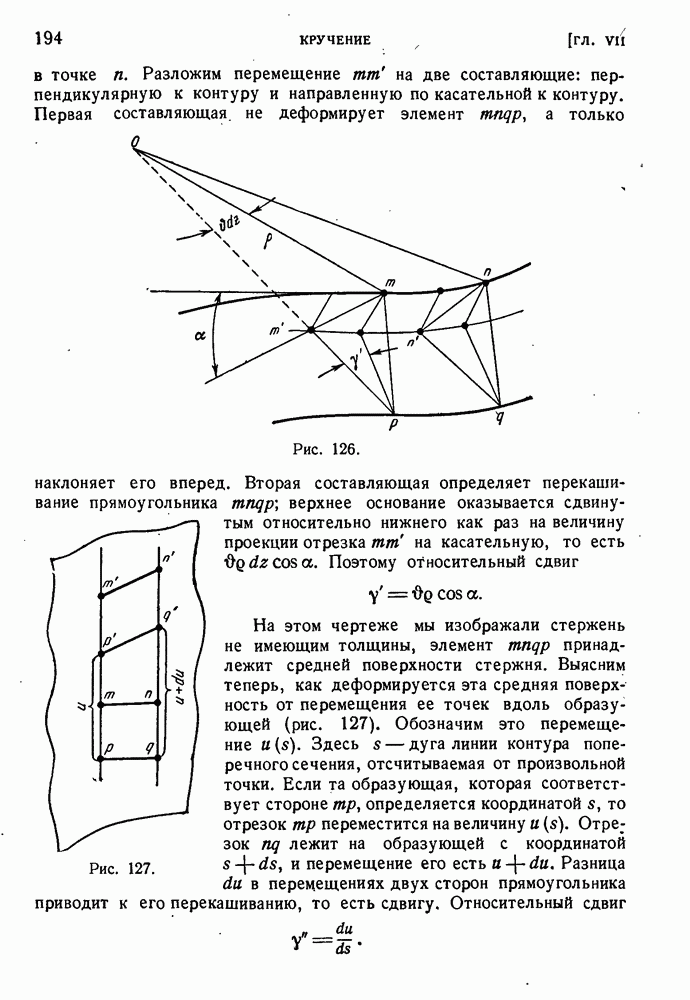
- § 89. Гипотеза жесткого контура.
- § 90. Кручение тонкостенных стержней замкнутого профиля.
- § 91. Кручение тонкостенных стержней открытого профиля.
- § 92. Кручение упругих стержией сплошного профиля.
- § 93. Опытное исследование кручения.
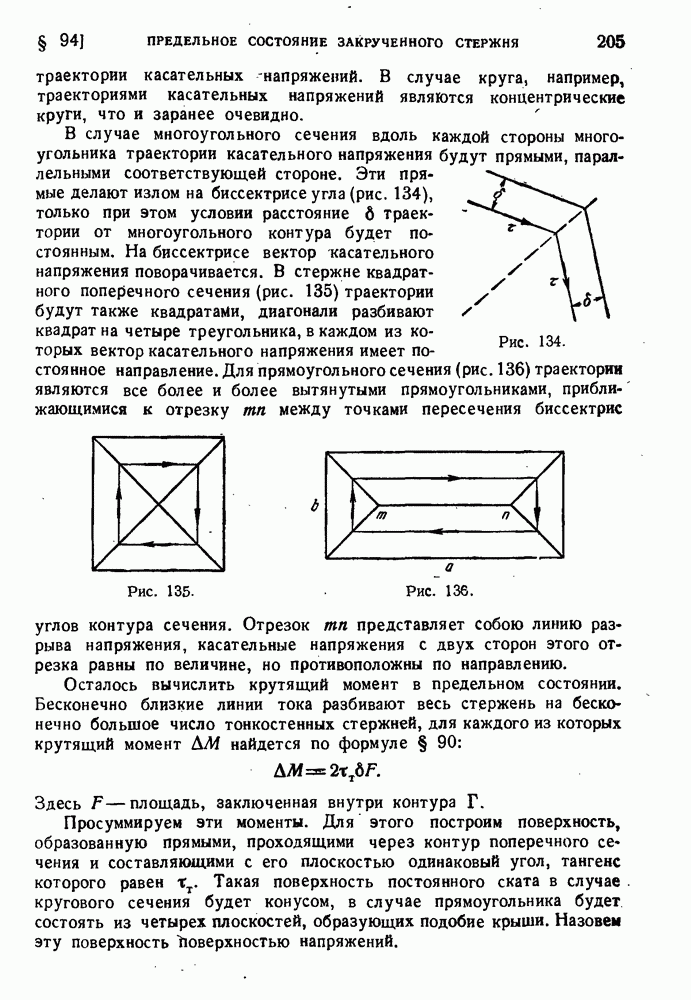
- § 94. Предельное состояние закрученного стержня из идеально-пластического материала.
- ГЛАВА VIII. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- § 96. Общие теоремы о моментах.
- § 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей.
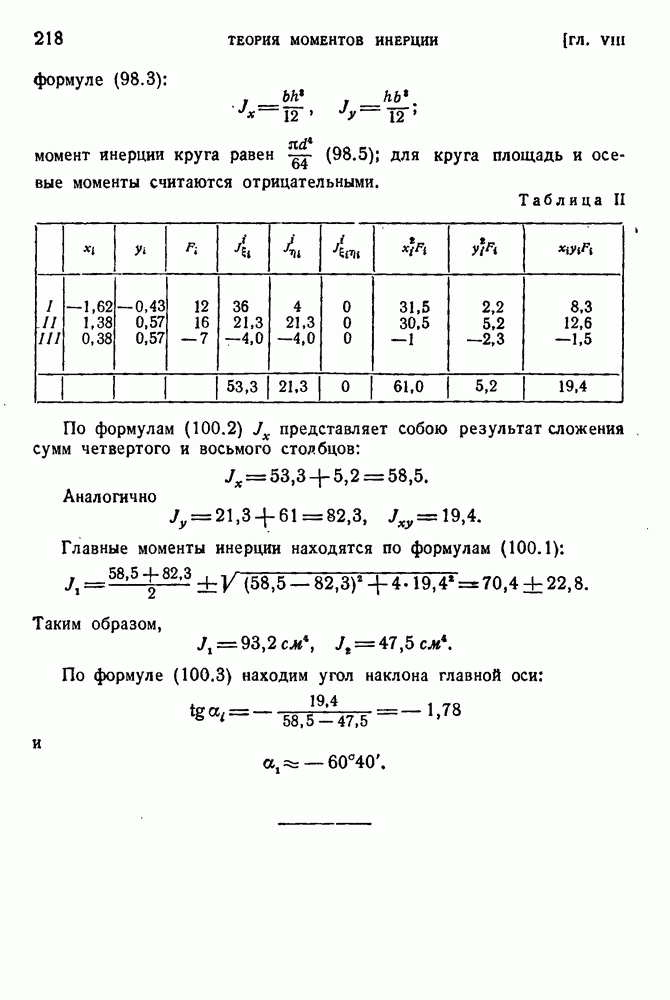
- § 98. Вычисление моментов инерции.
- § 99. Преобразование моментов инерции при повороте осей.
- § 100. Главные оси и главные моменты инерции.
- ГЛАВА IX. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
- § 101. Действие поперечных сил на балку.
- § 102. Гипотеза плоских сечений и принцип Сен-Венана.
- § 103. Нормальные напряжения при изгибе.
- § 104. Изгибающие моменты и перерезывающие силы.
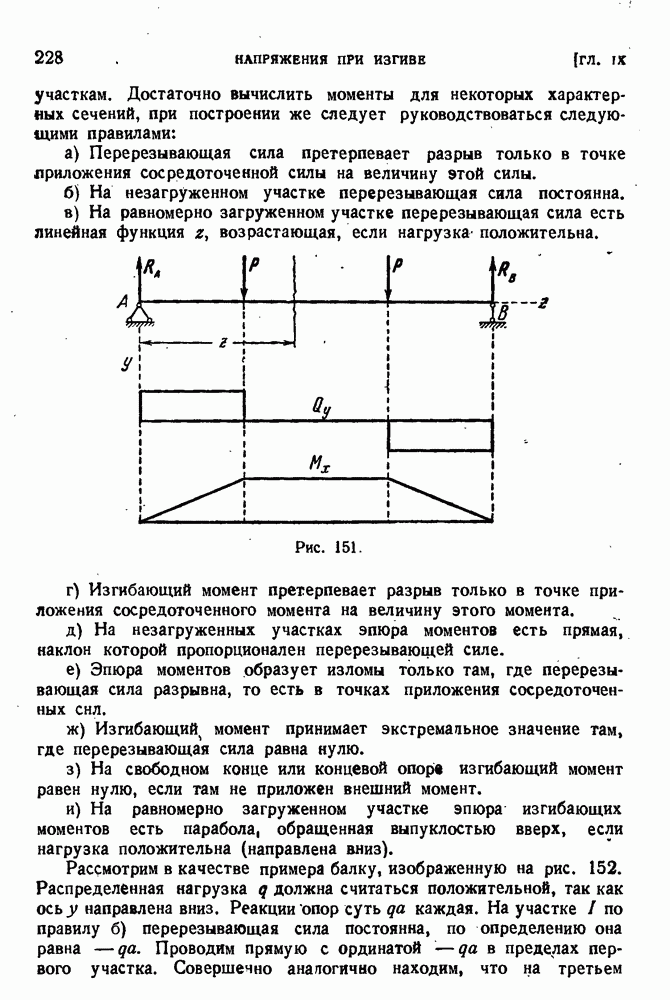
- § 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры.
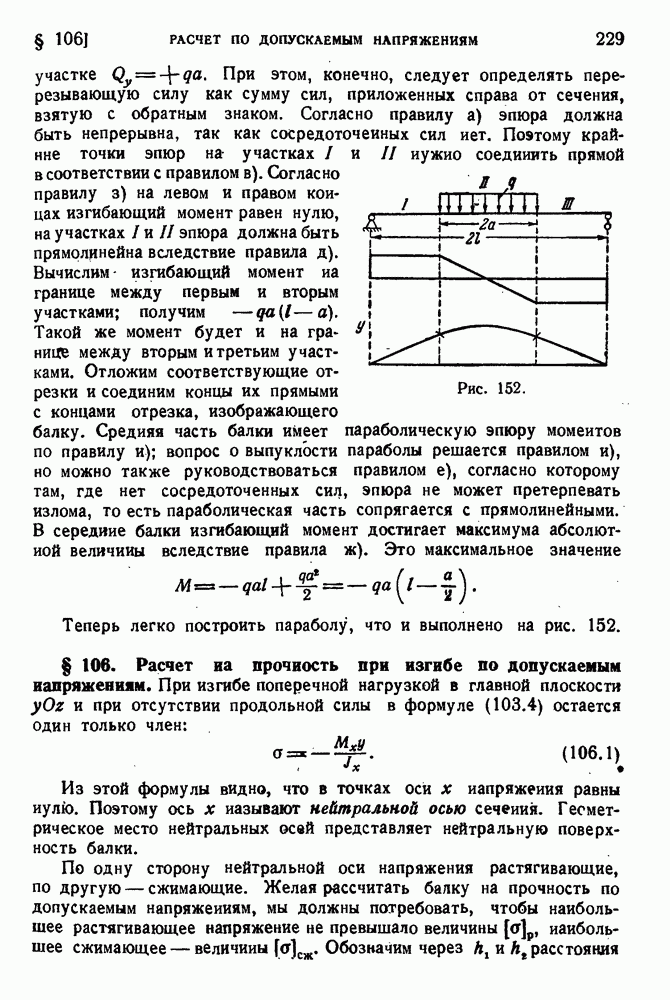
- § 106. Расчет на прочность при изгибе по допускаемым напряжениям.
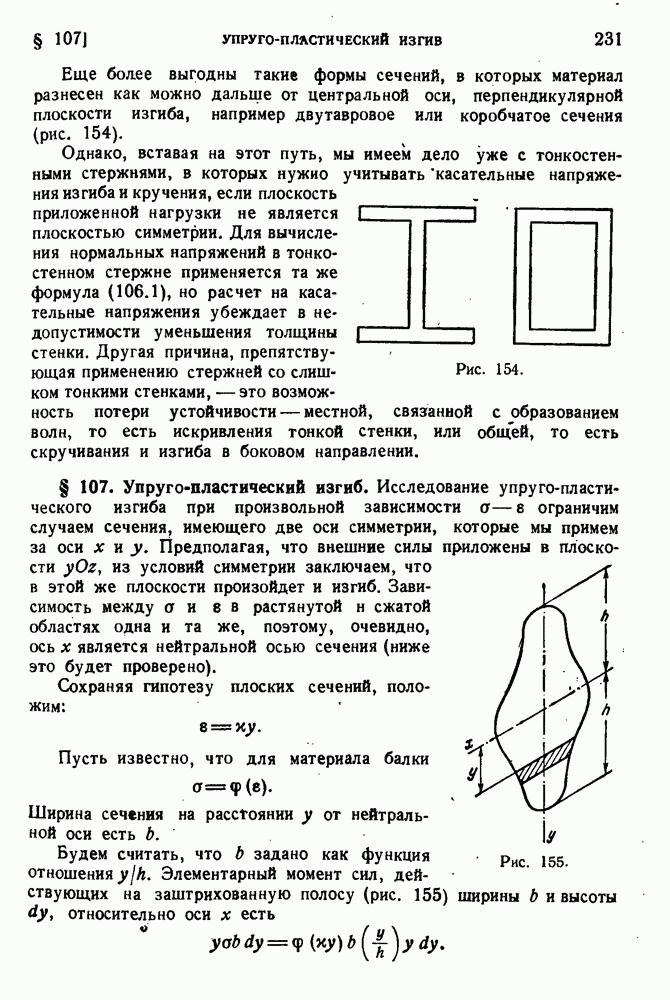
- § 107. Упруго-пластический изгиб.
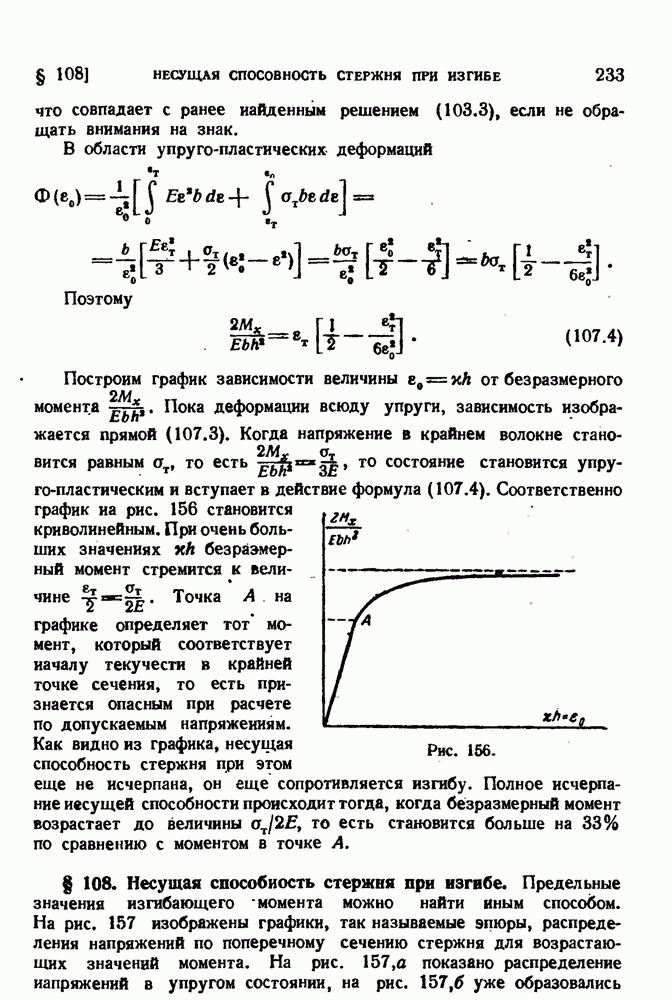
- § 108. Несущая способность стержня при изгибе.
- § 109. Принцип Сен-Венана.
- § 110. Внецентренное растяжение — сжатие.
- § 111. Ядро сечения.
- § 112. Несущая способность внецентренно сжатого стержня.
- § 113. Расчет составных балок.
- § 114. Изгиб кривого бруса.
- § 115. Нахождение нейтральной осн в кривом стержне.
- ГЛАВА X. ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- § 116. Дифференциальное уравнение изогнутой оси.
- § 117. Пределы применимости приближенной теории.
- § 118. Интегрирование уравнения изгиба.
- § 119. Примеры определения прогибов.
- § 120. Простейшие статически неопределенные задачи.
- § 121. Расчет статически неопределимых балок по способу допускаемых нагрузок.
- § 122. Изгиб стержней переменного сечения.
- § 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами.
- § 124. Продольно-поперечный изгиб.
- § 125. Изгиб балки на упругом основании.
- ГЛАВА XI. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
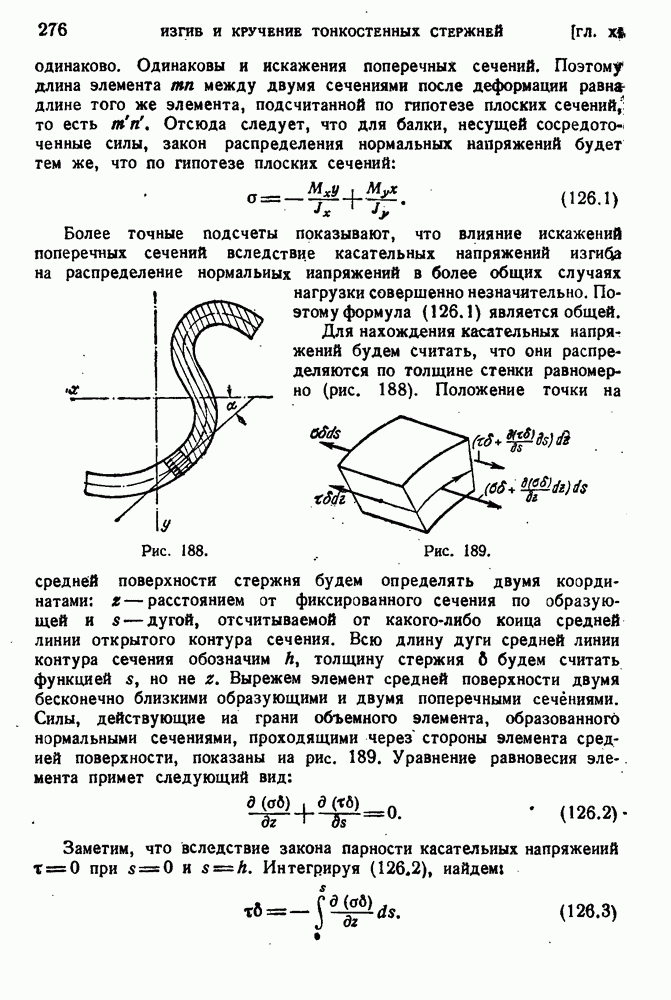
- § 126. Нормальные и касательные напряжения при изгибе.
- § 127. Касательные напряжении при изгибе в плоскости симметрии.
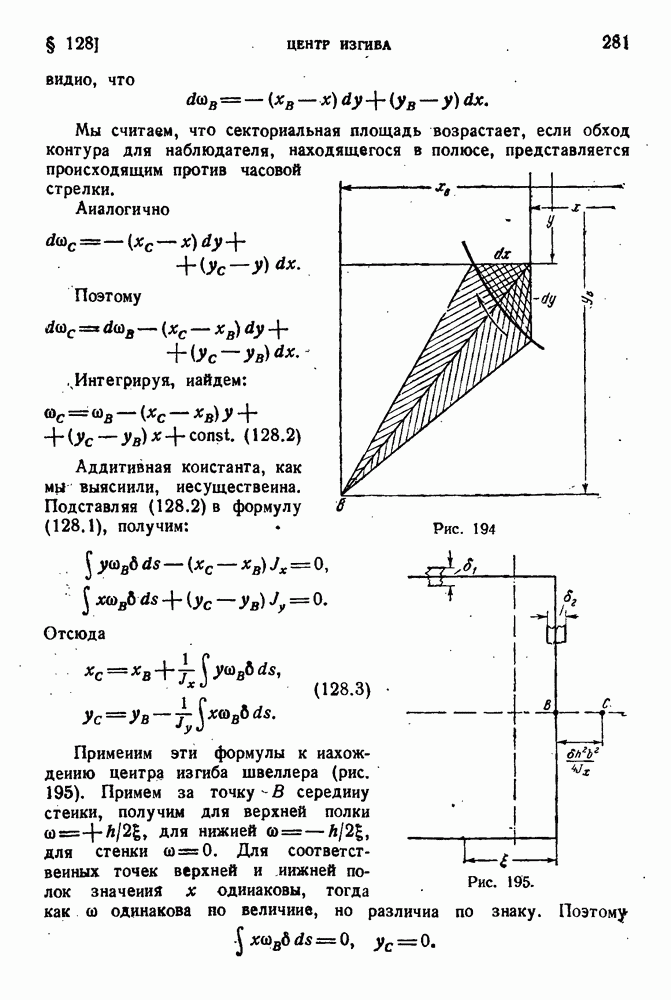
- § 128. Центр изгиба.
- § 129. Дополнительные напряжения при кручении.
- § 130. Закон секториальных площадей.
- § 131. Уравнение стесненного кручения.
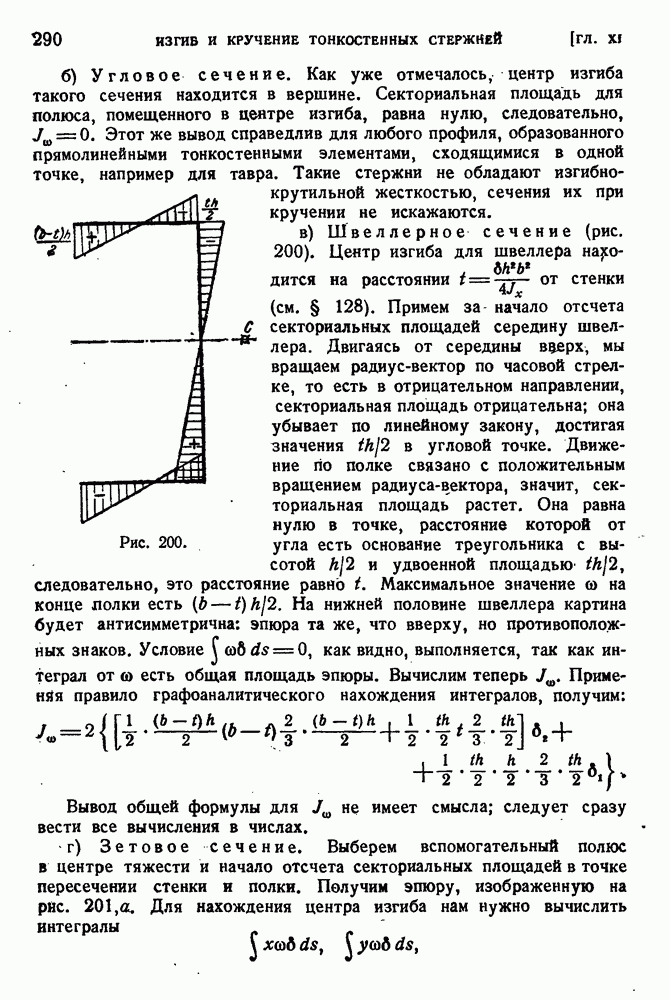
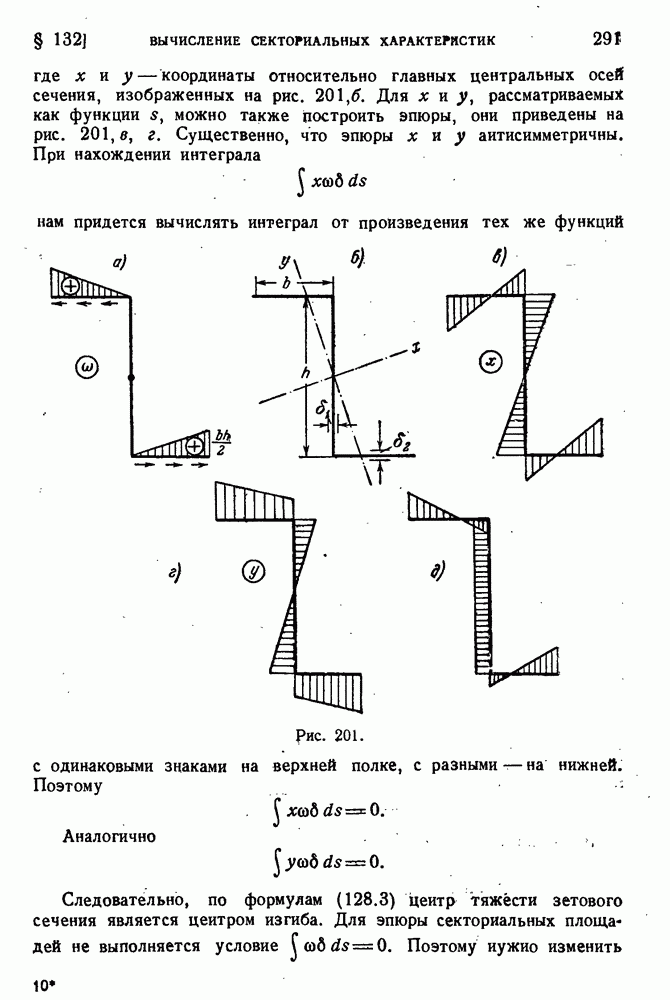
- § 132. Вычисление секториальных характеристик.
- § 133. Стержень, нагруженный бимоментом.
- § 134. Некоторые примеры стесненного кручения.
- ГЛАВА XII. УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ
- § 135. Постановка вопроса об устойчивости.
- § 136. Устойчивость сжатого упругого стержня.
- § 137. Эластика Эйлера.
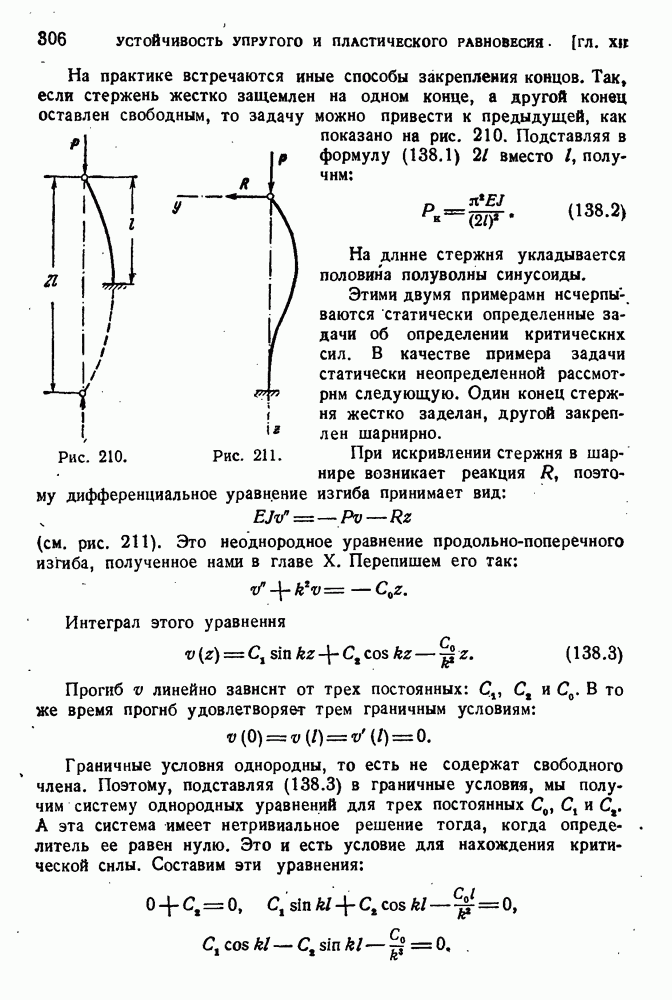
- § 138. Критические силы при иных видах закрепления стержня.
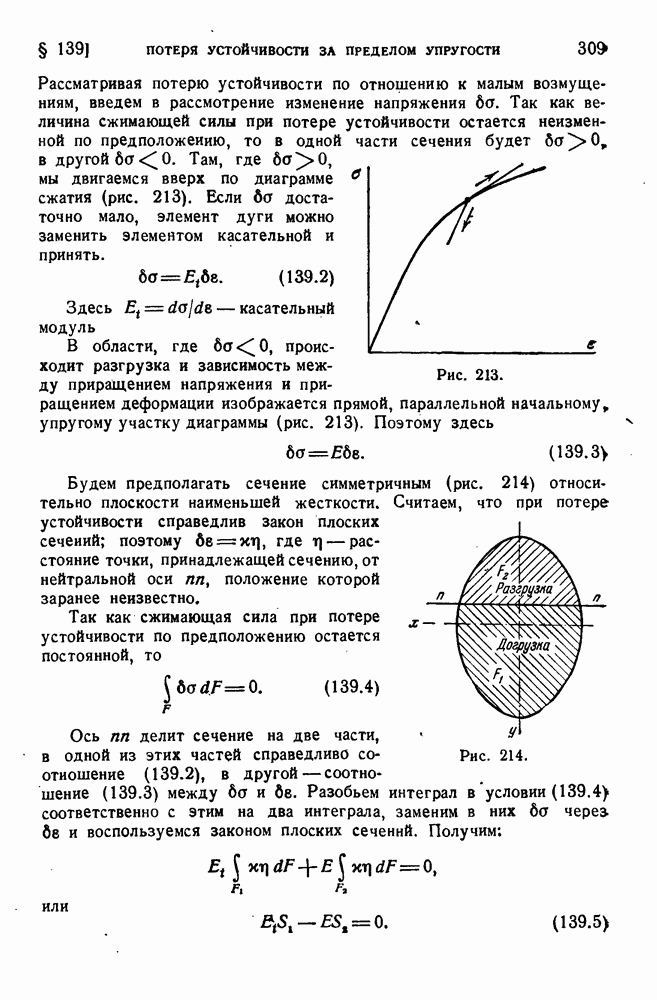
- § 139. Потеря устойчивости за пределом упругости.
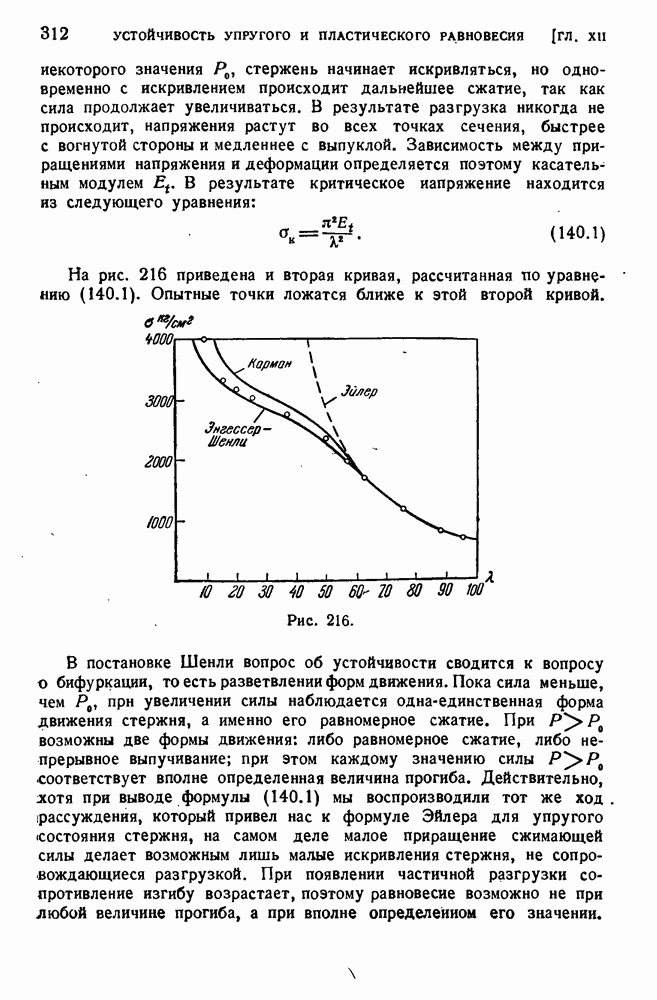
- § 140. Потеря устойчивости за пределом упругости (продолжение).
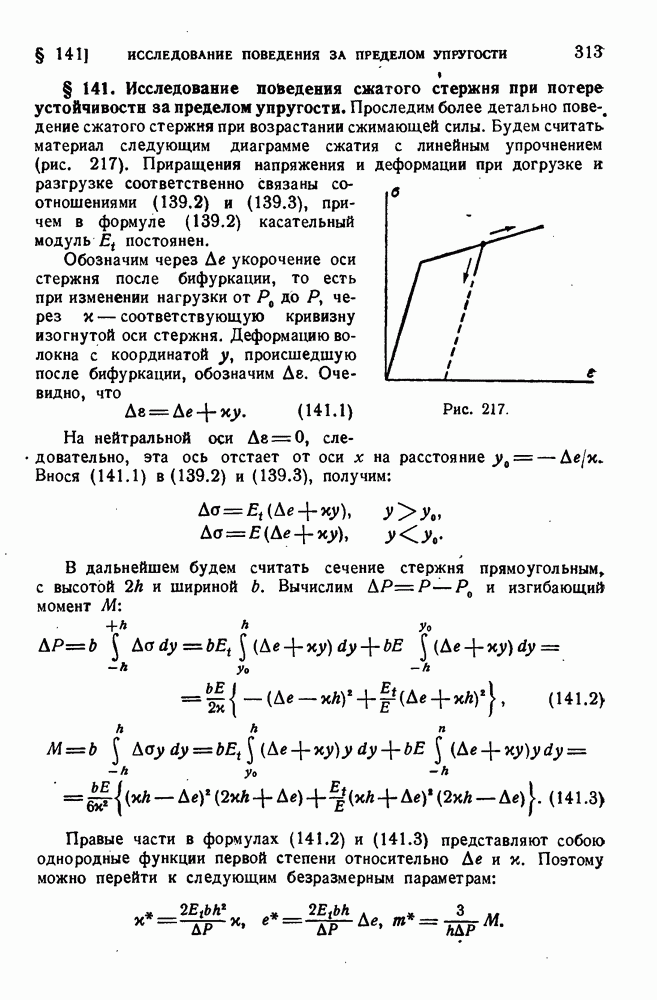
- § 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости.
- § 142. Расчет на устойчивость по эмпирическим формулам.
- ГЛАВА XIII. ТРУБЫ И ДИСКИ
- § 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности.
- § 144. Упругое состояние трубы. Формулы Ламе.
- § 145. Пластическое состояние трубы.
- § 146. Вращающиеся диски. Упругое состояние.
- § 147. Диск равного сопротивления.
- § 148. Предельное равновесие вращающегося диска.
- ГЛАВА XIV. ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 149. Обобщенные силы и обобщенные перемещения.
- § 150. Начало возможных перемещений для деформируемого тела.
- § 151. Теоремы Лагранжа и Кастильяно.
- § 152. Лииейиые упругие системы.
- § 153. Теорема о взаимности работ.
- § 154. Теорема Кастильяно для линейных упругих систем.
- § 155. Расчет винтовых пружин.
- § 156. Теорема о минимуме энергии.
- § 157. Интеграл перемещений.
- § 158. Графоаналитический способ вычислений интеграла перемещений.
- § 159. Расчет статически неопределимых систем по методу сил.
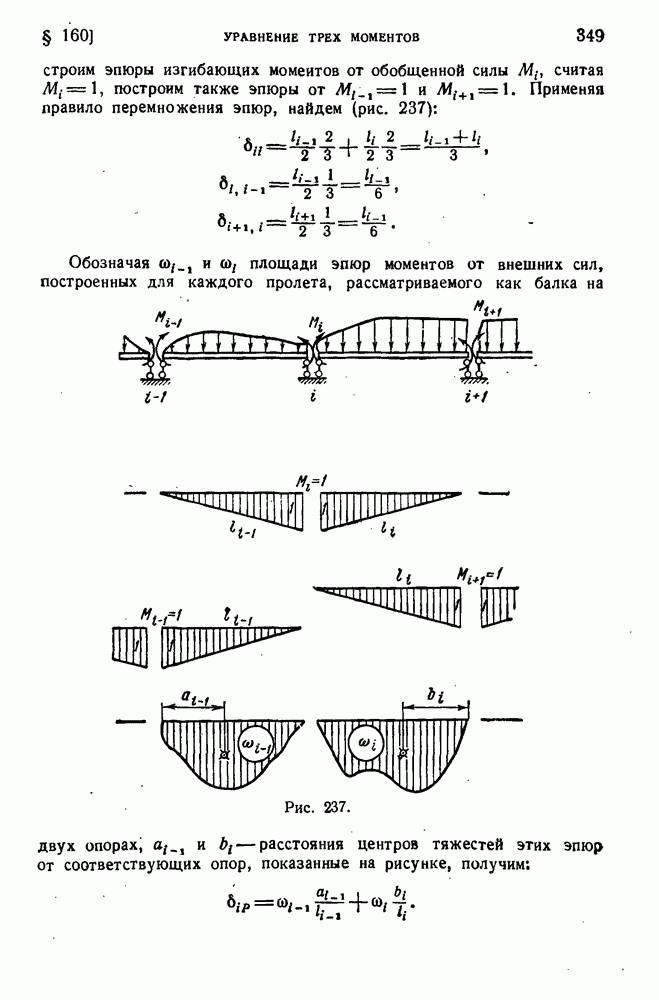
- § 160. Уравнение трех моментов.
- ГЛАВА XV. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
- § 161. Жестко-пластическое тело.
- § 162. Поверхности нагружения.
- § 163. Истинное и допустимые состояния элемента.
- § 164. Статический метод определения предельной нагрузки.
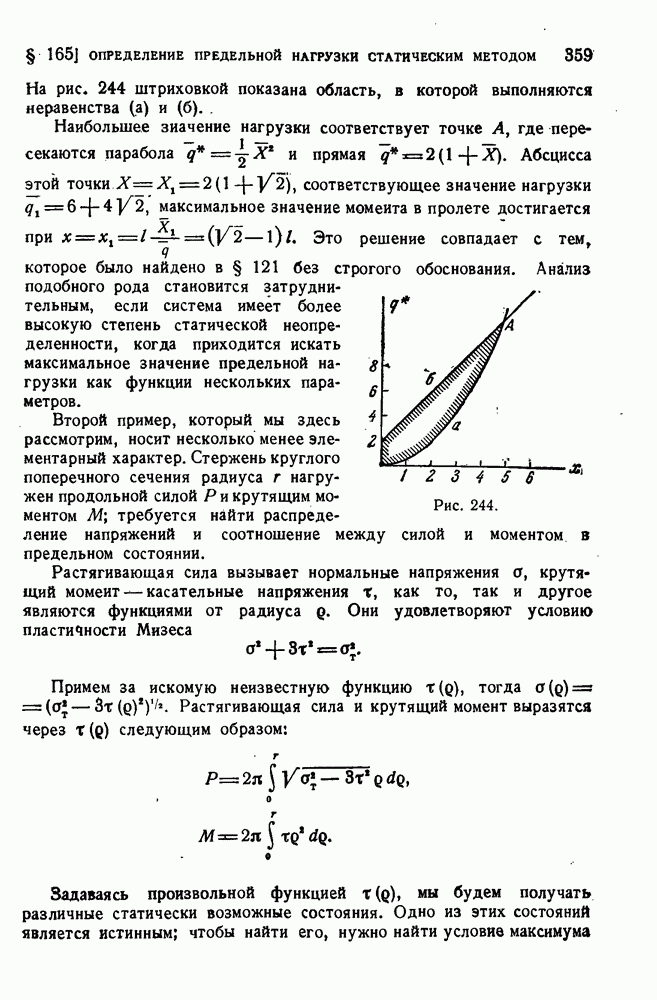
- § 165. Примеры определения предельной нагрузки статическим методом.
- § 166. Кинематически возможные состояния.
- § 167. Кинематический метод определения предельной нагрузки.
- § 168. Примеры определения предельной нагрузки кинематическим методом.
- § 169. Предельное равновесие пластинок.
- ГЛАВА XVI. ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 170. Колебания систем с конечным числом степеней свободы.
- § 171. Собственные частоты и главные формы колебаний.
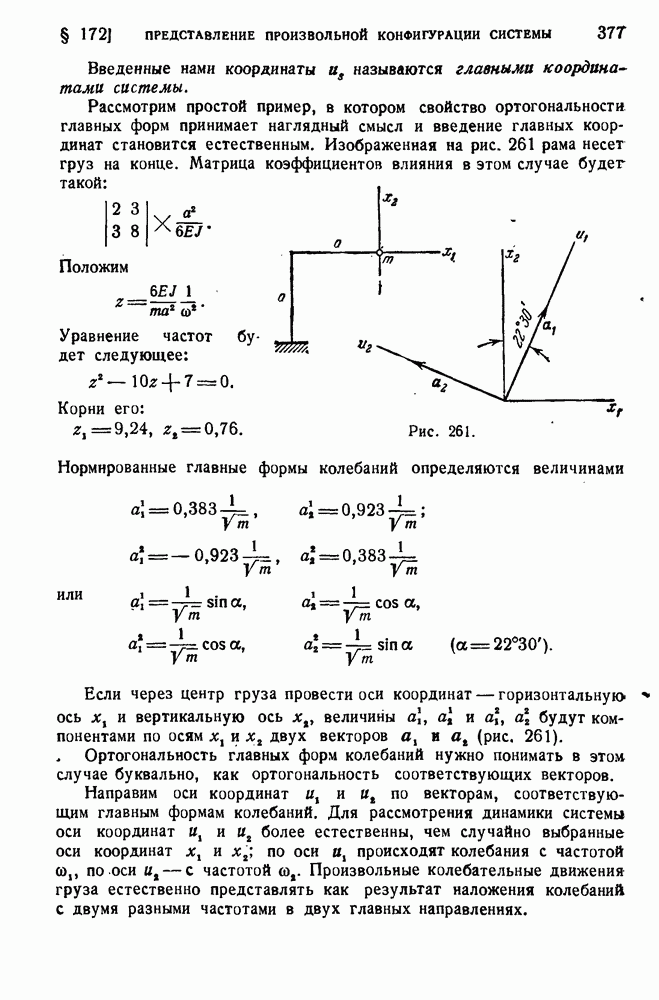
- § 172. Представление произвольной конфигурации системы через главные формы. Главные координаты.
- § 173. Формула и способ Релея.
- § 174. Нижние оценки для частоты основного тона.
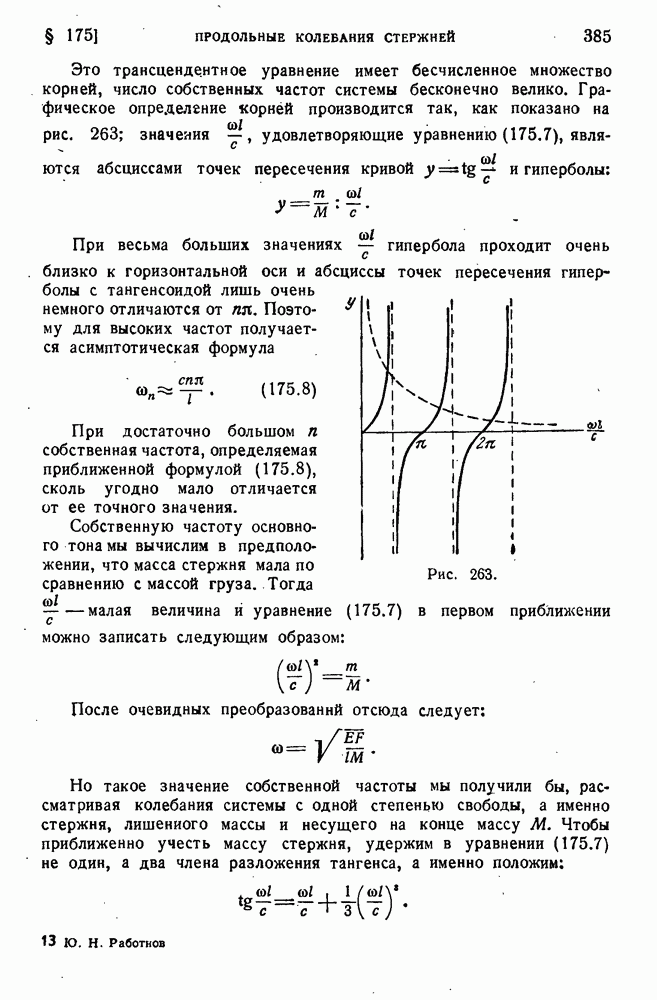
- § 175. Продольные колебания стержней.
- § 176. Поперечные колебания стержней.
- § 177. Колебания балок постоянного сечения.
- § 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня.
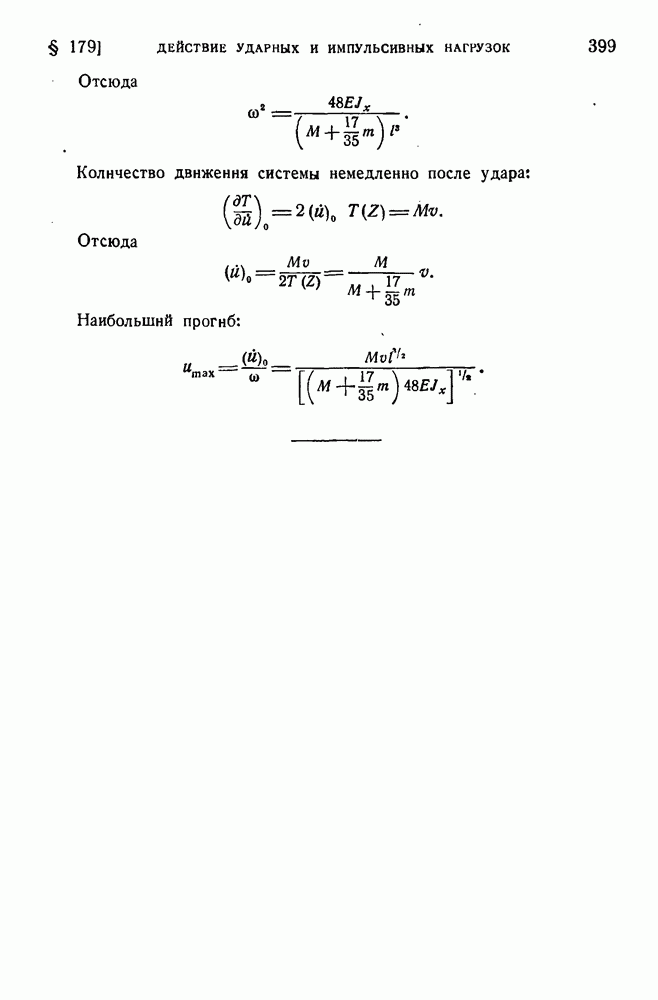
- § 179. Действие ударных и импульсивных нагрузок на упругие системы.
- ГЛАВА XVII. ТЕОРИИ ПРОЧНОСТИ
- § 180. Постановка вопроса о прочности.
- § 181. Хрупкое и пластическое разрушение.
- § 182. Теория прочности Мора.
- § 183. Механизм хрупкого разрушения.
- § 184. Прочность при низких температурах.
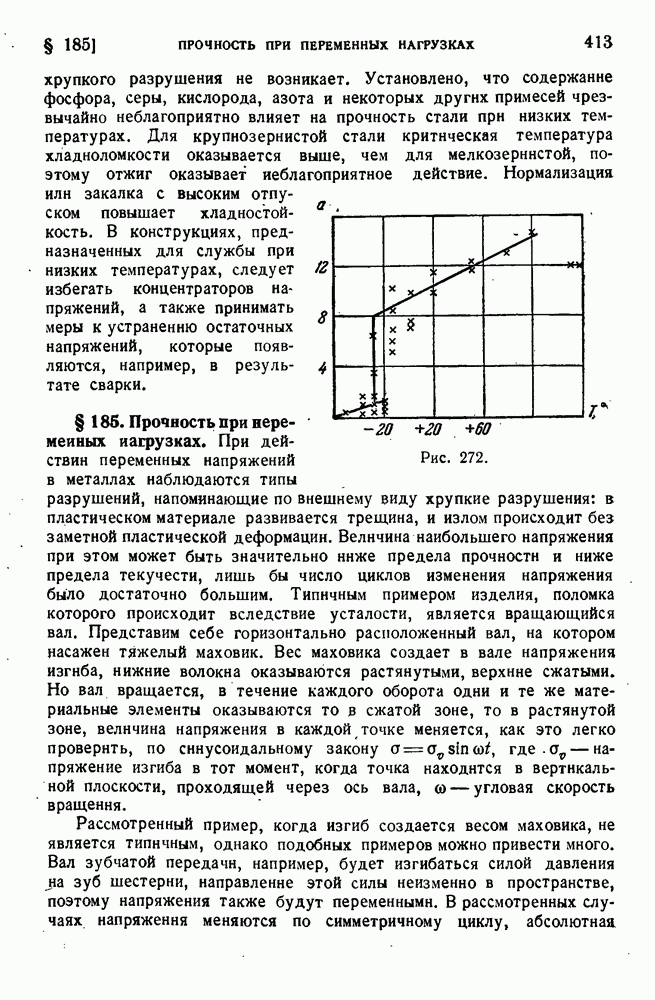
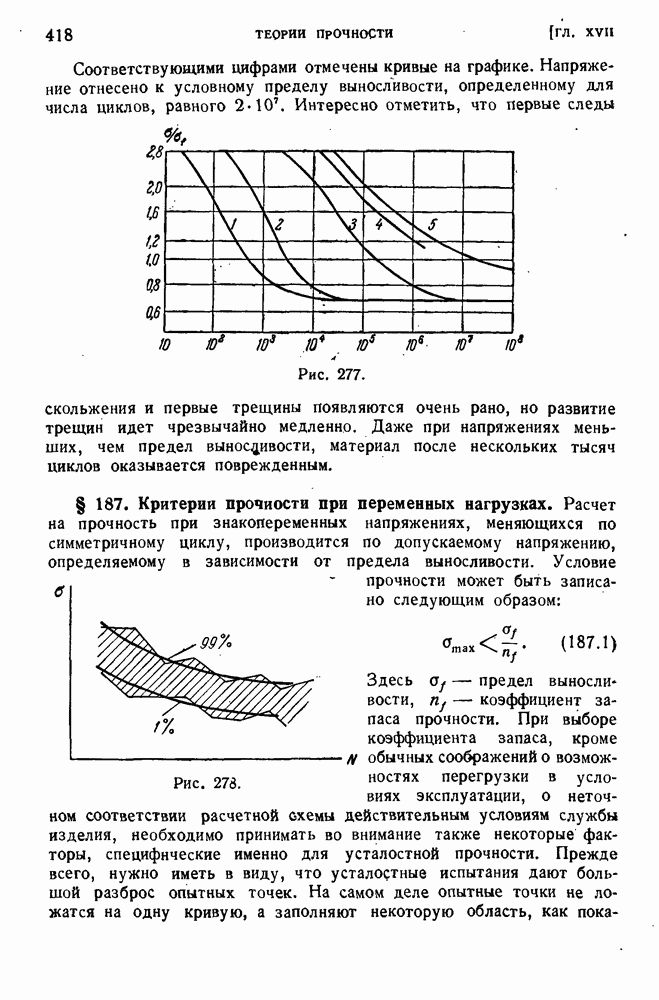
- § 185. Прочность при переменных нагрузках.
- § 186. Природа усталостного разрушения.
- § 187. Критерии прочности при переменных нагрузках.
- § 188. Влияние концентрации напряжений на усталостную прочность.
- § 189. Усталостная прочность при сложном напряженном состоянии.
- ГЛАВА XVIII. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
- § 190. Ползучесть металлов.
- § 191. Процесс ползучести.
- § 192. Длительное разрушение.
- § 193. Температурные зависимости ползучести и длительной прочности.
- § 194. Феноменологические теории одномерной ползучести.
- § 195. Релаксация напряжений.
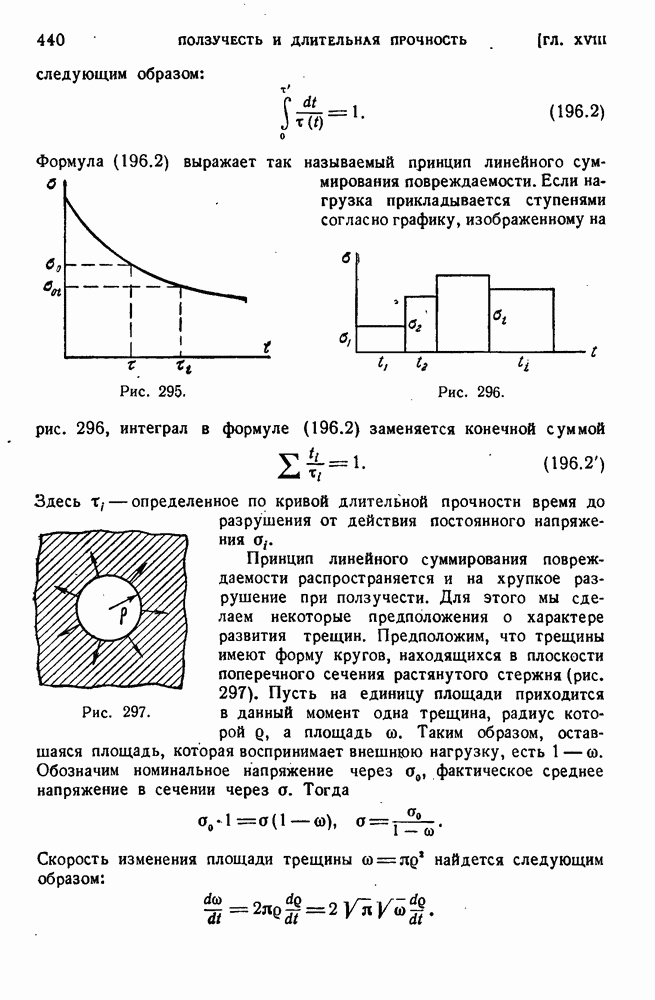
- § 196. Длительная прочность при переменных нагрузках.
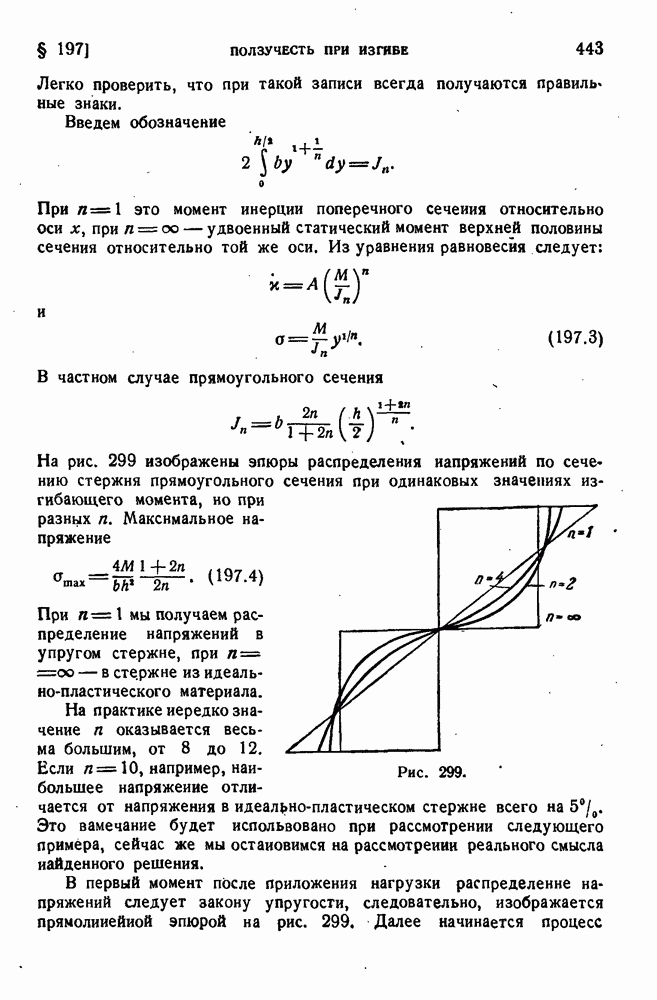
- § 197. Ползучесть при изгибе.
- § 198. Критическое время сжатого стержня.
- § 199. Ползучесть и длительная прочность при сложном напряженном состоянии.
- § 200. Вращающиеся диски в условиях ползучести.
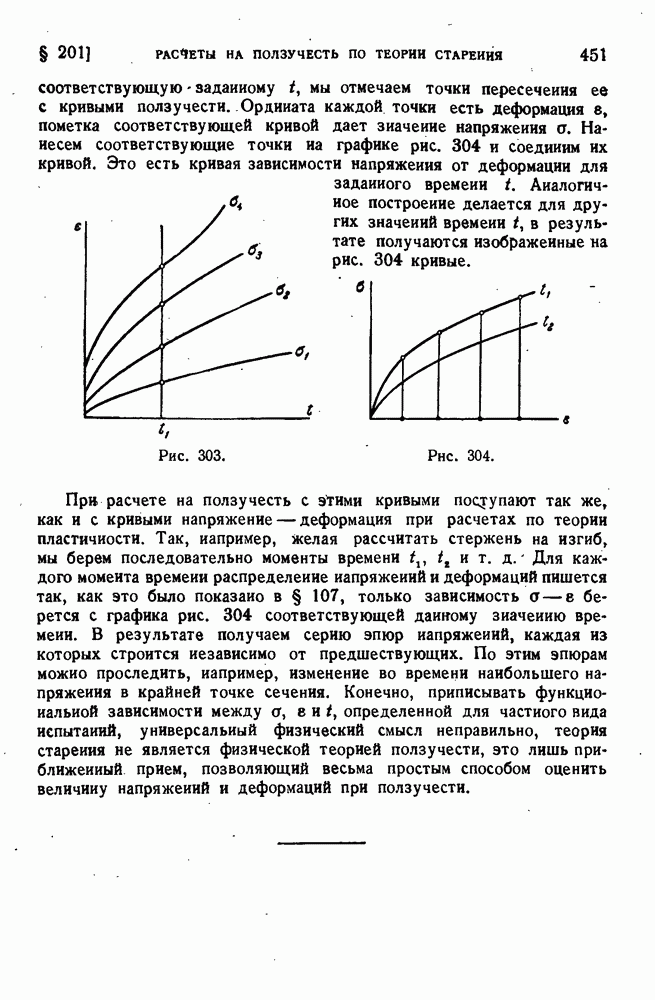
- § 201. Расчеты на ползучесть по теории старении.