| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
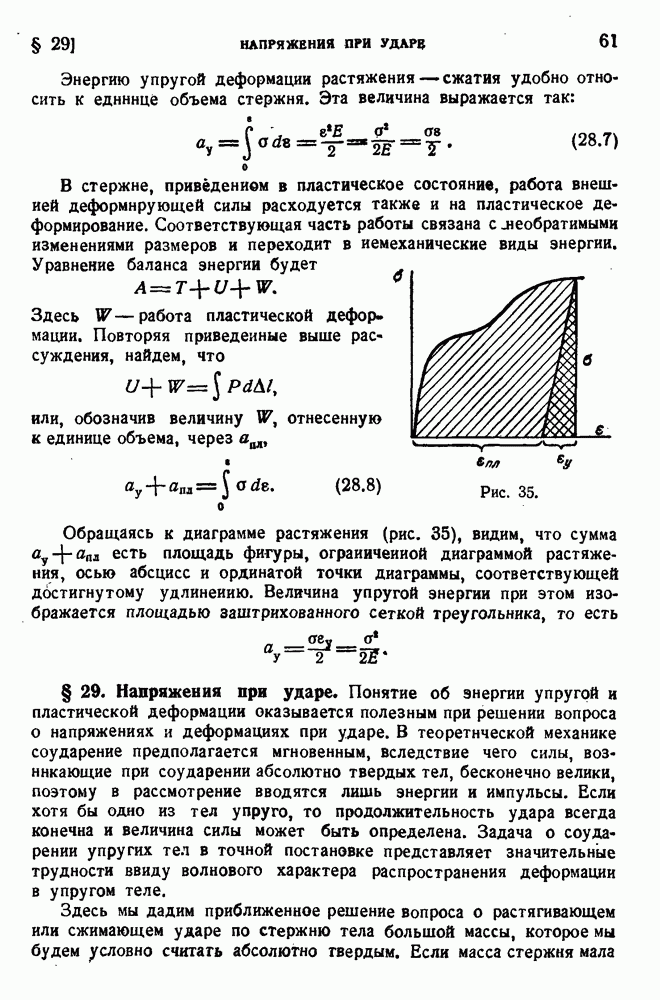
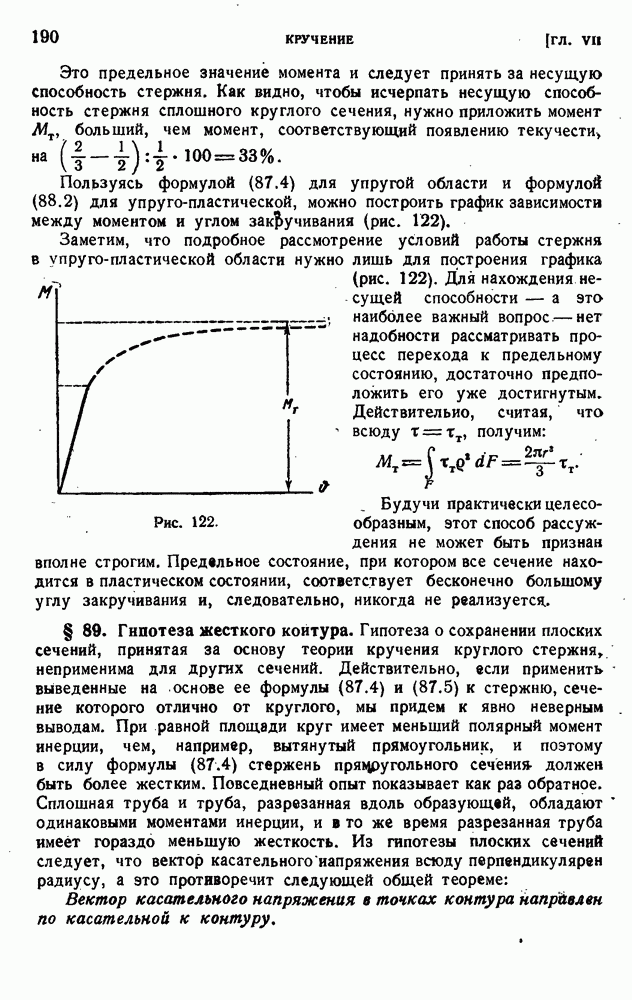
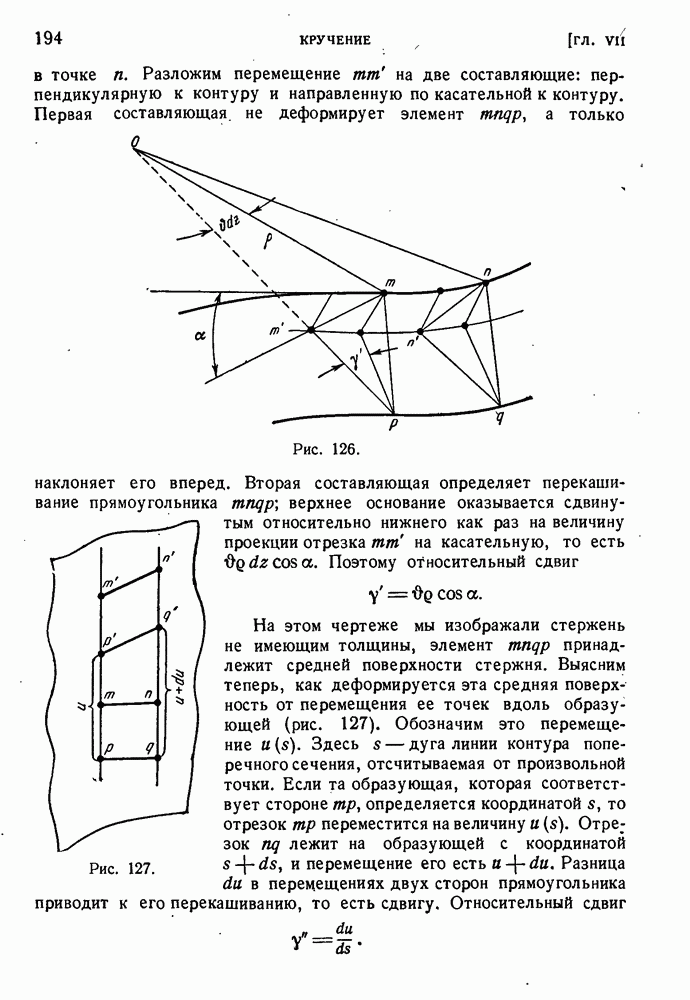
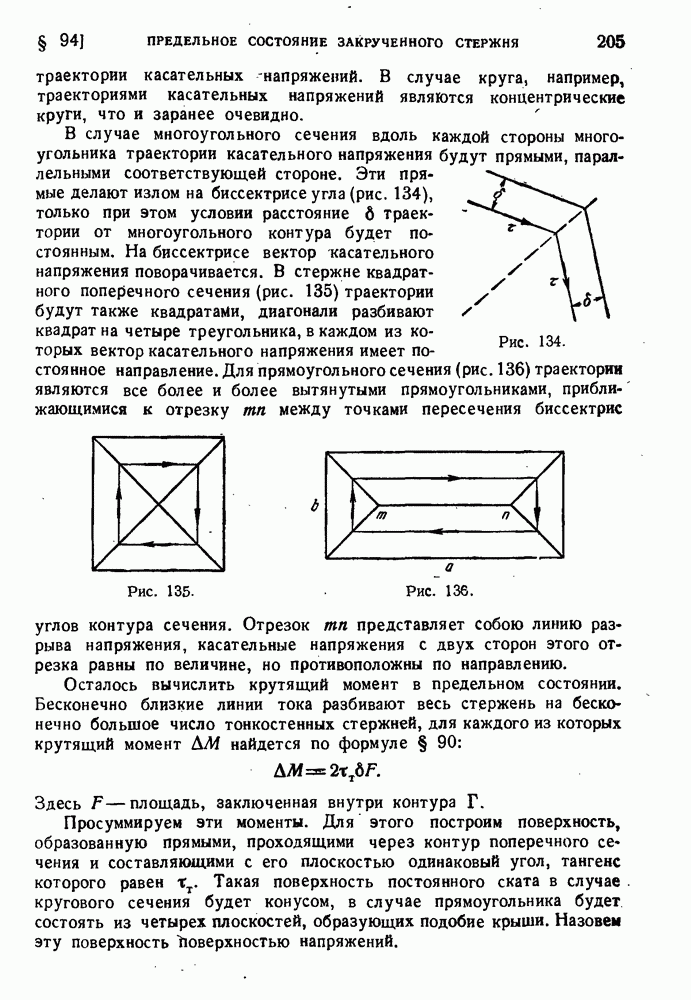
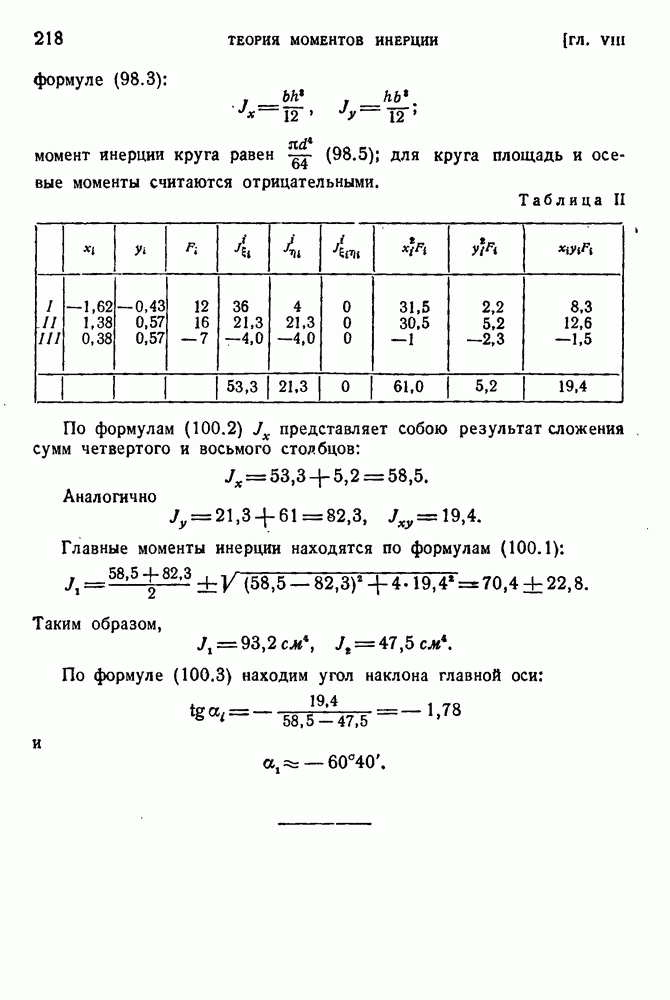
§ 50. Энергия изменения формы.
В конце прошлого столетии было высказано предположение о том, что переход в пластическое состояние свизан с достижением предельного значении энергией деформации на единицу объема (Бельтрами). Эта точка зрения была опровергнута опытом. Действительно, подвергая материал всестороннему сжатию, можно накопить в единице объема сколь угодно большую упругую энергию, лишь бы давление было достаточно велико. Однако ндея подобного энергетического критерии начала текучести представляется заманчивой, и для ее реализации необходимо суметь отделить энергию изменения объема от энергии сдвиговой деформации, или, как говорят, энергии изменения формы.
Представим себе, что наприженное состояние разложено на две составляющие, которые мы будем называть девиаторной частью тензора наприжений и его гидростатической частью.
Девнаторной частью тензора напряжений называют ту его часть, которая не меняетси от добавлении всестороннего растяжения или сжатии. Если тензор напряжений отнесен к главным осям, будем обозначать компоненты девиатора  . Гидростатическая часть — это выделиемое из общего наприженного состояния состояние всестороннего сжатия или растяжения. Компоненты гидростатической части тензора:
. Гидростатическая часть — это выделиемое из общего наприженного состояния состояние всестороннего сжатия или растяжения. Компоненты гидростатической части тензора:  . Теперь главные напряжении
. Теперь главные напряжении  могут быть представлены следующим образом:
могут быть представлены следующим образом:

Отсюда компоненты девиатора:

По определению компоненты девиатора не должны меняться от приложения к телу дополнительных напряжений всестороннего растяжения или сжатия. Пусть эти дополнительные напряжения равны q. Каждое из главных напряжений получает приращение, равное q; для того чтобы компоненты девиатора не изменились, необходимо, чтобы величина  также получила приращение, равное q. Для этого нужно принять
также получила приращение, равное q. Для этого нужно принять

На рис. 56 показано схематически разложение напряженного состояния на девиаторную и гидростатическую части. Оказывается, что потенциальная энергия упругой деформации может быть представлена

Рис. 56.
как сумма энергий, соответствующих девиаторной и гидростатической частям тензора напряжений. Первая называется энергией изменения формы, вторая — энергией изменения объема. Обозначим энергию изменения формы через  энергию изменения объема через
энергию изменения объема через  . Нам нужно доказать, что
. Нам нужно доказать, что

Следует заметить, что свойство аддитивности вообще на упругую энергию не распространяется, так как энергия является квадратичной функцией от напряжений. Если представить себе напряженное состояние тела как результат последовательного приложения двух систем напряжений, то вычисление конечной энергии можно производить следующим образом.
От приложения первой системы напряжений  в теле накапливается энергия
в теле накапливается энергия  . Прикладываем теперь вторую систему напряжений, которая вызывает деформации
. Прикладываем теперь вторую систему напряжений, которая вызывает деформации  они вычисляются по формулам закона Гука через напряжения
они вычисляются по формулам закона Гука через напряжения  так, как если бы первая система напряжений отсутствовала. Работа второй системы напряжений на своих перемещениях есть энергия
так, как если бы первая система напряжений отсутствовала. Работа второй системы напряжений на своих перемещениях есть энергия  . Но на деформациях
. Но на деформациях  производят работу и напряжения
производят работу и напряжения  первой системы, которые были приложены раньше. Обозначим эту работу
первой системы, которые были приложены раньше. Обозначим эту работу  и запишем:
и запишем:

Применяя эти рассуждения к нашему случаю, заметим, что гидростатическое напряженное состояние вызывает деформации:

Работа напряжений девиаторной части на этих деформациях есть

Складывая равенства (50.2) и принимая во внимание (50.3), получим:

Таким образом,  что и доказывает формулу (50.4). Для вычисления энергии изменения формы
что и доказывает формулу (50.4). Для вычисления энергии изменения формы  воспользуемся выражением (49.2) упругой энергии, заменив в нем
воспользуемся выражением (49.2) упругой энергии, заменив в нем  через
через  по формулам (50.2). Получим:
по формулам (50.2). Получим:

Для упрощения этого выражения воспользуемся тождеством (50.5). Возведем это тождество в квадрат:

С помощью (50.7) можно преобразовывать выражение (50.6) для энергии изменения формы различными способами. Например, исключая попарные произведения компонент девиатора, получим:

Исключая квадраты компонент девиатора, найдем:

Однако наиболее удобное выражение а получится, если умножить (50.7) на  и результат вычесть из (50.6). Таким образом мы придем к следующему результату:
и результат вычесть из (50.6). Таким образом мы придем к следующему результату:

Из формул (50.2) следует, что попарные разности компонент девиатора равны разности соответствующих компонент исходного тензора, поэтому предыдущую формулу на основании (44.3) и (41.2) можно заменить следующей:

Для нахождения энергии изменения объема  внесем в формулу (49.2) вместо
внесем в формулу (49.2) вместо  , величину
, величину  . Получим:
. Получим:

Условие постоянства октаэдрического касательного напряжения тождественно с условием постоянства упругой энергии изменения формы.
Губер в 1904 г. высказал предположение, что разрушение материала происходит тогда, когда достигается предельное значение либо полной упругой энергии, либо энергии изменения формы, в зависимости от того, отрицательно или положительно  . Когда гидростатическая часть тензора напряжений отрицательна, то есть происходит всестороннее сжатие, критерий прочности Губера совпадает с условием постоянства октаэдрического напряжения Мизеса. При всестороннем растяжении начало разрушения определяется, по Губеру, полной удельной энергией.
. Когда гидростатическая часть тензора напряжений отрицательна, то есть происходит всестороннее сжатие, критерий прочности Губера совпадает с условием постоянства октаэдрического напряжения Мизеса. При всестороннем растяжении начало разрушения определяется, по Губеру, полной удельной энергией.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Задачи и содержание сопротивления материалов.
- § 2. Сопротивление материалов и теоретическая механика.
- § 3. Статически неопределенные задачи.
- § 4. Внешние силы.
- § 5. Принцип отвердения.
- § 6. Недопустимость замены системы сил статически эквивалентной.
- § 7. Однородное тело.
- § 8. Внутренние силы.
- § 9. Напряжение.
- § 10. Простейшие типы напряженного состояния.
- § 11. Простейшие виды деформации.
- § 12. Упругость и пластичность.
- § 13. Закон Гука.
- § 14. Диаграмма пластичности.
- § 15. Тела изотропные и анизотропные.
- ГЛАВА II. РАСТЯЖЕНИЕ СЖАТИЕ
- § 16. Стержни и стержневые системы.
- § 17. Принцип Сен-Венана и гипотеза плоских сечений.
- § 18. Напряжения и деформации при растяжении.
- § 19. Расчеты на прочность при растижении и сжатии.
- § 20. Собственный вес и силы инерции.
- § 21. Стержни переменного сечения.
- § 22. Перемещения узлов стержневых систем.
- § 23. Статически неопределенные задачи на растяжение — сжатие.
- § 24. Температурные и монтажные напряжения.
- § 25. Общие соображения о расчете стержневых систем.
- § 26. Расчет статически неопределимых систем по допускаемым нагрузкам.
- § 27. Остаточные напряжения после пластической деформации.
- § 28. Потенциальная энергия растяжении.
- § 29. Напряжения при ударе.
- § 30. Распространение упругих волн в стержнях.
- § 31. Концентрации напряжений.
- § 32. Нелинейные задачи на растяжение — сжатие.
- ГЛАВА III. СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
- § 33. Напряжения на косых площадках при растяжении.
- § 34. Напряжения при двухосном растяжении.
- § 35. Круговая диаграмма Мора.
- § 36. Общий случай плоского напряженного состояния.
- § 37. Определение напряжений на произвольной площадке.
- § 38. Пространственное напряженное состояние.
- § 39. Главные напряжения.
- § 40. Главные касательные напряжения.
- § 41. Октаэдрическое напряжение.
- § 42. Закон Гука для главных осей.
- § 43. Изменение объема при упругой деформации.
- § 44. Чистый сдвиг.
- § 45. Деформация элемента объема в общем случае.
- § 46. Условие пластичности Треска — Сен-Венана.
- § 47. Условие пластичности Мизеса.
- § 48. Условия пластичности для плоского напряженного состояния.
- § 49. Потенциальная энергия упругой деформации.
- § 50. Энергия изменения формы.
- ГЛАВА IV. НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
- § 51. Расчеты на прочность изделий сложной формы.
- § 52. Безмоментные оболочки вращении.
- § 53. Местные напряжения в безмоментных оболочках.
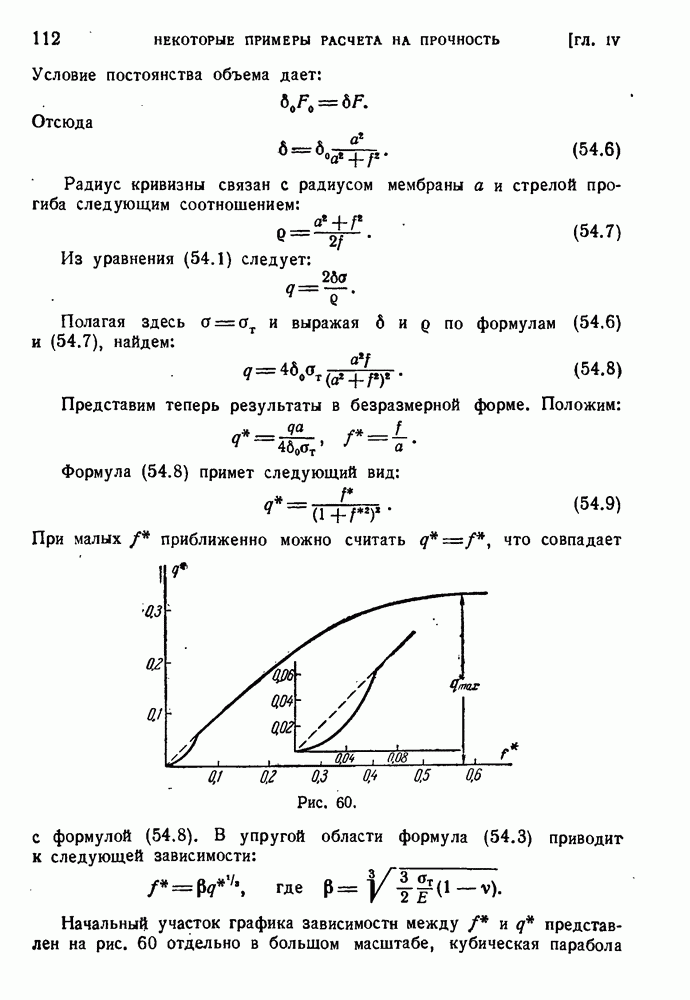
- § 54. Большие прогибы мембраны.
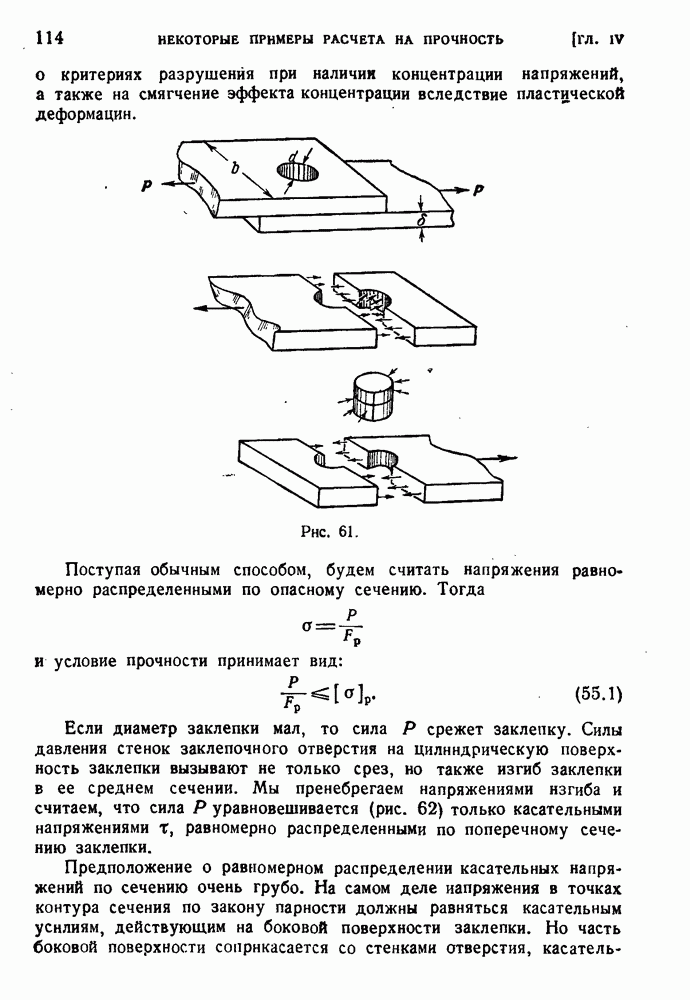
- § 55. Условные расчеты.
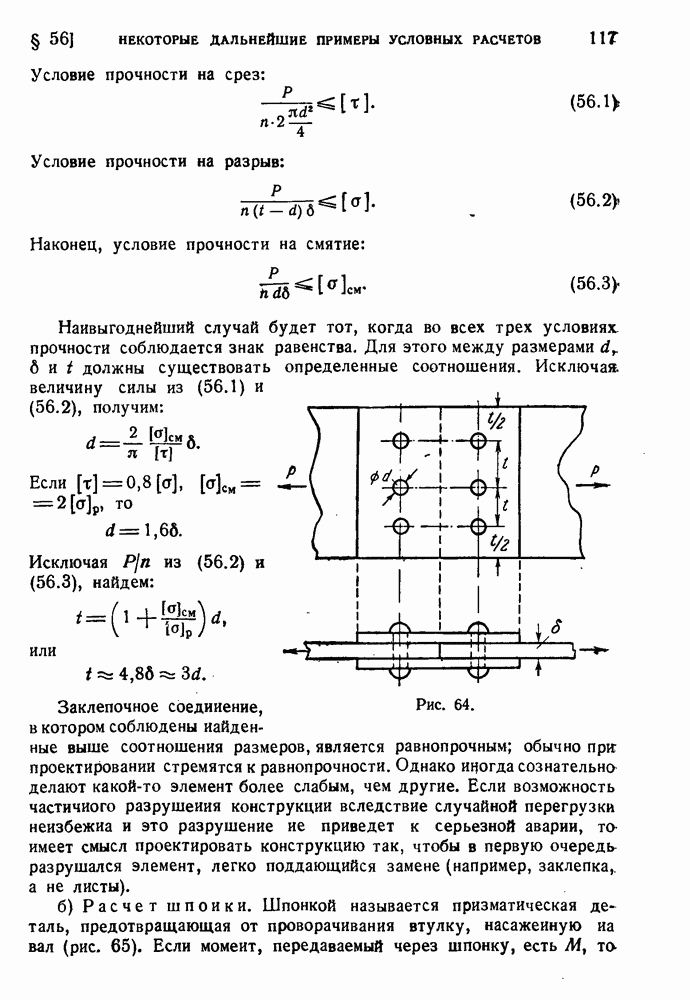
- § 56. Некоторые дальнейшие примеры условных расчетов.
- § 57. Расчет сварных соединений.
- ГЛАВА V. ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
- § 58. Задачи испытания материалов.
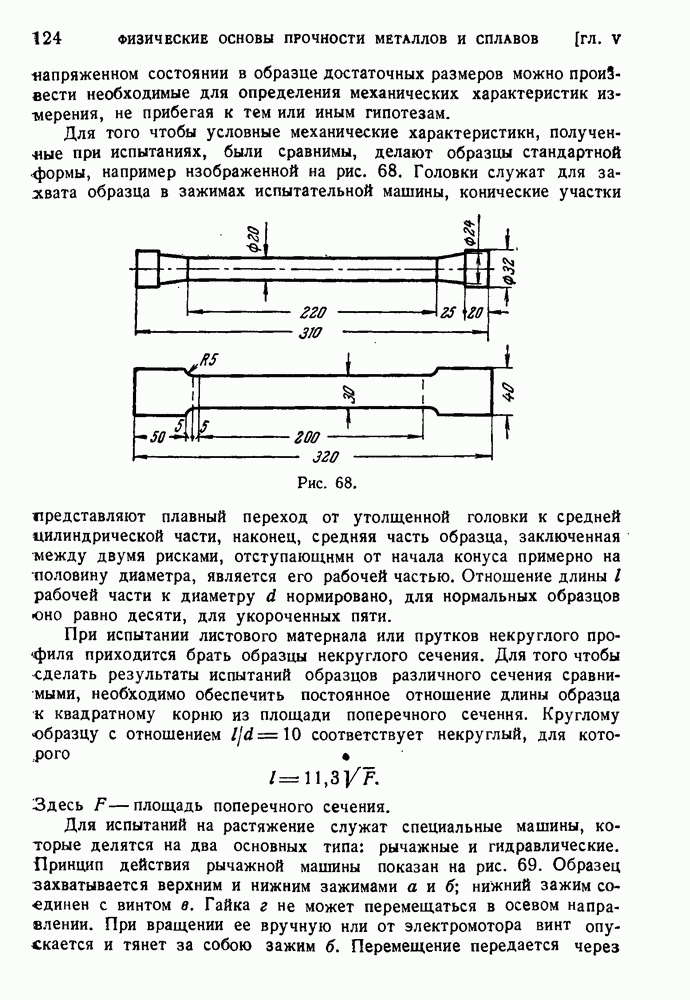
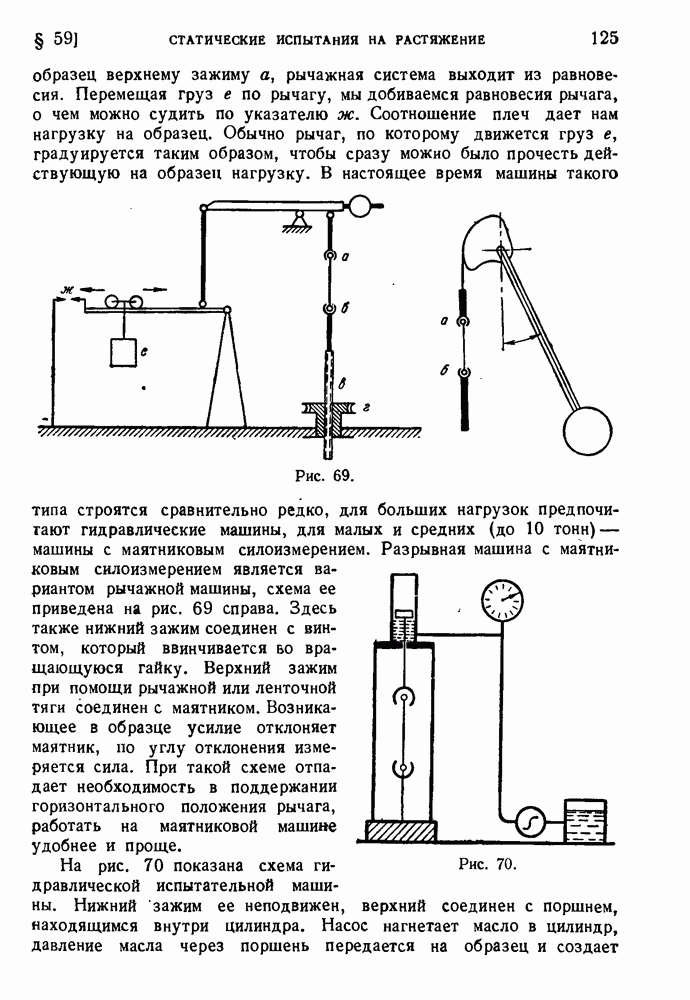
- § 59. Статические испытания на растяжение.
- § 60. Исследование металлов в области малых деформаций.
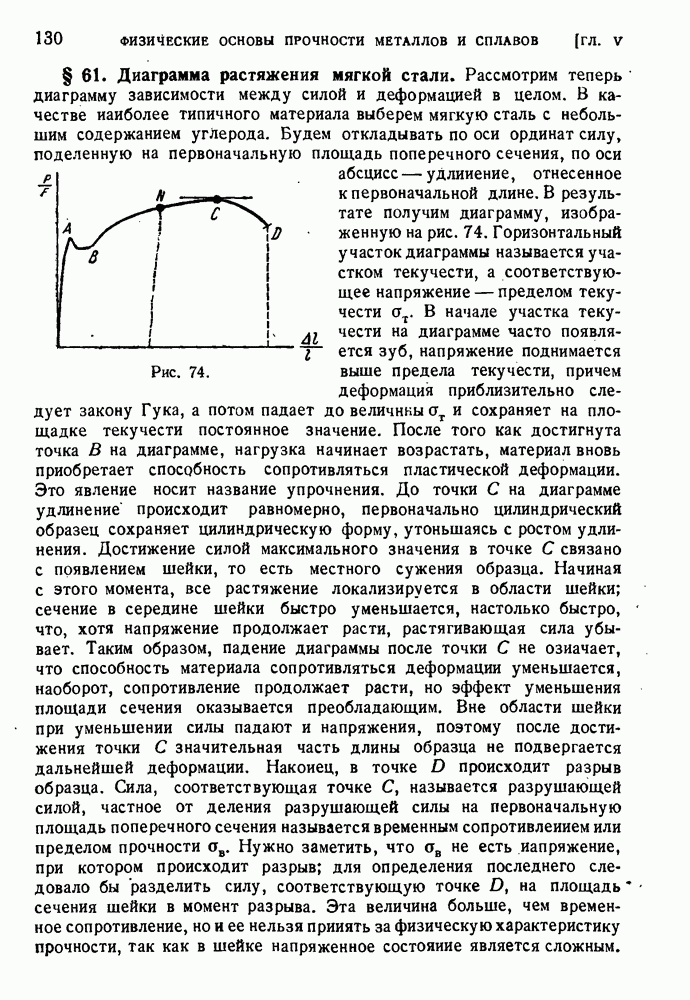
- § 61. Диаграмма растяжения мягкой стали.
- § 62. Опыты на сжатие.
- § 63. Строение и упругая деформация металлических кристаллов.
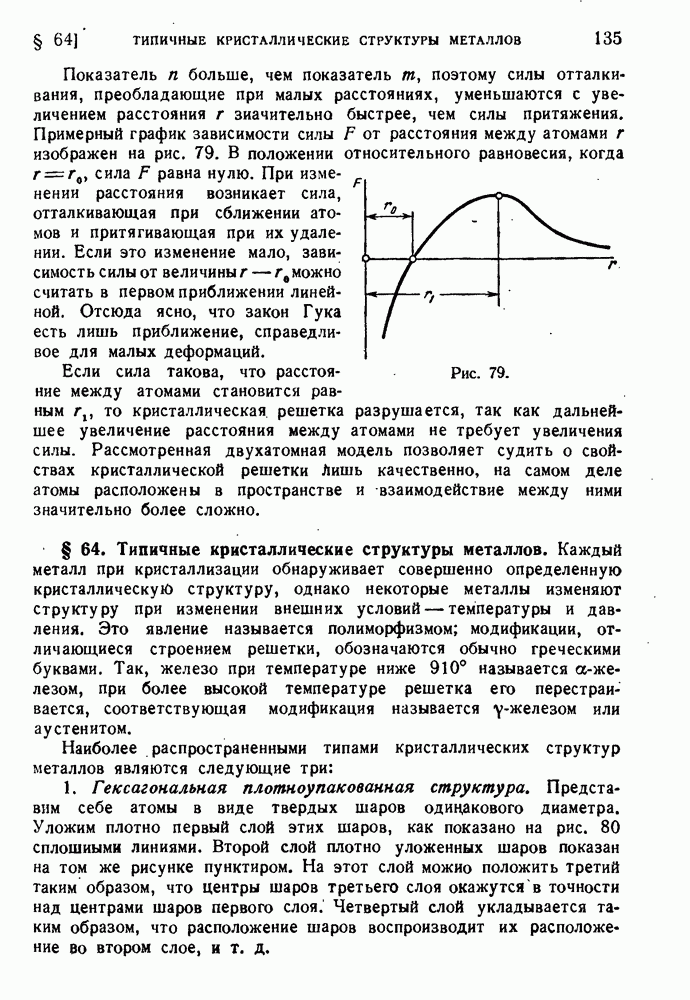
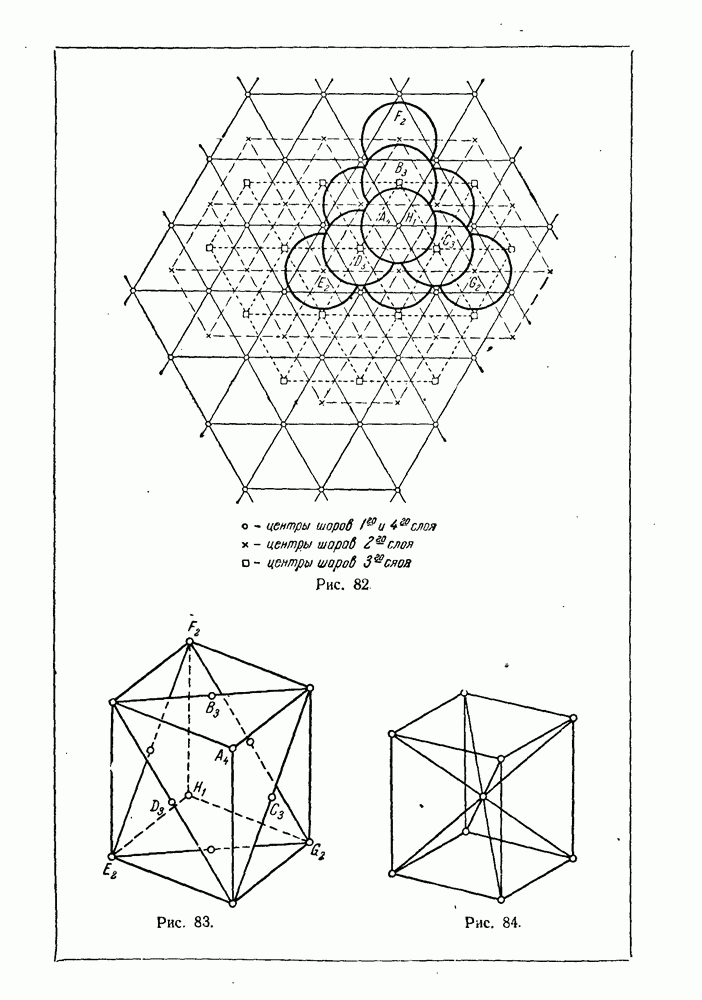
- § 64. Типичные кристаллические структуры металлов.
- § 65. Пластическая деформация монокристаллов.
- § 66. Прочность кристаллов и сопротивление пластическому деформированию.
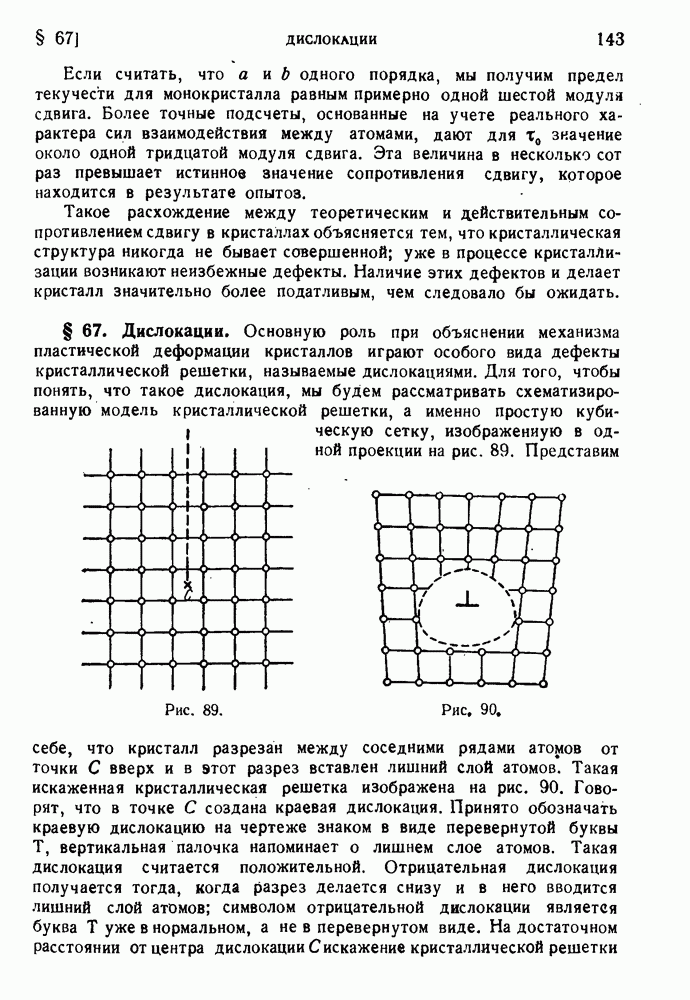
- § 67. Дислокации.
- § 68. Движение и равновесие дислокаций.
- § 69. Источники дислокаций.
- § 70. Границы блоков.
- § 71. Деформация поликристаллических металлов и сплавов.
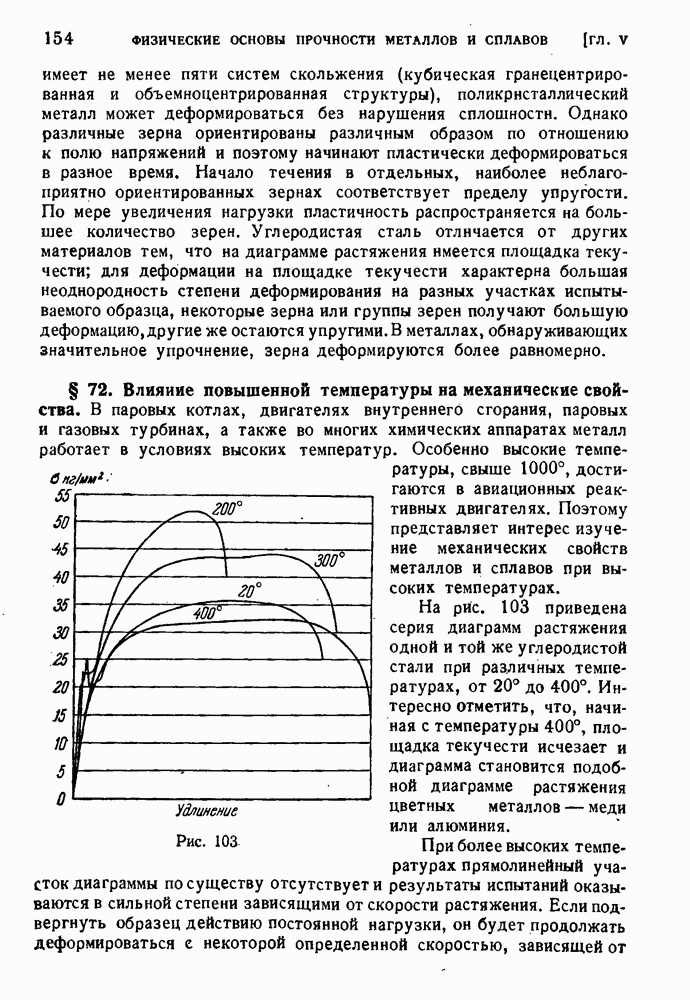
- § 72. Влияние повышенной температуры на механические свойства.
- § 73. Влияние скорости испытания.
- § 74. Испытании на твердость.
- ГЛАВА VI. ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ
- § 75. Основные принципы построения теории пластичности.
- § 76. Ассоциированный закон течения.
- § 77. Течение при условии пластичности Сен-Венана и Мизеса.
- § 78. Закон упрочнения.
- § 79. Деформационная теория пластичности.
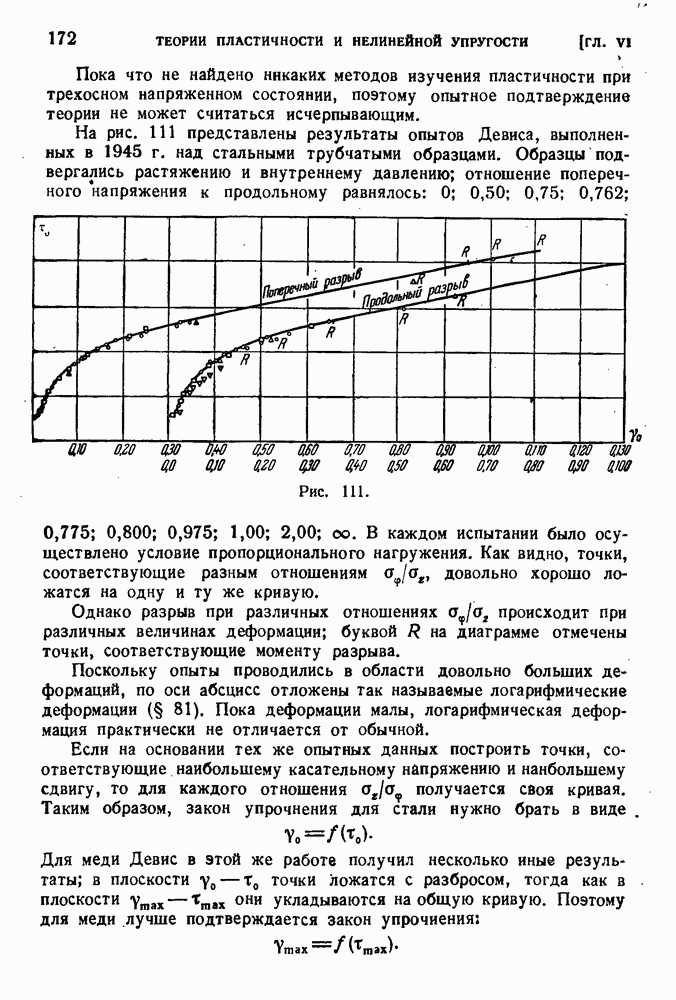
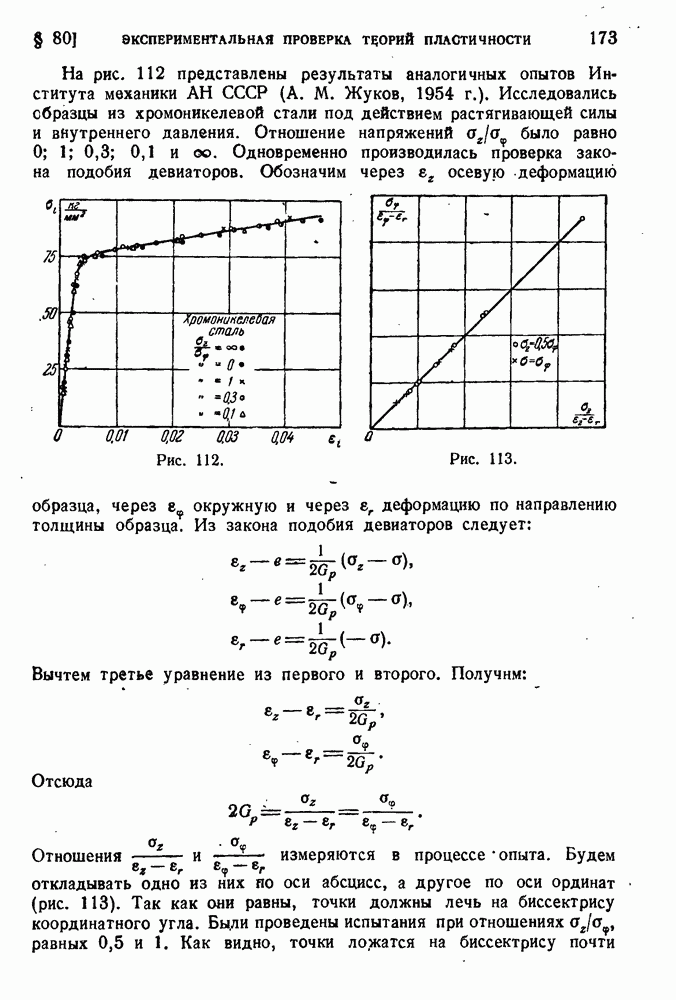
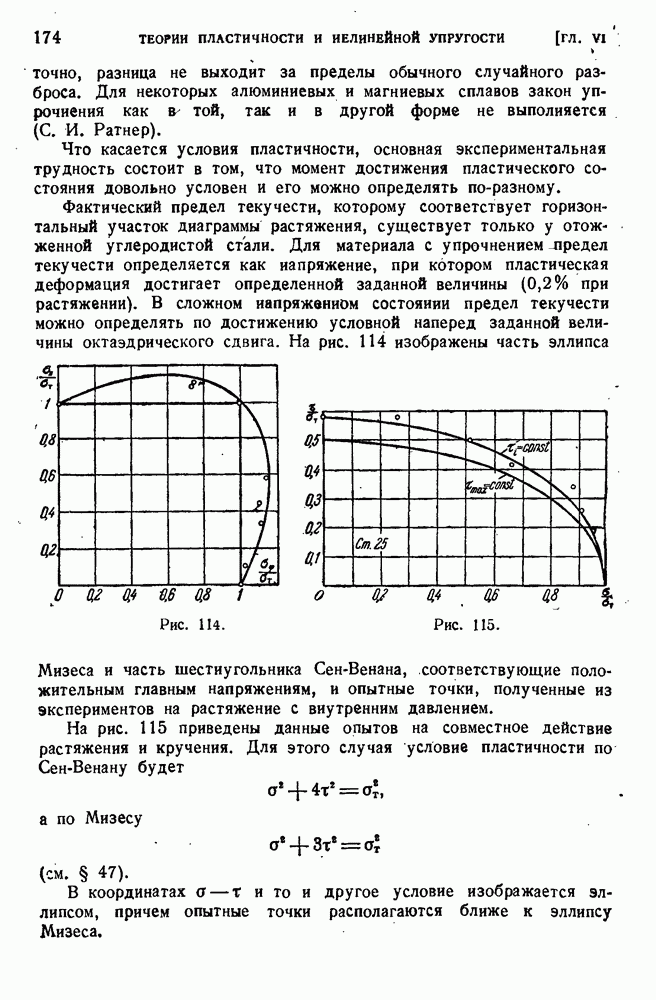
- § 80. Экспериментальная проверка теорий пластичности.
- § 81. Конечная деформация.
- § 82. Нелинейно упругое тело.
- § 83. Высокоэластические деформации.
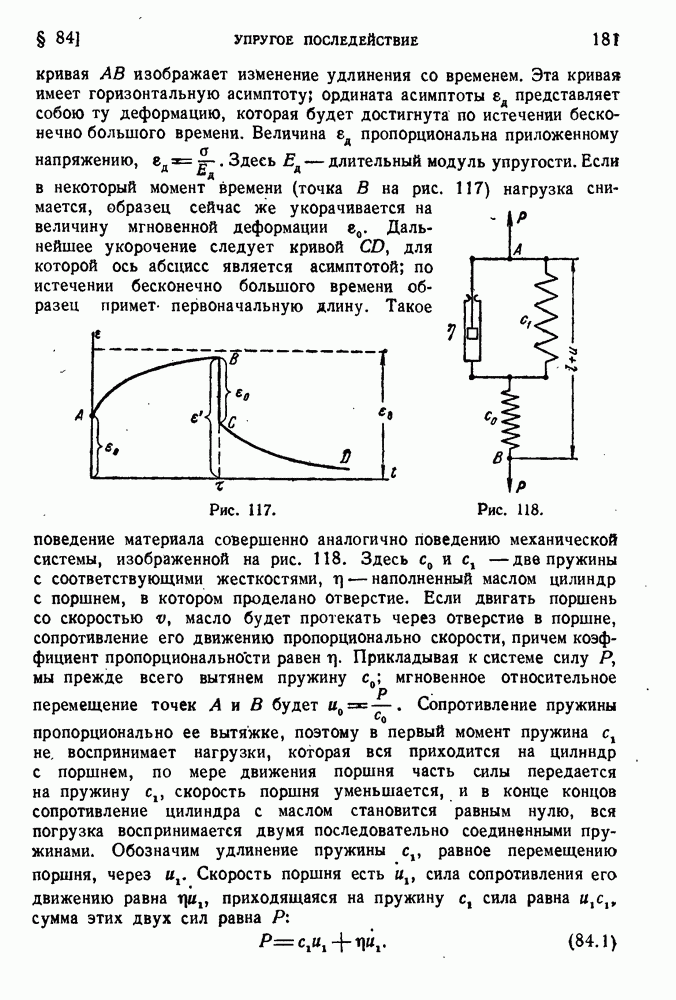
- § 84. Упругое последействие.
- § 85. Некоторые свойства вязко-упругого тела.
- § 86. Принцип суммирования Больцмана—Вольтерра.
- ГЛАВА VII. КРУЧЕНИЕ
- § 87. Кручение стержней круглого сечеиия.
- § 88. Упруго-пластическое кручение стержня круглого сечения.
- § 89. Гипотеза жесткого контура.
- § 90. Кручение тонкостенных стержней замкнутого профиля.
- § 91. Кручение тонкостенных стержней открытого профиля.
- § 92. Кручение упругих стержией сплошного профиля.
- § 93. Опытное исследование кручения.
- § 94. Предельное состояние закрученного стержня из идеально-пластического материала.
- ГЛАВА VIII. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- § 96. Общие теоремы о моментах.
- § 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей.
- § 98. Вычисление моментов инерции.
- § 99. Преобразование моментов инерции при повороте осей.
- § 100. Главные оси и главные моменты инерции.
- ГЛАВА IX. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
- § 101. Действие поперечных сил на балку.
- § 102. Гипотеза плоских сечений и принцип Сен-Венана.
- § 103. Нормальные напряжения при изгибе.
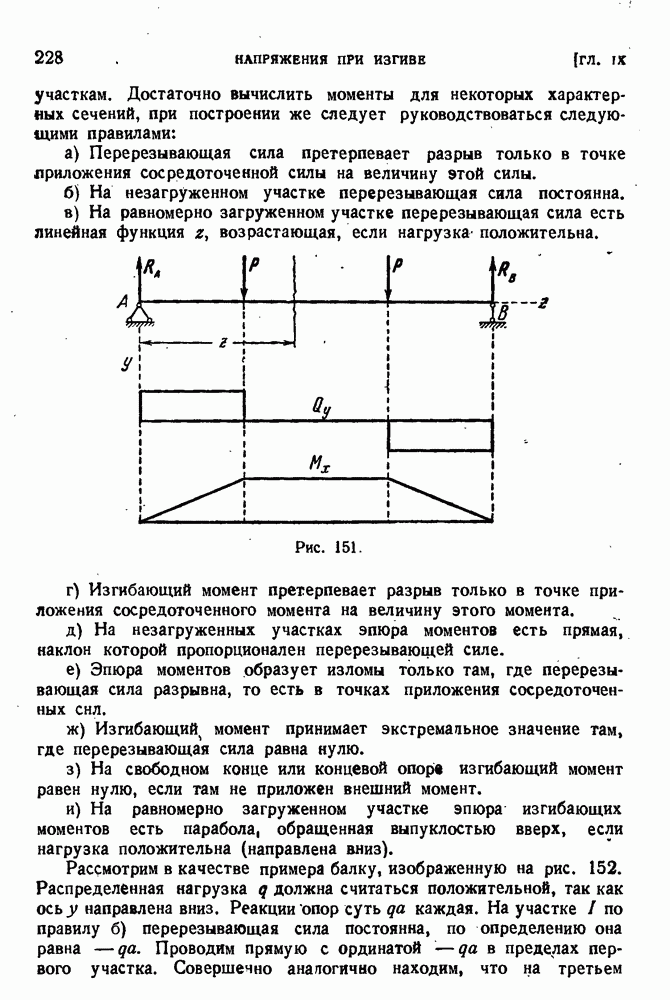
- § 104. Изгибающие моменты и перерезывающие силы.
- § 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры.
- § 106. Расчет на прочность при изгибе по допускаемым напряжениям.
- § 107. Упруго-пластический изгиб.
- § 108. Несущая способность стержня при изгибе.
- § 109. Принцип Сен-Венана.
- § 110. Внецентренное растяжение — сжатие.
- § 111. Ядро сечения.
- § 112. Несущая способность внецентренно сжатого стержня.
- § 113. Расчет составных балок.
- § 114. Изгиб кривого бруса.
- § 115. Нахождение нейтральной осн в кривом стержне.
- ГЛАВА X. ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- § 116. Дифференциальное уравнение изогнутой оси.
- § 117. Пределы применимости приближенной теории.
- § 118. Интегрирование уравнения изгиба.
- § 119. Примеры определения прогибов.
- § 120. Простейшие статически неопределенные задачи.
- § 121. Расчет статически неопределимых балок по способу допускаемых нагрузок.
- § 122. Изгиб стержней переменного сечения.
- § 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами.
- § 124. Продольно-поперечный изгиб.
- § 125. Изгиб балки на упругом основании.
- ГЛАВА XI. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
- § 126. Нормальные и касательные напряжения при изгибе.
- § 127. Касательные напряжении при изгибе в плоскости симметрии.
- § 128. Центр изгиба.
- § 129. Дополнительные напряжения при кручении.
- § 130. Закон секториальных площадей.
- § 131. Уравнение стесненного кручения.
- § 132. Вычисление секториальных характеристик.
- § 133. Стержень, нагруженный бимоментом.
- § 134. Некоторые примеры стесненного кручения.
- ГЛАВА XII. УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ
- § 135. Постановка вопроса об устойчивости.
- § 136. Устойчивость сжатого упругого стержня.
- § 137. Эластика Эйлера.
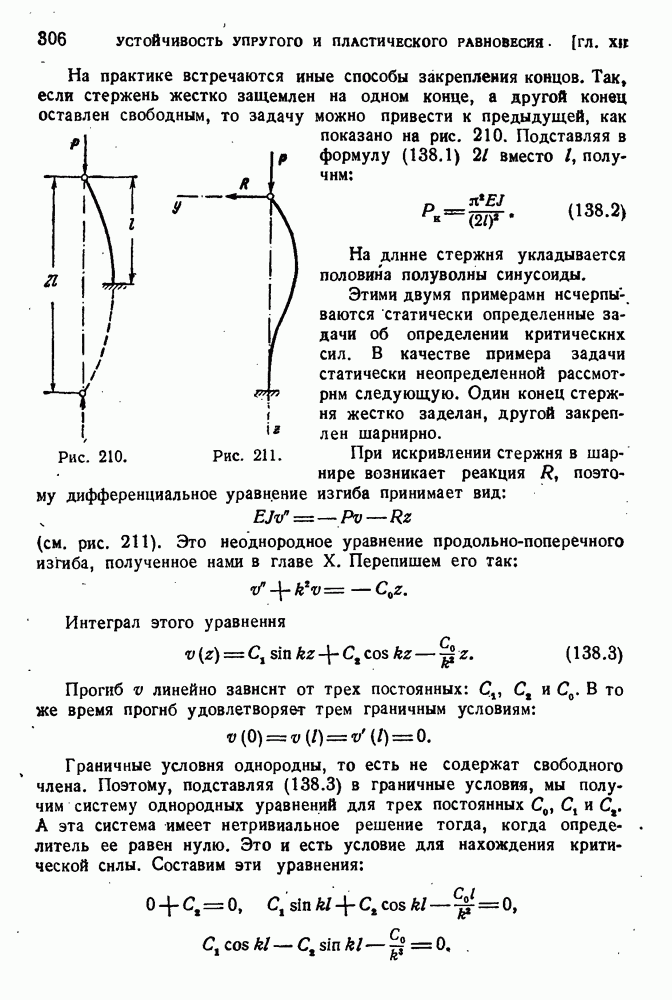
- § 138. Критические силы при иных видах закрепления стержня.
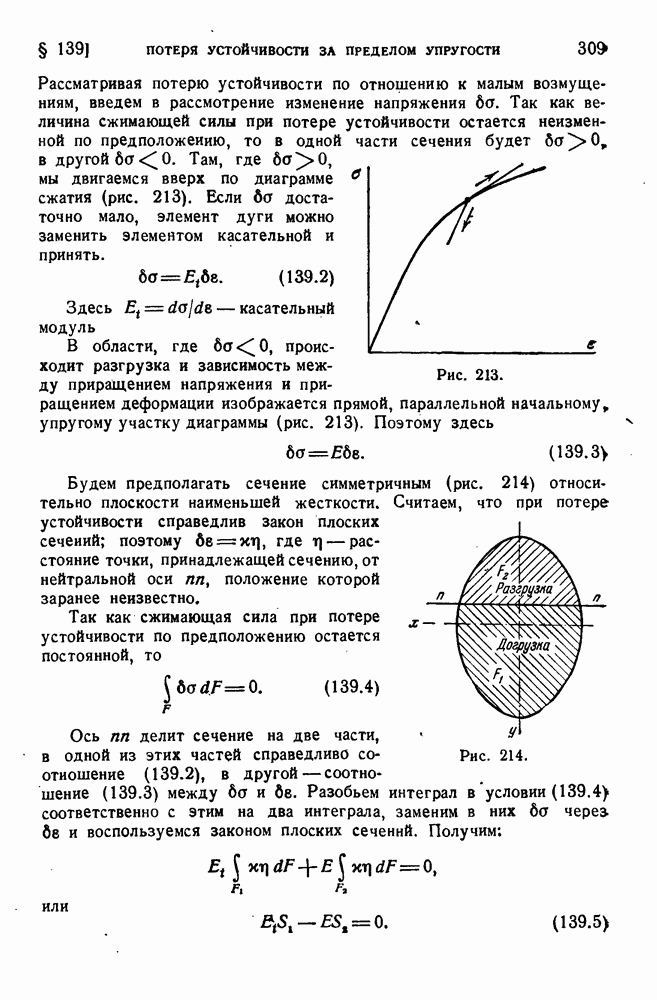
- § 139. Потеря устойчивости за пределом упругости.
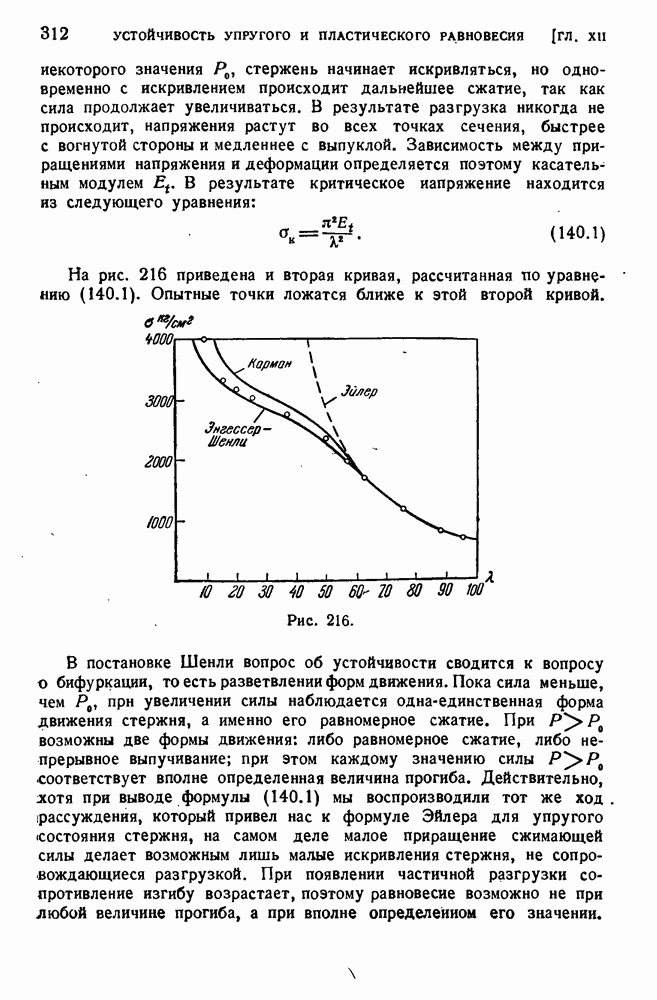
- § 140. Потеря устойчивости за пределом упругости (продолжение).
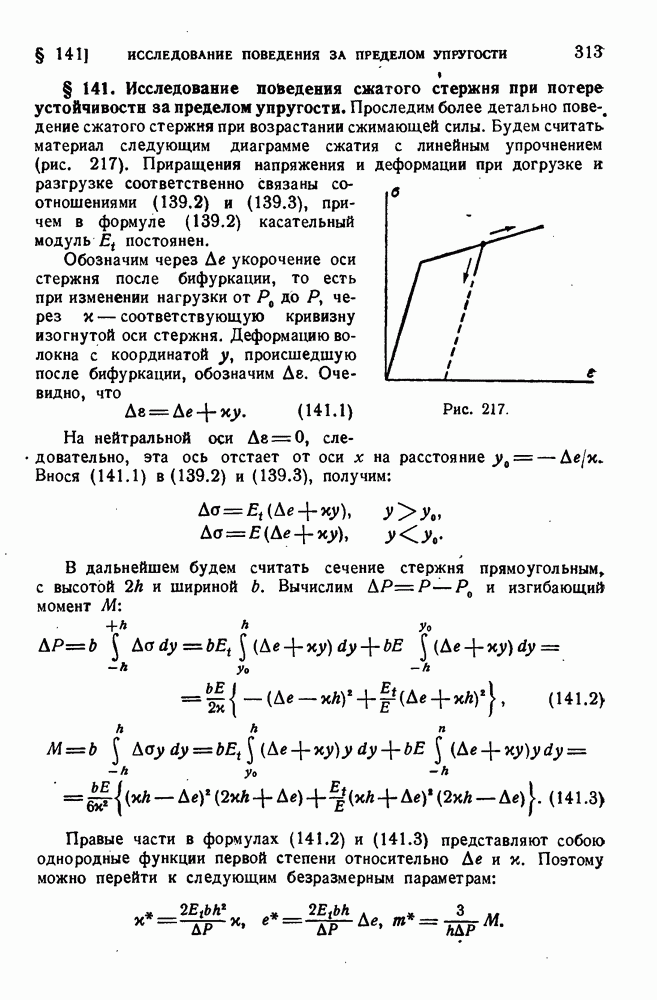
- § 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости.
- § 142. Расчет на устойчивость по эмпирическим формулам.
- ГЛАВА XIII. ТРУБЫ И ДИСКИ
- § 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности.
- § 144. Упругое состояние трубы. Формулы Ламе.
- § 145. Пластическое состояние трубы.
- § 146. Вращающиеся диски. Упругое состояние.
- § 147. Диск равного сопротивления.
- § 148. Предельное равновесие вращающегося диска.
- ГЛАВА XIV. ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 149. Обобщенные силы и обобщенные перемещения.
- § 150. Начало возможных перемещений для деформируемого тела.
- § 151. Теоремы Лагранжа и Кастильяно.
- § 152. Лииейиые упругие системы.
- § 153. Теорема о взаимности работ.
- § 154. Теорема Кастильяно для линейных упругих систем.
- § 155. Расчет винтовых пружин.
- § 156. Теорема о минимуме энергии.
- § 157. Интеграл перемещений.
- § 158. Графоаналитический способ вычислений интеграла перемещений.
- § 159. Расчет статически неопределимых систем по методу сил.
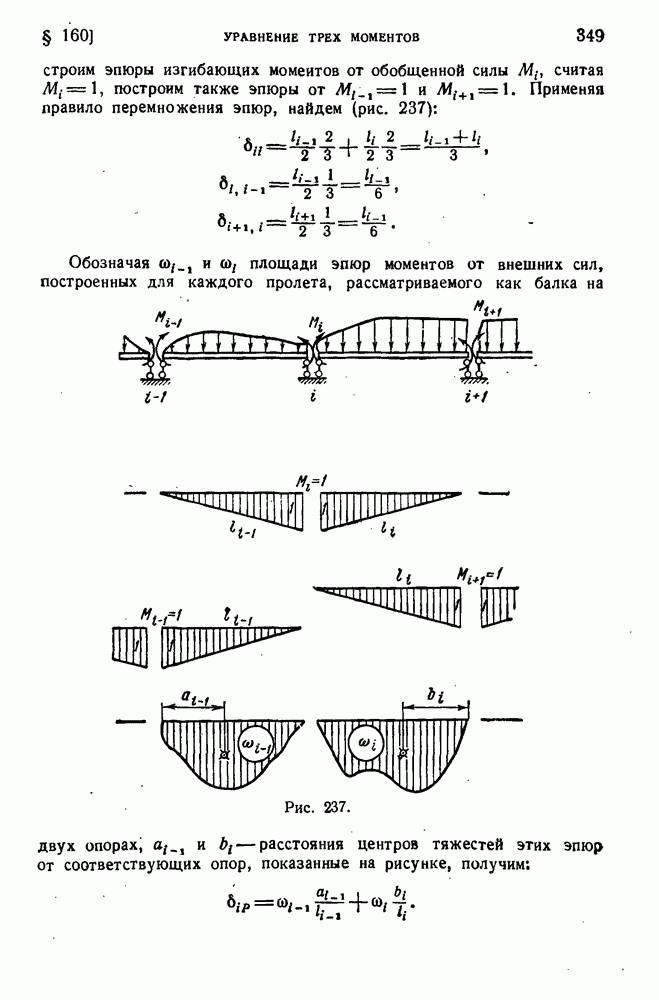
- § 160. Уравнение трех моментов.
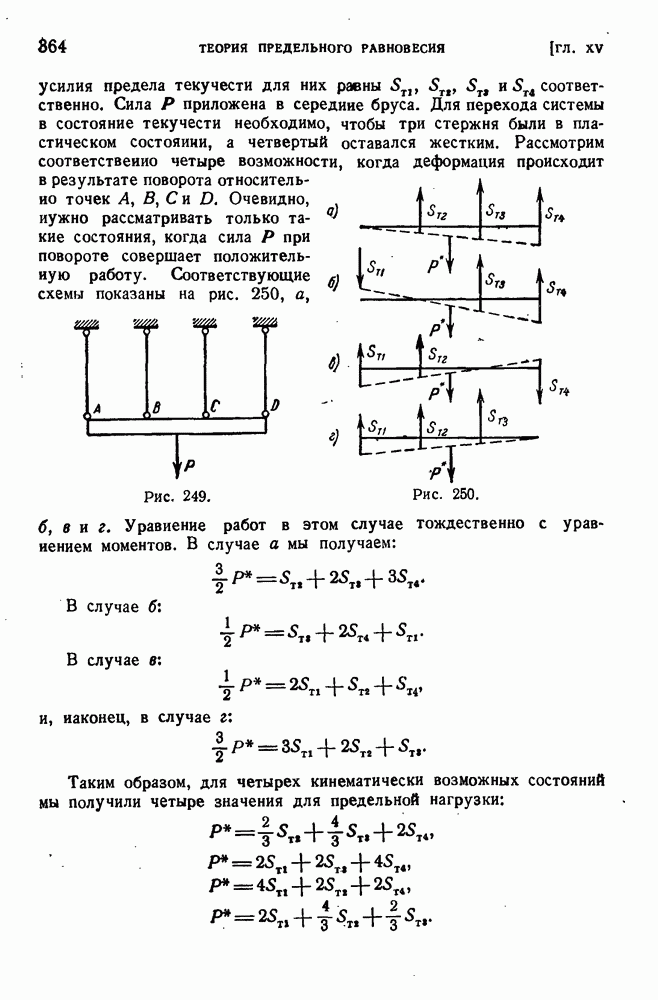
- ГЛАВА XV. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
- § 161. Жестко-пластическое тело.
- § 162. Поверхности нагружения.
- § 163. Истинное и допустимые состояния элемента.
- § 164. Статический метод определения предельной нагрузки.
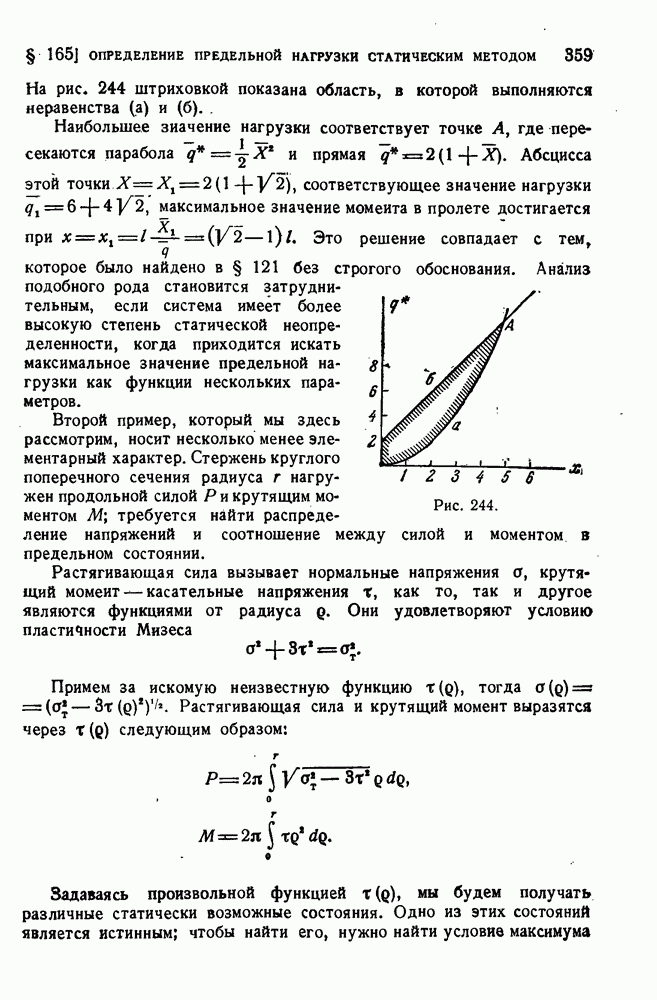
- § 165. Примеры определения предельной нагрузки статическим методом.
- § 166. Кинематически возможные состояния.
- § 167. Кинематический метод определения предельной нагрузки.
- § 168. Примеры определения предельной нагрузки кинематическим методом.
- § 169. Предельное равновесие пластинок.
- ГЛАВА XVI. ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 170. Колебания систем с конечным числом степеней свободы.
- § 171. Собственные частоты и главные формы колебаний.
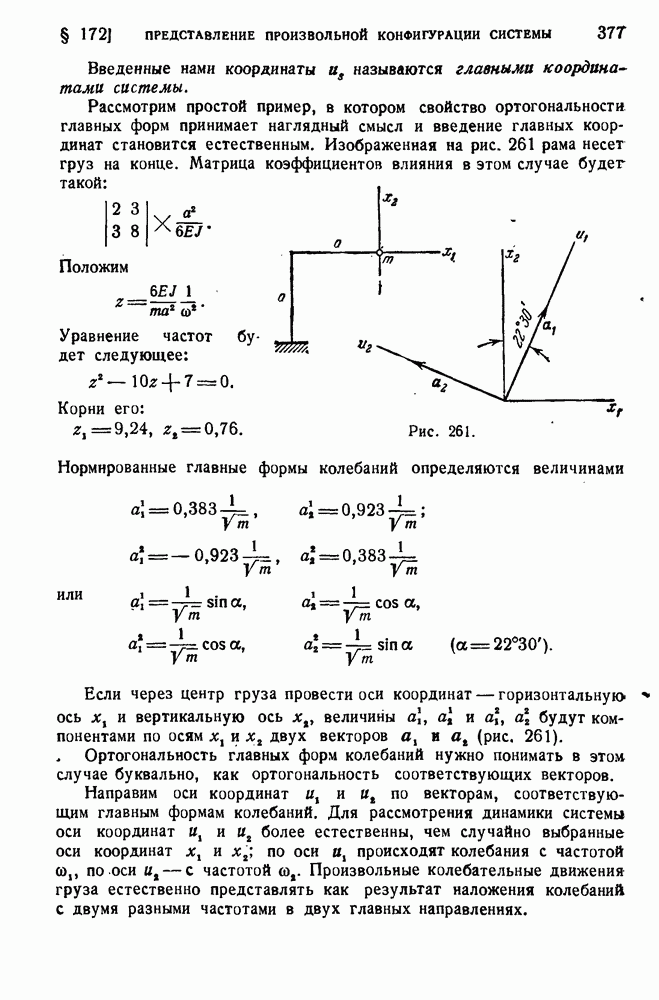
- § 172. Представление произвольной конфигурации системы через главные формы. Главные координаты.
- § 173. Формула и способ Релея.
- § 174. Нижние оценки для частоты основного тона.
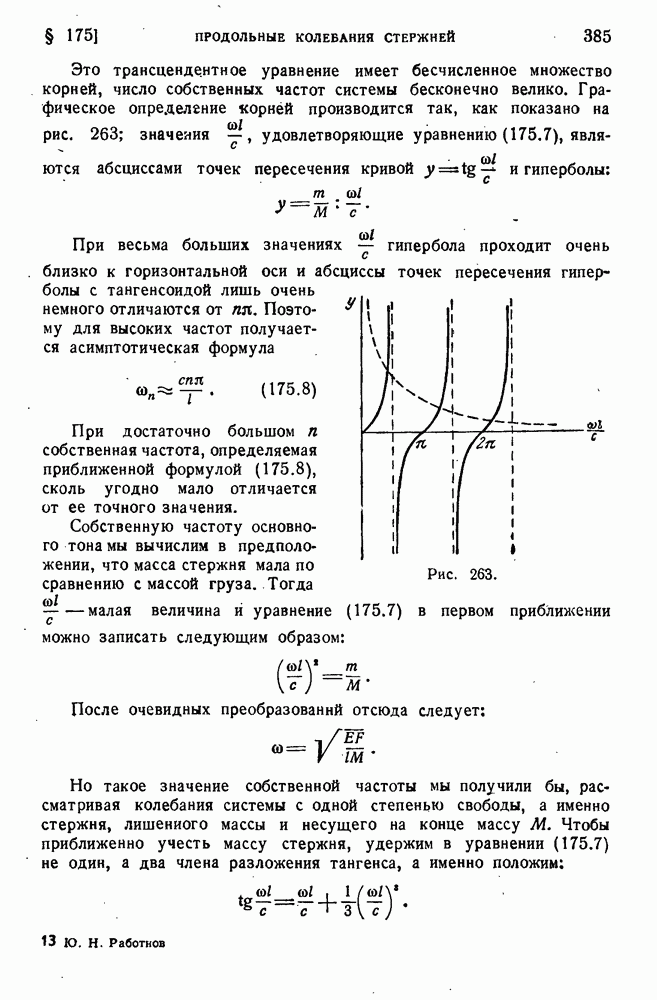
- § 175. Продольные колебания стержней.
- § 176. Поперечные колебания стержней.
- § 177. Колебания балок постоянного сечения.
- § 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня.
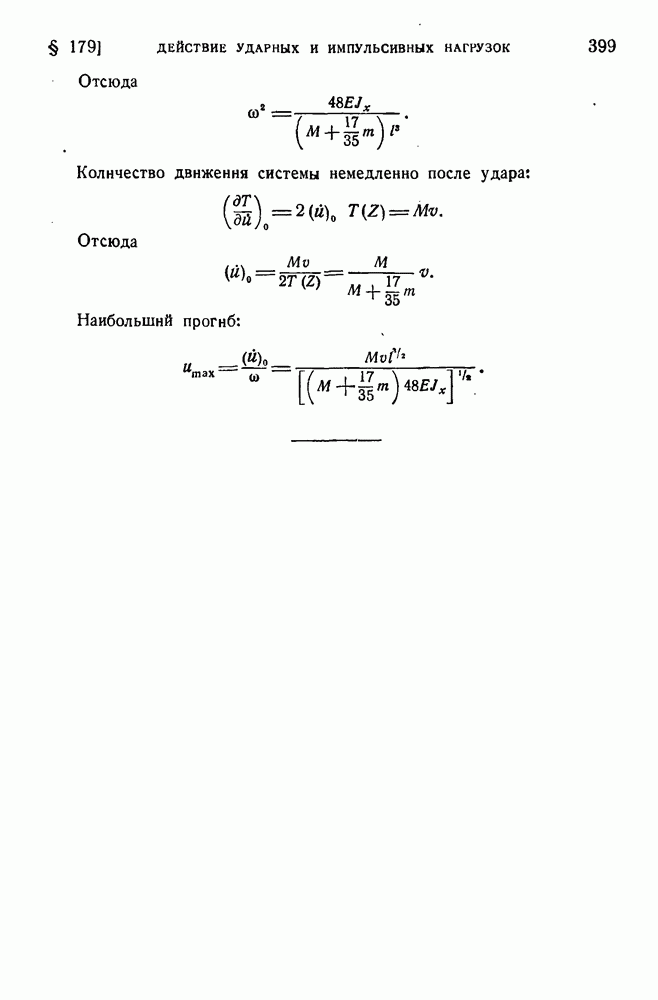
- § 179. Действие ударных и импульсивных нагрузок на упругие системы.
- ГЛАВА XVII. ТЕОРИИ ПРОЧНОСТИ
- § 180. Постановка вопроса о прочности.
- § 181. Хрупкое и пластическое разрушение.
- § 182. Теория прочности Мора.
- § 183. Механизм хрупкого разрушения.
- § 184. Прочность при низких температурах.
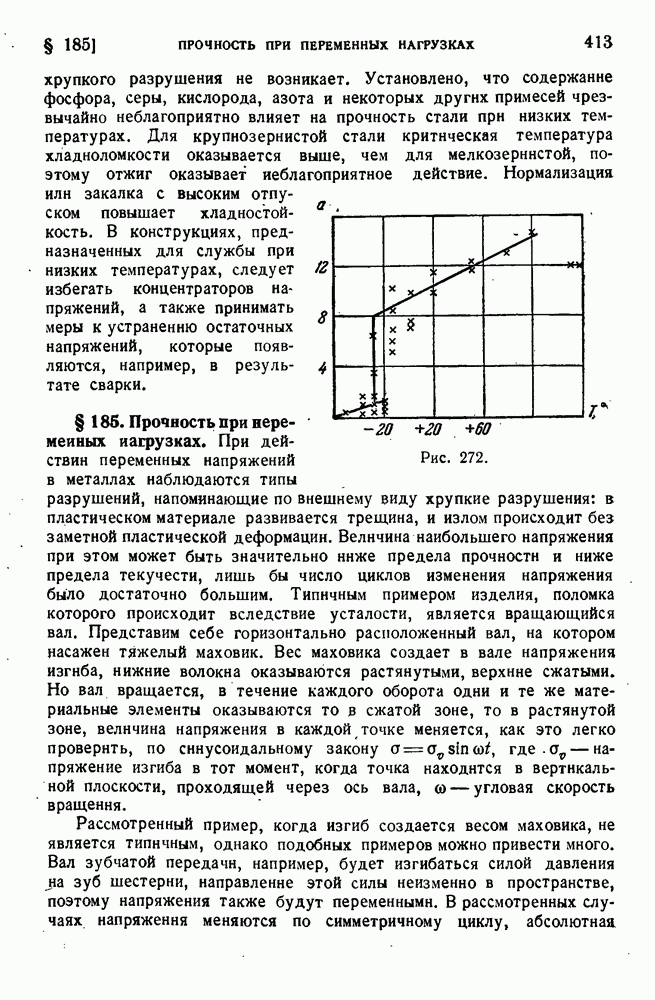
- § 185. Прочность при переменных нагрузках.
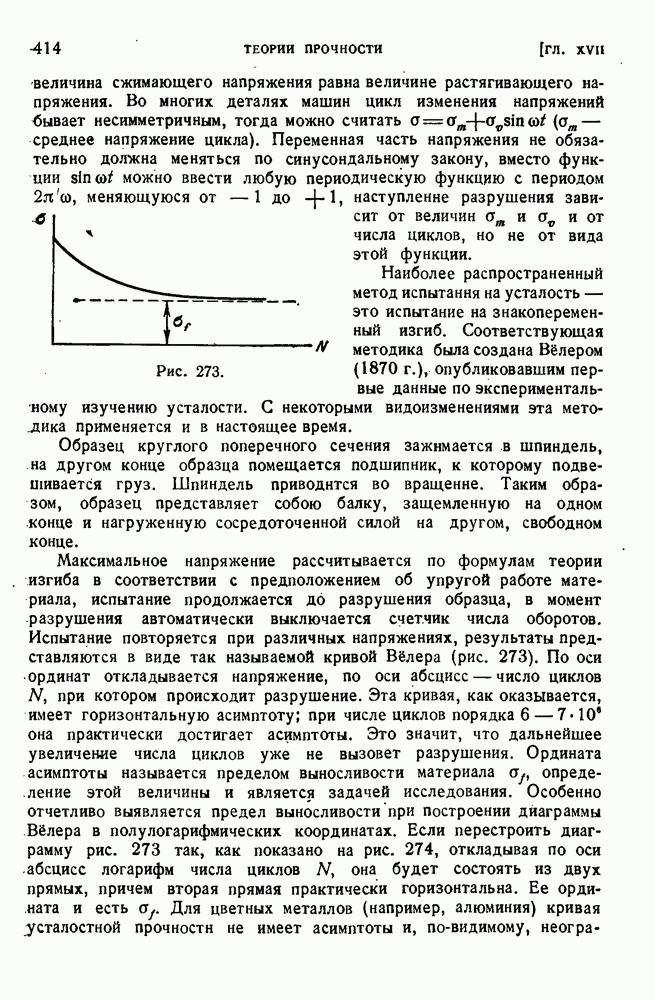
- § 186. Природа усталостного разрушения.
- § 187. Критерии прочности при переменных нагрузках.
- § 188. Влияние концентрации напряжений на усталостную прочность.
- § 189. Усталостная прочность при сложном напряженном состоянии.
- ГЛАВА XVIII. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
- § 190. Ползучесть металлов.
- § 191. Процесс ползучести.
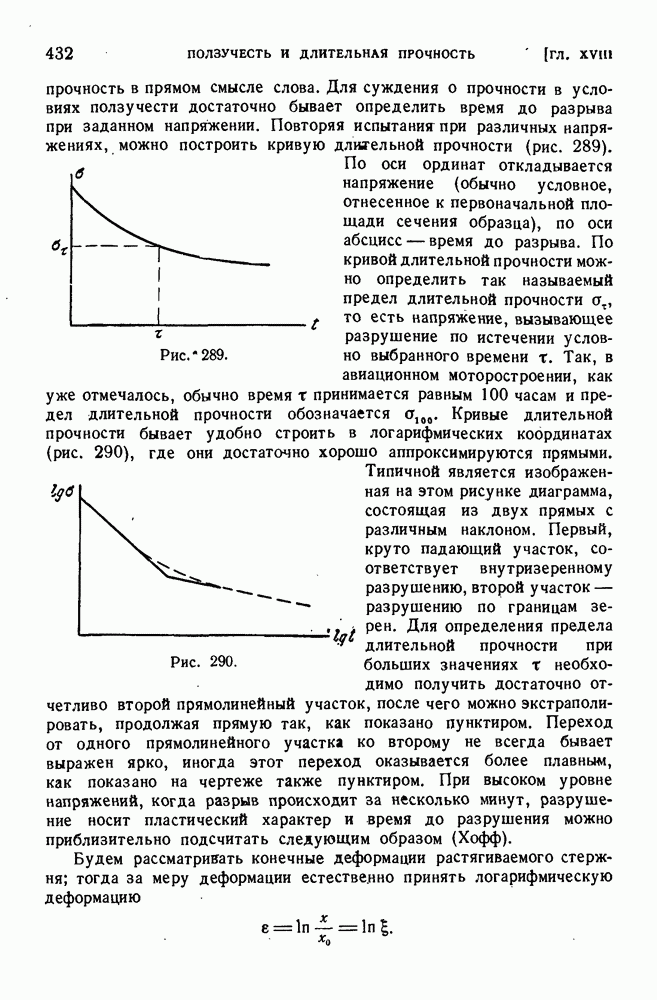
- § 192. Длительное разрушение.
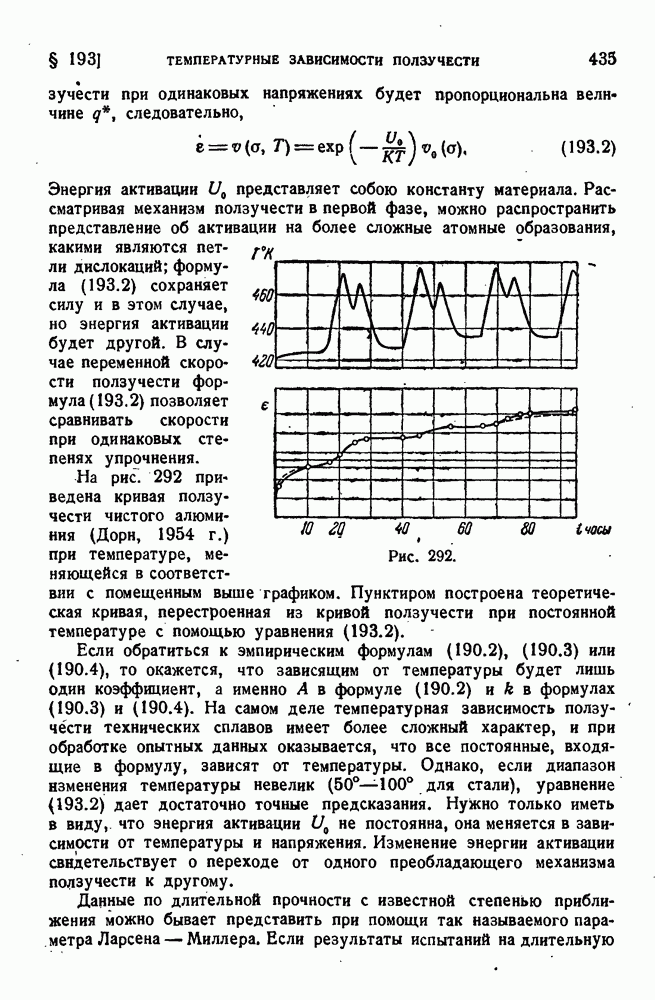
- § 193. Температурные зависимости ползучести и длительной прочности.
- § 194. Феноменологические теории одномерной ползучести.
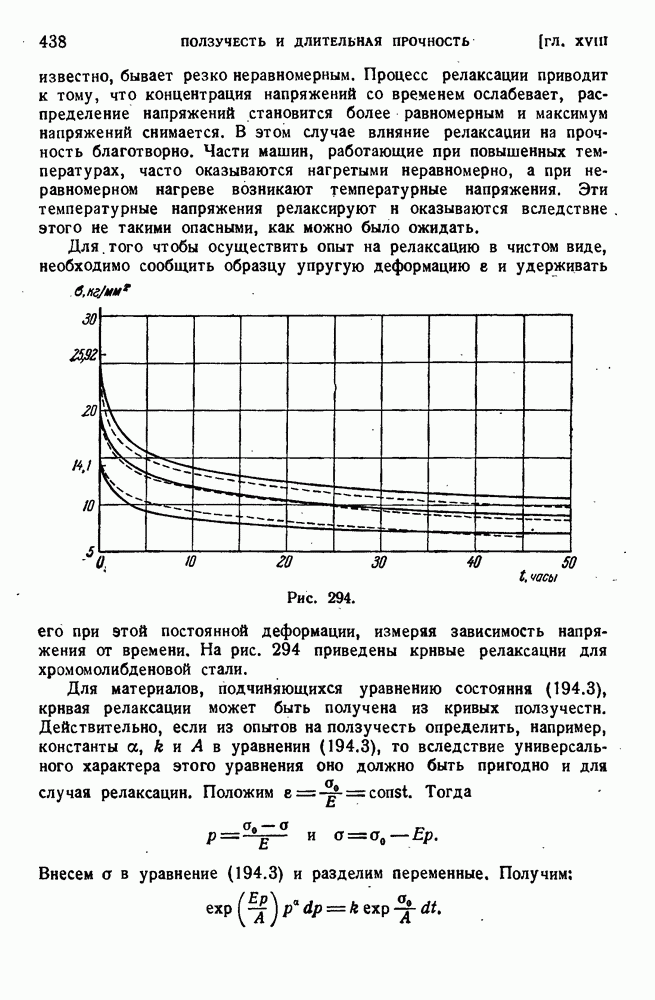
- § 195. Релаксация напряжений.
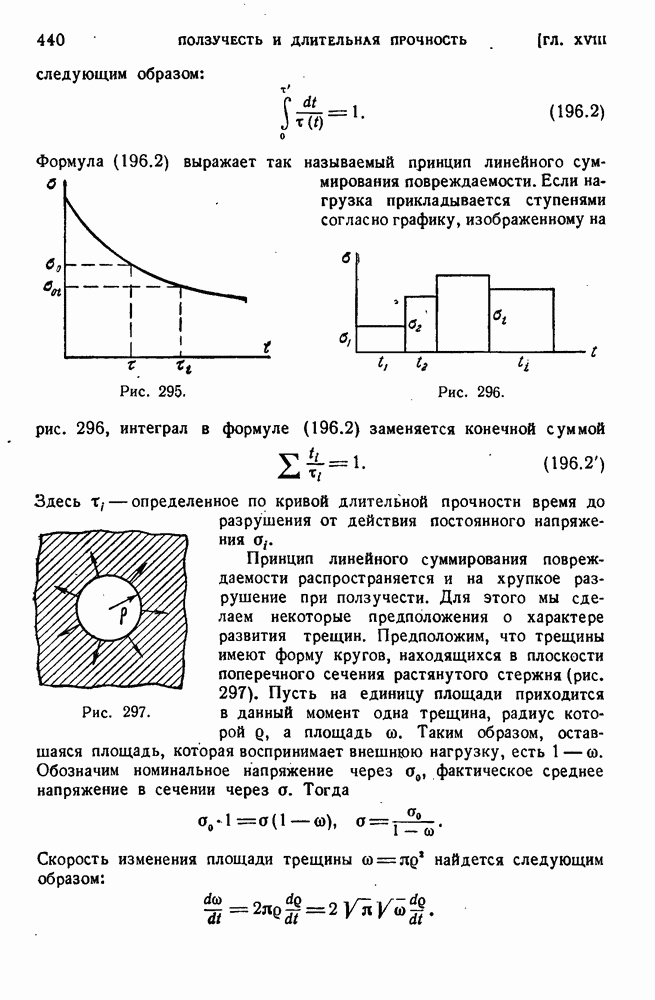
- § 196. Длительная прочность при переменных нагрузках.
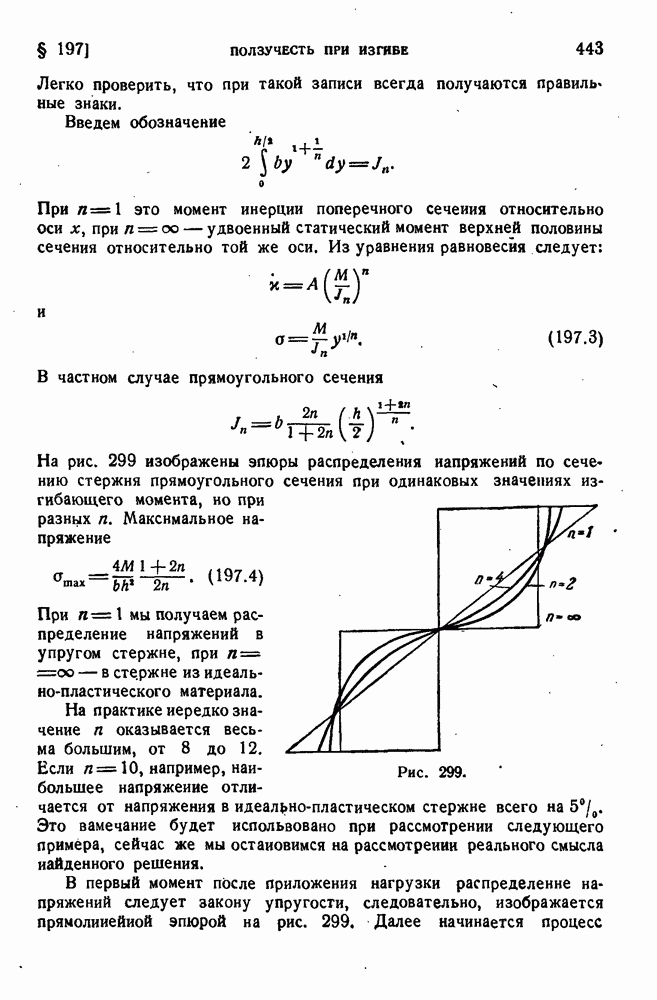
- § 197. Ползучесть при изгибе.
- § 198. Критическое время сжатого стержня.
- § 199. Ползучесть и длительная прочность при сложном напряженном состоянии.
- § 200. Вращающиеся диски в условиях ползучести.
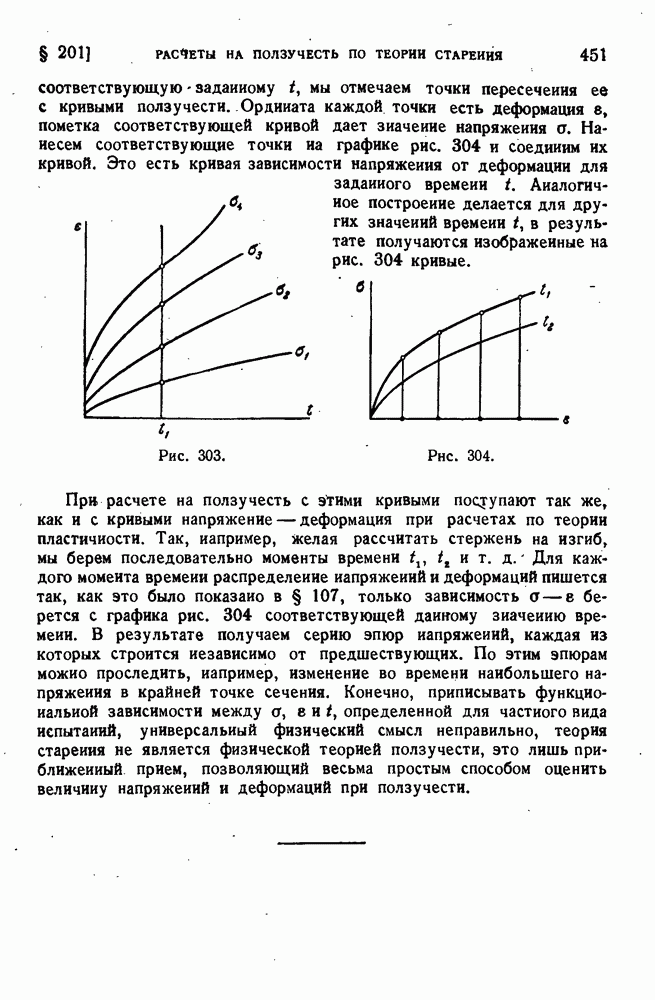
- § 201. Расчеты на ползучесть по теории старении.