| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
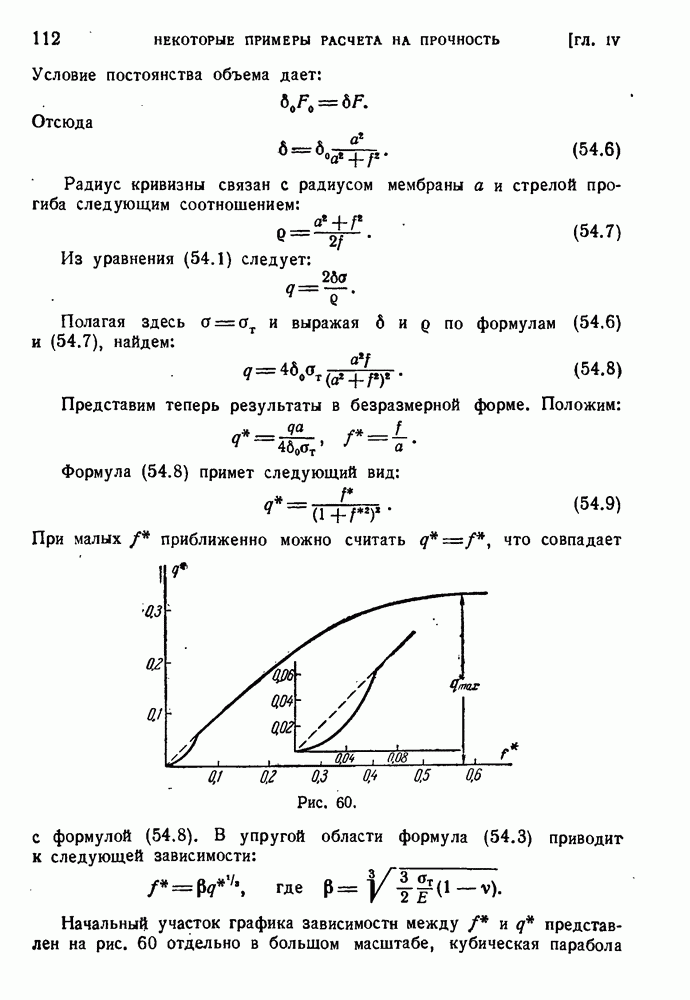
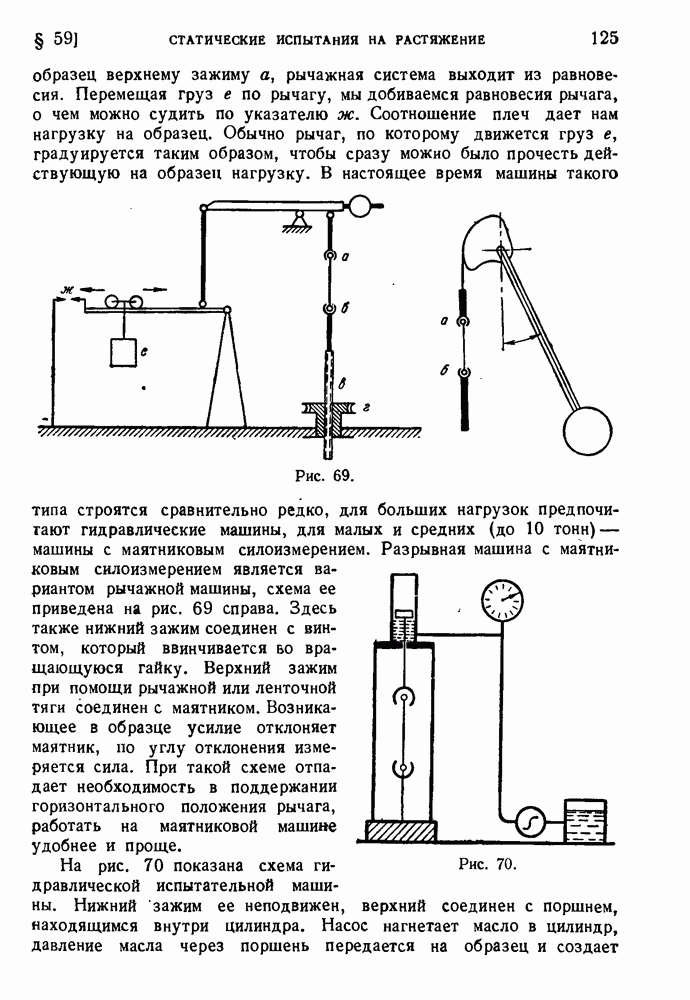
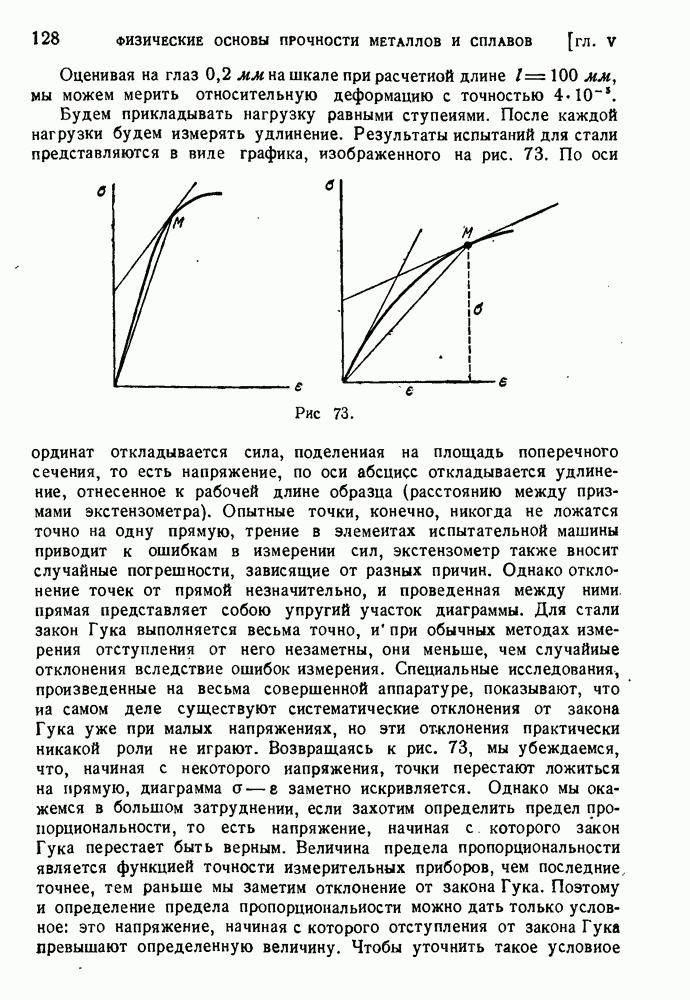
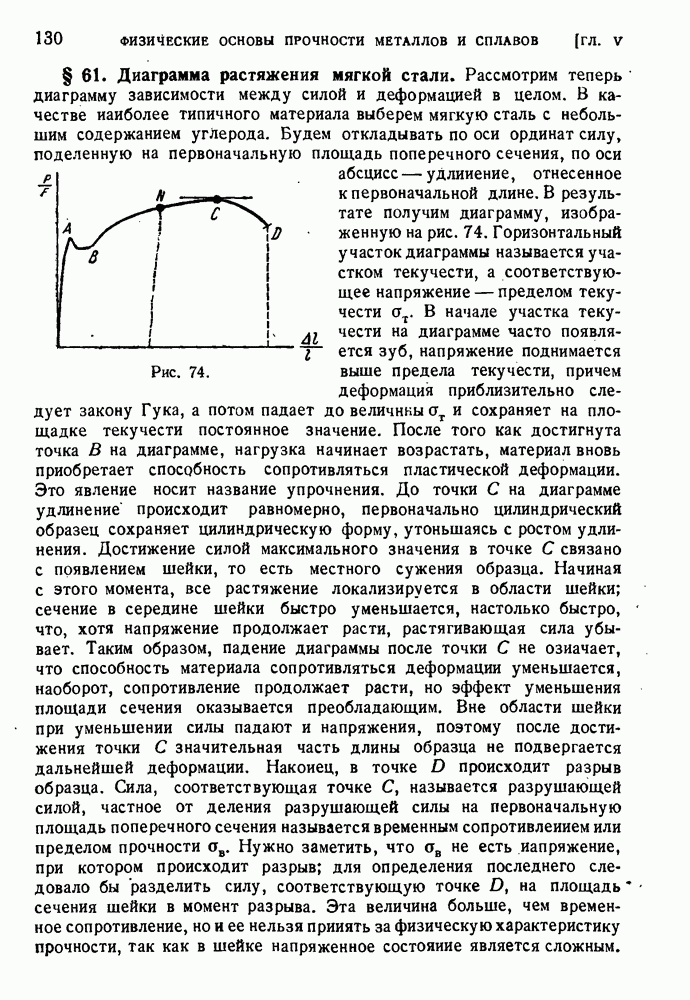
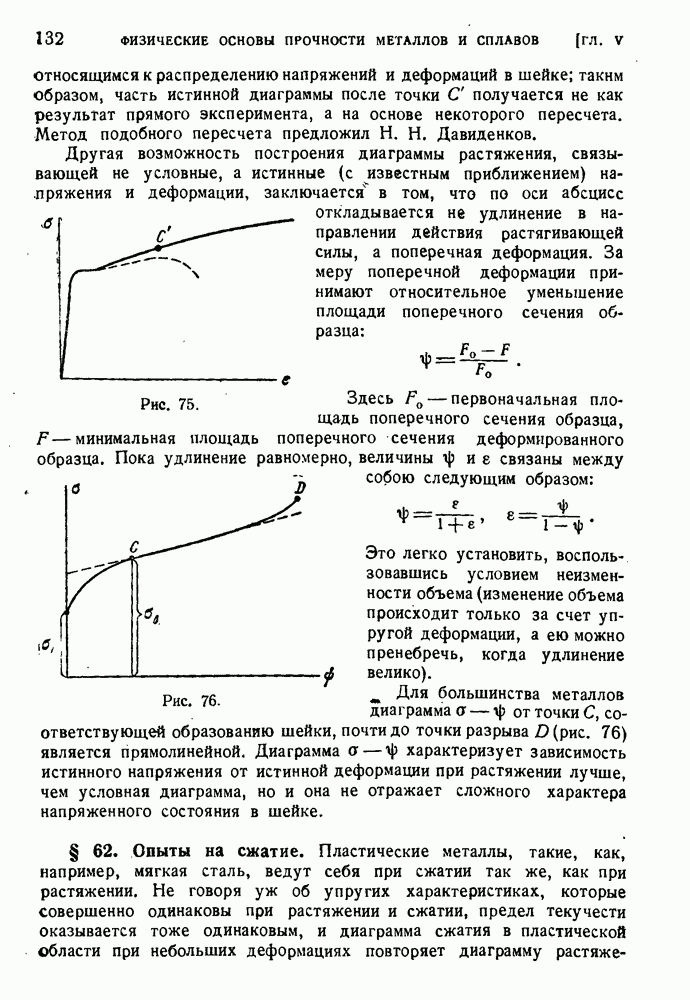
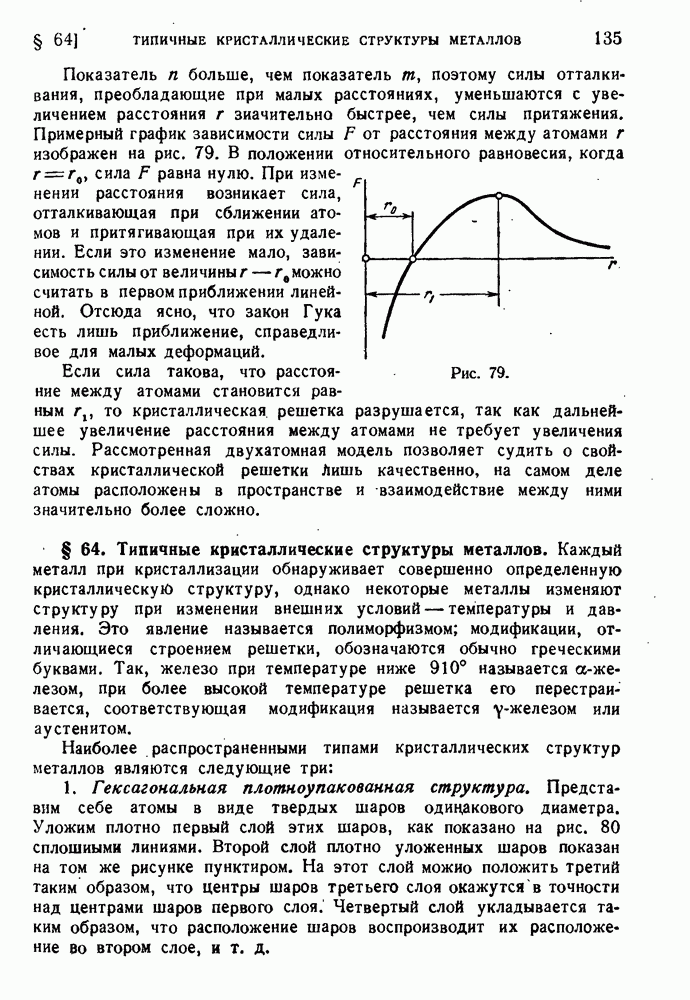
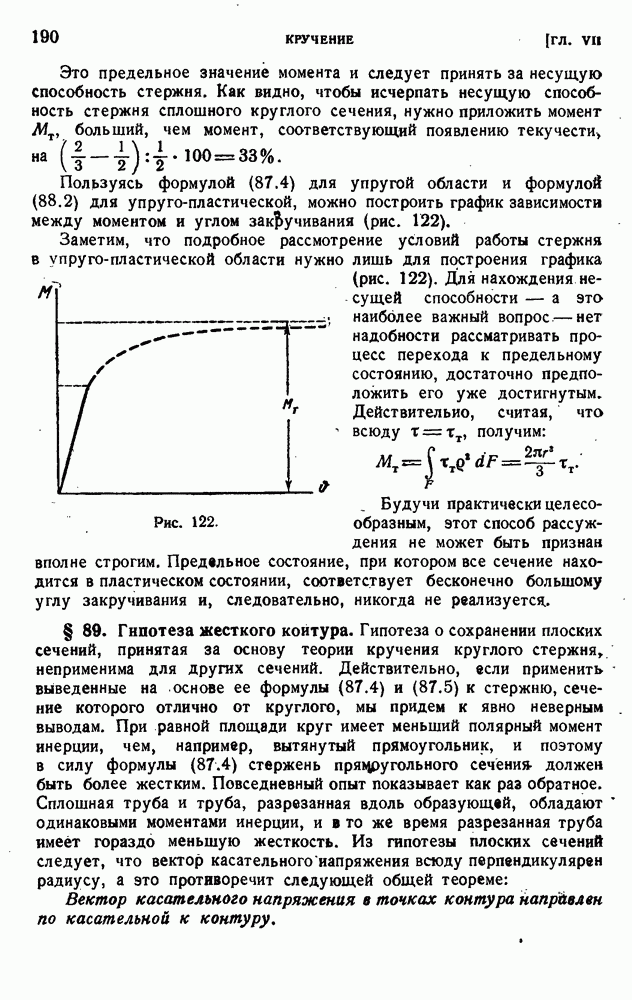
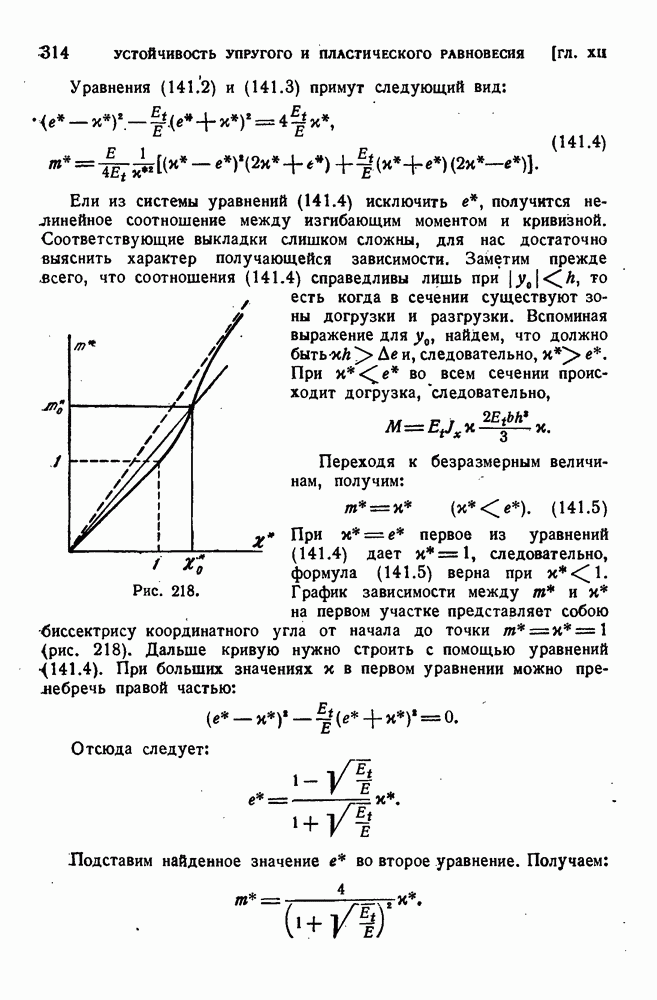
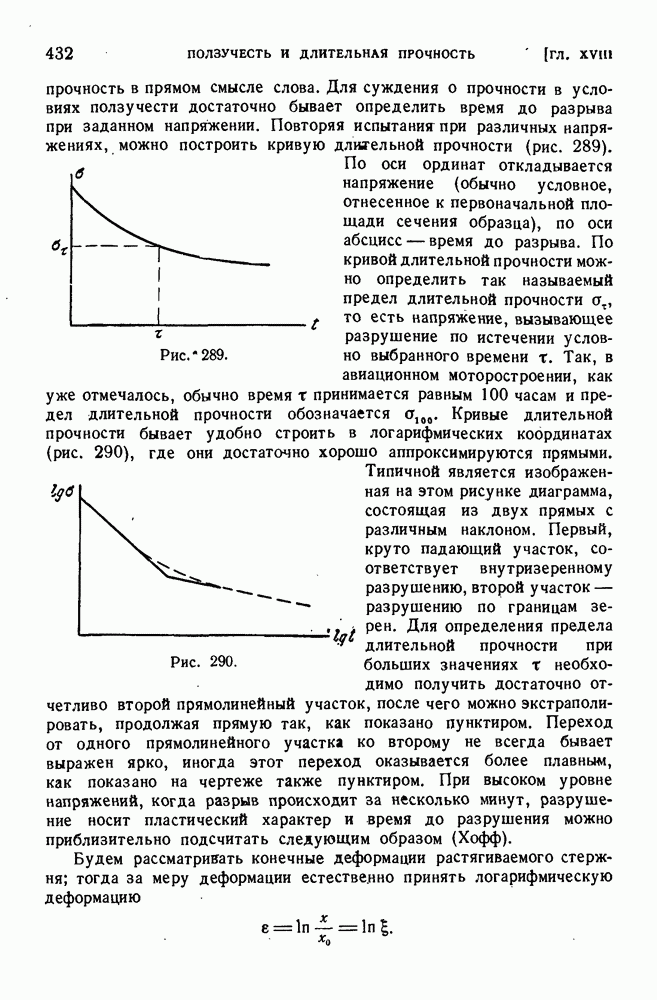
§ 80. Экспериментальная проверка теорий пластичности.
Начиная с 1928 г., когда было опубликовано фундаментальное исследование Лоде, посвященное экспериментальной проверке теории пластичности, этому вопросу было посвящено большое количество работ.
Подобные исследования ведутся у нас и за рубежом и в настоящее время, однако центральная проблема сейчас состоит в том, чтобы выяснить закономерности пластической деформации при непропорциональном нагружении. Универсальной теории пластичности, дающей достаточно надежные результаты при произвольном нагружении, пока еще не существует, вопрос находится в стадии накопления опытного материала и проверки разного рода гипотез, зачастую противоречащих друг другу. Вопрос о законах пластичности при пропорциональном нагружении для стали в настоящее время может считаться решенным, и только на этом вопросе мы здесь остановимся.
Единственный надежный способ создания в образце однородного напряженного состояния — это испытание тонкостенных трубок на совместное действие осевого растяжения, внутреннего давления и кручения.
Обозначим средний радиус трубки через R, толщину стенкн через  и определим напряжения, возникающие от растягивающей силы Р, внутреннего давления q и крутящего момента М.
и определим напряжения, возникающие от растягивающей силы Р, внутреннего давления q и крутящего момента М.
1. Растягивающая сила Р. Площадь сечения трубкн приближенно равна  . Направив ось z по образующей, найдем:
. Направив ось z по образующей, найдем:

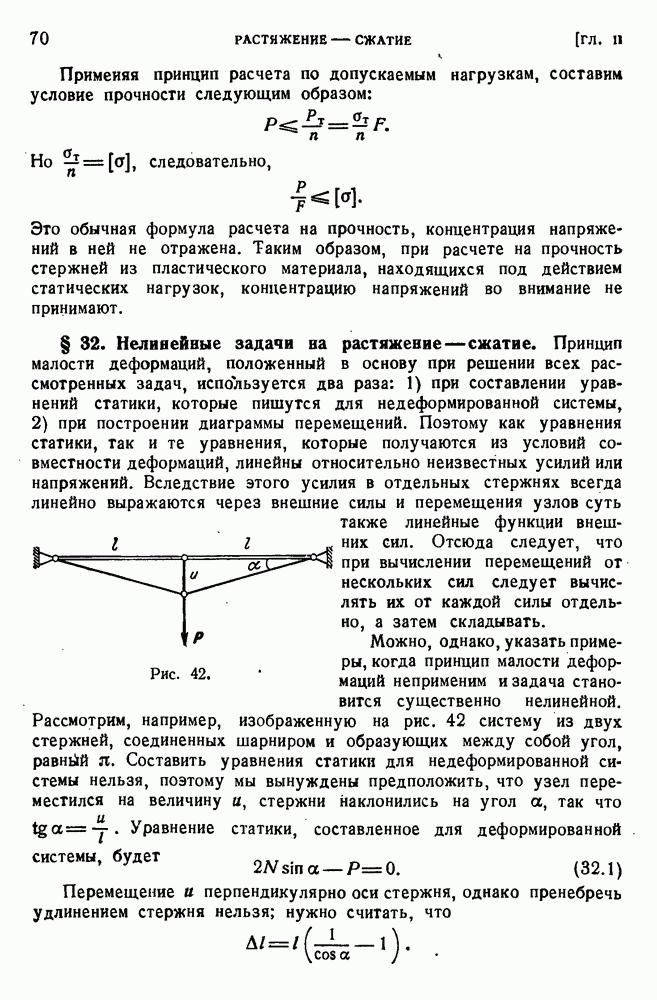
2. Внутреннее давление q. Внутреннее давление растягивает трубку в поперечном направлении, в продольных сечениях трубки возникают растягивающие напряжения, которые мы обозначим о. Для определения этих напряжений обратимся к рис. 110, где изображена иоловина трубки, рассеченной диаметральной плоскостью. Если длина трубки равна  то площадь сечения есть
то площадь сечения есть  . На этой площади действует растягивающее напряжение о, направленное параллельно оси у вниз.
. На этой площади действует растягивающее напряжение о, направленное параллельно оси у вниз.

Рис. 110.
Элементарная полоска  , выделенная вдоль образующей с угловой координатой
, выделенная вдоль образующей с угловой координатой  испытывает действие силы
испытывает действие силы

Проекция ее на вертикальную ось у равна

Составим уравнение равновесия, проектируя все силы на ось у. Получим:

Отсюда

3. Крутящий момент М. Предположим, что касательные напряжения распределены равномерно по сечению. Будем считать плечо их относительно оси трубки равным среднему радиусу трубки R. Приравняем момент внутренних сил в сечении внешнему моменту М. Получим:

Отсюда

Задавая по произволу Р, М и q, можно осуществить принципиально любое плоское напряженное состояние. Практически же, для того чтобы распределение напряжений по толщине было равномерным, нужно делать трубки достаточно тонкими ( ). Но при наличии сжимающих напряжений тонкая стенка теряет устойчивость, поэтому фактически удается обследовать область, в которой два главных напряжения положительны, а если одно из них отрицательно, то оно невелико по модулю по сравнению со вторым.
). Но при наличии сжимающих напряжений тонкая стенка теряет устойчивость, поэтому фактически удается обследовать область, в которой два главных напряжения положительны, а если одно из них отрицательно, то оно невелико по модулю по сравнению со вторым.
Пока что не найдено никаких методов изучения пластичности при трехосном напряженном состоянии, поэтому опытное подтверждение теории не может считаться исчерпывающим.
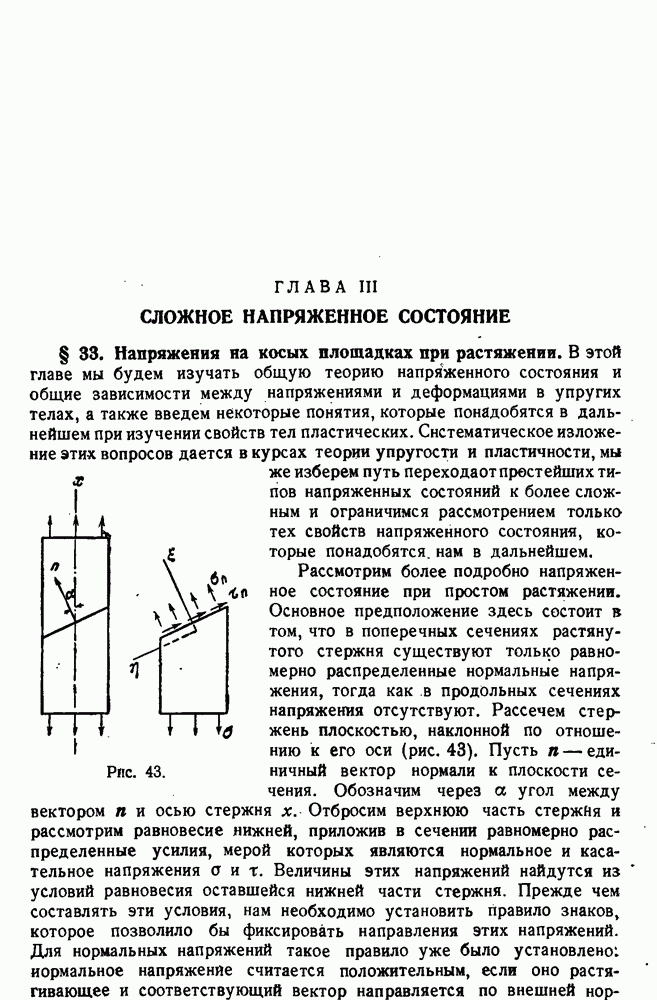
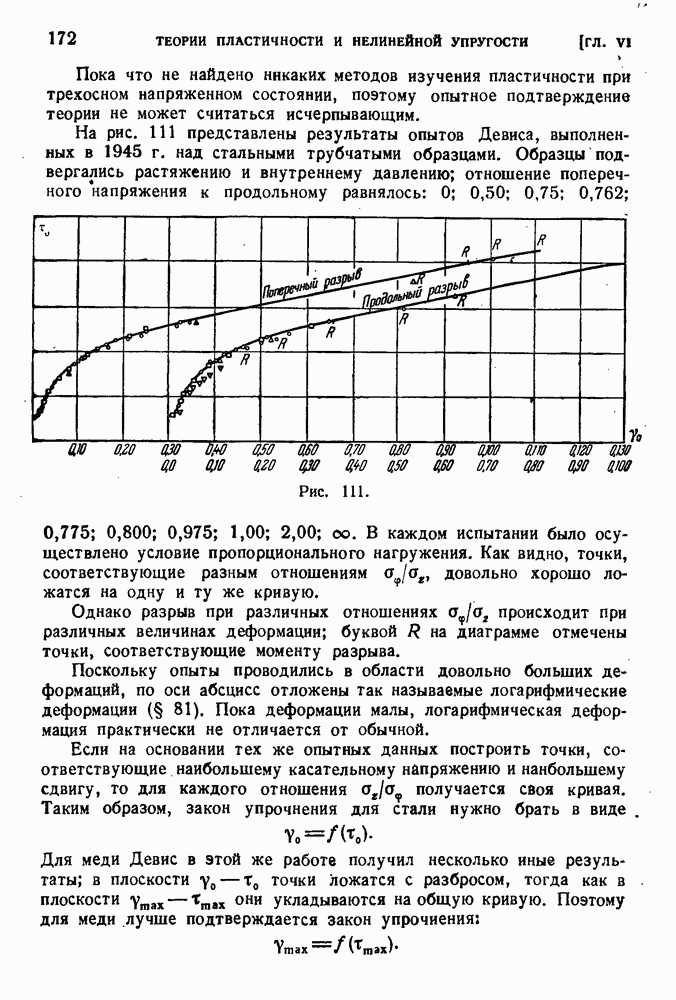
На рис. 111 представлены результаты опытов Девиса, выполненных в 1945 г. над стальными трубчатыми образцами. Образцы подвергались растяжению и внутреннему давлению; отношение поперечного напряжения к продольному равнялось: 0; 0,50; 0,75; 0,762; 0,775; 0,800; 0,975; 1,00; 2,00;  .
.

Рис. 111.
В каждом испытании было осуществлено условие пропорционального нагружения. Как видно, точки, соответствующие разным отношениям  довольно хорошо ложатся на одну и ту же кривую.
довольно хорошо ложатся на одну и ту же кривую.
Однако разрыв при различных отношениях  происходит при различных величинах деформации; буквой R на диаграмме отмечены точки, соответствующие моменту разрыва.
происходит при различных величинах деформации; буквой R на диаграмме отмечены точки, соответствующие моменту разрыва.
Поскольку опыты проводились в области довольно больших деформаций, по оси абсцисс отложены так называемые логарифмические деформации (§ 81). Пока деформации малы, логарифмическая деформация практически не отличается от обычной.
Если на основании тех же опытных данных построить точки, соответствующие наибольшему касательному напряжению и наибольшему сдвигу, то для каждого отношения  получается своя кривая. Таким образом, закон упрочнения для стали нужно брать в виде
получается своя кривая. Таким образом, закон упрочнения для стали нужно брать в виде

Для меди Девис в этой же работе получил несколько иные результаты; в плоскости  точки ложатся с разбросом, тогда как в плоскости
точки ложатся с разбросом, тогда как в плоскости  они укладываются на общую кривую. Поэтому для меди лучше подтверждается закон упрочнения:
они укладываются на общую кривую. Поэтому для меди лучше подтверждается закон упрочнения:

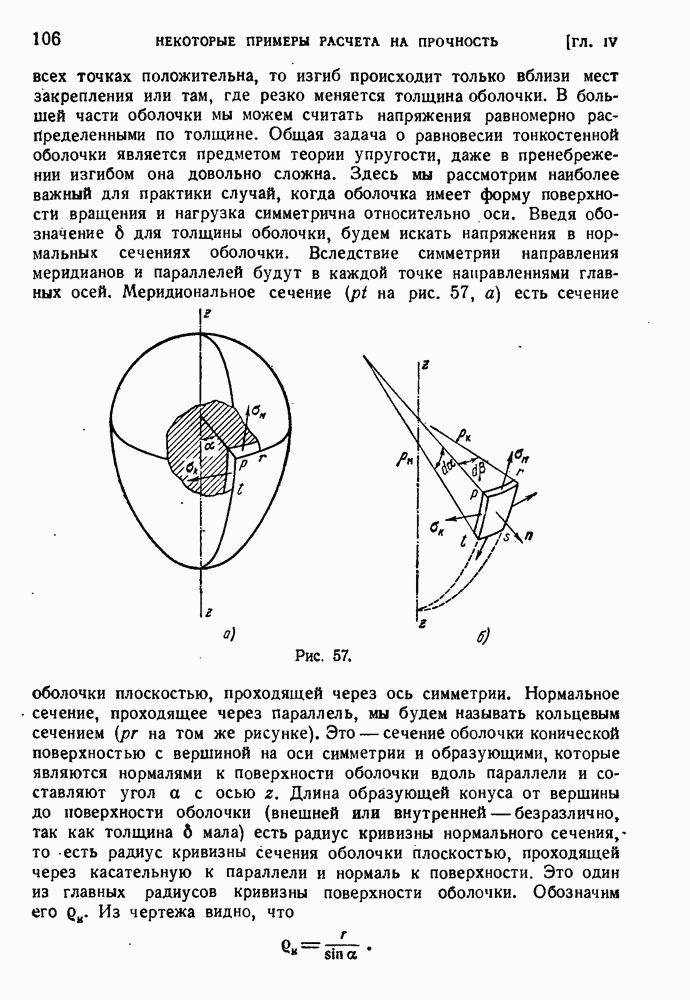
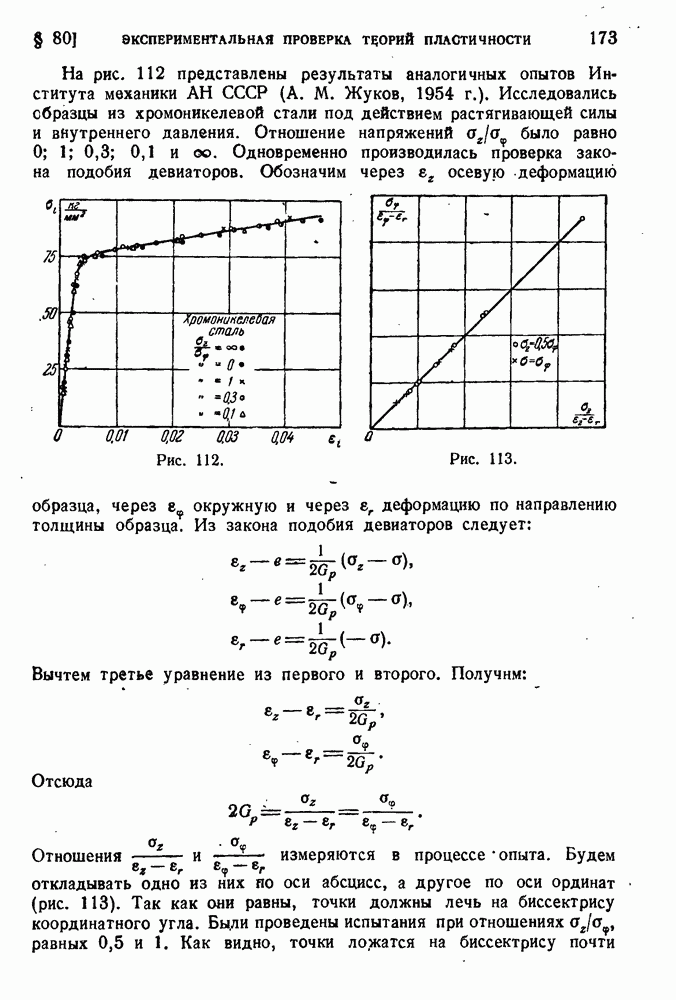
На рис. 112 представлены результаты аналогичных опытов Института механики АН СССР (А. М. Жуков, 1954 г.). Исследовались образцы из хромоникелевой стали под действием растягивающей силы и внутреннего давления. Отношение напряжений  было равно 0; 1; 0,3; 0,1 и
было равно 0; 1; 0,3; 0,1 и  . Одновременно производилась проверка закона подобия девиаторов.
. Одновременно производилась проверка закона подобия девиаторов.

Рис. 112.

Рис. 113.
Обозначим через  осевую деформацию образца, через
осевую деформацию образца, через  окружную и через
окружную и через  деформацию по направлению толщины образца. Из закона подобия девиаторов следует:
деформацию по направлению толщины образца. Из закона подобия девиаторов следует:

Вычтем третье уравнение из первого и второго. Получим:

Отсюда

Отношения  измеряются в процессе
измеряются в процессе  опыта. Будем откладывать одно из них по оси абсцисс, а другое по оси ординат (рис. 113). Так как они равны, точки должны лечь на биссектрису координатного угла. Были проведены испытания при отношениях
опыта. Будем откладывать одно из них по оси абсцисс, а другое по оси ординат (рис. 113). Так как они равны, точки должны лечь на биссектрису координатного угла. Были проведены испытания при отношениях  равных 0.5 и 1.
равных 0.5 и 1.
Как видно, точки ложатся на биссектрису почти точно, разница не выходит за пределы обычного случайного разброса. Для некоторых алюминиевых и магниевых сплавов закон упрочнения как той, так и в другой форме не выполняется (С. И. Ратнер).
Что касается условия пластичности, основная экспериментальная трудность состоит в том, что момент достижения пластического состояния довольно условен и его можно определять по-разному.
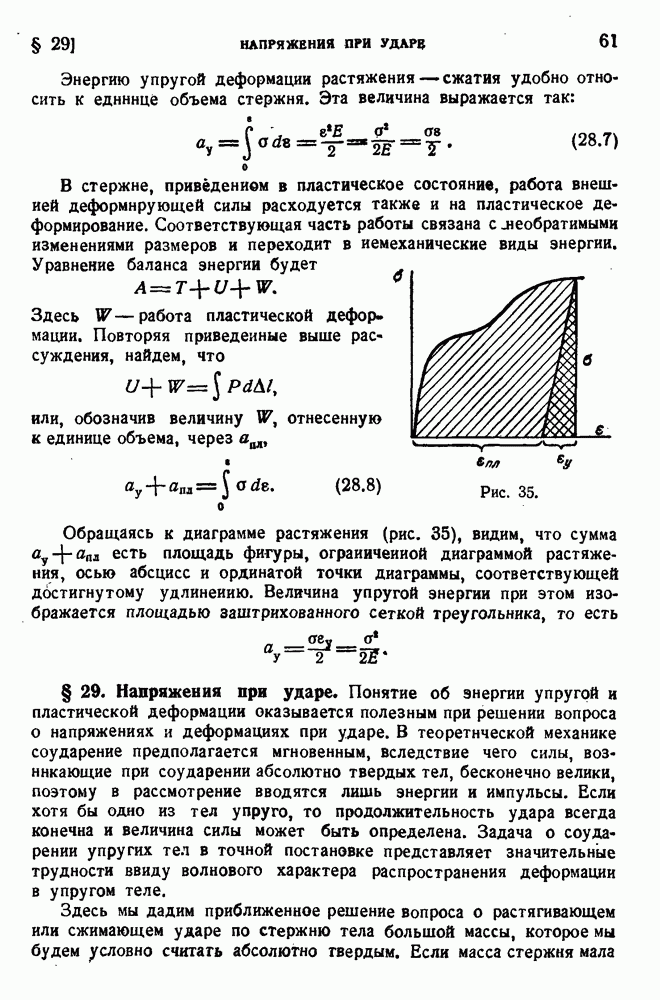
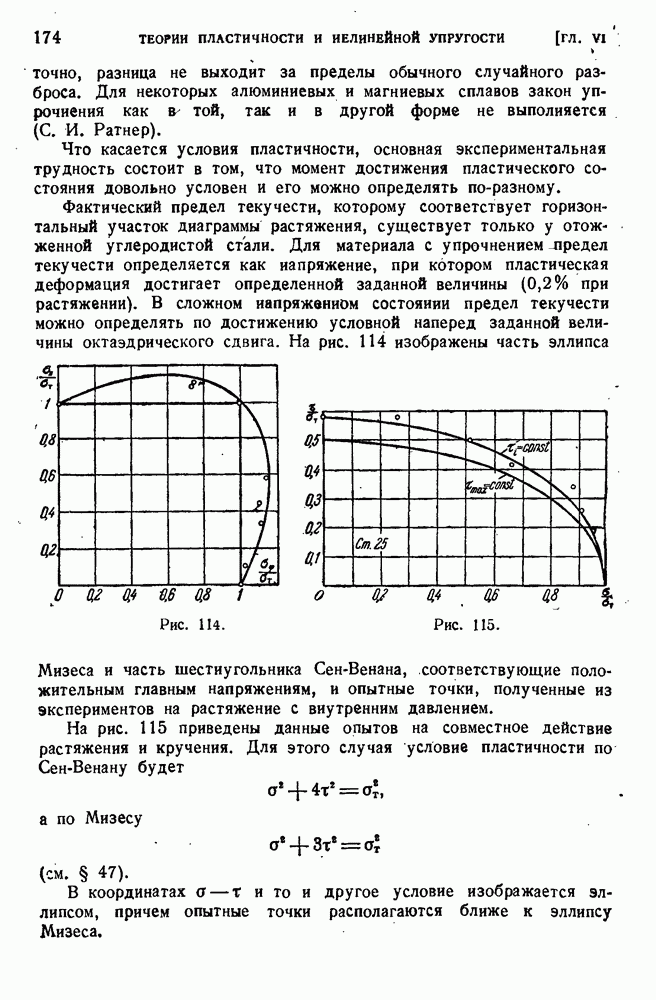
Фактический предел текучести, которому соответствует горизонтальный участок диаграммы растяжения, существует только у отожженной углеродистой стали. Для материала с упрочнением предел текучести определяется как напряжение, при котором пластическая деформация достигает определенной заданной величины (0,2% при растяжении). В сложном напряженном состоянии предел текучести можно определять по достижению условной наперед заданной величины октаэдрического сдвига. На рис. 114 изображены часть эллипса

Рис. 114.

Рис. 115.
Мизеса и часть шестиугольника Сен-Венана, соответствующие положительным главным напряжениям, и опытные точки, полученные из экспериментов на растяжение с внутренним давлением.
На рис. 115 приведены данные опытов на совместное действие растяжения и кручения. Для этого случая условие пластичности по Сен-Венану будет

а по Мизесу

(см. § 47).
В координатах  и то и другое условие изображается эллипсом, причем опытные точки располагаются ближе к эллипсу Мизеса.
и то и другое условие изображается эллипсом, причем опытные точки располагаются ближе к эллипсу Мизеса.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Задачи и содержание сопротивления материалов.
- § 2. Сопротивление материалов и теоретическая механика.
- § 3. Статически неопределенные задачи.
- § 4. Внешние силы.
- § 5. Принцип отвердения.
- § 6. Недопустимость замены системы сил статически эквивалентной.
- § 7. Однородное тело.
- § 8. Внутренние силы.
- § 9. Напряжение.
- § 10. Простейшие типы напряженного состояния.
- § 11. Простейшие виды деформации.
- § 12. Упругость и пластичность.
- § 13. Закон Гука.
- § 14. Диаграмма пластичности.
- § 15. Тела изотропные и анизотропные.
- ГЛАВА II. РАСТЯЖЕНИЕ СЖАТИЕ
- § 16. Стержни и стержневые системы.
- § 17. Принцип Сен-Венана и гипотеза плоских сечений.
- § 18. Напряжения и деформации при растяжении.
- § 19. Расчеты на прочность при растижении и сжатии.
- § 20. Собственный вес и силы инерции.
- § 21. Стержни переменного сечения.
- § 22. Перемещения узлов стержневых систем.
- § 23. Статически неопределенные задачи на растяжение — сжатие.
- § 24. Температурные и монтажные напряжения.
- § 25. Общие соображения о расчете стержневых систем.
- § 26. Расчет статически неопределимых систем по допускаемым нагрузкам.
- § 27. Остаточные напряжения после пластической деформации.
- § 28. Потенциальная энергия растяжении.
- § 29. Напряжения при ударе.
- § 30. Распространение упругих волн в стержнях.
- § 31. Концентрации напряжений.
- § 32. Нелинейные задачи на растяжение — сжатие.
- ГЛАВА III. СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
- § 33. Напряжения на косых площадках при растяжении.
- § 34. Напряжения при двухосном растяжении.
- § 35. Круговая диаграмма Мора.
- § 36. Общий случай плоского напряженного состояния.
- § 37. Определение напряжений на произвольной площадке.
- § 38. Пространственное напряженное состояние.
- § 39. Главные напряжения.
- § 40. Главные касательные напряжения.
- § 41. Октаэдрическое напряжение.
- § 42. Закон Гука для главных осей.
- § 43. Изменение объема при упругой деформации.
- § 44. Чистый сдвиг.
- § 45. Деформация элемента объема в общем случае.
- § 46. Условие пластичности Треска — Сен-Венана.
- § 47. Условие пластичности Мизеса.
- § 48. Условия пластичности для плоского напряженного состояния.
- § 49. Потенциальная энергия упругой деформации.
- § 50. Энергия изменения формы.
- ГЛАВА IV. НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
- § 51. Расчеты на прочность изделий сложной формы.
- § 52. Безмоментные оболочки вращении.
- § 53. Местные напряжения в безмоментных оболочках.
- § 54. Большие прогибы мембраны.
- § 55. Условные расчеты.
- § 56. Некоторые дальнейшие примеры условных расчетов.
- § 57. Расчет сварных соединений.
- ГЛАВА V. ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
- § 58. Задачи испытания материалов.
- § 59. Статические испытания на растяжение.
- § 60. Исследование металлов в области малых деформаций.
- § 61. Диаграмма растяжения мягкой стали.
- § 62. Опыты на сжатие.
- § 63. Строение и упругая деформация металлических кристаллов.
- § 64. Типичные кристаллические структуры металлов.
- § 65. Пластическая деформация монокристаллов.
- § 66. Прочность кристаллов и сопротивление пластическому деформированию.
- § 67. Дислокации.
- § 68. Движение и равновесие дислокаций.
- § 69. Источники дислокаций.
- § 70. Границы блоков.
- § 71. Деформация поликристаллических металлов и сплавов.
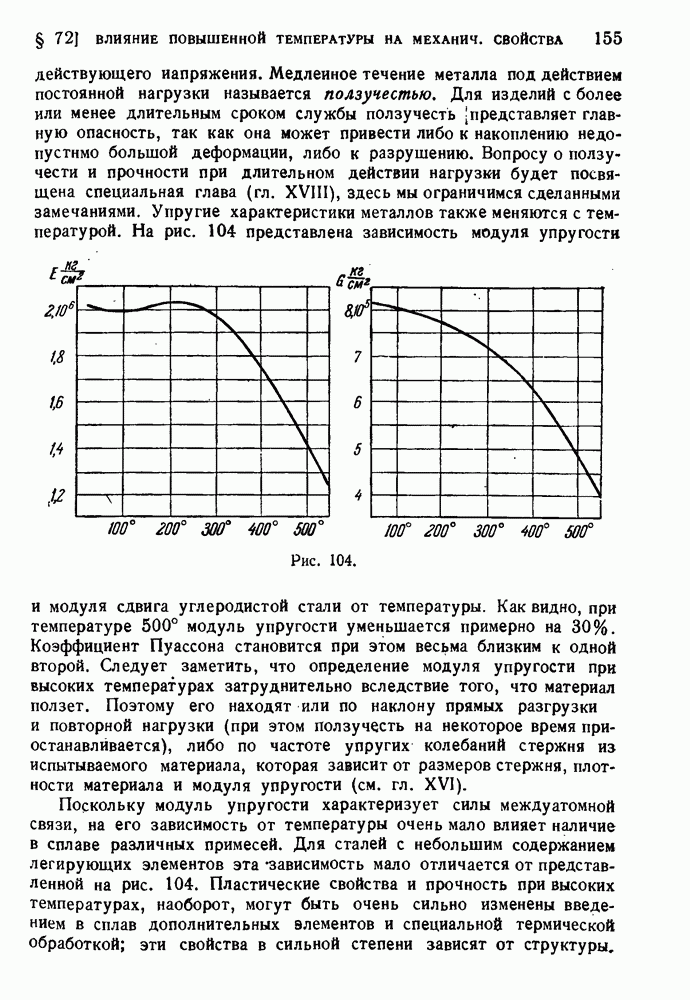
- § 72. Влияние повышенной температуры на механические свойства.
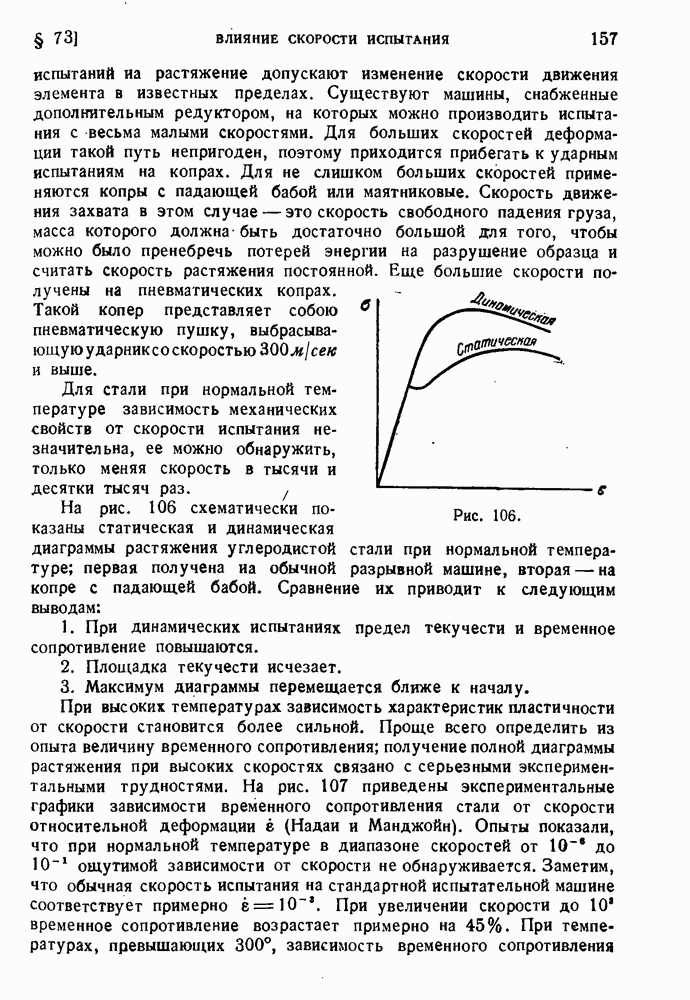
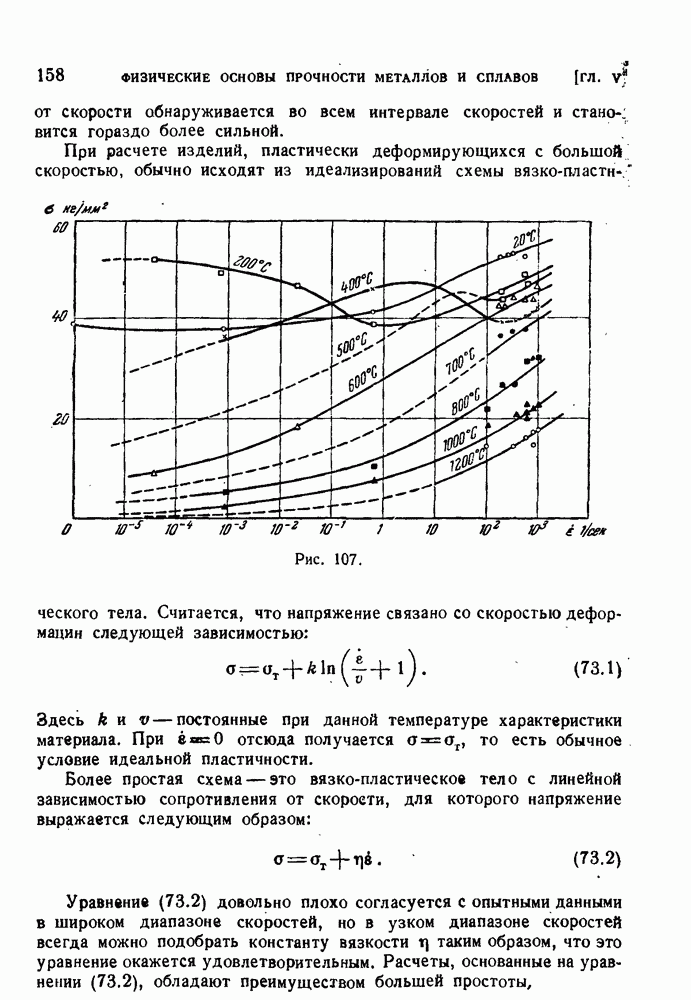
- § 73. Влияние скорости испытания.
- § 74. Испытании на твердость.
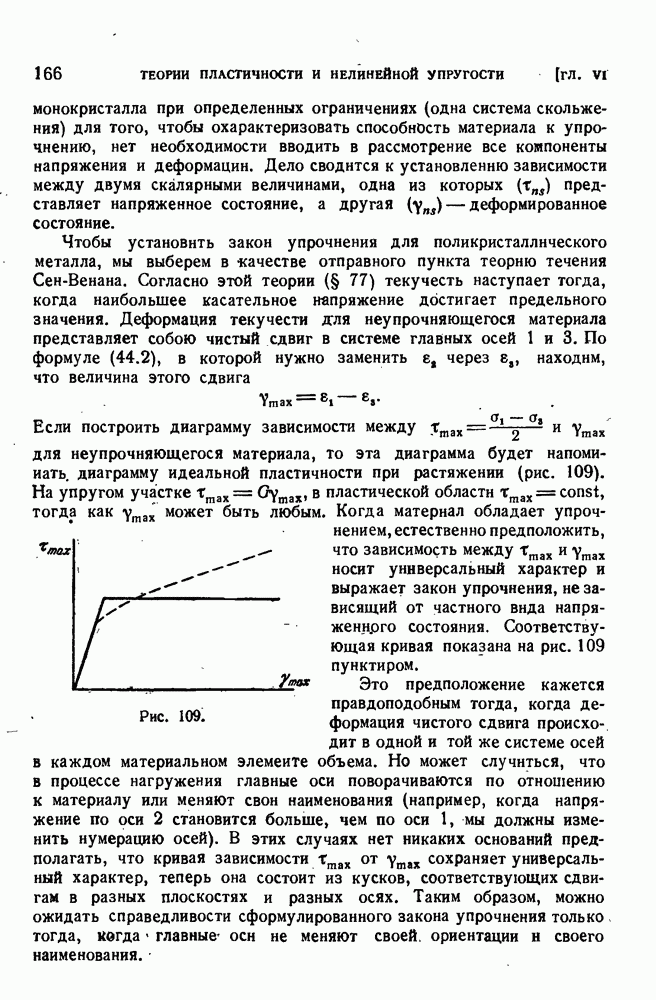
- ГЛАВА VI. ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ
- § 75. Основные принципы построения теории пластичности.
- § 76. Ассоциированный закон течения.
- § 77. Течение при условии пластичности Сен-Венана и Мизеса.
- § 78. Закон упрочнения.
- § 79. Деформационная теория пластичности.
- § 80. Экспериментальная проверка теорий пластичности.
- § 81. Конечная деформация.
- § 82. Нелинейно упругое тело.
- § 83. Высокоэластические деформации.
- § 84. Упругое последействие.
- § 85. Некоторые свойства вязко-упругого тела.
- § 86. Принцип суммирования Больцмана—Вольтерра.
- ГЛАВА VII. КРУЧЕНИЕ
- § 87. Кручение стержней круглого сечеиия.
- § 88. Упруго-пластическое кручение стержня круглого сечения.
- § 89. Гипотеза жесткого контура.
- § 90. Кручение тонкостенных стержней замкнутого профиля.
- § 91. Кручение тонкостенных стержней открытого профиля.
- § 92. Кручение упругих стержией сплошного профиля.
- § 93. Опытное исследование кручения.
- § 94. Предельное состояние закрученного стержня из идеально-пластического материала.
- ГЛАВА VIII. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- § 96. Общие теоремы о моментах.
- § 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей.
- § 98. Вычисление моментов инерции.
- § 99. Преобразование моментов инерции при повороте осей.
- § 100. Главные оси и главные моменты инерции.
- ГЛАВА IX. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
- § 101. Действие поперечных сил на балку.
- § 102. Гипотеза плоских сечений и принцип Сен-Венана.
- § 103. Нормальные напряжения при изгибе.
- § 104. Изгибающие моменты и перерезывающие силы.
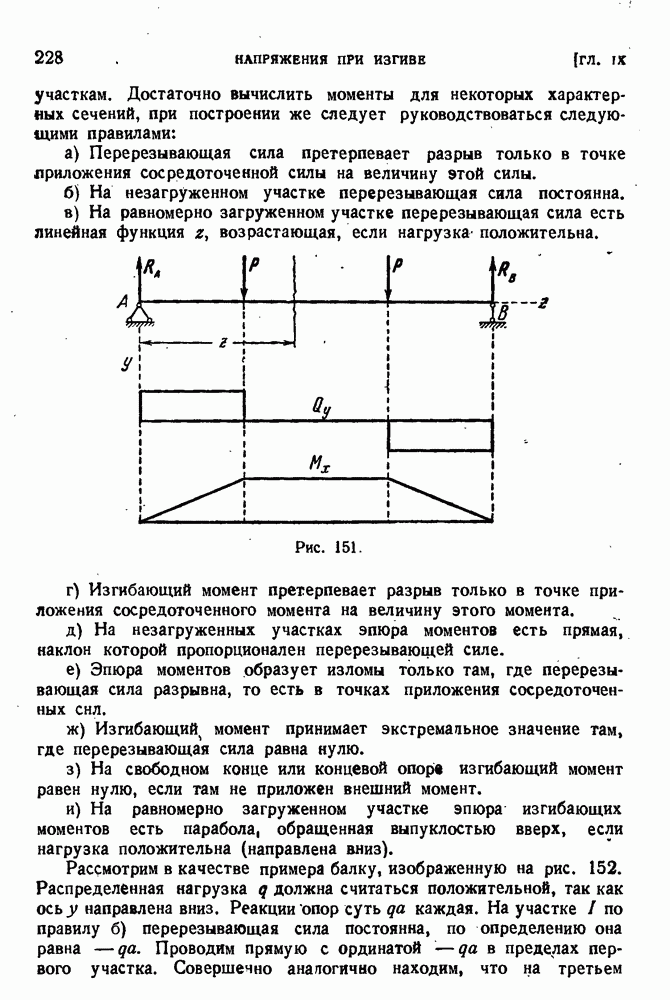
- § 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры.
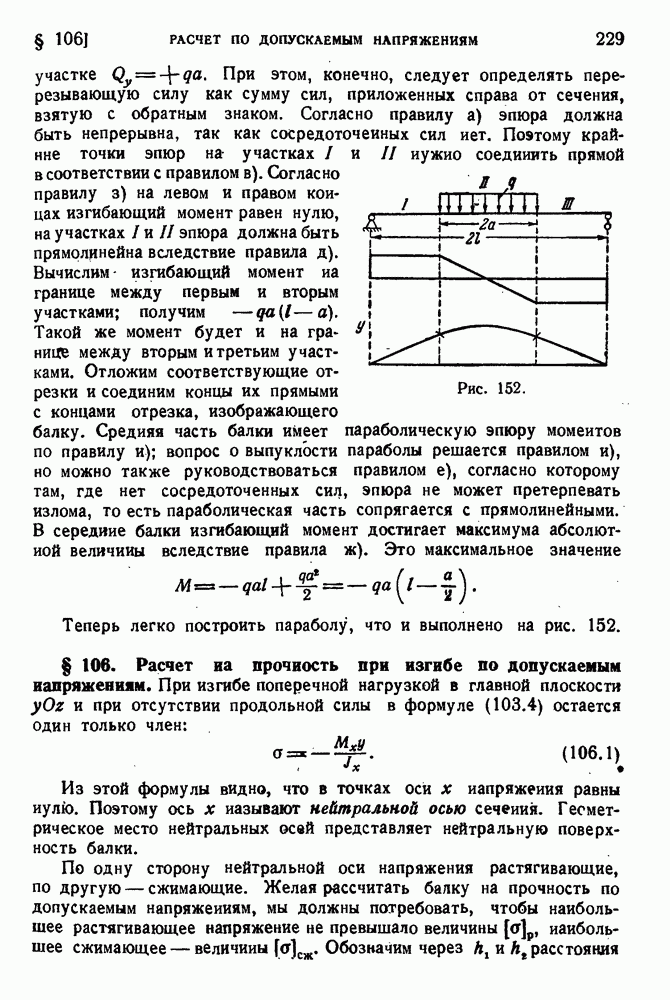
- § 106. Расчет на прочность при изгибе по допускаемым напряжениям.
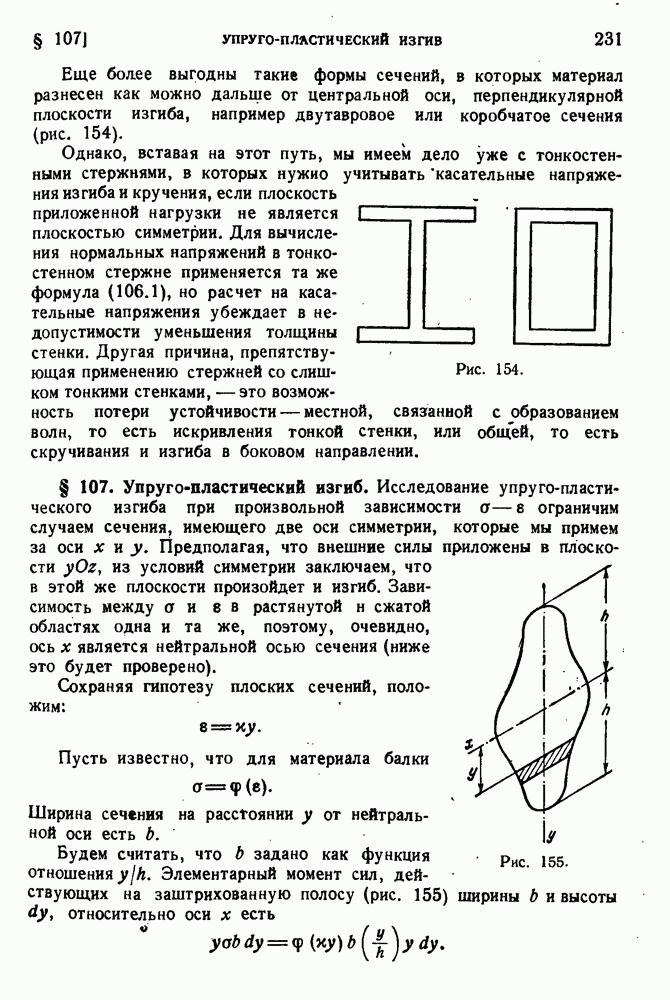
- § 107. Упруго-пластический изгиб.
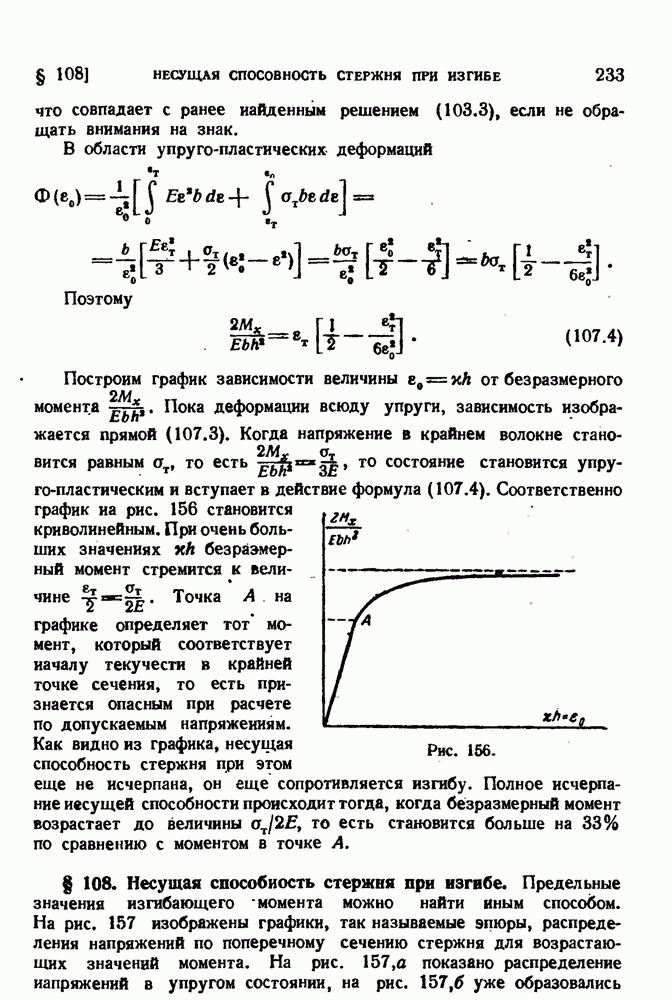
- § 108. Несущая способность стержня при изгибе.
- § 109. Принцип Сен-Венана.
- § 110. Внецентренное растяжение — сжатие.
- § 111. Ядро сечения.
- § 112. Несущая способность внецентренно сжатого стержня.
- § 113. Расчет составных балок.
- § 114. Изгиб кривого бруса.
- § 115. Нахождение нейтральной осн в кривом стержне.
- ГЛАВА X. ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- § 116. Дифференциальное уравнение изогнутой оси.
- § 117. Пределы применимости приближенной теории.
- § 118. Интегрирование уравнения изгиба.
- § 119. Примеры определения прогибов.
- § 120. Простейшие статически неопределенные задачи.
- § 121. Расчет статически неопределимых балок по способу допускаемых нагрузок.
- § 122. Изгиб стержней переменного сечения.
- § 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами.
- § 124. Продольно-поперечный изгиб.
- § 125. Изгиб балки на упругом основании.
- ГЛАВА XI. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
- § 126. Нормальные и касательные напряжения при изгибе.
- § 127. Касательные напряжении при изгибе в плоскости симметрии.
- § 128. Центр изгиба.
- § 129. Дополнительные напряжения при кручении.
- § 130. Закон секториальных площадей.
- § 131. Уравнение стесненного кручения.
- § 132. Вычисление секториальных характеристик.
- § 133. Стержень, нагруженный бимоментом.
- § 134. Некоторые примеры стесненного кручения.
- ГЛАВА XII. УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ
- § 135. Постановка вопроса об устойчивости.
- § 136. Устойчивость сжатого упругого стержня.
- § 137. Эластика Эйлера.
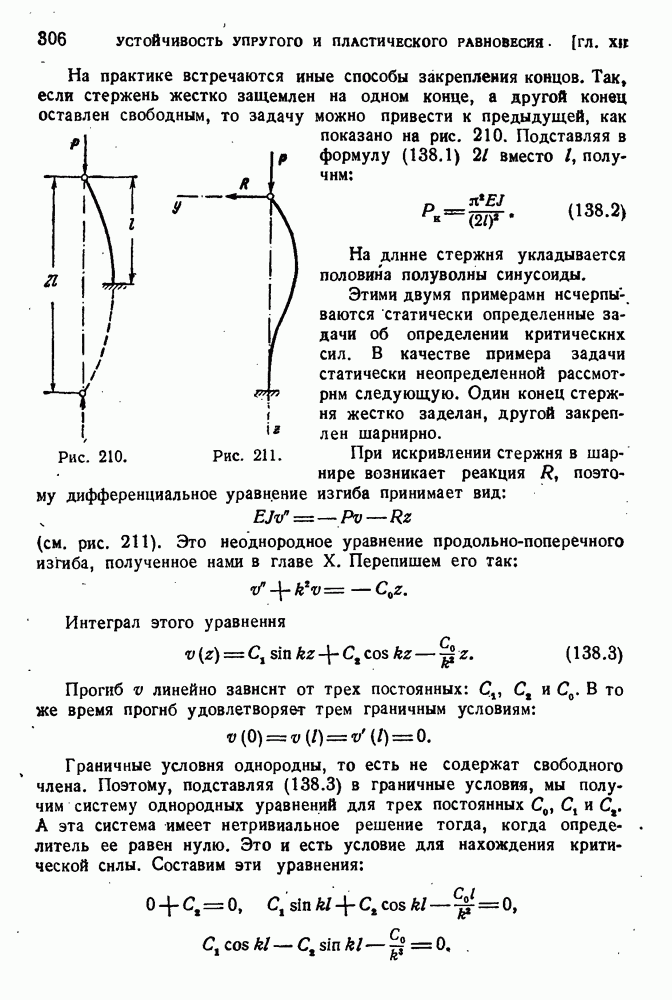
- § 138. Критические силы при иных видах закрепления стержня.
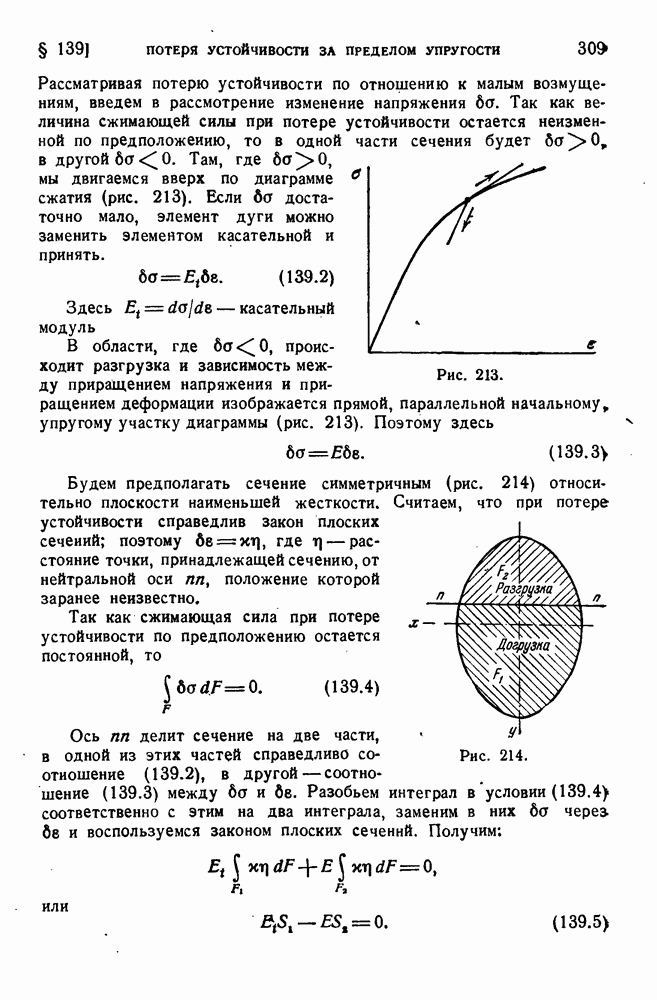
- § 139. Потеря устойчивости за пределом упругости.
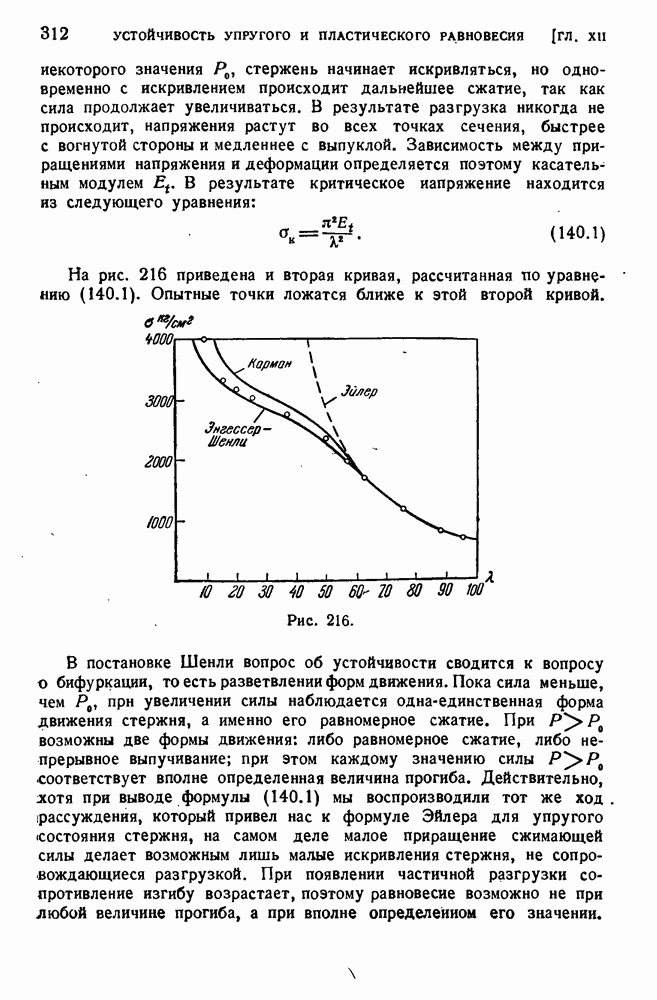
- § 140. Потеря устойчивости за пределом упругости (продолжение).
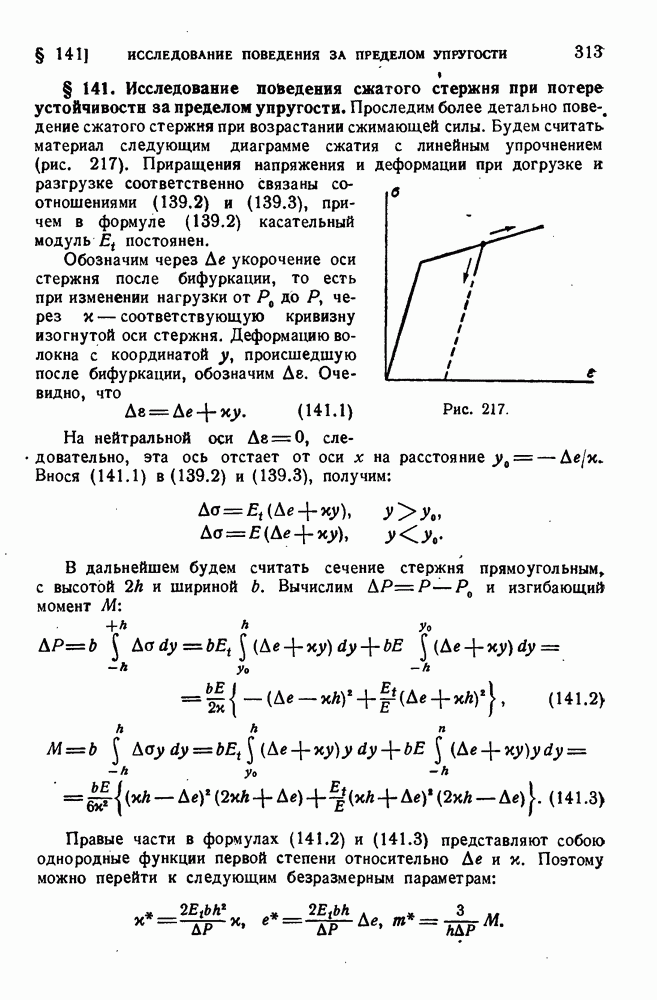
- § 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости.
- § 142. Расчет на устойчивость по эмпирическим формулам.
- ГЛАВА XIII. ТРУБЫ И ДИСКИ
- § 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности.
- § 144. Упругое состояние трубы. Формулы Ламе.
- § 145. Пластическое состояние трубы.
- § 146. Вращающиеся диски. Упругое состояние.
- § 147. Диск равного сопротивления.
- § 148. Предельное равновесие вращающегося диска.
- ГЛАВА XIV. ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 149. Обобщенные силы и обобщенные перемещения.
- § 150. Начало возможных перемещений для деформируемого тела.
- § 151. Теоремы Лагранжа и Кастильяно.
- § 152. Лииейиые упругие системы.
- § 153. Теорема о взаимности работ.
- § 154. Теорема Кастильяно для линейных упругих систем.
- § 155. Расчет винтовых пружин.
- § 156. Теорема о минимуме энергии.
- § 157. Интеграл перемещений.
- § 158. Графоаналитический способ вычислений интеграла перемещений.
- § 159. Расчет статически неопределимых систем по методу сил.
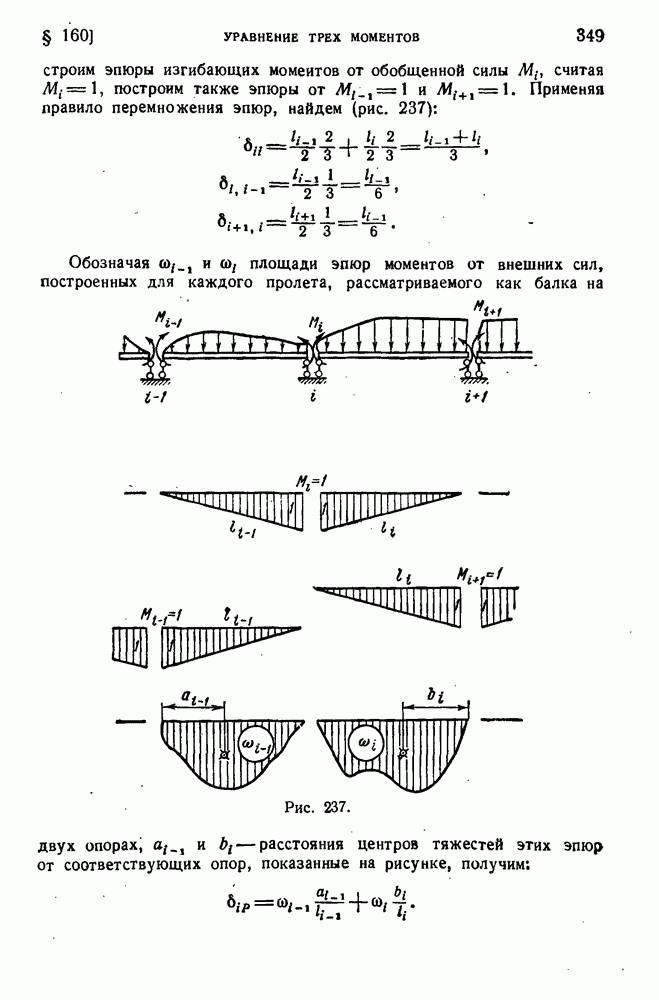
- § 160. Уравнение трех моментов.
- ГЛАВА XV. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
- § 161. Жестко-пластическое тело.
- § 162. Поверхности нагружения.
- § 163. Истинное и допустимые состояния элемента.
- § 164. Статический метод определения предельной нагрузки.
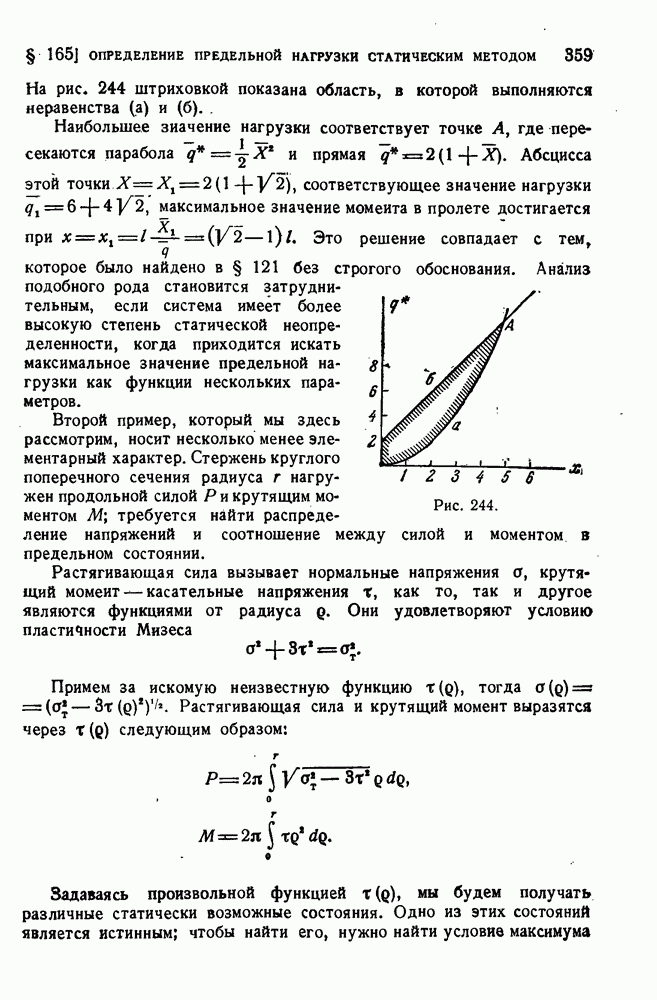
- § 165. Примеры определения предельной нагрузки статическим методом.
- § 166. Кинематически возможные состояния.
- § 167. Кинематический метод определения предельной нагрузки.
- § 168. Примеры определения предельной нагрузки кинематическим методом.
- § 169. Предельное равновесие пластинок.
- ГЛАВА XVI. ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 170. Колебания систем с конечным числом степеней свободы.
- § 171. Собственные частоты и главные формы колебаний.
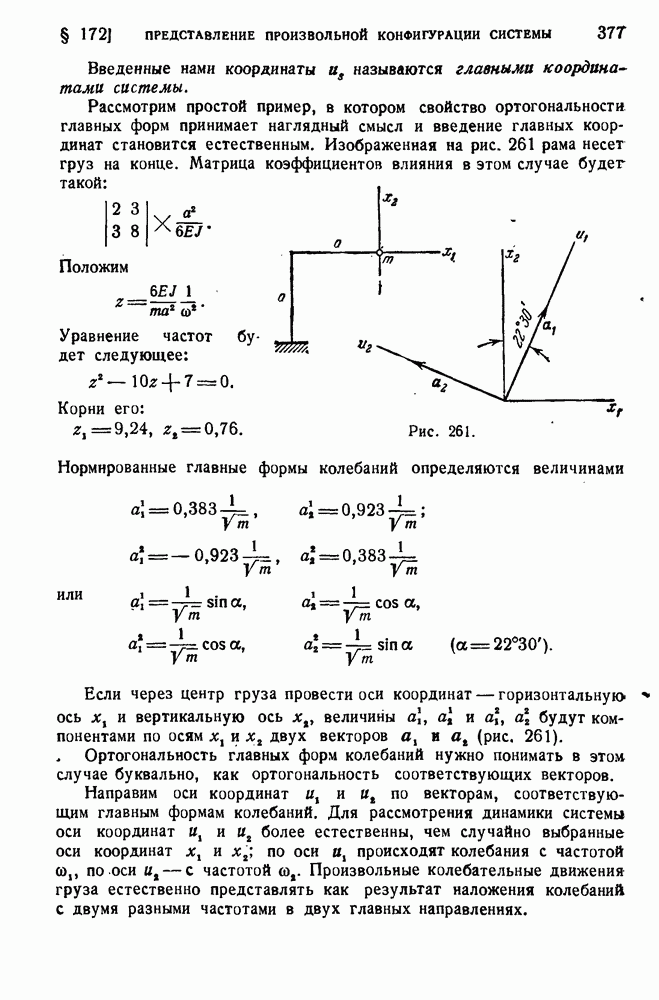
- § 172. Представление произвольной конфигурации системы через главные формы. Главные координаты.
- § 173. Формула и способ Релея.
- § 174. Нижние оценки для частоты основного тона.
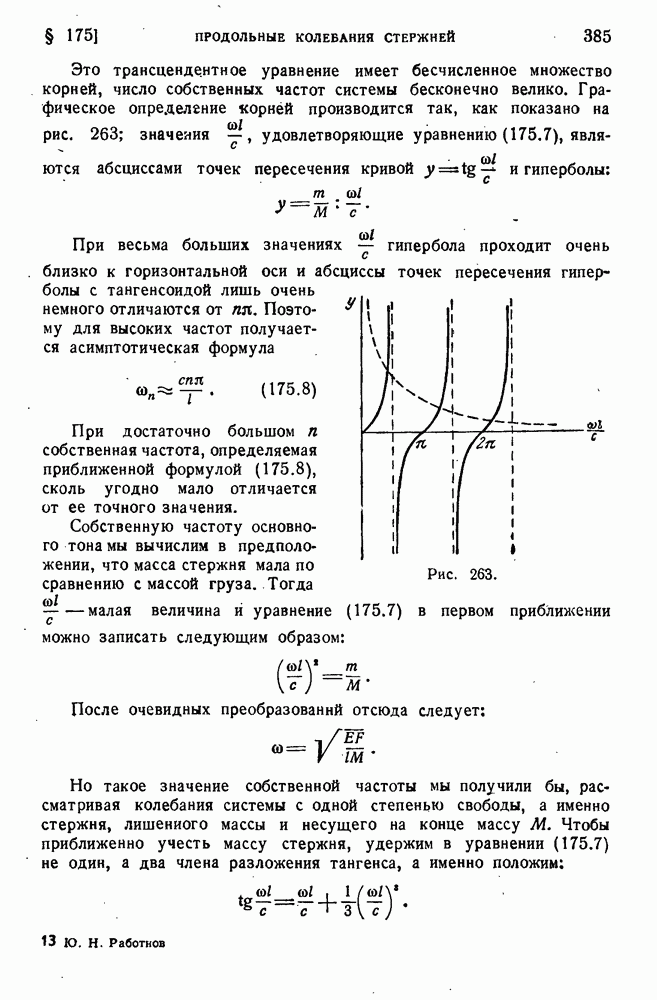
- § 175. Продольные колебания стержней.
- § 176. Поперечные колебания стержней.
- § 177. Колебания балок постоянного сечения.
- § 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня.
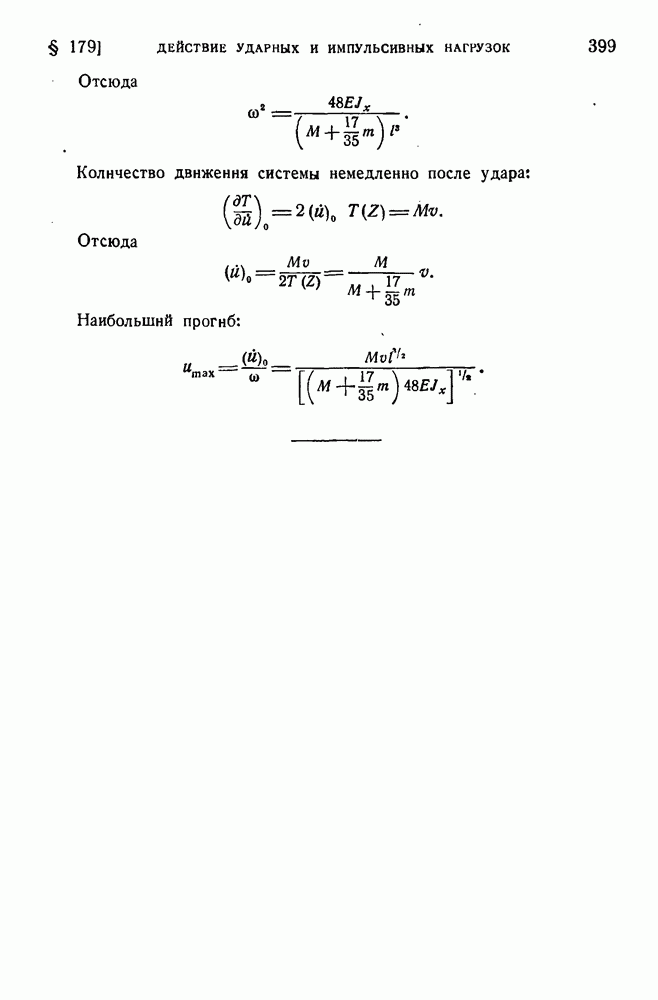
- § 179. Действие ударных и импульсивных нагрузок на упругие системы.
- ГЛАВА XVII. ТЕОРИИ ПРОЧНОСТИ
- § 180. Постановка вопроса о прочности.
- § 181. Хрупкое и пластическое разрушение.
- § 182. Теория прочности Мора.
- § 183. Механизм хрупкого разрушения.
- § 184. Прочность при низких температурах.
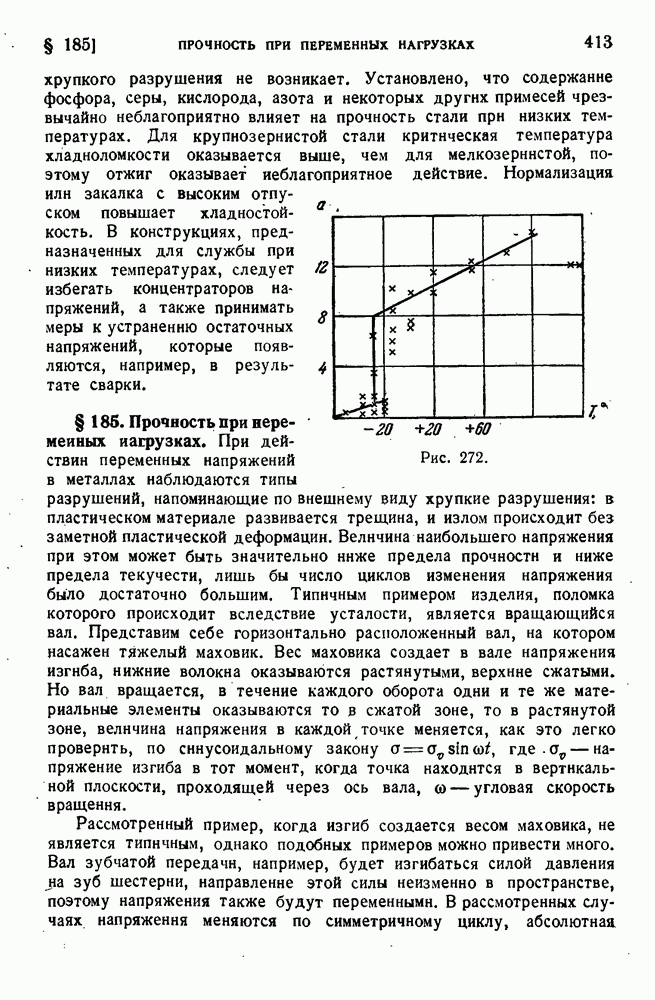
- § 185. Прочность при переменных нагрузках.
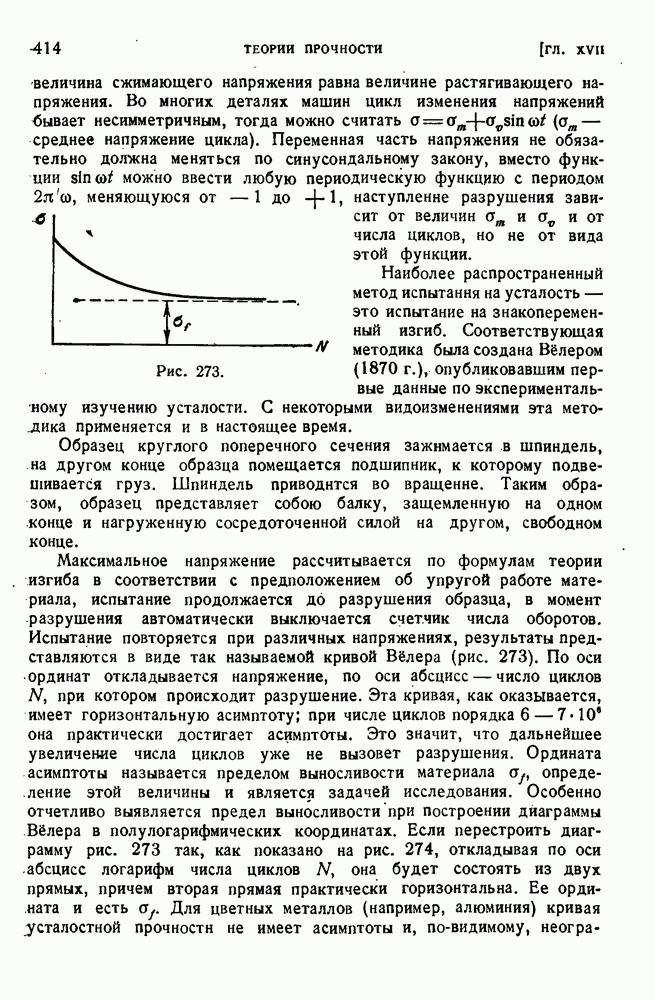
- § 186. Природа усталостного разрушения.
- § 187. Критерии прочности при переменных нагрузках.
- § 188. Влияние концентрации напряжений на усталостную прочность.
- § 189. Усталостная прочность при сложном напряженном состоянии.
- ГЛАВА XVIII. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
- § 190. Ползучесть металлов.
- § 191. Процесс ползучести.
- § 192. Длительное разрушение.
- § 193. Температурные зависимости ползучести и длительной прочности.
- § 194. Феноменологические теории одномерной ползучести.
- § 195. Релаксация напряжений.
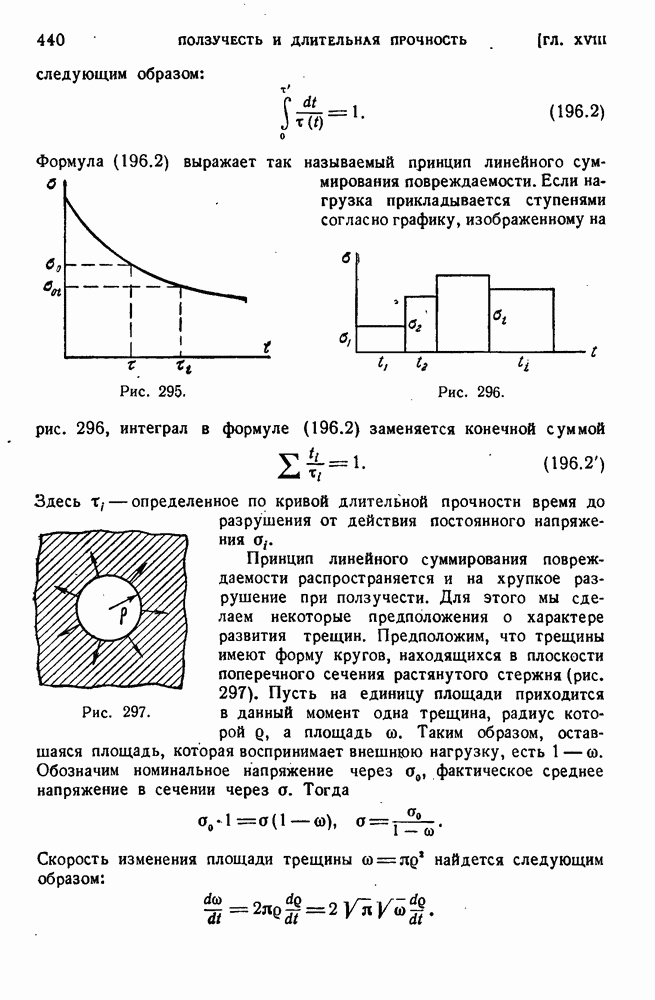
- § 196. Длительная прочность при переменных нагрузках.
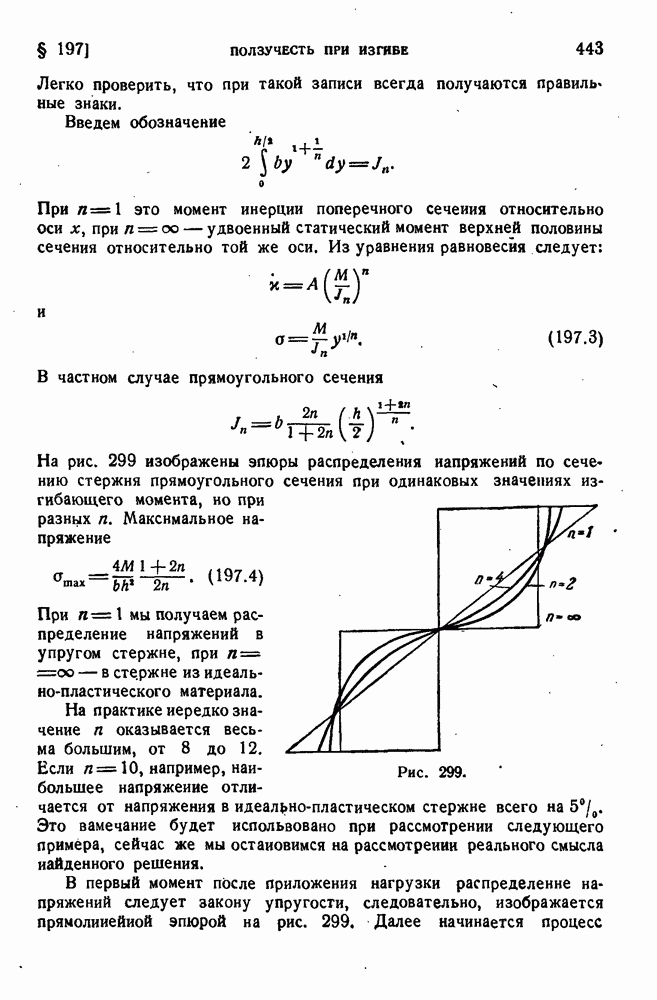
- § 197. Ползучесть при изгибе.
- § 198. Критическое время сжатого стержня.
- § 199. Ползучесть и длительная прочность при сложном напряженном состоянии.
- § 200. Вращающиеся диски в условиях ползучести.
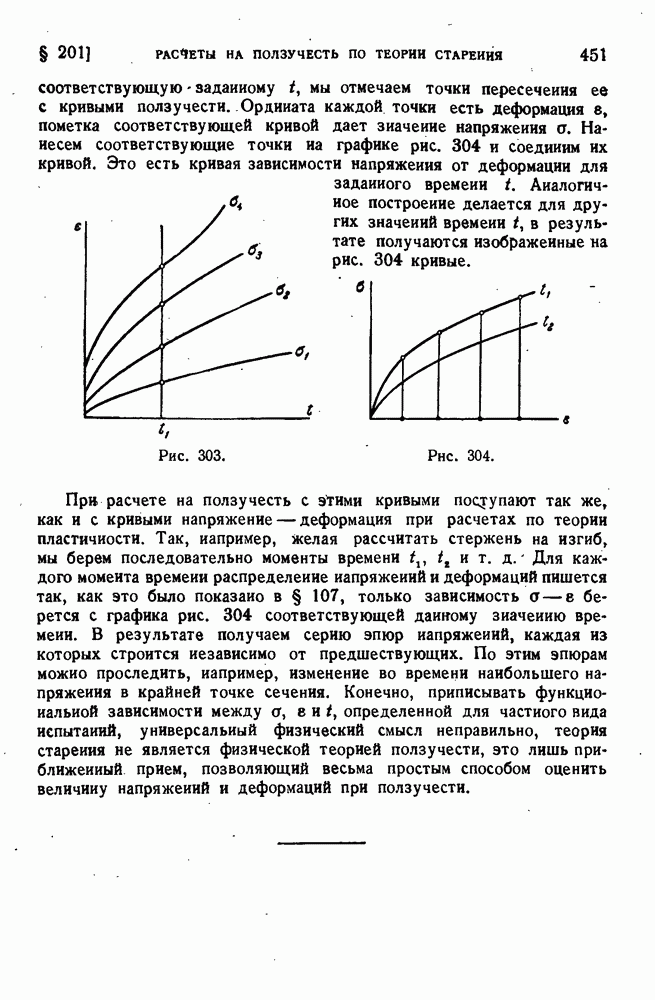
- § 201. Расчеты на ползучесть по теории старении.