| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
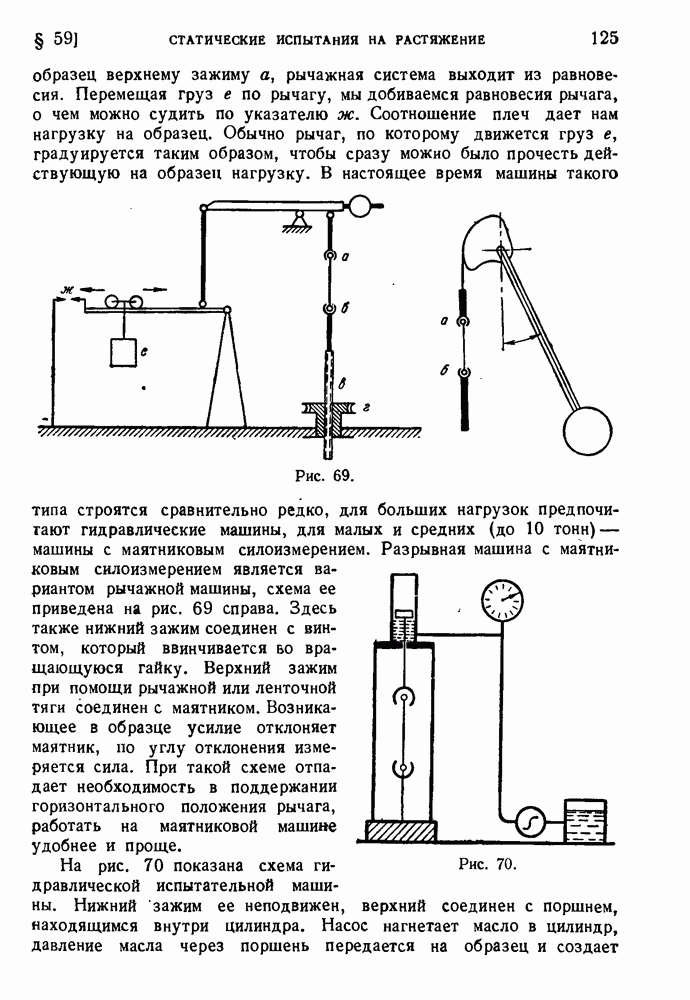
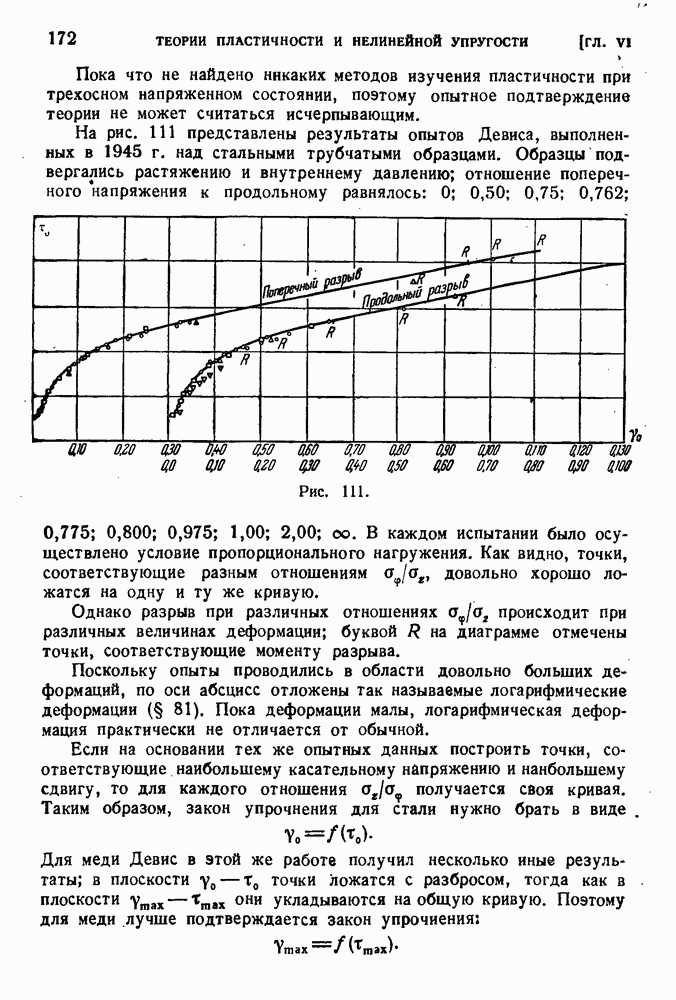
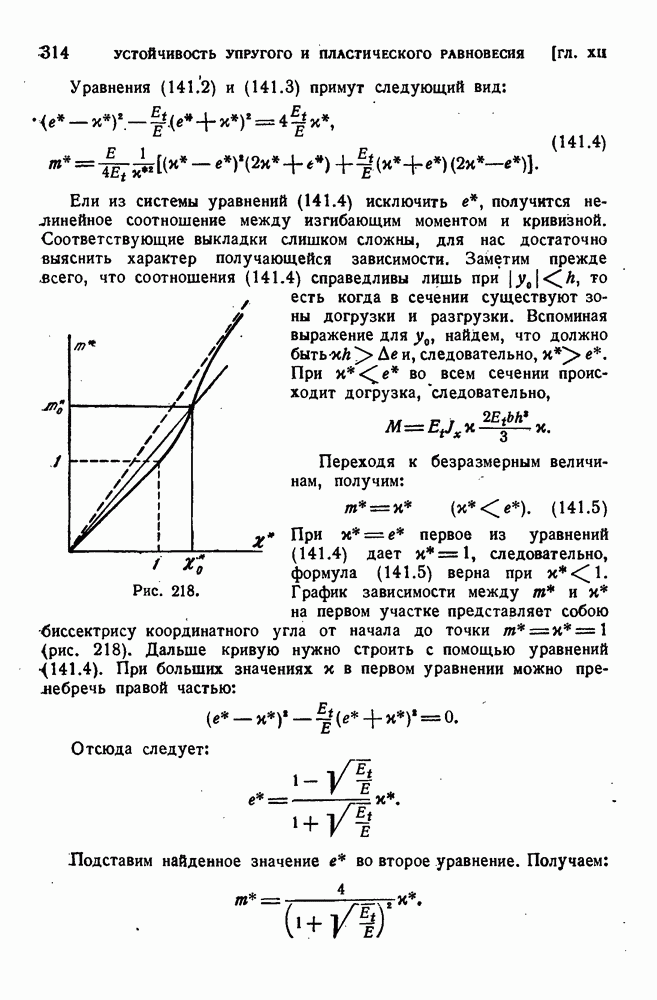
§ 60. Исследование металлов в области малых деформаций.
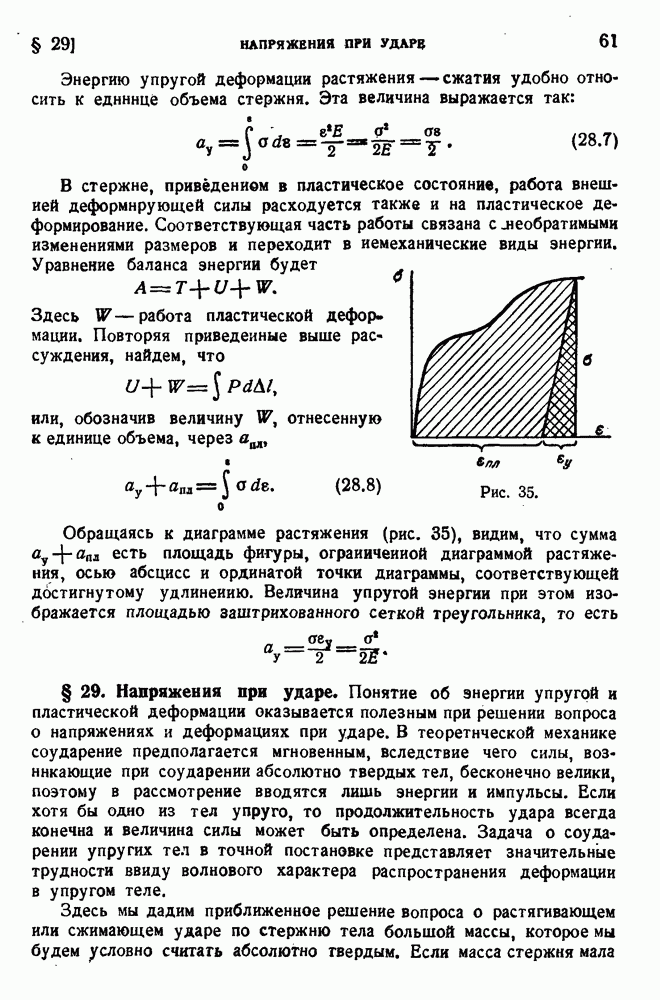
Измеряя малые деформации, соответствующие упругой области на диаграмме  , а также началу пластичности, следует заботиться об исключении различных искажающих факторов. Поэтому, например, нельзя измерять малые деформации по перемещению зажимов машины: обмятие головок образца и упругие деформации частей машины совершенно исказят результаты. Основное правило для измерения малых деформаций состоит в том, что измерения должны производиться на рабочей длине и прибор для измерения деформации, экстензометр, должен крепиться непосредственно на образце. На рис. 72 приведена схема зеркального экстензометра Мартенса. Шина а имеет на одном конце жестко с нею скрепленную призму
, а также началу пластичности, следует заботиться об исключении различных искажающих факторов. Поэтому, например, нельзя измерять малые деформации по перемещению зажимов машины: обмятие головок образца и упругие деформации частей машины совершенно исказят результаты. Основное правило для измерения малых деформаций состоит в том, что измерения должны производиться на рабочей длине и прибор для измерения деформации, экстензометр, должен крепиться непосредственно на образце. На рис. 72 приведена схема зеркального экстензометра Мартенса. Шина а имеет на одном конце жестко с нею скрепленную призму  , лезвие которой прижимается к образцу. На другом конце между образцом и шиной помещается ромбовидная призма в, изготовленнагя как одно целое со стержнем, как показано на рис. 72 внизу. Этот стержень с одной стороны несет зеркальце
, лезвие которой прижимается к образцу. На другом конце между образцом и шиной помещается ромбовидная призма в, изготовленнагя как одно целое со стержнем, как показано на рис. 72 внизу. Этот стержень с одной стороны несет зеркальце  , с другой — противовес. Диагональ ромбовидной призмы есть d. Шина прижимается к образцу струбцинкой. Зеркальце устанавливается так, чтобы через оптическую трубу
, с другой — противовес. Диагональ ромбовидной призмы есть d. Шина прижимается к образцу струбцинкой. Зеркальце устанавливается так, чтобы через оптическую трубу  было видно отражение в зеркале рейки
было видно отражение в зеркале рейки  со шкалой, разделенной на миллиметры.
со шкалой, разделенной на миллиметры.
Пусть начальный отсчет по шкале, то есть цифра, стоящая против нити в поле зрения трубы, есть s. Это значит, что луч, падающий из точки шкалы с пометкой  на зеркальце и образующий угол
на зеркальце и образующий угол  с нормалью к его поверхности, отражается под тем же углом
с нормалью к его поверхности, отражается под тем же углом  становясь направленным по оптической оси трубы. Предположим теперь, что образец растянулся, расстояние l между призмами получило приращение
становясь направленным по оптической оси трубы. Предположим теперь, что образец растянулся, расстояние l между призмами получило приращение  .
.

Рис. 72.
Подвижная призма, а вместе с нею и зеркальце повернулись на угол  на этот же угол повернулась нормаль к поверхности зеркальца. Угол между последней и оптической осью трубы стал
на этот же угол повернулась нормаль к поверхности зеркальца. Угол между последней и оптической осью трубы стал  . Угол между лучом падающим и лучом отраженным вместо
. Угол между лучом падающим и лучом отраженным вместо  стал
стал  а так как отраженный луч, направленный по оптической оси трубы, неподвижен, то на угол
а так как отраженный луч, направленный по оптической оси трубы, неподвижен, то на угол  повернулся луч падающий. Отсчет по шкале изменился на
повернулся луч падающий. Отсчет по шкале изменился на  считая шкалу приблизительно перпендикулярной лучу, получим:
считая шкалу приблизительно перпендикулярной лучу, получим:

Здесь L — расстояние от зеркальца до шкалы. Отсюда

Величина  есть увеличение прибора. Оно зависит от диагонали призмы d и фокусного расстояния трубы. Обычно
есть увеличение прибора. Оно зависит от диагонали призмы d и фокусного расстояния трубы. Обычно

Оценивая на глаз 0,2 мм на шкале при расчетной длине  , мы можем мерить относительную деформацию с точностью
, мы можем мерить относительную деформацию с точностью  .
.
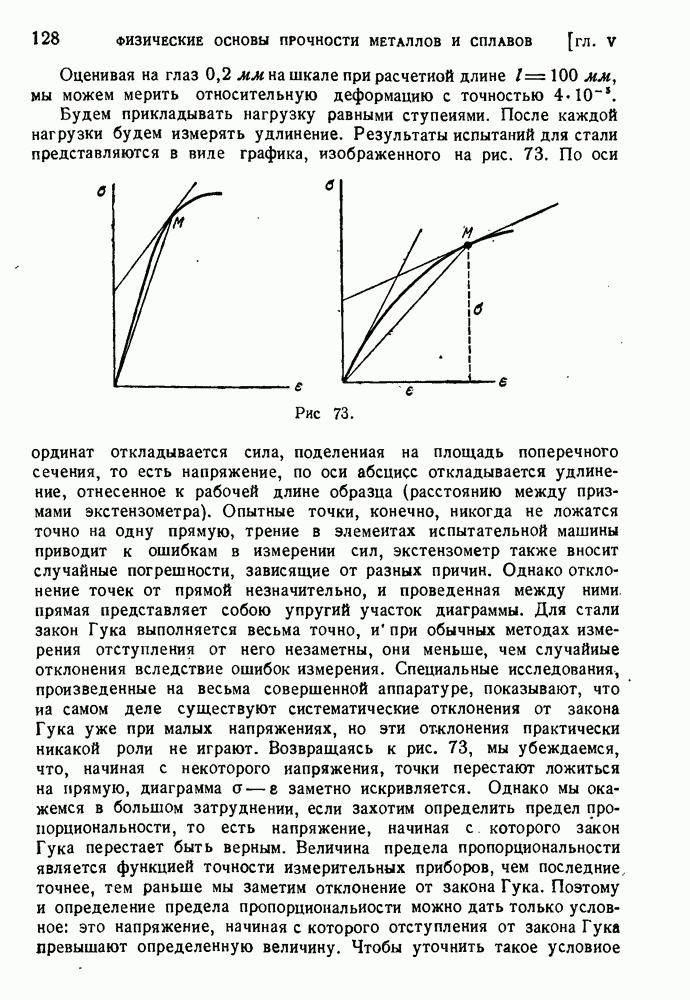
Будем прикладывать нагрузку равными ступенями. После каждой нагрузки будем измерять удлинение. Результаты испытаний для стали представляются в виде графика, изображенного на рис. 73.

Рис. 73.
По оси ординат откладывается сила, поделенная на площадь поперечного сечения, то есть напряжение, по оси абсцисс откладывается удлинение, отнесенное к рабочей длине образца (расстоянию между призмами экстензометра). Опытные точки, конечно, никогда не ложатся точно на одну прямую, трение в элементах испытательной машины приводит к ошибкам в измерении сил, экстензометр также вносит случайные погрешности, зависящие от разных причин. Однако отклонение точек от прямой незначительно, и проведенная между ними, прямая представляет собою упругий участок диаграммы. Для стали закон Гука выполняется весьма точно, и при обычных методах измерения отступления от него незаметны, они меньше, чем случайные отклонения вследствие ошибок измерения. Специальные исследования, произведенные на весьма совершенной аппаратуре, показывают, что на самом деле существуют систематические отклонения от закона Гука уже при малых напряжениях, но эти отклонения практически никакой роли не играют. Возвращаясь к рис. 73, мы убеждаемся, что, начиная с некоторого напряжения, точки перестают ложиться на прямую, диаграмма  заметно искривляется. Однако мы окажемся в большом затруднении, если захотим определить предел пропорциональности, то есть напряжение, начиная с которого закон Гука перестает быть верным. Величина предела пропорциональности является функцией точности измерительных приборов, чем последние, точнее, тем раньше мы заметим отклонение от закона Гука. Поэтому и определение предела пропорциональности можно дать только условное: это напряжение, начиная с которого отступления от закона Гука превышают определенную величину.
заметно искривляется. Однако мы окажемся в большом затруднении, если захотим определить предел пропорциональности, то есть напряжение, начиная с которого закон Гука перестает быть верным. Величина предела пропорциональности является функцией точности измерительных приборов, чем последние, точнее, тем раньше мы заметим отклонение от закона Гука. Поэтому и определение предела пропорциональности можно дать только условное: это напряжение, начиная с которого отступления от закона Гука превышают определенную величину.
Чтобы уточнить такое условное определение и дать точный способ определения предела пропорциональности, нужно сначала остановиться на нахождений модуля упругости.
Для стали и некоторых других достаточно прочных металлов и сплавов дело обстоит просто: мы проводим прямую, наилучшим образом проходящую через опытные точки и между ними; угловой коэффиилент этой прямой принимается за модуль упругости Е. Обычная ошибка при таком определении бывает порядка трех процентов. Но существуют материалы, у которых диаграмма  совсем не имеет прямолинейного участка, например чугун. Для таких материалов модуля упругости в обычном смысле не существует, вместо него вводится понятие о так называемом секущем модуле, который представляет собою угловой коэффициент луча, проведенного из начала координат в некоторую точку М диаграммы:
совсем не имеет прямолинейного участка, например чугун. Для таких материалов модуля упругости в обычном смысле не существует, вместо него вводится понятие о так называемом секущем модуле, который представляет собою угловой коэффициент луча, проведенного из начала координат в некоторую точку М диаграммы:

Секущий модуль — это переменная величина, ее можно считать функцией напряжения, соответствующего точке М. Когда говорят о модуле упругости чугуна, например, и применяют для расчета чугунных изделий закон Гука, имеют в виду некоторое среднее значение секущего модуля, соответствующее диапазону рабочих напряжений.
Наряду с секущим модулем введем касательный модуль, представляющий собою угловой коэффициент касательной к линии  :
:

Как видно, при  при изменении а касательный модуль
при изменении а касательный модуль  меняется значительно быстрее, чем
меняется значительно быстрее, чем  Возвращаясь к рис. 73, мы видим, что за пределом пропорциональности секущий модуль изменился мало по сравнению с его значением на прямолинейном участке, тогда как касательный модуль изменился весьма заметно. За предел пропорциональности обычно принимают напряжение, при котором касательный модуль превышает на определенное число процентов (например, на 50%) модуль упругости для прямолинейной части диаграммы.
Возвращаясь к рис. 73, мы видим, что за пределом пропорциональности секущий модуль изменился мало по сравнению с его значением на прямолинейном участке, тогда как касательный модуль изменился весьма заметно. За предел пропорциональности обычно принимают напряжение, при котором касательный модуль превышает на определенное число процентов (например, на 50%) модуль упругости для прямолинейной части диаграммы.
Описанный опыт не доставляет нам никаких сведений об упругих свойствах материала. Желая найти предел упругости, после каждой нагрузки разгружают образец и следят за появлением остаточной деформации. Более точные приборы, конечно, позволят обнаружить остаточную деформацию раньше, поэтому предел упругости определяют как напряжение, начиная с которого остаточное удлинение превышает некоторую условную величину (от  до
до  по разным нормам).
по разным нормам).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Задачи и содержание сопротивления материалов.
- § 2. Сопротивление материалов и теоретическая механика.
- § 3. Статически неопределенные задачи.
- § 4. Внешние силы.
- § 5. Принцип отвердения.
- § 6. Недопустимость замены системы сил статически эквивалентной.
- § 7. Однородное тело.
- § 8. Внутренние силы.
- § 9. Напряжение.
- § 10. Простейшие типы напряженного состояния.
- § 11. Простейшие виды деформации.
- § 12. Упругость и пластичность.
- § 13. Закон Гука.
- § 14. Диаграмма пластичности.
- § 15. Тела изотропные и анизотропные.
- ГЛАВА II. РАСТЯЖЕНИЕ СЖАТИЕ
- § 16. Стержни и стержневые системы.
- § 17. Принцип Сен-Венана и гипотеза плоских сечений.
- § 18. Напряжения и деформации при растяжении.
- § 19. Расчеты на прочность при растижении и сжатии.
- § 20. Собственный вес и силы инерции.
- § 21. Стержни переменного сечения.
- § 22. Перемещения узлов стержневых систем.
- § 23. Статически неопределенные задачи на растяжение — сжатие.
- § 24. Температурные и монтажные напряжения.
- § 25. Общие соображения о расчете стержневых систем.
- § 26. Расчет статически неопределимых систем по допускаемым нагрузкам.
- § 27. Остаточные напряжения после пластической деформации.
- § 28. Потенциальная энергия растяжении.
- § 29. Напряжения при ударе.
- § 30. Распространение упругих волн в стержнях.
- § 31. Концентрации напряжений.
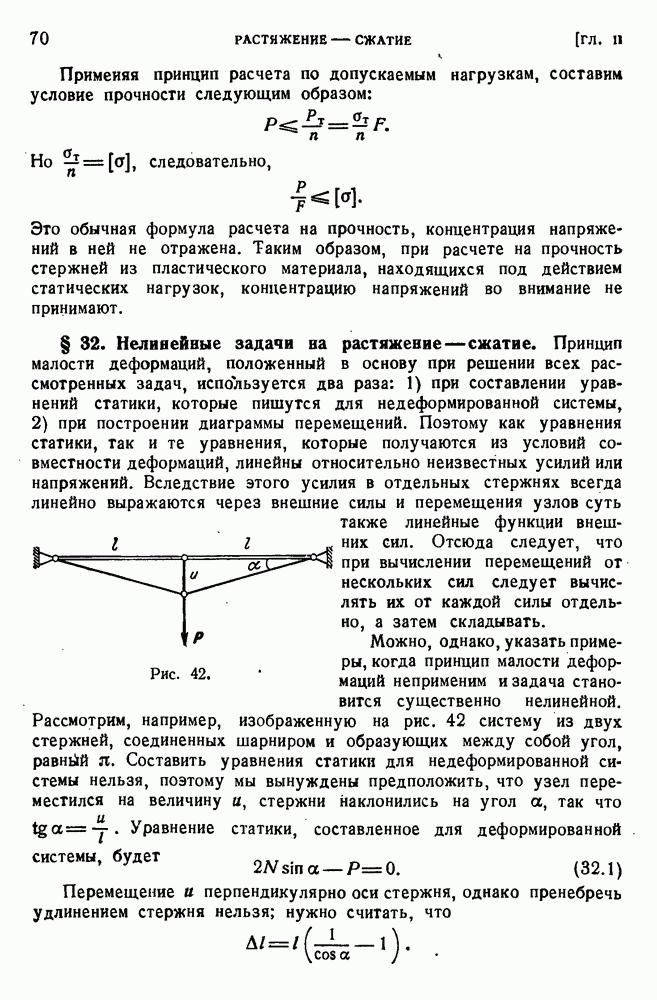
- § 32. Нелинейные задачи на растяжение — сжатие.
- ГЛАВА III. СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
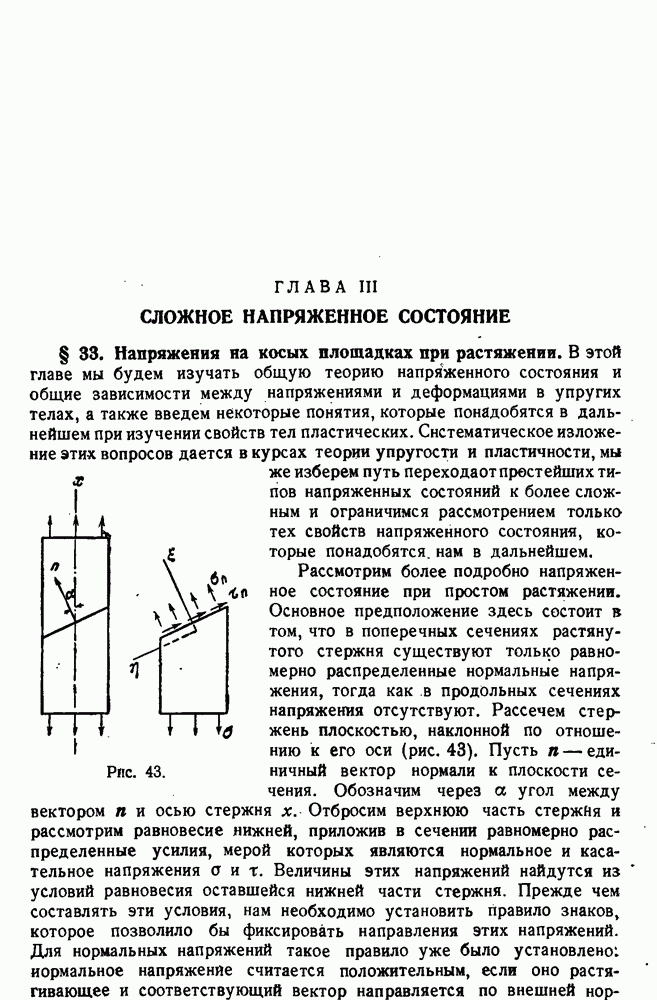
- § 33. Напряжения на косых площадках при растяжении.
- § 34. Напряжения при двухосном растяжении.
- § 35. Круговая диаграмма Мора.
- § 36. Общий случай плоского напряженного состояния.
- § 37. Определение напряжений на произвольной площадке.
- § 38. Пространственное напряженное состояние.
- § 39. Главные напряжения.
- § 40. Главные касательные напряжения.
- § 41. Октаэдрическое напряжение.
- § 42. Закон Гука для главных осей.
- § 43. Изменение объема при упругой деформации.
- § 44. Чистый сдвиг.
- § 45. Деформация элемента объема в общем случае.
- § 46. Условие пластичности Треска — Сен-Венана.
- § 47. Условие пластичности Мизеса.
- § 48. Условия пластичности для плоского напряженного состояния.
- § 49. Потенциальная энергия упругой деформации.
- § 50. Энергия изменения формы.
- ГЛАВА IV. НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
- § 51. Расчеты на прочность изделий сложной формы.
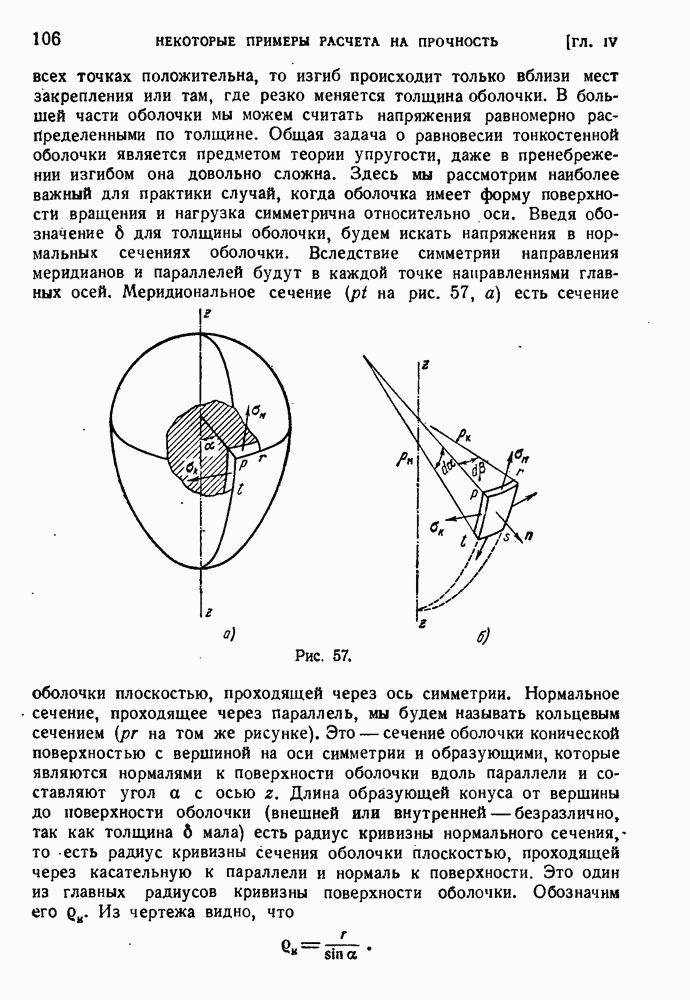
- § 52. Безмоментные оболочки вращении.
- § 53. Местные напряжения в безмоментных оболочках.
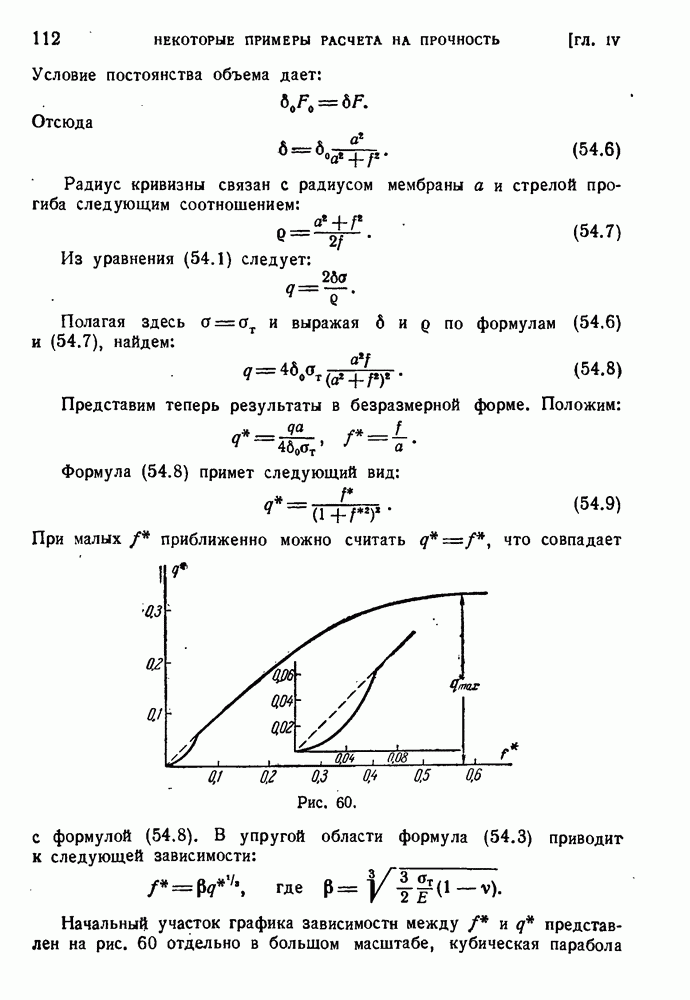
- § 54. Большие прогибы мембраны.
- § 55. Условные расчеты.
- § 56. Некоторые дальнейшие примеры условных расчетов.
- § 57. Расчет сварных соединений.
- ГЛАВА V. ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
- § 58. Задачи испытания материалов.
- § 59. Статические испытания на растяжение.
- § 60. Исследование металлов в области малых деформаций.
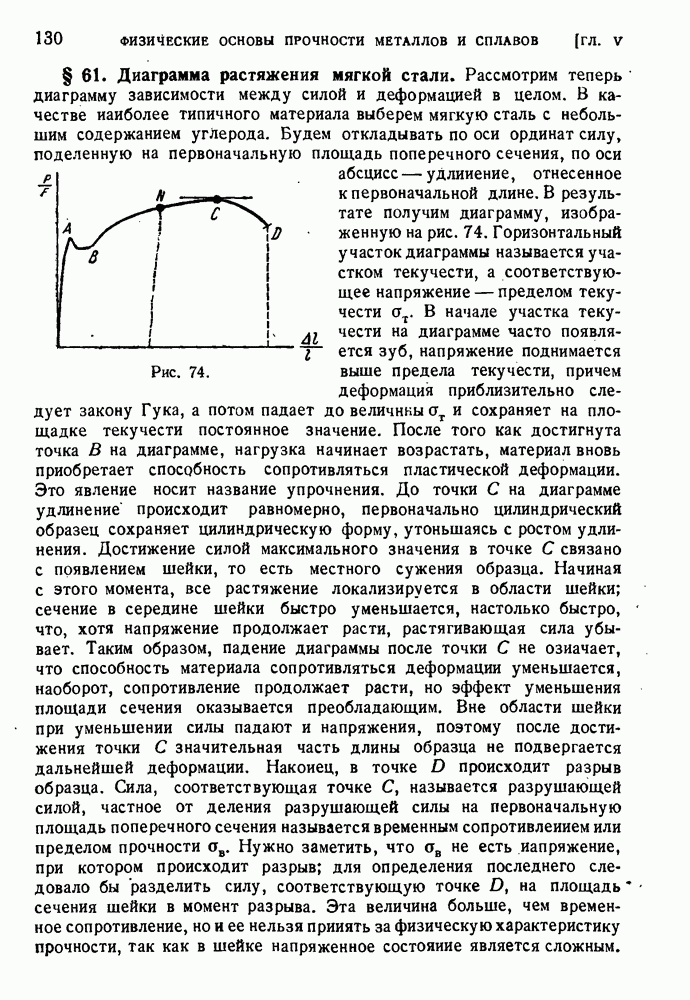
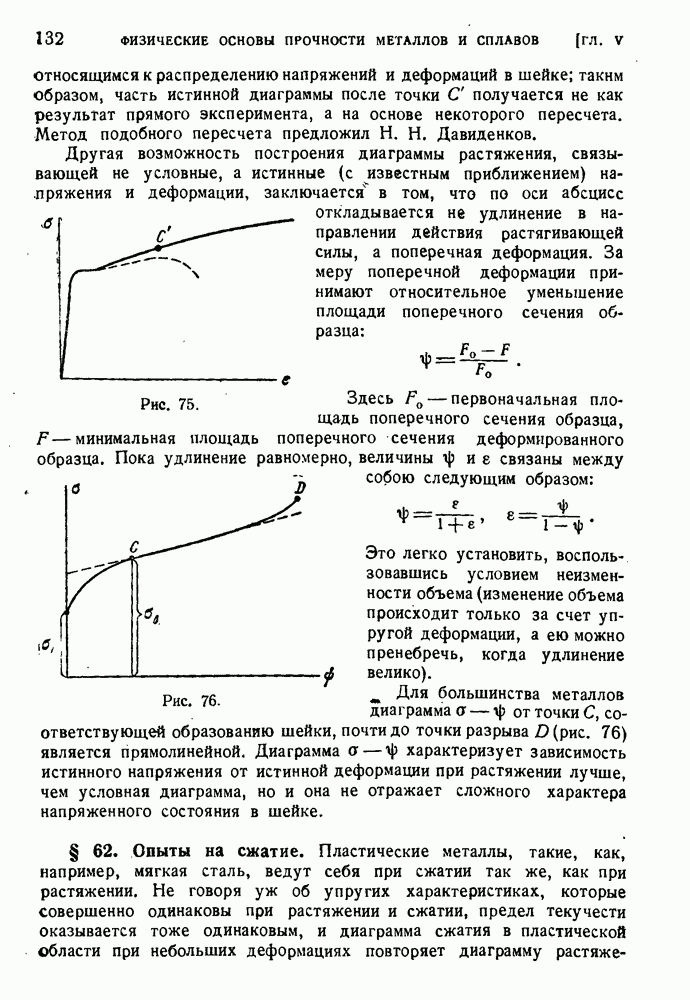
- § 61. Диаграмма растяжения мягкой стали.
- § 62. Опыты на сжатие.
- § 63. Строение и упругая деформация металлических кристаллов.
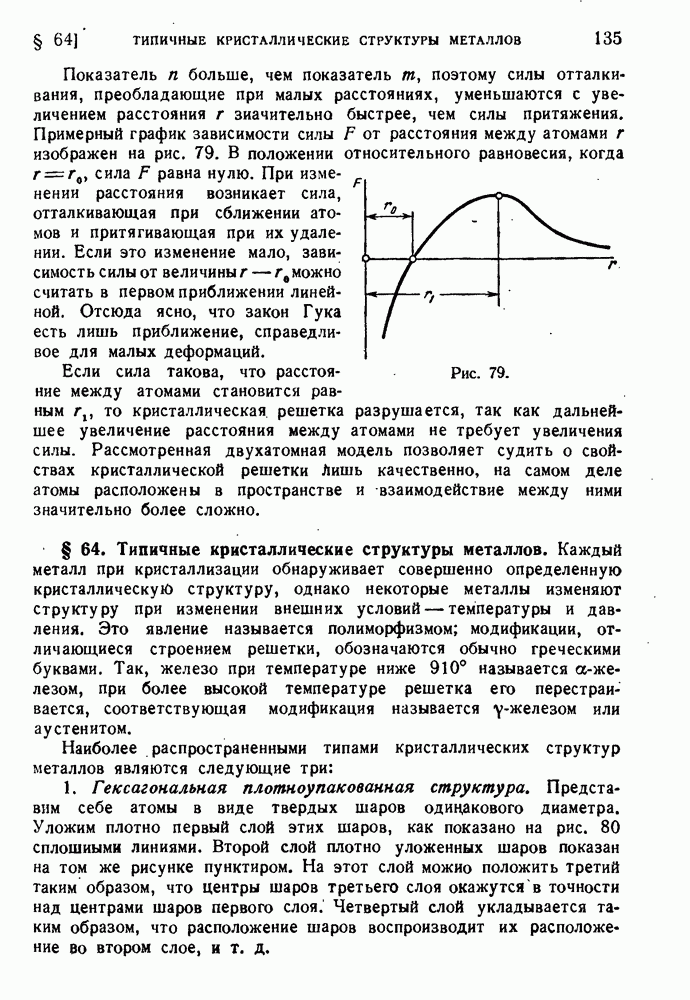
- § 64. Типичные кристаллические структуры металлов.
- § 65. Пластическая деформация монокристаллов.
- § 66. Прочность кристаллов и сопротивление пластическому деформированию.
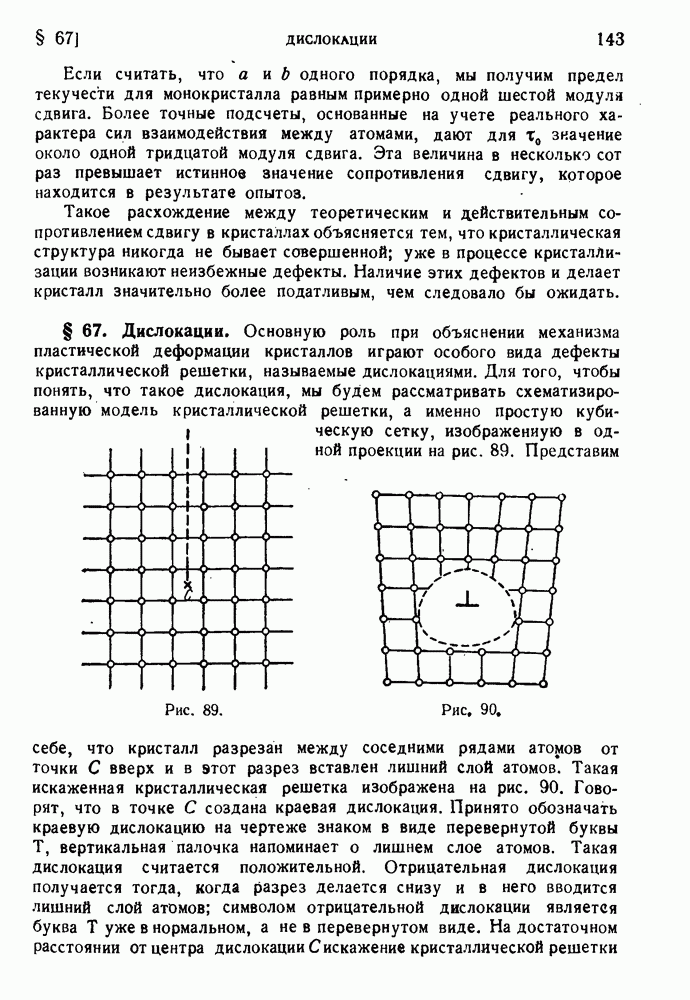
- § 67. Дислокации.
- § 68. Движение и равновесие дислокаций.
- § 69. Источники дислокаций.
- § 70. Границы блоков.
- § 71. Деформация поликристаллических металлов и сплавов.
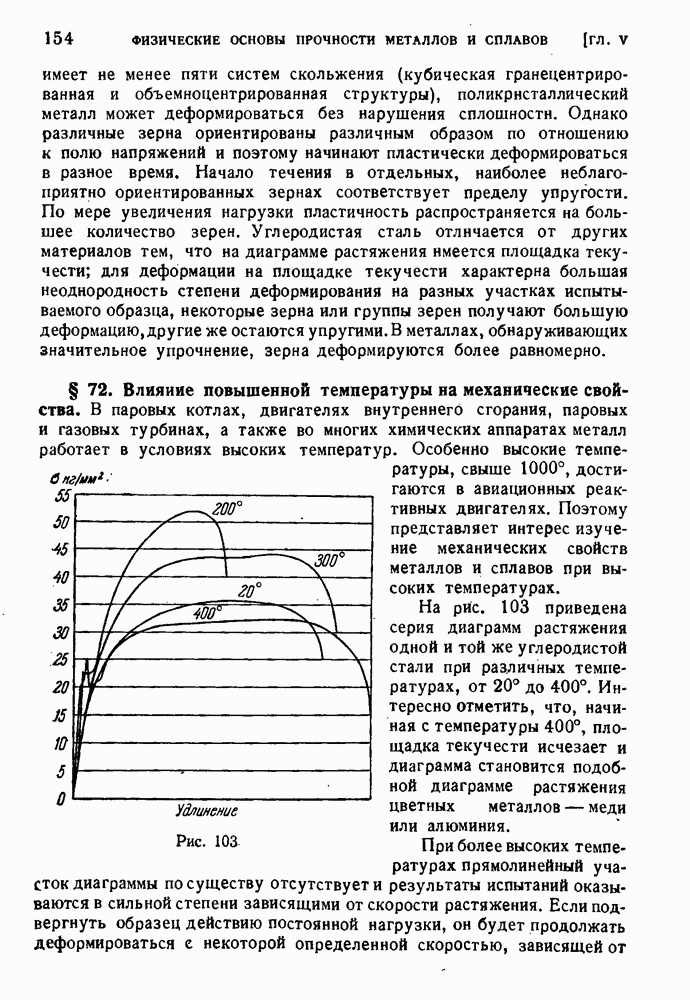
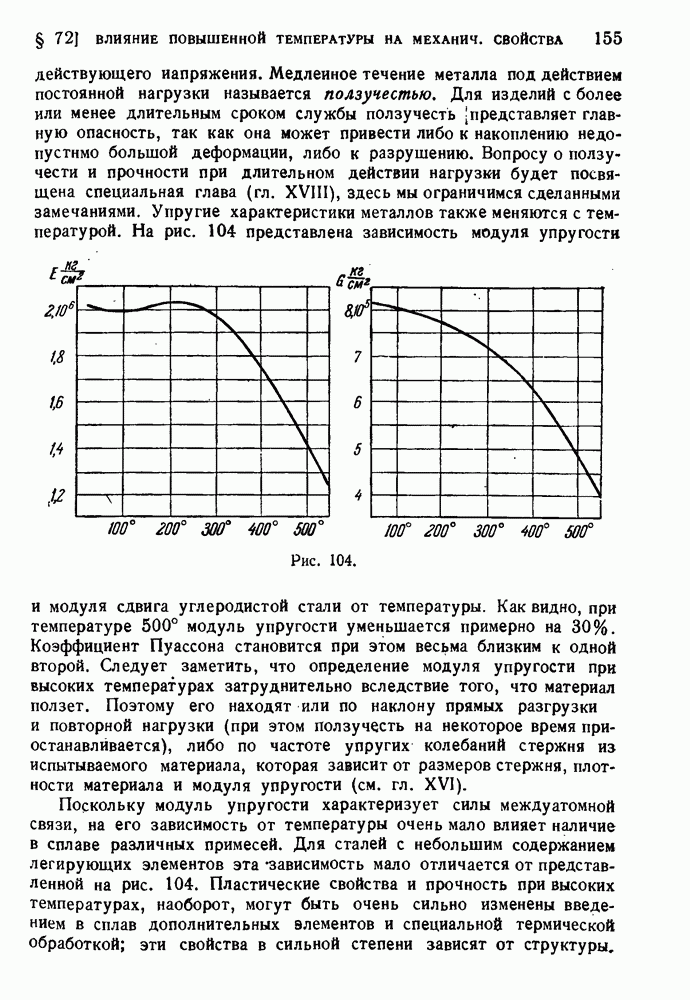
- § 72. Влияние повышенной температуры на механические свойства.
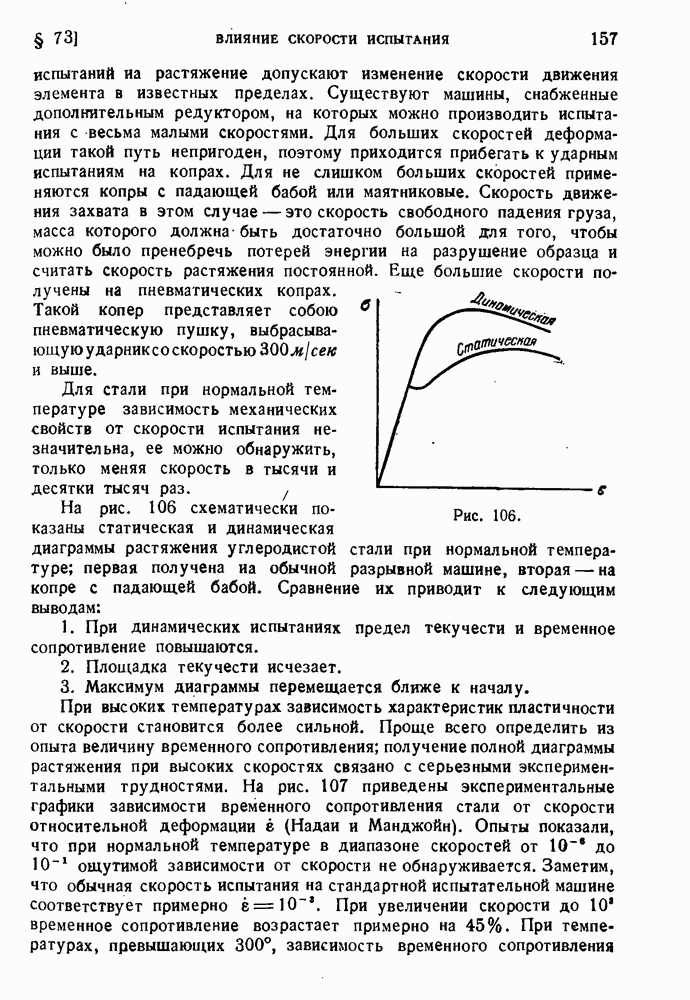
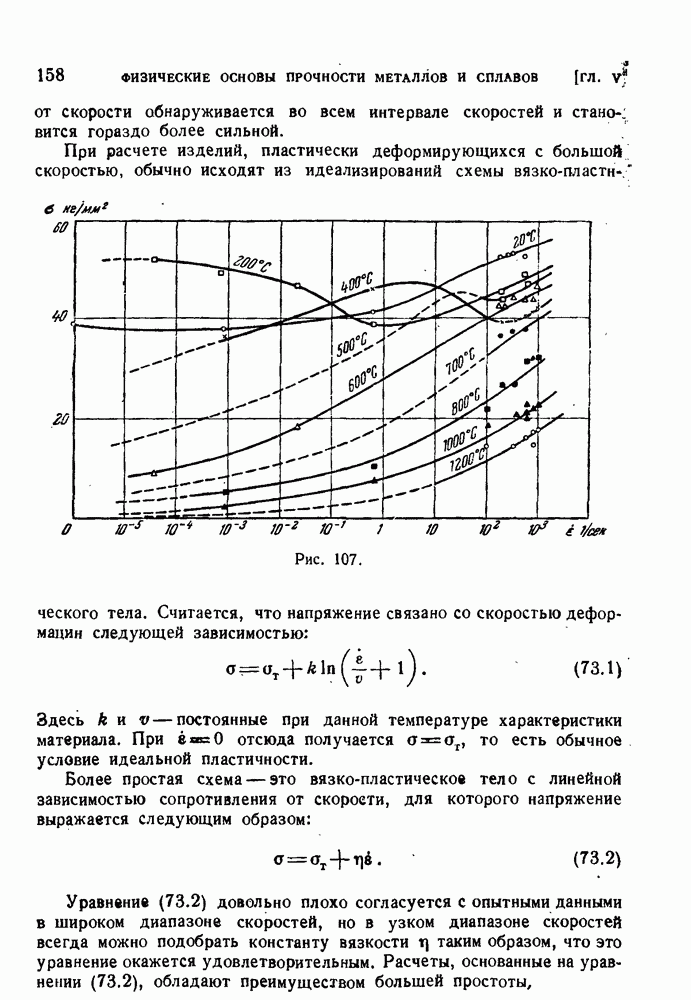
- § 73. Влияние скорости испытания.
- § 74. Испытании на твердость.
- ГЛАВА VI. ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ
- § 75. Основные принципы построения теории пластичности.
- § 76. Ассоциированный закон течения.
- § 77. Течение при условии пластичности Сен-Венана и Мизеса.
- § 78. Закон упрочнения.
- § 79. Деформационная теория пластичности.
- § 80. Экспериментальная проверка теорий пластичности.
- § 81. Конечная деформация.
- § 82. Нелинейно упругое тело.
- § 83. Высокоэластические деформации.
- § 84. Упругое последействие.
- § 85. Некоторые свойства вязко-упругого тела.
- § 86. Принцип суммирования Больцмана—Вольтерра.
- ГЛАВА VII. КРУЧЕНИЕ
- § 87. Кручение стержней круглого сечеиия.
- § 88. Упруго-пластическое кручение стержня круглого сечения.
- § 89. Гипотеза жесткого контура.
- § 90. Кручение тонкостенных стержней замкнутого профиля.
- § 91. Кручение тонкостенных стержней открытого профиля.
- § 92. Кручение упругих стержией сплошного профиля.
- § 93. Опытное исследование кручения.
- § 94. Предельное состояние закрученного стержня из идеально-пластического материала.
- ГЛАВА VIII. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- § 96. Общие теоремы о моментах.
- § 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей.
- § 98. Вычисление моментов инерции.
- § 99. Преобразование моментов инерции при повороте осей.
- § 100. Главные оси и главные моменты инерции.
- ГЛАВА IX. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
- § 101. Действие поперечных сил на балку.
- § 102. Гипотеза плоских сечений и принцип Сен-Венана.
- § 103. Нормальные напряжения при изгибе.
- § 104. Изгибающие моменты и перерезывающие силы.
- § 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры.
- § 106. Расчет на прочность при изгибе по допускаемым напряжениям.
- § 107. Упруго-пластический изгиб.
- § 108. Несущая способность стержня при изгибе.
- § 109. Принцип Сен-Венана.
- § 110. Внецентренное растяжение — сжатие.
- § 111. Ядро сечения.
- § 112. Несущая способность внецентренно сжатого стержня.
- § 113. Расчет составных балок.
- § 114. Изгиб кривого бруса.
- § 115. Нахождение нейтральной осн в кривом стержне.
- ГЛАВА X. ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- § 116. Дифференциальное уравнение изогнутой оси.
- § 117. Пределы применимости приближенной теории.
- § 118. Интегрирование уравнения изгиба.
- § 119. Примеры определения прогибов.
- § 120. Простейшие статически неопределенные задачи.
- § 121. Расчет статически неопределимых балок по способу допускаемых нагрузок.
- § 122. Изгиб стержней переменного сечения.
- § 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами.
- § 124. Продольно-поперечный изгиб.
- § 125. Изгиб балки на упругом основании.
- ГЛАВА XI. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
- § 126. Нормальные и касательные напряжения при изгибе.
- § 127. Касательные напряжении при изгибе в плоскости симметрии.
- § 128. Центр изгиба.
- § 129. Дополнительные напряжения при кручении.
- § 130. Закон секториальных площадей.
- § 131. Уравнение стесненного кручения.
- § 132. Вычисление секториальных характеристик.
- § 133. Стержень, нагруженный бимоментом.
- § 134. Некоторые примеры стесненного кручения.
- ГЛАВА XII. УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ
- § 135. Постановка вопроса об устойчивости.
- § 136. Устойчивость сжатого упругого стержня.
- § 137. Эластика Эйлера.
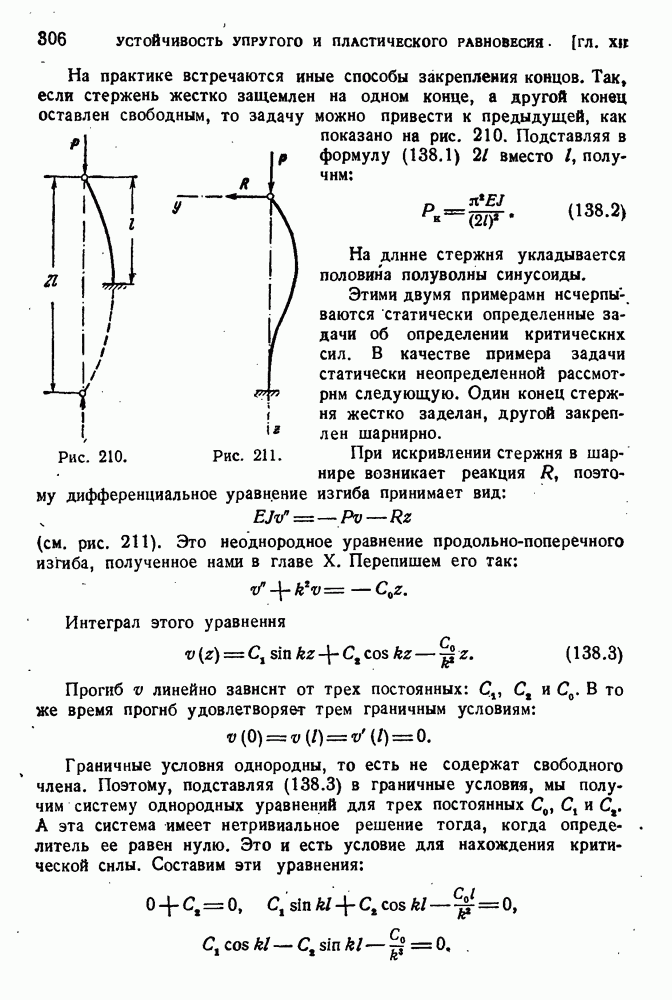
- § 138. Критические силы при иных видах закрепления стержня.
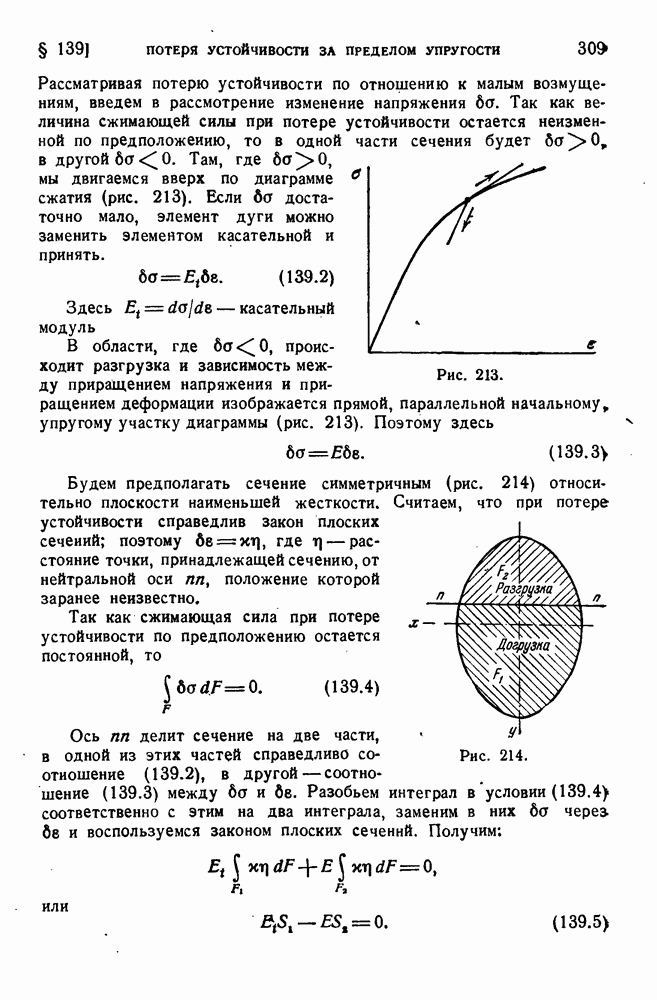
- § 139. Потеря устойчивости за пределом упругости.
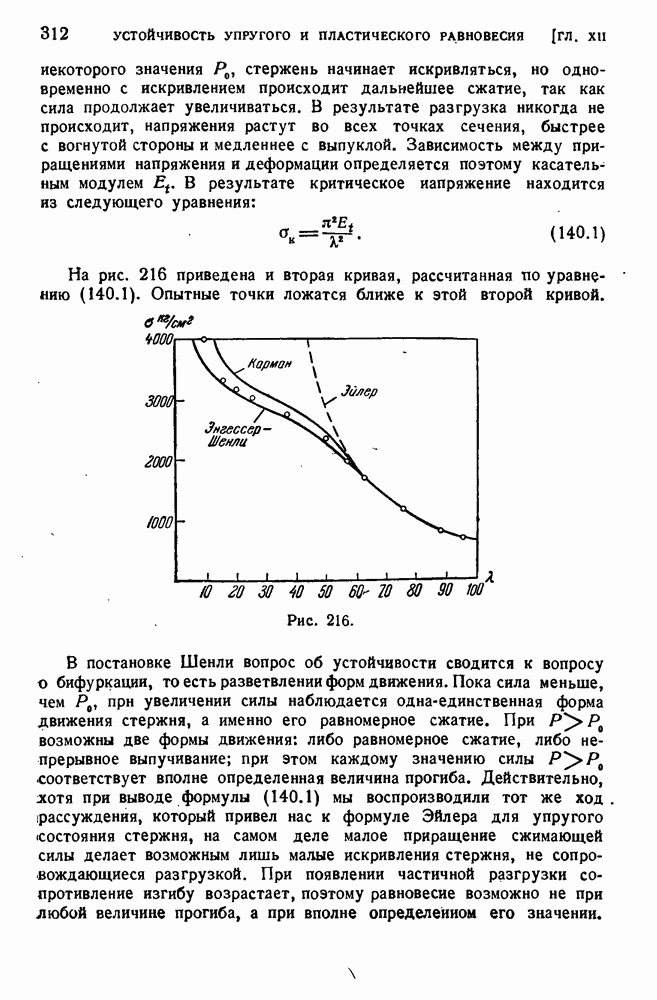
- § 140. Потеря устойчивости за пределом упругости (продолжение).
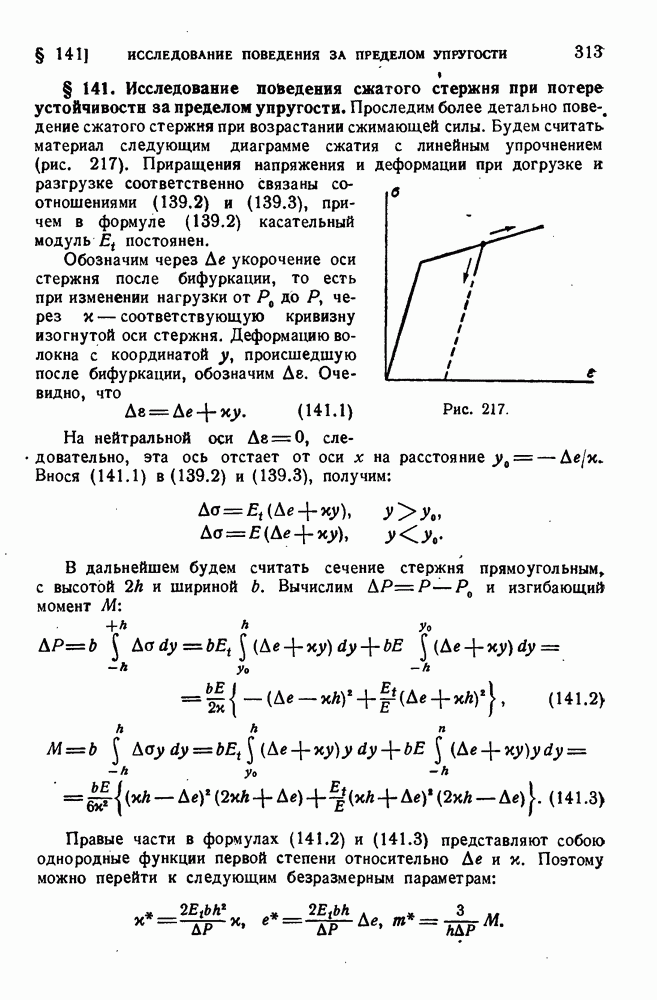
- § 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости.
- § 142. Расчет на устойчивость по эмпирическим формулам.
- ГЛАВА XIII. ТРУБЫ И ДИСКИ
- § 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности.
- § 144. Упругое состояние трубы. Формулы Ламе.
- § 145. Пластическое состояние трубы.
- § 146. Вращающиеся диски. Упругое состояние.
- § 147. Диск равного сопротивления.
- § 148. Предельное равновесие вращающегося диска.
- ГЛАВА XIV. ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 149. Обобщенные силы и обобщенные перемещения.
- § 150. Начало возможных перемещений для деформируемого тела.
- § 151. Теоремы Лагранжа и Кастильяно.
- § 152. Лииейиые упругие системы.
- § 153. Теорема о взаимности работ.
- § 154. Теорема Кастильяно для линейных упругих систем.
- § 155. Расчет винтовых пружин.
- § 156. Теорема о минимуме энергии.
- § 157. Интеграл перемещений.
- § 158. Графоаналитический способ вычислений интеграла перемещений.
- § 159. Расчет статически неопределимых систем по методу сил.
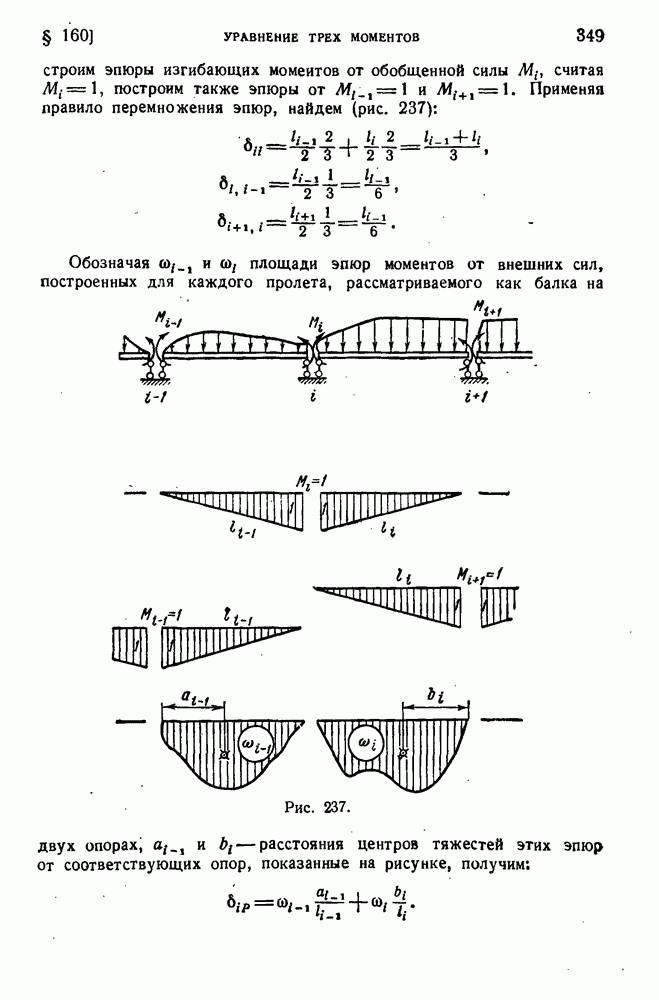
- § 160. Уравнение трех моментов.
- ГЛАВА XV. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
- § 161. Жестко-пластическое тело.
- § 162. Поверхности нагружения.
- § 163. Истинное и допустимые состояния элемента.
- § 164. Статический метод определения предельной нагрузки.
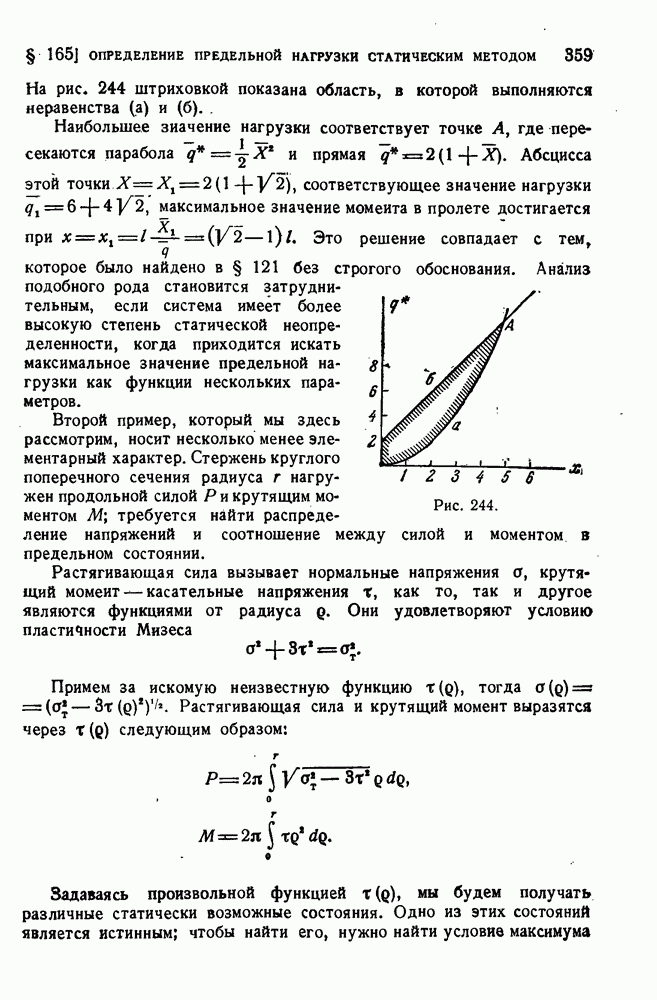
- § 165. Примеры определения предельной нагрузки статическим методом.
- § 166. Кинематически возможные состояния.
- § 167. Кинематический метод определения предельной нагрузки.
- § 168. Примеры определения предельной нагрузки кинематическим методом.
- § 169. Предельное равновесие пластинок.
- ГЛАВА XVI. ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 170. Колебания систем с конечным числом степеней свободы.
- § 171. Собственные частоты и главные формы колебаний.
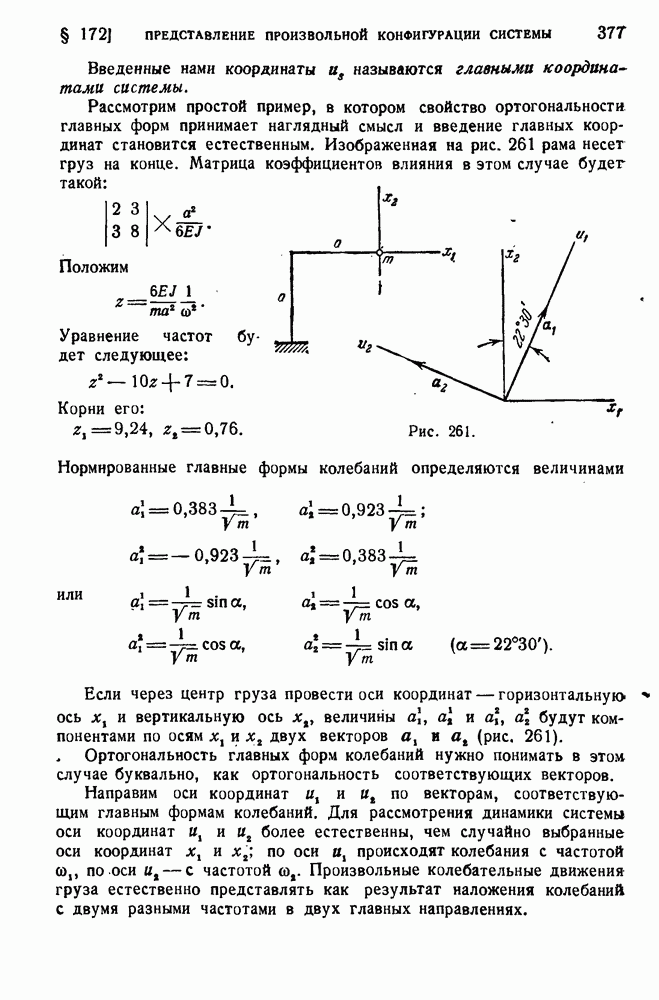
- § 172. Представление произвольной конфигурации системы через главные формы. Главные координаты.
- § 173. Формула и способ Релея.
- § 174. Нижние оценки для частоты основного тона.
- § 175. Продольные колебания стержней.
- § 176. Поперечные колебания стержней.
- § 177. Колебания балок постоянного сечения.
- § 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня.
- § 179. Действие ударных и импульсивных нагрузок на упругие системы.
- ГЛАВА XVII. ТЕОРИИ ПРОЧНОСТИ
- § 180. Постановка вопроса о прочности.
- § 181. Хрупкое и пластическое разрушение.
- § 182. Теория прочности Мора.
- § 183. Механизм хрупкого разрушения.
- § 184. Прочность при низких температурах.
- § 185. Прочность при переменных нагрузках.
- § 186. Природа усталостного разрушения.
- § 187. Критерии прочности при переменных нагрузках.
- § 188. Влияние концентрации напряжений на усталостную прочность.
- § 189. Усталостная прочность при сложном напряженном состоянии.
- ГЛАВА XVIII. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
- § 190. Ползучесть металлов.
- § 191. Процесс ползучести.
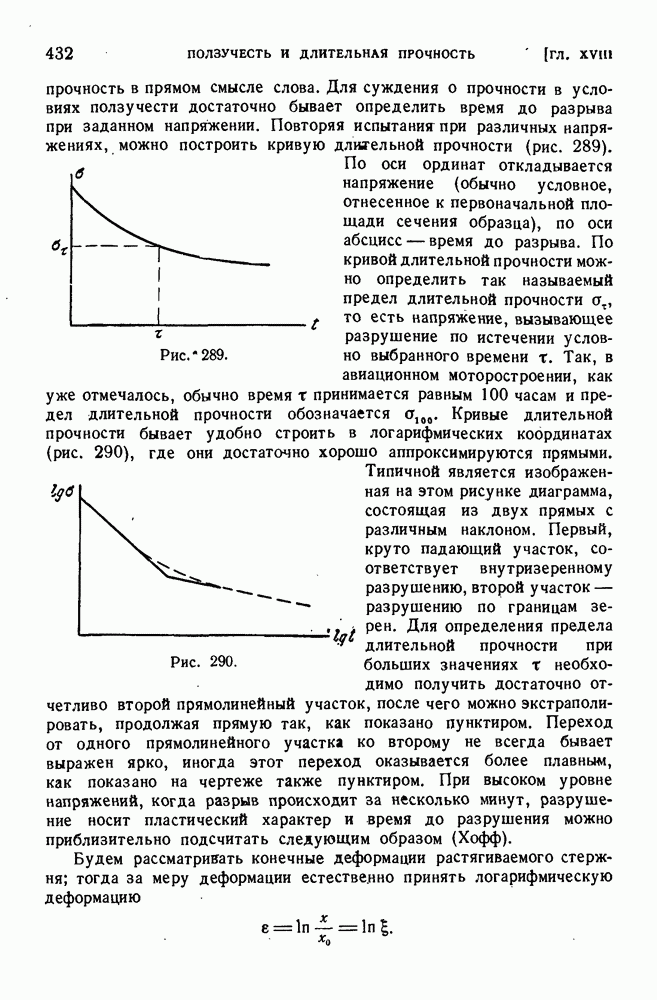
- § 192. Длительное разрушение.
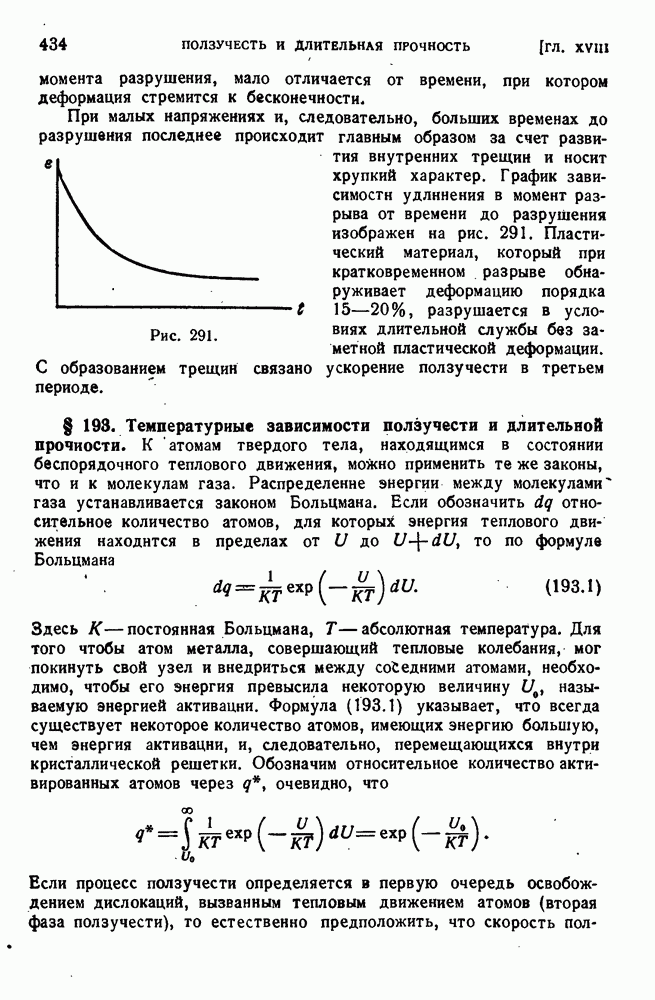
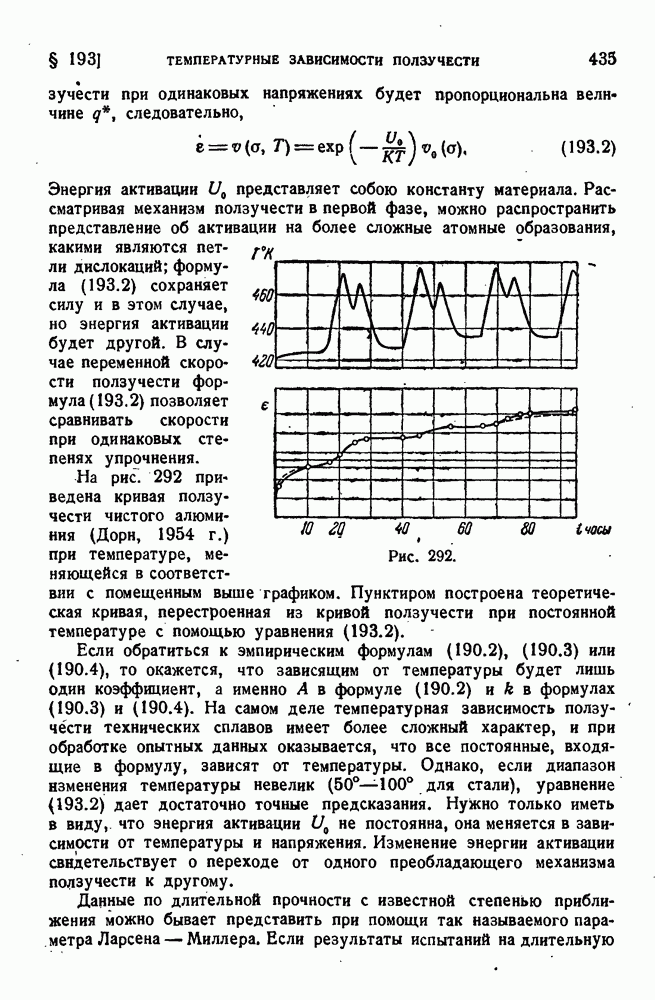
- § 193. Температурные зависимости ползучести и длительной прочности.
- § 194. Феноменологические теории одномерной ползучести.
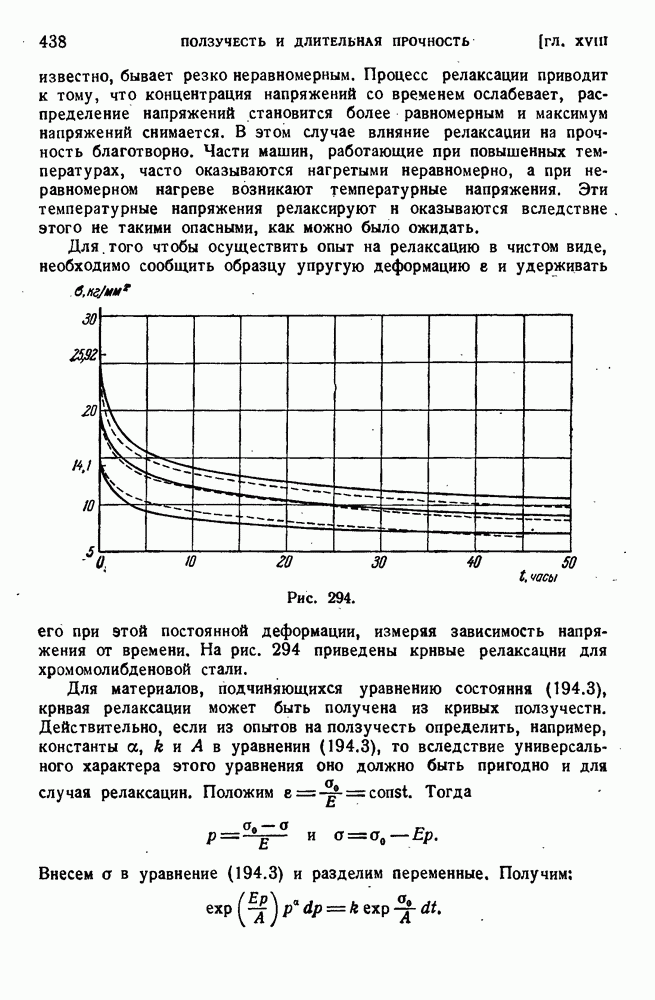
- § 195. Релаксация напряжений.
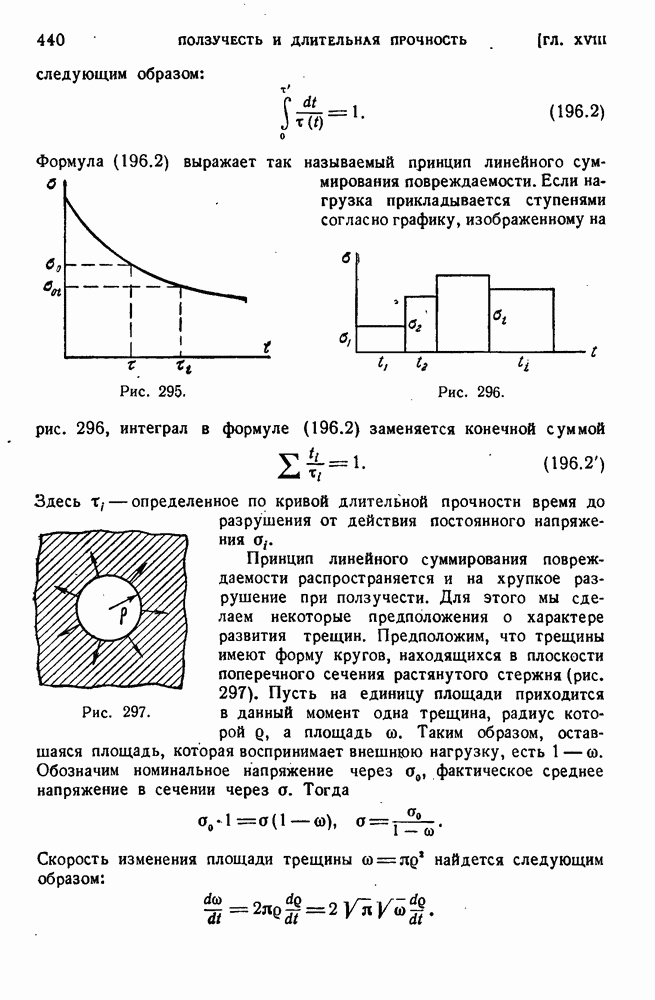
- § 196. Длительная прочность при переменных нагрузках.
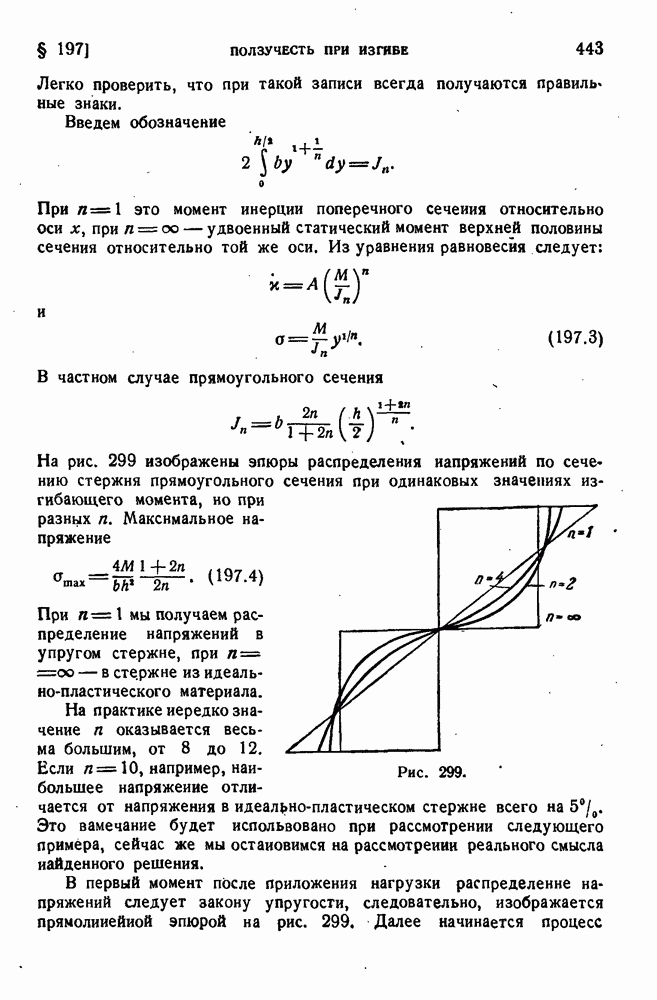
- § 197. Ползучесть при изгибе.
- § 198. Критическое время сжатого стержня.
- § 199. Ползучесть и длительная прочность при сложном напряженном состоянии.
- § 200. Вращающиеся диски в условиях ползучести.
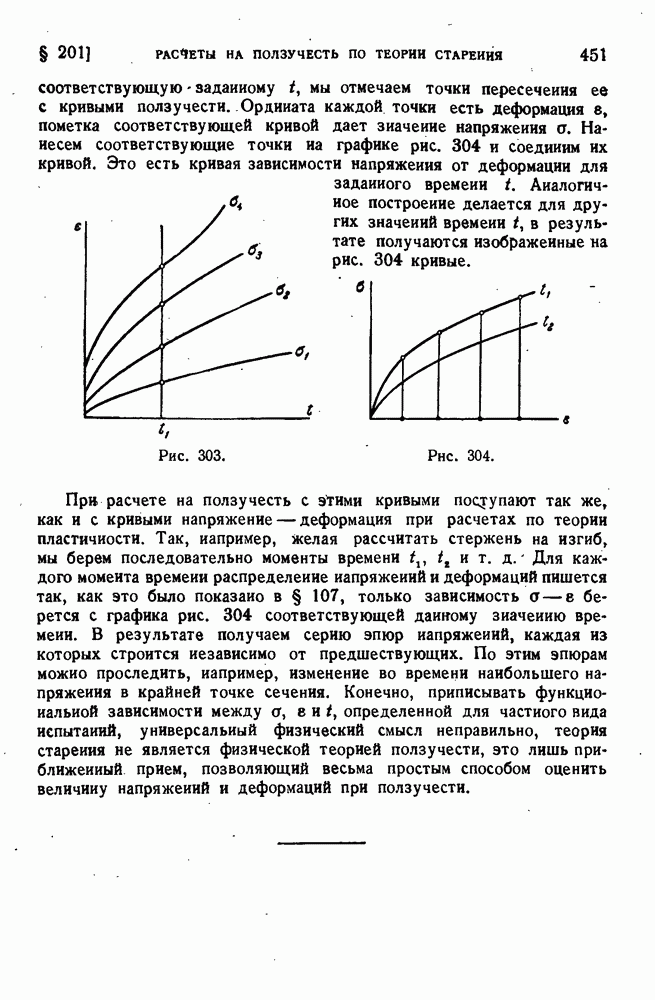
- § 201. Расчеты на ползучесть по теории старении.