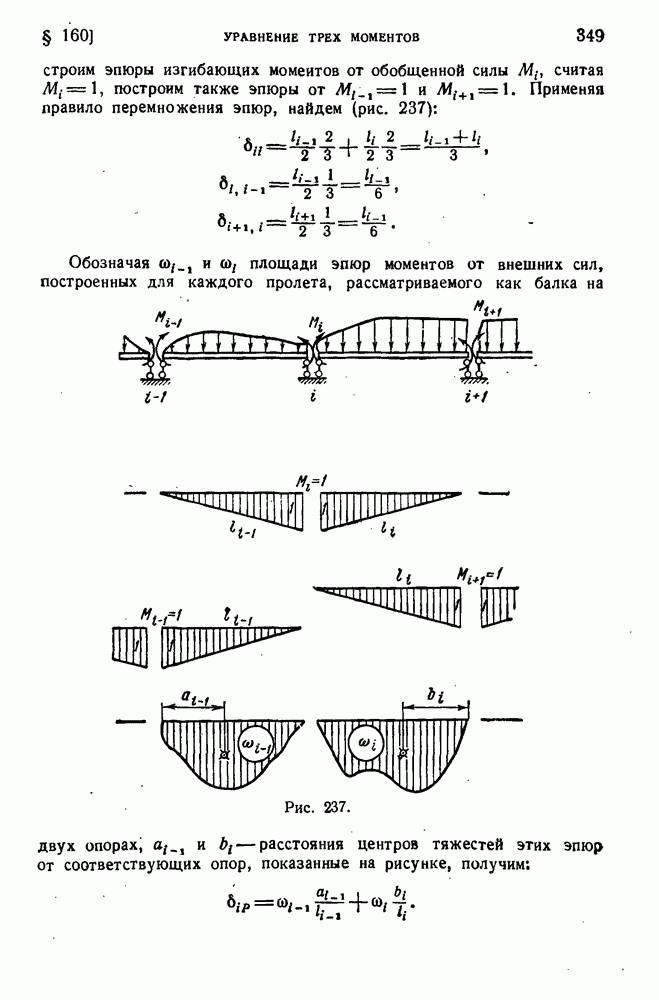
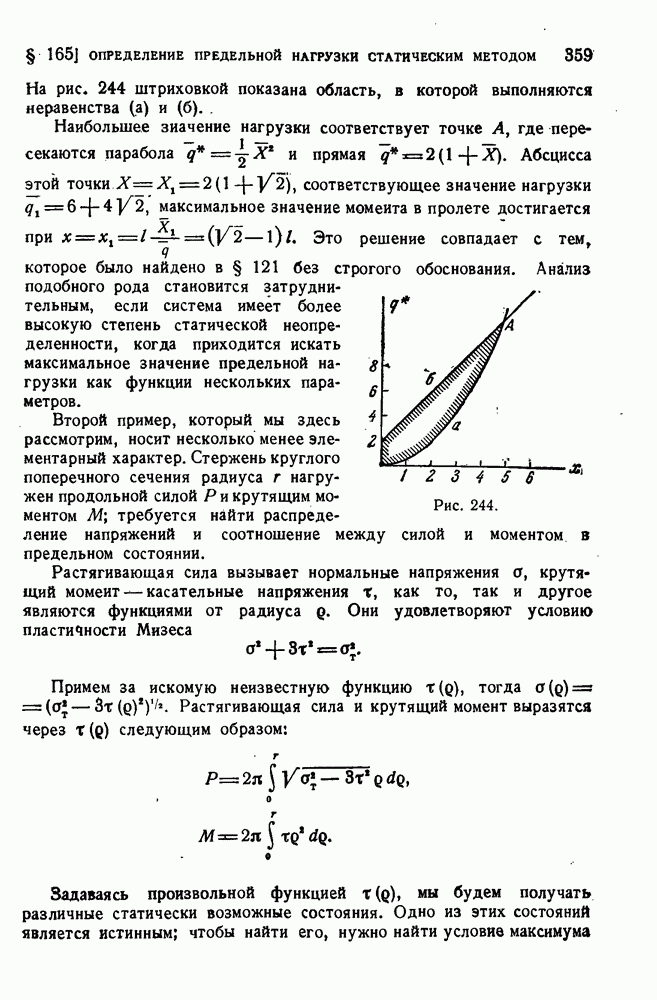
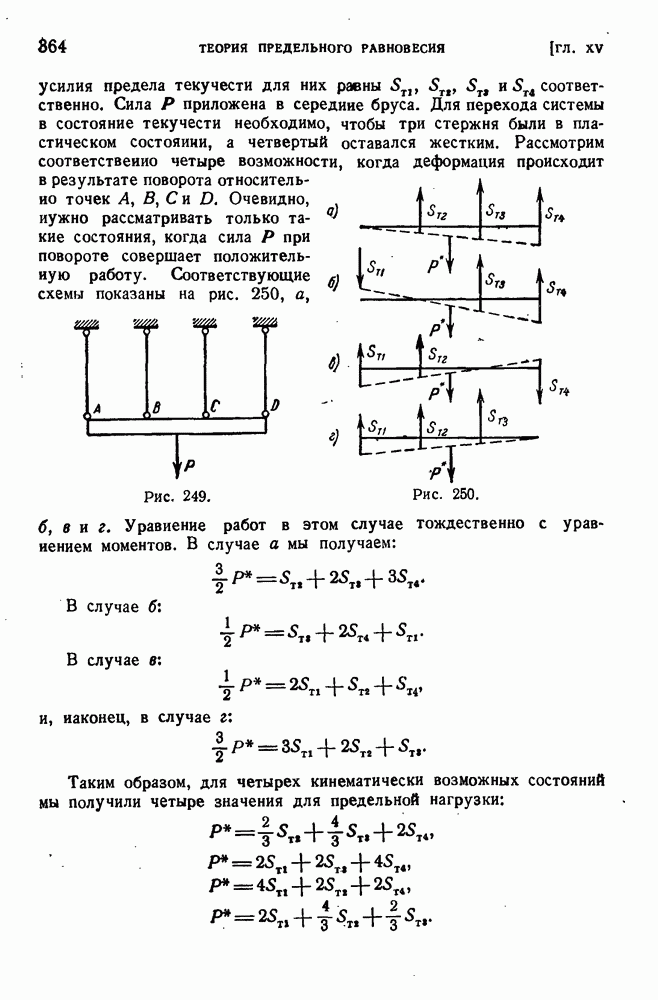
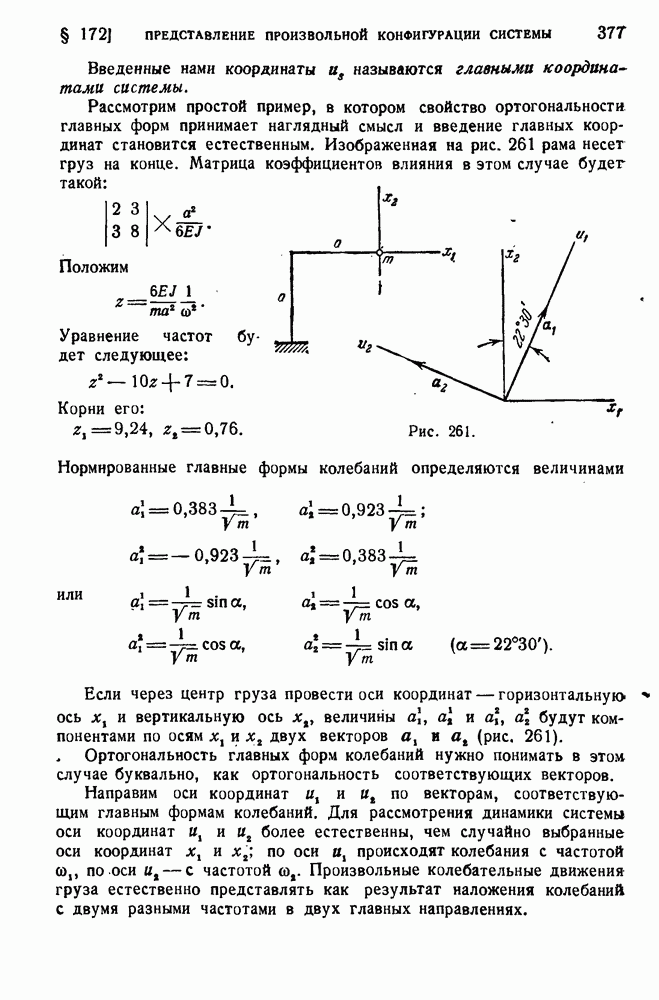
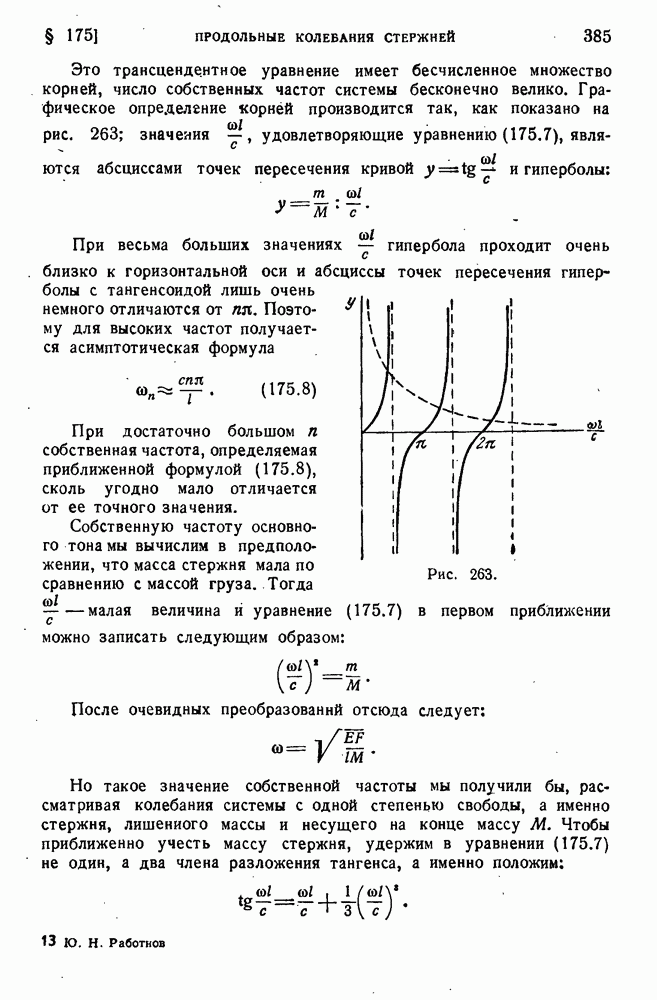
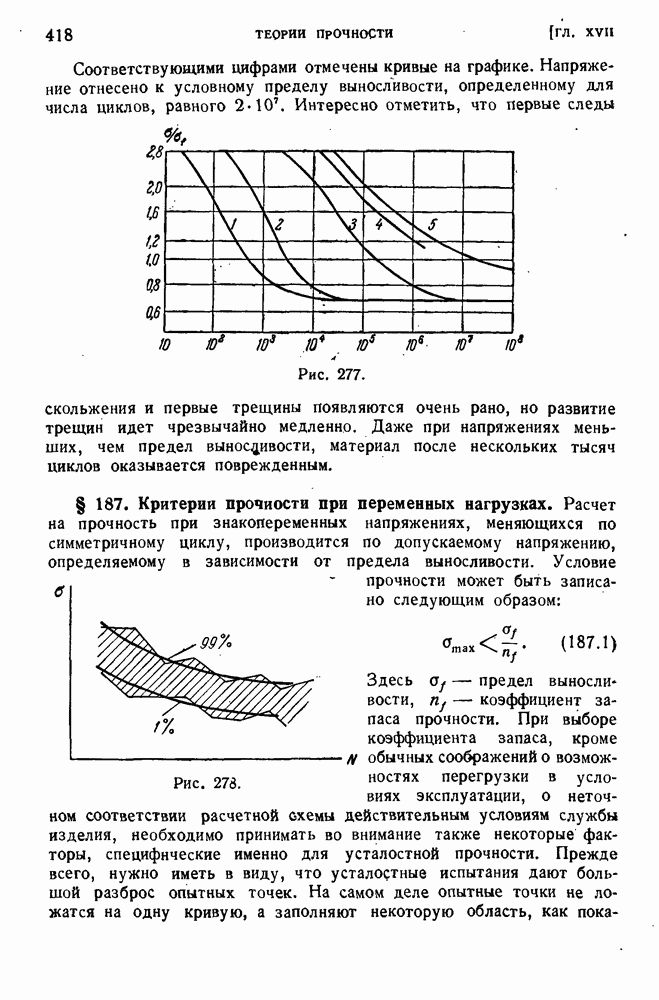
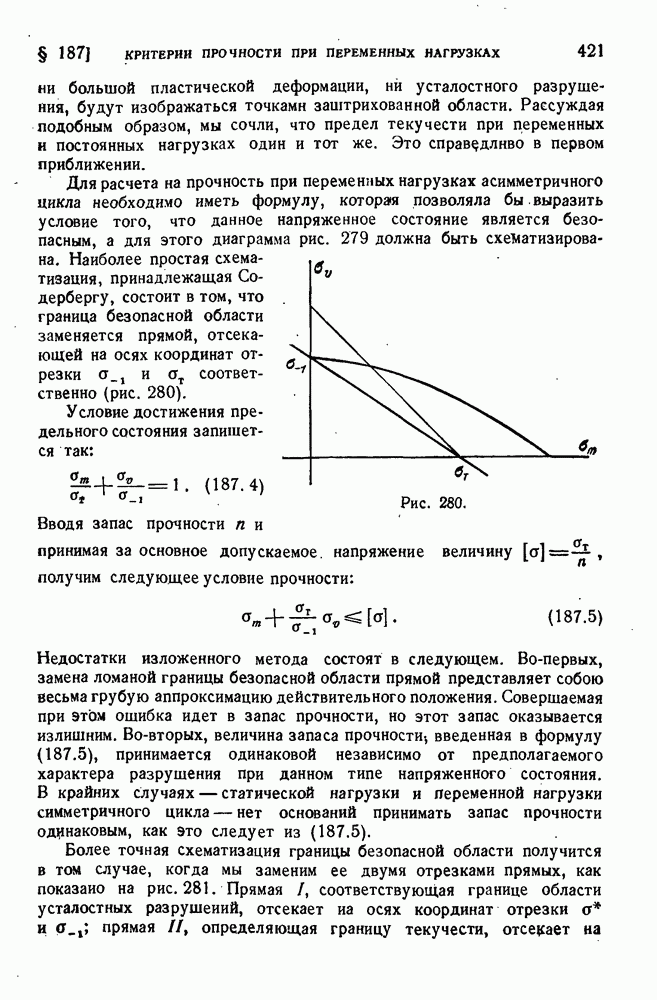
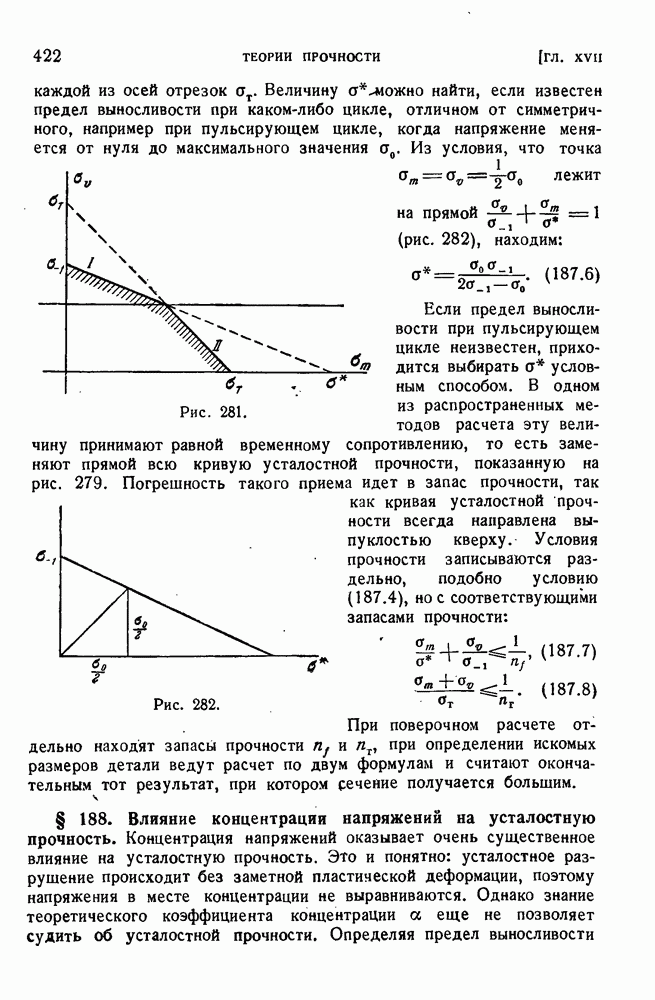
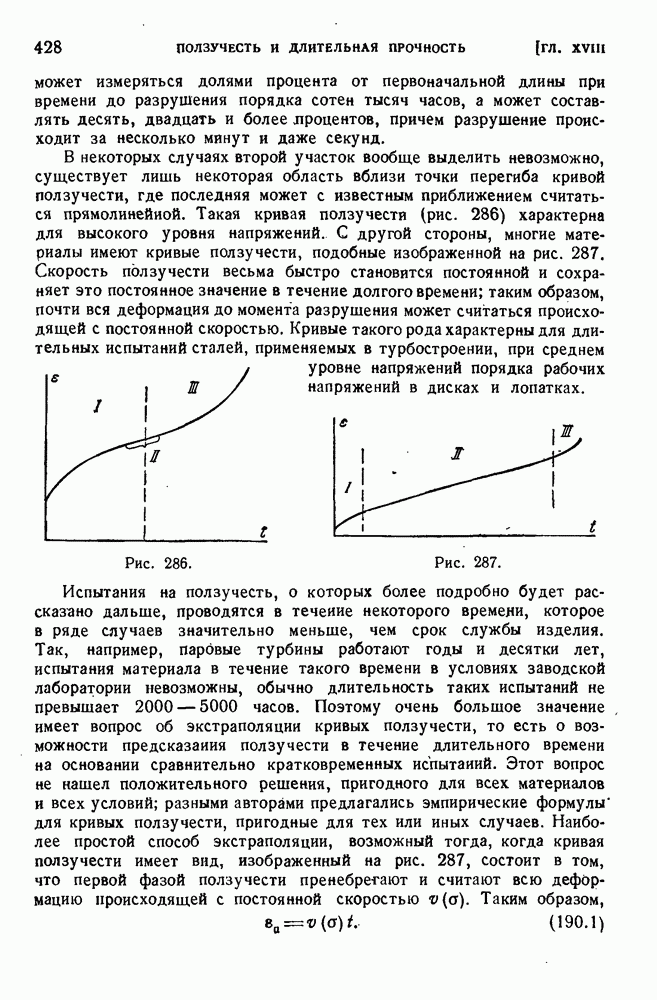
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 27. Остаточные напряжения после пластической деформации.
Если удалить внешние силы, стержни, претерпевшие пластические деформации, не вернутся в исходное состояние и не дадут вернуться в исходное состояние тем стержням, которые остались упругими. В системе появятся остаточные напряжения и деформации. Определение остаточных напряжений и деформаций производится на основании теоремы о разгрузке. Для доказательства этой теоремы заметим, что соотношения (26.3) и (26.4) справедливы для любого состояния системы независимо от того, находятся ее элементы в упругом или пластическом состоянии. Изменение нагрузок сказывается лишь на величинах  . При отсутствии нагрузок мы получаем:
. При отсутствии нагрузок мы получаем:

Вычтем из уравнений (26.3) уравнения (27.1) и из (26.4) — (27.2). Получим:

Здесь  может быть упругой или пластической деформацией; в последнем случае соответствующее
может быть упругой или пластической деформацией; в последнем случае соответствующее  .
.
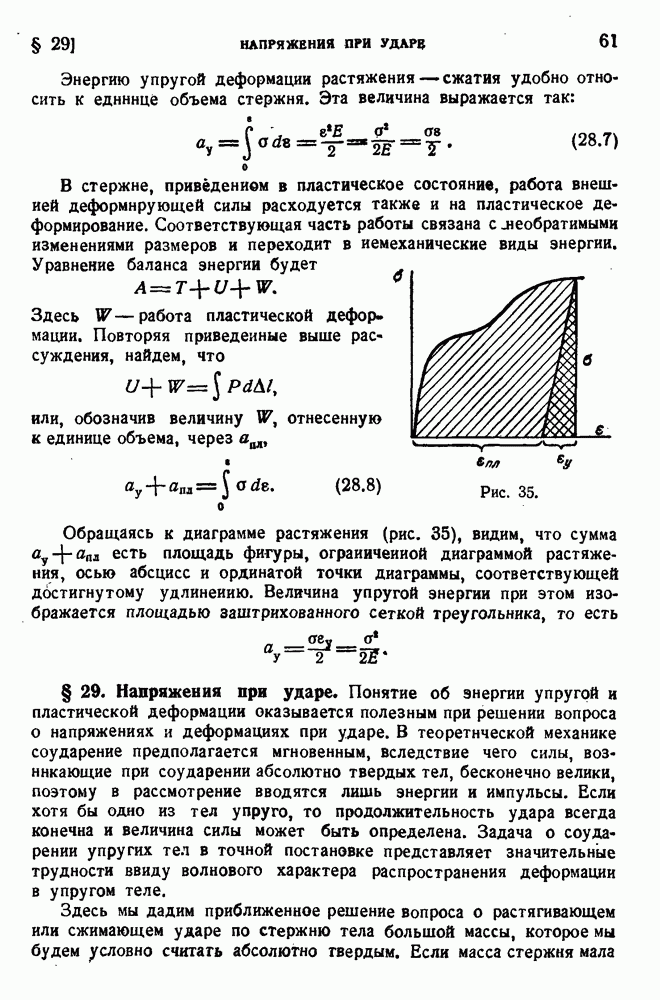
Обращаясь к диаграмме пластичности на рис. 34, убеждаемся, что как в том, так и в другом случае

Положим:

Величины  связаны следующими уравнениями:
связаны следующими уравнениями:

Но это — уравнения для решения статически неопределенной задачи в предположении упругости стержней. Решая эти уравнения, найдем  и вычислим остаточные напряжения и деформации по формулам:
и вычислим остаточные напряжения и деформации по формулам:

Таким образом, получаем следующую теорему о разгрузке:
Для определения напряжений и деформаций, остающихся в системе после снятия нагрузки, нужно вычесть из действительных напряжений и деформаций, соответствующих данной нагрузке, те напряжения и деформации, которые получаются при этой нагрузке в предположении упругости всех элементов.

Рис. 34.
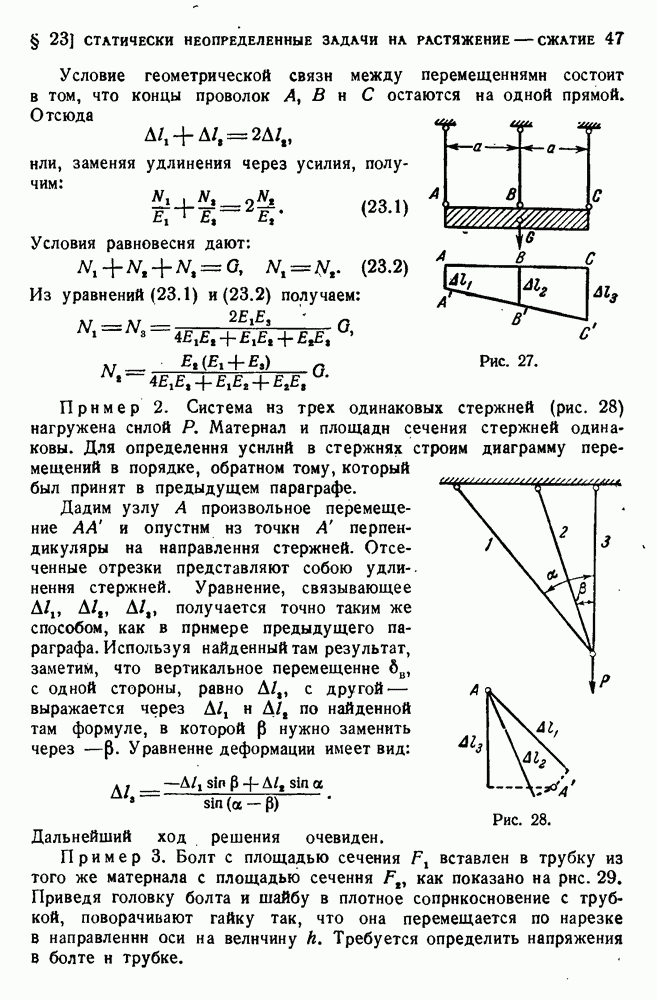
Определим для примера остаточные напряжения в системе из трех стержней, изображенной на рис. 33, если все стержни были выведены за предел текучести. Соответствующая нагрузка есть  фиктивные усилия, вычисленные в предположении упругости стержней, равны
фиктивные усилия, вычисленные в предположении упругости стержней, равны

Следовательно,

Предположим теперь, что разгруженная система нагружается вторично. Усилия, соответствующие нагрузке Р, можно определить так, как если бы никаких остаточных напряжений не было, а потом прибавить к ним остаточные напряжения. Пока материал упруг, получаем:

Из этих формул видно, что при повторной нагрузке система ведет себя совсем иначе, нежели при первой. Теперь предел текучести при увеличении силы Р достигается в обоих стержнях одновременно, когда  .
.
Обобщая этот результат, можем утверждать следующее:
При повторной нагрузке все элементы остаются упругими до тех пор, пока новая нагрузка не превышает той, от которой произведена разгрузка.
Как это правило, так и теорема о разгрузке справедливы лишь тогда, когда не возникают вторичные пластические деформации. Это значит, что остаточные напряжения при разгрузке, вычисленные в предположении упругой разгрузки, нигде не превышают предела текучести. В рассмотренном примере  , а
, а  Можно опасаться того, что остаточное сжимающее напряжение во втором стержне окажется по абсолютной величине больше предела текучести. В этом случае говорят о вторичных пластических деформациях; если они появляются, все рассуждения, конечно, становятся неверными. В данном примере легко проверить, что вторичные пластические деформации невозможны.
Можно опасаться того, что остаточное сжимающее напряжение во втором стержне окажется по абсолютной величине больше предела текучести. В этом случае говорят о вторичных пластических деформациях; если они появляются, все рассуждения, конечно, становятся неверными. В данном примере легко проверить, что вторичные пластические деформации невозможны.
Заметим, что теорема о разгрузке может быть обобщена на случай вторичных пластических деформаций. Фиктивные напряжения и деформации  при этом нужно вычислять с учетом возможности пластических деформаций, но при удвоенном пределе текучести.
при этом нужно вычислять с учетом возможности пластических деформаций, но при удвоенном пределе текучести.
Детальное выяснение обстоятельств последовательного перехода стержней из упругого состояния в пластическое само по себе редко бывает интересно; важно знать несущую способность системы, то есть ту нагрузку, при которой система становится изменяемой. В примере § 26 для определения величины РТ нужно было просто предположить, что в каждом стержне напряжения равны, и из условия равновесия найти эту силу. В сложных стержневых системах далеко не всегда бывает ясно, в каких именно элементах наступает текучесть. Поэтому необходимо или производить полный анализ по вышеописанной схеме, или же пользоваться общими методами, которые будут изложены в главе XV.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Задачи и содержание сопротивления материалов.
- § 2. Сопротивление материалов и теоретическая механика.
- § 3. Статически неопределенные задачи.
- § 4. Внешние силы.
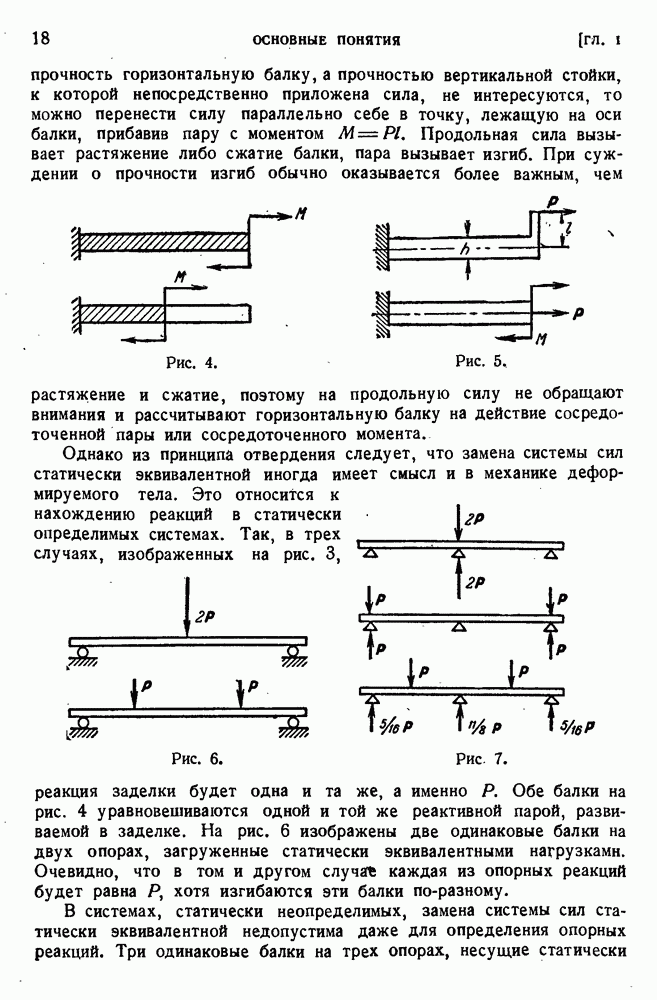
- § 5. Принцип отвердения.
- § 6. Недопустимость замены системы сил статически эквивалентной.
- § 7. Однородное тело.
- § 8. Внутренние силы.
- § 9. Напряжение.
- § 10. Простейшие типы напряженного состояния.
- § 11. Простейшие виды деформации.
- § 12. Упругость и пластичность.
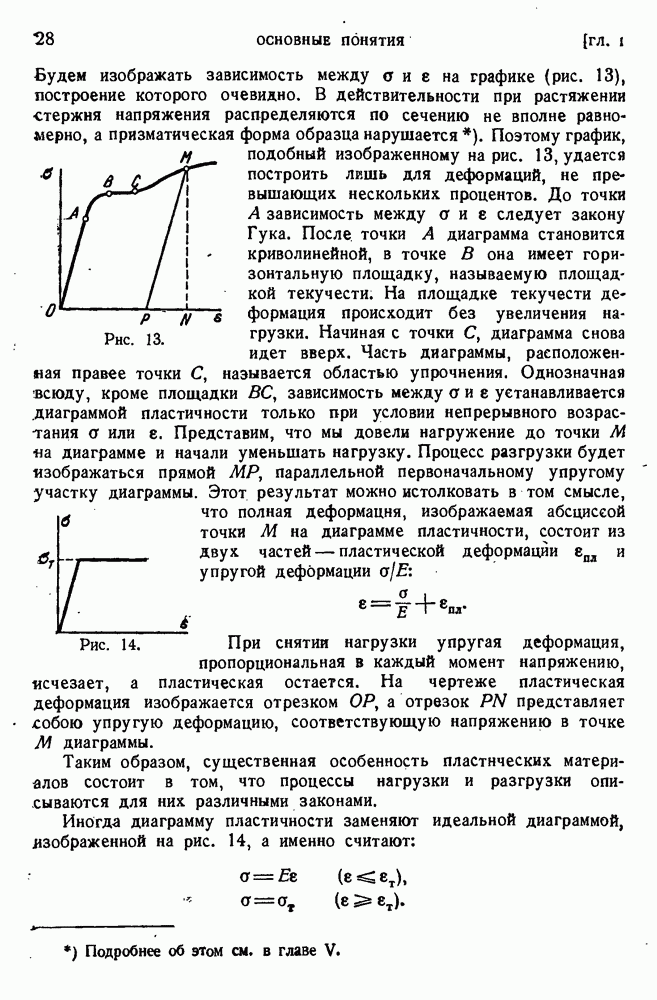
- § 13. Закон Гука.
- § 14. Диаграмма пластичности.
- § 15. Тела изотропные и анизотропные.
- ГЛАВА II. РАСТЯЖЕНИЕ СЖАТИЕ
- § 16. Стержни и стержневые системы.
- § 17. Принцип Сен-Венана и гипотеза плоских сечений.
- § 18. Напряжения и деформации при растяжении.
- § 19. Расчеты на прочность при растижении и сжатии.
- § 20. Собственный вес и силы инерции.
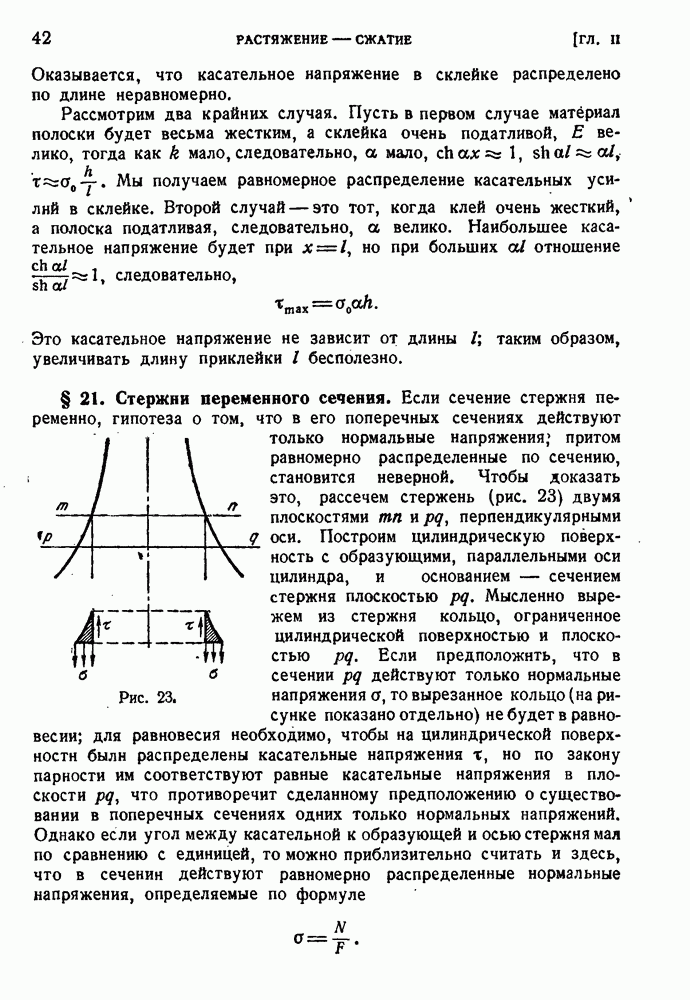
- § 21. Стержни переменного сечения.
- § 22. Перемещения узлов стержневых систем.
- § 23. Статически неопределенные задачи на растяжение — сжатие.
- § 24. Температурные и монтажные напряжения.
- § 25. Общие соображения о расчете стержневых систем.
- § 26. Расчет статически неопределимых систем по допускаемым нагрузкам.
- § 27. Остаточные напряжения после пластической деформации.
- § 28. Потенциальная энергия растяжении.
- § 29. Напряжения при ударе.
- § 30. Распространение упругих волн в стержнях.
- § 31. Концентрации напряжений.
- § 32. Нелинейные задачи на растяжение — сжатие.
- ГЛАВА III. СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
- § 33. Напряжения на косых площадках при растяжении.
- § 34. Напряжения при двухосном растяжении.
- § 35. Круговая диаграмма Мора.
- § 36. Общий случай плоского напряженного состояния.
- § 37. Определение напряжений на произвольной площадке.
- § 38. Пространственное напряженное состояние.
- § 39. Главные напряжения.
- § 40. Главные касательные напряжения.
- § 41. Октаэдрическое напряжение.
- § 42. Закон Гука для главных осей.
- § 43. Изменение объема при упругой деформации.
- § 44. Чистый сдвиг.
- § 45. Деформация элемента объема в общем случае.
- § 46. Условие пластичности Треска — Сен-Венана.
- § 47. Условие пластичности Мизеса.
- § 48. Условия пластичности для плоского напряженного состояния.
- § 49. Потенциальная энергия упругой деформации.
- § 50. Энергия изменения формы.
- ГЛАВА IV. НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
- § 51. Расчеты на прочность изделий сложной формы.
- § 52. Безмоментные оболочки вращении.
- § 53. Местные напряжения в безмоментных оболочках.
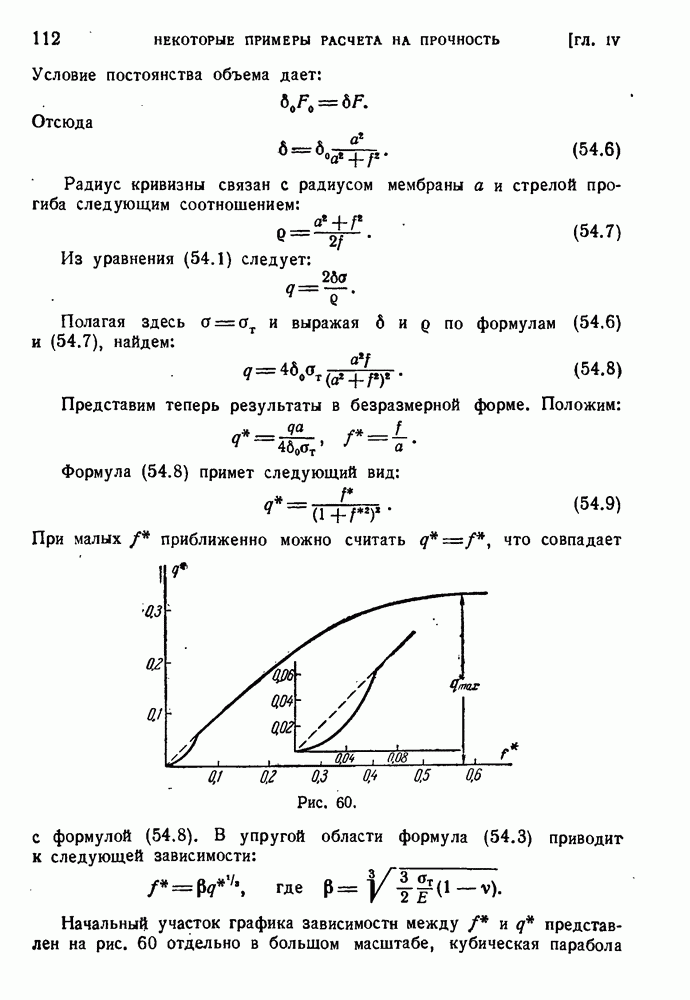
- § 54. Большие прогибы мембраны.
- § 55. Условные расчеты.
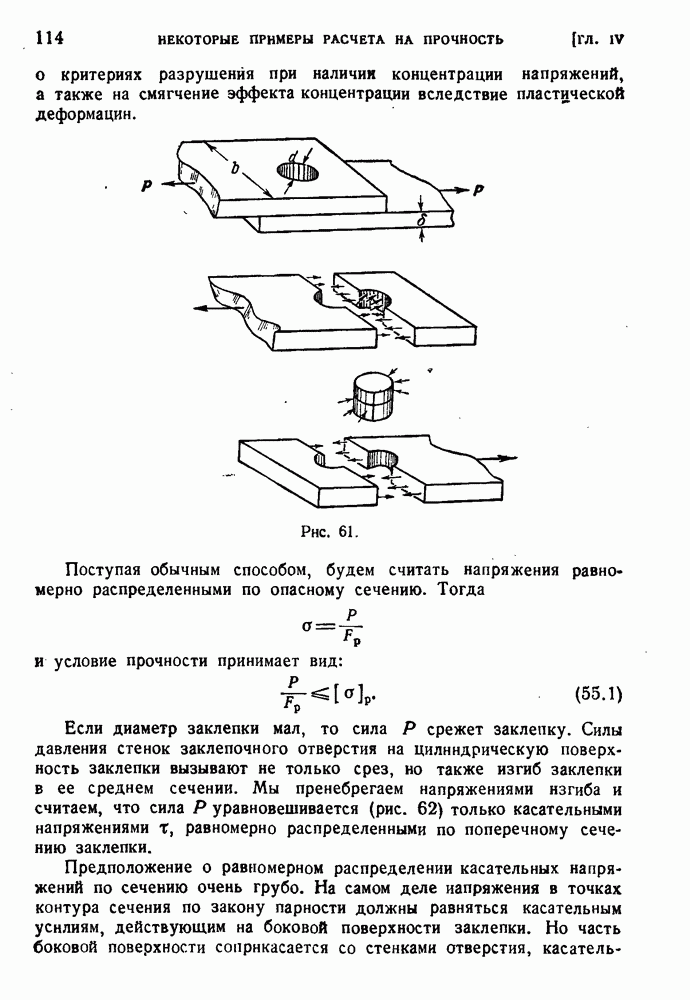
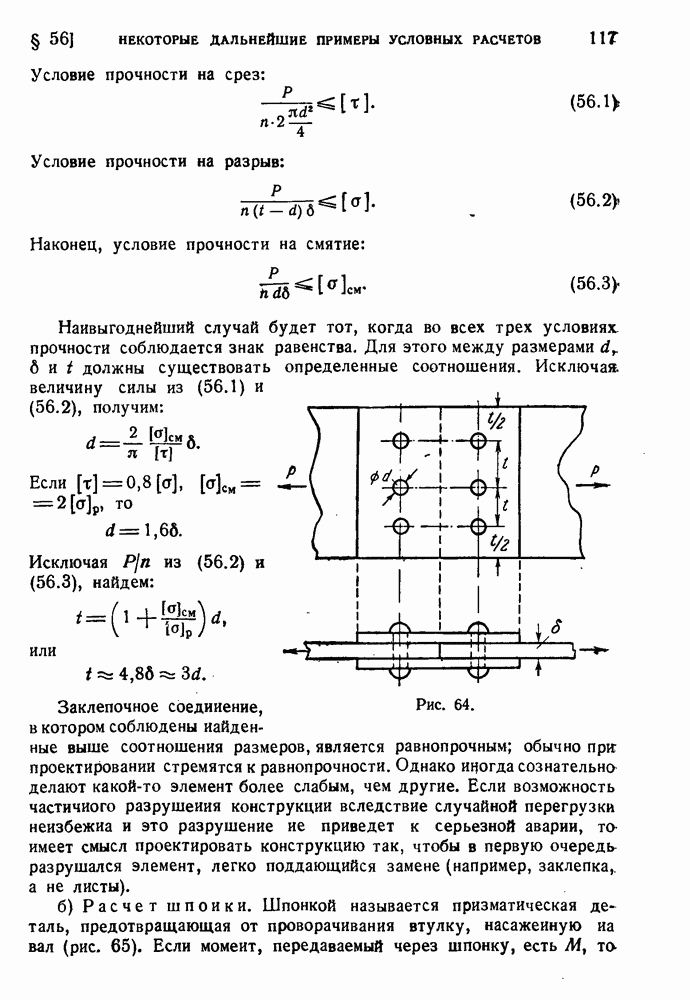
- § 56. Некоторые дальнейшие примеры условных расчетов.
- § 57. Расчет сварных соединений.
- ГЛАВА V. ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
- § 58. Задачи испытания материалов.
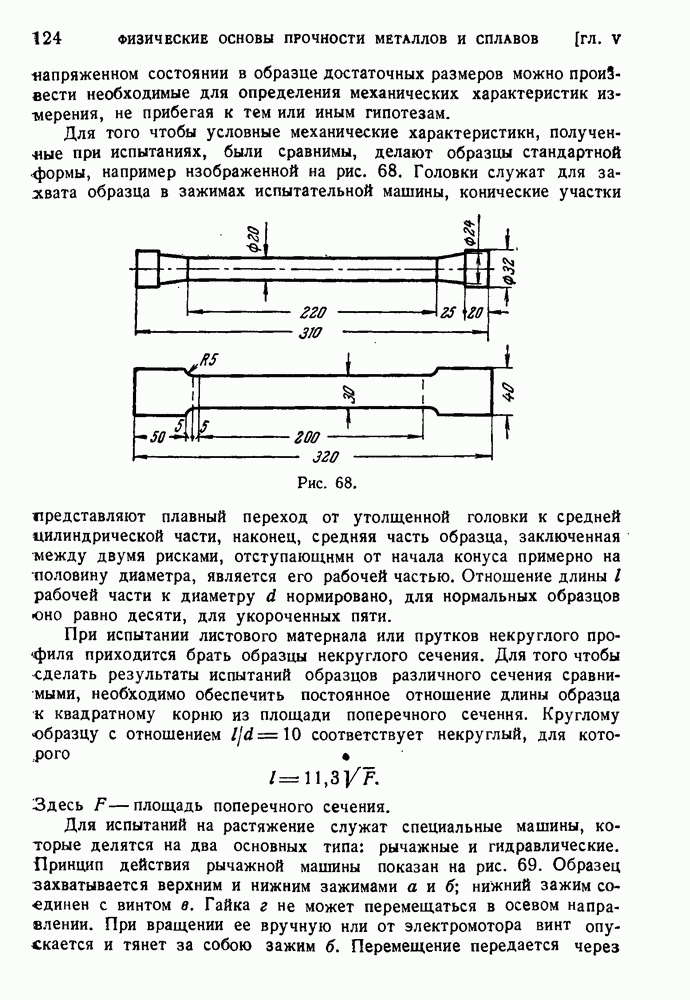
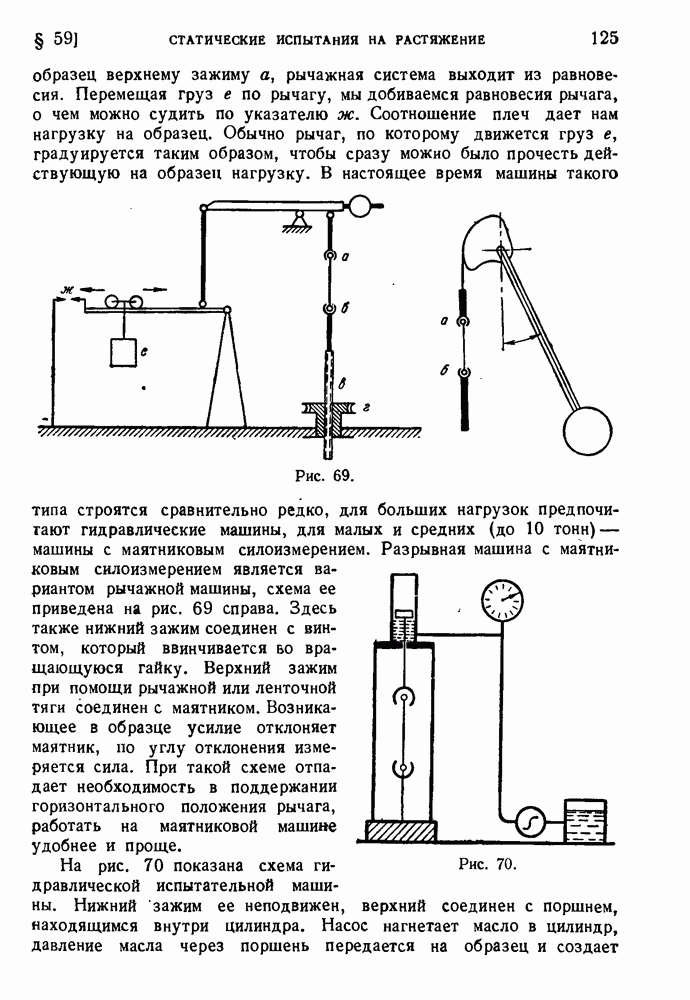
- § 59. Статические испытания на растяжение.
- § 60. Исследование металлов в области малых деформаций.
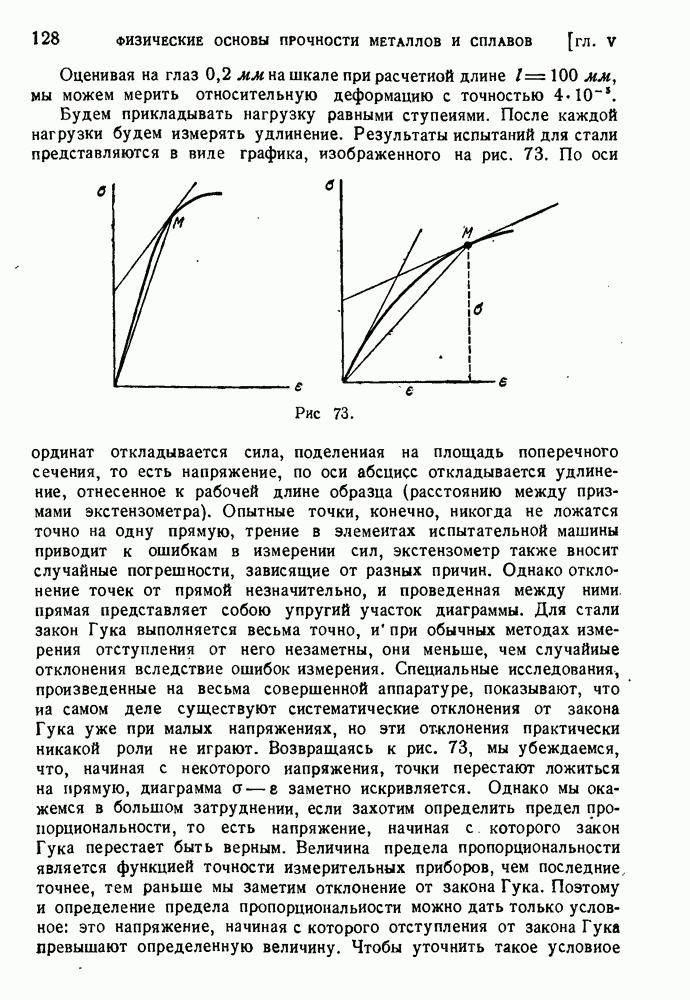
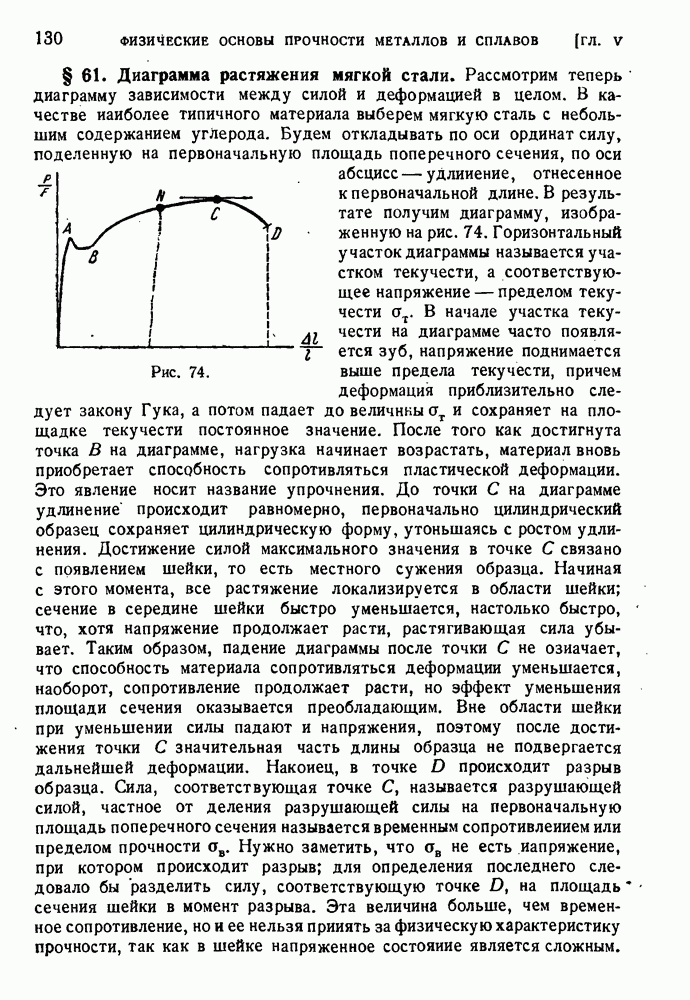
- § 61. Диаграмма растяжения мягкой стали.
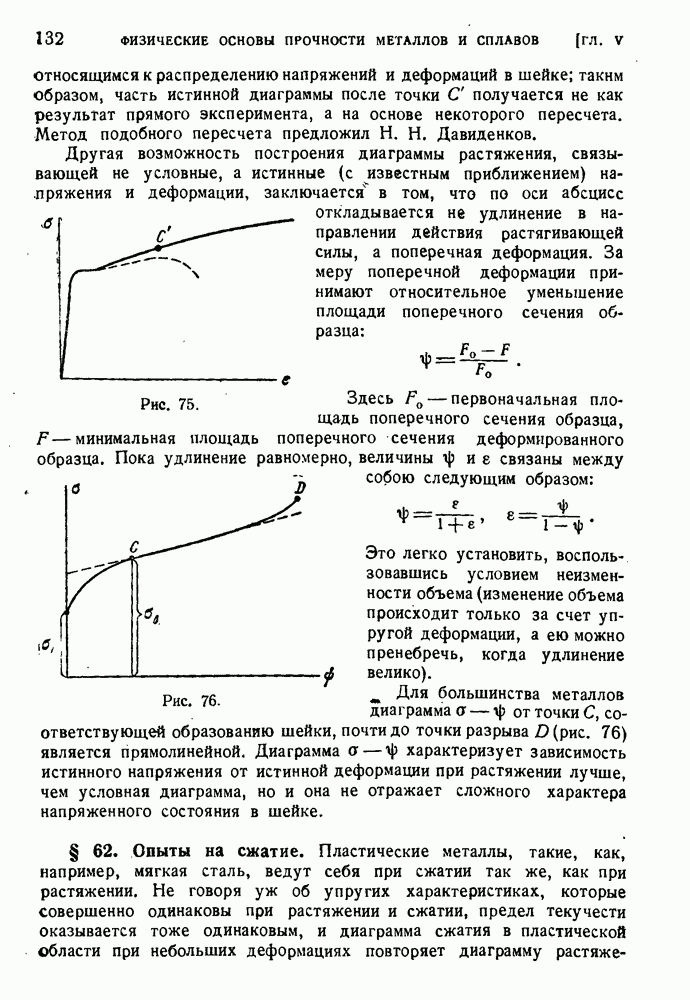
- § 62. Опыты на сжатие.
- § 63. Строение и упругая деформация металлических кристаллов.
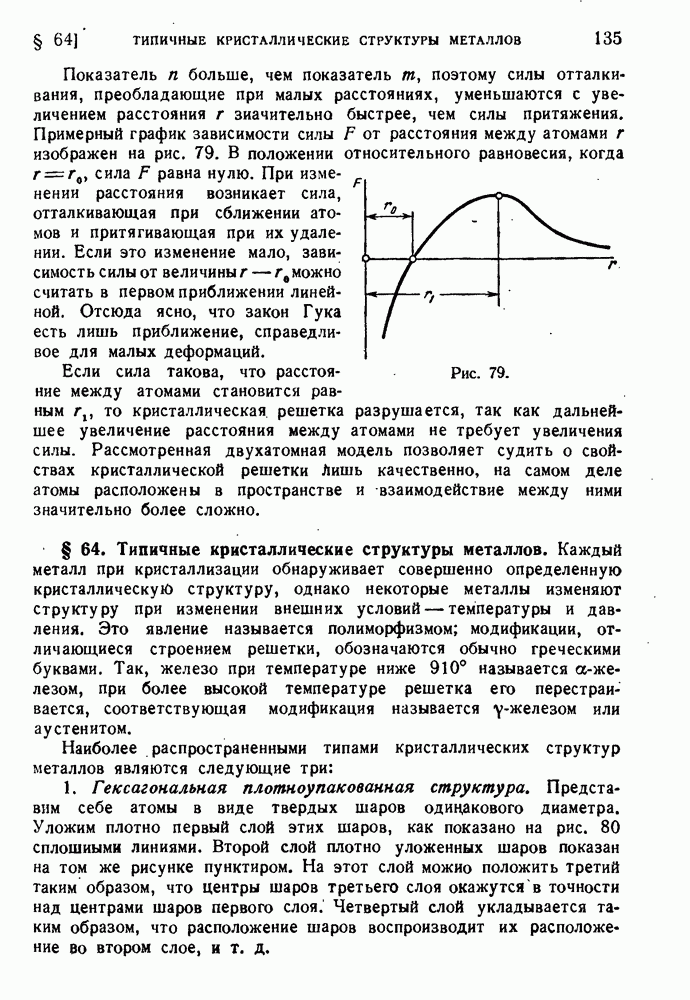
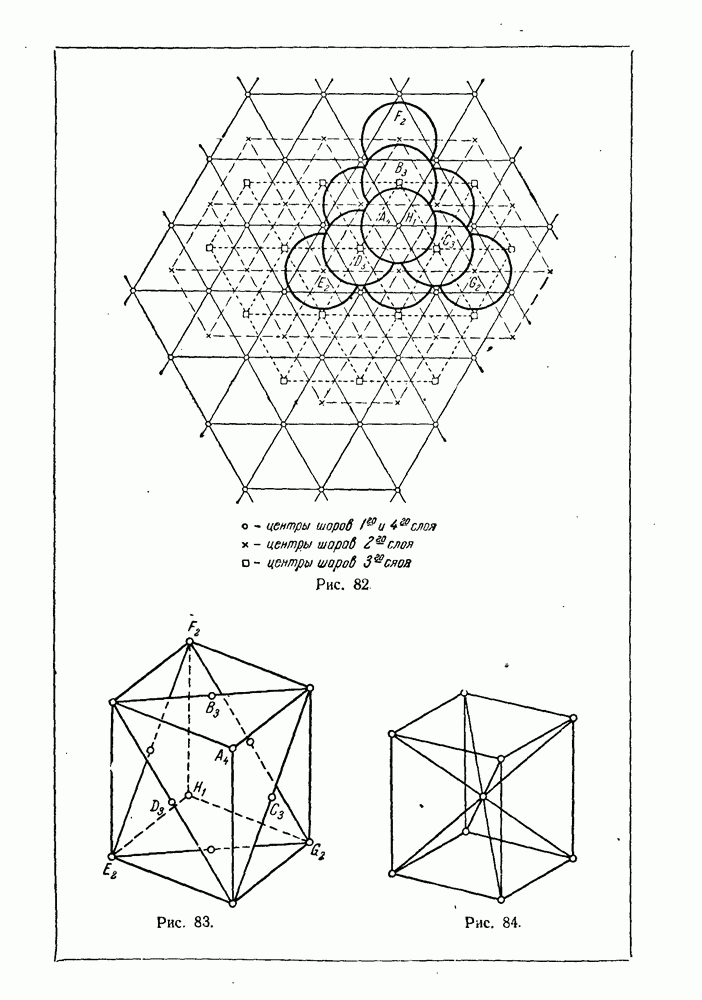
- § 64. Типичные кристаллические структуры металлов.
- § 65. Пластическая деформация монокристаллов.
- § 66. Прочность кристаллов и сопротивление пластическому деформированию.
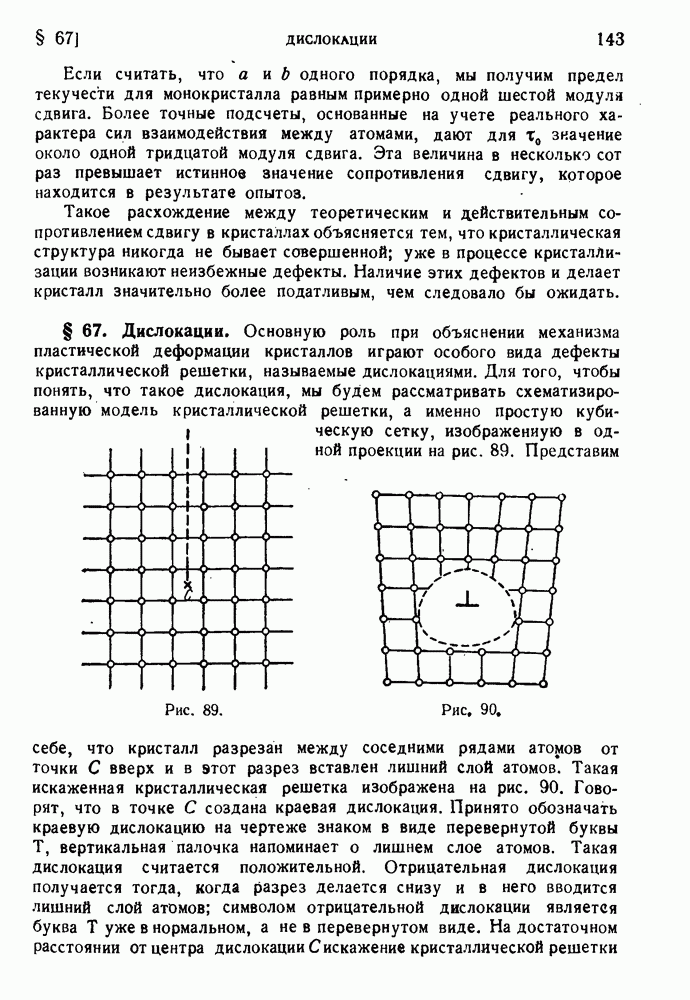
- § 67. Дислокации.
- § 68. Движение и равновесие дислокаций.
- § 69. Источники дислокаций.
- § 70. Границы блоков.
- § 71. Деформация поликристаллических металлов и сплавов.
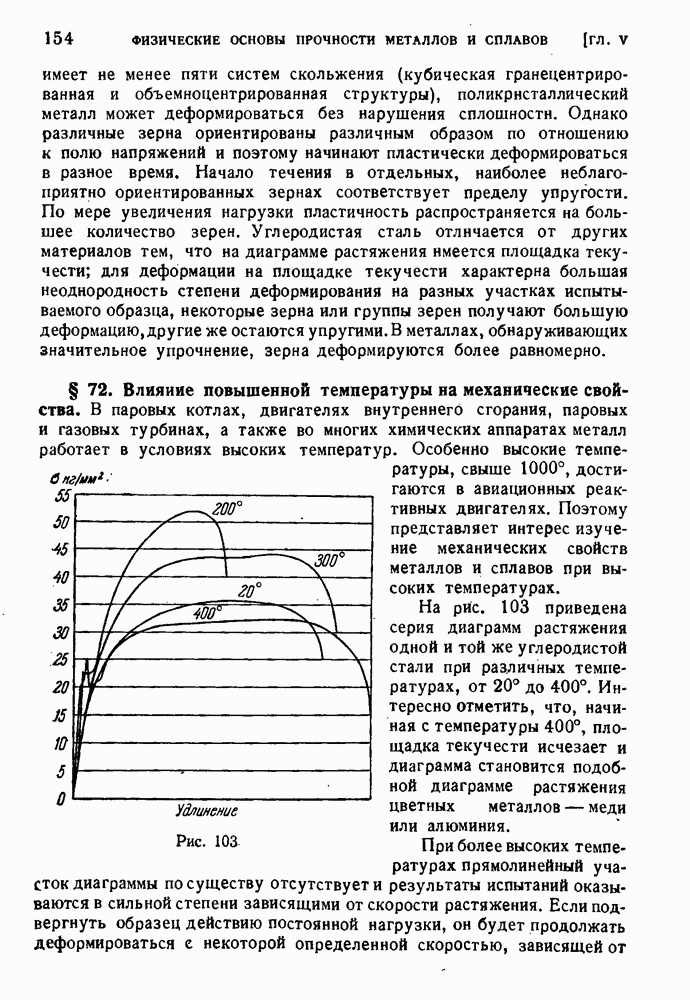
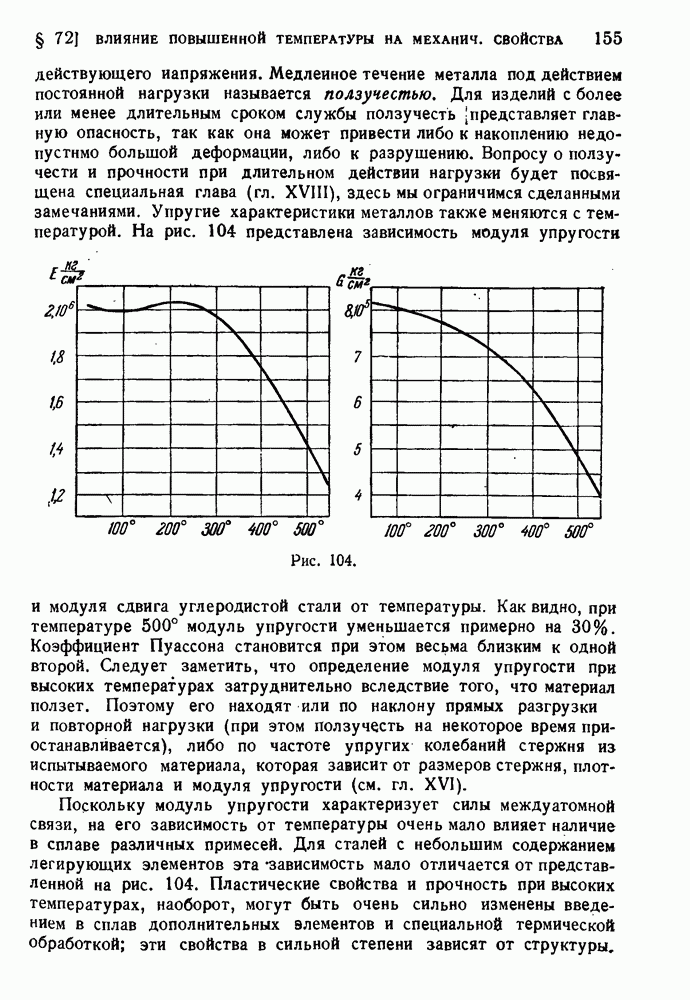
- § 72. Влияние повышенной температуры на механические свойства.
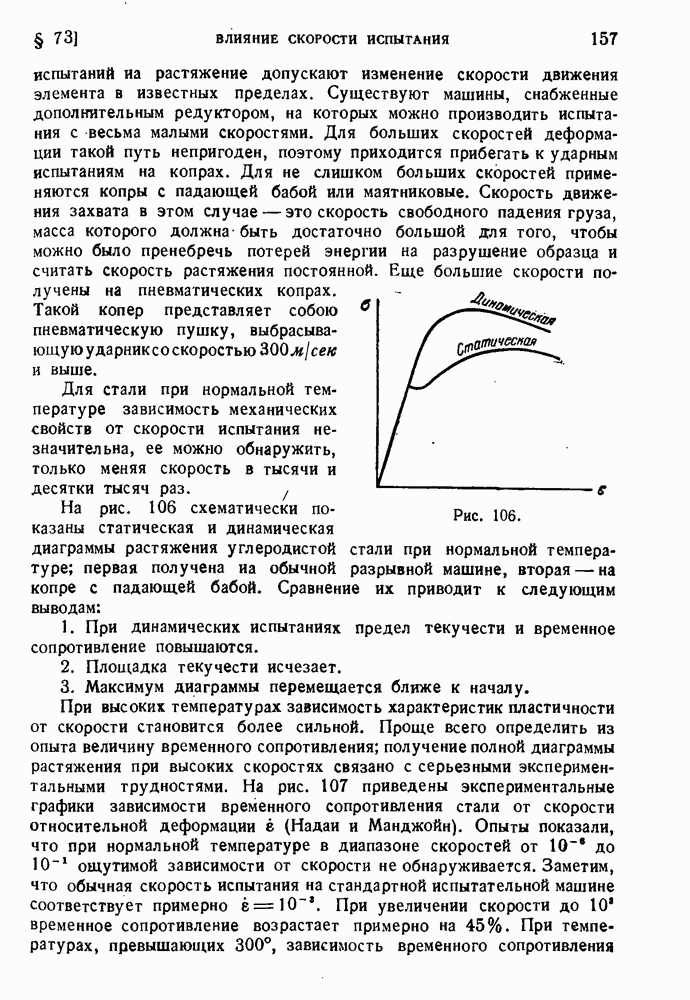
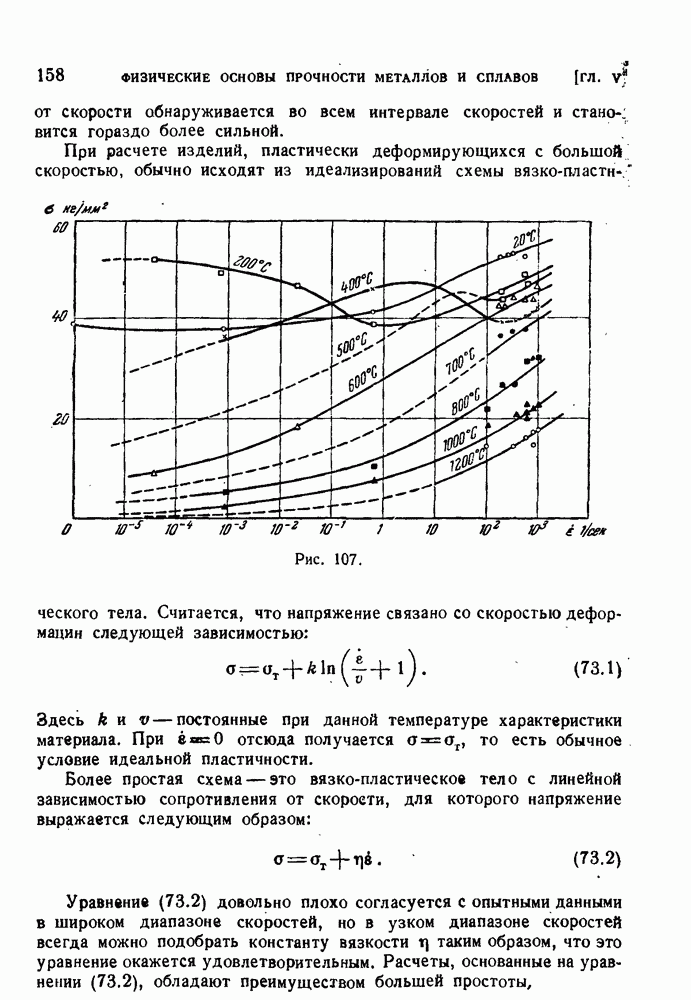
- § 73. Влияние скорости испытания.
- § 74. Испытании на твердость.
- ГЛАВА VI. ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ
- § 75. Основные принципы построения теории пластичности.
- § 76. Ассоциированный закон течения.
- § 77. Течение при условии пластичности Сен-Венана и Мизеса.
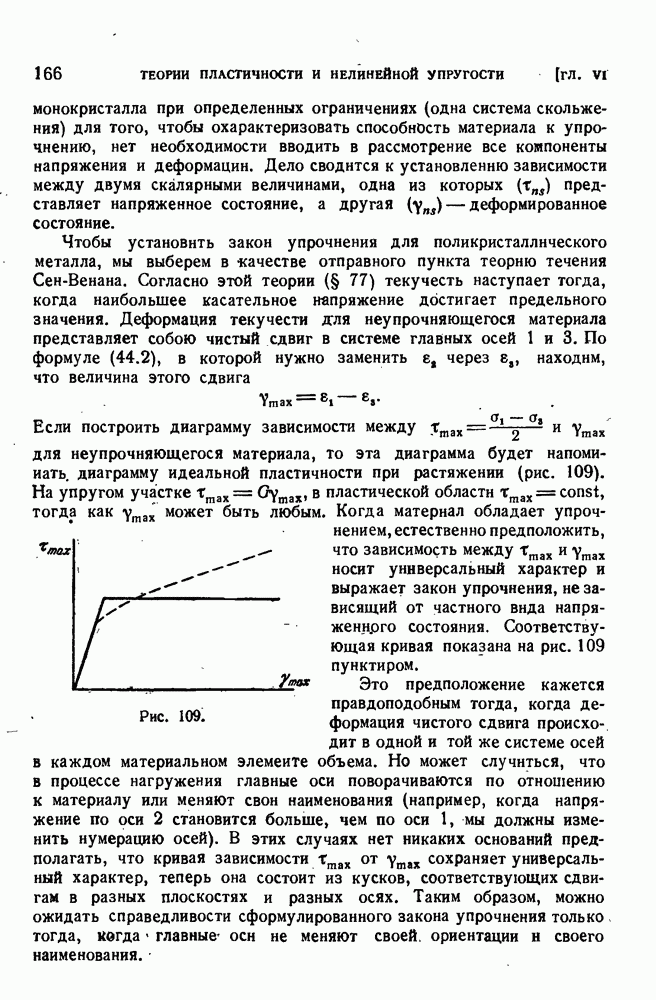
- § 78. Закон упрочнения.
- § 79. Деформационная теория пластичности.
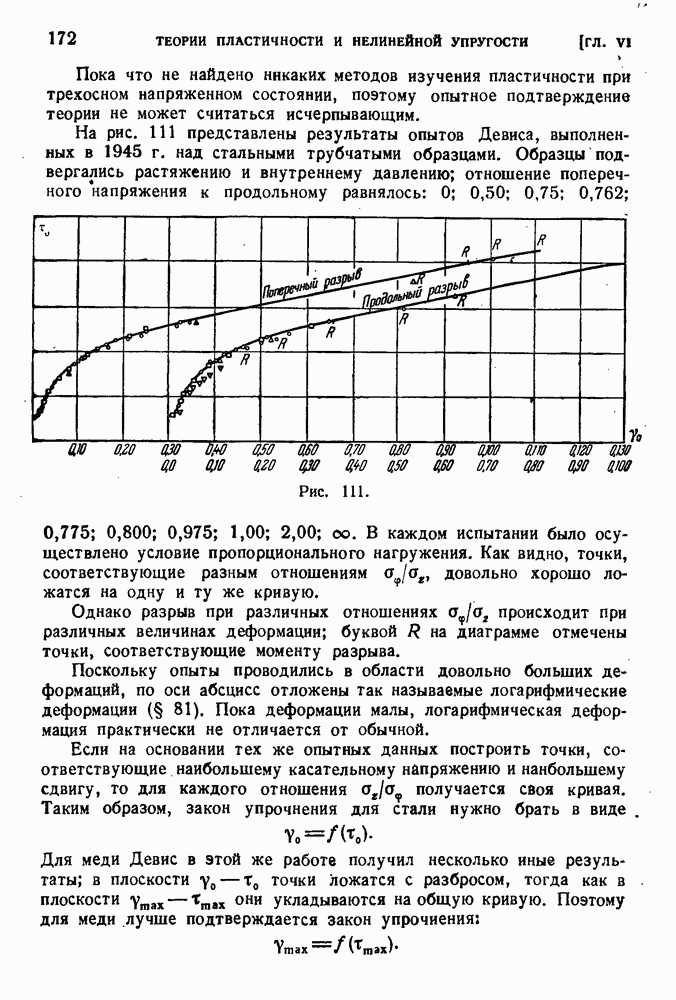
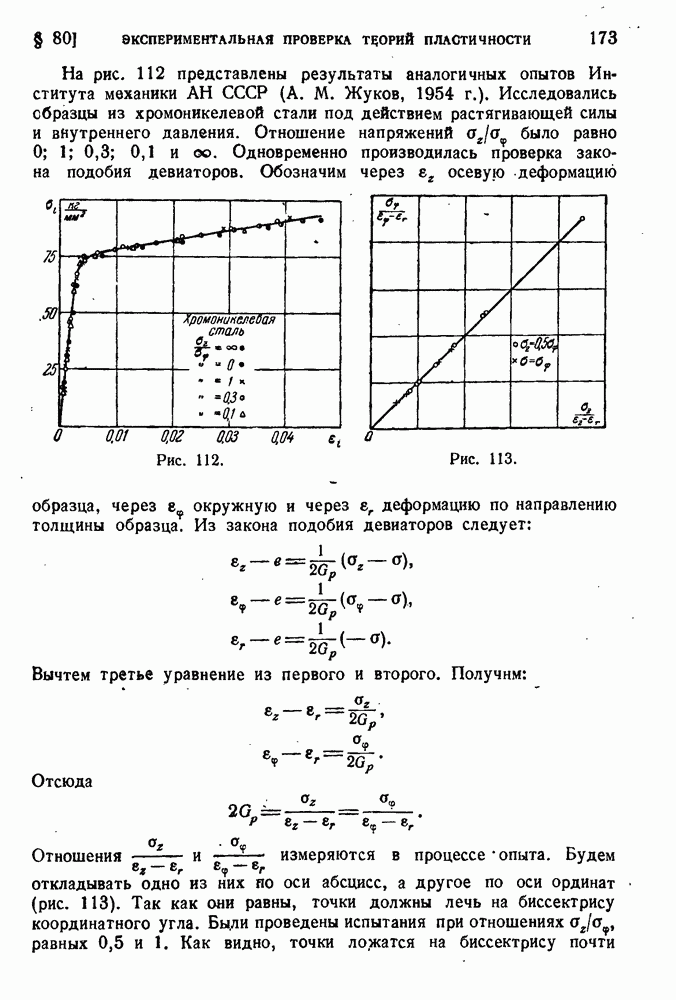
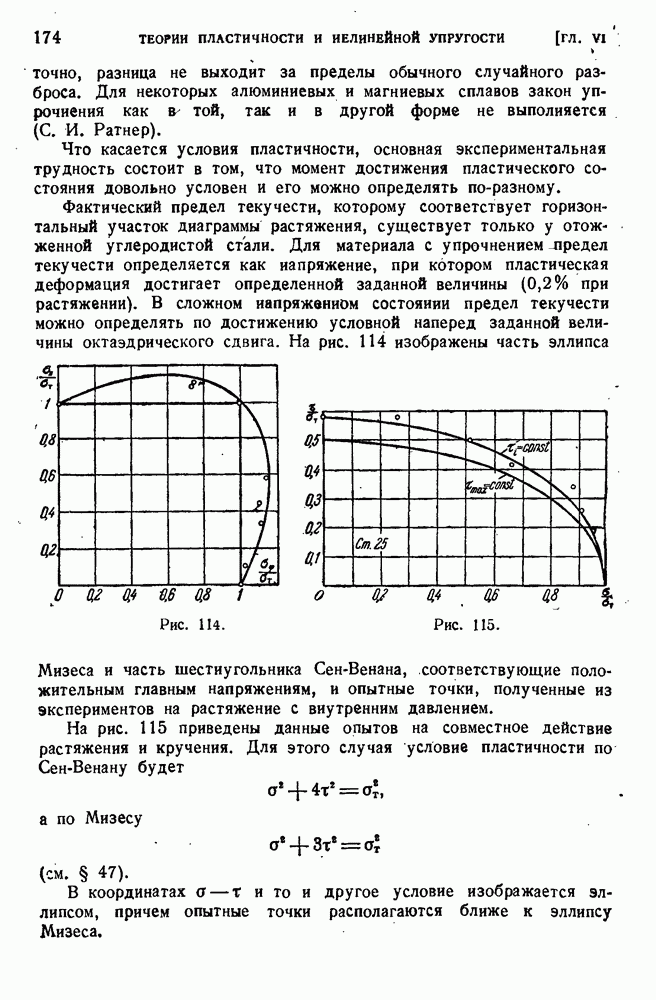
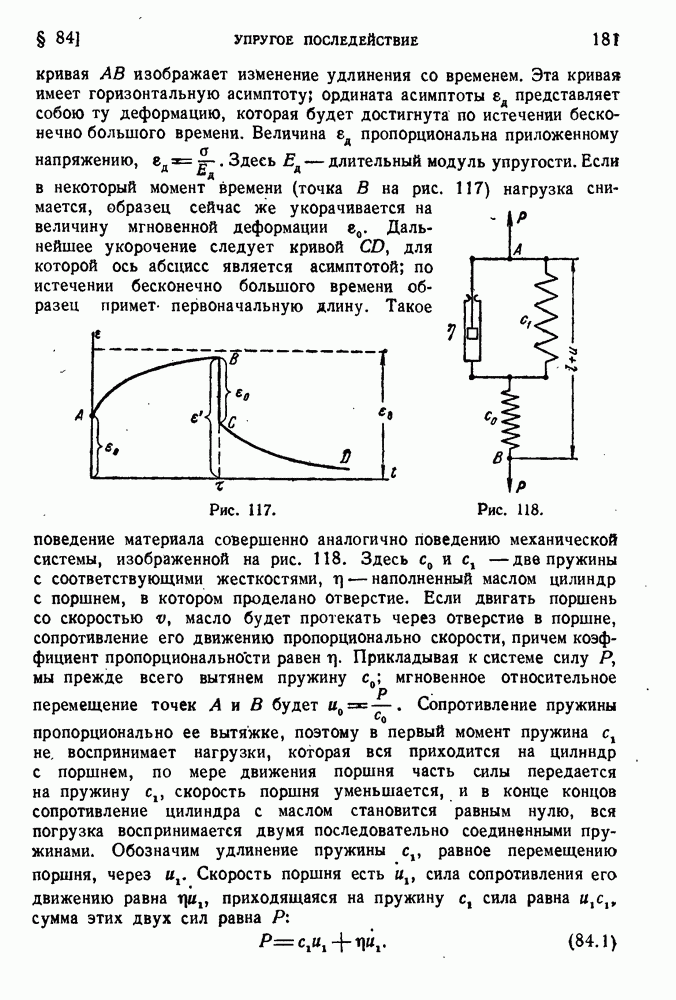
- § 80. Экспериментальная проверка теорий пластичности.
- § 81. Конечная деформация.
- § 82. Нелинейно упругое тело.
- § 83. Высокоэластические деформации.
- § 84. Упругое последействие.
- § 85. Некоторые свойства вязко-упругого тела.
- § 86. Принцип суммирования Больцмана—Вольтерра.
- ГЛАВА VII. КРУЧЕНИЕ
- § 87. Кручение стержней круглого сечеиия.
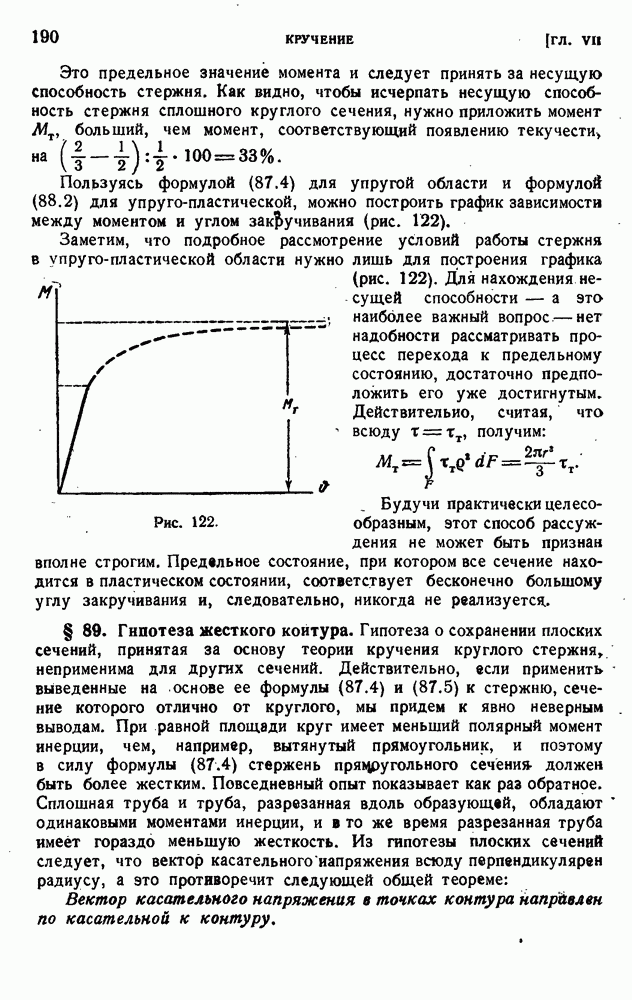
- § 88. Упруго-пластическое кручение стержня круглого сечения.
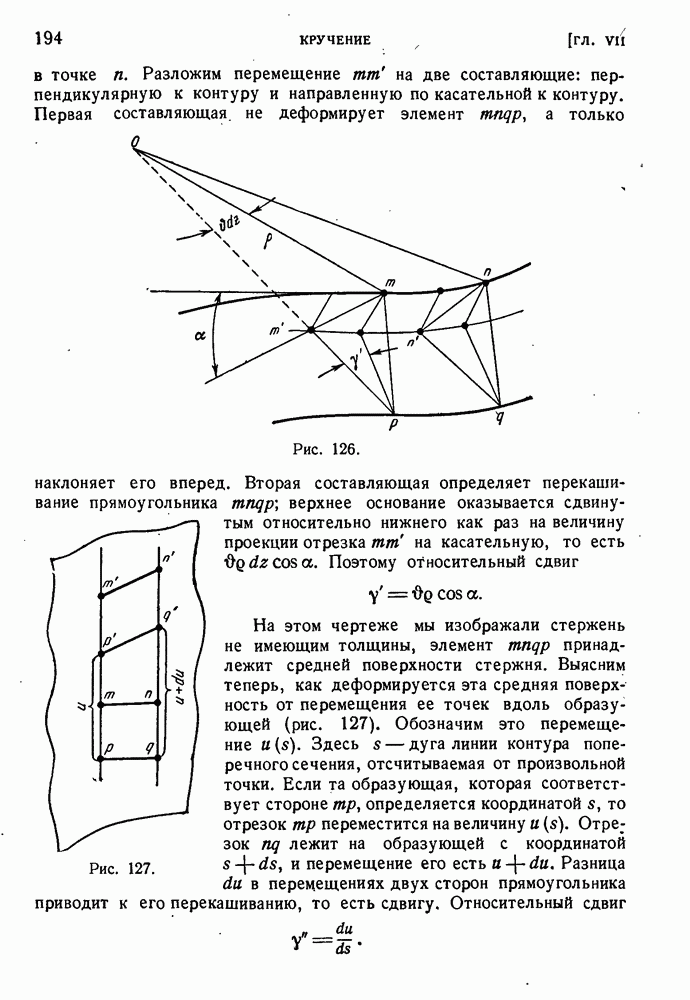
- § 89. Гипотеза жесткого контура.
- § 90. Кручение тонкостенных стержней замкнутого профиля.
- § 91. Кручение тонкостенных стержней открытого профиля.
- § 92. Кручение упругих стержией сплошного профиля.
- § 93. Опытное исследование кручения.
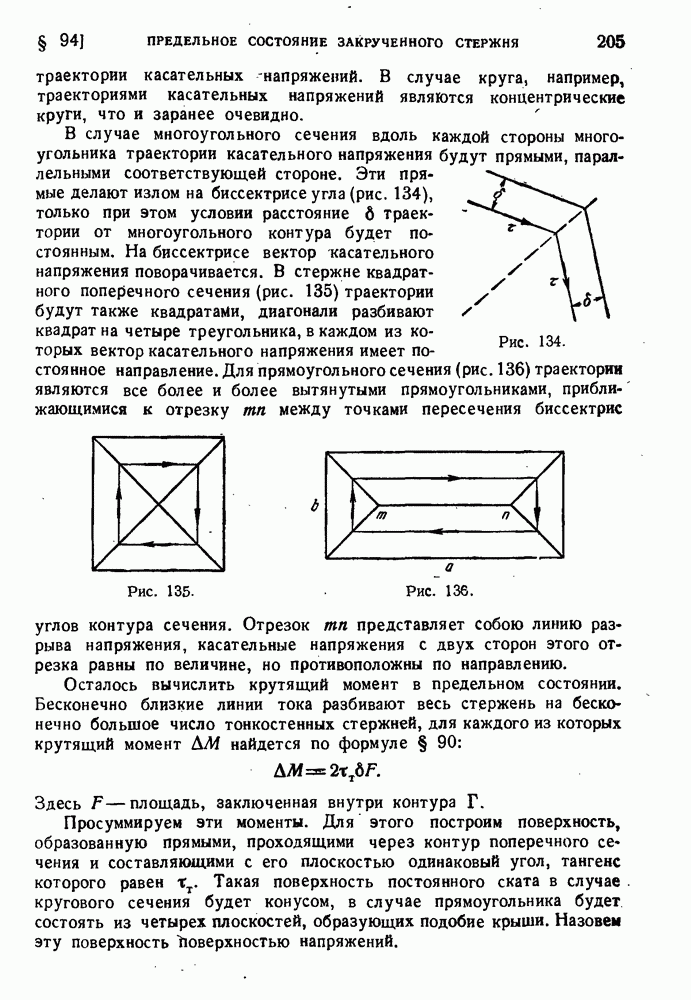
- § 94. Предельное состояние закрученного стержня из идеально-пластического материала.
- ГЛАВА VIII. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
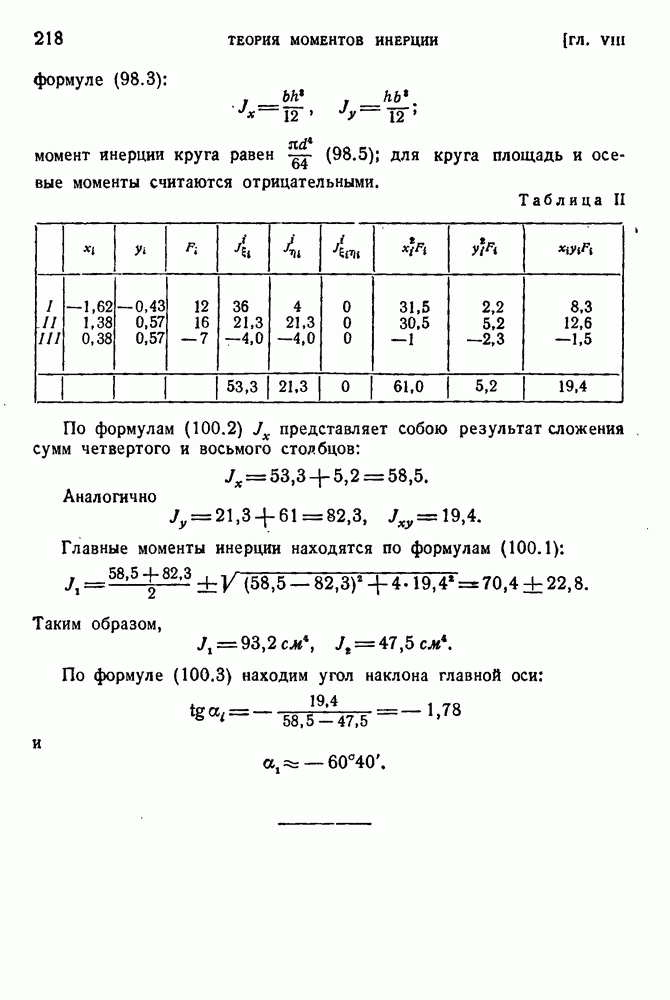
- § 96. Общие теоремы о моментах.
- § 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей.
- § 98. Вычисление моментов инерции.
- § 99. Преобразование моментов инерции при повороте осей.
- § 100. Главные оси и главные моменты инерции.
- ГЛАВА IX. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
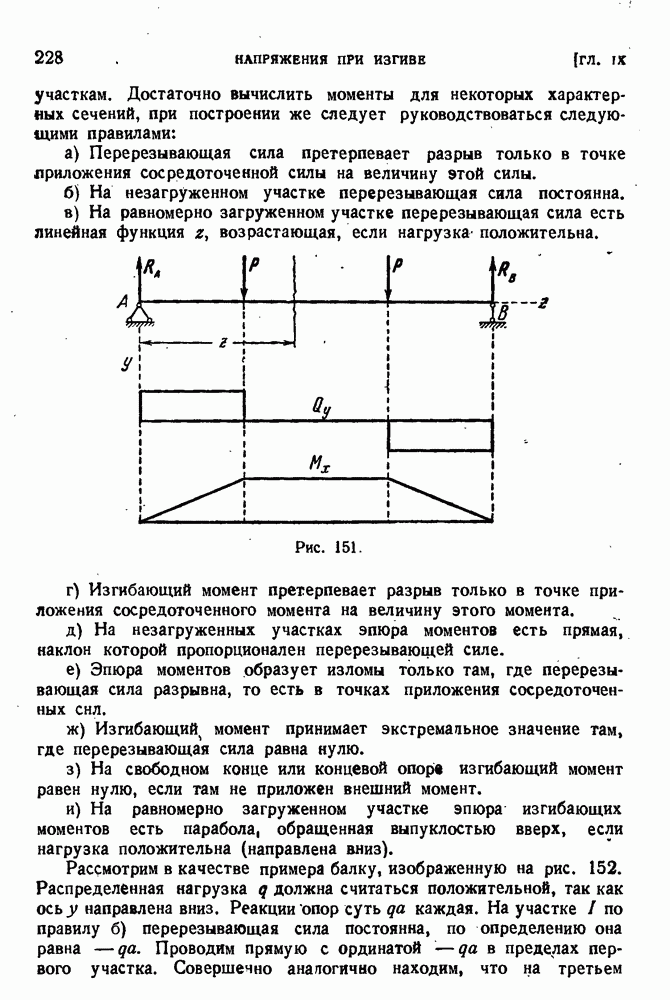
- § 101. Действие поперечных сил на балку.
- § 102. Гипотеза плоских сечений и принцип Сен-Венана.
- § 103. Нормальные напряжения при изгибе.
- § 104. Изгибающие моменты и перерезывающие силы.
- § 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры.
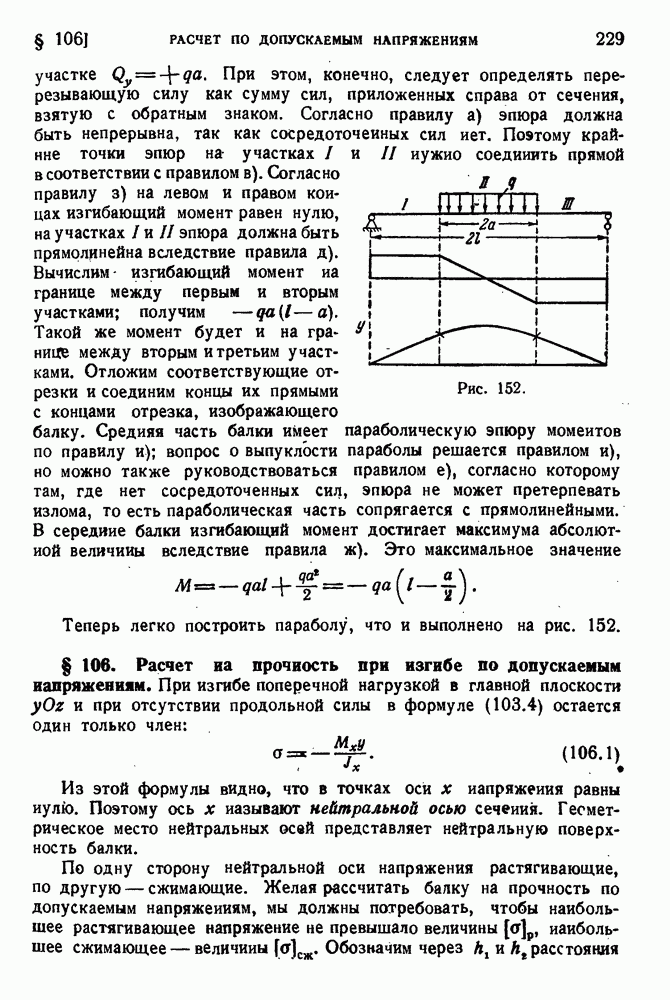
- § 106. Расчет на прочность при изгибе по допускаемым напряжениям.
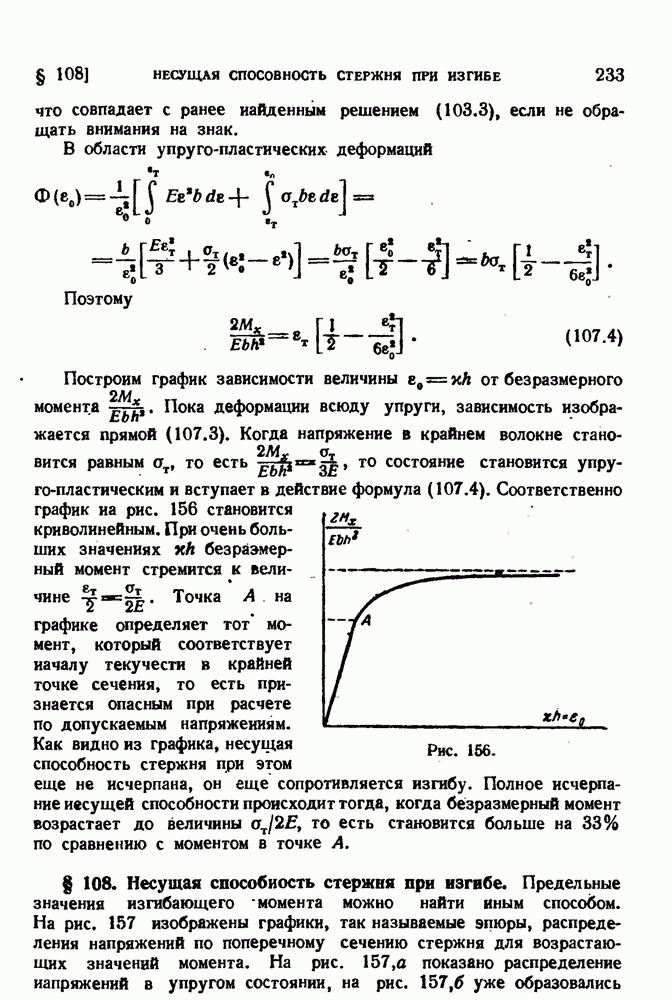
- § 107. Упруго-пластический изгиб.
- § 108. Несущая способность стержня при изгибе.
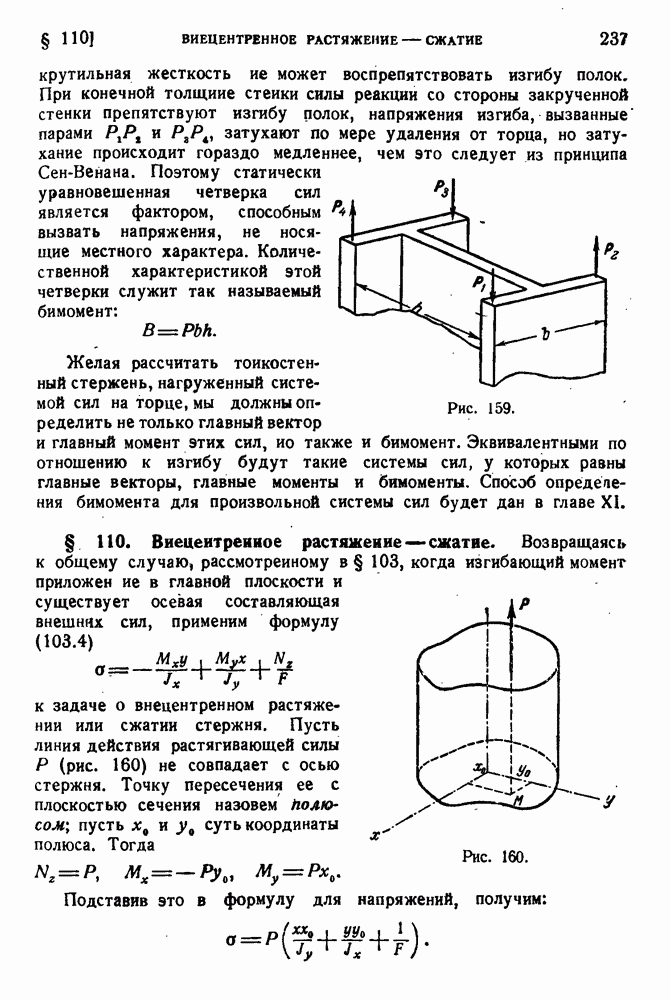
- § 109. Принцип Сен-Венана.
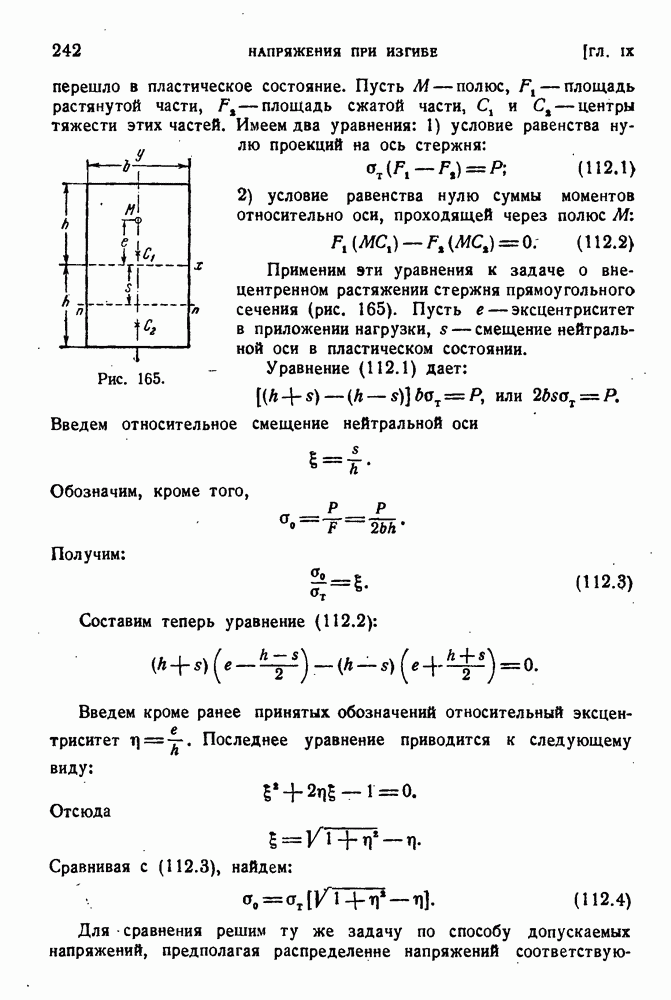
- § 110. Внецентренное растяжение — сжатие.
- § 111. Ядро сечения.
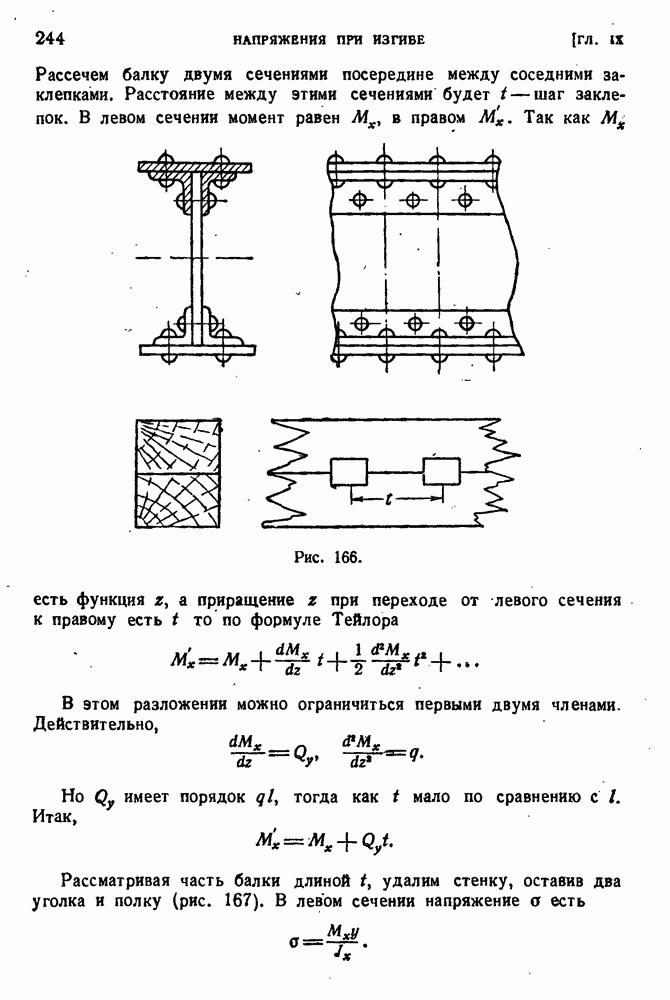
- § 112. Несущая способность внецентренно сжатого стержня.
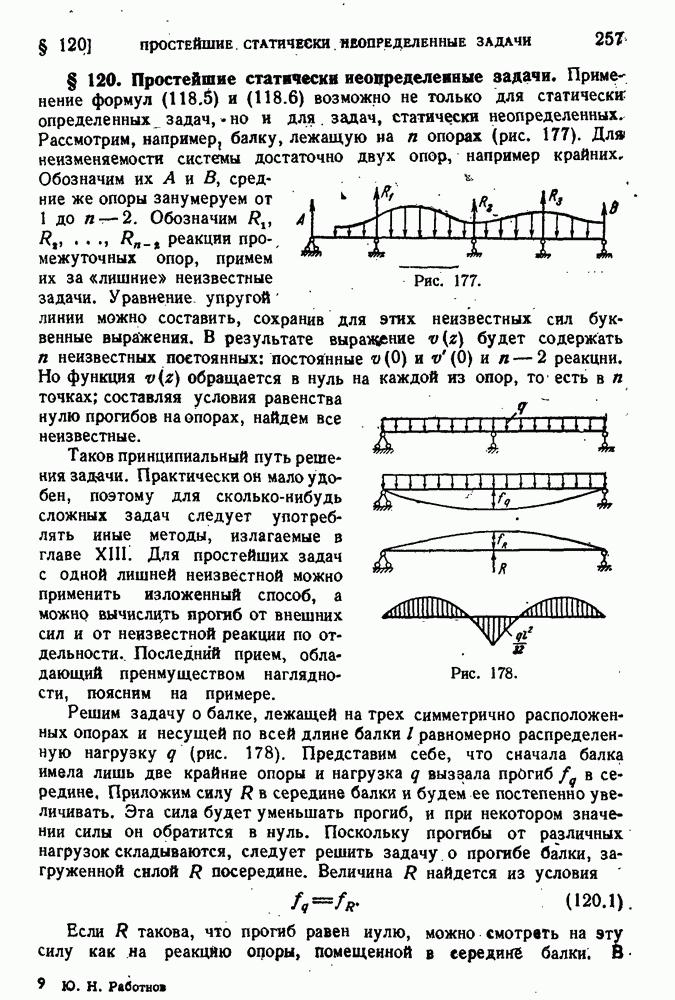
- § 113. Расчет составных балок.
- § 114. Изгиб кривого бруса.
- § 115. Нахождение нейтральной осн в кривом стержне.
- ГЛАВА X. ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- § 116. Дифференциальное уравнение изогнутой оси.
- § 117. Пределы применимости приближенной теории.
- § 118. Интегрирование уравнения изгиба.
- § 119. Примеры определения прогибов.
- § 120. Простейшие статически неопределенные задачи.
- § 121. Расчет статически неопределимых балок по способу допускаемых нагрузок.
- § 122. Изгиб стержней переменного сечения.
- § 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами.
- § 124. Продольно-поперечный изгиб.
- § 125. Изгиб балки на упругом основании.
- ГЛАВА XI. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
- § 126. Нормальные и касательные напряжения при изгибе.
- § 127. Касательные напряжении при изгибе в плоскости симметрии.
- § 128. Центр изгиба.
- § 129. Дополнительные напряжения при кручении.
- § 130. Закон секториальных площадей.
- § 131. Уравнение стесненного кручения.
- § 132. Вычисление секториальных характеристик.
- § 133. Стержень, нагруженный бимоментом.
- § 134. Некоторые примеры стесненного кручения.
- ГЛАВА XII. УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ
- § 135. Постановка вопроса об устойчивости.
- § 136. Устойчивость сжатого упругого стержня.
- § 137. Эластика Эйлера.
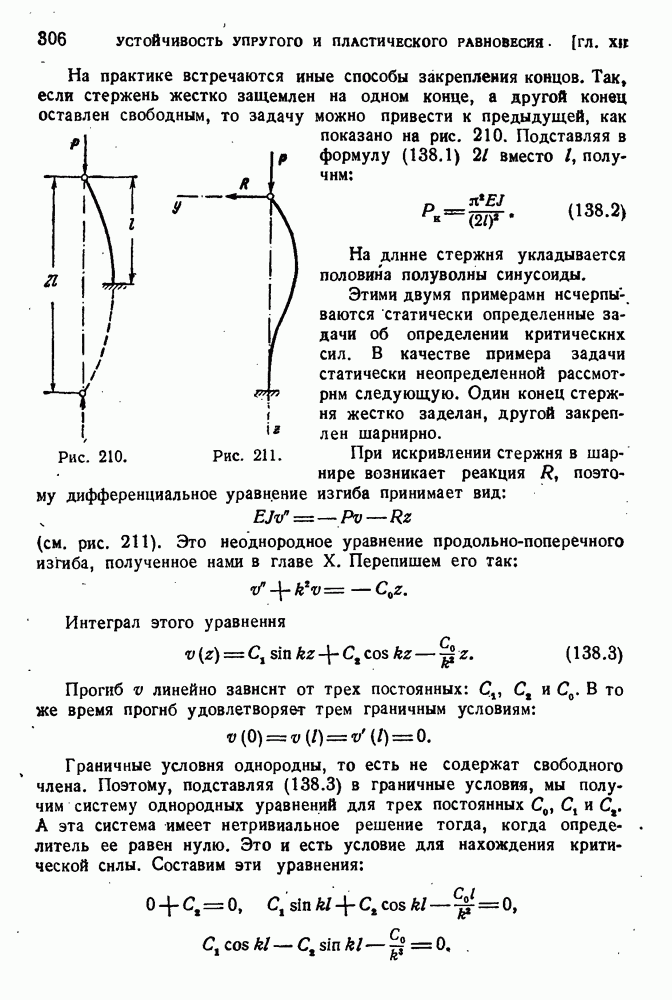
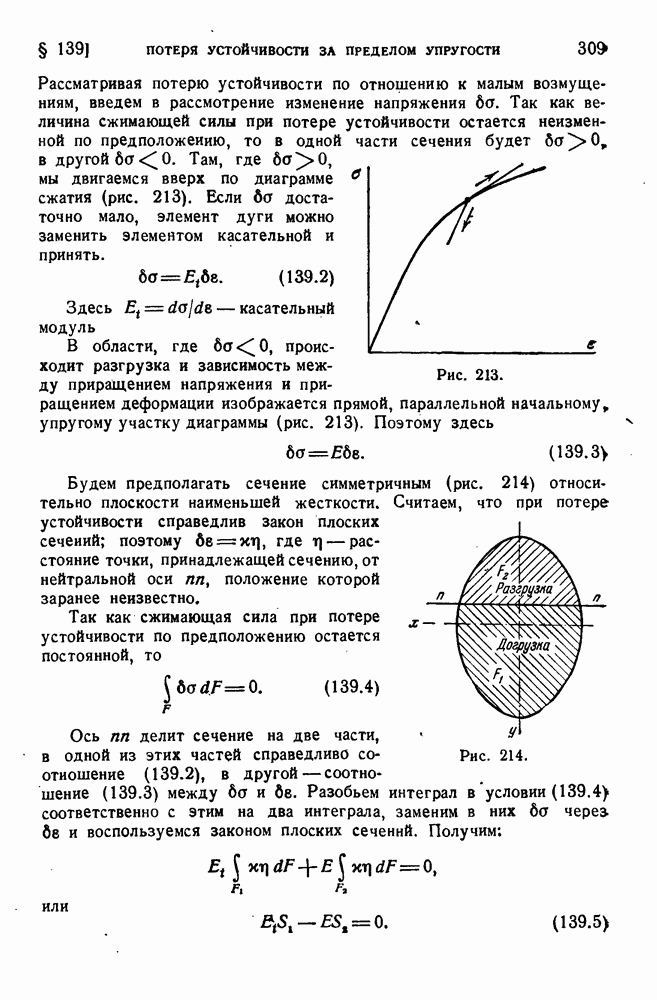
- § 138. Критические силы при иных видах закрепления стержня.
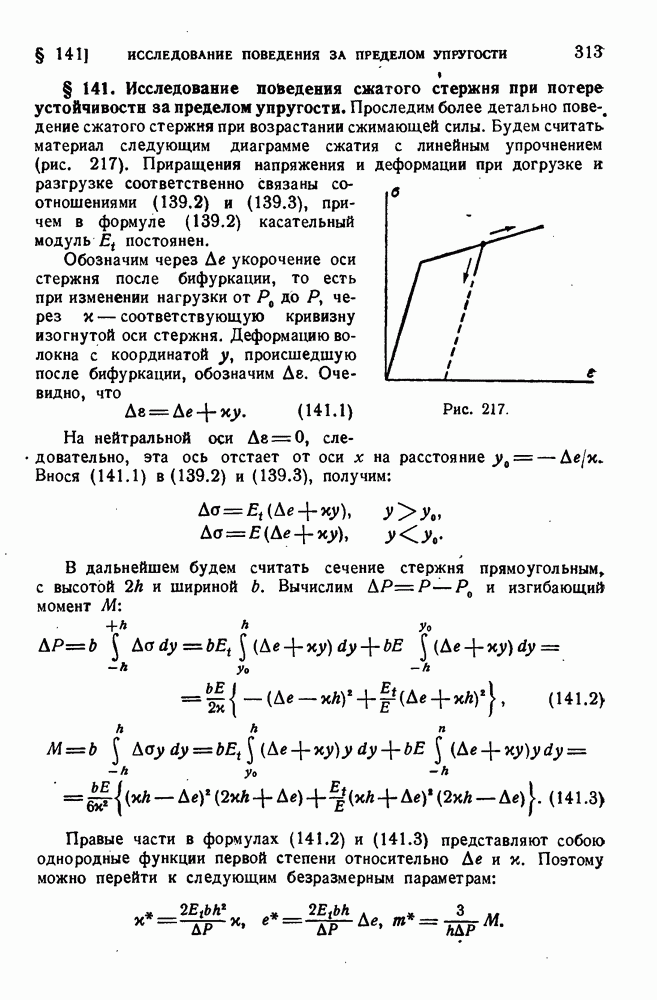
- § 139. Потеря устойчивости за пределом упругости.
- § 140. Потеря устойчивости за пределом упругости (продолжение).
- § 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости.
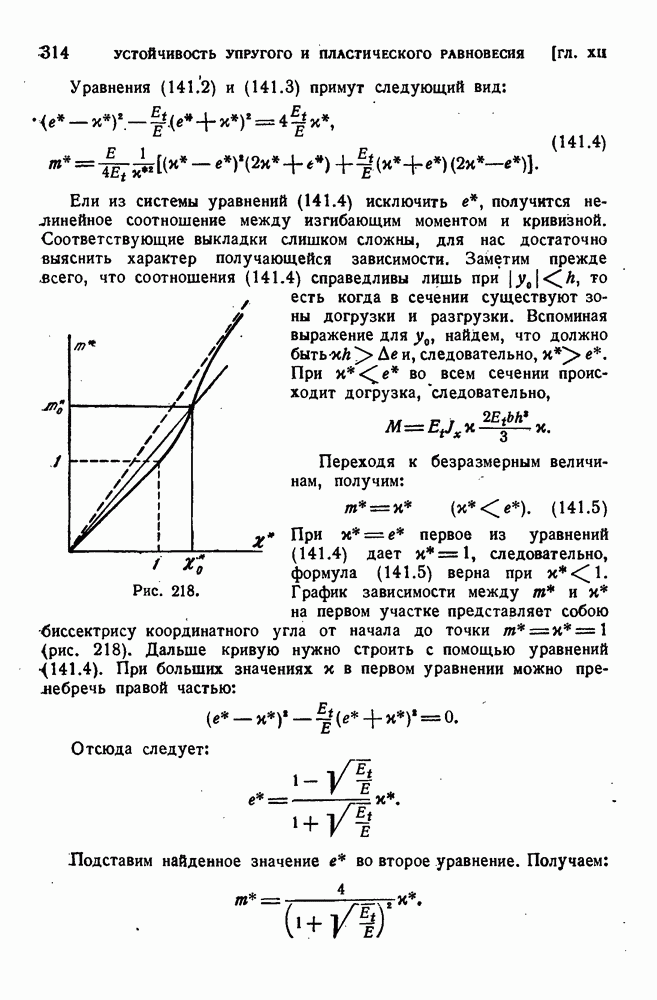
- § 142. Расчет на устойчивость по эмпирическим формулам.
- ГЛАВА XIII. ТРУБЫ И ДИСКИ
- § 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности.
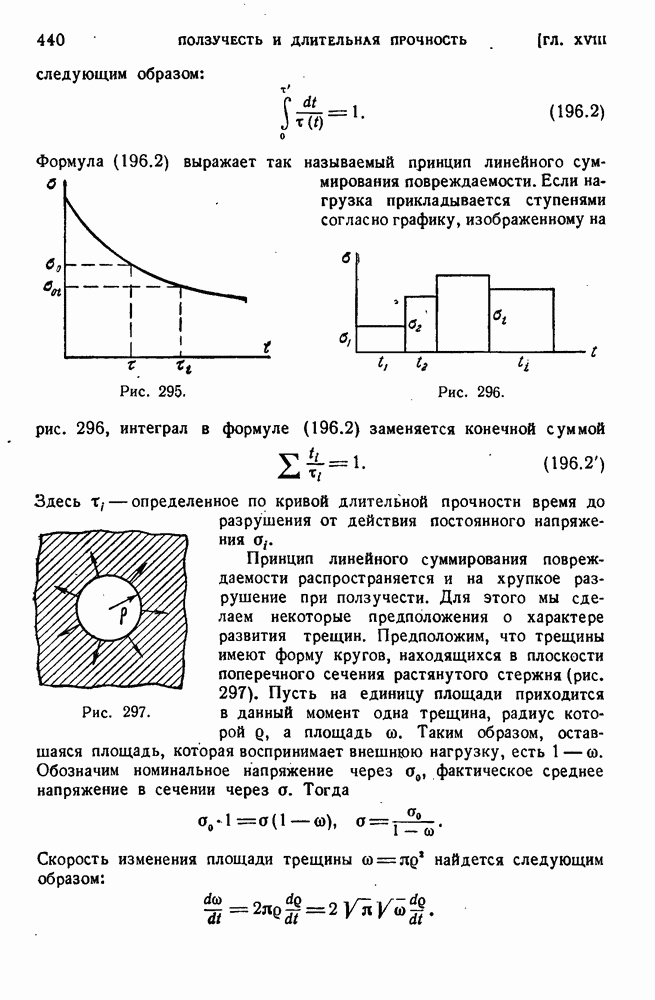
- § 144. Упругое состояние трубы. Формулы Ламе.
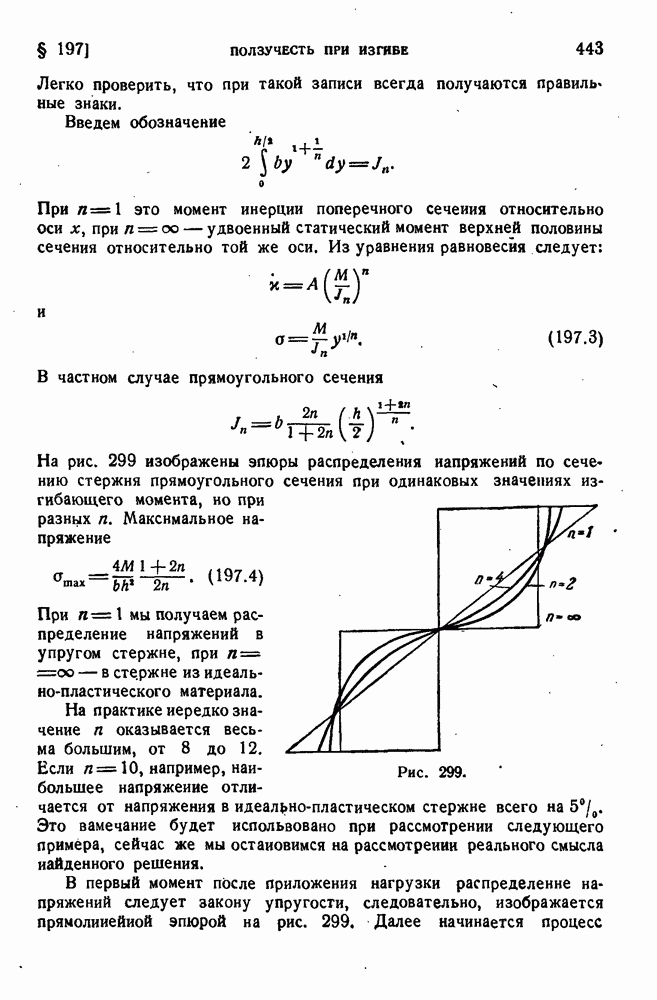
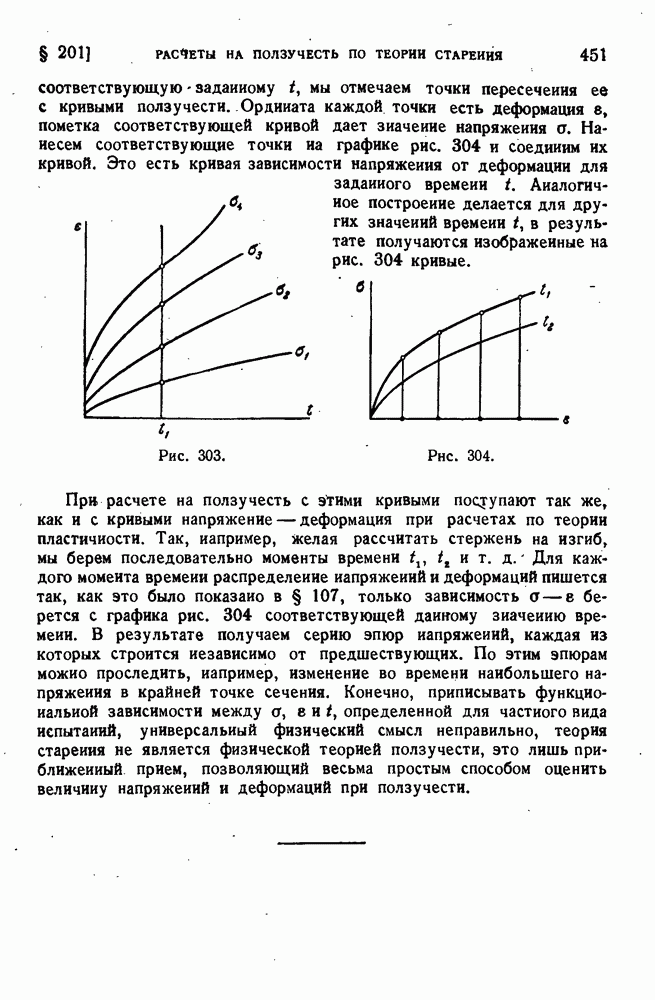
- § 145. Пластическое состояние трубы.
- § 146. Вращающиеся диски. Упругое состояние.
- § 147. Диск равного сопротивления.
- § 148. Предельное равновесие вращающегося диска.
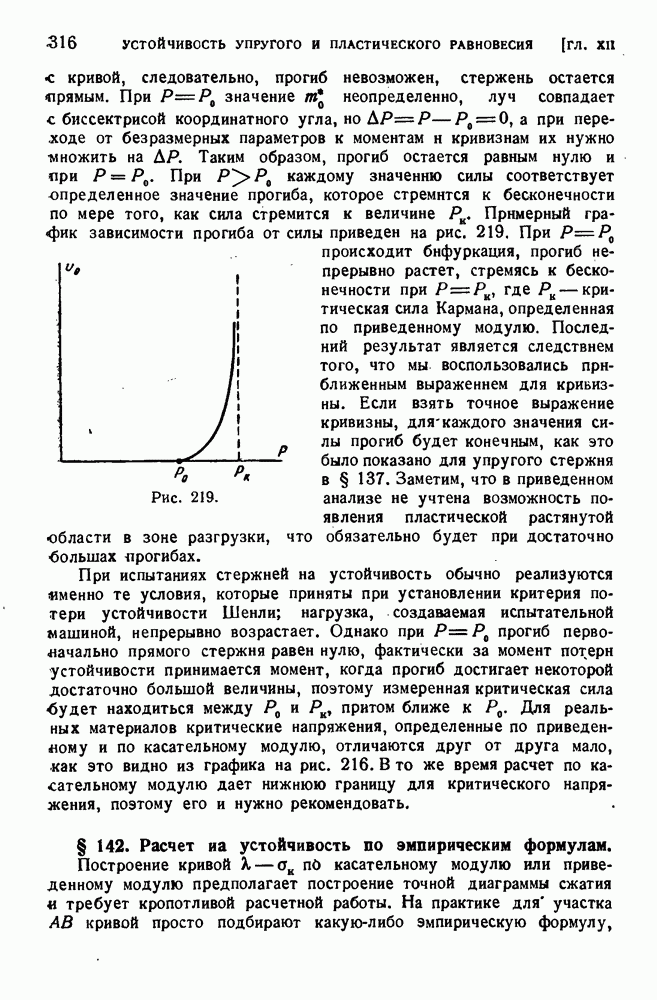
- ГЛАВА XIV. ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 149. Обобщенные силы и обобщенные перемещения.
- § 150. Начало возможных перемещений для деформируемого тела.
- § 151. Теоремы Лагранжа и Кастильяно.
- § 152. Лииейиые упругие системы.
- § 153. Теорема о взаимности работ.
- § 154. Теорема Кастильяно для линейных упругих систем.
- § 155. Расчет винтовых пружин.
- § 156. Теорема о минимуме энергии.
- § 157. Интеграл перемещений.
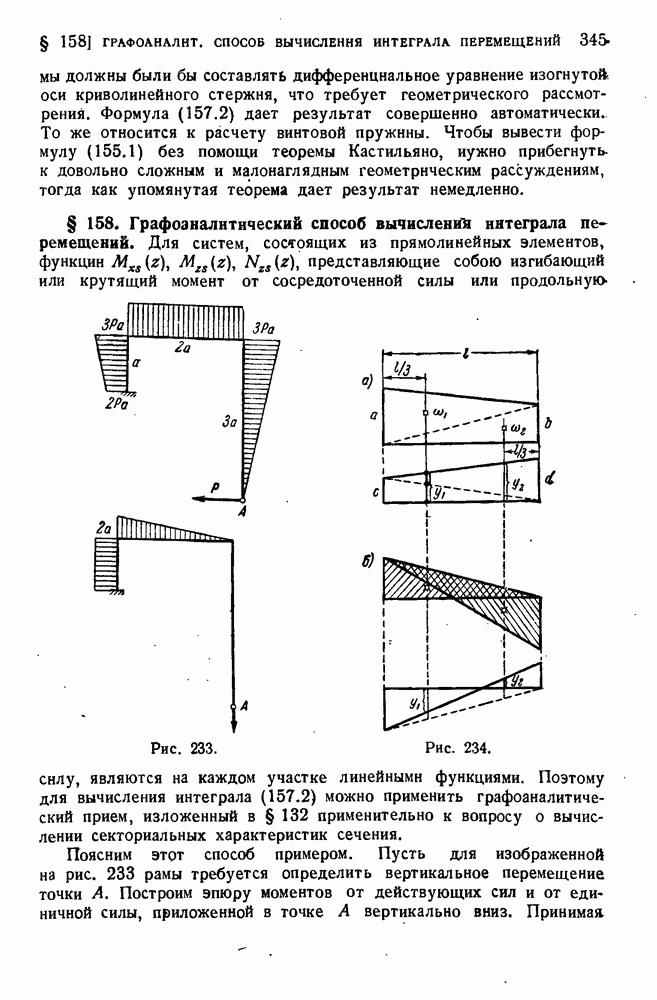
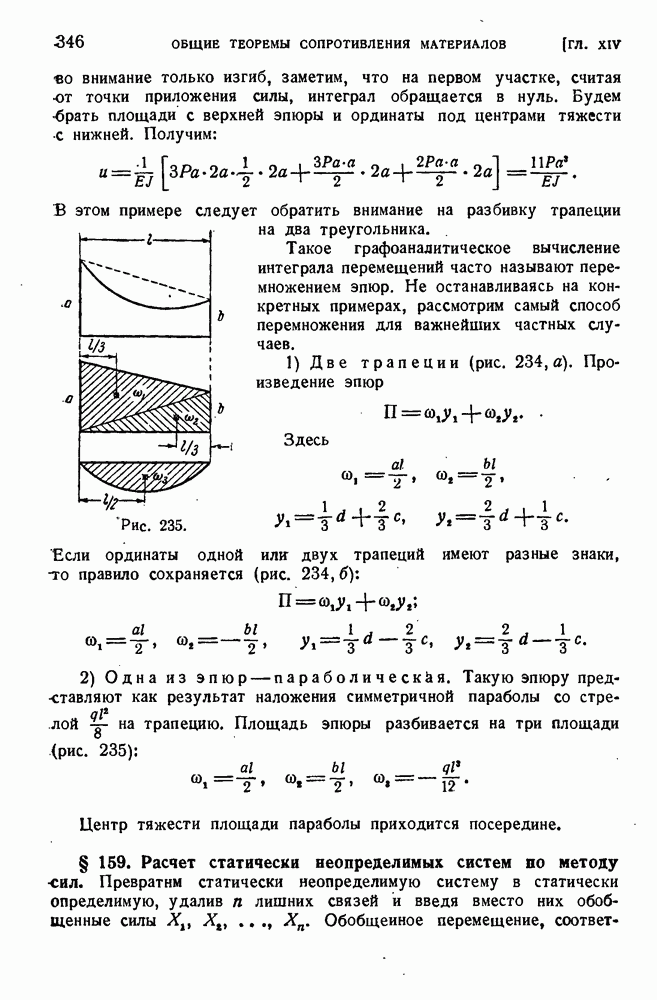
- § 158. Графоаналитический способ вычислений интеграла перемещений.
- § 159. Расчет статически неопределимых систем по методу сил.
- § 160. Уравнение трех моментов.
- ГЛАВА XV. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
- § 161. Жестко-пластическое тело.
- § 162. Поверхности нагружения.
- § 163. Истинное и допустимые состояния элемента.
- § 164. Статический метод определения предельной нагрузки.
- § 165. Примеры определения предельной нагрузки статическим методом.
- § 166. Кинематически возможные состояния.
- § 167. Кинематический метод определения предельной нагрузки.
- § 168. Примеры определения предельной нагрузки кинематическим методом.
- § 169. Предельное равновесие пластинок.
- ГЛАВА XVI. ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 170. Колебания систем с конечным числом степеней свободы.
- § 171. Собственные частоты и главные формы колебаний.
- § 172. Представление произвольной конфигурации системы через главные формы. Главные координаты.
- § 173. Формула и способ Релея.
- § 174. Нижние оценки для частоты основного тона.
- § 175. Продольные колебания стержней.
- § 176. Поперечные колебания стержней.
- § 177. Колебания балок постоянного сечения.
- § 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня.
- § 179. Действие ударных и импульсивных нагрузок на упругие системы.
- ГЛАВА XVII. ТЕОРИИ ПРОЧНОСТИ
- § 180. Постановка вопроса о прочности.
- § 181. Хрупкое и пластическое разрушение.
- § 182. Теория прочности Мора.
- § 183. Механизм хрупкого разрушения.
- § 184. Прочность при низких температурах.
- § 185. Прочность при переменных нагрузках.
- § 186. Природа усталостного разрушения.
- § 187. Критерии прочности при переменных нагрузках.
- § 188. Влияние концентрации напряжений на усталостную прочность.
- § 189. Усталостная прочность при сложном напряженном состоянии.
- ГЛАВА XVIII. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
- § 190. Ползучесть металлов.
- § 191. Процесс ползучести.
- § 192. Длительное разрушение.
- § 193. Температурные зависимости ползучести и длительной прочности.
- § 194. Феноменологические теории одномерной ползучести.
- § 195. Релаксация напряжений.
- § 196. Длительная прочность при переменных нагрузках.
- § 197. Ползучесть при изгибе.
- § 198. Критическое время сжатого стержня.
- § 199. Ползучесть и длительная прочность при сложном напряженном состоянии.
- § 200. Вращающиеся диски в условиях ползучести.
- § 201. Расчеты на ползучесть по теории старении.