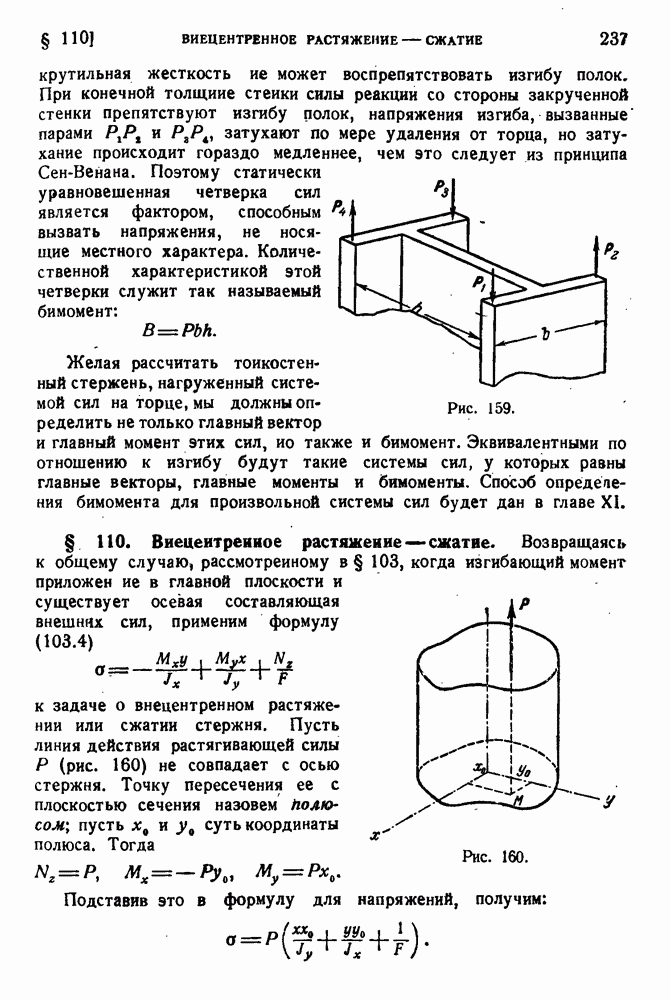
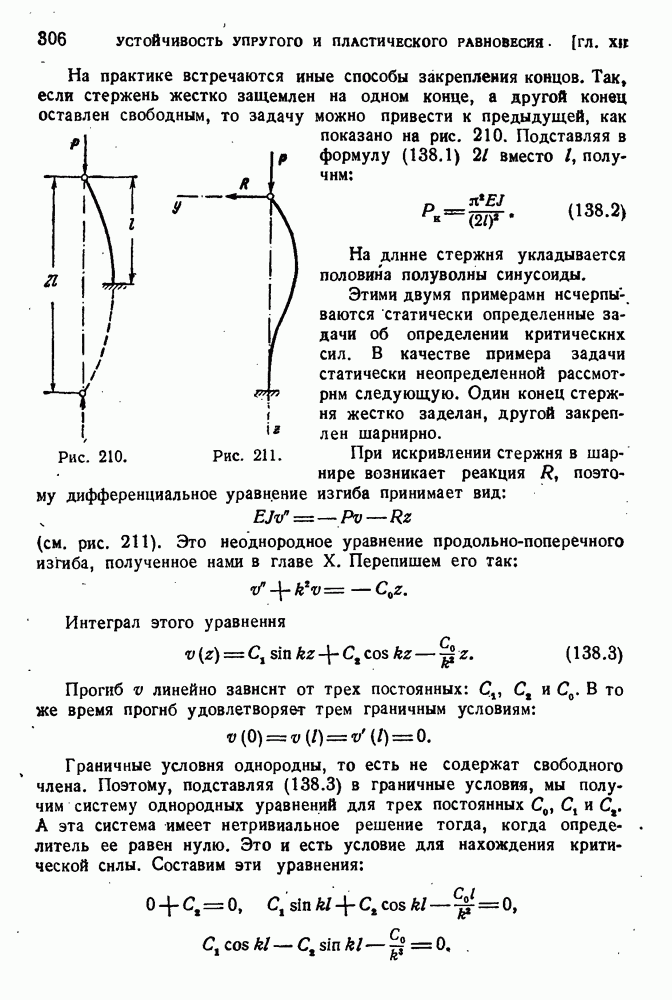
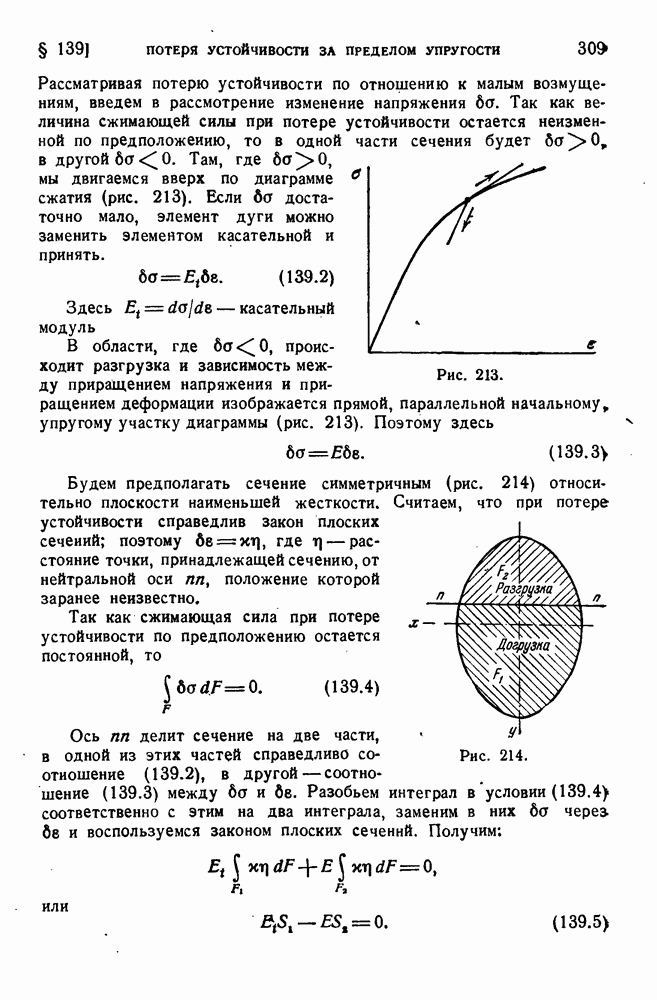
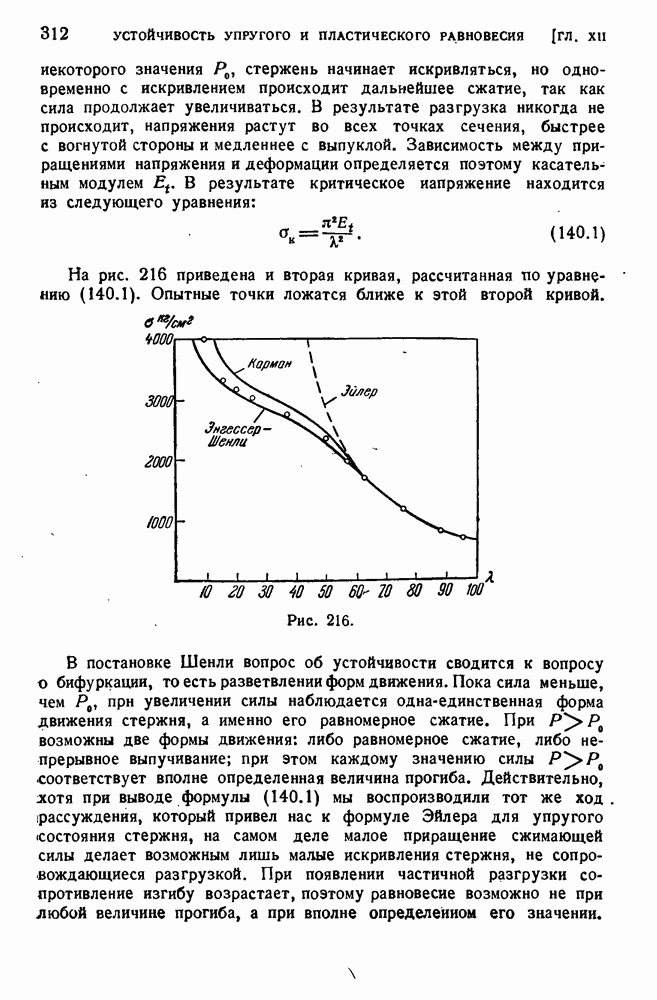
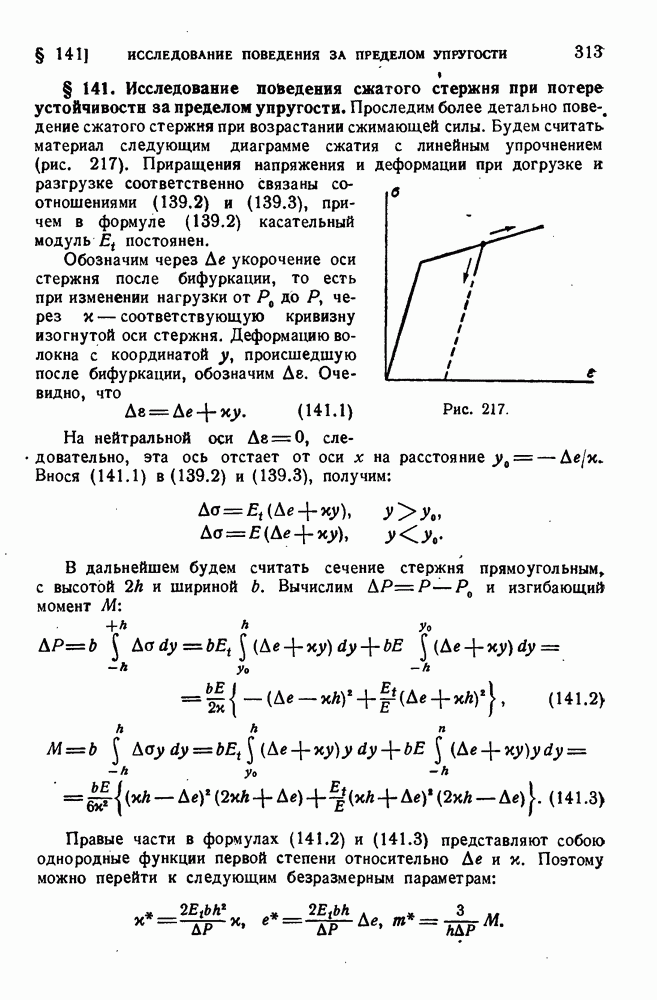
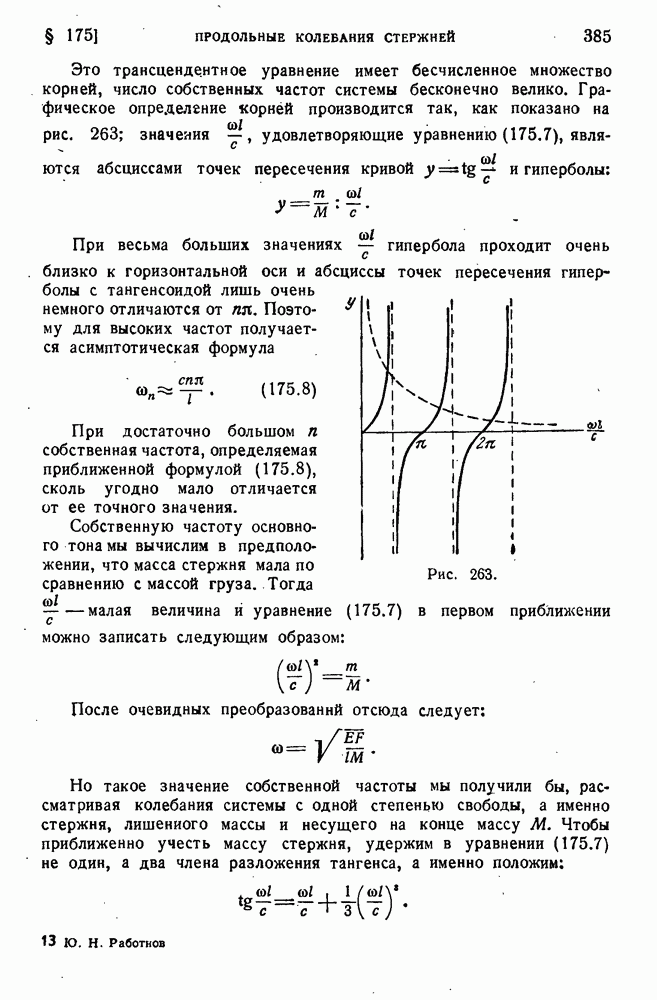
| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
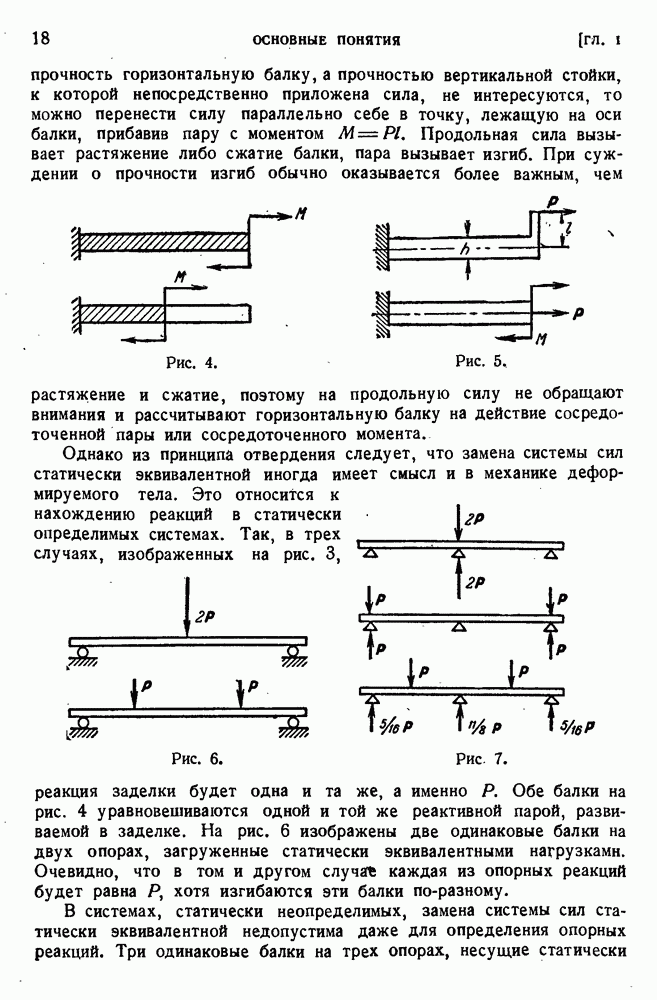
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
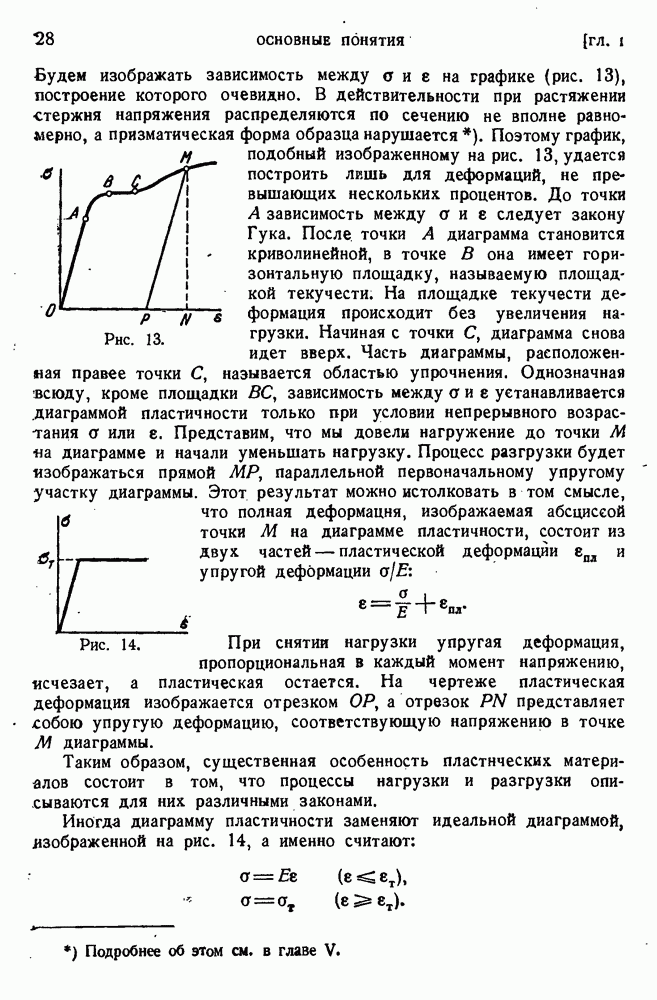
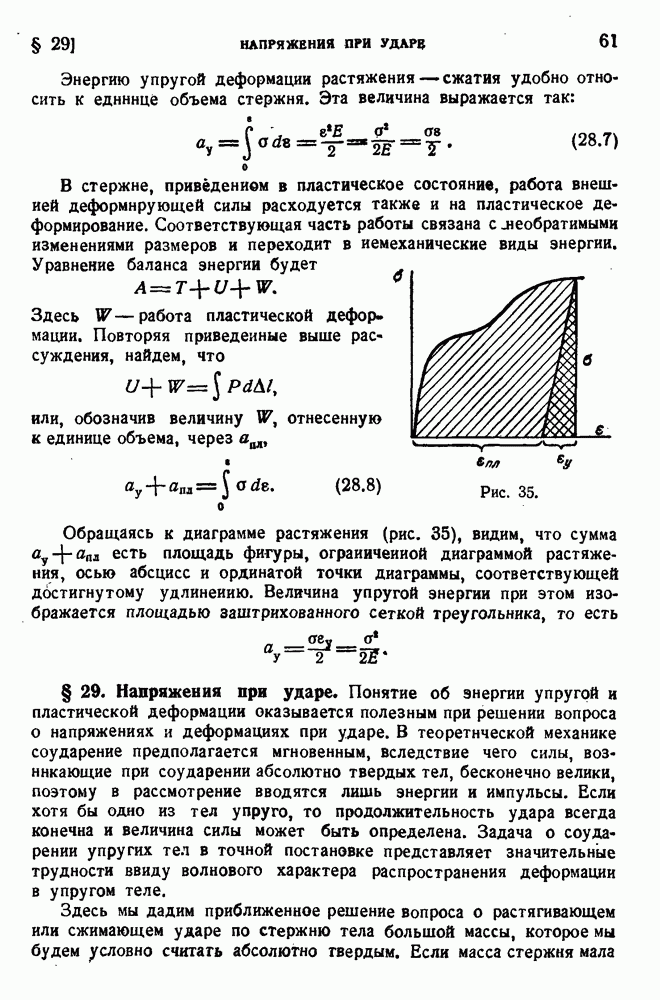
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
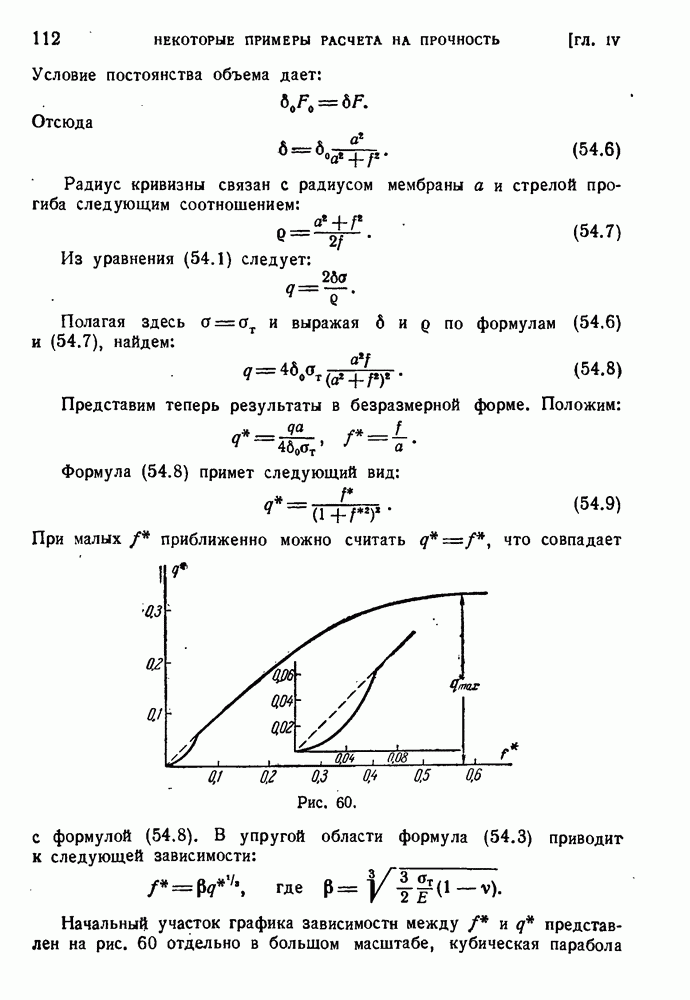
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
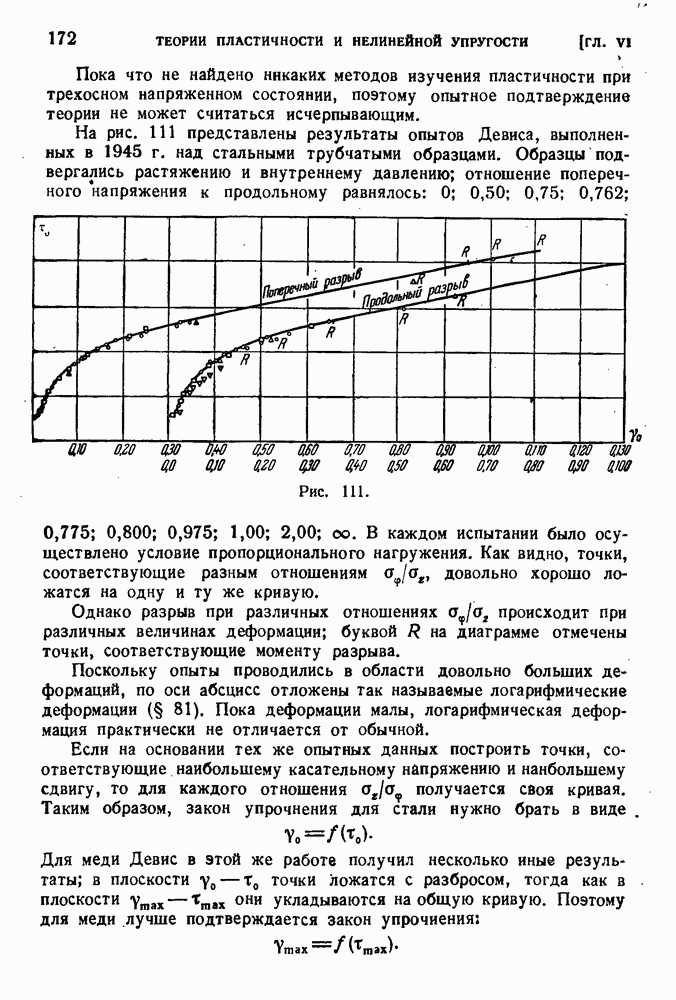
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
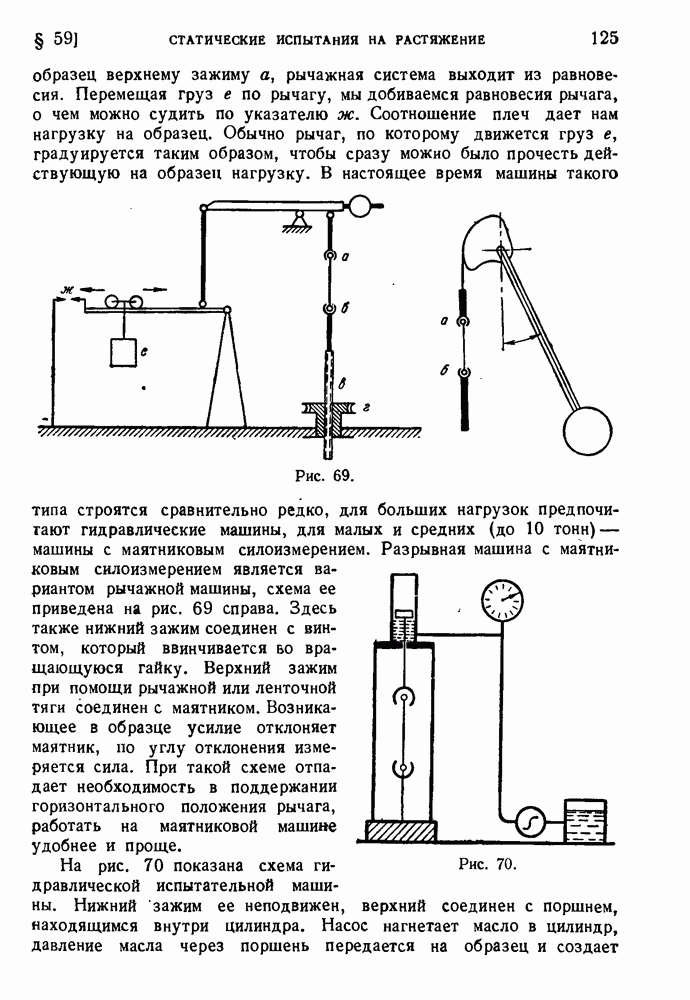
126
127
128
129
130
131
132
133
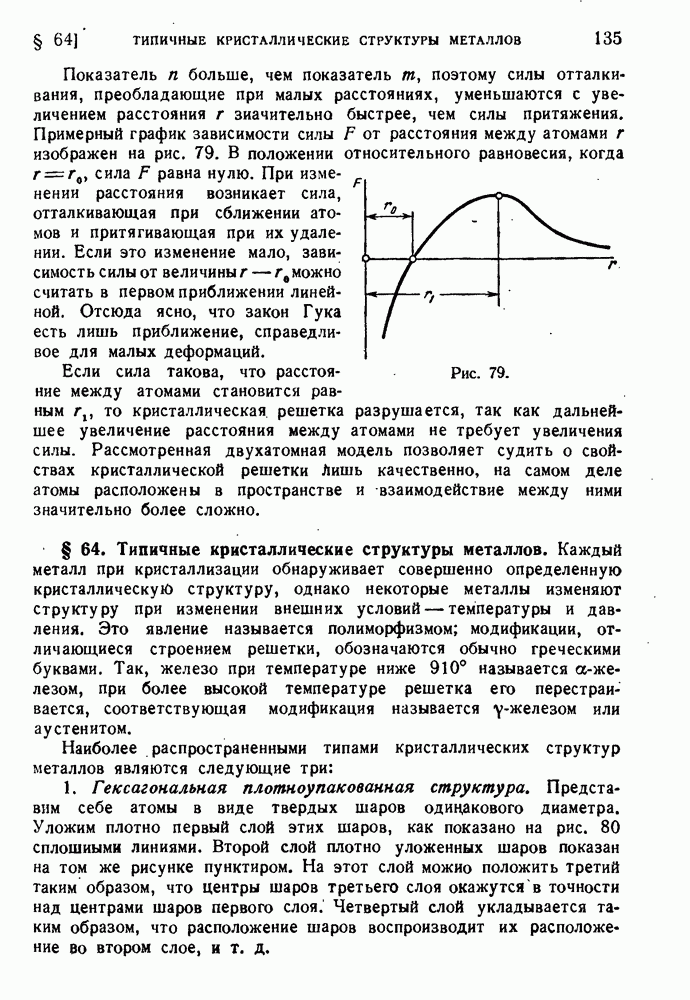
134
135
136
137
138
139
140
141
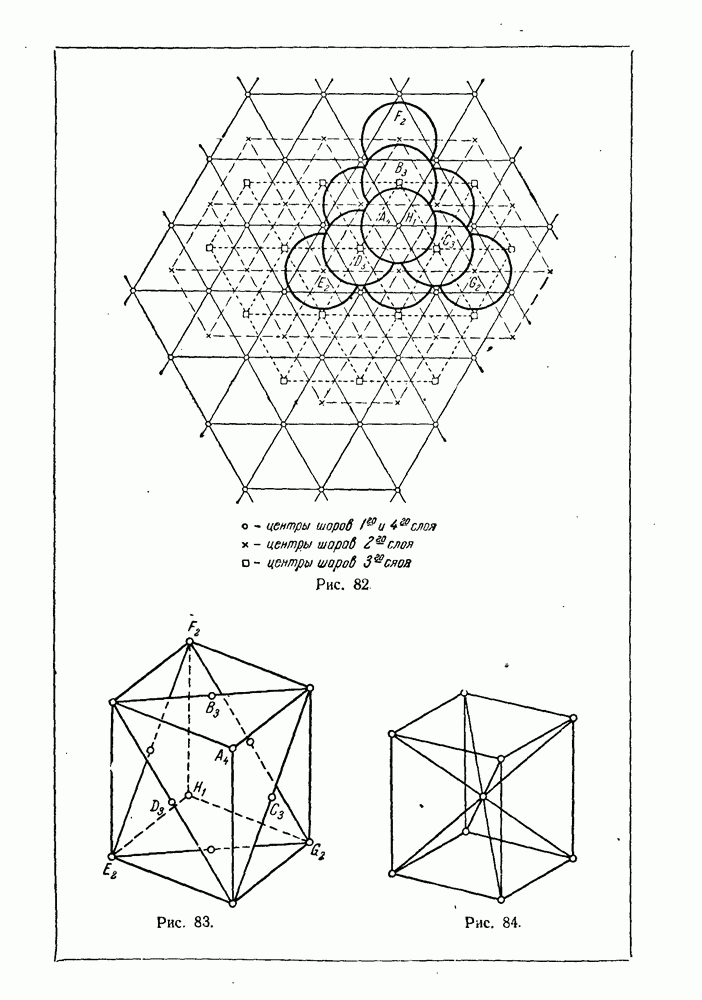
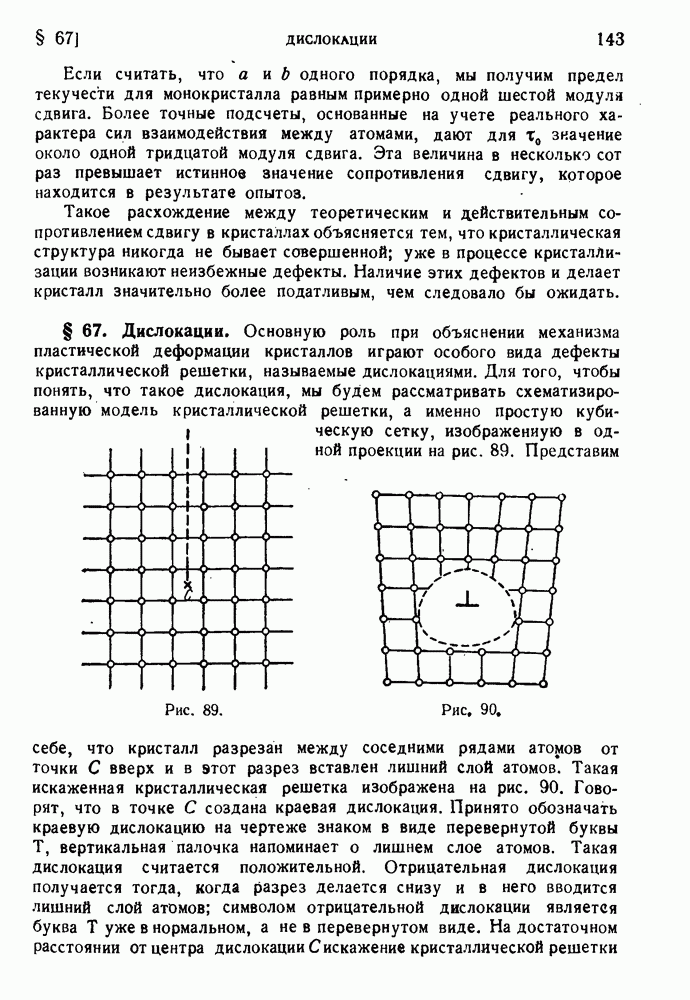
142
143
144
145
146
147
148
149
150
151
152
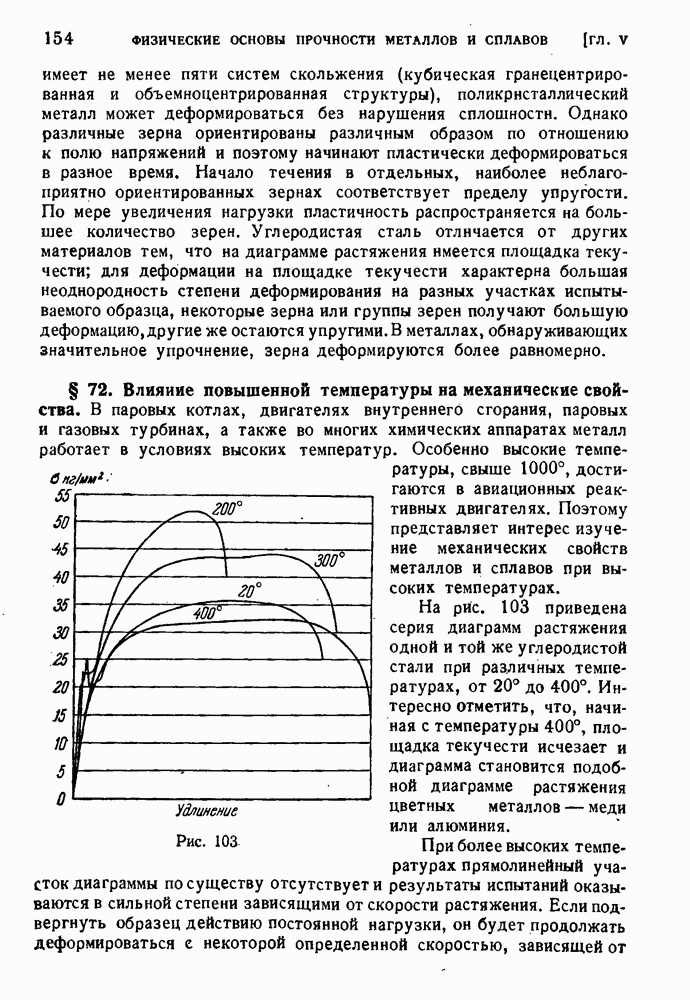
153
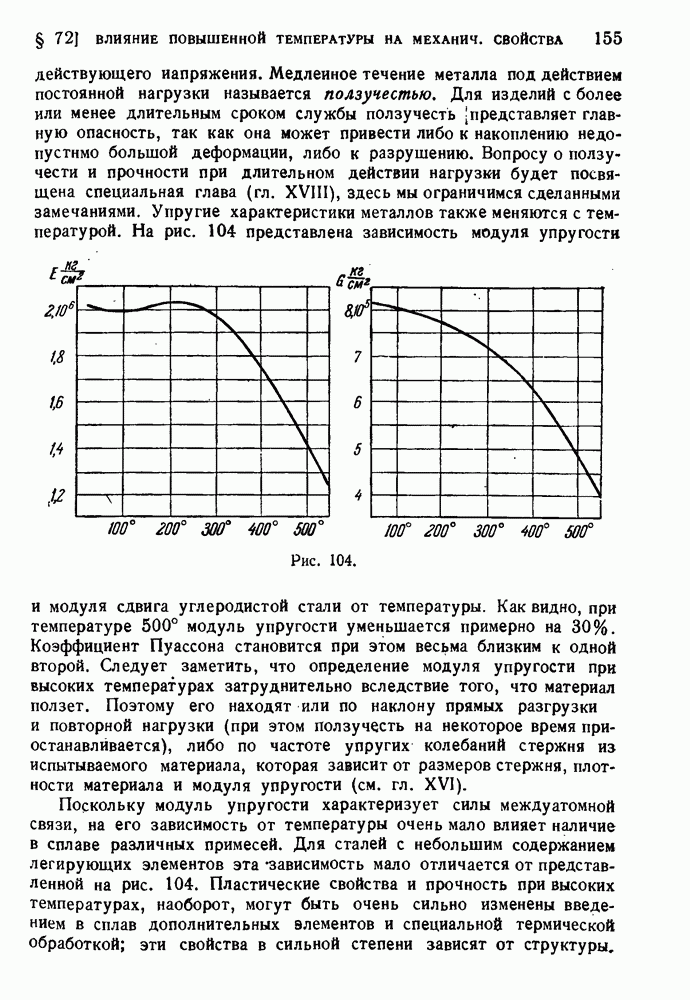
154
155
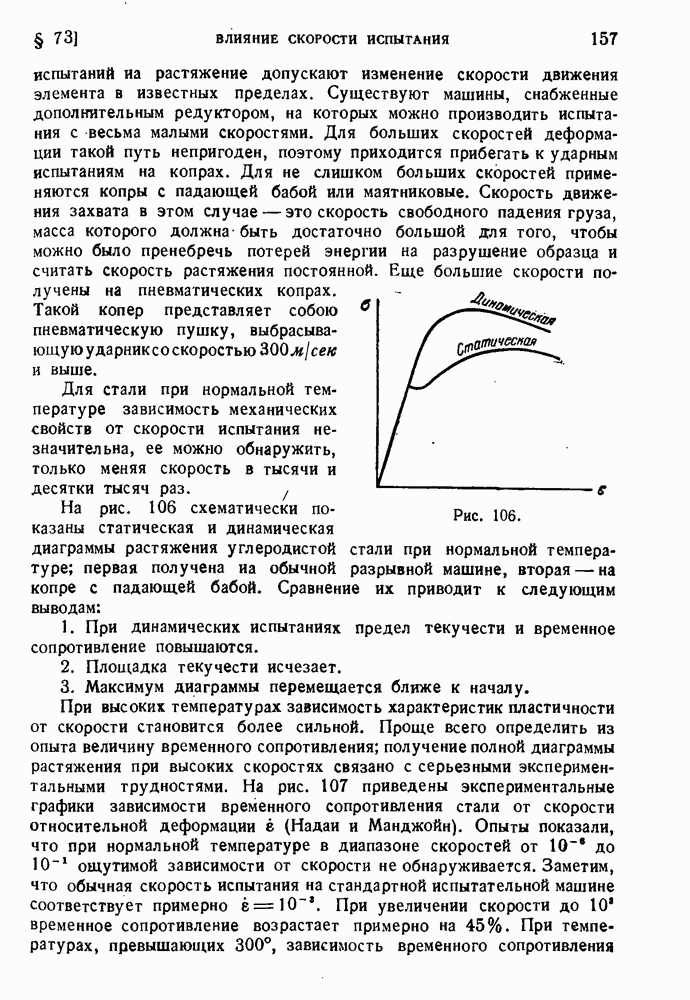
156
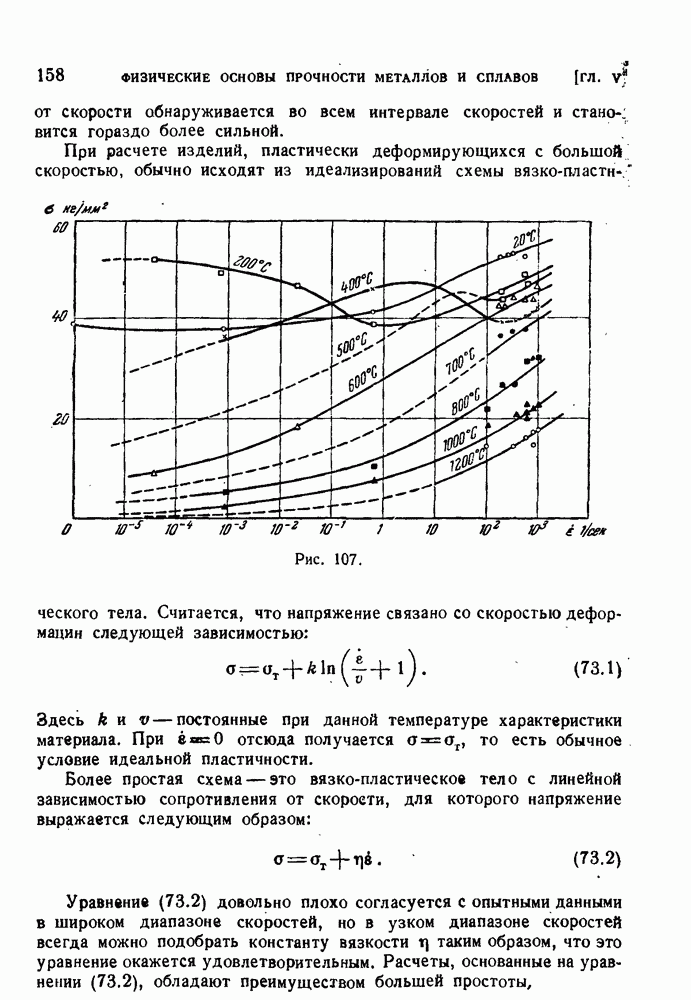
157
158
159
160
161
162
163
164
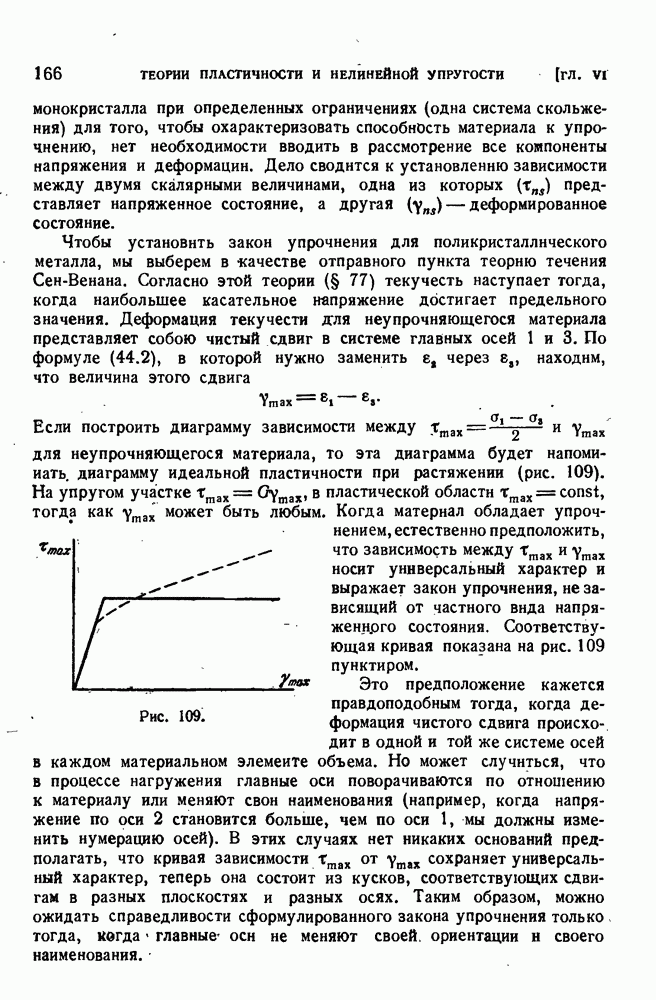
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
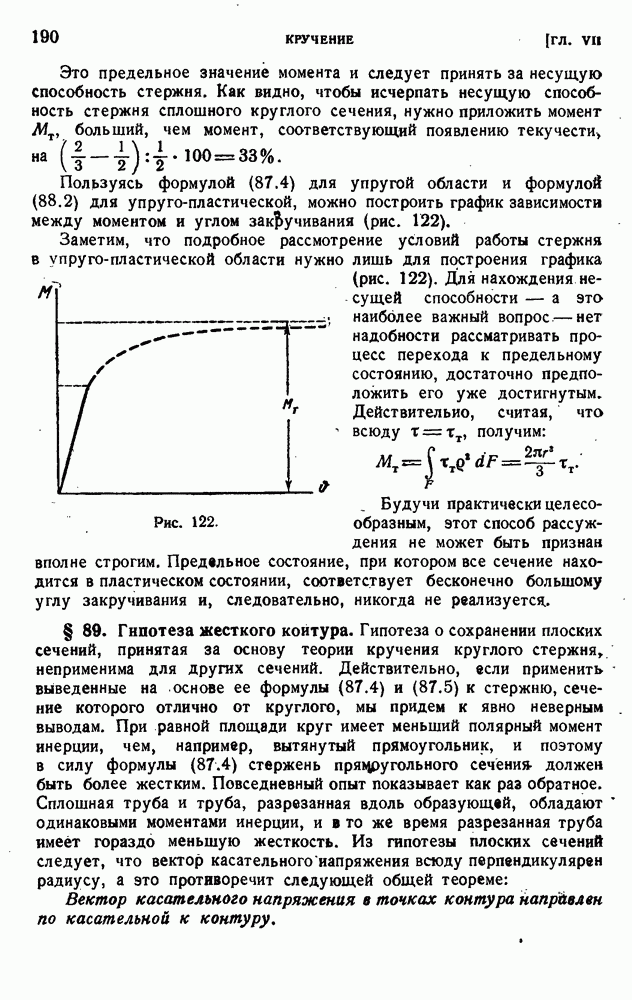
189
190
191
192
193
194
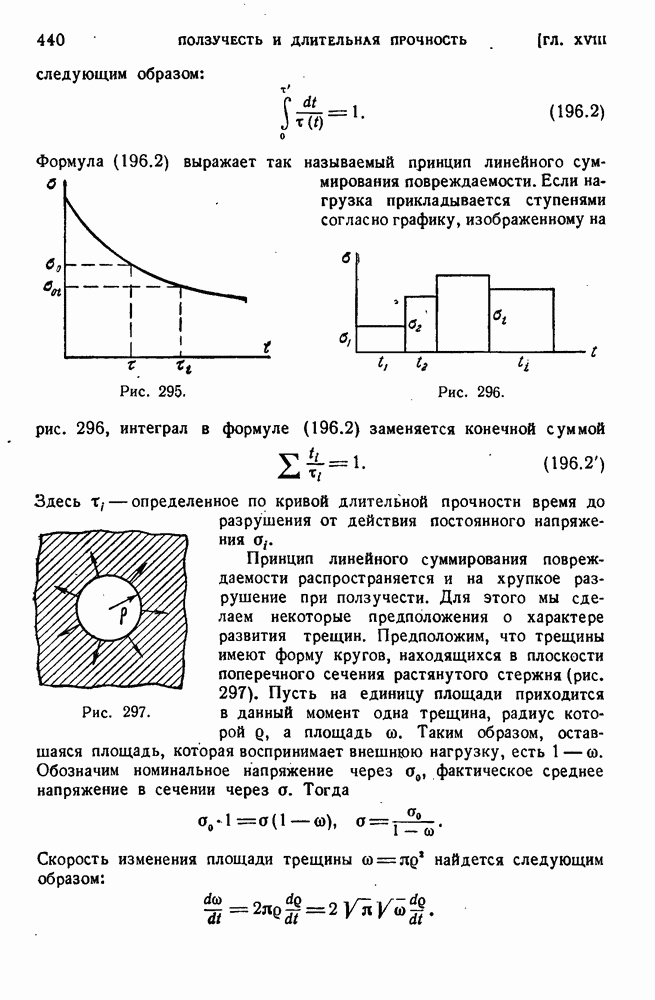
195
196
197
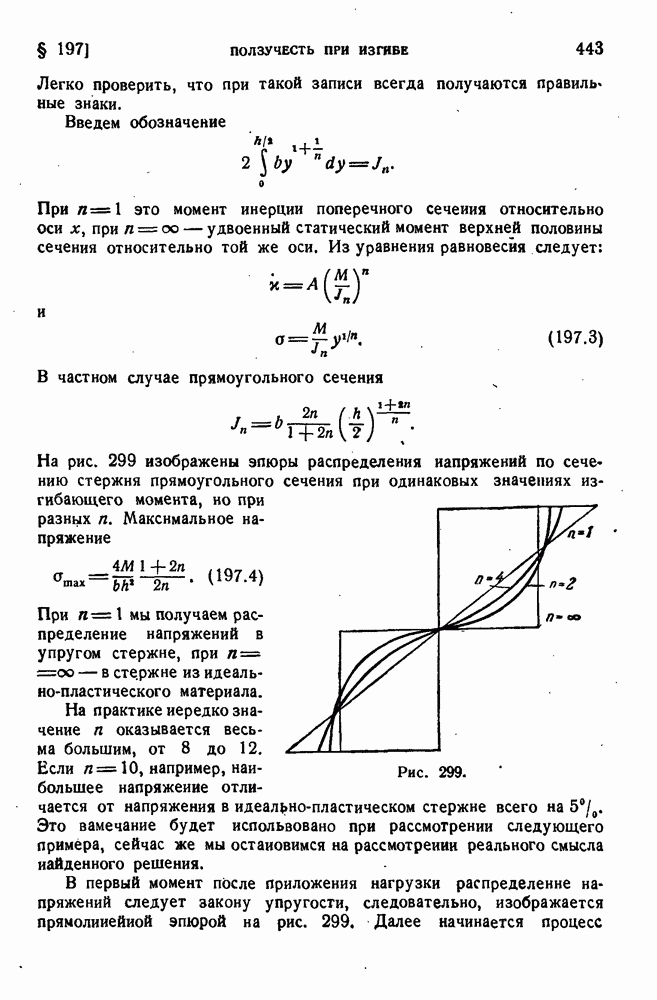
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
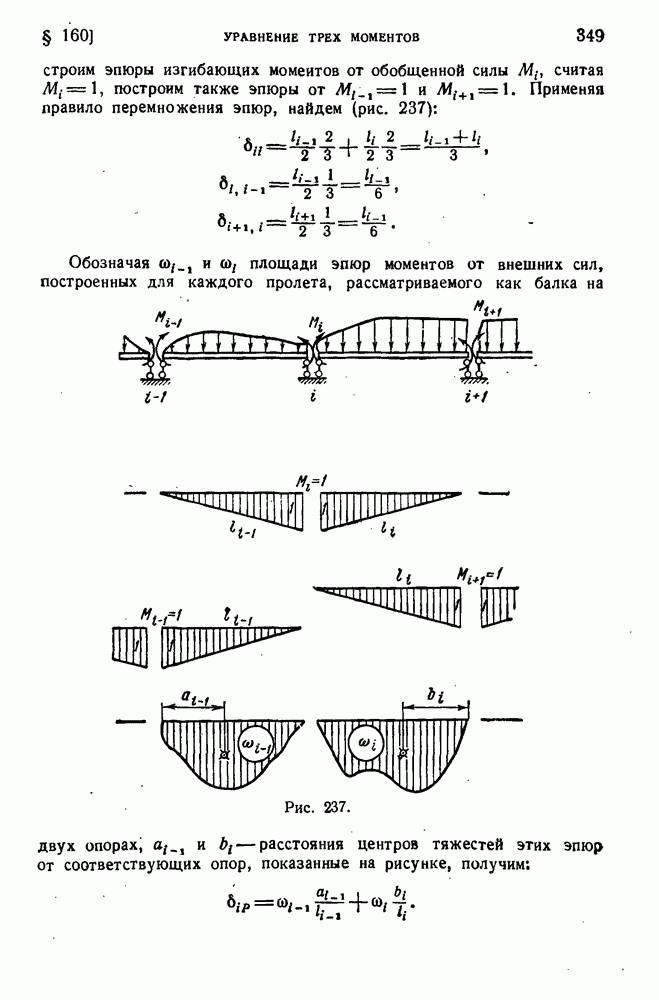
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
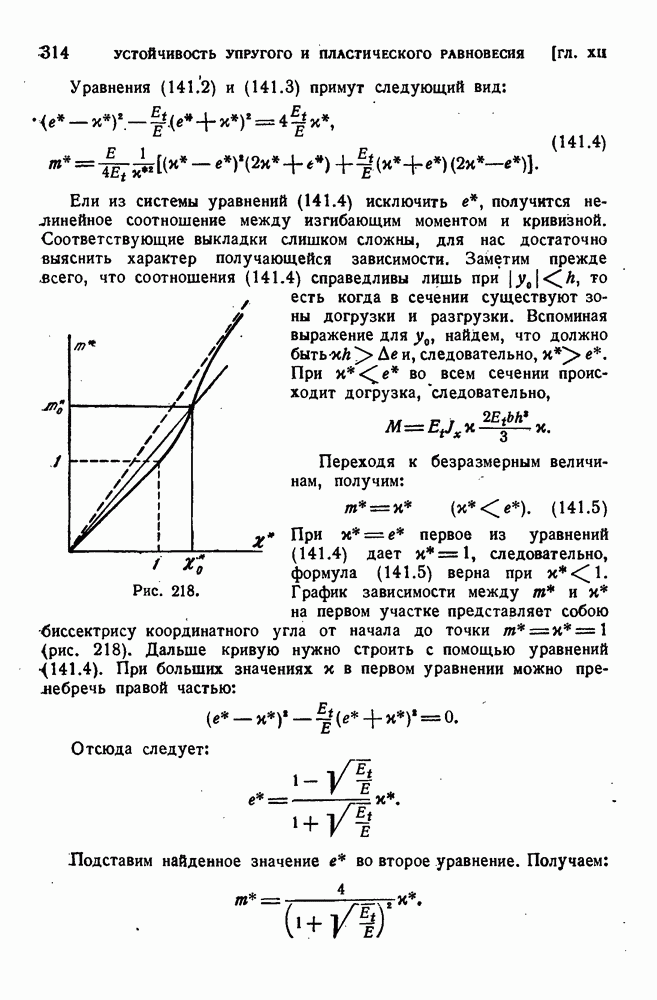
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
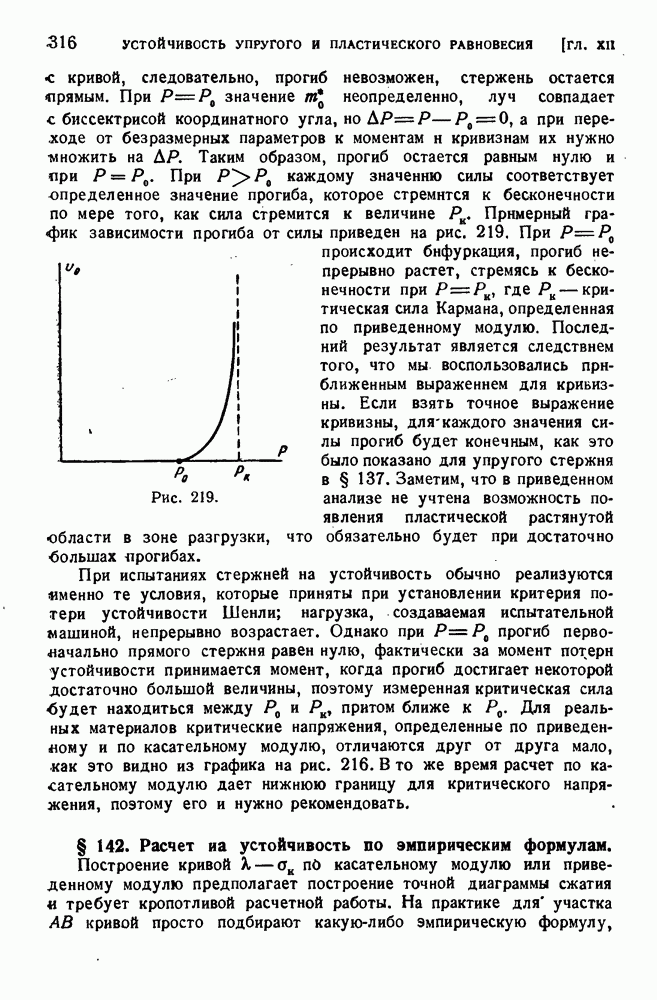
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
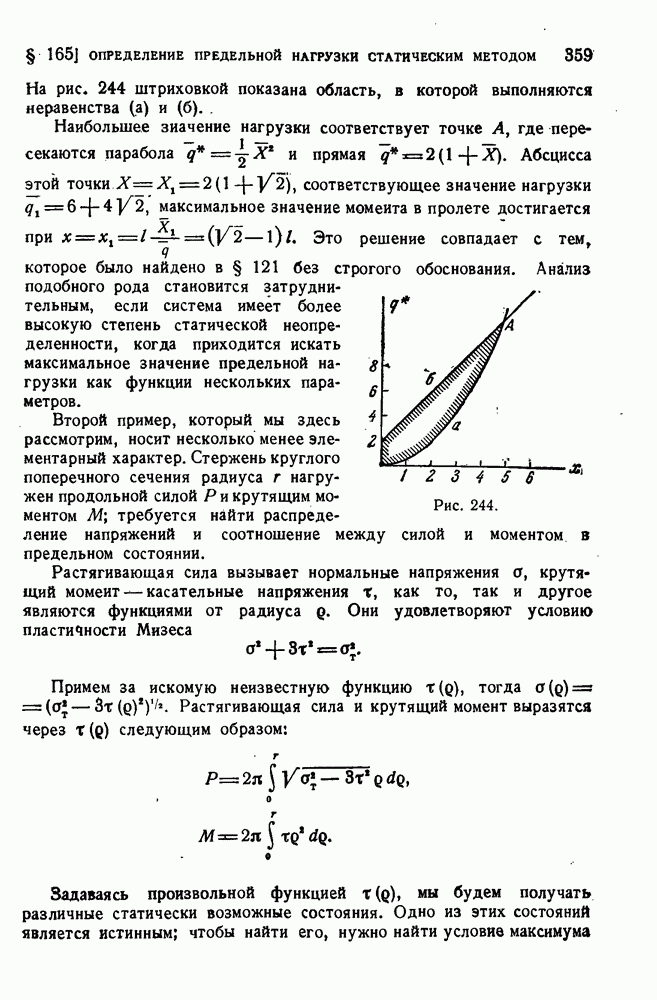
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 128. Центр изгиба.
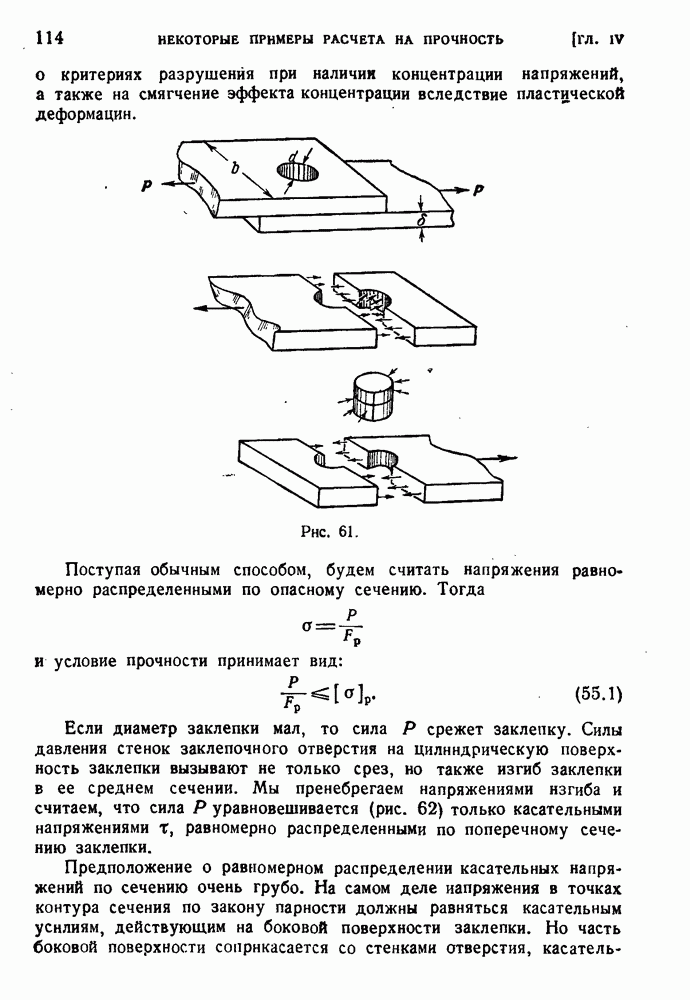
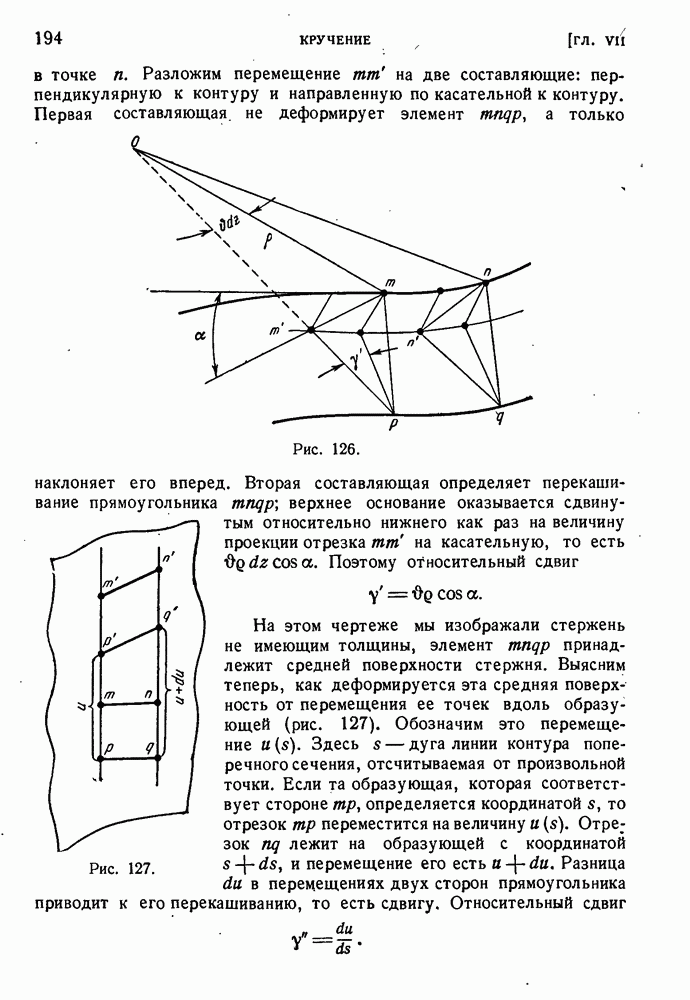
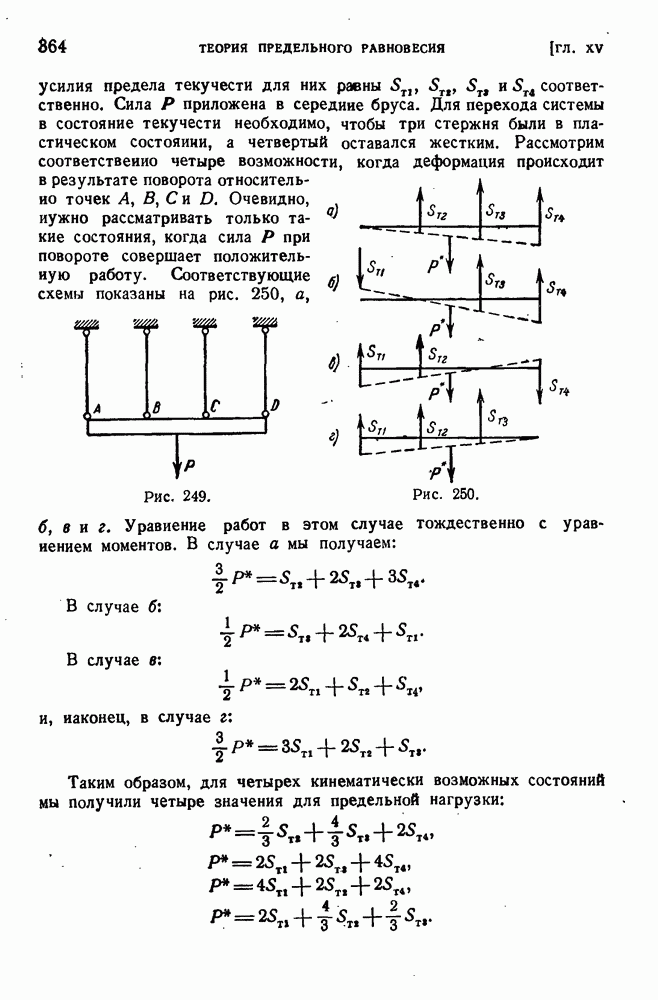
Предположим теперь, что сечение стержня несимметрично. Покажем, что существует такая ось, параллельная, оси стержня, что силы, действующие в любой проходящей через эту ось плоскости, не вызывают кручения. Точку пересечения этой оси с плоскостью сечеиия называют центром изгиба. Если такая точка С существует, то касательные силы в сечении приводятся к равнодействующей, проходящей через эту точку.
Отсюда следует, что сумма моментов всех касательных сил в сечении относительно точки С равна нулю. На элемент  с координатами х, у действует сила
с координатами х, у действует сила  (рис. 192); момент ее относительно точки С есть
(рис. 192); момент ее относительно точки С есть


Рис. 192.
где  — длина перпендикуляра, опущенного из точки С на касательную. Если С есть центр изгиба, то
— длина перпендикуляра, опущенного из точки С на касательную. Если С есть центр изгиба, то

Но  — это удвоенная площадь треугольника с основанием
— это удвоенная площадь треугольника с основанием  и вершиной в точке С. Положим
и вершиной в точке С. Положим  . Таким образом,
. Таким образом,

Применим формулу интегрирования по частям. Получим:

Но  обращается в нуль при
обращается в нуль при  . Воспользуемся, кроме того, для преобразования интеграла уравнением (126.2), вспомнив, что
. Воспользуемся, кроме того, для преобразования интеграла уравнением (126.2), вспомнив, что

как показано в § 126. Окончательный результат будет следующий:

а так как  произвольны, положение центра изгиба определяется следующими условиями:
произвольны, положение центра изгиба определяется следующими условиями:
 (128.1)
(128.1)
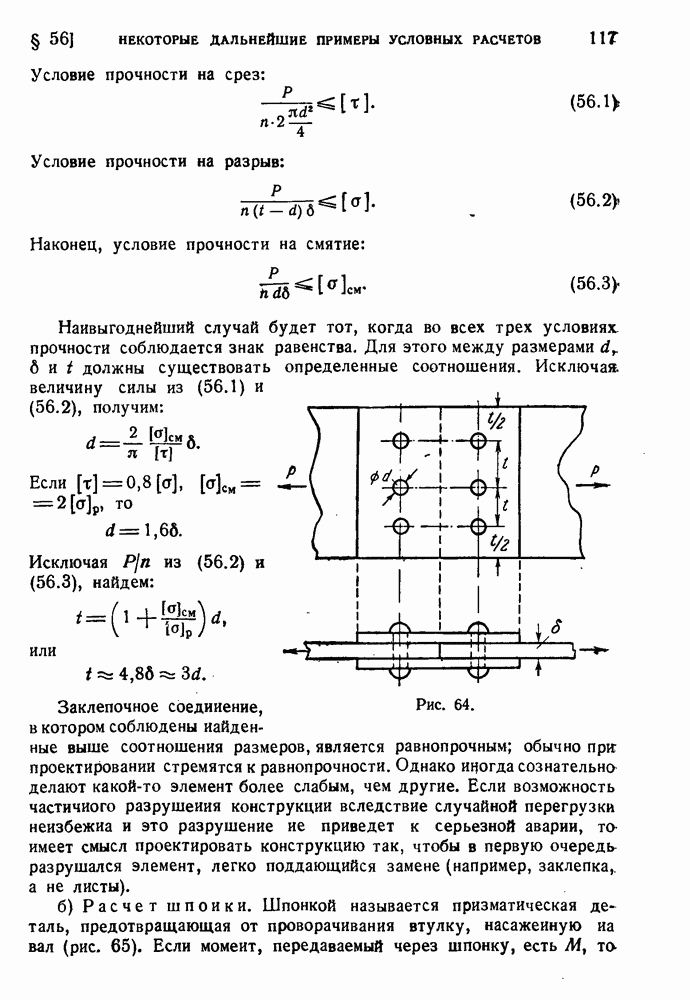
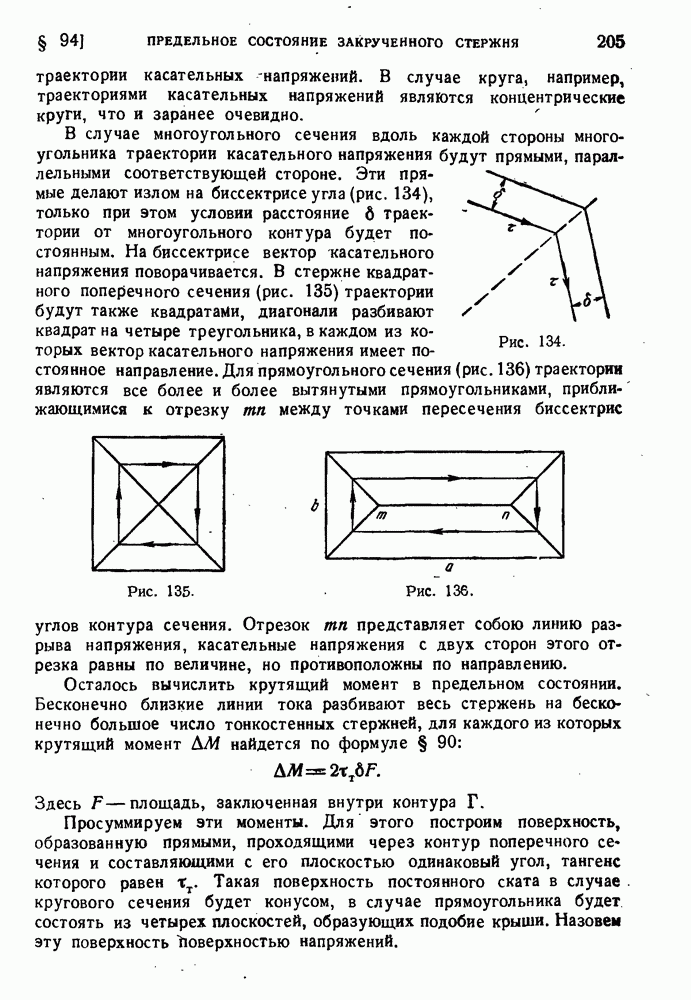
Совершенно элементарно находится центр изгиба для углового профиля. Если принять за полюс вершину, то секториальная площадь  равна нулю, поэтому условия (128.1) выполняются, и вершина есть центр изгиба (рис. 193).
равна нулю, поэтому условия (128.1) выполняются, и вершина есть центр изгиба (рис. 193).

Рис. 193.
Аналогично для таврового сечения центр изгиба находится в точке пересечения стенки с полкой. Заметим, что в формуле (128.1) к величине  можно прибавить любую постоянную величину. Действительно,
можно прибавить любую постоянную величину. Действительно,

так как оси х и у предполагаются центральными и статический момент площади сечения относительно оси х равен нулю. Вследствие этого замечания секториальную площадь <а можно отсчитывать не от конца профиля, а от какой-либо его. промежуточной точки.
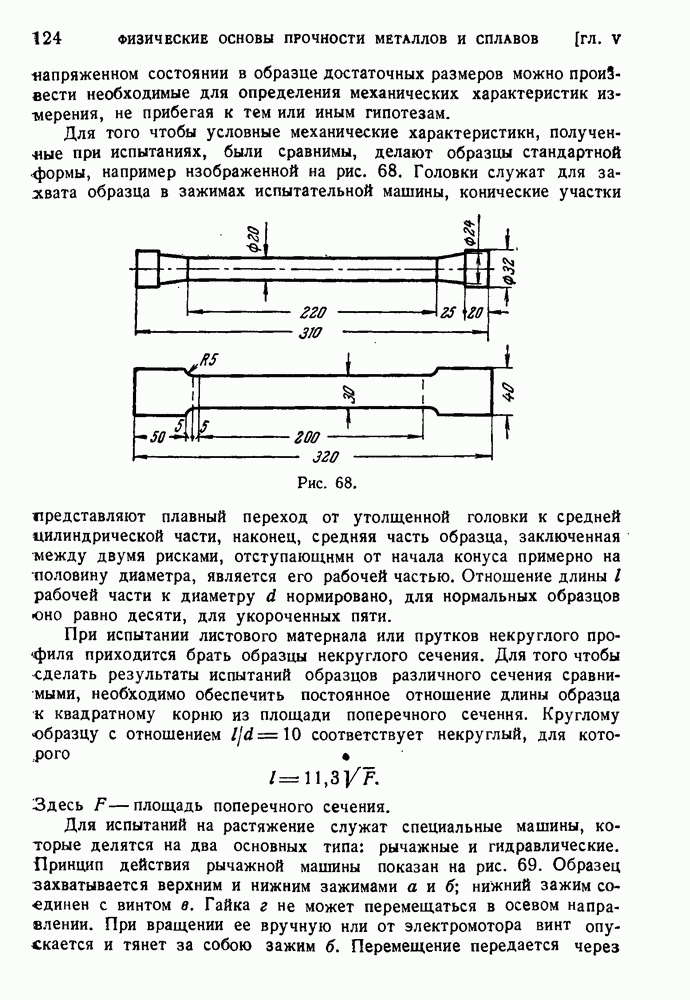
Для фактического нахождения центра изгиба важно иметь формулу, непосредственно определяющую его координаты. Для этого возьмем некоторую произвольную точку В и примем ее за полюс секторнальной площади  . Установим связь между
. Установим связь между  .
.
Из рис. 194 видно, что


Рис. 194.
Мы считаем, что секториальная площадь возрастает, если обход контура для наблюдателя, находящегося в полюсе, представляется происходящим против часовой стрелки.
Аналогично

Поэтому

Интегрируя, найдем:
 (128.2)
(128.2)
Аддитивная константа, как мы выяснили, несущественна.
Подставляя (128.2) в формулу (128.1), получим:

Отсюда
 (128.3)
(128.3)
Применим эти формулы к нахождению центра изгиба швеллера (рис. 195). Примем за точку В середину стенки, получим для верхней полки  , нижней
, нижней  , для стенки
, для стенки  . Для соответственных точек верхней и нижней полок значений х одинаковы, тогда как
. Для соответственных точек верхней и нижней полок значений х одинаковы, тогда как  одинакова по величине, но различна по знаку. Поэтому
одинакова по величине, но различна по знаку. Поэтому


Рис. 195.
Для  получим формулу
получим формулу

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Задачи и содержание сопротивления материалов.
- § 2. Сопротивление материалов и теоретическая механика.
- § 3. Статически неопределенные задачи.
- § 4. Внешние силы.
- § 5. Принцип отвердения.
- § 6. Недопустимость замены системы сил статически эквивалентной.
- § 7. Однородное тело.
- § 8. Внутренние силы.
- § 9. Напряжение.
- § 10. Простейшие типы напряженного состояния.
- § 11. Простейшие виды деформации.
- § 12. Упругость и пластичность.
- § 13. Закон Гука.
- § 14. Диаграмма пластичности.
- § 15. Тела изотропные и анизотропные.
- ГЛАВА II. РАСТЯЖЕНИЕ СЖАТИЕ
- § 16. Стержни и стержневые системы.
- § 17. Принцип Сен-Венана и гипотеза плоских сечений.
- § 18. Напряжения и деформации при растяжении.
- § 19. Расчеты на прочность при растижении и сжатии.
- § 20. Собственный вес и силы инерции.
- § 21. Стержни переменного сечения.
- § 22. Перемещения узлов стержневых систем.
- § 23. Статически неопределенные задачи на растяжение — сжатие.
- § 24. Температурные и монтажные напряжения.
- § 25. Общие соображения о расчете стержневых систем.
- § 26. Расчет статически неопределимых систем по допускаемым нагрузкам.
- § 27. Остаточные напряжения после пластической деформации.
- § 28. Потенциальная энергия растяжении.
- § 29. Напряжения при ударе.
- § 30. Распространение упругих волн в стержнях.
- § 31. Концентрации напряжений.
- § 32. Нелинейные задачи на растяжение — сжатие.
- ГЛАВА III. СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
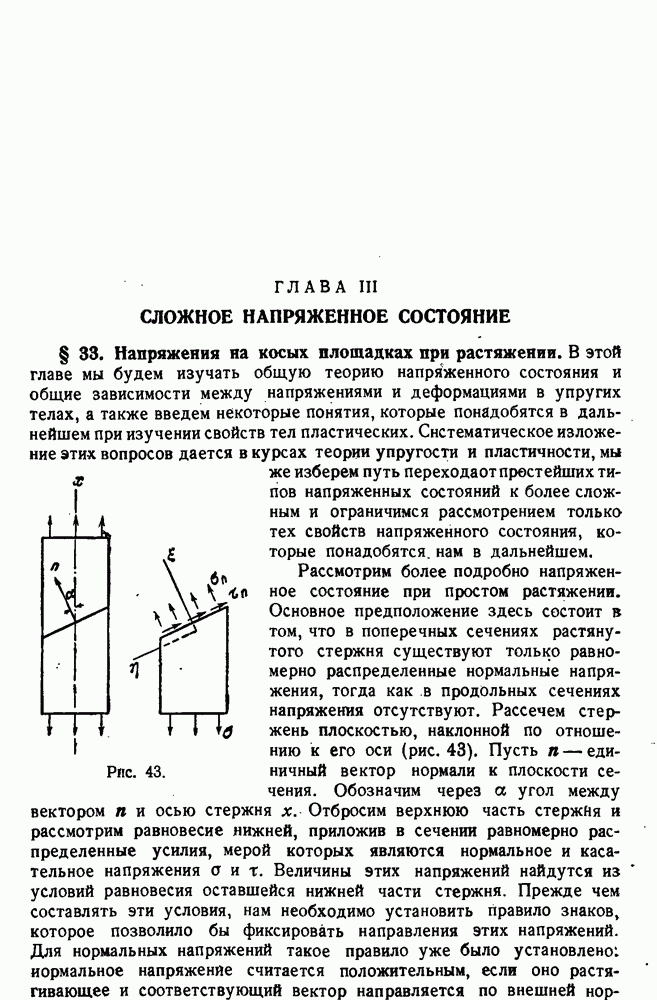
- § 33. Напряжения на косых площадках при растяжении.
- § 34. Напряжения при двухосном растяжении.
- § 35. Круговая диаграмма Мора.
- § 36. Общий случай плоского напряженного состояния.
- § 37. Определение напряжений на произвольной площадке.
- § 38. Пространственное напряженное состояние.
- § 39. Главные напряжения.
- § 40. Главные касательные напряжения.
- § 41. Октаэдрическое напряжение.
- § 42. Закон Гука для главных осей.
- § 43. Изменение объема при упругой деформации.
- § 44. Чистый сдвиг.
- § 45. Деформация элемента объема в общем случае.
- § 46. Условие пластичности Треска — Сен-Венана.
- § 47. Условие пластичности Мизеса.
- § 48. Условия пластичности для плоского напряженного состояния.
- § 49. Потенциальная энергия упругой деформации.
- § 50. Энергия изменения формы.
- ГЛАВА IV. НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
- § 51. Расчеты на прочность изделий сложной формы.
- § 52. Безмоментные оболочки вращении.
- § 53. Местные напряжения в безмоментных оболочках.
- § 54. Большие прогибы мембраны.
- § 55. Условные расчеты.
- § 56. Некоторые дальнейшие примеры условных расчетов.
- § 57. Расчет сварных соединений.
- ГЛАВА V. ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
- § 58. Задачи испытания материалов.
- § 59. Статические испытания на растяжение.
- § 60. Исследование металлов в области малых деформаций.
- § 61. Диаграмма растяжения мягкой стали.
- § 62. Опыты на сжатие.
- § 63. Строение и упругая деформация металлических кристаллов.
- § 64. Типичные кристаллические структуры металлов.
- § 65. Пластическая деформация монокристаллов.
- § 66. Прочность кристаллов и сопротивление пластическому деформированию.
- § 67. Дислокации.
- § 68. Движение и равновесие дислокаций.
- § 69. Источники дислокаций.
- § 70. Границы блоков.
- § 71. Деформация поликристаллических металлов и сплавов.
- § 72. Влияние повышенной температуры на механические свойства.
- § 73. Влияние скорости испытания.
- § 74. Испытании на твердость.
- ГЛАВА VI. ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ
- § 75. Основные принципы построения теории пластичности.
- § 76. Ассоциированный закон течения.
- § 77. Течение при условии пластичности Сен-Венана и Мизеса.
- § 78. Закон упрочнения.
- § 79. Деформационная теория пластичности.
- § 80. Экспериментальная проверка теорий пластичности.
- § 81. Конечная деформация.
- § 82. Нелинейно упругое тело.
- § 83. Высокоэластические деформации.
- § 84. Упругое последействие.
- § 85. Некоторые свойства вязко-упругого тела.
- § 86. Принцип суммирования Больцмана—Вольтерра.
- ГЛАВА VII. КРУЧЕНИЕ
- § 87. Кручение стержней круглого сечеиия.
- § 88. Упруго-пластическое кручение стержня круглого сечения.
- § 89. Гипотеза жесткого контура.
- § 90. Кручение тонкостенных стержней замкнутого профиля.
- § 91. Кручение тонкостенных стержней открытого профиля.
- § 92. Кручение упругих стержией сплошного профиля.
- § 93. Опытное исследование кручения.
- § 94. Предельное состояние закрученного стержня из идеально-пластического материала.
- ГЛАВА VIII. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- § 96. Общие теоремы о моментах.
- § 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей.
- § 98. Вычисление моментов инерции.
- § 99. Преобразование моментов инерции при повороте осей.
- § 100. Главные оси и главные моменты инерции.
- ГЛАВА IX. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
- § 101. Действие поперечных сил на балку.
- § 102. Гипотеза плоских сечений и принцип Сен-Венана.
- § 103. Нормальные напряжения при изгибе.
- § 104. Изгибающие моменты и перерезывающие силы.
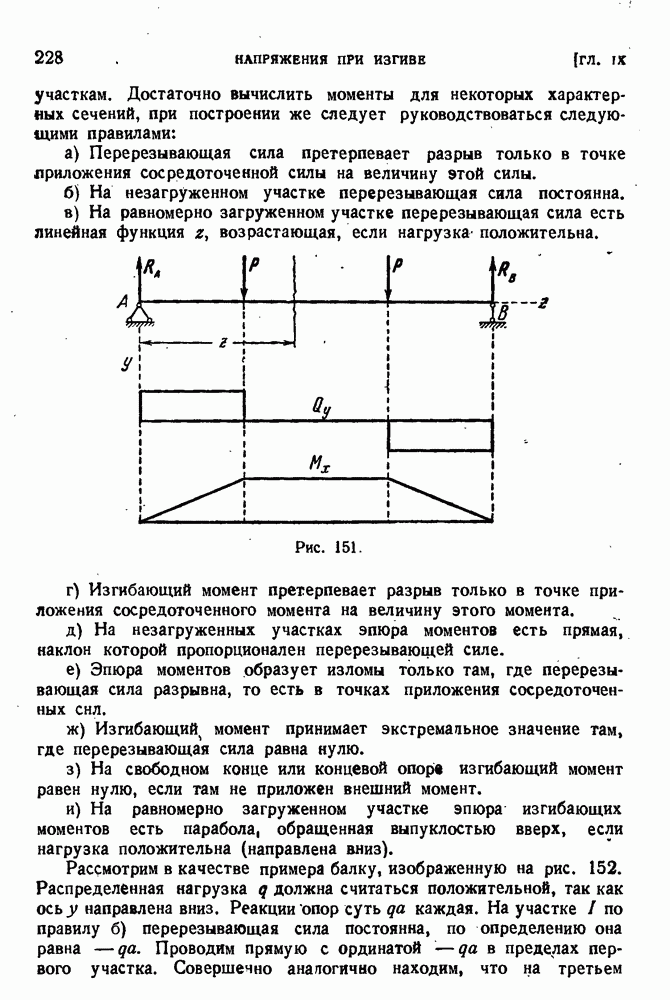
- § 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры.
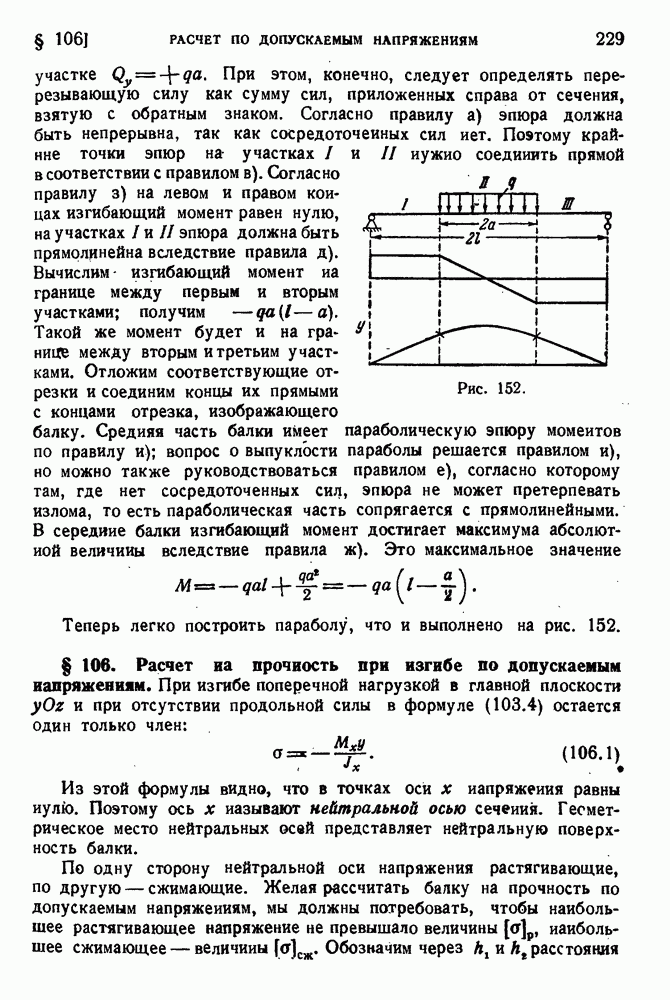
- § 106. Расчет на прочность при изгибе по допускаемым напряжениям.
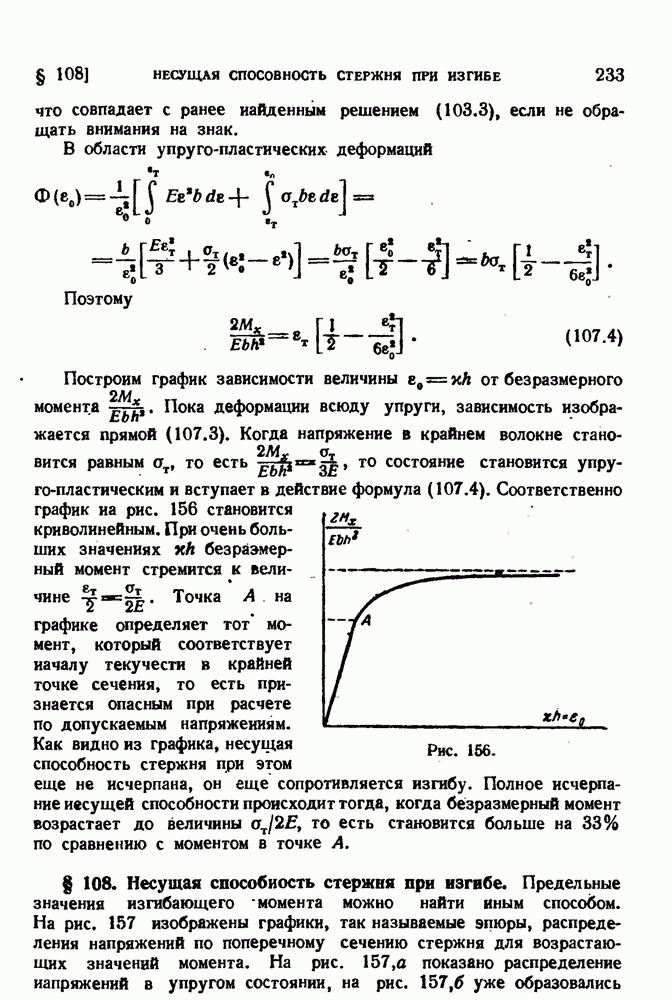
- § 107. Упруго-пластический изгиб.
- § 108. Несущая способность стержня при изгибе.
- § 109. Принцип Сен-Венана.
- § 110. Внецентренное растяжение — сжатие.
- § 111. Ядро сечения.
- § 112. Несущая способность внецентренно сжатого стержня.
- § 113. Расчет составных балок.
- § 114. Изгиб кривого бруса.
- § 115. Нахождение нейтральной осн в кривом стержне.
- ГЛАВА X. ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- § 116. Дифференциальное уравнение изогнутой оси.
- § 117. Пределы применимости приближенной теории.
- § 118. Интегрирование уравнения изгиба.
- § 119. Примеры определения прогибов.
- § 120. Простейшие статически неопределенные задачи.
- § 121. Расчет статически неопределимых балок по способу допускаемых нагрузок.
- § 122. Изгиб стержней переменного сечения.
- § 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами.
- § 124. Продольно-поперечный изгиб.
- § 125. Изгиб балки на упругом основании.
- ГЛАВА XI. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
- § 126. Нормальные и касательные напряжения при изгибе.
- § 127. Касательные напряжении при изгибе в плоскости симметрии.
- § 128. Центр изгиба.
- § 129. Дополнительные напряжения при кручении.
- § 130. Закон секториальных площадей.
- § 131. Уравнение стесненного кручения.
- § 132. Вычисление секториальных характеристик.
- § 133. Стержень, нагруженный бимоментом.
- § 134. Некоторые примеры стесненного кручения.
- ГЛАВА XII. УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ
- § 135. Постановка вопроса об устойчивости.
- § 136. Устойчивость сжатого упругого стержня.
- § 137. Эластика Эйлера.
- § 138. Критические силы при иных видах закрепления стержня.
- § 139. Потеря устойчивости за пределом упругости.
- § 140. Потеря устойчивости за пределом упругости (продолжение).
- § 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости.
- § 142. Расчет на устойчивость по эмпирическим формулам.
- ГЛАВА XIII. ТРУБЫ И ДИСКИ
- § 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности.
- § 144. Упругое состояние трубы. Формулы Ламе.
- § 145. Пластическое состояние трубы.
- § 146. Вращающиеся диски. Упругое состояние.
- § 147. Диск равного сопротивления.
- § 148. Предельное равновесие вращающегося диска.
- ГЛАВА XIV. ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 149. Обобщенные силы и обобщенные перемещения.
- § 150. Начало возможных перемещений для деформируемого тела.
- § 151. Теоремы Лагранжа и Кастильяно.
- § 152. Лииейиые упругие системы.
- § 153. Теорема о взаимности работ.
- § 154. Теорема Кастильяно для линейных упругих систем.
- § 155. Расчет винтовых пружин.
- § 156. Теорема о минимуме энергии.
- § 157. Интеграл перемещений.
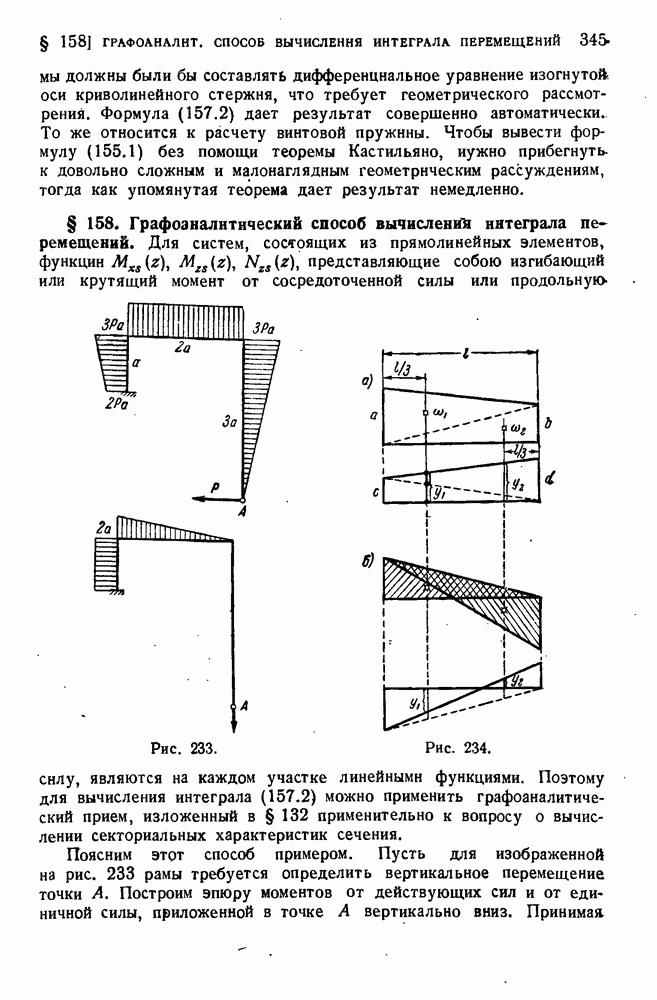
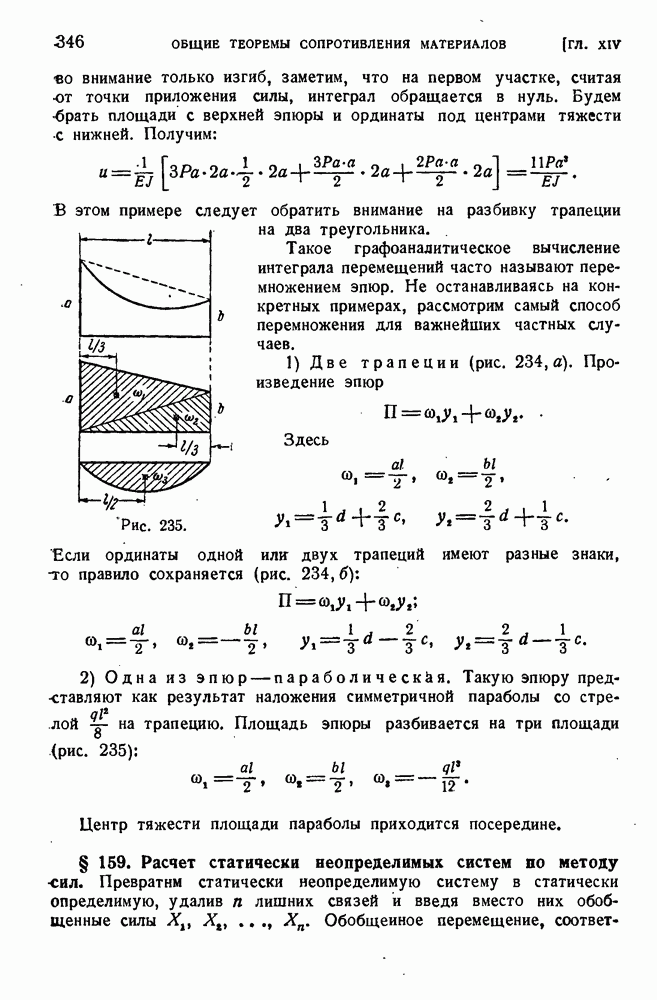
- § 158. Графоаналитический способ вычислений интеграла перемещений.
- § 159. Расчет статически неопределимых систем по методу сил.
- § 160. Уравнение трех моментов.
- ГЛАВА XV. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
- § 161. Жестко-пластическое тело.
- § 162. Поверхности нагружения.
- § 163. Истинное и допустимые состояния элемента.
- § 164. Статический метод определения предельной нагрузки.
- § 165. Примеры определения предельной нагрузки статическим методом.
- § 166. Кинематически возможные состояния.
- § 167. Кинематический метод определения предельной нагрузки.
- § 168. Примеры определения предельной нагрузки кинематическим методом.
- § 169. Предельное равновесие пластинок.
- ГЛАВА XVI. ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 170. Колебания систем с конечным числом степеней свободы.
- § 171. Собственные частоты и главные формы колебаний.
- § 172. Представление произвольной конфигурации системы через главные формы. Главные координаты.
- § 173. Формула и способ Релея.
- § 174. Нижние оценки для частоты основного тона.
- § 175. Продольные колебания стержней.
- § 176. Поперечные колебания стержней.
- § 177. Колебания балок постоянного сечения.
- § 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня.
- § 179. Действие ударных и импульсивных нагрузок на упругие системы.
- ГЛАВА XVII. ТЕОРИИ ПРОЧНОСТИ
- § 180. Постановка вопроса о прочности.
- § 181. Хрупкое и пластическое разрушение.
- § 182. Теория прочности Мора.
- § 183. Механизм хрупкого разрушения.
- § 184. Прочность при низких температурах.
- § 185. Прочность при переменных нагрузках.
- § 186. Природа усталостного разрушения.
- § 187. Критерии прочности при переменных нагрузках.
- § 188. Влияние концентрации напряжений на усталостную прочность.
- § 189. Усталостная прочность при сложном напряженном состоянии.
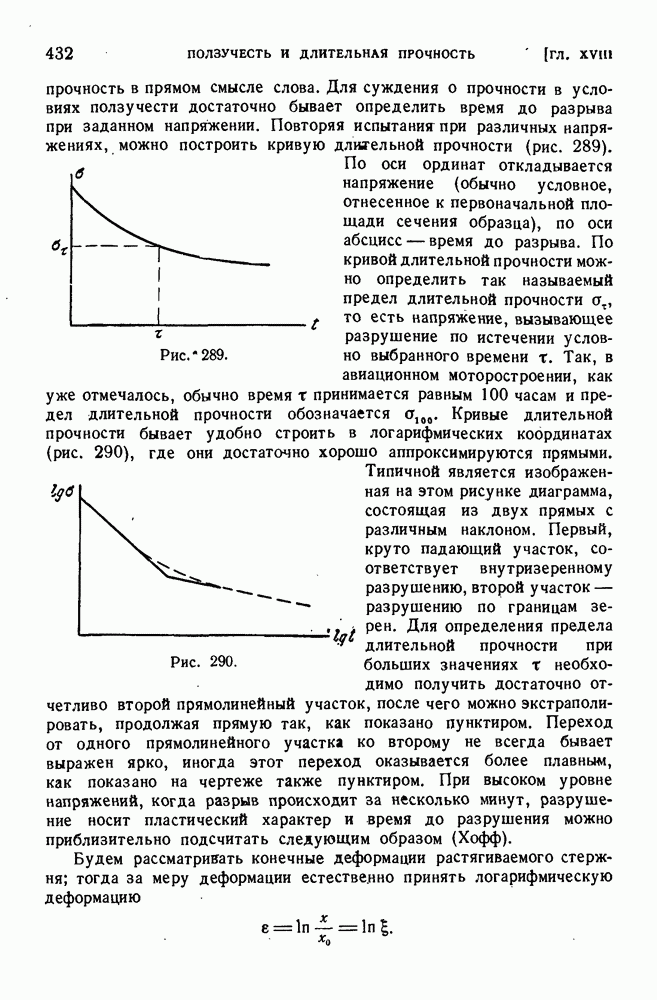
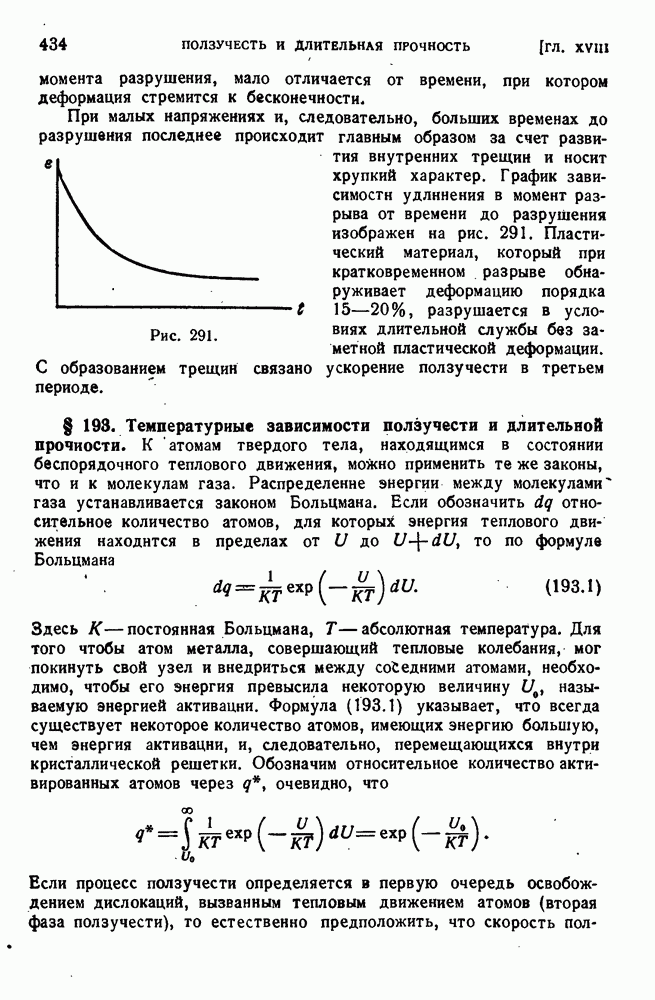
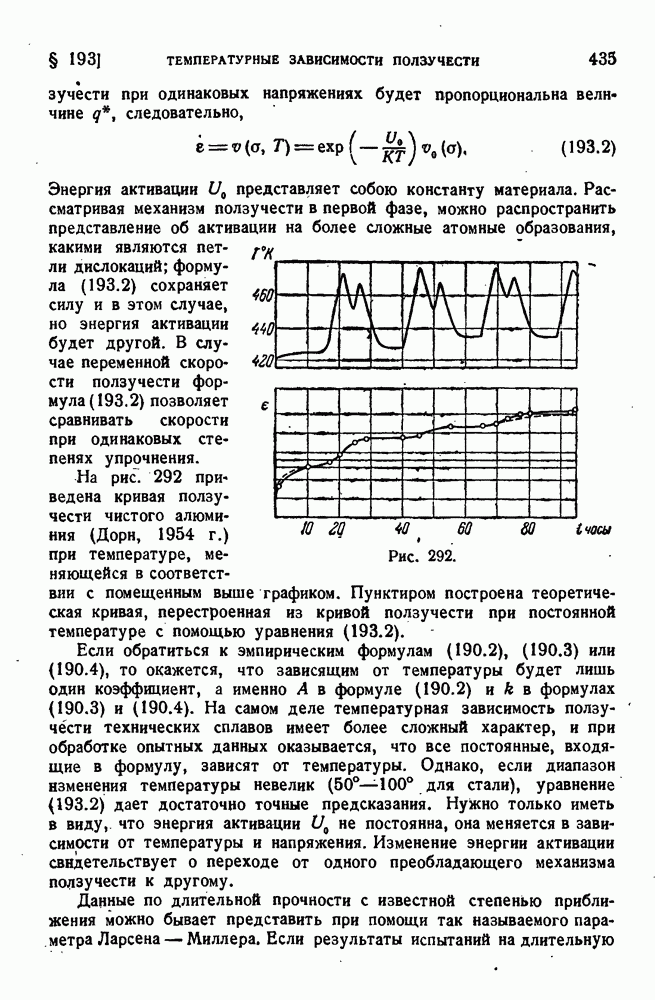
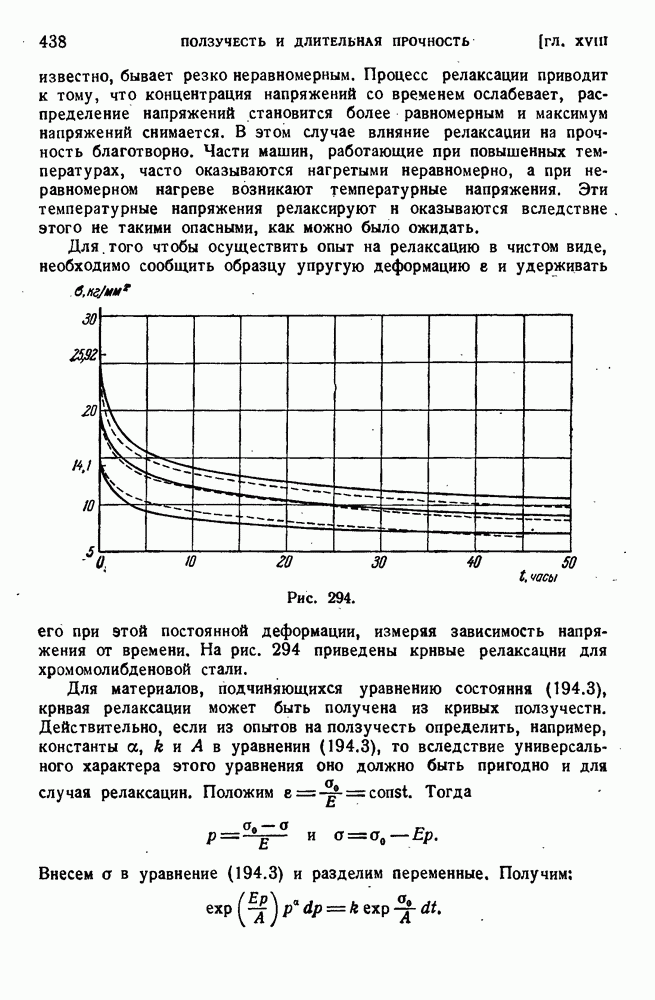
- ГЛАВА XVIII. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
- § 190. Ползучесть металлов.
- § 191. Процесс ползучести.
- § 192. Длительное разрушение.
- § 193. Температурные зависимости ползучести и длительной прочности.
- § 194. Феноменологические теории одномерной ползучести.
- § 195. Релаксация напряжений.
- § 196. Длительная прочность при переменных нагрузках.
- § 197. Ползучесть при изгибе.
- § 198. Критическое время сжатого стержня.
- § 199. Ползучесть и длительная прочность при сложном напряженном состоянии.
- § 200. Вращающиеся диски в условиях ползучести.
- § 201. Расчеты на ползучесть по теории старении.