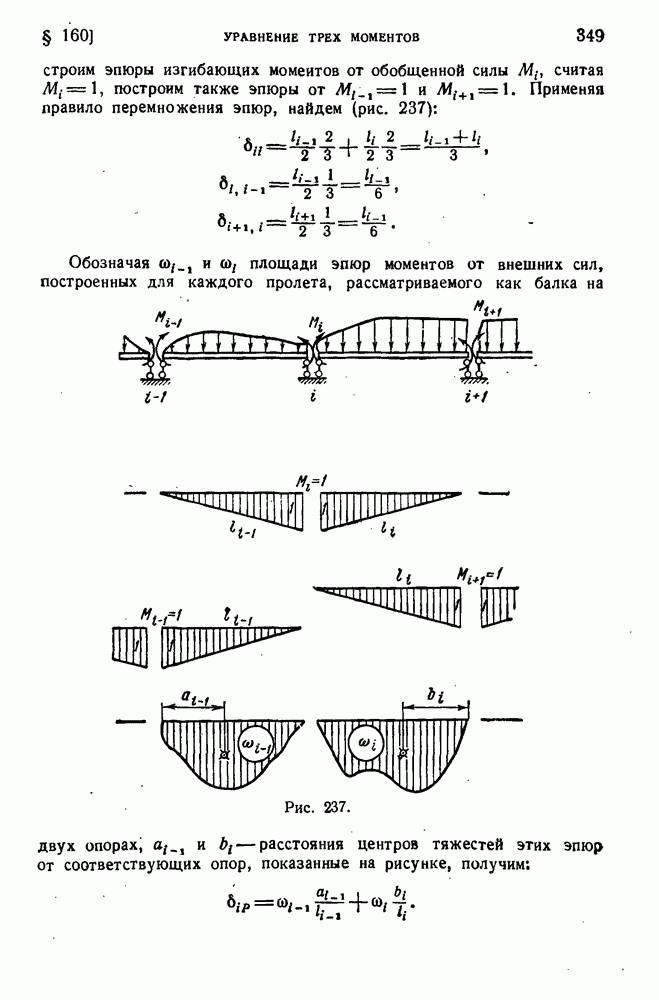
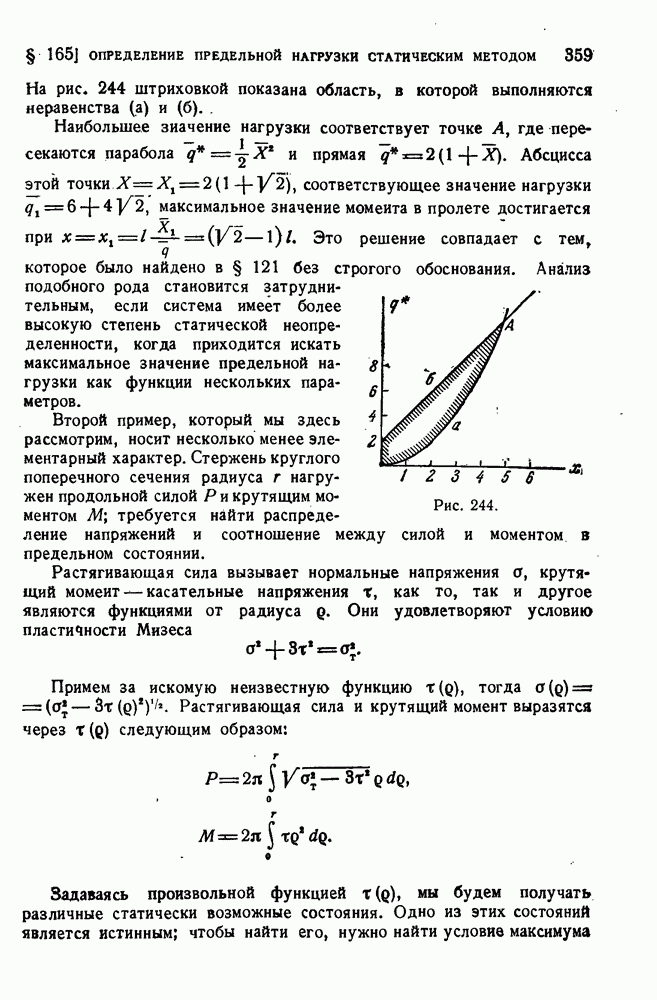
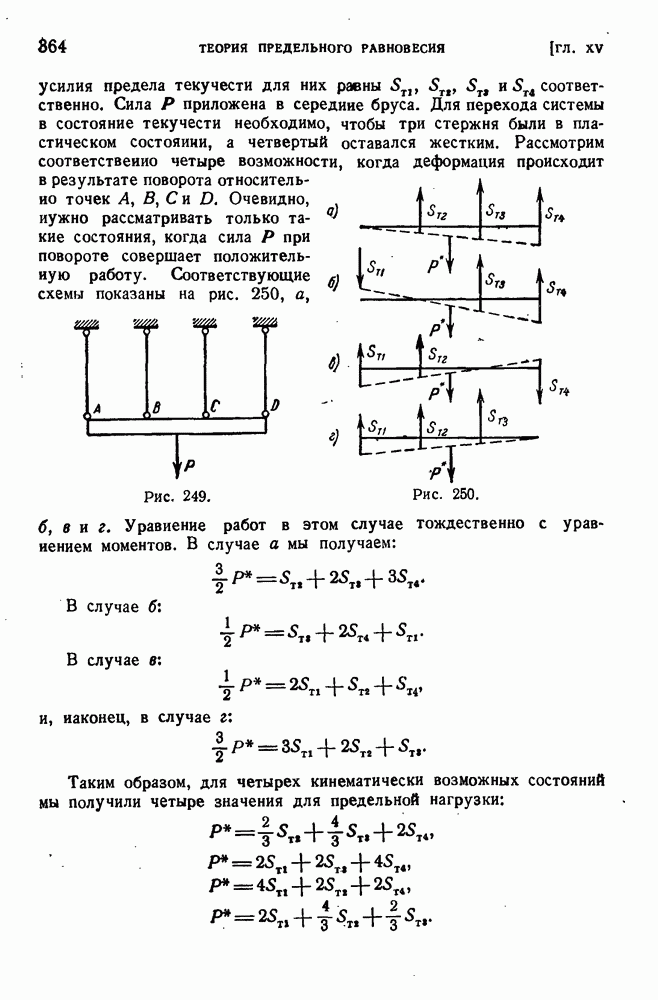
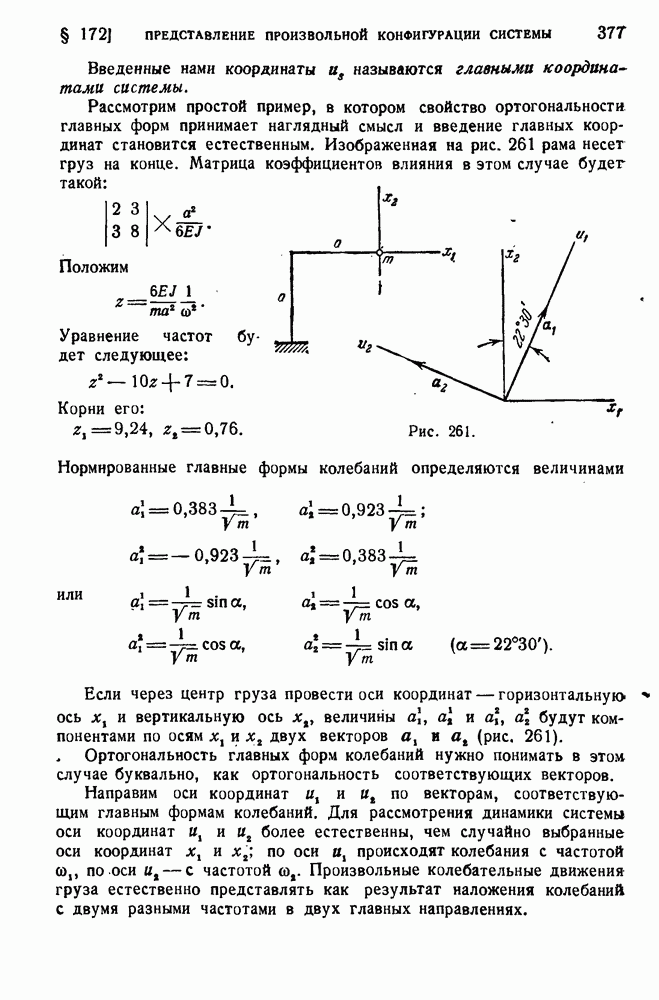
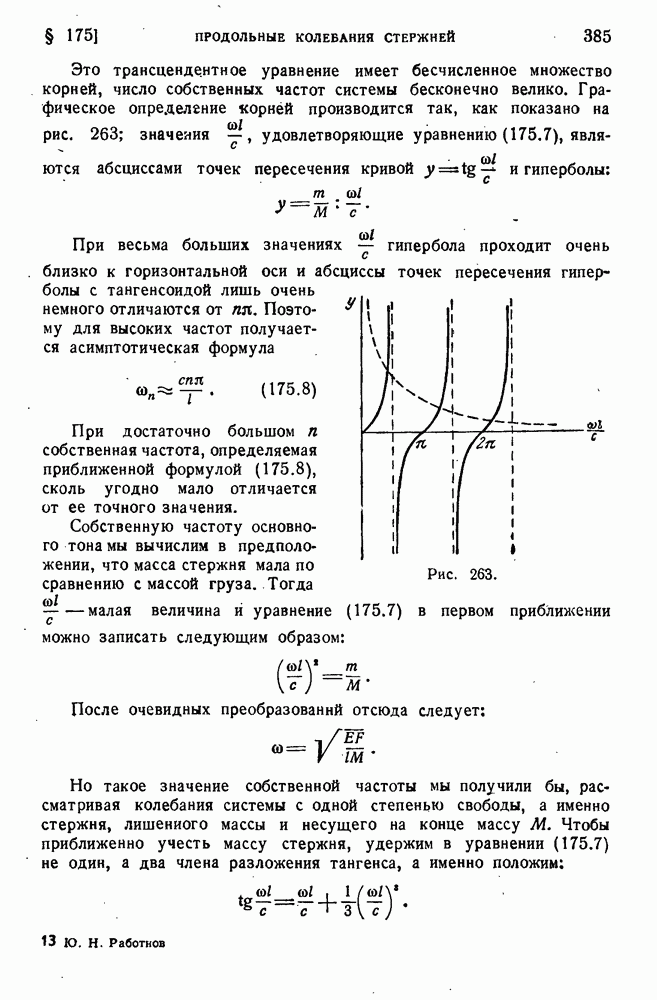
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 69. Источники дислокаций.
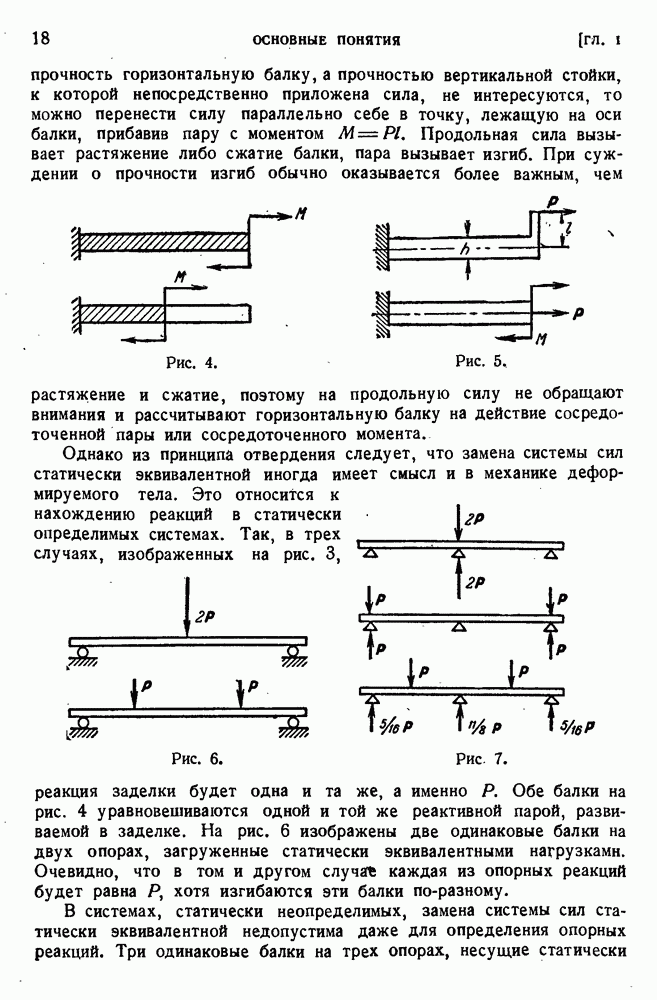
Как мы видели, пластическая деформация кристаллов связана с выходом дислокаций наружу или блокированием их на границах зерен; таким образом, казалось бы, что после определенной величины пластической деформации кристалл должен освободиться от дислокаций и потерять возможность пластической деформации. На самом деле этого не наблюдается, наоборот, число дислокаций в результате пластической деформации увеличивается. Следовательно, должен существовать некоторый механизм порождения новых дислокаций в процессе пластической деформации.
Чтобы рассмотреть этот механизм, нам придется сначала ввести понятие о дислокациях более общего вида, чем краевые дислокации. Вообще можно представить себе, что ось дислокации является произвольной пространственной кривой Г, замкнутой или уходящей двумя концами в бесконечность. На рис. 95 изображена замкнутая линия дислокации.
Чтобы произвести дислокацию, нужно провести через контур Г произвольную поверхность  , сделать по этой поверхности разрез и сместить стороны разреза друг относительна друга на величину вектора Бюргерса
, сделать по этой поверхности разрез и сместить стороны разреза друг относительна друга на величину вектора Бюргерса  После этого стороны разреза соединяются, причем для восстановления сплошности либо добавляется материал, либо убирается лишний. Приведенному определению удовлетворяет, очевидно, и краевая дислокация; осью ее является бесконечная прямая, замыкающаяся в бесконечна удаленной точке, поэтому поверхностью разреза является бесконечная полуплоскость. Те же соображения, что и в случае краевой дислокации, убеждают нас в том, что дислокация общего вида может перемещаться по цилиндрической поверхности, образующая которой параллельна вектору Бюргерса.
После этого стороны разреза соединяются, причем для восстановления сплошности либо добавляется материал, либо убирается лишний. Приведенному определению удовлетворяет, очевидно, и краевая дислокация; осью ее является бесконечная прямая, замыкающаяся в бесконечна удаленной точке, поэтому поверхностью разреза является бесконечная полуплоскость. Те же соображения, что и в случае краевой дислокации, убеждают нас в том, что дислокация общего вида может перемещаться по цилиндрической поверхности, образующая которой параллельна вектору Бюргерса.
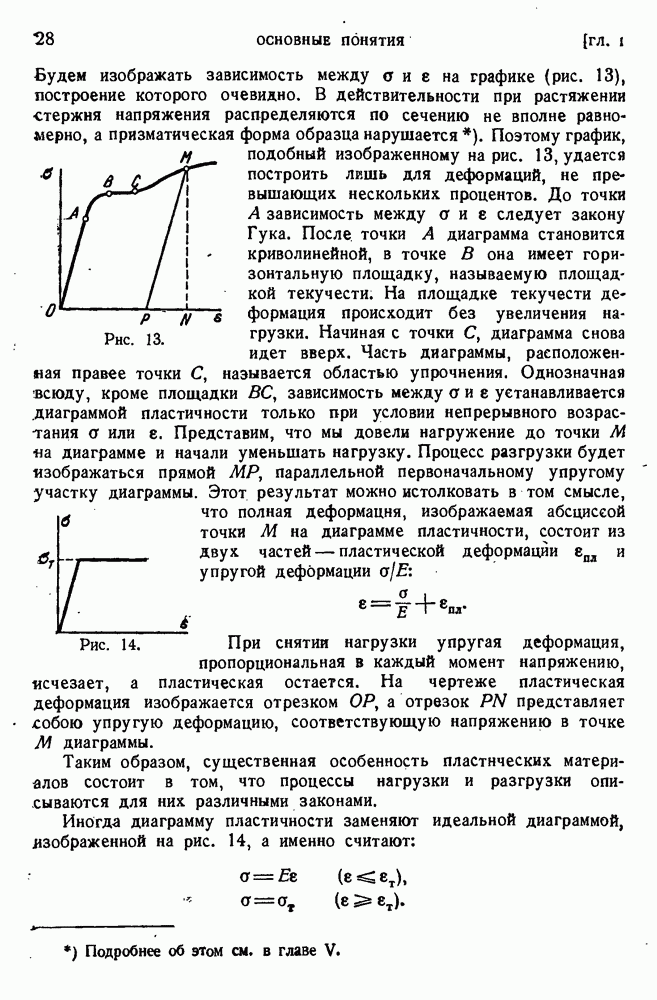
Представим себе теперь, что в кристалле существует произвольная дислокация с криволинейной осью. В реальной кристаллической структуре такая дислокация имеет очень ограниченную возможность для движения, оно возможно только тогда, когда дислокация лежит в плоскости возможного сдвига для кристалла и вектор Бюргерса параллелен этой плоскости. Но может случиться, что элемент  линии дислокации (рис. 96) удовлетворяет этим условиям, то есть
линии дислокации (рис. 96) удовлетворяет этим условиям, то есть

Рис. 95.

Рис. 96.

Рис. 97.
он лежит в плоскости наиболее плотной упаковки атомов и вектор Бюргерса находится в этой же плоскости. Если в плоскости скольжения действует касательное напряжение, созданное внешними силами, то линия дислокации стремится переместиться. Однако концы ее удерживаются в точках  и q, и поэтому она изгибается по некоторой кривой. Чтобы определить форму этой кривой, мы применим к равновесию дислокации принцип возможных перемещений, справедливый для любой механической системы. Пусть
и q, и поэтому она изгибается по некоторой кривой. Чтобы определить форму этой кривой, мы применим к равновесию дислокации принцип возможных перемещений, справедливый для любой механической системы. Пусть  элемент длины линии дислокации, Q — радиус кривизны (рис. 97). Сообщим точкам линии дислокации перемещение
элемент длины линии дислокации, Q — радиус кривизны (рис. 97). Сообщим точкам линии дислокации перемещение  в направлении нормали; элемент
в направлении нормали; элемент  займет положение
займет положение  .
.
На заштрихованной площади  произошло дополнительное смещение сторон разреза на величину вектора Бюргерса
произошло дополнительное смещение сторон разреза на величину вектора Бюргерса  при этом необходимо было преодолеть сопротивление от действующих в плоскости скольжения касательных напряжений, то есть затратить работу
при этом необходимо было преодолеть сопротивление от действующих в плоскости скольжения касательных напряжений, то есть затратить работу  . Элемент
. Элемент  больше, чем элемент
больше, чем элемент  на величину
на величину  из чертежа видно, что
из чертежа видно, что  . Так как энергия дислокации на единицу длины есть энергия элемента
. Так как энергия дислокации на единицу длины есть энергия элемента  увеличилась на
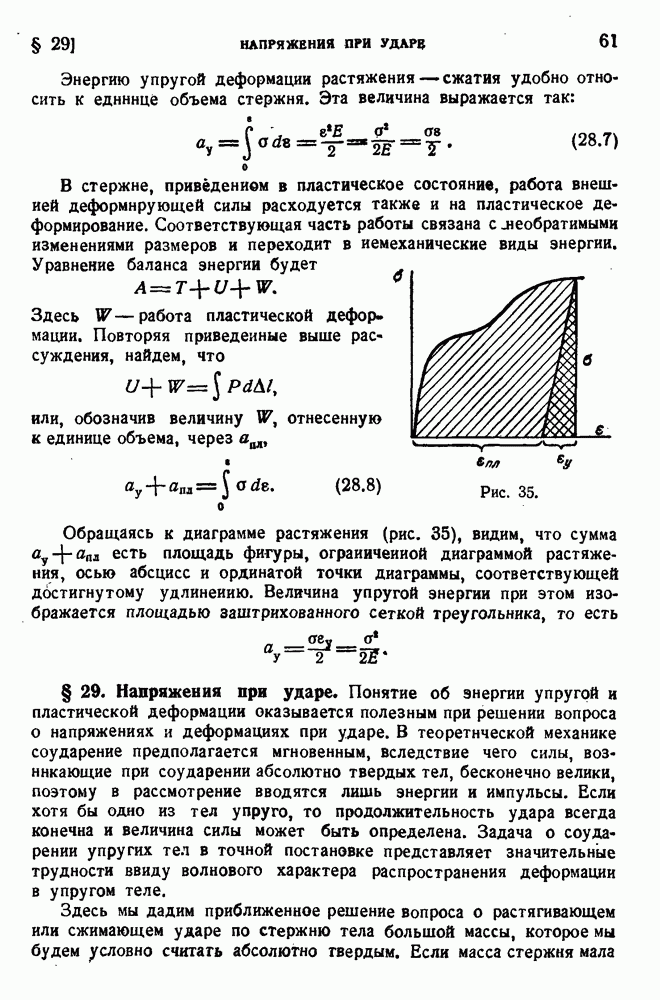
увеличилась на  . Приравнивая эту величину работе касательных напряжений, получим:
. Приравнивая эту величину работе касательных напряжений, получим:

Отсюда

Линия дислокации является окружностью, проходящей через точки  .
.
Энергия на единицу длины произвольной дислокации определяется с достаточной степенью той же формулой, что и для краевой дислокации, а имеиио  Поэтому
Поэтому

Обращаясь к рис. 96, мы видим, что минимальный радиус окружности, проходящий через точки  и q, равен
и q, равен  где L — расстояние
где L — расстояние  то есть длина источника дислокаций. Отсюда максимальное значение
то есть длина источника дислокаций. Отсюда максимальное значение  равно
равно

Если внешнее напряжение меньше критического, деформация сдвига, являющаяся результатом перемещения линии дислокации, обратима; она исчезнет при снятии нагрузки. Таким образом, наличие источников несколько понижает модуль сдвига материала. Такое понижение упругих постоянных в результате пластической деформации, увеличивающей число дислокаций, наблюдается в действительности.
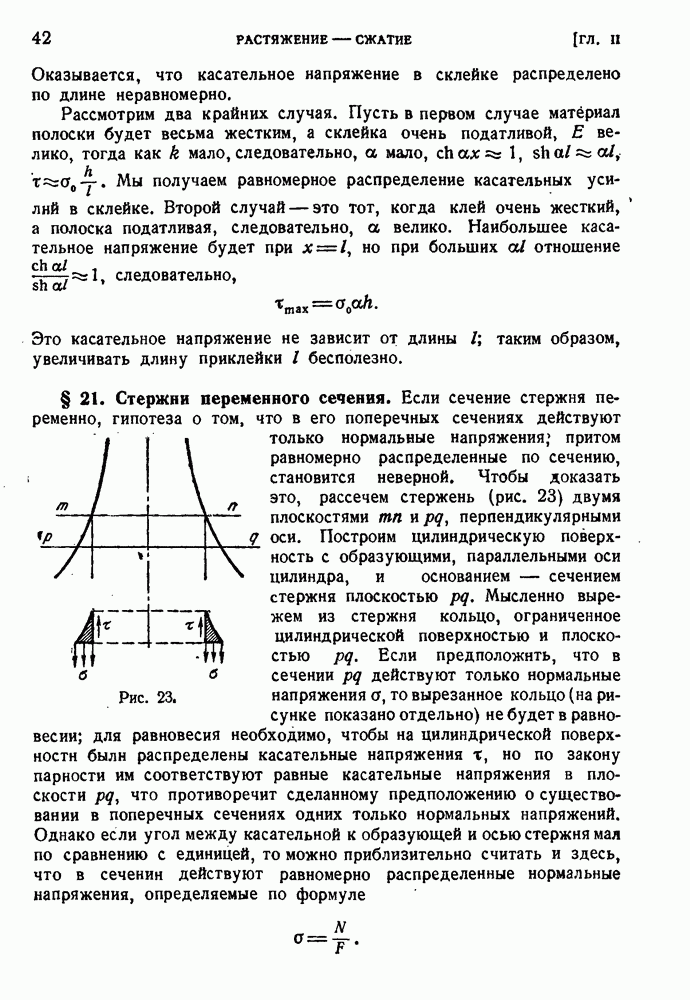
Но если касательное напряжение достигает критического значения, равновесие дуги дислокации становится неустойчивым, эта дуга неограниченно расширяется, ометая значительную площадь, на которой происходит сдвиг. Макроскопический эффект такого срыва дислокации представляет собою сдвиг на величину вектора Бюргерса.. Заметим, что уравнение равновесия линии дислокации (69.1) имеет тот же вид, что и уравнение равновесия гибкой нити с постоянным натяжением W, нагруженной постоянным давлением, нормальным к нити в каждой точке и равным произведению  . Как мы уже отметили, после достижения критического напряжения дуга дислокации будет неограниченно расширяться, причем радиус ее кривизны увеличивается.
. Как мы уже отметили, после достижения критического напряжения дуга дислокации будет неограниченно расширяться, причем радиус ее кривизны увеличивается.
Формула (69.1) показывает, что такое расширение возможно при уменьшающемся напряжении. На самом же деле напряжение остается постоянным, поэтому расширение дислокации носит динамический характер. Мы не в состоянии точно исследовать этот динамический процесс, но можем высказать некоторые качественные соображения по этому поводу. Естественно предполагать, что движение линии дислокации встречает сопротивление, увеличивающееся с увеличением скорости, поэтому середина дуги дислокации будет двигаться медленнее, а концы — быстрее. Кривая перестанет быть дугой окружности и сплющится. Последовательные формы линии дислокации в процессе ее движения показаны на рис. 98; в конце концов кривая коснется сама себя в точке М. Отрезки  линии дислокации могут рассматриваться как отрезки прямолинейных дислокаций разных знаков. В момент касания они сольются и взаимно уничтожатся; в результате образуется замкнутое кольцо дислокации и криволинейная дислокация, соединяющая точки
линии дислокации могут рассматриваться как отрезки прямолинейных дислокаций разных знаков. В момент касания они сольются и взаимно уничтожатся; в результате образуется замкнутое кольцо дислокации и криволинейная дислокация, соединяющая точки  как показано на рис. 98 сплошными линиями. Кольцо под действием «давления»
как показано на рис. 98 сплошными линиями. Кольцо под действием «давления»  немедленно примет круговую формуй будет продолжать неограниченно расширяться, дислокация, соединяющая точки
немедленно примет круговую формуй будет продолжать неограниченно расширяться, дислокация, соединяющая точки  и q, выпрямится, снова выгнется вправо, и весь процесс будет повторяться неограниченное число раз.
и q, выпрямится, снова выгнется вправо, и весь процесс будет повторяться неограниченное число раз.

Рис. 98.
Таким образом, один источник может породить любое количество кольцевых дислокаций; выход каждой из них на поверхность означает сдвиг на величину вектора Бюргерса или одного междуатомного расстояния. Приведенная модель носит название модели Франка — Рида. Эта модель описывает неограниченную пластическую деформацию кристалла, не содержащего примесей и имеющего минимальное количество внутренних дефектов.
Формула (69.3) дает величину предела текучести для данного кристалла.
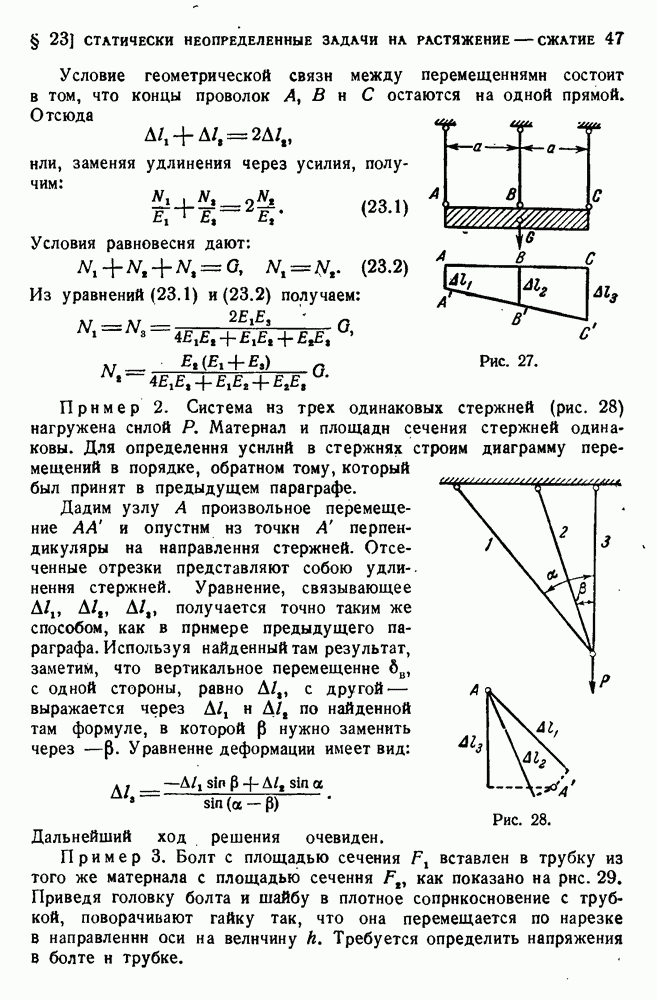
В действительности кольца дислокаций не имеют возможности расширяться неограниченно: в реальном кристалле всегда имеются препятствия для движения дислокаций. Представим себе, что препятствие имеет форму кольца, в центре которого находится источник.
Первая дислокация останавливается на препятствии, вторая стремится расшириться под действием напряжения  но она в то же время испытывает силу отталкивания со стороны первой. В результате образуется система кольцевых дислокаций, изображенная на рис. 99. Эти дислокации создают поле напряжений в теле. Касательное напряжение, действующее со стороны отдельных дислокаций на источник, противоположно напряжению
но она в то же время испытывает силу отталкивания со стороны первой. В результате образуется система кольцевых дислокаций, изображенная на рис. 99. Эти дислокации создают поле напряжений в теле. Касательное напряжение, действующее со стороны отдельных дислокаций на источник, противоположно напряжению  в результате критическое напряжение источника увеличивается с каждой отделившейся дислокацией и в конце концов становится равным действующему напряжению.
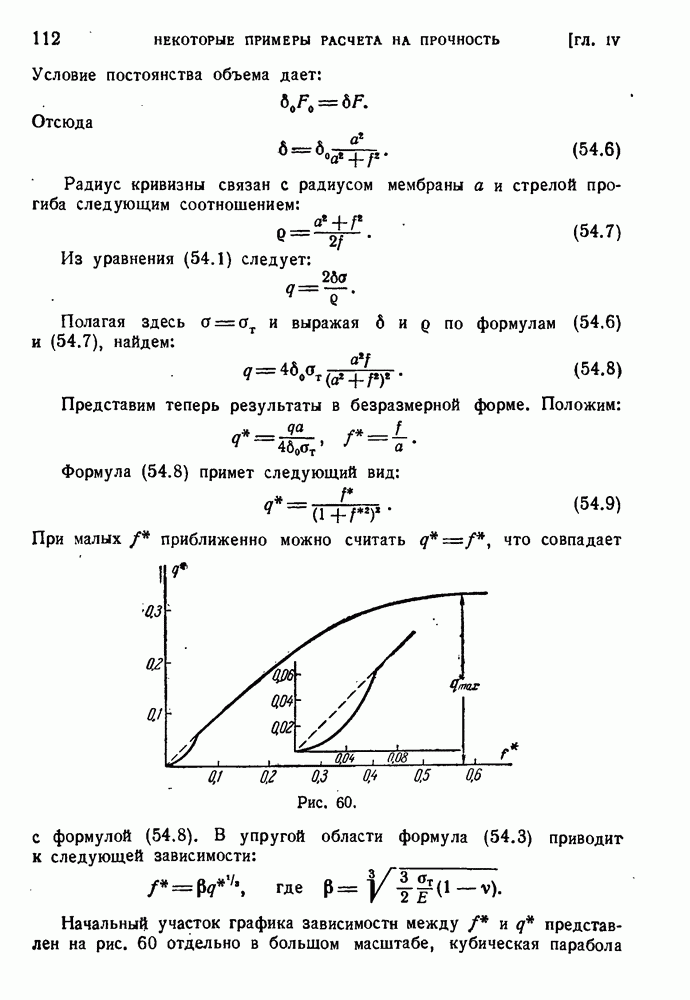
в результате критическое напряжение источника увеличивается с каждой отделившейся дислокацией и в конце концов становится равным действующему напряжению.

Рис. 99.
Таким образом, если дислокации не имеют возможности свободно выходить на поверхность, а задерживаются препятствиями, при данном касательном напряжении источник может породить лишь определенное число дислокаций, чему соответствует определенная конечная пластическая деформация. Для дальнейшей деформации нужно увеличить напряжение. Такого рода поведение характерно для упрочняющихся материалов.
На самом деле очень мало вероятности, чтобы препятствие имело кольцевую форму, притом с центром, совпадающим с источником. Кольца дислокаций при дальнейшем движении сильно деформируются, и рассмотреть все многообразие возможных форм не представляется возможным; поэтому обычно рассматривают самую простую модель группы краевых дислокаций в плоскости скольжения, задержанных препятствием (рис. 100). Условия равновесия такой группы известны совершенно точно; можно указать расстояние между дислокациями в состоянии равновесия под действием напряжения  и сил взаимного отталкивания дислокаций.
и сил взаимного отталкивания дислокаций.

Рис. 100.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Задачи и содержание сопротивления материалов.
- § 2. Сопротивление материалов и теоретическая механика.
- § 3. Статически неопределенные задачи.
- § 4. Внешние силы.
- § 5. Принцип отвердения.
- § 6. Недопустимость замены системы сил статически эквивалентной.
- § 7. Однородное тело.
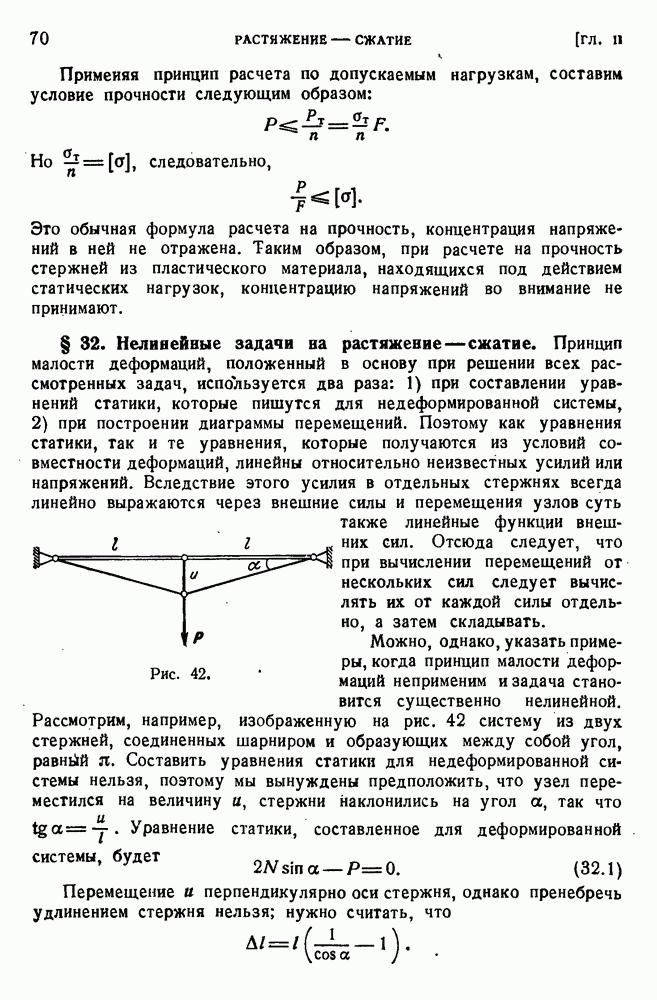
- § 8. Внутренние силы.
- § 9. Напряжение.
- § 10. Простейшие типы напряженного состояния.
- § 11. Простейшие виды деформации.
- § 12. Упругость и пластичность.
- § 13. Закон Гука.
- § 14. Диаграмма пластичности.
- § 15. Тела изотропные и анизотропные.
- ГЛАВА II. РАСТЯЖЕНИЕ СЖАТИЕ
- § 16. Стержни и стержневые системы.
- § 17. Принцип Сен-Венана и гипотеза плоских сечений.
- § 18. Напряжения и деформации при растяжении.
- § 19. Расчеты на прочность при растижении и сжатии.
- § 20. Собственный вес и силы инерции.
- § 21. Стержни переменного сечения.
- § 22. Перемещения узлов стержневых систем.
- § 23. Статически неопределенные задачи на растяжение — сжатие.
- § 24. Температурные и монтажные напряжения.
- § 25. Общие соображения о расчете стержневых систем.
- § 26. Расчет статически неопределимых систем по допускаемым нагрузкам.
- § 27. Остаточные напряжения после пластической деформации.
- § 28. Потенциальная энергия растяжении.
- § 29. Напряжения при ударе.
- § 30. Распространение упругих волн в стержнях.
- § 31. Концентрации напряжений.
- § 32. Нелинейные задачи на растяжение — сжатие.
- ГЛАВА III. СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
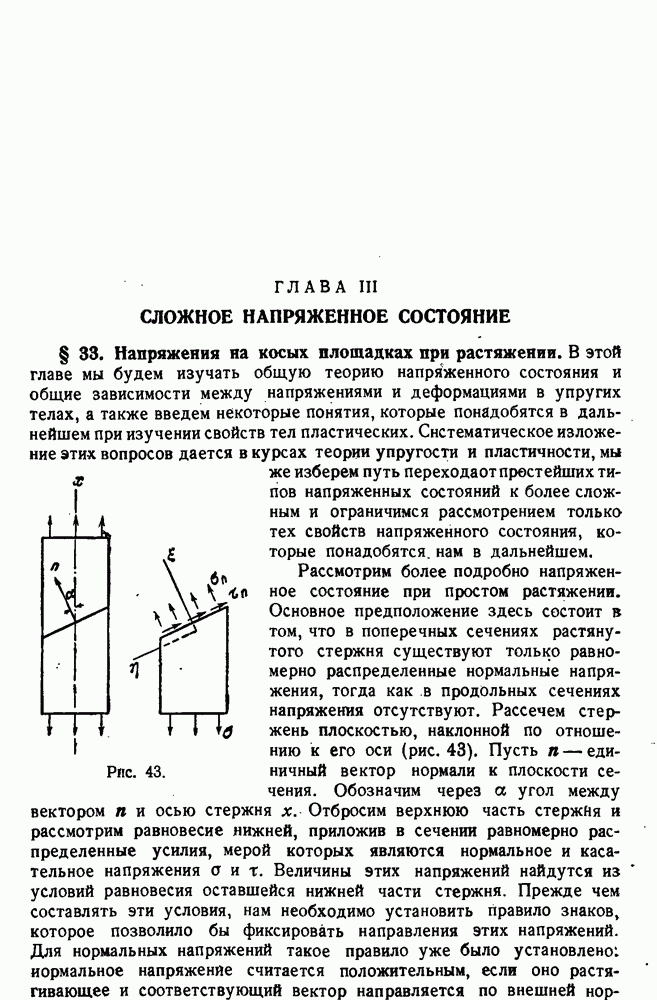
- § 33. Напряжения на косых площадках при растяжении.
- § 34. Напряжения при двухосном растяжении.
- § 35. Круговая диаграмма Мора.
- § 36. Общий случай плоского напряженного состояния.
- § 37. Определение напряжений на произвольной площадке.
- § 38. Пространственное напряженное состояние.
- § 39. Главные напряжения.
- § 40. Главные касательные напряжения.
- § 41. Октаэдрическое напряжение.
- § 42. Закон Гука для главных осей.
- § 43. Изменение объема при упругой деформации.
- § 44. Чистый сдвиг.
- § 45. Деформация элемента объема в общем случае.
- § 46. Условие пластичности Треска — Сен-Венана.
- § 47. Условие пластичности Мизеса.
- § 48. Условия пластичности для плоского напряженного состояния.
- § 49. Потенциальная энергия упругой деформации.
- § 50. Энергия изменения формы.
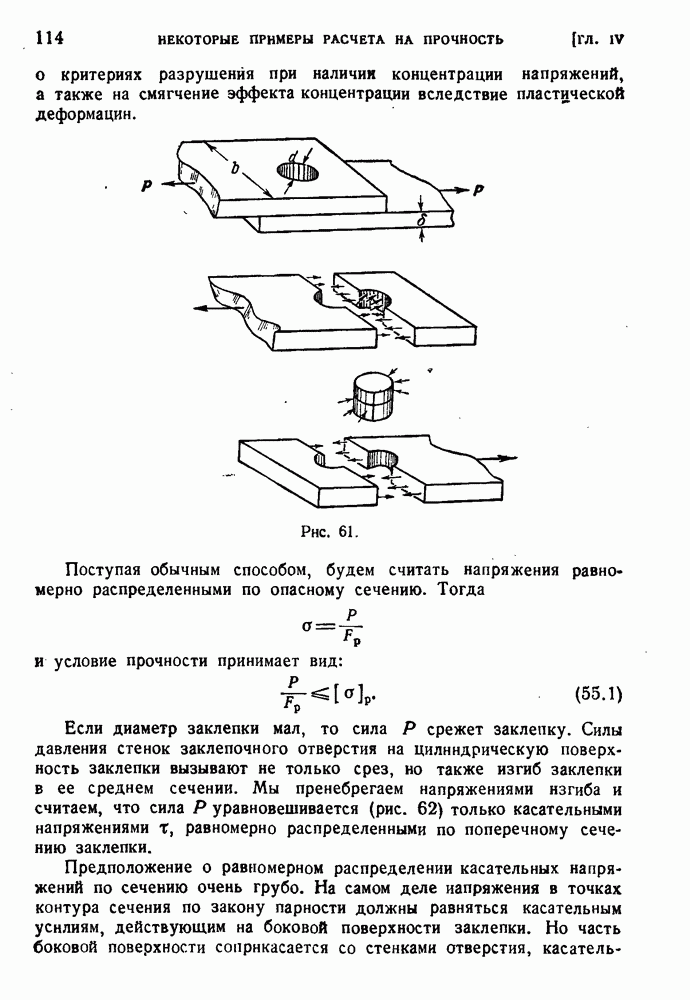
- ГЛАВА IV. НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
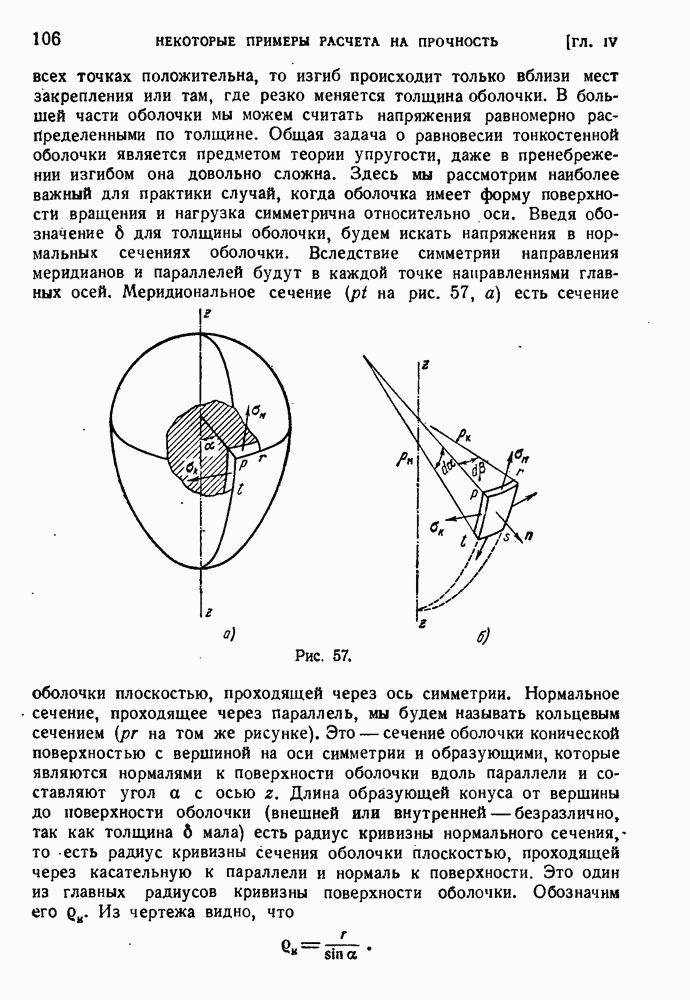
- § 51. Расчеты на прочность изделий сложной формы.
- § 52. Безмоментные оболочки вращении.
- § 53. Местные напряжения в безмоментных оболочках.
- § 54. Большие прогибы мембраны.
- § 55. Условные расчеты.
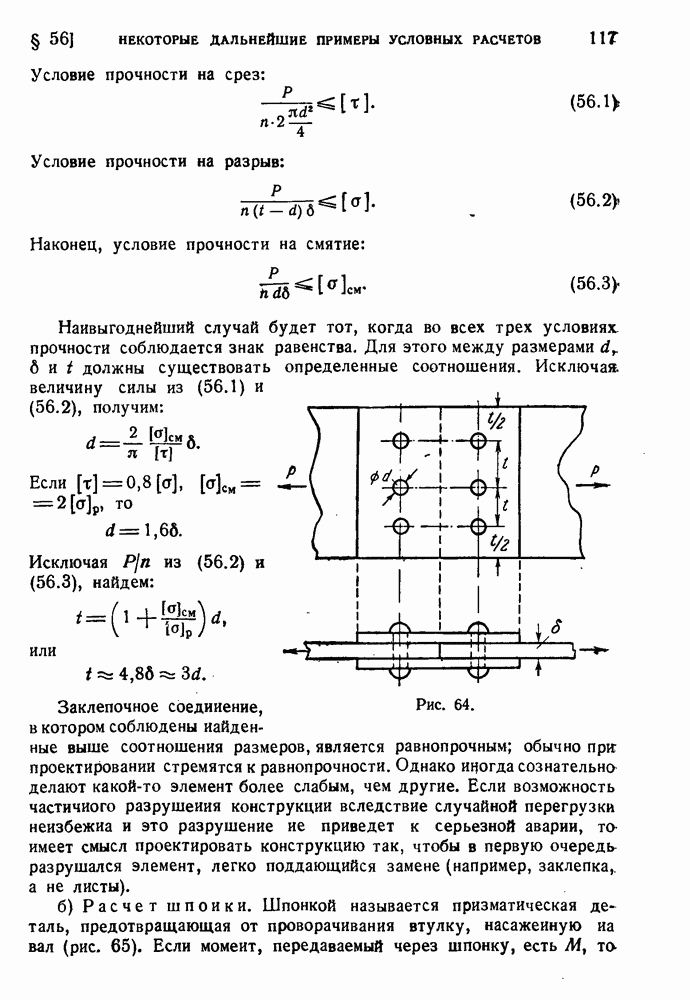
- § 56. Некоторые дальнейшие примеры условных расчетов.
- § 57. Расчет сварных соединений.
- ГЛАВА V. ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
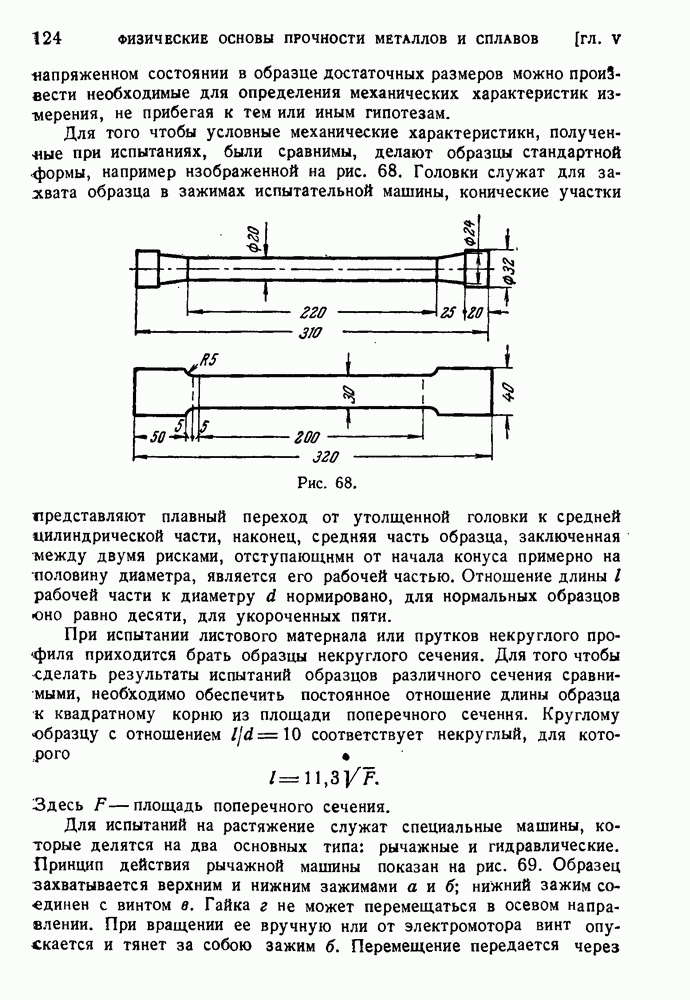
- § 58. Задачи испытания материалов.
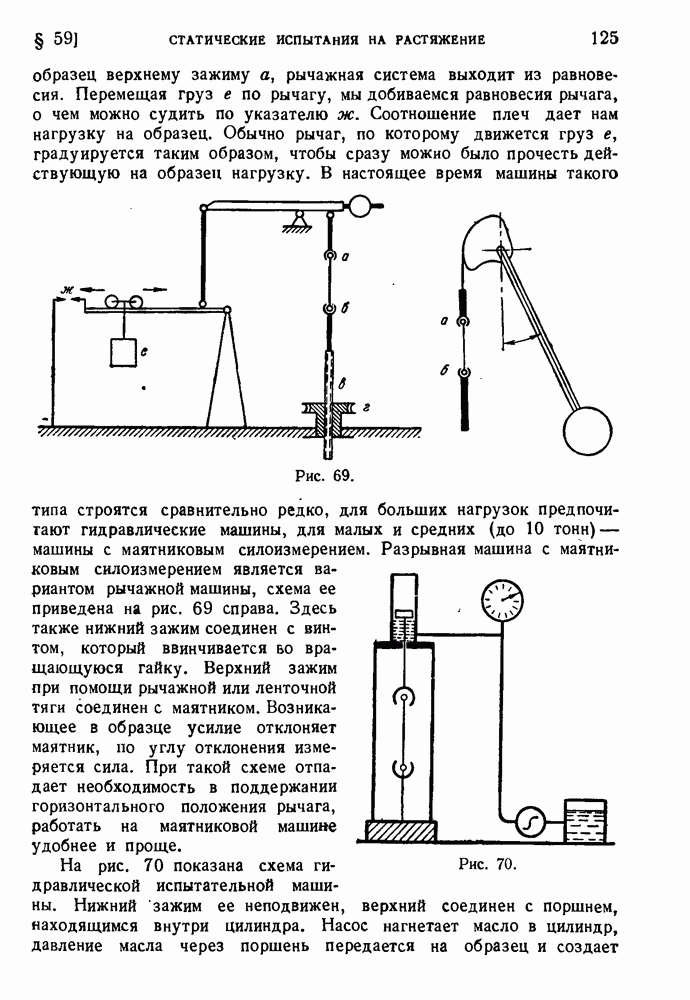
- § 59. Статические испытания на растяжение.
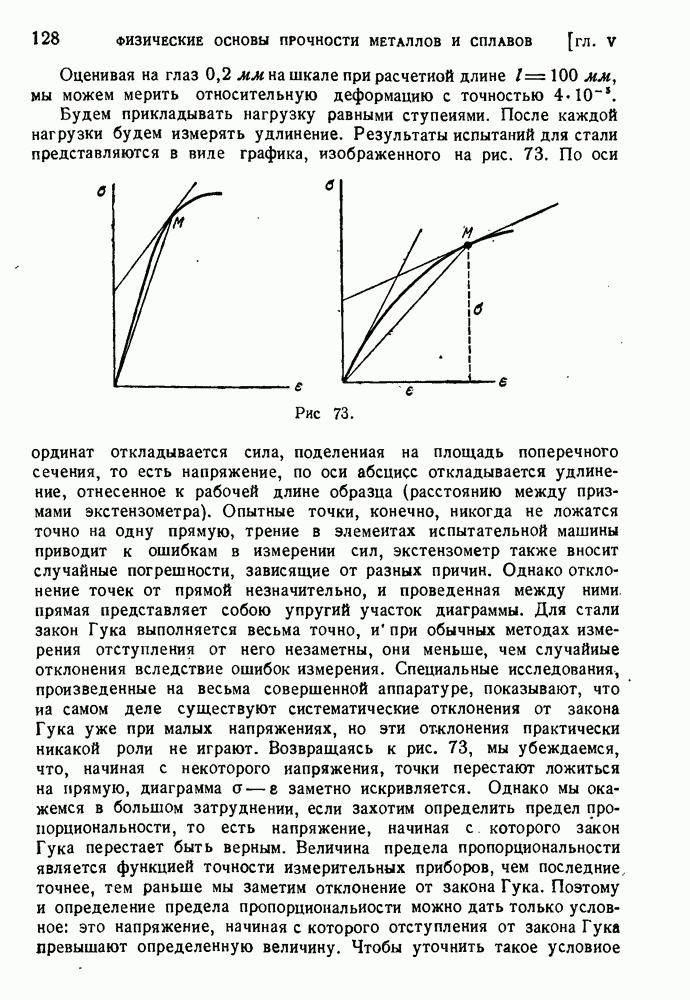
- § 60. Исследование металлов в области малых деформаций.
- § 61. Диаграмма растяжения мягкой стали.
- § 62. Опыты на сжатие.
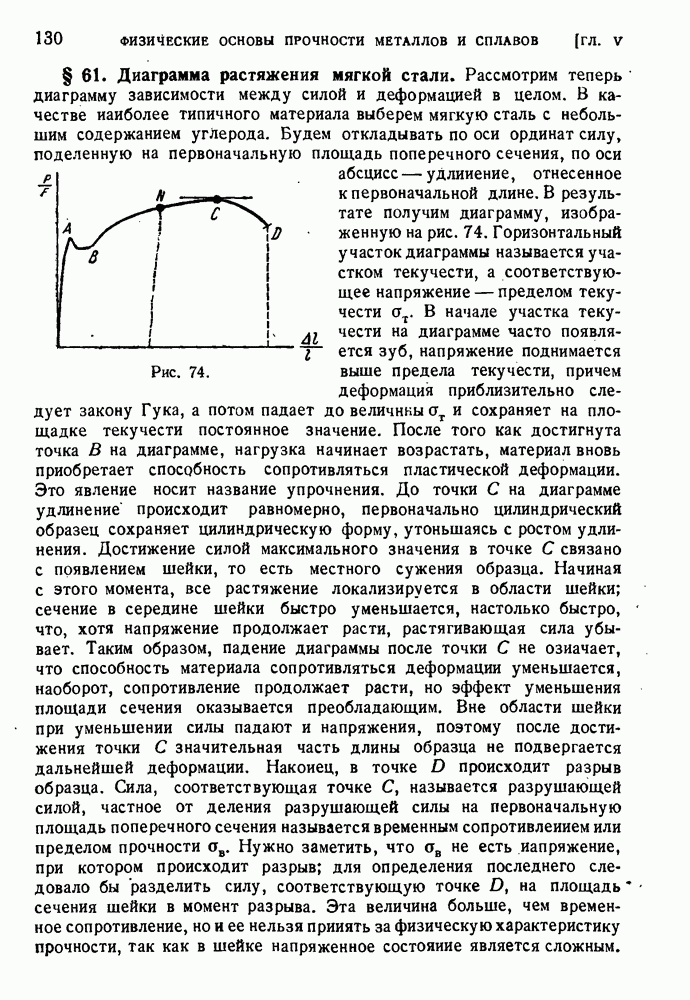
- § 63. Строение и упругая деформация металлических кристаллов.
- § 64. Типичные кристаллические структуры металлов.
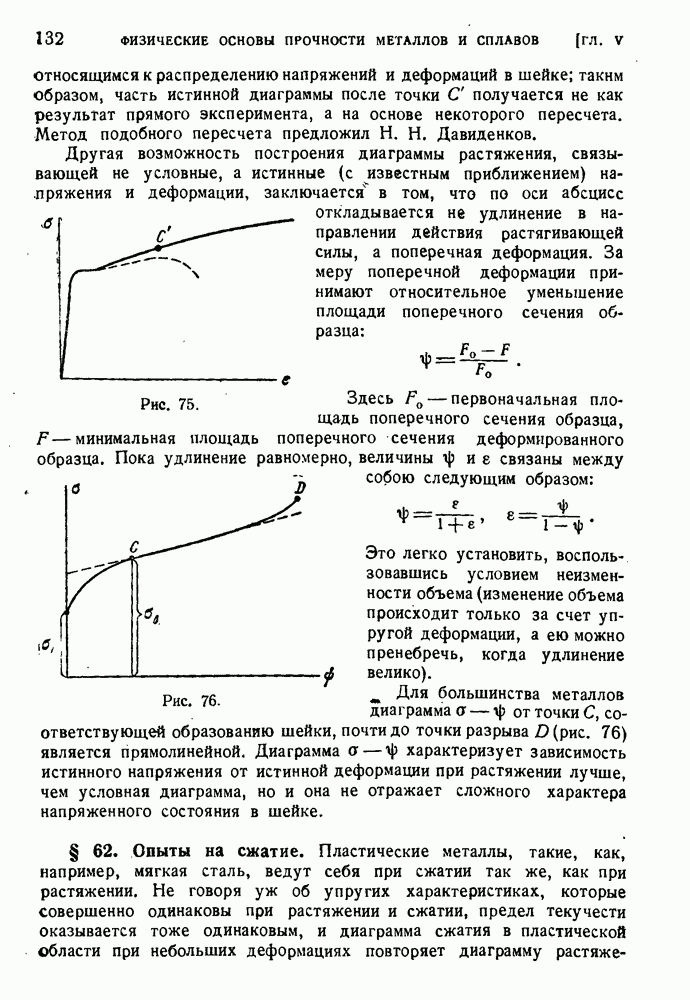
- § 65. Пластическая деформация монокристаллов.
- § 66. Прочность кристаллов и сопротивление пластическому деформированию.
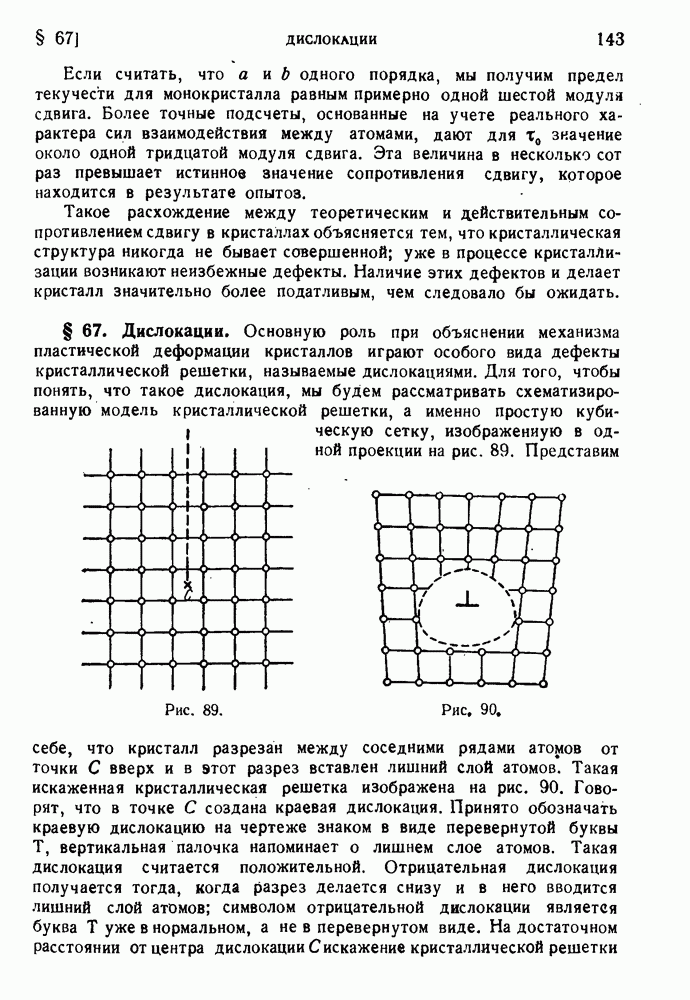
- § 67. Дислокации.
- § 68. Движение и равновесие дислокаций.
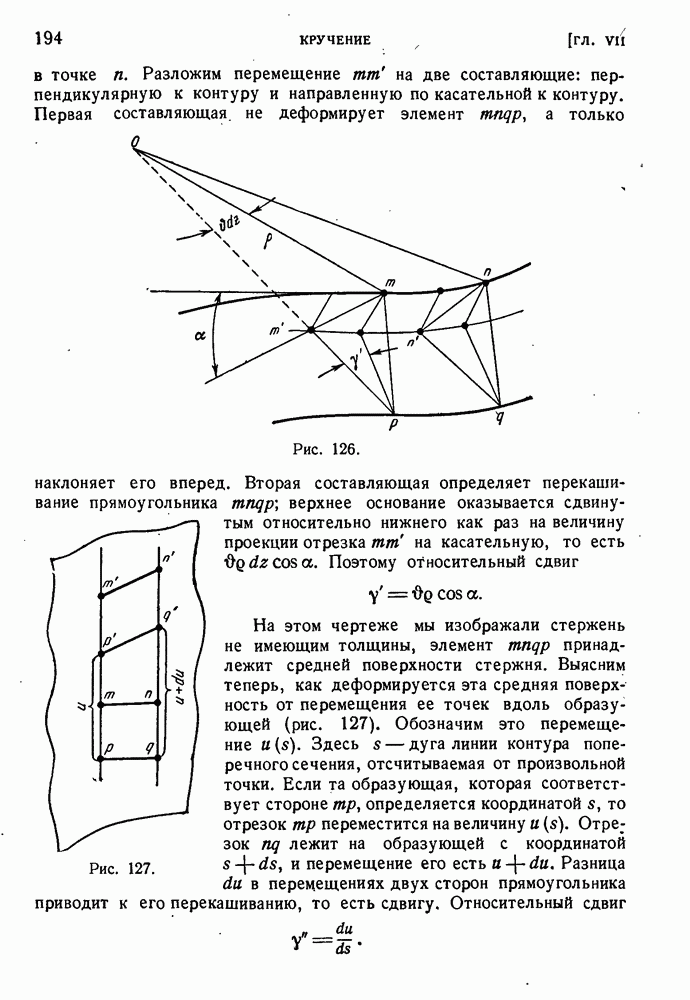
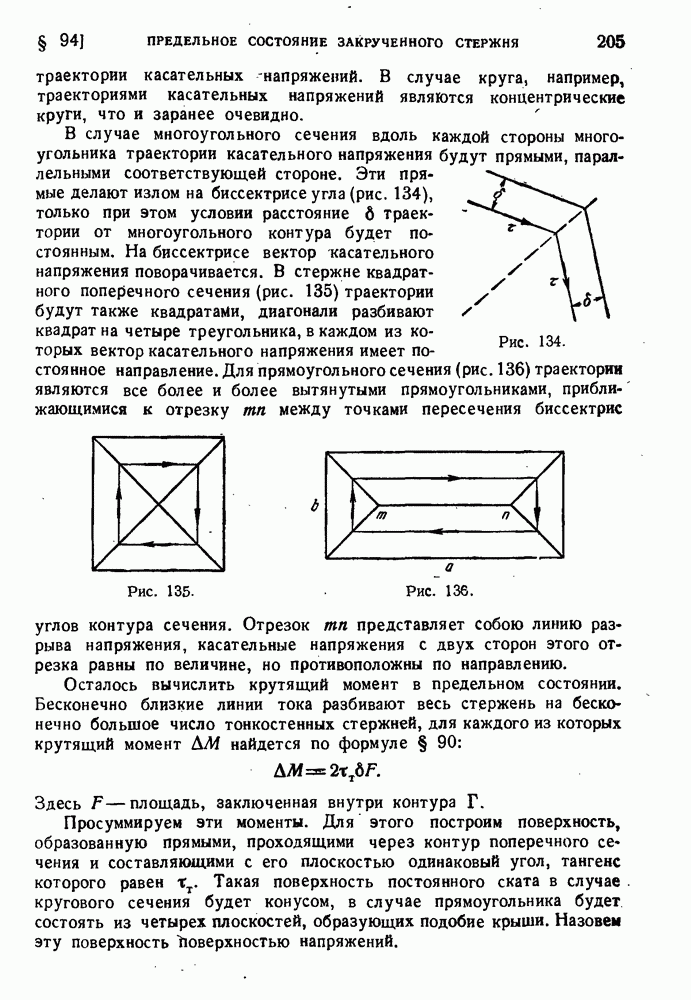
- § 69. Источники дислокаций.
- § 70. Границы блоков.
- § 71. Деформация поликристаллических металлов и сплавов.
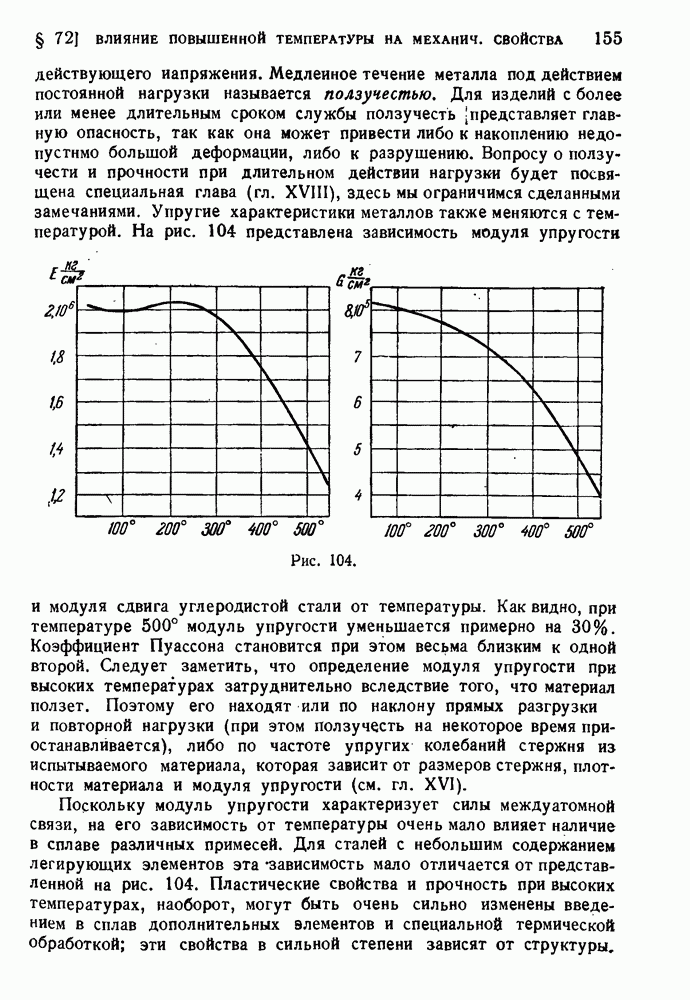
- § 72. Влияние повышенной температуры на механические свойства.
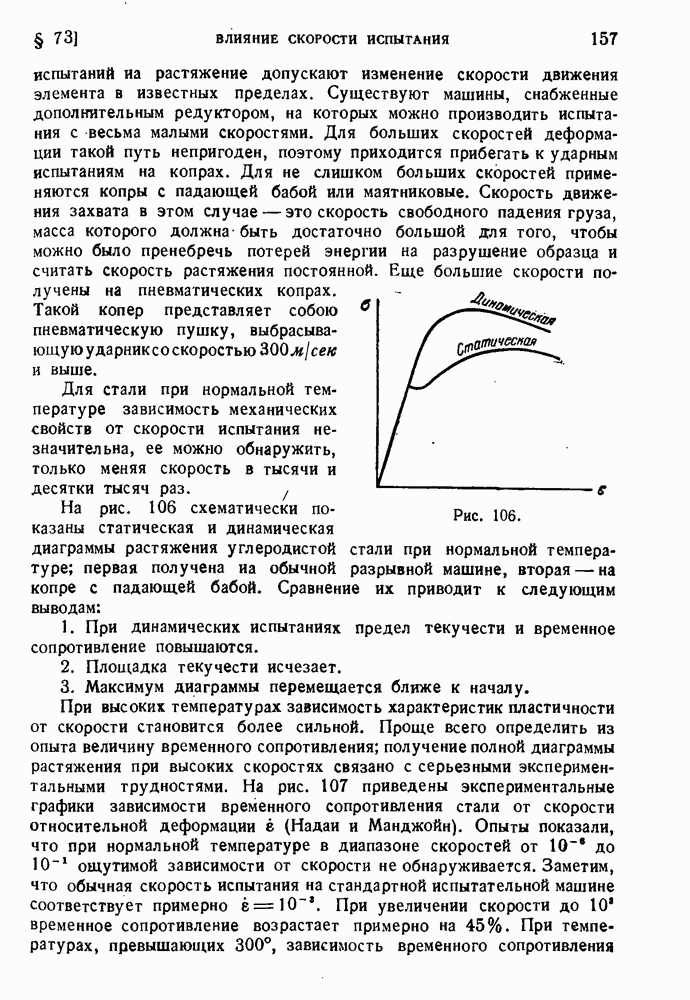
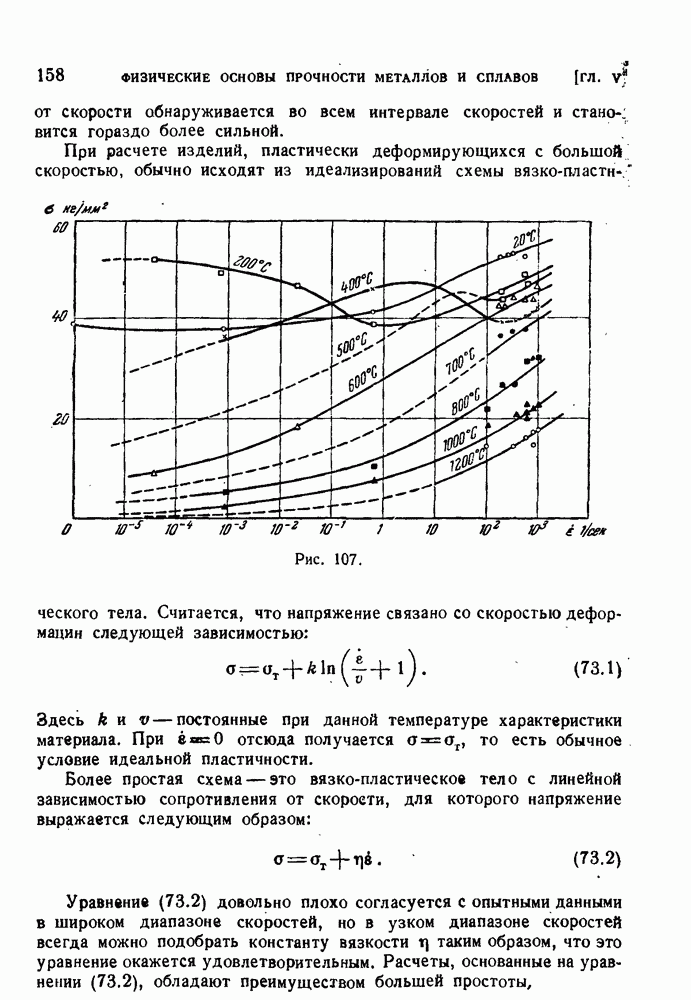
- § 73. Влияние скорости испытания.
- § 74. Испытании на твердость.
- ГЛАВА VI. ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ
- § 75. Основные принципы построения теории пластичности.
- § 76. Ассоциированный закон течения.
- § 77. Течение при условии пластичности Сен-Венана и Мизеса.
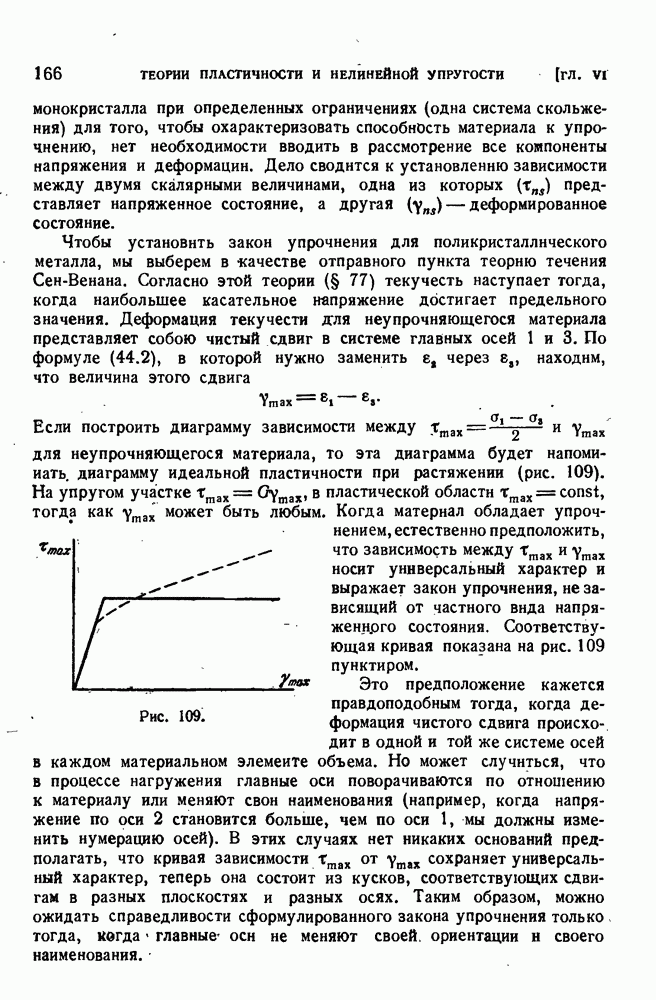
- § 78. Закон упрочнения.
- § 79. Деформационная теория пластичности.
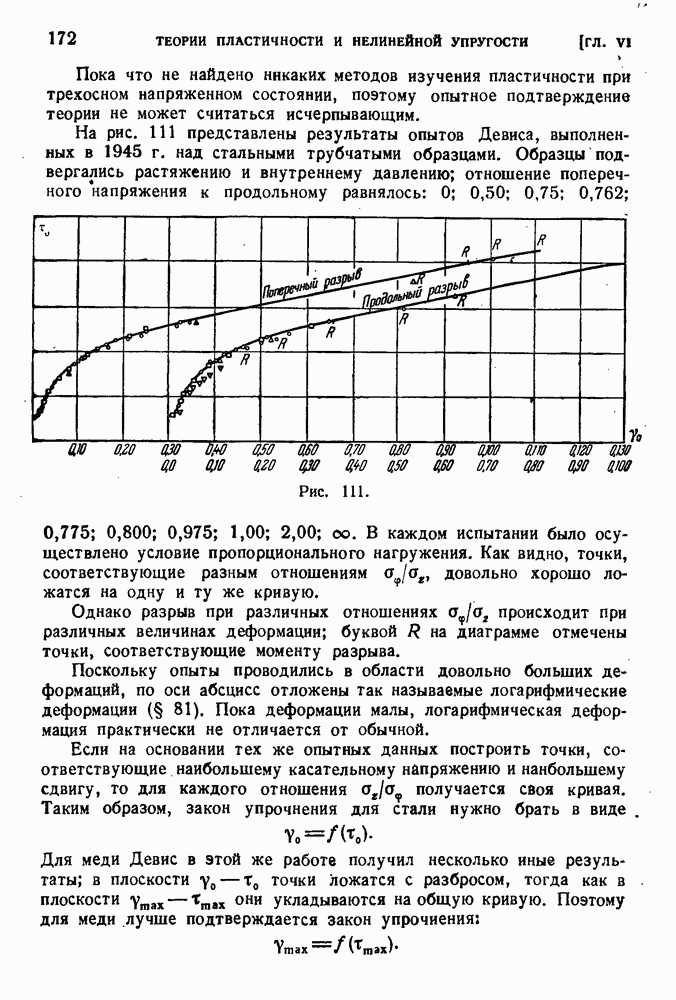
- § 80. Экспериментальная проверка теорий пластичности.
- § 81. Конечная деформация.
- § 82. Нелинейно упругое тело.
- § 83. Высокоэластические деформации.
- § 84. Упругое последействие.
- § 85. Некоторые свойства вязко-упругого тела.
- § 86. Принцип суммирования Больцмана—Вольтерра.
- ГЛАВА VII. КРУЧЕНИЕ
- § 87. Кручение стержней круглого сечеиия.
- § 88. Упруго-пластическое кручение стержня круглого сечения.
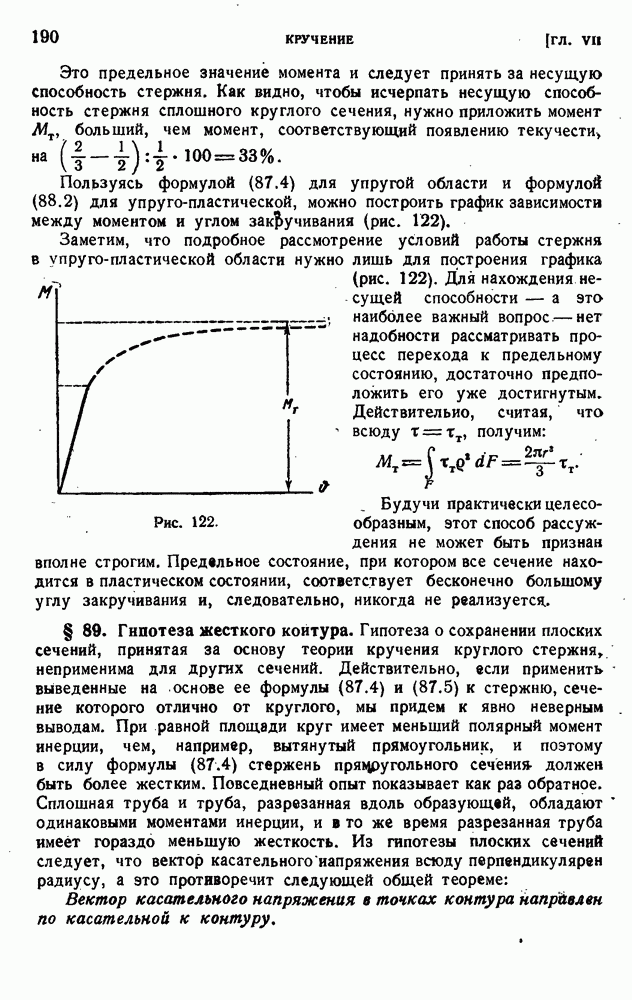
- § 89. Гипотеза жесткого контура.
- § 90. Кручение тонкостенных стержней замкнутого профиля.
- § 91. Кручение тонкостенных стержней открытого профиля.
- § 92. Кручение упругих стержией сплошного профиля.
- § 93. Опытное исследование кручения.
- § 94. Предельное состояние закрученного стержня из идеально-пластического материала.
- ГЛАВА VIII. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
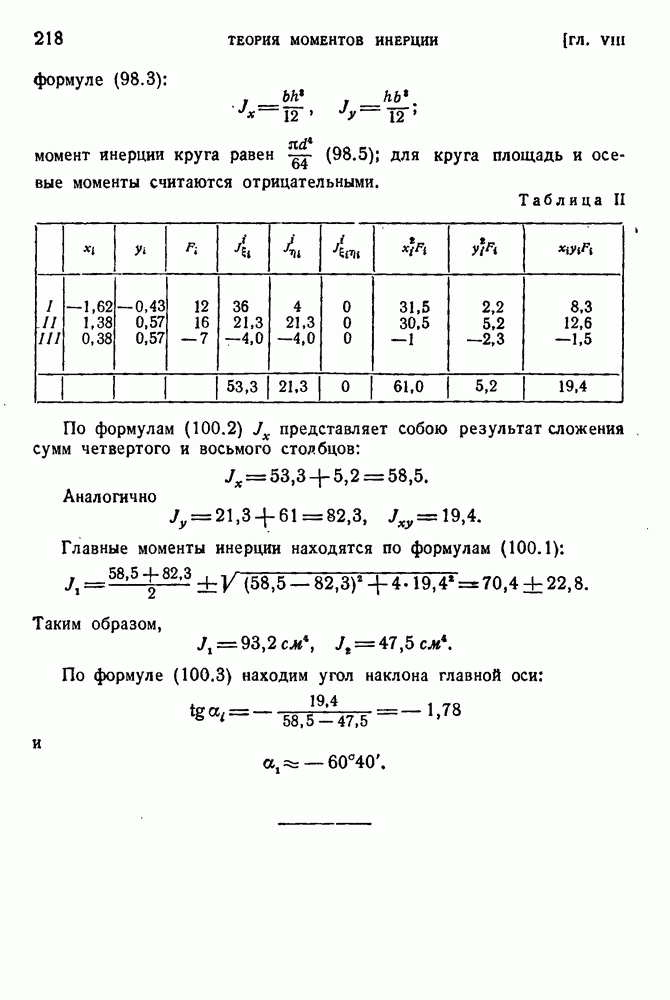
- § 96. Общие теоремы о моментах.
- § 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей.
- § 98. Вычисление моментов инерции.
- § 99. Преобразование моментов инерции при повороте осей.
- § 100. Главные оси и главные моменты инерции.
- ГЛАВА IX. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
- § 101. Действие поперечных сил на балку.
- § 102. Гипотеза плоских сечений и принцип Сен-Венана.
- § 103. Нормальные напряжения при изгибе.
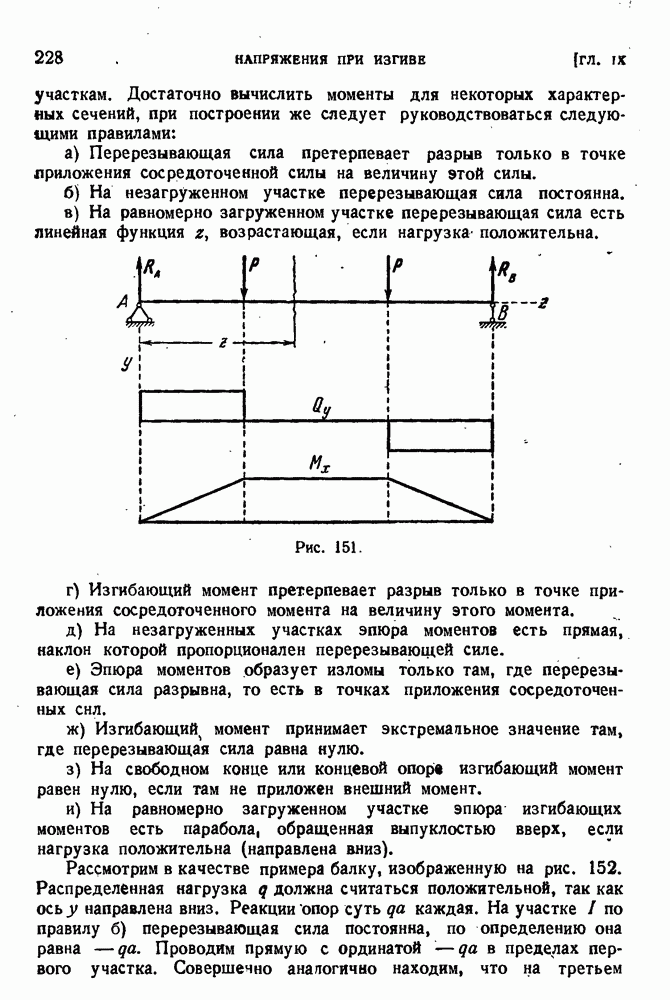
- § 104. Изгибающие моменты и перерезывающие силы.
- § 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры.
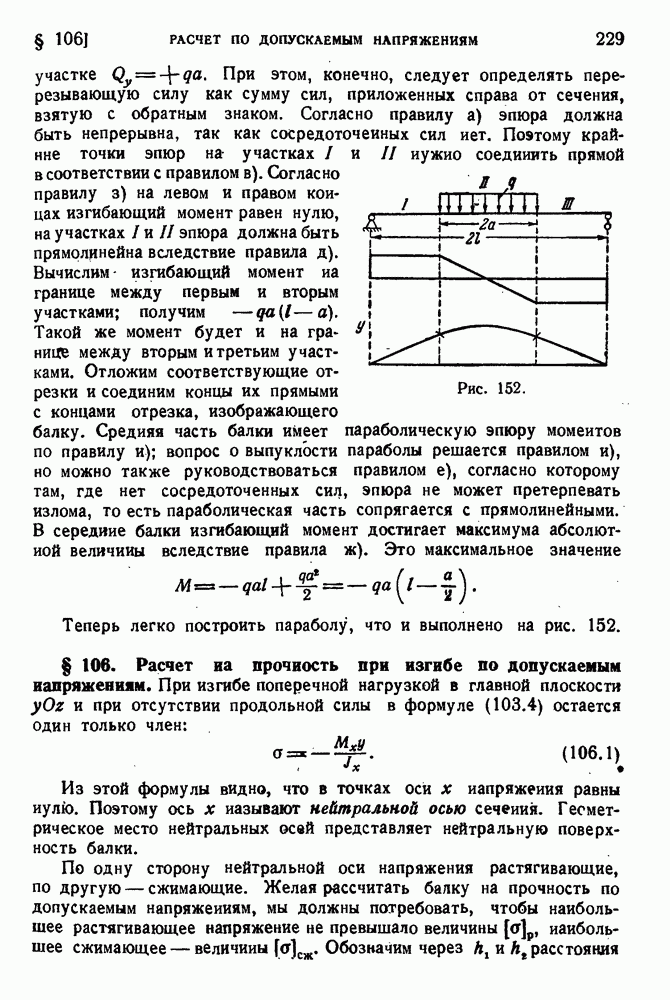
- § 106. Расчет на прочность при изгибе по допускаемым напряжениям.
- § 107. Упруго-пластический изгиб.
- § 108. Несущая способность стержня при изгибе.
- § 109. Принцип Сен-Венана.
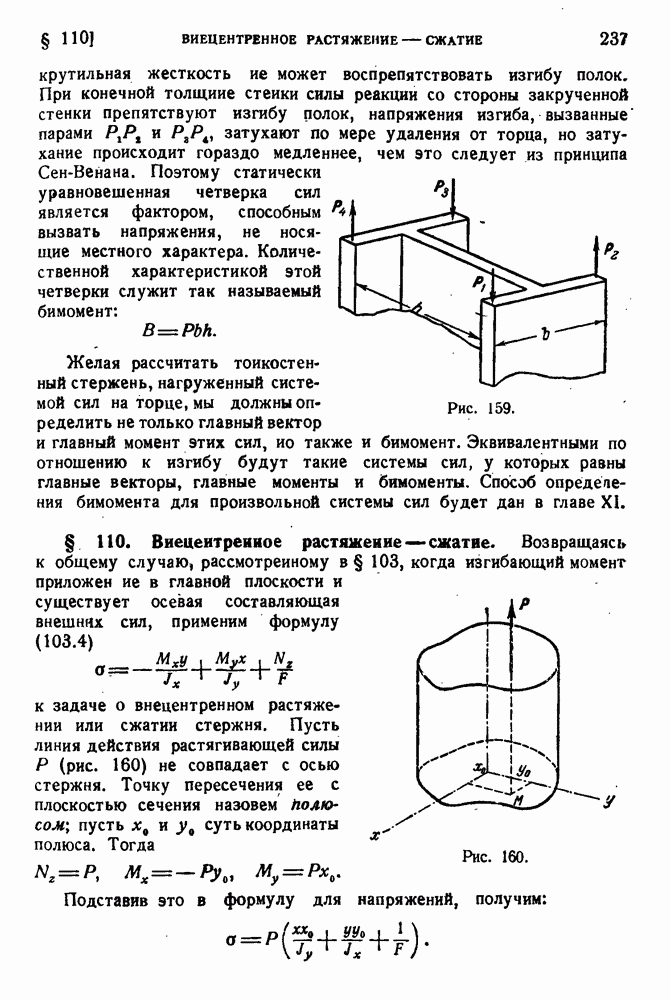
- § 110. Внецентренное растяжение — сжатие.
- § 111. Ядро сечения.
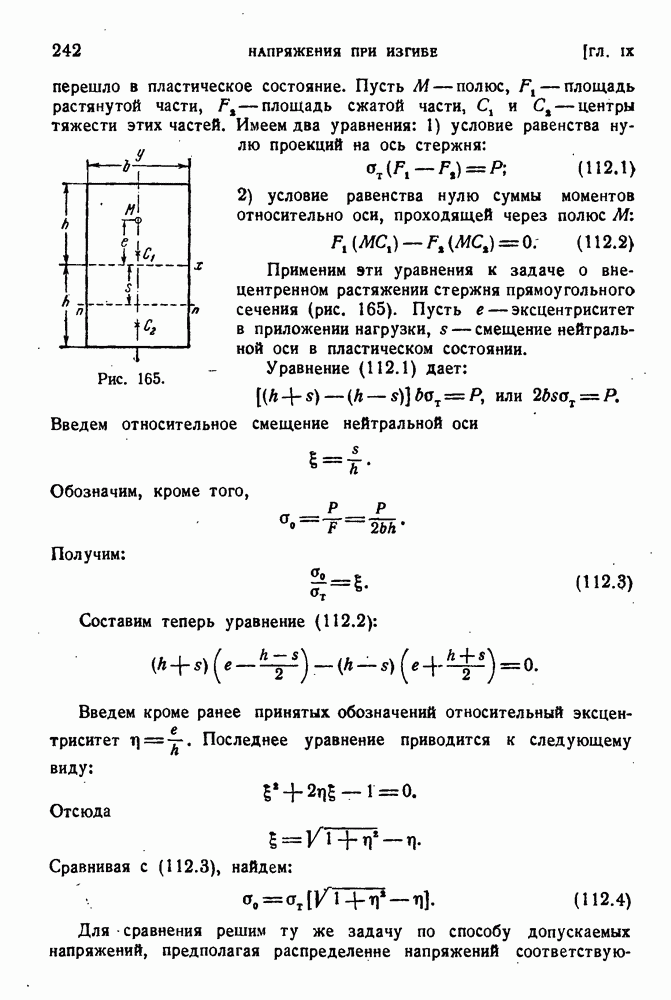
- § 112. Несущая способность внецентренно сжатого стержня.
- § 113. Расчет составных балок.
- § 114. Изгиб кривого бруса.
- § 115. Нахождение нейтральной осн в кривом стержне.
- ГЛАВА X. ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- § 116. Дифференциальное уравнение изогнутой оси.
- § 117. Пределы применимости приближенной теории.
- § 118. Интегрирование уравнения изгиба.
- § 119. Примеры определения прогибов.
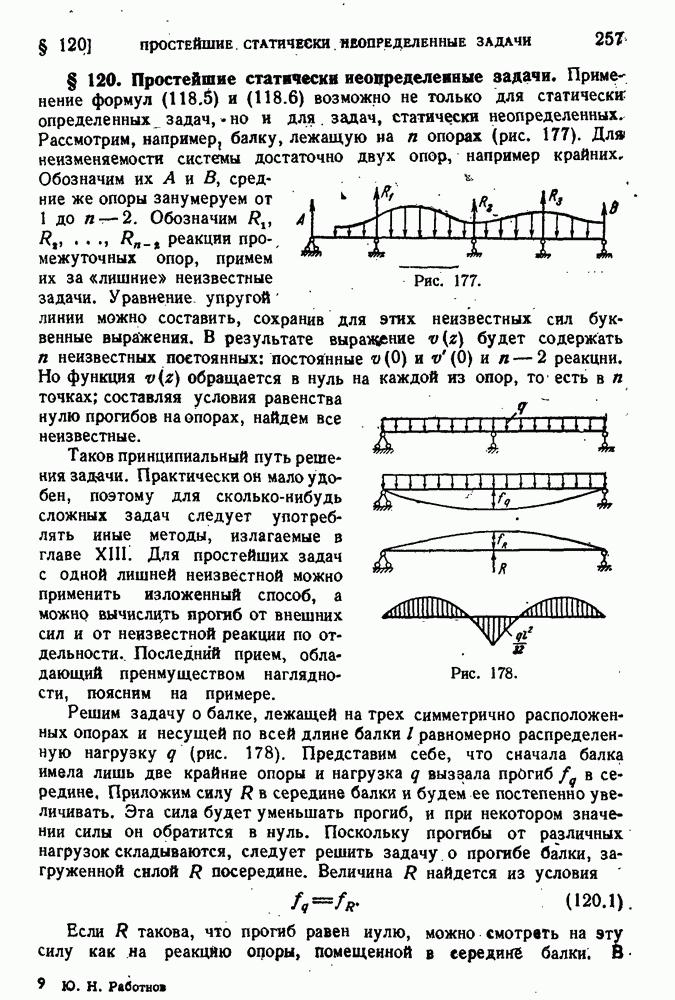
- § 120. Простейшие статически неопределенные задачи.
- § 121. Расчет статически неопределимых балок по способу допускаемых нагрузок.
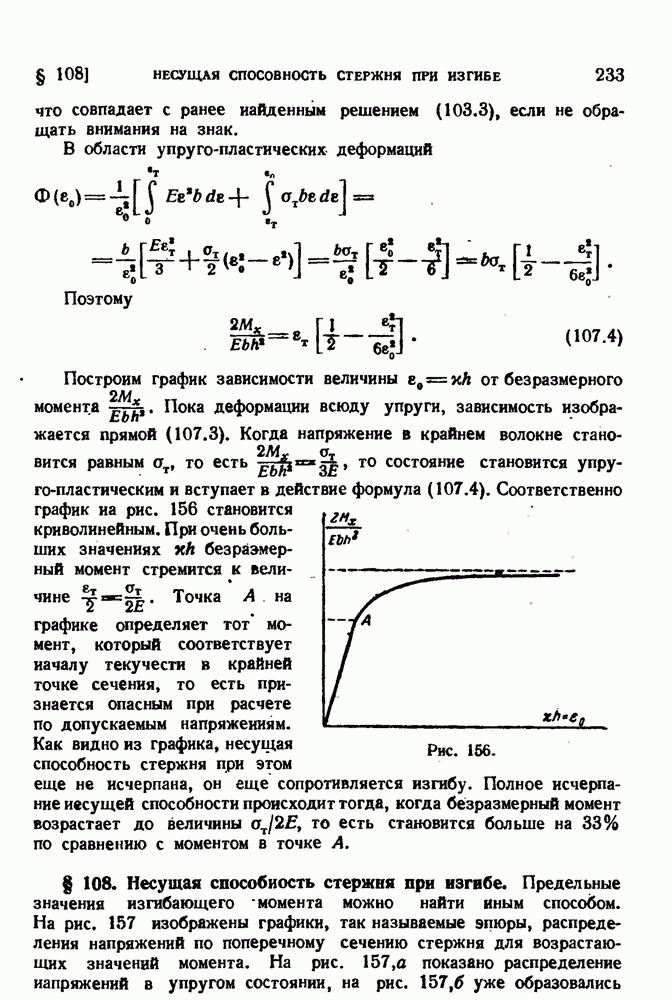
- § 122. Изгиб стержней переменного сечения.
- § 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами.
- § 124. Продольно-поперечный изгиб.
- § 125. Изгиб балки на упругом основании.
- ГЛАВА XI. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
- § 126. Нормальные и касательные напряжения при изгибе.
- § 127. Касательные напряжении при изгибе в плоскости симметрии.
- § 128. Центр изгиба.
- § 129. Дополнительные напряжения при кручении.
- § 130. Закон секториальных площадей.
- § 131. Уравнение стесненного кручения.
- § 132. Вычисление секториальных характеристик.
- § 133. Стержень, нагруженный бимоментом.
- § 134. Некоторые примеры стесненного кручения.
- ГЛАВА XII. УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ
- § 135. Постановка вопроса об устойчивости.
- § 136. Устойчивость сжатого упругого стержня.
- § 137. Эластика Эйлера.
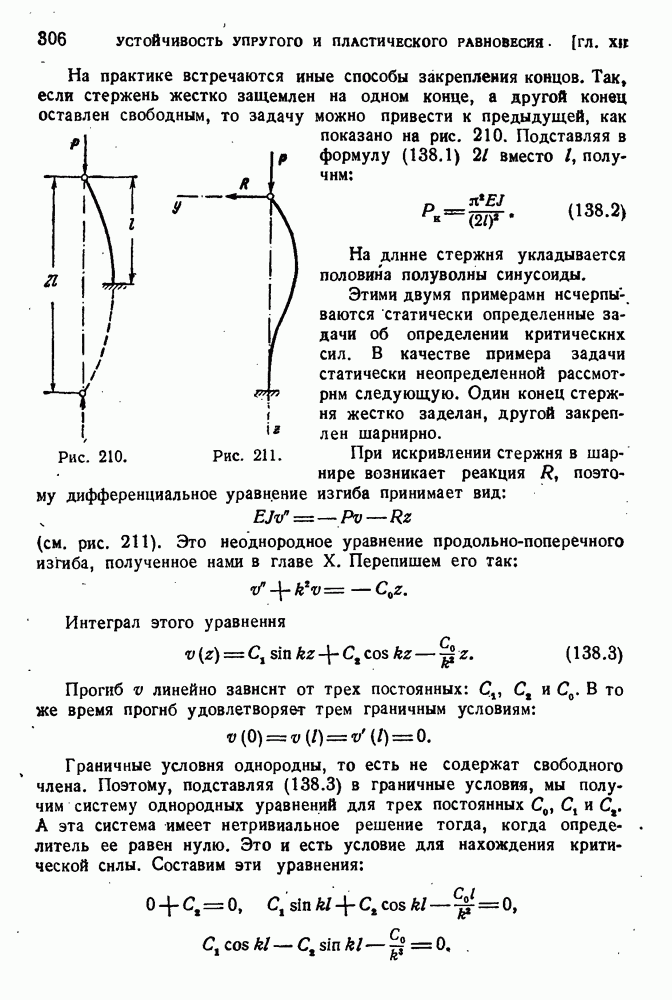
- § 138. Критические силы при иных видах закрепления стержня.
- § 139. Потеря устойчивости за пределом упругости.
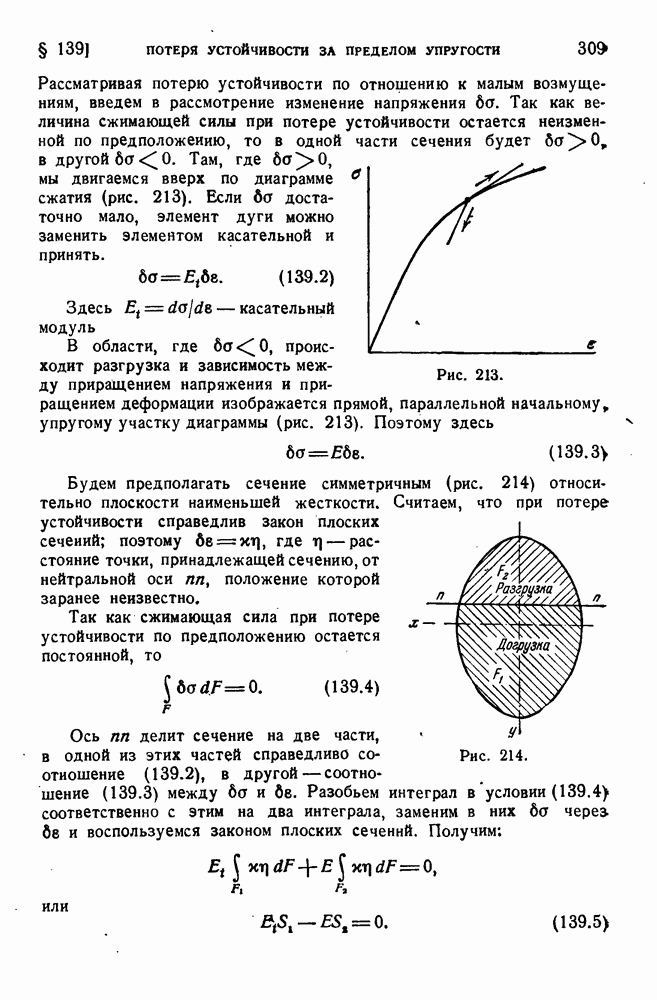
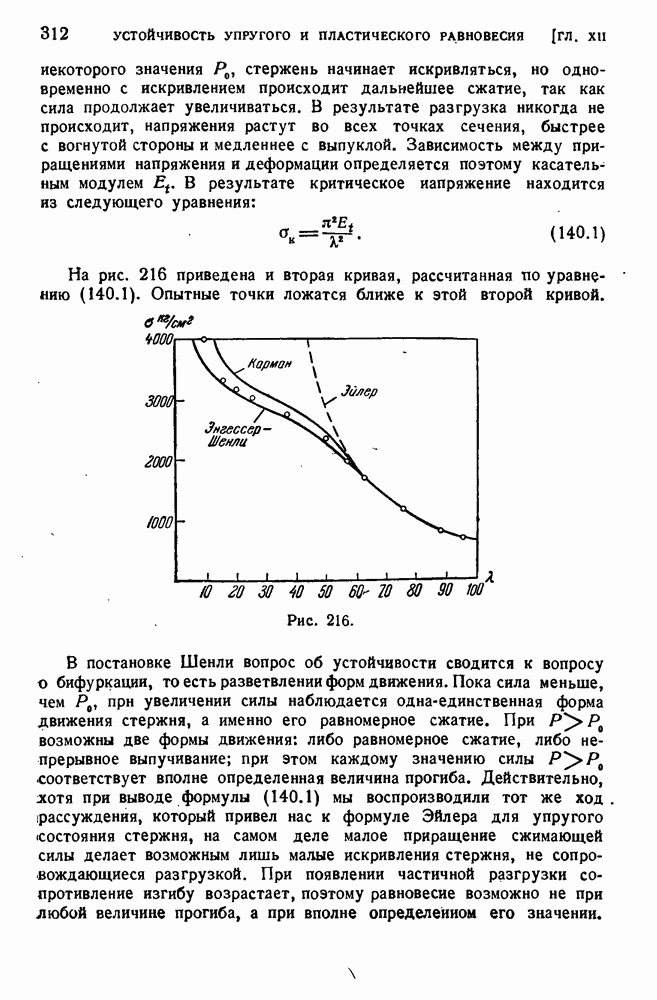
- § 140. Потеря устойчивости за пределом упругости (продолжение).
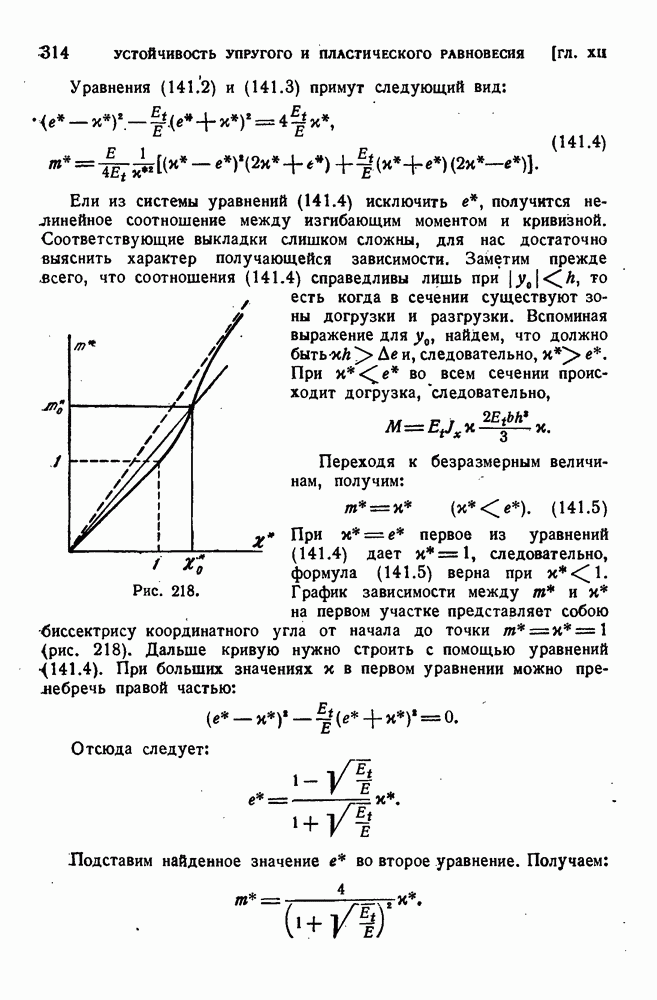
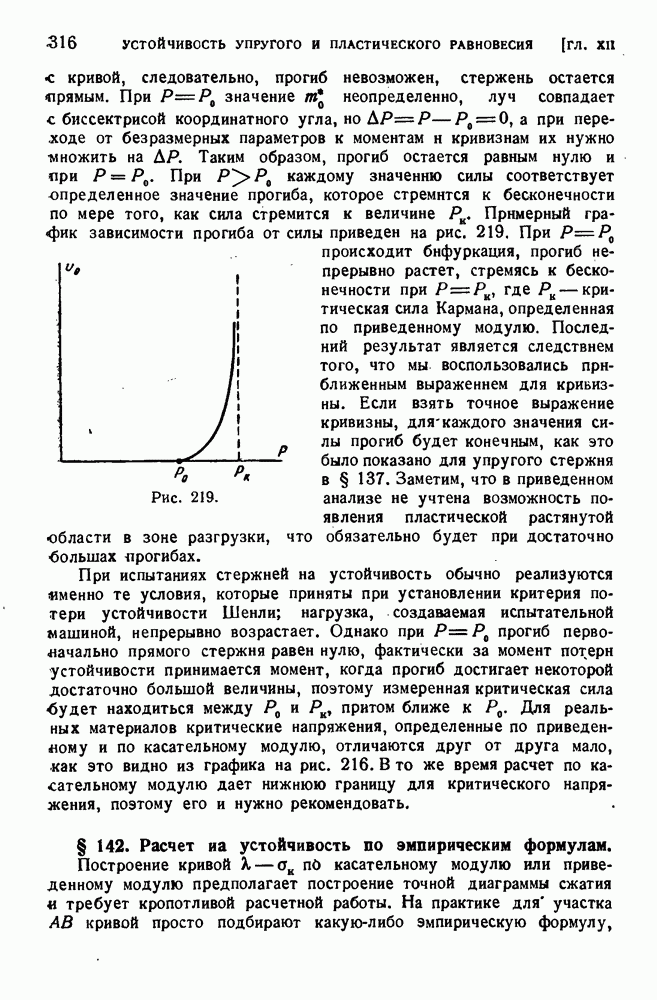
- § 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости.
- § 142. Расчет на устойчивость по эмпирическим формулам.
- ГЛАВА XIII. ТРУБЫ И ДИСКИ
- § 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности.
- § 144. Упругое состояние трубы. Формулы Ламе.
- § 145. Пластическое состояние трубы.
- § 146. Вращающиеся диски. Упругое состояние.
- § 147. Диск равного сопротивления.
- § 148. Предельное равновесие вращающегося диска.
- ГЛАВА XIV. ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 149. Обобщенные силы и обобщенные перемещения.
- § 150. Начало возможных перемещений для деформируемого тела.
- § 151. Теоремы Лагранжа и Кастильяно.
- § 152. Лииейиые упругие системы.
- § 153. Теорема о взаимности работ.
- § 154. Теорема Кастильяно для линейных упругих систем.
- § 155. Расчет винтовых пружин.
- § 156. Теорема о минимуме энергии.
- § 157. Интеграл перемещений.
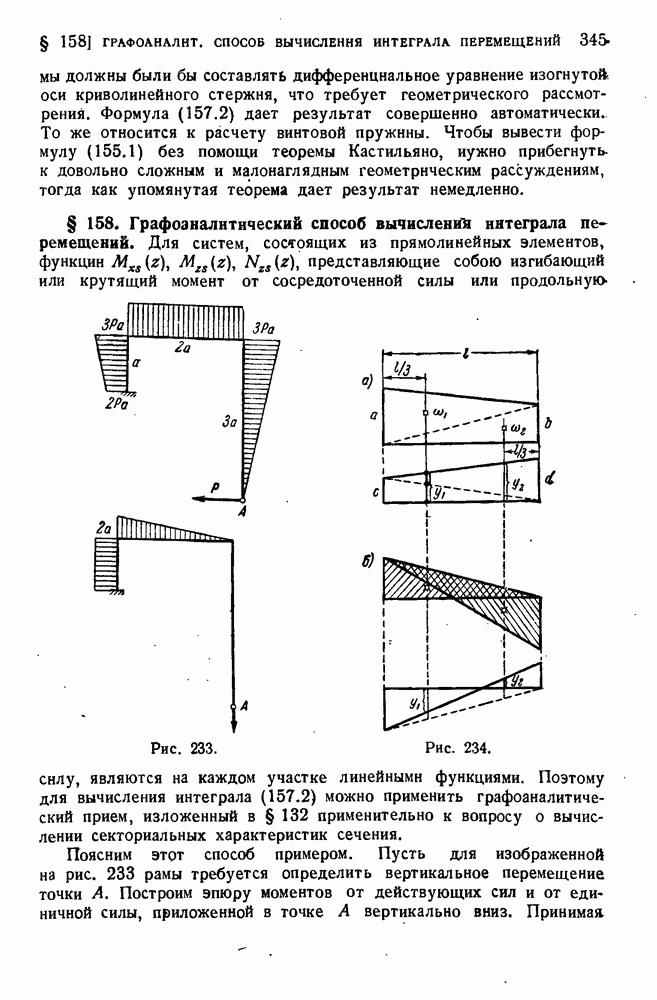
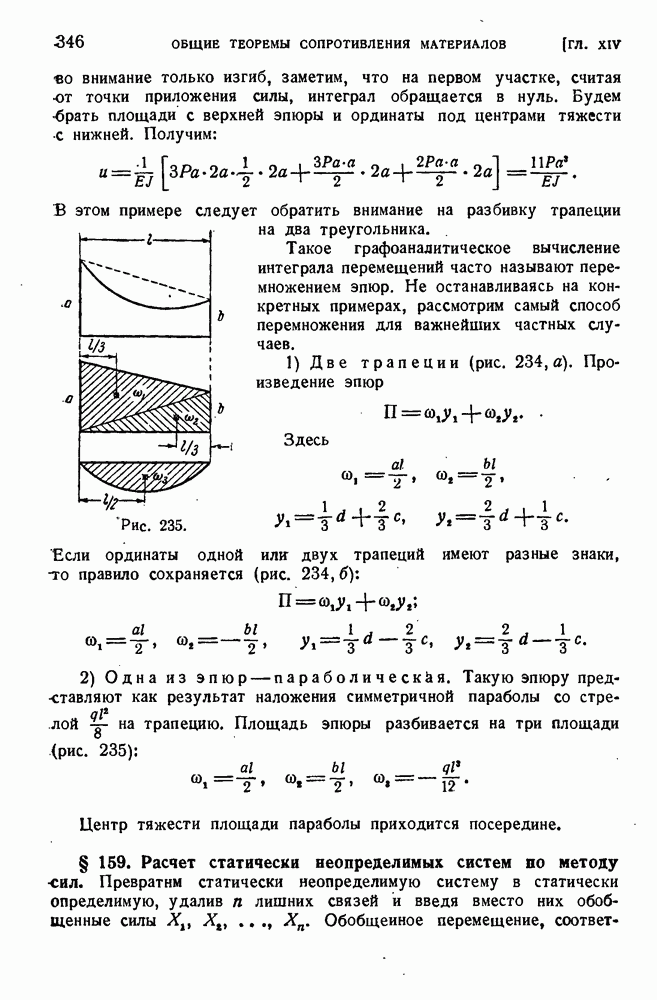
- § 158. Графоаналитический способ вычислений интеграла перемещений.
- § 159. Расчет статически неопределимых систем по методу сил.
- § 160. Уравнение трех моментов.
- ГЛАВА XV. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
- § 161. Жестко-пластическое тело.
- § 162. Поверхности нагружения.
- § 163. Истинное и допустимые состояния элемента.
- § 164. Статический метод определения предельной нагрузки.
- § 165. Примеры определения предельной нагрузки статическим методом.
- § 166. Кинематически возможные состояния.
- § 167. Кинематический метод определения предельной нагрузки.
- § 168. Примеры определения предельной нагрузки кинематическим методом.
- § 169. Предельное равновесие пластинок.
- ГЛАВА XVI. ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 170. Колебания систем с конечным числом степеней свободы.
- § 171. Собственные частоты и главные формы колебаний.
- § 172. Представление произвольной конфигурации системы через главные формы. Главные координаты.
- § 173. Формула и способ Релея.
- § 174. Нижние оценки для частоты основного тона.
- § 175. Продольные колебания стержней.
- § 176. Поперечные колебания стержней.
- § 177. Колебания балок постоянного сечения.
- § 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня.
- § 179. Действие ударных и импульсивных нагрузок на упругие системы.
- ГЛАВА XVII. ТЕОРИИ ПРОЧНОСТИ
- § 180. Постановка вопроса о прочности.
- § 181. Хрупкое и пластическое разрушение.
- § 182. Теория прочности Мора.
- § 183. Механизм хрупкого разрушения.
- § 184. Прочность при низких температурах.
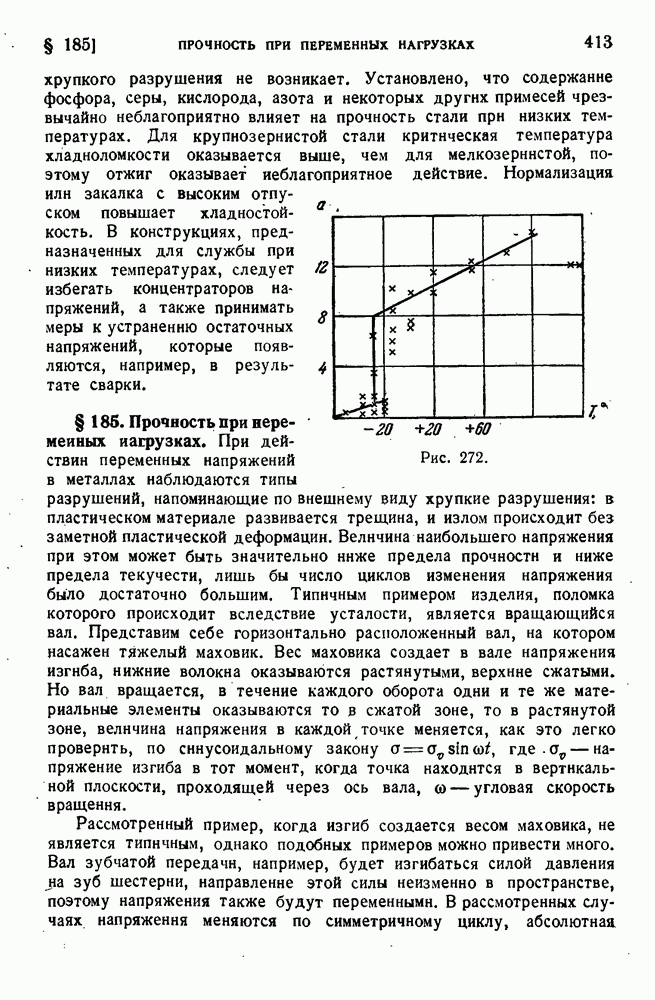
- § 185. Прочность при переменных нагрузках.
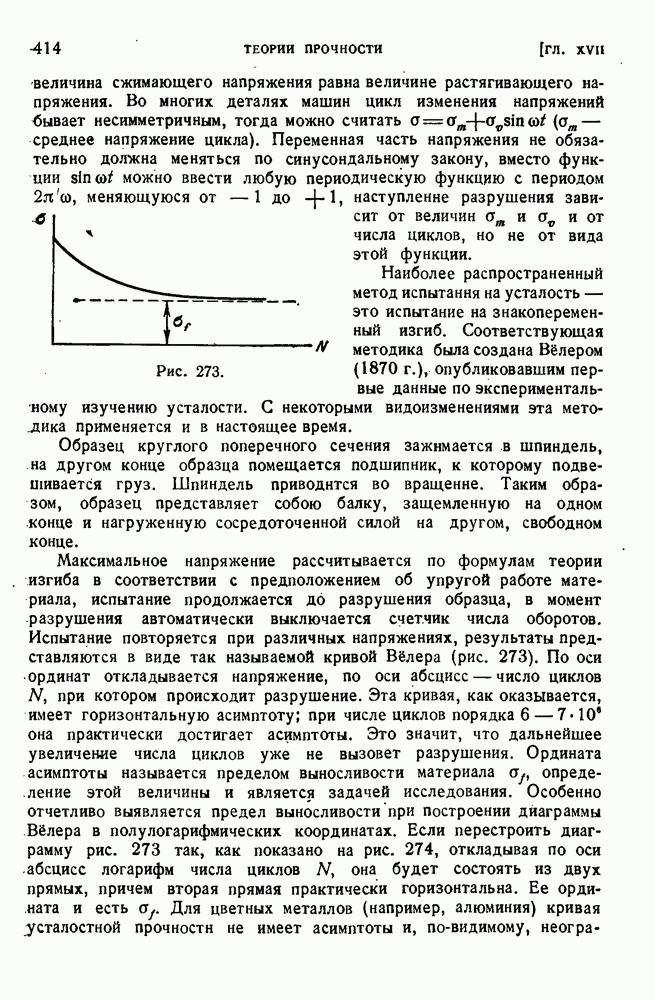
- § 186. Природа усталостного разрушения.
- § 187. Критерии прочности при переменных нагрузках.
- § 188. Влияние концентрации напряжений на усталостную прочность.
- § 189. Усталостная прочность при сложном напряженном состоянии.
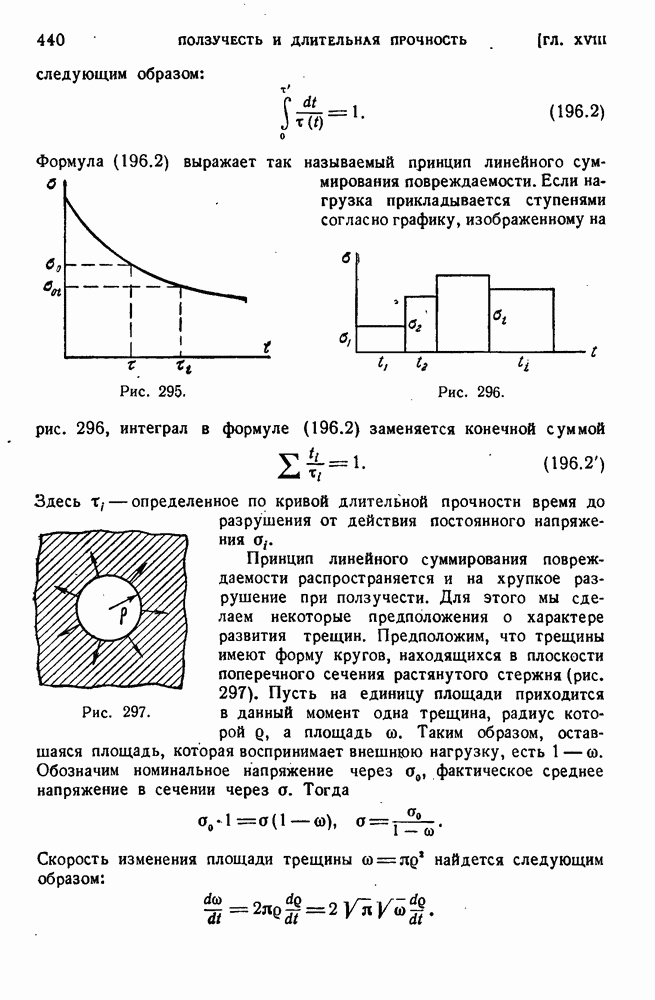
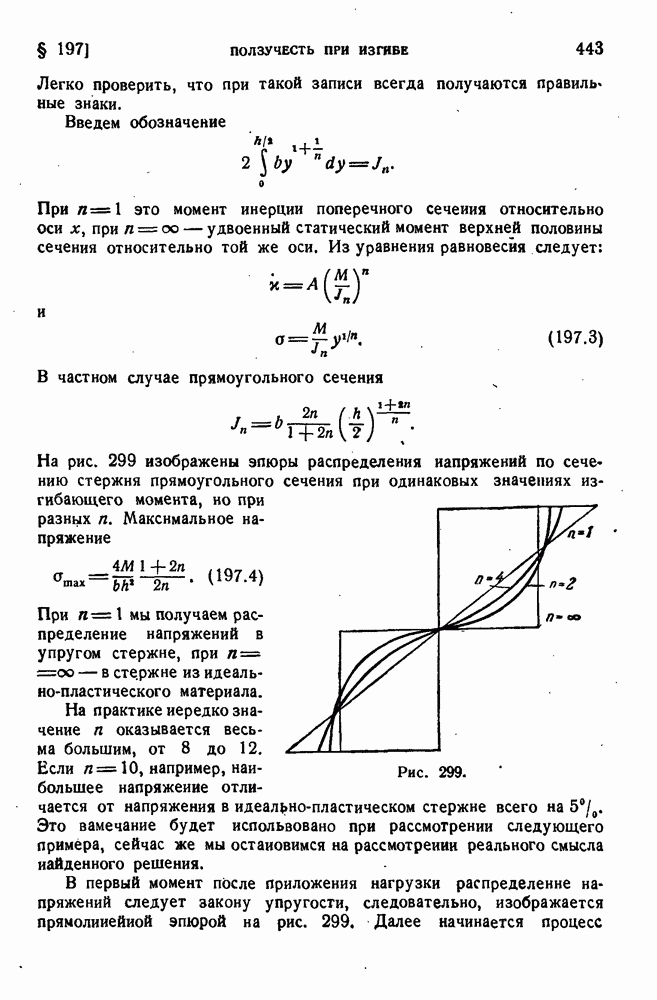
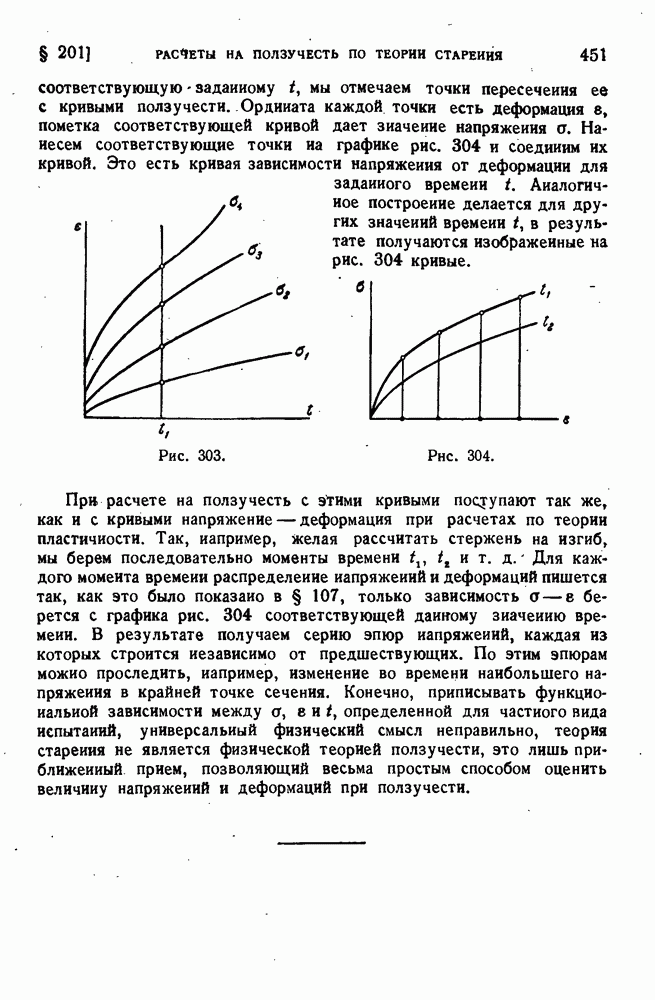
- ГЛАВА XVIII. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
- § 190. Ползучесть металлов.
- § 191. Процесс ползучести.
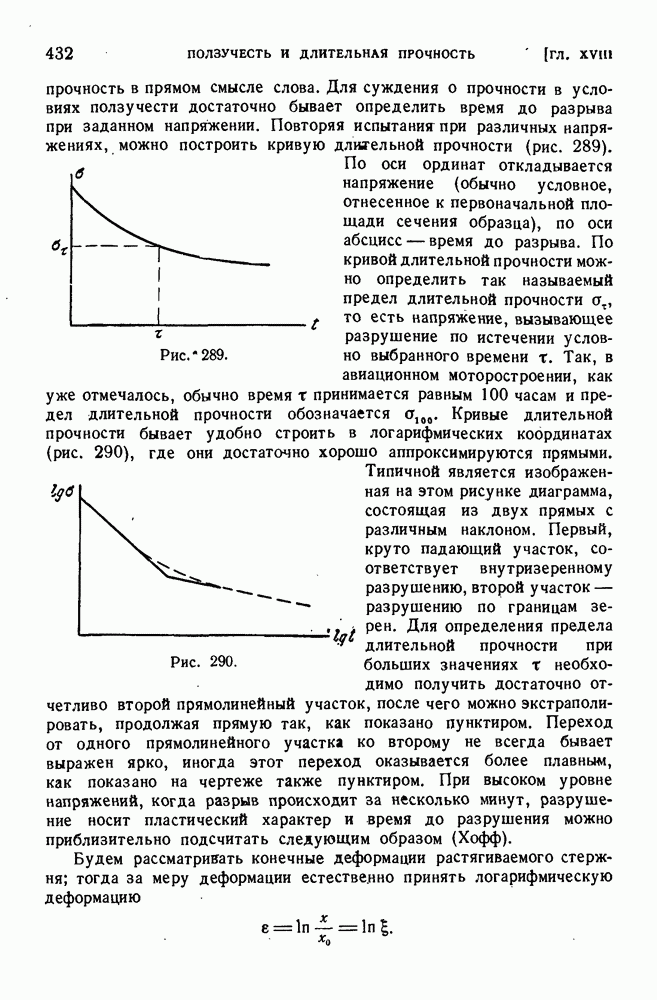
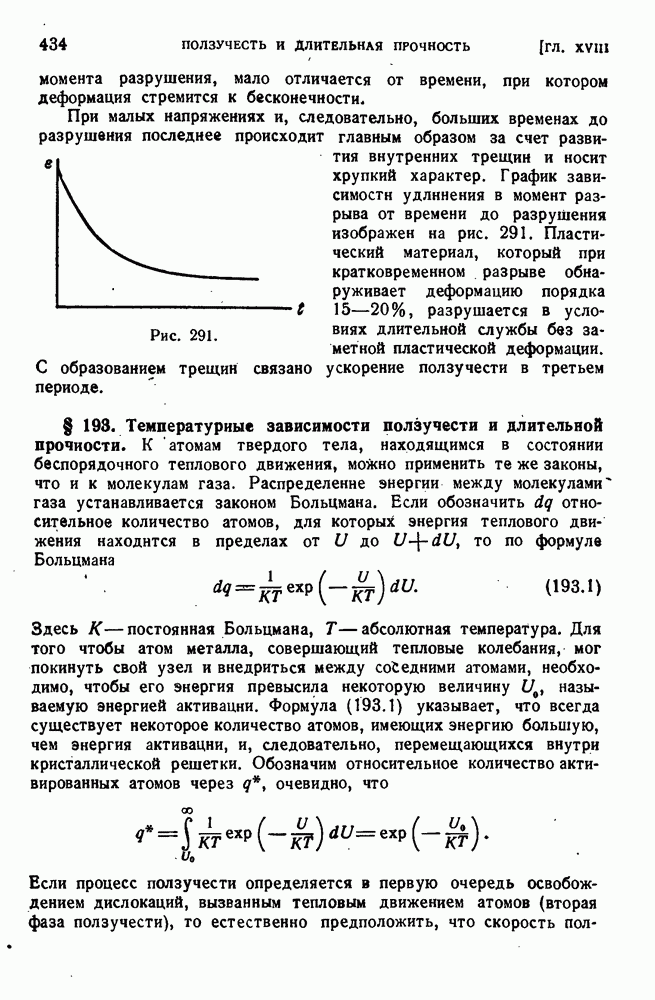
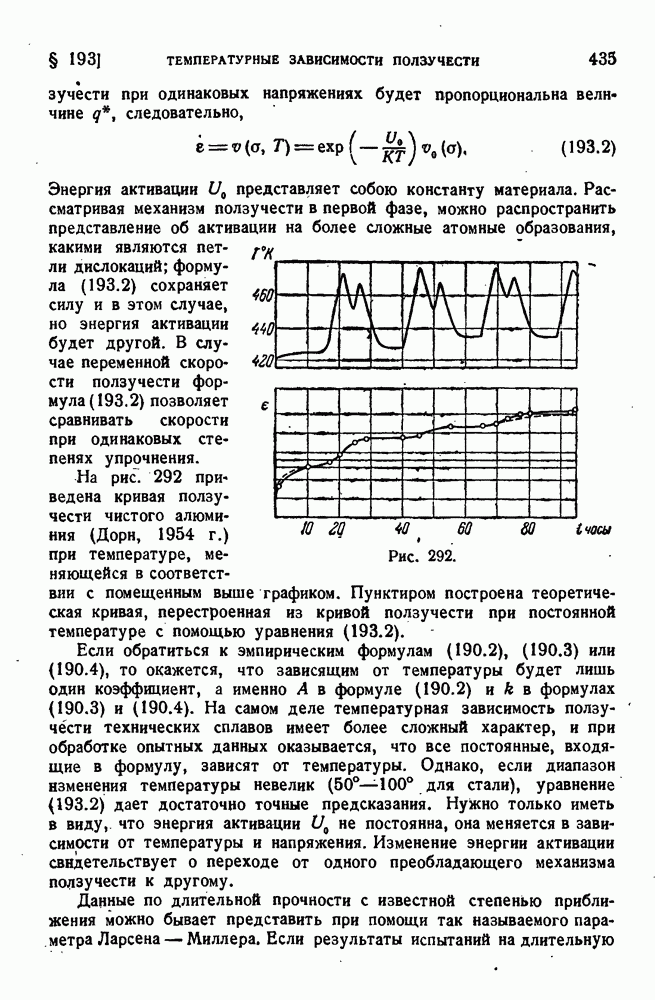
- § 192. Длительное разрушение.
- § 193. Температурные зависимости ползучести и длительной прочности.
- § 194. Феноменологические теории одномерной ползучести.
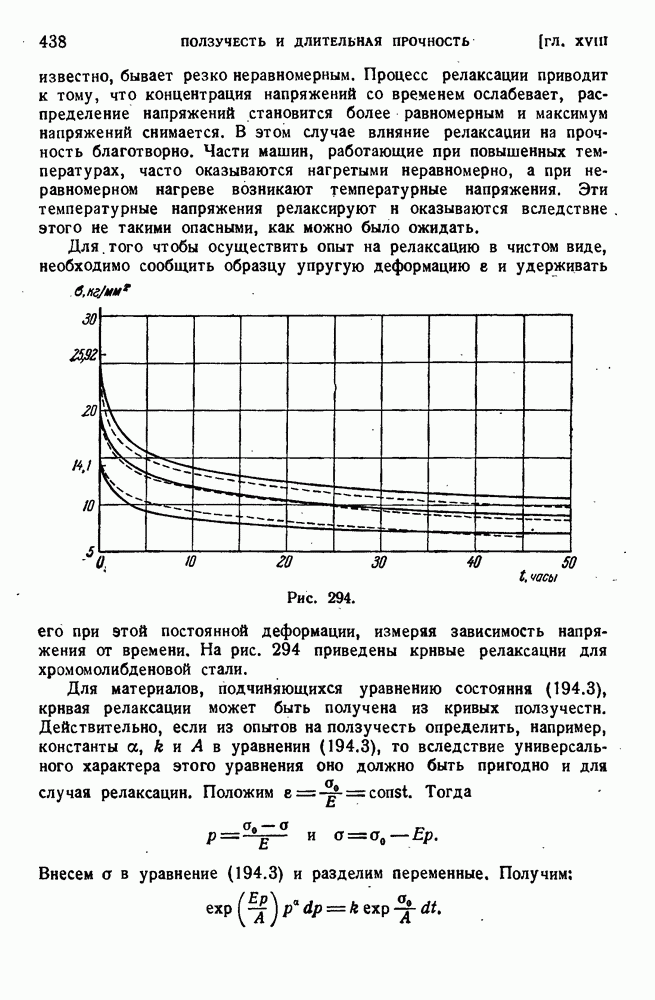
- § 195. Релаксация напряжений.
- § 196. Длительная прочность при переменных нагрузках.
- § 197. Ползучесть при изгибе.
- § 198. Критическое время сжатого стержня.
- § 199. Ползучесть и длительная прочность при сложном напряженном состоянии.
- § 200. Вращающиеся диски в условиях ползучести.
- § 201. Расчеты на ползучесть по теории старении.