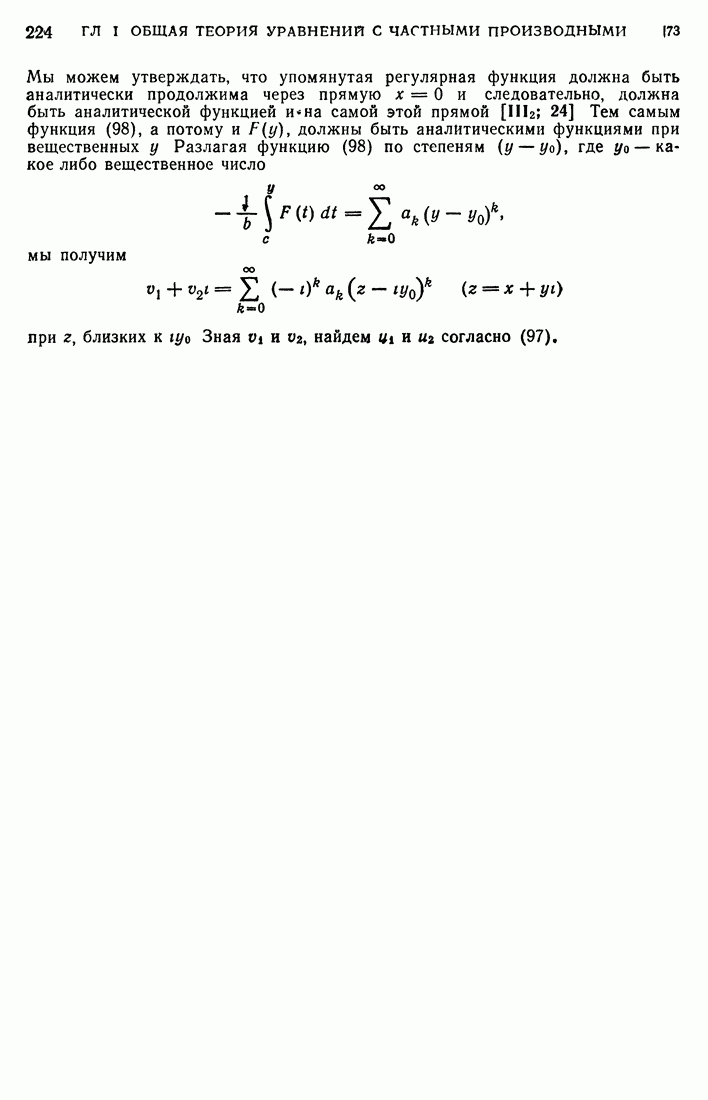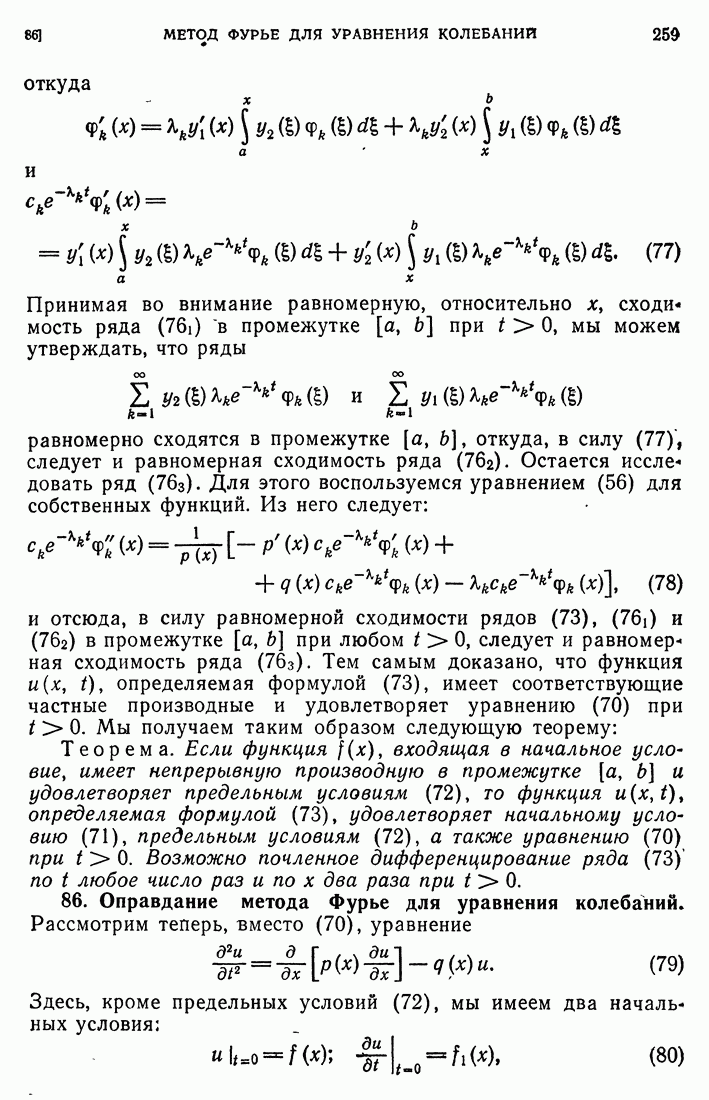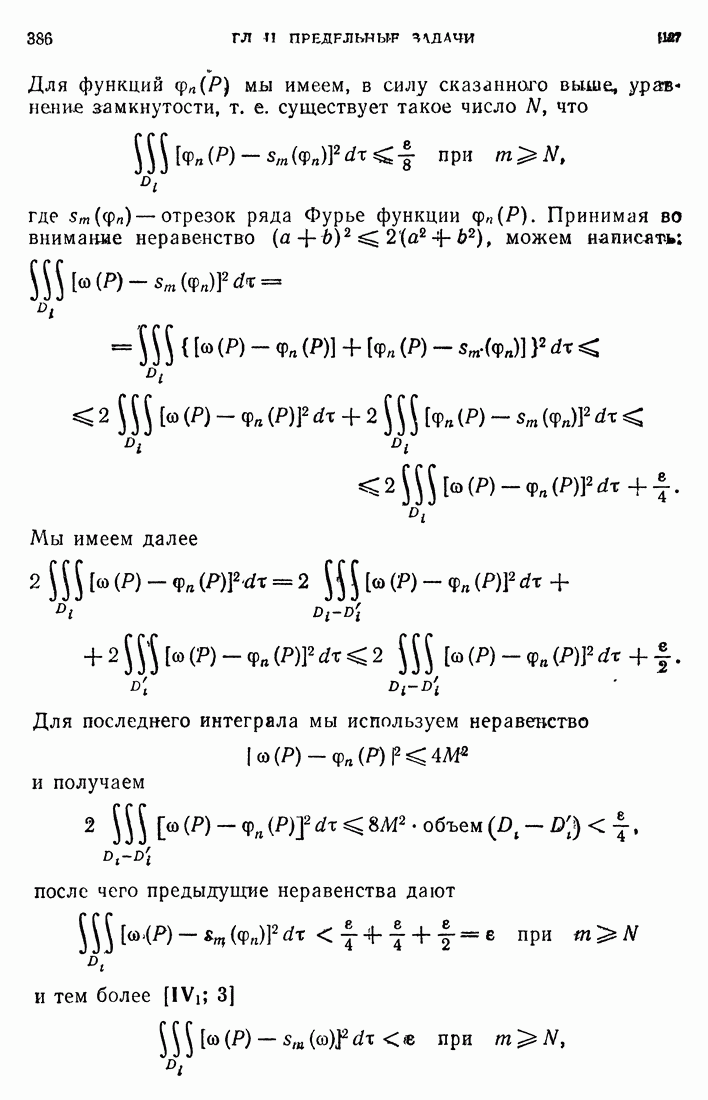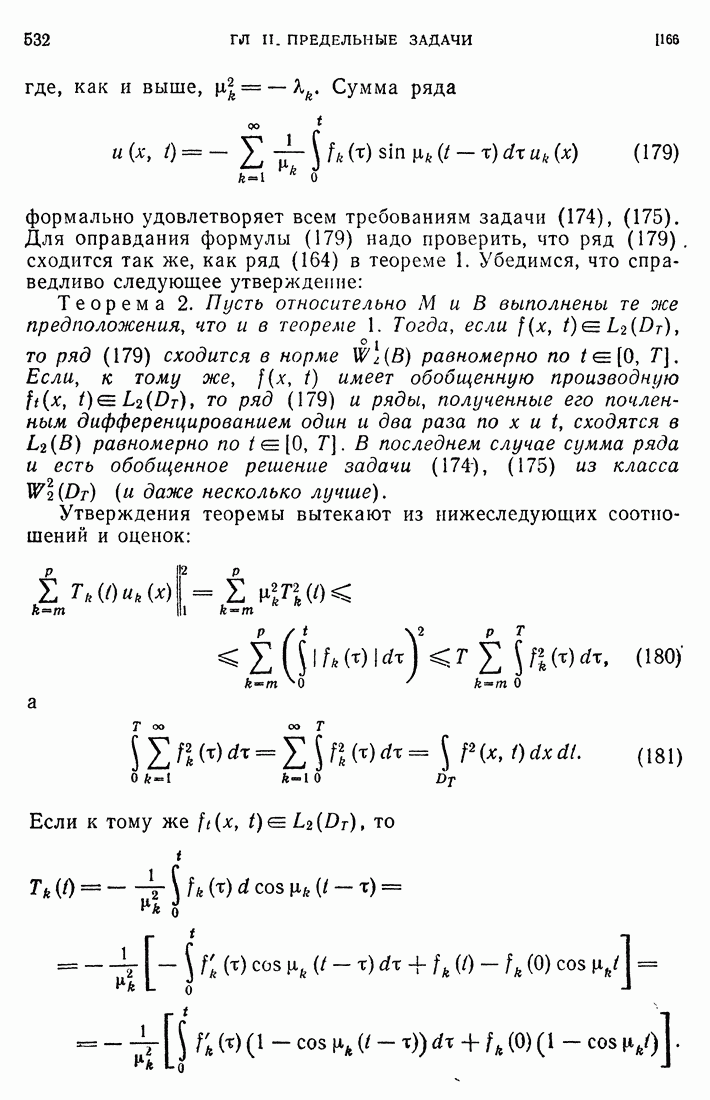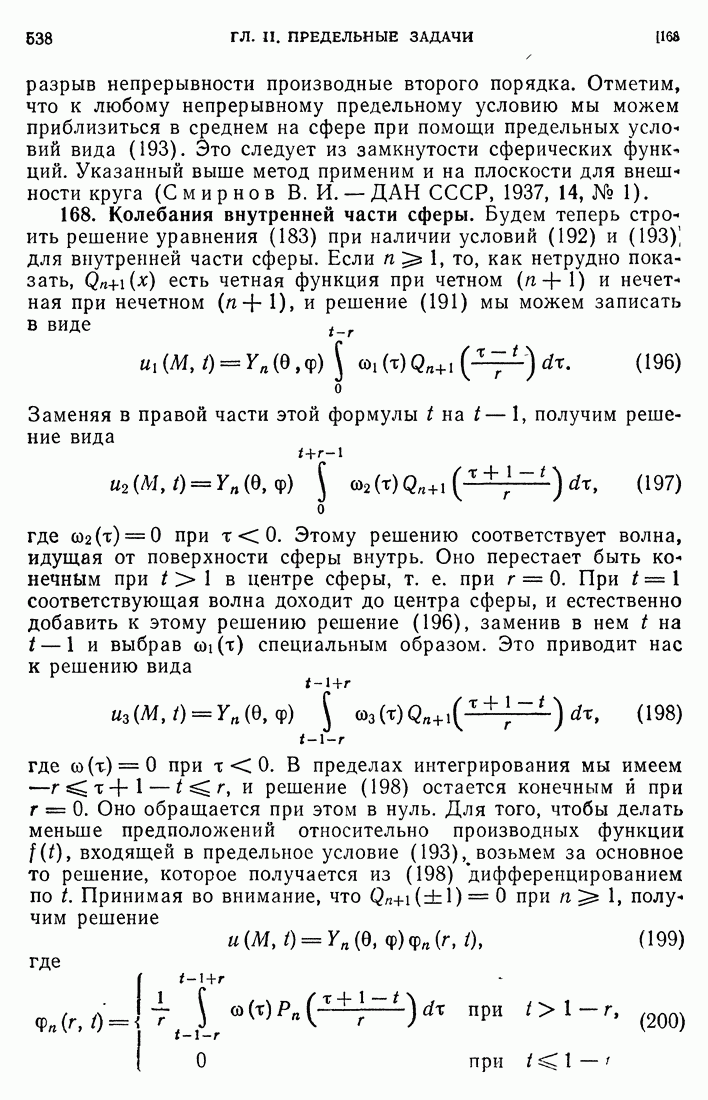| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
107. Единственность решения задачи Неймана.
В настоящем параграфе мы дадим доказательство единственности решения внутренней задачи Неймана без предположения правильности нормальной производной. Предварительно рассмотрим тело некоторого специального вида и построим в этом теле гармоническую функцию, обладающую некоторыми свойствами, которые будут ниже указаны. Пусть  тело, ограниченное поверхностью
тело, ограниченное поверхностью

и плоскостью  , где k, а и
, где k, а и  положительные постоянные. Точку (0, 0, 0) назовем вершиной этого тела, и обозначим ее
положительные постоянные. Точку (0, 0, 0) назовем вершиной этого тела, и обозначим ее  Буквою а обозначим ту часть границы этого тела, которая лежит в плоскости
Буквою а обозначим ту часть границы этого тела, которая лежит в плоскости  и буквою
и буквою  — остальную часть границы тела. Пусть далее
— остальную часть границы тела. Пусть далее  две вещественные постоянные, причем
две вещественные постоянные, причем  Построим функцию
Построим функцию  гармоническую внутри тела
гармоническую внутри тела  непрерывную вплоть до границы, и такую, что
непрерывную вплоть до границы, и такую, что  на
на  на
на  . Если
. Если  угол между радиусом-вектором и осью z и
угол между радиусом-вектором и осью z и  - функция Лежандра
- функция Лежандра  то, как известно
то, как известно  при любом
при любом  функция
функция  будет гармонической внутри тела
будет гармонической внутри тела  Будем строить
Будем строить  в виде
в виде

где у и  — положительные постоянные, которые будут определены позднее. Мы имеем, очевидно,
— положительные постоянные, которые будут определены позднее. Мы имеем, очевидно,  . Покажем, прежде всего, что при всех
. Покажем, прежде всего, что при всех  , достаточно близких к нулю,
, достаточно близких к нулю,

Функция  есть сумма гипергеометрического ряда:
есть сумма гипергеометрического ряда:

вследствие чего можно написать:

или

Мы считаем  , так что множители, соответствующие
, так что множители, соответствующие  , положительны, а остальные
, положительны, а остальные  отрицательны. Относя к этим последним множителям
отрицательны. Относя к этим последним множителям  можем записать их в виде
можем записать их в виде

Таким образом, выделяя первые два множителя, получаем неравенство

т. е.

откуда и следует, что  если
если  . Таким образом, (118) доказано при всех положительных р, достаточно близких к нулю. Фиксируем
. Таким образом, (118) доказано при всех положительных р, достаточно близких к нулю. Фиксируем  так, чтобы оно удовлетворяло этому условию, а также условию
так, чтобы оно удовлетворяло этому условию, а также условию  , где а из уравнения (116). Принимая во внимание, что
, где а из уравнения (116). Принимая во внимание, что  получаем на поверхности (116)
получаем на поверхности (116)

где  , и, окончательно, на поверхности (116)
, и, окончательно, на поверхности (116)

Если  , то и, в силу
, то и, в силу  квадратная скобка имеет при этом отрицательный предел. Таким образом, мы можем фиксировать положительное число h настолько малым, чтобы на всей части
квадратная скобка имеет при этом отрицательный предел. Таким образом, мы можем фиксировать положительное число h настолько малым, чтобы на всей части  поверхности тела
поверхности тела  иметь
иметь

Выберем, наконец, положительное число  настолько малым, чтобы формула (117) давала
настолько малым, чтобы формула (117) давала  на
на  . Построенная функция
. Построенная функция  удовлетворяет всем указанным выше условиям. На оси тела
удовлетворяет всем указанным выше условиям. На оси тела  ), т. е. на оси Z, мы имеем
), т. е. на оси Z, мы имеем

Если М — переменная точка этой оси, то

Докажем теперь теорему:
Теорема. Если  — функция, гармоническая внутри
— функция, гармоническая внутри  отличная от постоянной,
отличная от постоянной,  конечная точная нижняя граница значений
конечная точная нижняя граница значений  внутри
внутри  и существует такая точка
и существует такая точка  на S, что
на S, что  при стремлении М изнутри к
при стремлении М изнутри к  , то при стремлении М к
, то при стремлении М к  по нормали, отношение
по нормали, отношение

остается больше некоторого положительного числа.
Мы считаем, что существует тело  которое касается S в точке
которое касается S в точке  и все точки которого, кроме
и все точки которого, кроме  , лежат внутри S. Число h фиксировано настолько малым, чтобы иметь
, лежат внутри S. Число h фиксировано настолько малым, чтобы иметь  на всей части
на всей части  поверхности упомянутого тела. Пусть
поверхности упомянутого тела. Пусть  наименьшее значение
наименьшее значение  на части а поверхности
на части а поверхности  Так как
Так как  отлична от постоянно, то
отлична от постоянно, то  и, выбрав у достаточно малым, мы можем построить
и, выбрав у достаточно малым, мы можем построить  с указанными выше свойствами. При этом
с указанными выше свойствами. При этом  на остальной части поверхности
на остальной части поверхности  При этом, направив ось Z по внутренней нормали к S в точке
При этом, направив ось Z по внутренней нормали к S в точке  получим
получим

что и доказывает теорему.
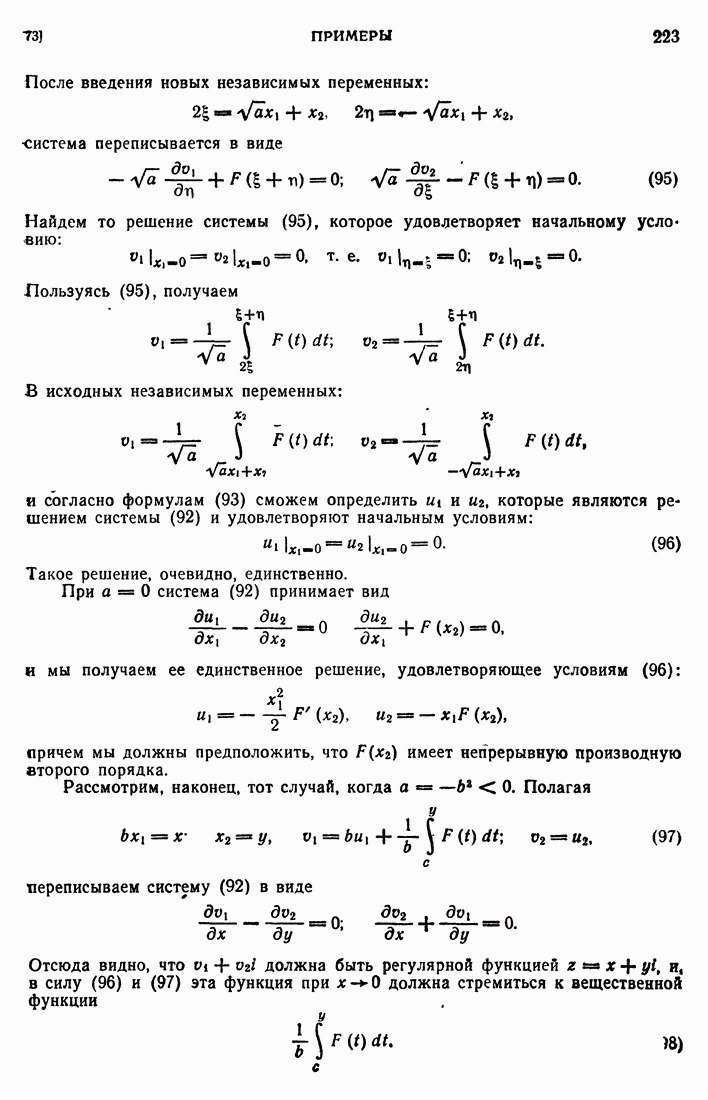
Из доказанной теоремы непосредственно следует единственность решения задачи Неймана в следующем смысле:
Если гармоническая внутри  функция
функция  непрерывна вплоть до S, и
непрерывна вплоть до S, и  на всей поверхности S, то
на всей поверхности S, то  постоянна. Пусть
постоянна. Пусть  точка S, где
точка S, где  имеет наименьшее значение. Из (122) непосредственно следует, что производная по нормали в точке
имеет наименьшее значение. Из (122) непосредственно следует, что производная по нормали в точке  не может стремиться к нулю, когда
не может стремиться к нулю, когда  оставаясь на нормали. Если бы это было так, то из формулы конечных приращений мы получили бы
оставаясь на нормали. Если бы это было так, то из формулы конечных приращений мы получили бы

что противоречит (122).
Совершенно аналогично проводится доказательство единственности и для внешней задачи Неймана.
Приведенное выше доказательство было дано в совместной работе М. В. Келдыша и М. А. Лаврентьева (ДАН СССР, 1937, 16, № 3).
Если можно коснуться поверхности S изнутри сферой, то доказательство теоремы единственности проводится элементарно (Заремба С. — УМН, 1946, 1, № 3—4).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
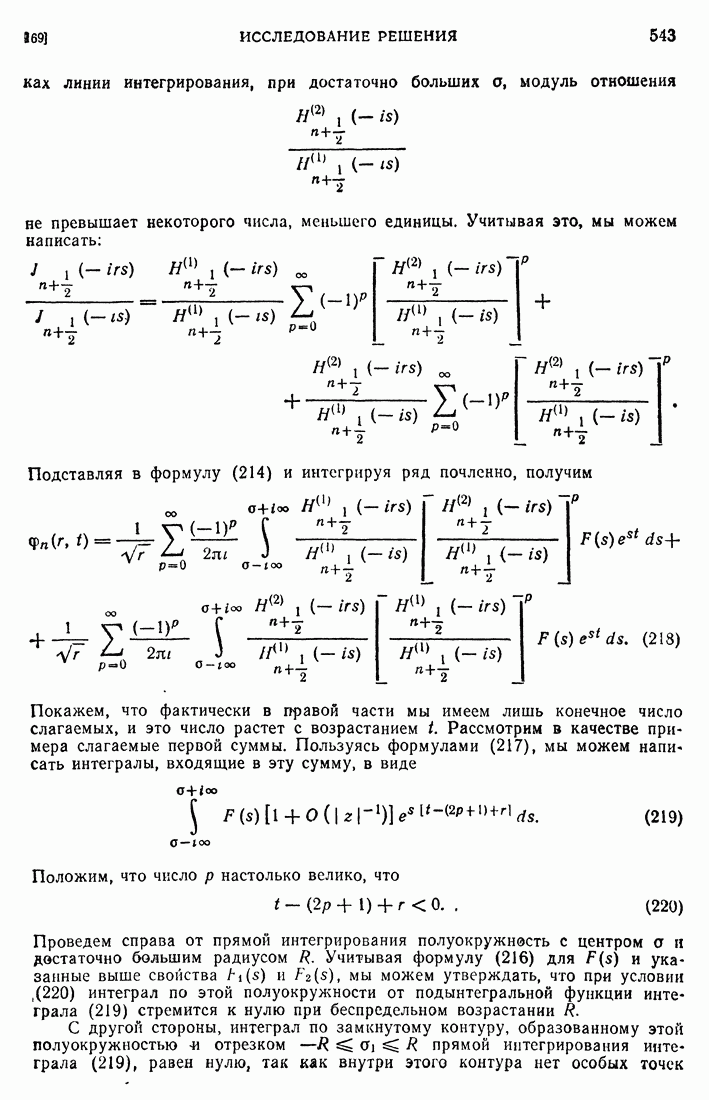
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.