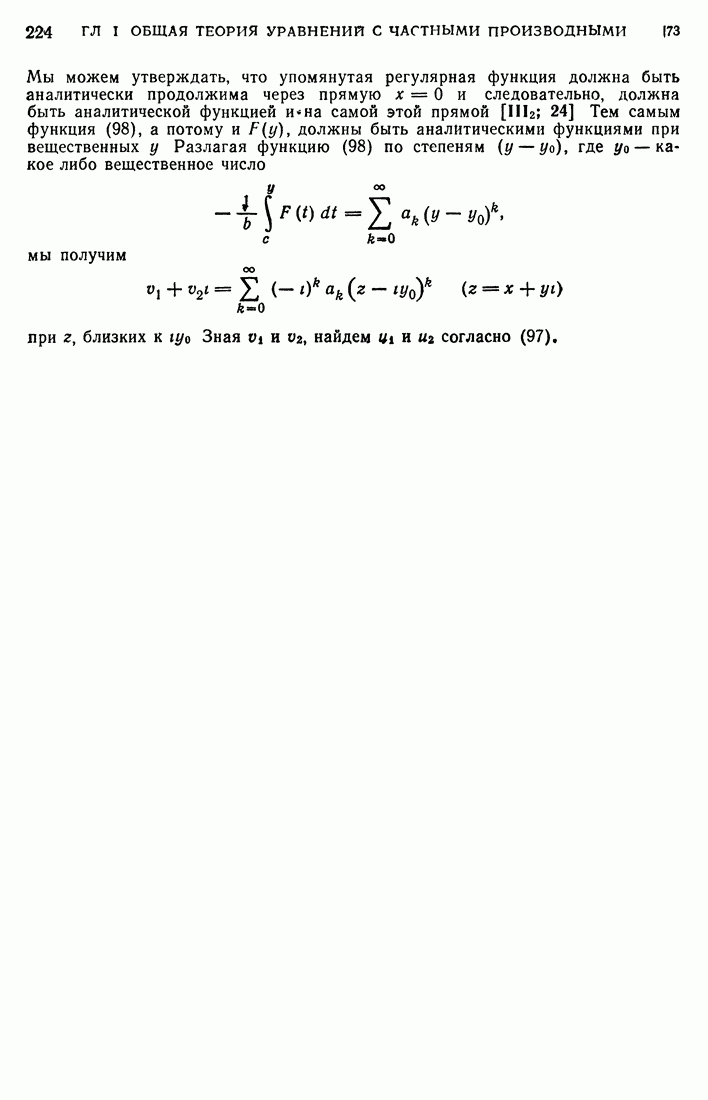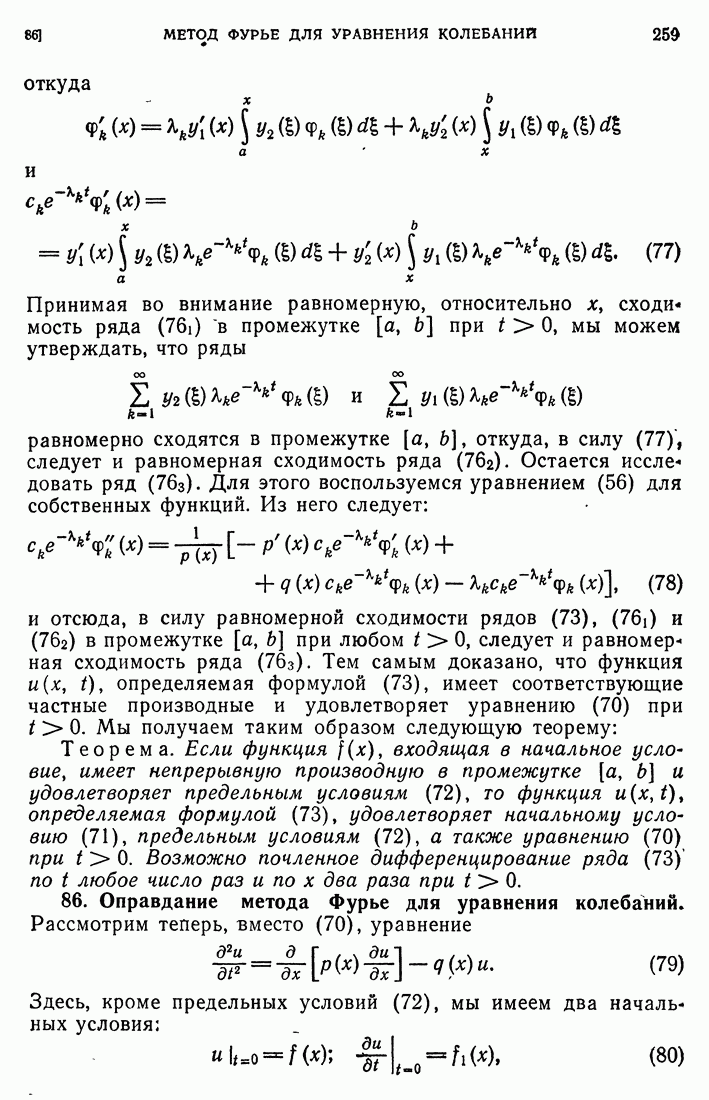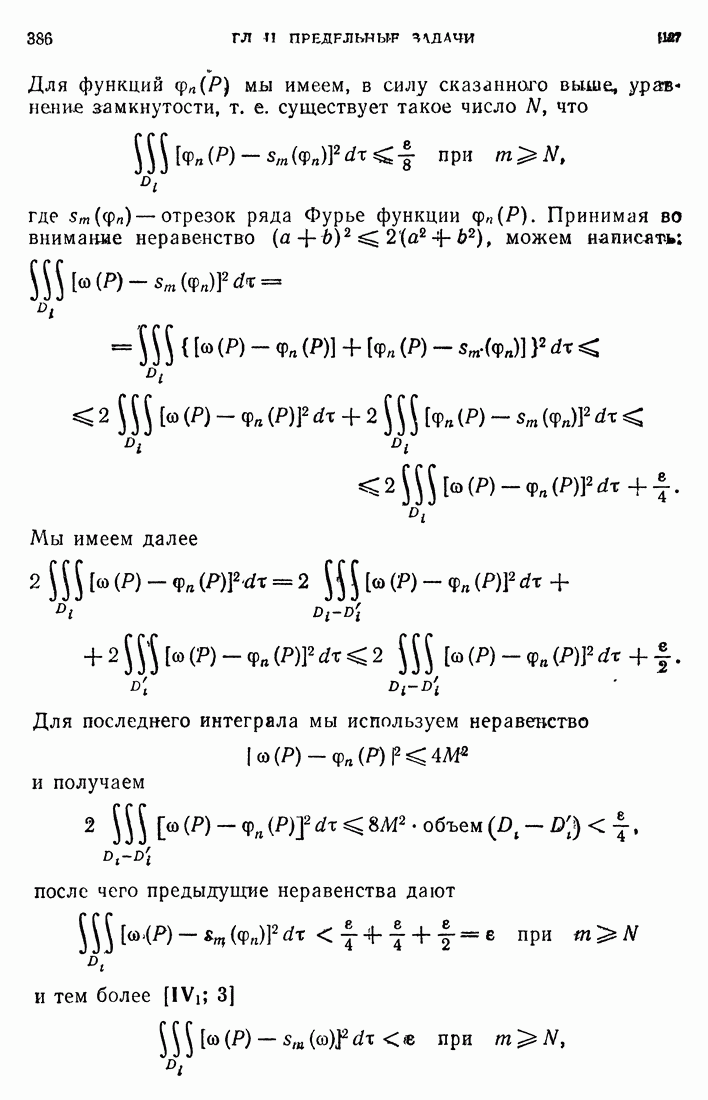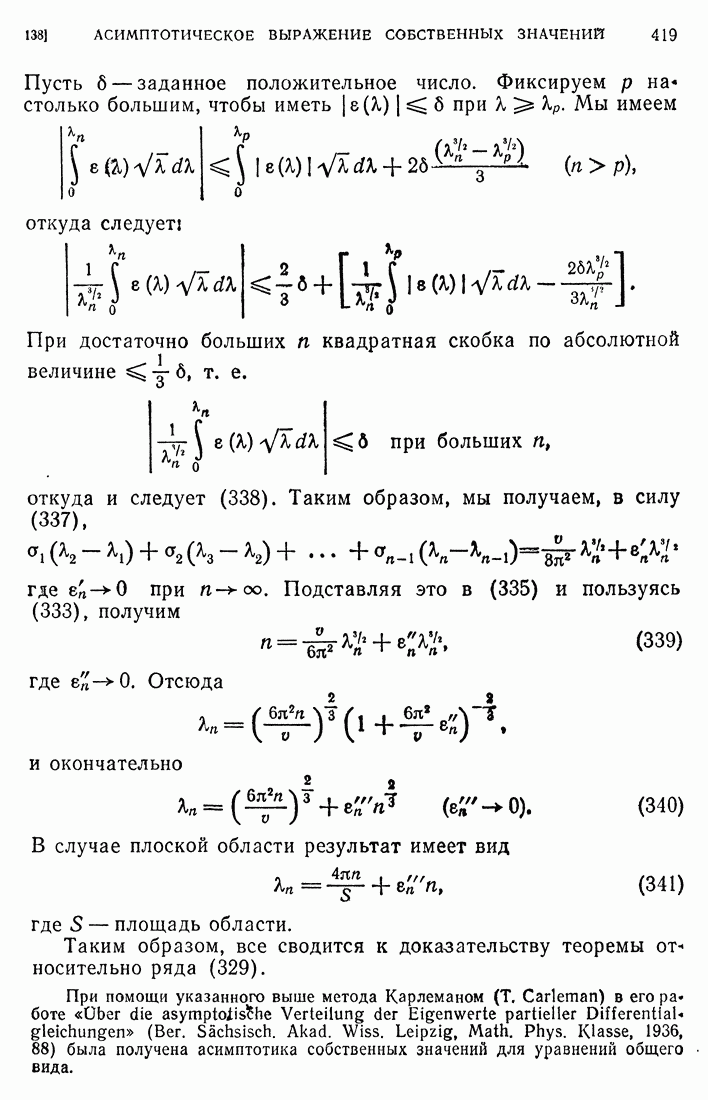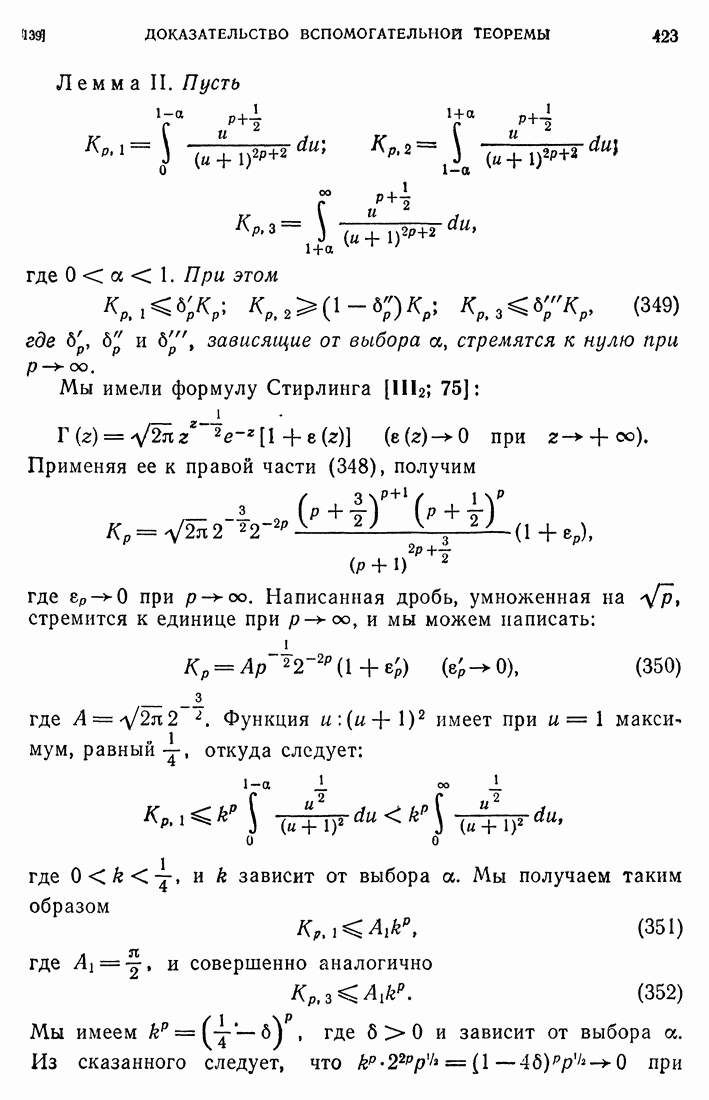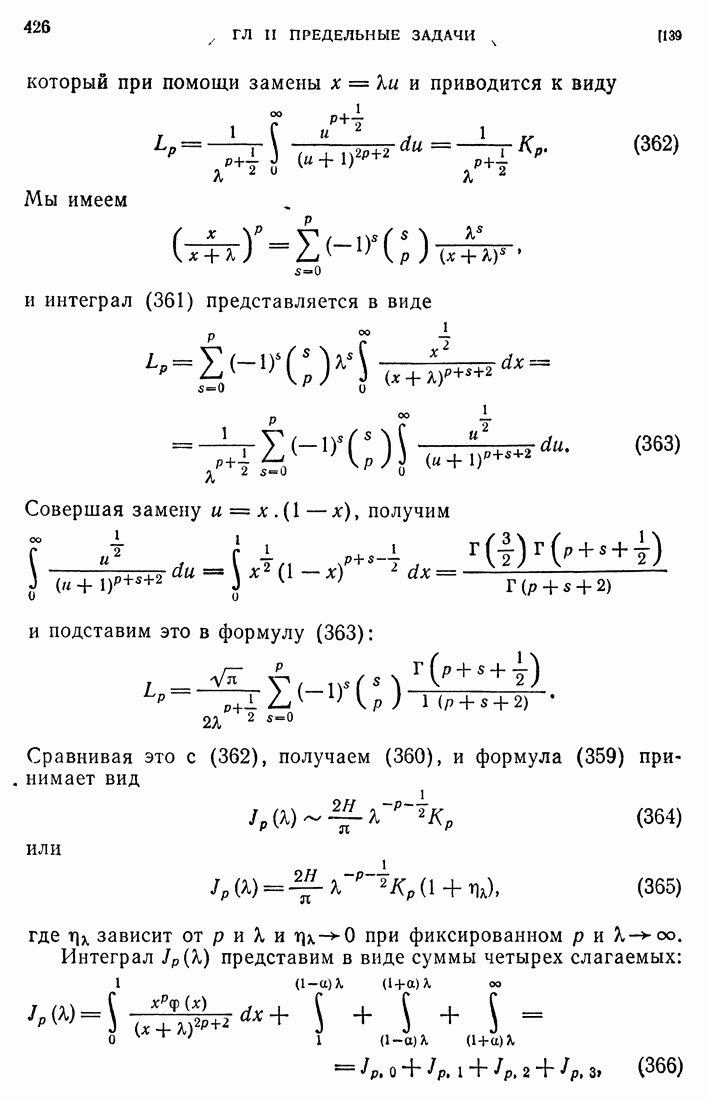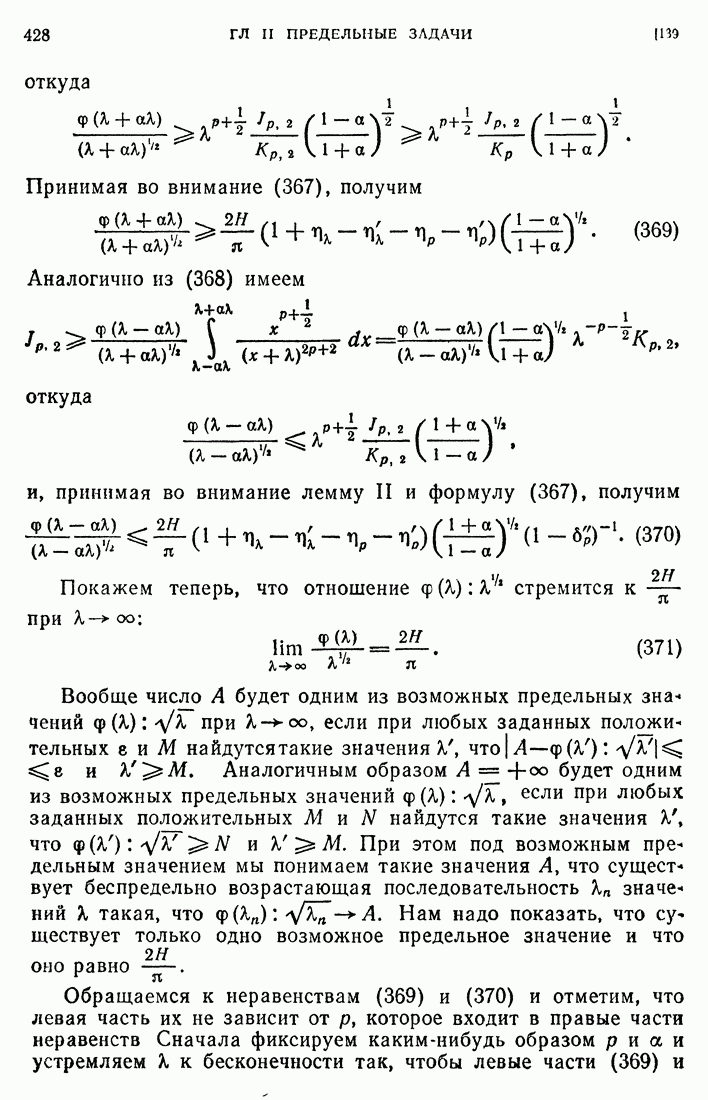| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Оно справедливо для любой функции v, принадлежащей т. е. v из  имеющей обобщенные производные первого порядка, суммируемые по D. Граница
имеющей обобщенные производные первого порядка, суммируемые по D. Граница  области D должна обладать некоторой регулярностью, например принадлежать классу СК Неравенство (428) справедливо и для более широкого класса областей: для областей с липшицевыми границами. Мы не будем давать их точного определения, но из приводимого ниже вывода нетрудно усмотреть, какие свойства S достаточны для справедливости (428). Неравенство (428) потребуется нам лишь для функций v, принадлежащих
области D должна обладать некоторой регулярностью, например принадлежать классу СК Неравенство (428) справедливо и для более широкого класса областей: для областей с липшицевыми границами. Мы не будем давать их точного определения, но из приводимого ниже вывода нетрудно усмотреть, какие свойства S достаточны для справедливости (428). Неравенство (428) потребуется нам лишь для функций v, принадлежащих  Поэтому мы ограничимся его доказательством лишь для таких v. Из этого факта и плотности
Поэтому мы ограничимся его доказательством лишь для таких v. Из этого факта и плотности  следует справедливость (428) для любой
следует справедливость (428) для любой  Возьмем в произвольной точке
Возьмем в произвольной точке  местную декартову систему координат
местную декартову систему координат  и кусок
и кусок  поверхности S, имеющий уравнение
поверхности S, имеющий уравнение 

Пусть  таково, что область
таково, что область  принадлежит D. Функцию
принадлежит D. Функцию  будем считать не прерывно дифференцируемой в
будем считать не прерывно дифференцируемой в  Функцию v, принадлежащую
Функцию v, принадлежащую  рассмотрим как функцию координат
рассмотрим как функцию координат  в В силу теоремы Ньютона — Лейбница
в В силу теоремы Ньютона — Лейбница

Возьмем от обеих частей (429) модули, результат умножим на  и проинтегрируем по
и проинтегрируем по  . Это и элементарные оценки дают следующие соотношения:
. Это и элементарные оценки дают следующие соотношения:

для  . Постоянная
. Постоянная  есть мажоранта для
есть мажоранта для  Проинтегрируем теперь неравенство
Проинтегрируем теперь неравенство
(430) по  в пределах от 0 до
в пределах от 0 до  и результат умножим на В правой части появится интеграл
и результат умножим на В правой части появится интеграл

который не превосходит  Таким образом мы приходим к неравенству
Таким образом мы приходим к неравенству

Предполагая, что поверхность S можно покрыть конечным числом кусков типа  мы придем к неравенству (428), суммируя (431) по всем таким кускам.
мы придем к неравенству (428), суммируя (431) по всем таким кускам.
Определим теперь пространство  Оно есть замкнутое подпространство гильбертова пространства
Оно есть замкнутое подпространство гильбертова пространства  которое определено в
которое определено в  . Напомним, что
. Напомним, что  состоит из всех квадратично суммируемых по D функций, имеющих квадратично суммируемые по
состоит из всех квадратично суммируемых по D функций, имеющих квадратично суммируемые по  производные до второго порядка. Скалярное произведение в
производные до второго порядка. Скалярное произведение в  определяется так:
определяется так:

где  является полным гильбертовым пространством. Норму в нем будем обозначать
является полным гильбертовым пространством. Норму в нем будем обозначать  а иногда, короче,
а иногда, короче, 
Подпространство  состоит из тех элементов
состоит из тех элементов  которые обращаются в нуль на границе S области D. При «хороших» границах S в
которые обращаются в нуль на границе S области D. При «хороших» границах S в  плотно множество функций из
плотно множество функций из  равных нулю на S. Чтобы не доказывать этот важный для нас факт, определим
равных нулю на S. Чтобы не доказывать этот важный для нас факт, определим  иначе:
иначе:  есть замыкание в норме
есть замыкание в норме  множества С(D) функций и
множества С(D) функций и  равных нулю на S. (Мы ввели здесь обозначение
равных нулю на S. (Мы ввели здесь обозначение  ; не следует его смешивать с обозначением
; не следует его смешивать с обозначением  множества всех дважды непрерывно дифференцируемых
множества всех дважды непрерывно дифференцируемых
функций, имеющих компактные носители, лежащие в D. Элементы  равны нулю не только на S, но и в ее окрестности.)
равны нулю не только на S, но и в ее окрестности.)  есть полное гильбертово пространство с тем же скалярным произведением, что и в Для гладких (и даже липшицевых) границ S множество
есть полное гильбертово пространство с тем же скалярным произведением, что и в Для гладких (и даже липшицевых) границ S множество  принадлежит множеству
принадлежит множеству  Мы предоставляем читателю доказать это утверждение самостоятельно.
Мы предоставляем читателю доказать это утверждение самостоятельно.
Теперь мы переходим к получению оценки нормы в  решений и задачи (403) через нормы и и f в
решений и задачи (403) через нормы и и f в  Для этого, помимо усдовий (413) о коэффициентах L, будем считать, что а, имеют ограниченные об. производные первого порядка, т. е.
Для этого, помимо усдовий (413) о коэффициентах L, будем считать, что а, имеют ограниченные об. производные первого порядка, т. е.

Кроме того, предположим, что S принадлежит классу  допустимых ослаблениях этого условия см. замечание в конце данного пункта). Эта оценка есть следствие неравенства
допустимых ослаблениях этого условия см. замечание в конце данного пункта). Эта оценка есть следствие неравенства

справедливого для любой функции  . Оно и называется вторым основным неравенством для эллиптических операторов Постоянная
. Оно и называется вторым основным неравенством для эллиптических операторов Постоянная  в нем определяется некоторыми характеристиками границы области D и постоянными
в нем определяется некоторыми характеристиками границы области D и постоянными  и из условий (413), (433). Неравенство (434) достаточно доказать лишь для и
и из условий (413), (433). Неравенство (434) достаточно доказать лишь для и  ибо
ибо  плотно в
плотно в  Действительно, любое и из
Действительно, любое и из  можно аппроксимировать в норме
можно аппроксимировать в норме  функциями
функциями  из
из  Пусть (434) верно для всех
Пусть (434) верно для всех  . В силу указанной сходимости
. В силу указанной сходимости  к и в (434), взятом для
к и в (434), взятом для  можно Перейти к пределу по
можно Перейти к пределу по  и Получить (434) для
и Получить (434) для  . Итак, пусть и
. Итак, пусть и  . Рассмотрим
. Рассмотрим  и оценим его снизу следующим образом:
и оценим его снизу следующим образом:

Здесь и ниже, если не оговорено противное, по повторяющимся днажды индексам подразумевается суммирование от 1 до  — произвольное число из интервала (0, 1), а постоянная
— произвольное число из интервала (0, 1), а постоянная  , так же, как и вводимые ниже постоянные С, определяются числовыми параметрами из условий (413), (433), и возможно, областью D. Преобразуем интеграл
, так же, как и вводимые ниже постоянные С, определяются числовыми параметрами из условий (413), (433), и возможно, областью D. Преобразуем интеграл  с помощью двукратного интегрирования по частям (см. (107 [48]) к виду
с помощью двукратного интегрирования по частям (см. (107 [48]) к виду

где

Из (436) следует неравенство

в котором использовано следующее сокращенное обозначение

Покажем, что в силу (413) имеет место оценка

Для этого зафиксируем произвольную точку  и введем в ее окрестности новые декартовы координаты:
и введем в ее окрестности новые декартовы координаты:  . Ортогональную матрицу
. Ортогональную матрицу  выберем так, чтобы она приводила квадратичную форму
выберем так, чтобы она приводила квадратичную форму  к диагональному виду, т. е. чтобы
к диагональному виду, т. е. чтобы

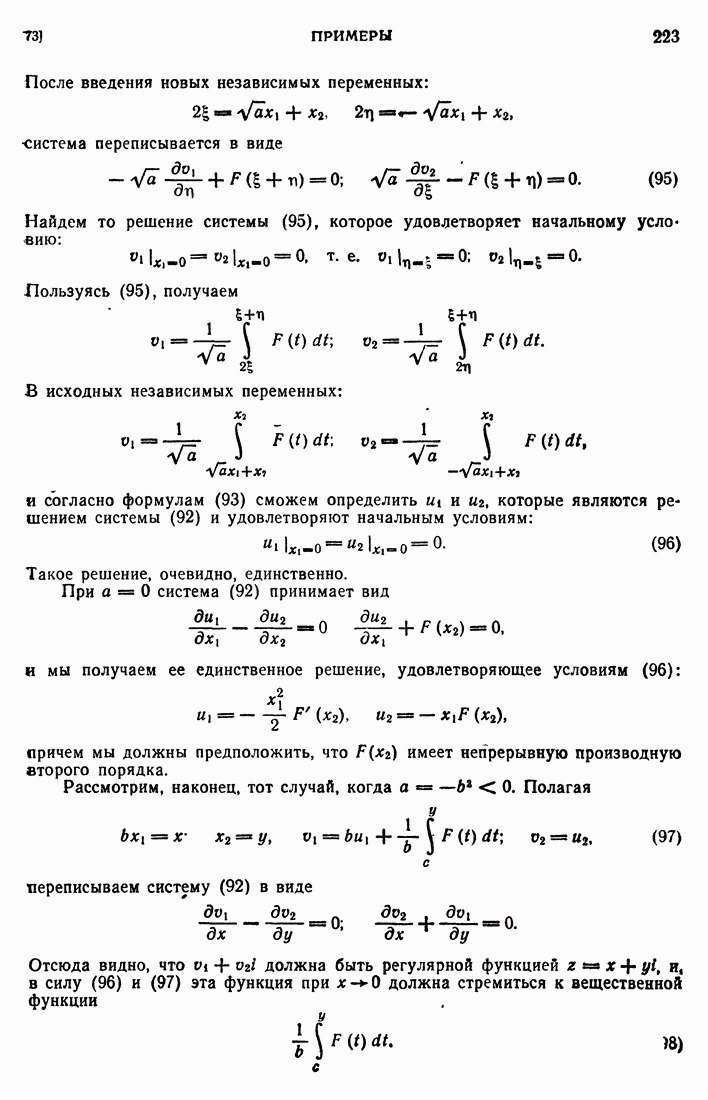
где  собственные числа формы
собственные числа формы  символ Кронекера. Тогда, учитывая условие (413) и закон преобразования
символ Кронекера. Тогда, учитывая условие (413) и закон преобразования  при переходе к координатам
при переходе к координатам  получим
получим

Но, как легко проверить,  и поэтому неравенство (439) действительно имеет место для всех точек
и поэтому неравенство (439) действительно имеет место для всех точек  из D. Благодаря (437) и (439) из (435) следует неравенство
из D. Благодаря (437) и (439) из (435) следует неравенство

а из этого неравенства — неравенство

Здесь  произвольное положительное число,
произвольное положительное число,  — произвольное число из
— произвольное число из  При
При  и (440) примет вид
и (440) примет вид

До сих пор мы не использовали обращение и в нуль на S. Покажем, что если воспользоваться этим условием, то интеграл
может быть преобразован к виду, не содержащему вторые производные и по  . Этот факт является центральным при выводе неравенства (434). Чтобы доказать это, рассмотрим произвольную точку
. Этот факт является центральным при выводе неравенства (434). Чтобы доказать это, рассмотрим произвольную точку  на поверхности
на поверхности  и введем в ней местные декартовы координаты
и введем в ней местные декартовы координаты  , т. е. такие, что ось
, т. е. такие, что ось  направлена по внешней нормали
направлена по внешней нормали  к
к  в точке
в точке  и матрица
и матрица  -ортогональна. Пусть
-ортогональна. Пусть  есть уравнение поверхности S в окрестности начала координат
есть уравнение поверхности S в окрестности начала координат  . По условию, функция
. По условию, функция  . В силу ортогональности матрицы
. В силу ортогональности матрицы  имеем
имеем  , и потому
, и потому  . Рассмотрим выражение
. Рассмотрим выражение  в точке
в точке  и перейдем в нем к координатам у.
и перейдем в нем к координатам у.

где

Используем теперь граничное условие  . Вблизи точки
. Вблизи точки  , координаты
, координаты  которой равны нулю, это условие имеет вид
которой равны нулю, это условие имеет вид

причем оно выполняется тождественно по  вблизи
вблизи  . Продифференцируем это тождество по
. Продифференцируем это тождество по  и учтем, что в точке
и учтем, что в точке  точке
точке  это даст
это даст

 Благодаря
Благодаря 

При  и произвольном q, а также при
и произвольном q, а также при  и произвольном
и произвольном  члены, стоящие в круглой скобке (444) взаимно сокращаются, что вместе с (443) дает для
члены, стоящие в круглой скобке (444) взаимно сокращаются, что вместе с (443) дает для  представление
представление

Будем считать, что координаты  в касательной плоскости к S в точке
в касательной плоскости к S в точке  выбраны так, что все смешанные
выбраны так, что все смешанные
производные  в точке
в точке  равны нулю (этого, как известно, всегда можно добиться за счет ортогонального преобразования координат
равны нулю (этого, как известно, всегда можно добиться за счет ортогонального преобразования координат  ). Тогда
). Тогда

В силу предположения:  найдется такое неотрицательное число К, что
найдется такое неотрицательное число К, что

для всех точек  поверхности S. Если, в частности, D есть выпуклая область, то в качестве К можно взять нуль. Из условия (413) следует, что
поверхности S. Если, в частности, D есть выпуклая область, то в качестве К можно взять нуль. Из условия (413) следует, что  и поэтому
и поэтому

Благодаря этому из неравенства (441) получаем

Для оценки граничного интеграла при  воспользуемся неравенством (428), взяв в нем
воспользуемся неравенством (428), взяв в нем  :
:

где  — любое положительное число. Постоянная
— любое положительное число. Постоянная  равна константе С из (428). Подставим в (449) эту оценку гранитного
равна константе С из (428). Подставим в (449) эту оценку гранитного
интеграла, взяв  и приведем подобные члены:
и приведем подобные члены:

Прибавив к обеим ее частям член  получим
получим

С другой стороны, для любой функции  справедливы соотношения
справедливы соотношения

 . Используем его с
. Используем его с  для оценки сверху члена
для оценки сверху члена  имеющегося в правой части (451). В результате этого элементарные преобразования приведут нас к неравенству
имеющегося в правой части (451). В результате этого элементарные преобразования приведут нас к неравенству

из которого следует интересующее нас неравенство (434). Как сказано выше, все постоянные. С, определяются D и известными нам параметрами из условий (413), (433). Они могут быть выписаны явно, что легко сделать, следуя только что приведенному выводу неравенства (434).
Если и есть решение задачи (403) из пространства  то благодаря неравенству (434) мы можем оценить его норму в
то благодаря неравенству (434) мы можем оценить его норму в  через
через  , а именно:
, а именно:

Если же  таково, что выполняется неравенство (420), то отсюда и из (421) следует возможность оценить
таково, что выполняется неравенство (420), то отсюда и из (421) следует возможность оценить  только через
только через  :
:

Замечание. Из данного нами доказательства неравенства  видно, что от области D были использованы лишь две характеристики: постоянная С из (428) и постоянная К из (447), причем условие (447) может нарушаться в отдельных точках S и даже на целых множествах точек S поверхностной меры нуль.
видно, что от области D были использованы лишь две характеристики: постоянная С из (428) и постоянная К из (447), причем условие (447) может нарушаться в отдельных точках S и даже на целых множествах точек S поверхностной меры нуль.
Весь вывод сохраняется для широкого класса областей D (например, для любых многогранников).
Неравенство (434) и приведенный здесь вывод взят из работы О. А. Ладыженской (ДАН СССР, 1951, 79, с. 723—725). Такое же неравенство было установлено ею и для общих однородных краевых условии вида L — где означает дифференцирование по направлению, не касающемуся поверхности S и гладко меняющемуся при переходе от одной точки поверхности к другой. Более того, были даны оценки, обобщающие неравенство (434) на случай производных и любого порядка (полные доказательства имеются в книге: Ладыженская О. А. Смешанная задача для гиперболического уравнения. — М.: Гостехиздат, 1953). Неравенство (434) для первого краевого условия (т. е. для  ) независимо от О. А. Ладыженской и другим способом было доказано Каччопполи (Giorn. Mat. Battaglini, 1950-51, 80, p. 186-212). Частный случай (434), когда D есть круг, извлекается из работ С. Н. Бернштейна (Math. Ann., 1906, 62, S. 253-271; 1910, 69, S. 82-131). Примечательной особенностью двумерного случая является то, что неравенство (434) место для операторов
) независимо от О. А. Ладыженской и другим способом было доказано Каччопполи (Giorn. Mat. Battaglini, 1950-51, 80, p. 186-212). Частный случай (434), когда D есть круг, извлекается из работ С. Н. Бернштейна (Math. Ann., 1906, 62, S. 253-271; 1910, 69, S. 82-131). Примечательной особенностью двумерного случая является то, что неравенство (434) место для операторов

старшие коэффициенты  которых могут быть произвольными
которых могут быть произвольными  измеримыми функциями, удовлетворяющими лишь условиям (413). Этот факт доказывается с помощью приема С. Н. Бернштейна, сводящего данный вопрос для L к аналогичному вопросу для оператора Лапласа, и приема О. А. Ладыженской преобразования и оценки контурного интеграла
измеримыми функциями, удовлетворяющими лишь условиям (413). Этот факт доказывается с помощью приема С. Н. Бернштейна, сводящего данный вопрос для L к аналогичному вопросу для оператора Лапласа, и приема О. А. Ладыженской преобразования и оценки контурного интеграла  изложенного выше. При размерности пространства
изложенного выше. При размерности пространства  большей двух, прием С. Н. Бернштейна не работает и, оказывается, для справедливости неравенства (434) необходимо накладывать те или иные дополнительные ограничения на коэффициенты
большей двух, прием С. Н. Бернштейна не работает и, оказывается, для справедливости неравенства (434) необходимо накладывать те или иные дополнительные ограничения на коэффициенты  нас — это условие
нас — это условие  ) (см. по этому поводу главы I и III книги; Ладыженская О. А., Уральцева Н. Н. Линейные и квазилинейные уравнения эллиптического типа. — М.: Наука, 1973).
) (см. по этому поводу главы I и III книги; Ладыженская О. А., Уральцева Н. Н. Линейные и квазилинейные уравнения эллиптического типа. — М.: Наука, 1973).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.