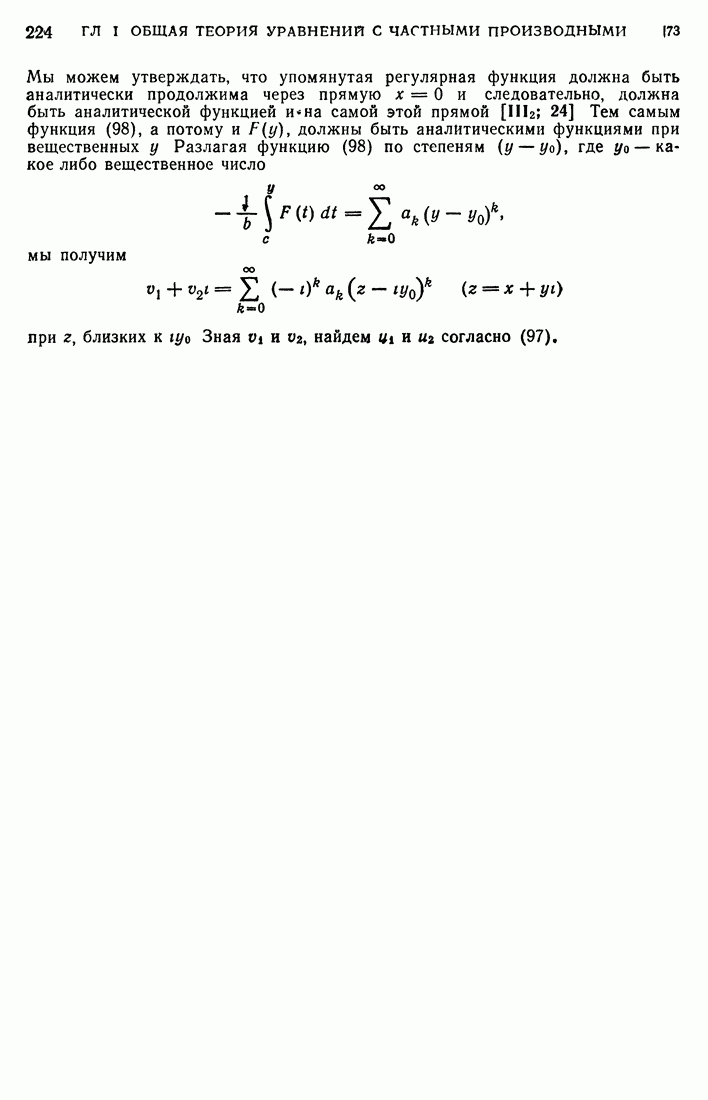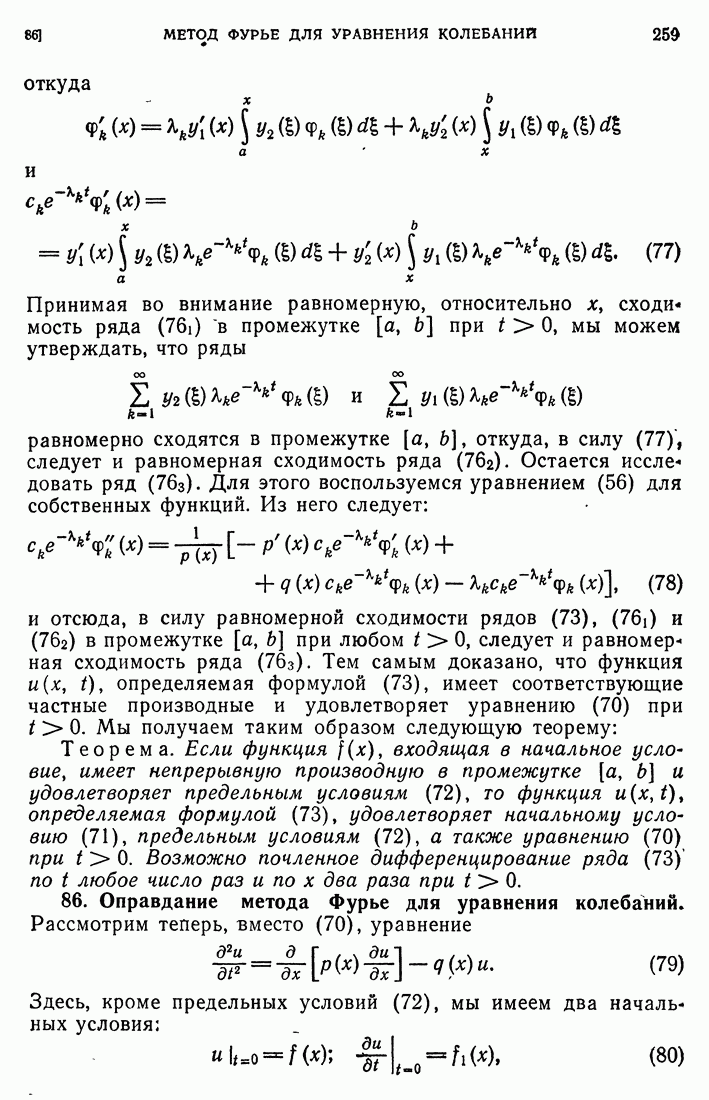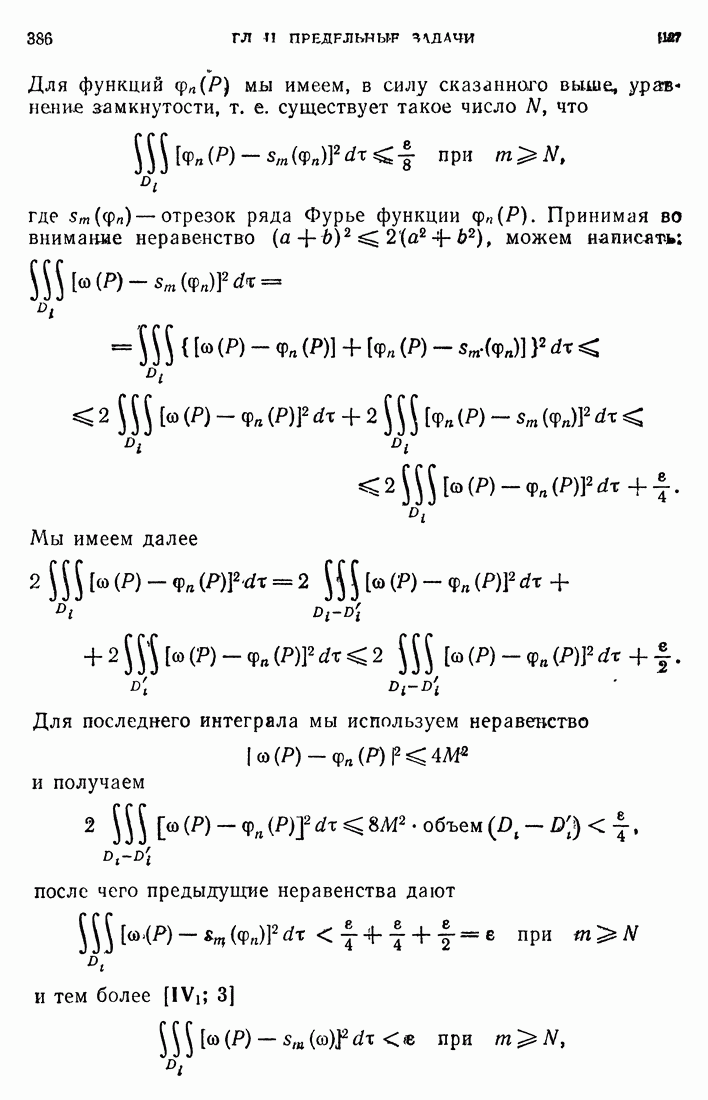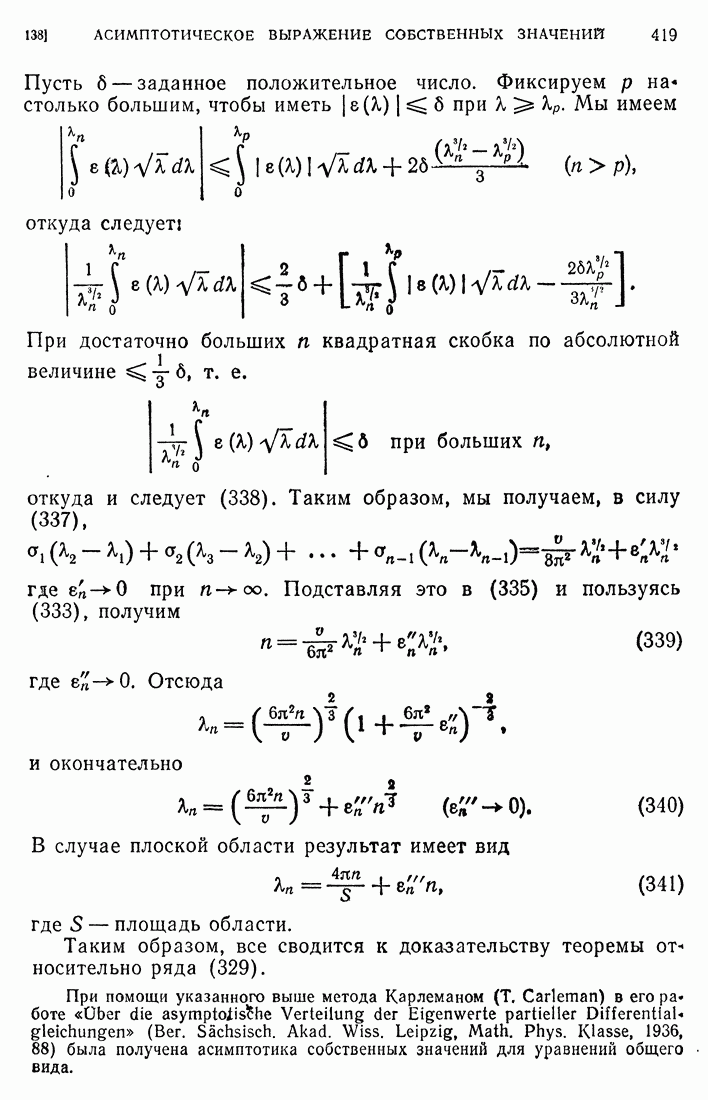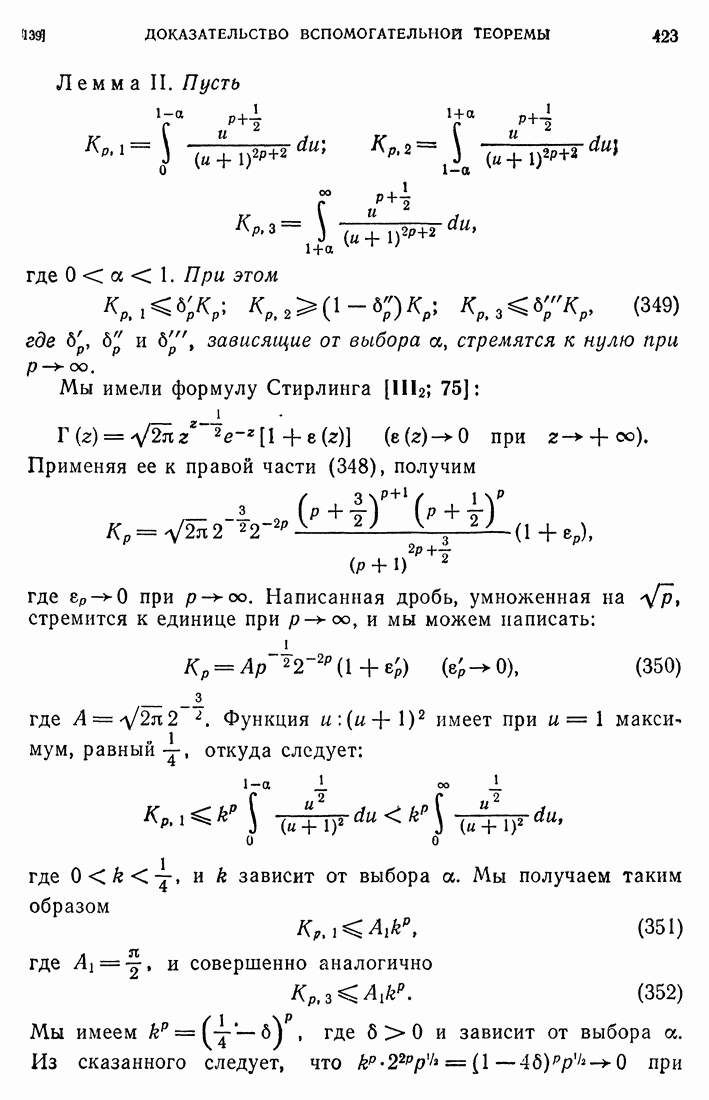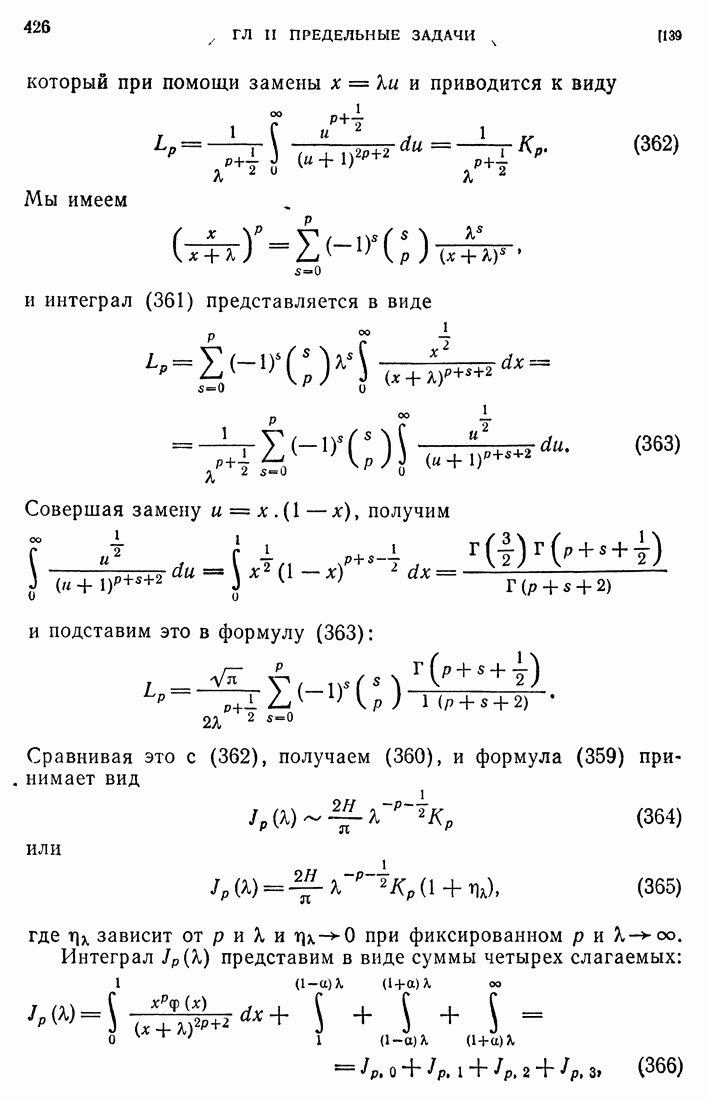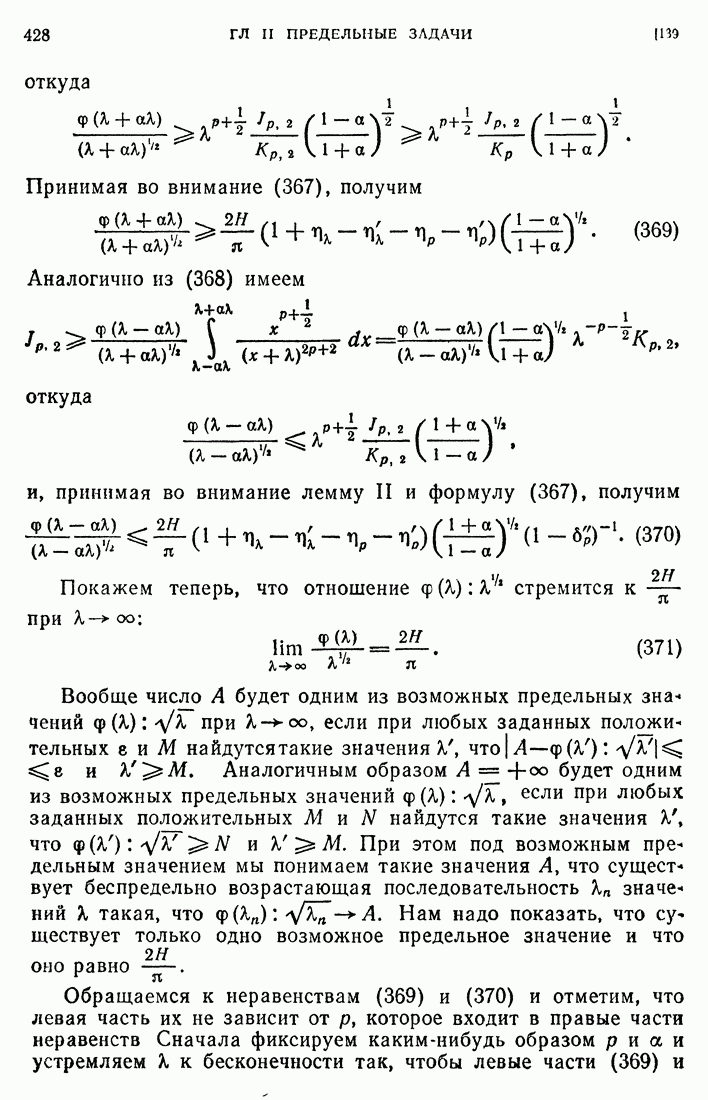| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
105. Внешние задачи в случае плоскости.
Функцию  гармоническую в окрестности бесконечно далекой точки, мы назовем регулярной в бесконечно далекой точке, если при стремлении точки М к бесконечности функция
гармоническую в окрестности бесконечно далекой точки, мы назовем регулярной в бесконечно далекой точке, если при стремлении точки М к бесконечности функция  имеет конечный предел. Выясним смысл этого определения. Построим в окрестности бесконечно далекой точки функцию
имеет конечный предел. Выясним смысл этого определения. Построим в окрестности бесконечно далекой точки функцию  гармонически сопряженную с
гармонически сопряженную с  . При обходе бесконечно далекой точки против часовой стрелки функция
. При обходе бесконечно далекой точки против часовой стрелки функция  может приобрести постоянное слагаемое, которое мы обозначим через у. Функция комплексного переменного
может приобрести постоянное слагаемое, которое мы обозначим через у. Функция комплексного переменного

будет однозначной и регулярной в окрестности бесконечно далекой точки и, следовательно, должна разлагаться в этой окрестности в ряд Лорана по целым степеням  . Покажем, что в этом разложении вовсе нет членов с положительными степенями
. Покажем, что в этом разложении вовсе нет членов с положительными степенями  . Действительно, если бы таких членов было бы бесконечное множество, то функция
. Действительно, если бы таких членов было бы бесконечное множество, то функция  при
при  могла бы принимать значения, сколь угодно близкие к любому наперед заданному числу
могла бы принимать значения, сколь угодно близкие к любому наперед заданному числу  а на самом деле вещественная часть функции, т. е.
а на самом деле вещественная часть функции, т. е.  или стремится к бесконечности, если
или стремится к бесконечности, если  так как, по условию,
так как, по условию,  имеет конечный предел, или имеет конечный предел при
имеет конечный предел, или имеет конечный предел при  если
если 
Если бы членов с положительными степенями было конечное число, т. е. если бы

то мы имели бы

( вещественной части).
вещественной части).
Если разделить обе части равенства на  и устремить
и устремить  к бесконечности при фиксированном
к бесконечности при фиксированном  то левая часть будет очевидно стремиться к нулю, а правая будет иметь предел
то левая часть будет очевидно стремиться к нулю, а правая будет иметь предел  зависящий от
зависящий от  который не всегда равен нулю. Мы придем, таким образом, к противоречию и, следовательно, в разложении
который не всегда равен нулю. Мы придем, таким образом, к противоречию и, следовательно, в разложении  будеттолько свободный член и члены с отрицательными степенями:
будеттолько свободный член и члены с отрицательными степенями:

При  функция
функция  имеет конечный и определенный предел
имеет конечный и определенный предел  и отсюда непосредственно вытекает, что постоянная
и отсюда непосредственно вытекает, что постоянная
у должна быть равна нулю, т. е. если  регулярна в бесконечно далекой точке и
регулярна в бесконечно далекой точке и  сопряженная функция, то
сопряженная функция, то  имеет в окрестности бесконечно далекой точки разложение (105). Из предыдущих рассуждений непосредственно вытекает, что для получения этого результата достаточно предположить, что
имеет в окрестности бесконечно далекой точки разложение (105). Из предыдущих рассуждений непосредственно вытекает, что для получения этого результата достаточно предположить, что  просто ограничена по абсолютной величине в окрестности бесконечно далекой точки. Отсюда уже будет вытекать разложение (105) и, тем самым, существование конечного предела
просто ограничена по абсолютной величине в окрестности бесконечно далекой точки. Отсюда уже будет вытекать разложение (105) и, тем самым, существование конечного предела  при стремлении точки М к бесконечности.
при стремлении точки М к бесконечности.
Внешняя задача Дирихле сводится к нахождению функцин  гармонической вне замкнутого контура l, регулярной
гармонической вне замкнутого контура l, регулярной  бесконечности и принимающей на контуре
бесконечности и принимающей на контуре  заданные значения
заданные значения  Пусть
Пусть  — некоторая точка, находящаяся внутри
— некоторая точка, находящаяся внутри  Совершим конформное преобразование плоскости
Совершим конформное преобразование плоскости 
Часть плоскости, находящаяся вне l, перейдет в некоторую ограниченную область В, гармонические функции перейдут в гармонические функции  , точка
, точка  перейдет в
перейдет в  будет регулярной функцией от w при
будет регулярной функцией от w при  Формулированная выше внешняя задача Дирихле перейдет во внутреннюю задачу для преобразованной области, и мы, очевидно, можем иметь только одно решение поставленной задачи.
Формулированная выше внешняя задача Дирихле перейдет во внутреннюю задачу для преобразованной области, и мы, очевидно, можем иметь только одно решение поставленной задачи.
Пользуясь разложением (105), дифференцируя его по z и принимая во внимание, что

мы можем утверждать, что если гармоническая функция  регулярна в бесконечно далекой точке, то произведения
регулярна в бесконечно далекой точке, то произведения  и
и  где
где  остаются ограниченными при беспредельном удалении точки М. Отсюда непосредственно вытекает, что и произведение
остаются ограниченными при беспредельном удалении точки М. Отсюда непосредственно вытекает, что и произведение  где m — любое направление, которое может и изменяться при перемещении точки М, остается ограниченным при беспредельном удалении точки М. Если В есть часть плоскости, находящаяся вне замкнутого контура
где m — любое направление, которое может и изменяться при перемещении точки М, остается ограниченным при беспредельном удалении точки М. Если В есть часть плоскости, находящаяся вне замкнутого контура  функции, гармонические в В, непрерывные в бесконечно далекой точке и непрерывные вместе с производными первого порядка вплоть до контура, то имеют место формулы
функции, гармонические в В, непрерывные в бесконечно далекой точке и непрерывные вместе с производными первого порядка вплоть до контура, то имеют место формулы

где n — направление нормали к  внешней по отношению к области В. Формулы доказываются совершенно так же, как это делалось в [102] для трехмерного случая. Достаточно иметь в виду, что на окружности С с центром в фиксированной точке О и радиусом R произведения v и и имеют оценку а длина окружности
внешней по отношению к области В. Формулы доказываются совершенно так же, как это делалось в [102] для трехмерного случая. Достаточно иметь в виду, что на окружности С с центром в фиксированной точке О и радиусом R произведения v и и имеют оценку а длина окружности  . Как и в [102], формулы (106) и (107) остаются справедливыми, если вместо непрерывности производных первого порядка вплоть до
. Как и в [102], формулы (106) и (107) остаются справедливыми, если вместо непрерывности производных первого порядка вплоть до  потребовать существования правильных нормальных производных
потребовать существования правильных нормальных производных  .
.
Переходим к внешней задаче Неймана, когда на l имеется предельное условие

при стремлении М к N по нормали, и сохраняется требование регулярности функции  на бесконечности. Пусть решение задачи
на бесконечности. Пусть решение задачи  существует, и предположим, что
существует, и предположим, что  имеет правильную нормальную производную на
имеет правильную нормальную производную на  Проводя окружность С достаточно большого радиуса R и применяя формулу (107) к
Проводя окружность С достаточно большого радиуса R и применяя формулу (107) к  для области, ограниченной l и С, получим
для области, ограниченной l и С, получим

Но на С производная имеет порядок  откуда следует, что интеграл по С стремится к нулю при и мы получаем в пределе, в силу (108),
откуда следует, что интеграл по С стремится к нулю при и мы получаем в пределе, в силу (108),

Это необходимое условие мы получили и для внутренней задачи Неймана. Пользуясь формулой (106), можно доказать единственность решения внешней задачи Неймана при условии правильности нормальной производной  . В трехмерном пространстве мы
. В трехмерном пространстве мы  будем иметь условия, аналогичного (110) для разрешимости внешней задачи Неймана.
будем иметь условия, аналогичного (110) для разрешимости внешней задачи Неймана.
Отметим тот факт, что основное сингулярное решение  не будет регулярным в бесконечно далекой точке. При
не будет регулярным в бесконечно далекой точке. При  оно стремится к
оно стремится к  . Второе сингулярное решение
. Второе сингулярное решение  , соответствующее диполю, уже будет регулярным в бесконечно далекой точке, и оно обращается в этой точке в нуль, В трехмерном
, соответствующее диполю, уже будет регулярным в бесконечно далекой точке, и оно обращается в этой точке в нуль, В трехмерном
пространстве не только потенциал диполя, но и основное сингулярное решение у обращается в бесконечно далекой точке в нуль.
Потенциал простого слоя (81), дающий гармоническую функцию вне  не будет, вообще говоря, регулярным в бесконечно далекой точке. Если общий заряд равен нулю, т. е. если
не будет, вообще говоря, регулярным в бесконечно далекой точке. Если общий заряд равен нулю, т. е. если

то в этом частном случае потенциал (81) будет регулярным. Действительно, пусть R — расстояние точки М до начала. Вводя в интеграл (111) множитель  не зависящий от переменной точки интегрирования N, мы можем написать потенциал (81) в виде
не зависящий от переменной точки интегрирования N, мы можем написать потенциал (81) в виде

и при беспредельном удалении точки М выражение  стремится к нулю равномерно по отношению к точкам
стремится к нулю равномерно по отношению к точкам  лежащим на l. Таким образом, мы видим, что потенциал действительно будет регулярным в бесконечно далекой точке и равным нулю.
лежащим на l. Таким образом, мы видим, что потенциал действительно будет регулярным в бесконечно далекой точке и равным нулю.
Докажем еще одно свойство гармонических функций. Положим, что  гармоническая функция в некотором круге, центр которого примем за начало координат
гармоническая функция в некотором круге, центр которого примем за начало координат  кроме, может быть, самого начала, и ограничена по абсолютной величине в этом круге. Покажем, что существует предел
кроме, может быть, самого начала, и ограничена по абсолютной величине в этом круге. Покажем, что существует предел  при
при  и если принять этот предел за значение
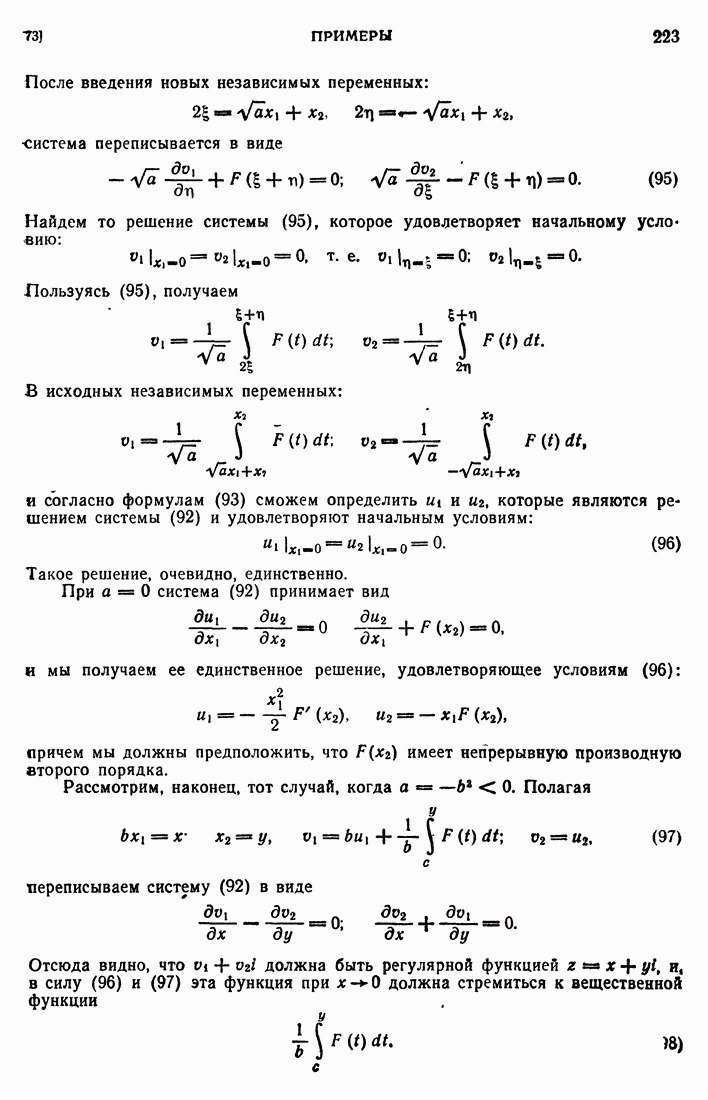
и если принять этот предел за значение  , то
, то  будет гармонической во всем круге, включая начало. Чтобы убедиться в этом, достаточно проделать те рассуждения, которые привели нас к разложению (105), заменив бесконечно далекую точку началом. Вместо (105) будем иметь
будет гармонической во всем круге, включая начало. Чтобы убедиться в этом, достаточно проделать те рассуждения, которые привели нас к разложению (105), заменив бесконечно далекую точку началом. Вместо (105) будем иметь

откуда и следует наше утверждение.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.