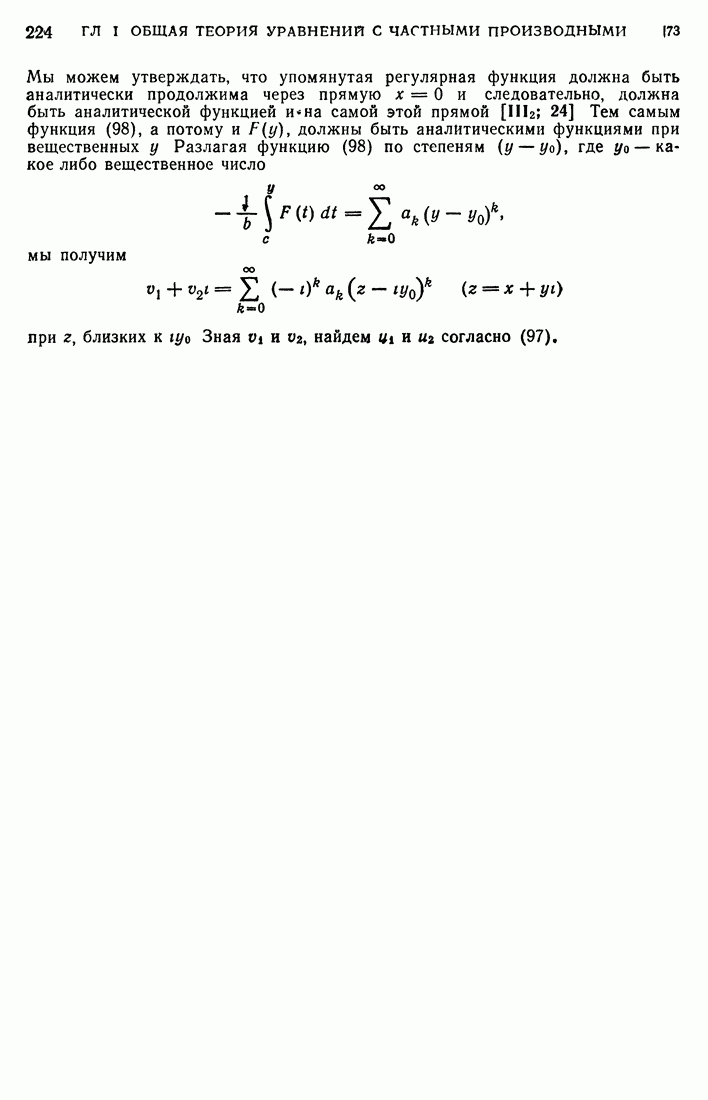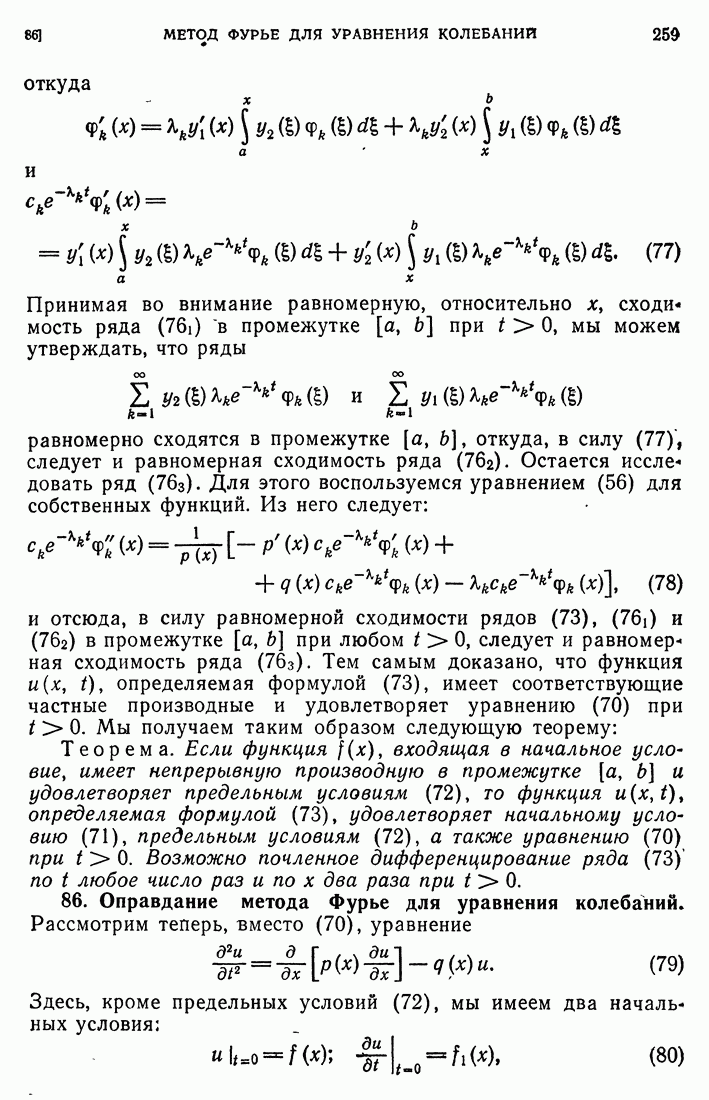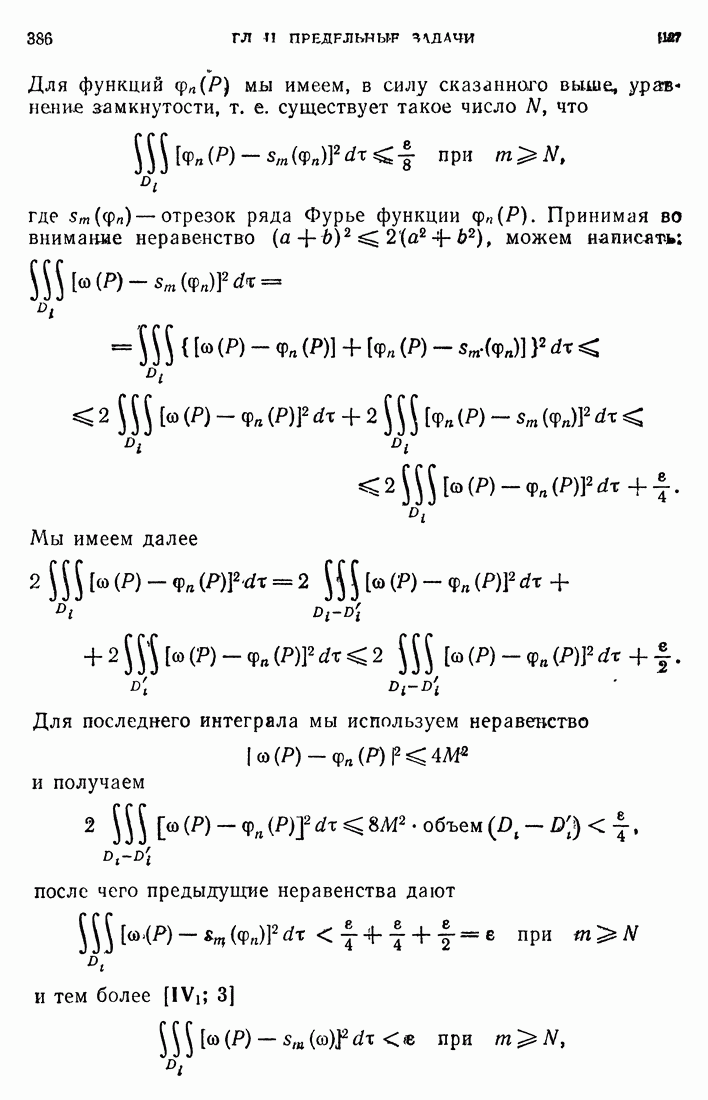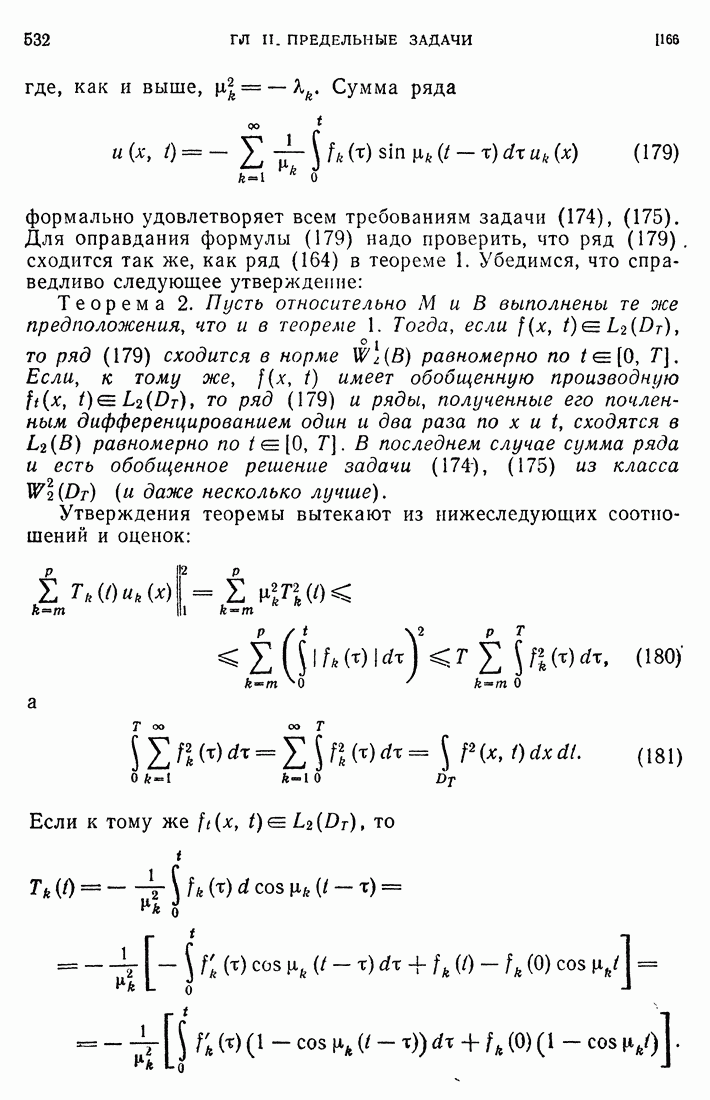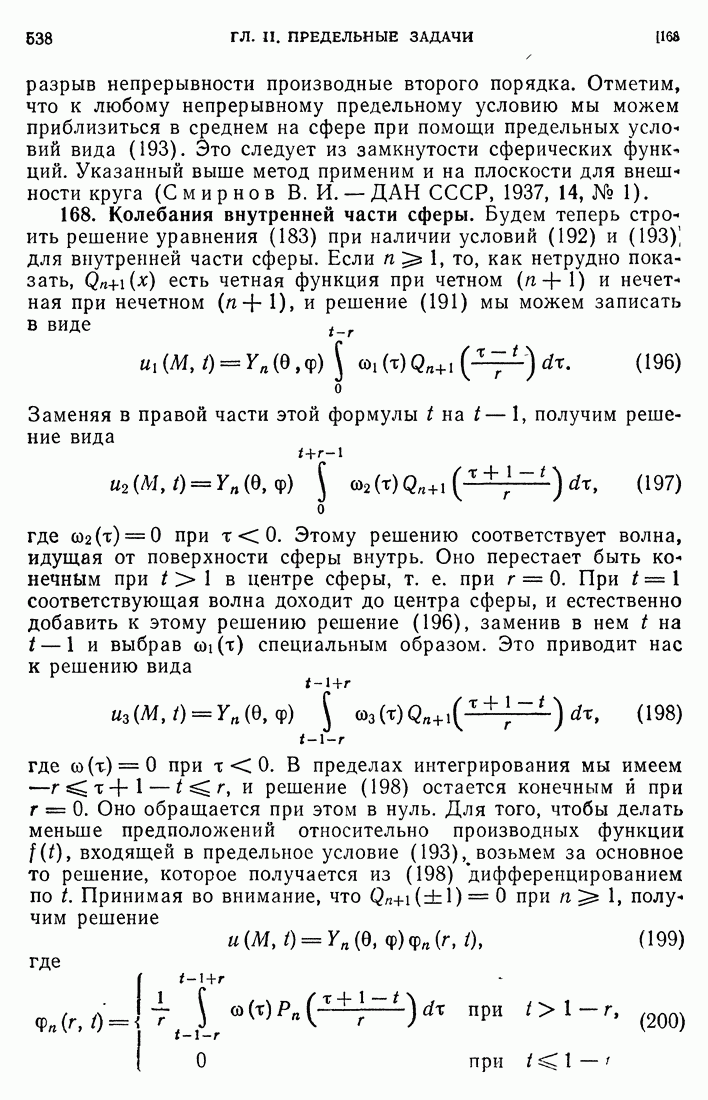| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
124. Функция Грина в случае плоскости.
Рассмотрение функции Грина на плоскости представляет некоторые особенности по сравнению со случаем пространства. Мы будем рассматривать функцию Грина для ограниченной области  с контуром
с контуром  при предельном условии (189) на
при предельном условии (189) на 
Определим, как и в [123], функцию  на плоскости:
на плоскости:

Построим, как это мы делали в [123], потенциал простого слоя;

где  есть расстояние от Р до переменной точки N на
есть расстояние от Р до переменной точки N на  . Предельные значения его нормальной производной на
. Предельные значения его нормальной производной на  со стороны
со стороны  равны
равны

где  — направление MQ и
— направление MQ и  — направление нормали к
— направление нормали к  в точке М, внешней по отношению к замкнутому контуру
в точке М, внешней по отношению к замкнутому контуру  Составим теперь гармоническую в
Составим теперь гармоническую в  функцию
функцию

имеющую правильную нормальную производную на  равную нулю. Проведем внутри
равную нулю. Проведем внутри  какой-либо замкнутый обходящий вокруг
какой-либо замкнутый обходящий вокруг  контур
контур  , и применим формулу Грина при
, и применим формулу Грина при  к области, ограниченной
к области, ограниченной  . Мы имеем
. Мы имеем

причем в обоих случаях  — есть внешняя нормаль по отношению к замкнутому контуру. Отсюда, в силу того, что
— есть внешняя нормаль по отношению к замкнутому контуру. Отсюда, в силу того, что 

Но

где  есть направление
есть направление  направление
направление  . Интегрируя по l, меняя порядок интегрирования
. Интегрируя по l, меняя порядок интегрирования  и принимая во внимание, что точки Q и N находятся внутри
и принимая во внимание, что точки Q и N находятся внутри  получим, в силу (83),
получим, в силу (83),

Мы можем теперь переписать (209) в виде

При беспредельном удалении точки Р отношение  равномерно стремится к единице, т. е. при любом заданном положительном
равномерно стремится к единице, т. е. при любом заданном положительном  существует такое положительное число М, что
существует такое положительное число М, что  при любом положении N на
при любом положении N на  если только
если только 
Таким образом, функция (211), гармоническая в  имеет на l правильную нормальную производную, равную нулю, и стремится к нулю при беспредельном удалении точки Р. К такой функции применима формула
имеет на l правильную нормальную производную, равную нулю, и стремится к нулю при беспредельном удалении точки Р. К такой функции применима формула

из которой следует, что  т. е.
т. е.

Отсюда, как и в [123], непосредственно следует, что потенциал простого слоя (207) совпадает с функцией  определенной равенством (206), на всей плоскости, и можно утверждать, что
определенной равенством (206), на всей плоскости, и можно утверждать, что  имеет на l правильную нормальную производную. Далее, как и в [123], можно утверждать, что
имеет на l правильную нормальную производную. Далее, как и в [123], можно утверждать, что  имеет в
имеет в  непрерывные производные первого порядка вплоть до L. Доказательство симметричности
непрерывные производные первого порядка вплоть до L. Доказательство симметричности  проводится совершенно так же, как и в [123]. Для круга радиуса R функция Грина имеет вид
проводится совершенно так же, как и в [123]. Для круга радиуса R функция Грина имеет вид

при тех же обозначениях, что и в [123]. Это приводит к следующим оценкам:

Для решения задачи Дирихле в  имеет место формула, аналогичная
имеет место формула, аналогичная 
Функция Грина оператора Лапласа для плоской односвязной области при предельном условии (189) тесно связана с функцией, совершающей конформное преобразование упомянутой об ласти на круг  Пусть В — односвязная область с контуром
Пусть В — односвязная область с контуром  некоторая внутренняя точка этой области. Пусть, далее,
некоторая внутренняя точка этой области. Пусть, далее,  - функция, совершающая кон формное преобразование В на единичный круг, причем
- функция, совершающая кон формное преобразование В на единичный круг, причем  т. е. точка
т. е. точка  переходит в центр упомянутого круга. При не которых условиях гладкости контура
переходит в центр упомянутого круга. При не которых условиях гладкости контура  непрерывна вплотт до окружности
непрерывна вплотт до окружности  и преобразует ее в контур
и преобразует ее в контур 
Из однолистности преобразования вытекает, что  имеет в точке
имеет в точке  простой корень:
простой корень:

Образуем функцию

Нетрудно проверить, что это и будет функция Грина для области В с полюсом  . Действительно,
. Действительно,  представляет собою вещественную часть
представляет собою вещественную часть  и, следовательно, удовлетворяет уравнению Лапласа. Согласно (214), бесконечная часть функции (215) в точке
и, следовательно, удовлетворяет уравнению Лапласа. Согласно (214), бесконечная часть функции (215) в точке  будет
будет  и, наконец контур
и, наконец контур  области В переходит в окружность единичного круга т. е.
области В переходит в окружность единичного круга т. е.  на контуре
на контуре  а функция (215) при этом обращается в нуль.
а функция (215) при этом обращается в нуль.
Обозначим через  функцию, гармонически сопряженную с (215). Мы имеем
функцию, гармонически сопряженную с (215). Мы имеем

и, следовательно, можем выразить  через функцию Грина и сопряженную с ней функцию:
через функцию Грина и сопряженную с ней функцию:

Функция Н определена с точностью до постоянного слагаемого, и тем самым в правой части последней формулы мы имеем произвольный постоянный множитель, по модулю равный единице, что соответствует произвольному повороту единичного круга  вокруг начала.
вокруг начала.
Положим, что контур  области В обладает следующим свойством: угол
области В обладает следующим свойством: угол  образованный касательной к
образованный касательной к  каким-либо фиксированным направлением, как функция длины дуги
каким-либо фиксированным направлением, как функция длины дуги  удовлетворяет условию Липшица
удовлетворяет условию Липшица

где b и  — положительные постоянные. Доказывается, что при этом производная
— положительные постоянные. Доказывается, что при этом производная  непрерывна вплоть до
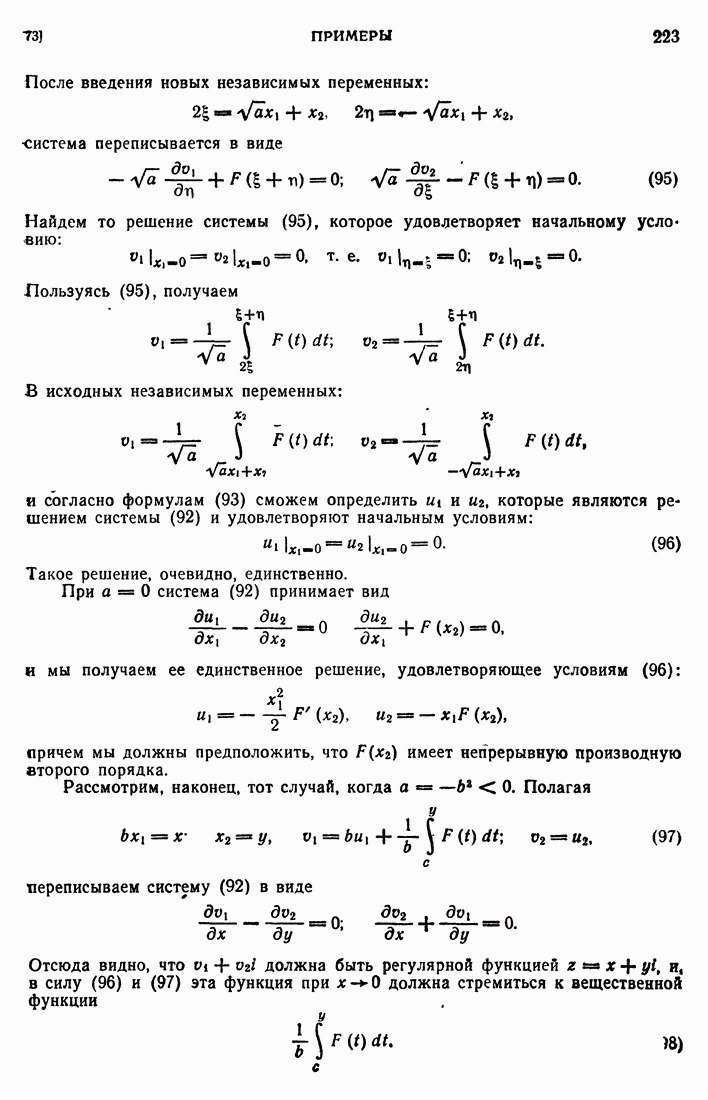
непрерывна вплоть до  и существуют такие две положительные постоянные
и существуют такие две положительные постоянные  и М, что
и М, что

Эти постоянные зависят, конечно, от выбора той точки  которая переходит в начало координат на плоскости w. Зафиксируем эту точку
которая переходит в начало координат на плоскости w. Зафиксируем эту точку  и будем теперь строить общее конформное преобразование В на круг
и будем теперь строить общее конформное преобразование В на круг  при условии, что в начало координат переходит какая-либо точка
при условии, что в начало координат переходит какая-либо точка  , лежащая внутри В. Для этого надо совершить сначала конформное преобразование
, лежащая внутри В. Для этого надо совершить сначала конформное преобразование  а затем преобразовать круг 1 в себя так, чтобы точка
а затем преобразовать круг 1 в себя так, чтобы точка  перешла в начало координат. Это последнее преобразование есть дробно-линейное преобразование, и окончательно мы получаем, отбрасывая постоянный множитель с модулем, равным единице,
перешла в начало координат. Это последнее преобразование есть дробно-линейное преобразование, и окончательно мы получаем, отбрасывая постоянный множитель с модулем, равным единице,

где, как всегда,  знак вещественной части и
знак вещественной части и  - функция Грина области В с полюсом в точке z. Дифференцируя по
- функция Грина области В с полюсом в точке z. Дифференцируя по  где за
где за  можно принять любое направление, получим
можно принять любое направление, получим

или, заменяя вещественную часть модулем,

и, принимая во внимание, что  получим
получим 

Пусть  функция, обратная функции
функция, обратная функции  Она определена в круге
Она определена в круге  . Из (218) следует, что
. Из (218) следует, что  и мы получаем
и мы получаем

причем указанное интегрирование можно производить по прямолинейному отрезку. Последнее неравенство дает  и, принимая во внимание
и, принимая во внимание  получаем, в силу последнего неравенства
получаем, в силу последнего неравенства

где  — расстояние точек z и
— расстояние точек z и  . Таким образом, при сделанном относительно контура I предположении, мы получаем оценку производной функции Грира по любому направлению, зависящую только от расстояния
. Таким образом, при сделанном относительно контура I предположении, мы получаем оценку производной функции Грира по любому направлению, зависящую только от расстояния  .
.
Если область В — многосвязна, и каждый из ограничивающих ее замкну  контуров удоилетворяет указанному выше условию, то можно и в этом случае получить оценку вида (219). Указанное выше доказательство оценки (219), а также и доказательство для многосвязной области, которое я не привожу, было мне сообщено Г. М. Голузиным.
контуров удоилетворяет указанному выше условию, то можно и в этом случае получить оценку вида (219). Указанное выше доказательство оценки (219), а также и доказательство для многосвязной области, которое я не привожу, было мне сообщено Г. М. Голузиным.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
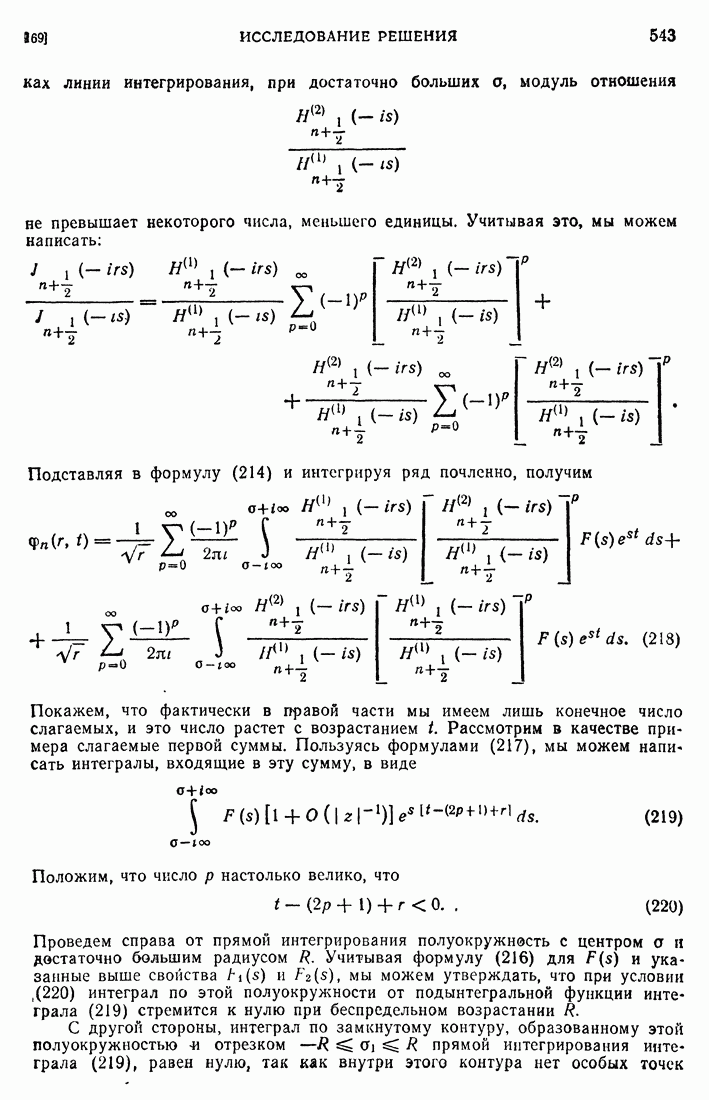
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.