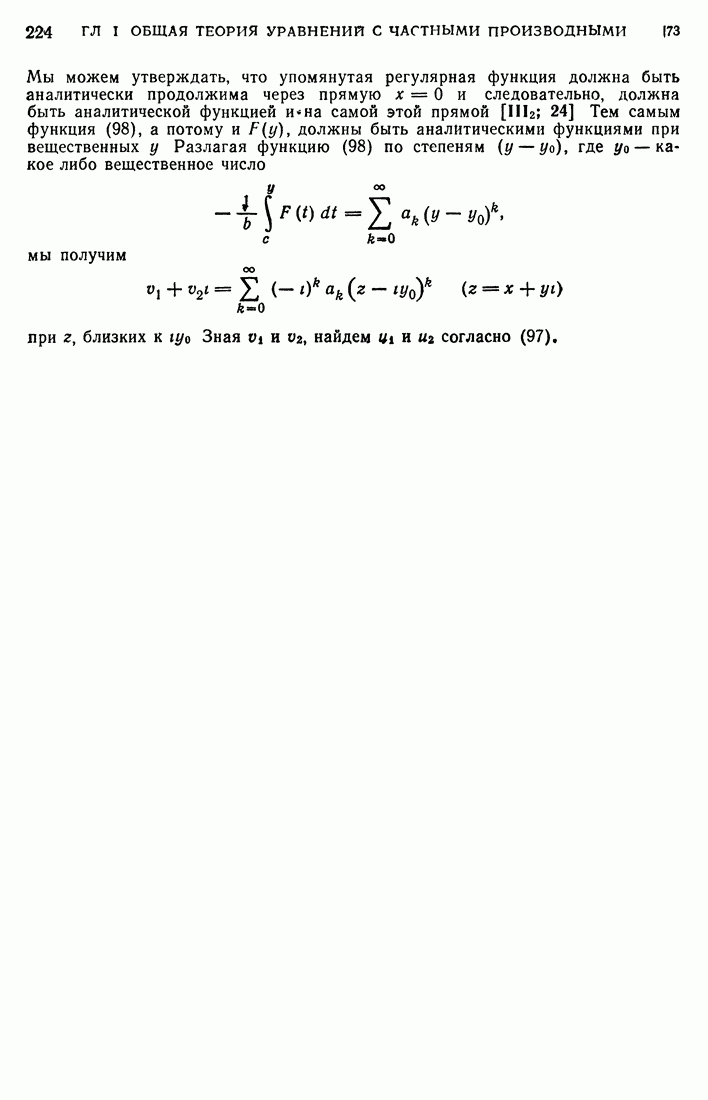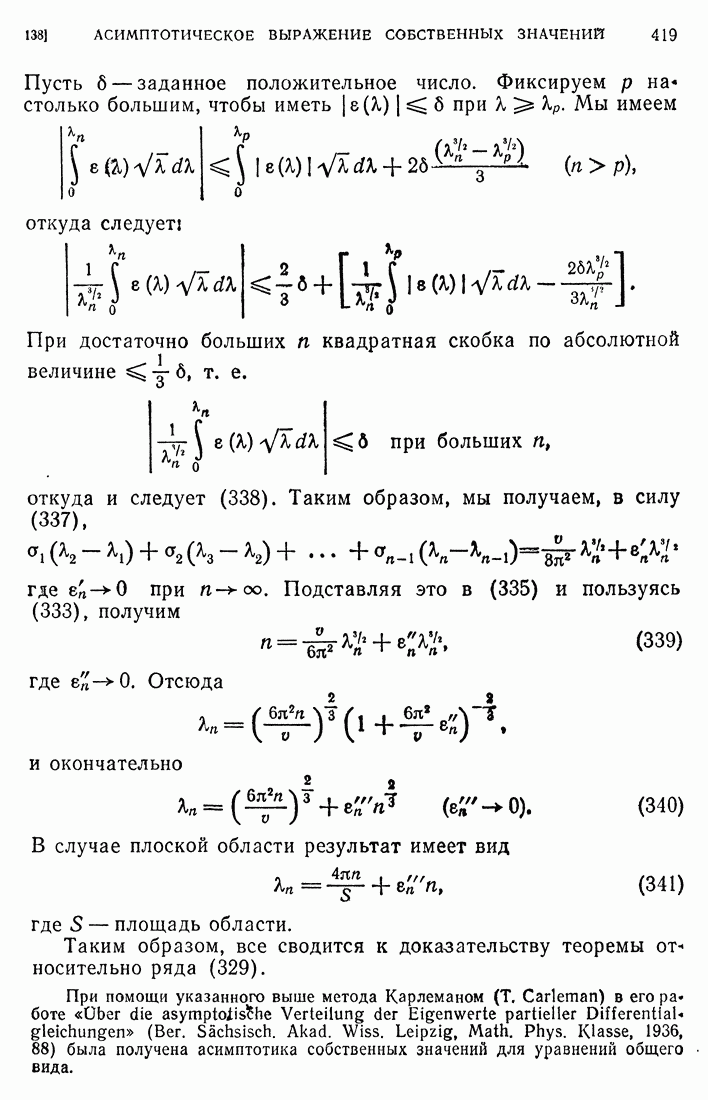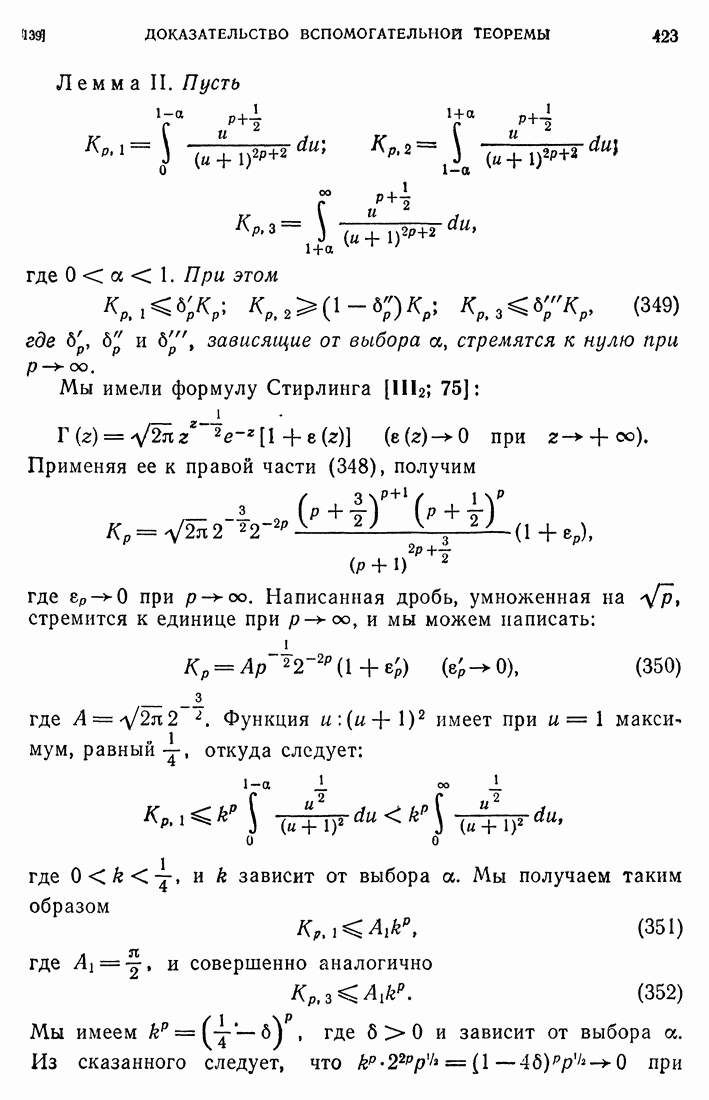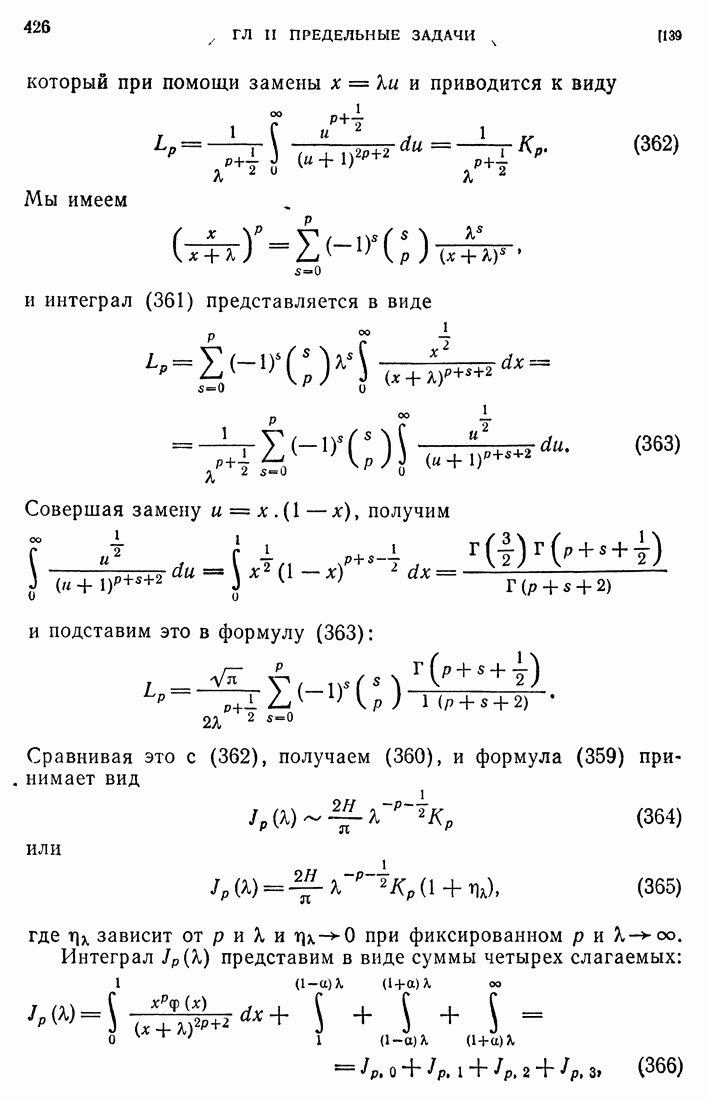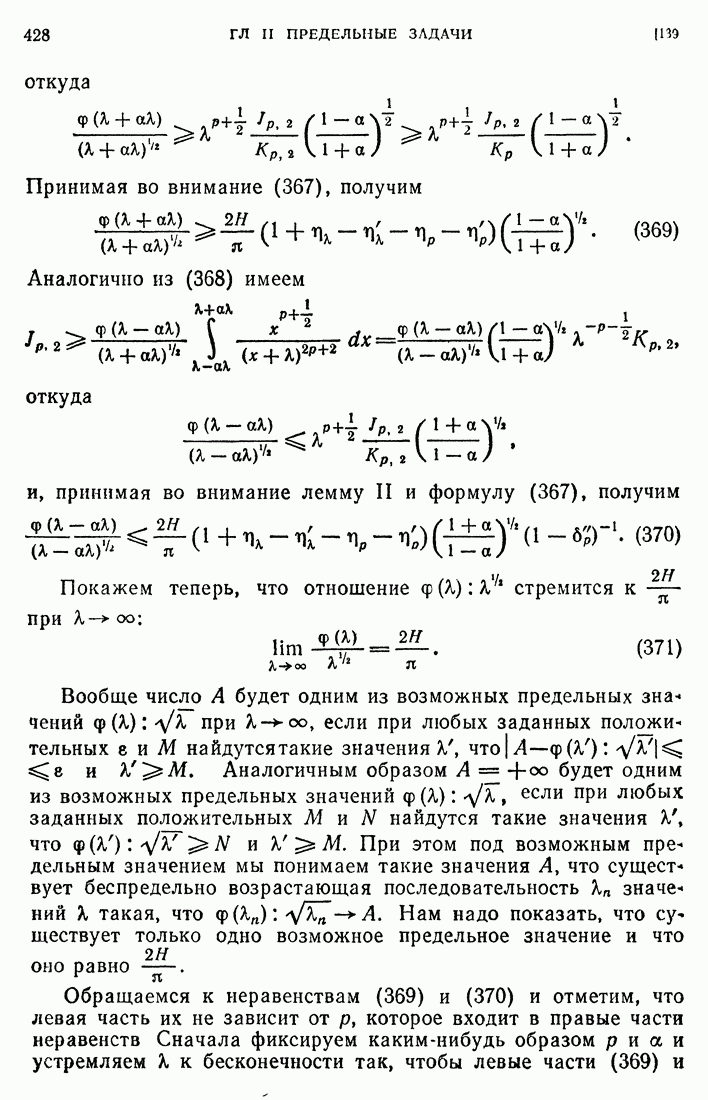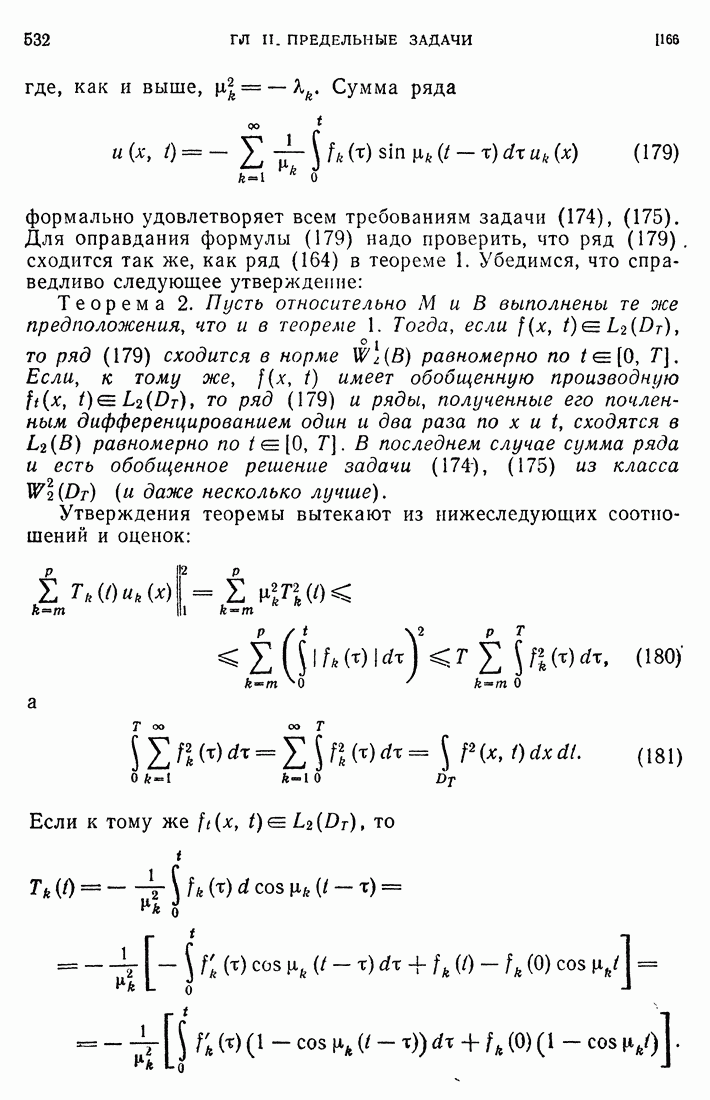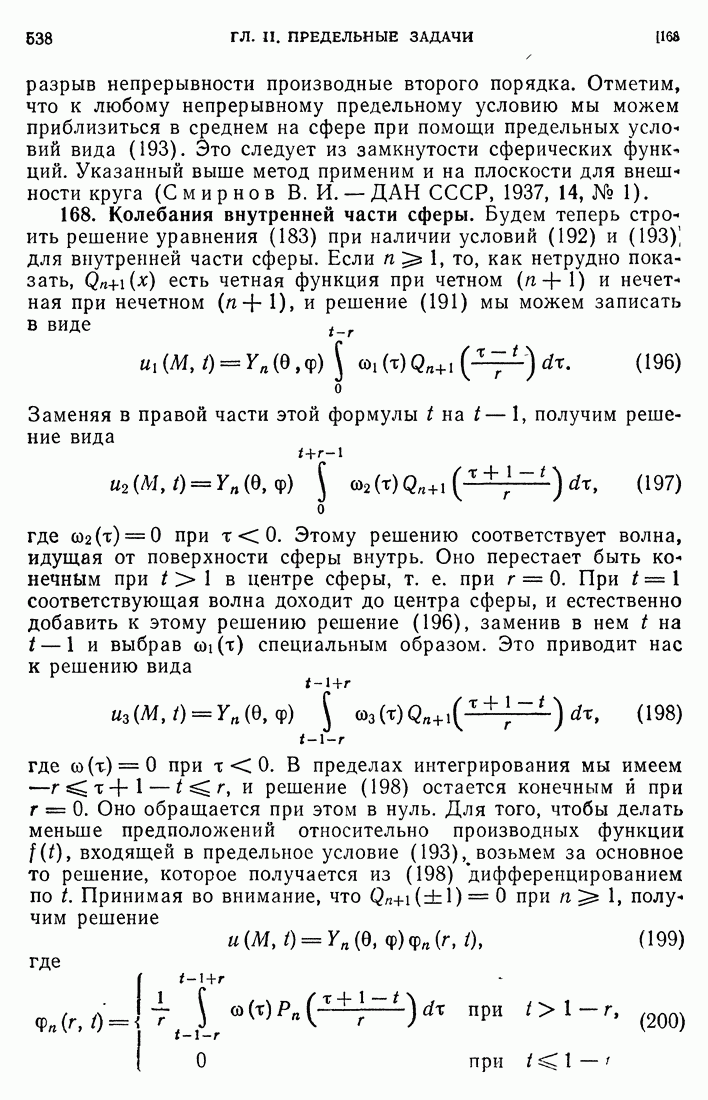| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
150. О спектре симметричного оператора.
Рассмотрим симметричные дифференциальные операторы L вида (402), т. е. такие, для которых оператор L, сопряженный L по Лагранжу (его выражение дается равенством (480)), совпадает с L, Они имеют вид

Изучим для них спектральную задачу

в ограниченной области D, считая, что для коэффициентов L и области D выполнены условия теоремы 2 [148]. Из результатов, доказанных в [149], следует, что для неограниченного оператора L, заданного на плотном множестве  пространства
пространства  равенством (488), сопряженным оператором является он сам с той же областью определения
равенством (488), сопряженным оператором является он сам с той же областью определения  . В этом случае говорят, что L является самосопряженным оператором, и записывают это в виде равенства
. В этом случае говорят, что L является самосопряженным оператором, и записывают это в виде равенства  . Соответствующая ему квадратичная форма
. Соответствующая ему квадратичная форма  имеет вид
имеет вид

Так как по условию  , то при
, то при

где  есть положительная постоянная из неравенства (423) [145]. Согласно результатам [148] для
есть положительная постоянная из неравенства (423) [145]. Согласно результатам [148] для  существует обратный оператор
существует обратный оператор  который является вполне непрерывным, самосопряженным оператором в пространстве
который является вполне непрерывным, самосопряженным оператором в пространстве  Ввиду этого для него справедливы теоремы, доказанные в
Ввиду этого для него справедливы теоремы, доказанные в  . А именно, его спектр (полный) состоит не более чем из счетного числа вещественных чисел, которые мы обозначим через
. А именно, его спектр (полный) состоит не более чем из счетного числа вещественных чисел, которые мы обозначим через  Каждому
Каждому  соответствует конечное число линейно независимых решений уравнения
соответствует конечное число линейно независимых решений уравнения

являющихся элементами  . Так как
. Так как  обратим, то число
обратим, то число  не есть точка спектра
не есть точка спектра  . т. е. ни одно
. т. е. ни одно  не совпадает с нулем), и потому число различных собственных значений
не совпадает с нулем), и потому число различных собственных значений  неограничено. Из свойств оператора
неограничено. Из свойств оператора  следует, что
следует, что  принадлежат
принадлежат  и потому любое
и потому любое  есть решение задачи
есть решение задачи

 и, наоборот, любое решение задачи (492), принадлежащее
и, наоборот, любое решение задачи (492), принадлежащее  , есть решение уравнения (491). В свою очередь, задача (492) есть не что иное, как задача (489)
, есть решение уравнения (491). В свою очередь, задача (492) есть не что иное, как задача (489)  Из неравенства (490) следует, что все
Из неравенства (490) следует, что все  отрицательны
отрицательны 
Действительно, для  неравенство (490) дает оценку
неравенство (490) дает оценку

Опять-таки в силу свойств, установленных в  для вполне непрерывных симметрических операторов, собственные числа
для вполне непрерывных симметрических операторов, собственные числа  можно считать занумерованными в порядке их возрастания. Кроме того, каждое собственное значение удобно записывать в последовательности столько раз, какова его кратность, и каждому из них сопоставить одну нормированную в
можно считать занумерованными в порядке их возрастания. Кроме того, каждое собственное значение удобно записывать в последовательности столько раз, какова его кратность, и каждому из них сопоставить одну нормированную в  собственную функцию
собственную функцию  причем выбрать их так, чтобы они все были ортогональны друг другу. В соответствии со сказанным, мы будем считать, что
причем выбрать их так, чтобы они все были ортогональны друг другу. В соответствии со сказанным, мы будем считать, что

и соответствующие им собственные функции удовлетворяют условиям

Спектр оператора L при условии Дирихле состоит из чисел  соответствует собственная функция
соответствует собственная функция  решение задачи (489) при
решение задачи (489) при  . Все функции
. Все функции  как отмечалось выше, суть элементы
как отмечалось выше, суть элементы  . Ясно, что
. Ясно, что  при
при 
Займемся теперь теоремами разложения по системе собственных функций  . Теорема
. Теорема  утверждает, что система
утверждает, что система  образует базис в
образует базис в  , т. е. любая функция f из
, т. е. любая функция f из  разлагается по ней в ряд Фурье
разлагается по ней в ряд Фурье

сходящийся к ней в норме  , и
, и

Покажем теперь, что если  то ряд (495) сходится к ней в норме
то ряд (495) сходится к ней в норме  , т. е. ряд (495) допускает почленное дифференцирование по
, т. е. ряд (495) допускает почленное дифференцирование по  один и два раза и полученные при этом ряды (заметим, что они уже не ортогональны в
один и два раза и полученные при этом ряды (заметим, что они уже не ортогональны в  сходятся в
сходятся в  к соответствующим производным
к соответствующим производным  Для доказательства этого рассмотрим
Для доказательства этого рассмотрим  как гильбертово пространство со скалярным произведением, определенным равенством (432), и нормой
как гильбертово пространство со скалярным произведением, определенным равенством (432), и нормой 
Введем в  новое скалярное произведение
новое скалярное произведение

Соответствующая ему норма, которую мы обозначим через  эквивалентна норме
эквивалентна норме  (см. об этом [147]). Действительно, неравенство
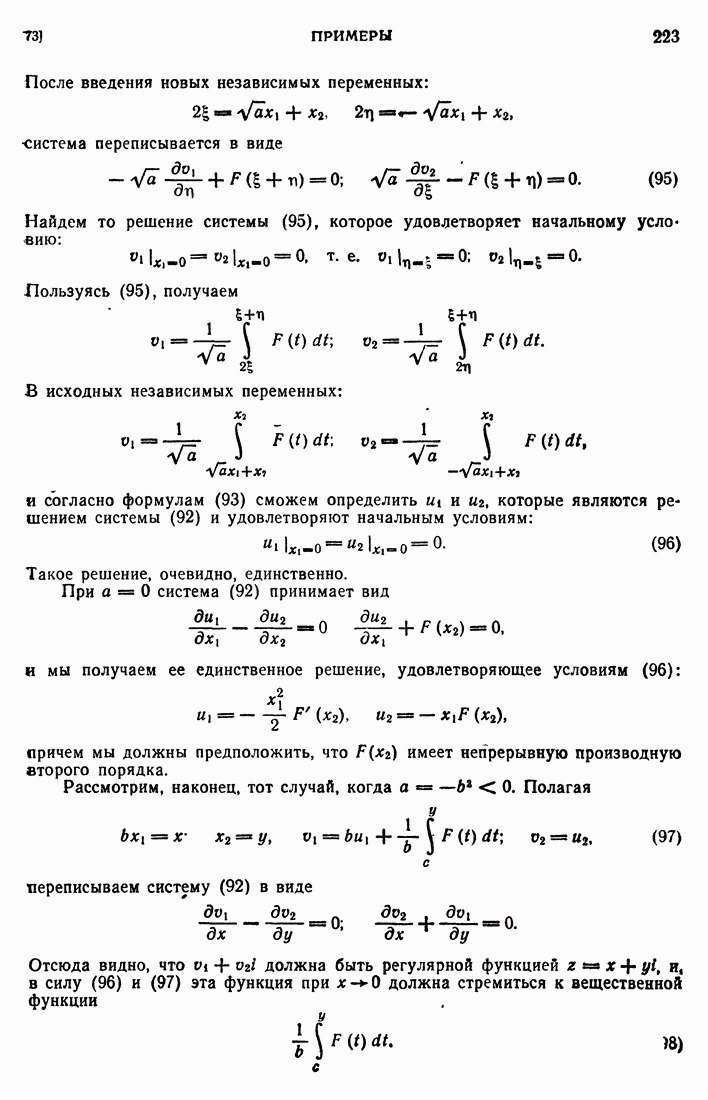
(см. об этом [147]). Действительно, неравенство

для любой и  следует непосредственно из ограниченности
следует непосредственно из ограниченности  . Обратное неравенство
. Обратное неравенство

есть не что иное, как неравенство (461). Итак, эквивалентность норм  доказана. Функции
доказана. Функции  принадлежат
принадлежат  следовательно, ему принадлежат и конечные отрезки ряда (495). Кроме того, функции
следовательно, ему принадлежат и конечные отрезки ряда (495). Кроме того, функции  ортогональны друг другу в смысле нового скалярного произведения, ибо из (492) следует, что
ортогональны друг другу в смысле нового скалярного произведения, ибо из (492) следует, что

Ввиду этого просто подсчитать величину

При этом мы использовали то, что  . Числовой же ряд
. Числовой же ряд  сходится и равен
сходится и равен  ибо
ибо 
(см. (496)). Поэтому функции  образуют последовательность Коши в пространстве
образуют последовательность Коши в пространстве  , а так как оно полное, то существует элемент
, а так как оно полное, то существует элемент  , к которому
, к которому  сходятся в норме
сходятся в норме  . Но, с другой стороны, мы знаем, что
. Но, с другой стороны, мы знаем, что  сходится в
сходится в  следовательно,
следовательно,  Итак, мы доказали, что для
Итак, мы доказали, что для  ряд (495) сходится в норме пространства
ряд (495) сходится в норме пространства  (т. е. в любой из норм
(т. е. в любой из норм  ), и потому
), и потому

причем этот ряд сходится в норме  и
и

Докажем еще такое предложение: если  , то ряд (495) сходится к ней в норме
, то ряд (495) сходится к ней в норме  , т. е. ряд (495) и ряды, полученные однократным почленным дифференцированием ряда
, т. е. ряд (495) и ряды, полученные однократным почленным дифференцированием ряда  по
по  сходятся в норме
сходятся в норме  соответственно. Для этого введем в гильбертово пространство
соответственно. Для этого введем в гильбертово пространство  новое скалярное произведение
новое скалярное произведение

Из (490) и ограниченности  следует, что соответствующая ему норма
следует, что соответствующая ему норма  эквивалентна исходной норме
эквивалентна исходной норме  пространства
пространства  . Собственные функции
. Собственные функции  принадлежат
принадлежат  и ортогональны по отношению к скалярному произведению
и ортогональны по отношению к скалярному произведению  ибо
ибо

Функции  образуют, тем самым, ортонормированную систему функций в пространстве
образуют, тем самым, ортонормированную систему функций в пространстве  с новым скалярным произведением. Поэтому для любой
с новым скалярным произведением. Поэтому для любой  из
из  и системы
и системы  справедливо неравенство Бесселя
справедливо неравенство Бесселя 

С другой стороны,

и

Сопоставляя эти соотношения, видим, что функции  образуют последовательность Коши в пространстве
образуют последовательность Коши в пространстве  и потому существует элемент
и потому существует элемент  этого пространства, к которому
этого пространства, к которому  сходится в любой из двух норм
сходится в любой из двух норм

Но так как  сходится к
сходится к  в норме
в норме  , то
, то  и
и

Подытожим доказанные в этом пункте факты в виде теоремы (см. в связи с нею замечание на с. 390):
Теорема 1. Пусть для симметричного оператора L, определенного равенством (488), и области D выполнены условия теоремы 2 из [148]. Тогда весь спектр задачи (489) (или, что то же, спектр оператора L в области D при условии Дирихле) состоит из счетного числа вещественных значений  стремящихся при
стремящихся при  и меньших числа мажорирующего коэффициент
и меньших числа мажорирующего коэффициент  Соответствующие им собственные функции (1 можно ортонормировать в
Соответствующие им собственные функции (1 можно ортонормировать в  . Они образуют базис в пространствах
. Они образуют базис в пространствах  , так что ряд Фурье (495) по ним для любой функции f из
, так что ряд Фурье (495) по ним для любой функции f из  сходится к f в норме
сходится к f в норме  для любой f из
для любой f из  сходится к f в норме
сходится к f в норме  а для любой
а для любой  из
из  сходится к f в норме
сходится к f в норме  Кроме того, имеют место равенства (496) для
Кроме того, имеют место равенства (496) для  равенство
равенство  для f из
для f из  и равенства (497) и (498) для f из
и равенства (497) и (498) для f из 
Изложенное здесь доказательство сходимости рядов (495) в пространстве  принадлежит О. А. Ладыженской. Более того, это было сделано ею для всех трех классических краевых условий, причем не только в пространстве
принадлежит О. А. Ладыженской. Более того, это было сделано ею для всех трех классических краевых условий, причем не только в пространстве  но и во всех пространствах
но и во всех пространствах  с целыми l (см. гл. II книги:
с целыми l (см. гл. II книги:
Ладыженская О. А. Смешанная задача для гиперболических уравнений. - М.; Физматгиз, 1953).
Собственные функции и собственные значения оператора  обладают рядом экстремальных свойств аналогичных тем, которые мы установили ранее для интегральных операторов с симметрическими ядрами, для вполне непрерывных симметрических операторов в
обладают рядом экстремальных свойств аналогичных тем, которые мы установили ранее для интегральных операторов с симметрическими ядрами, для вполне непрерывных симметрических операторов в  для обыкновенных дифференциальных операторов типа Штурма — Лиувилля [88], для оператора Лапласа [129] при условии Дирихле. Так, например, из равенств (496) и (502), справедливых для любой функции
для обыкновенных дифференциальных операторов типа Штурма — Лиувилля [88], для оператора Лапласа [129] при условии Дирихле. Так, например, из равенств (496) и (502), справедливых для любой функции  из
из  легко доказывается следующая теорема:
легко доказывается следующая теорема:
Теорема 2. Наименьшее значение квадратичного функционала

на множестве функций f из  равно
равно  первому собственному значению, взятому с обратным знаком. Оно реализуется на первой собственной функции
первому собственному значению, взятому с обратным знаком. Оно реализуется на первой собственной функции  Второе собственное значение, взятое с обратным знаком, дает наименьшее значение
Второе собственное значение, взятое с обратным знаком, дает наименьшее значение  на множестве функций f из
на множестве функций f из  подчиняющихся двум условиям:
подчиняющихся двум условиям:  . Оно реализуется на собственных функциях, соответствующих
. Оно реализуется на собственных функциях, соответствующих  (обозначим одно из решений этой задачи через
(обозначим одно из решений этой задачи через  ). Следующая собственная функция
). Следующая собственная функция  находится, как решение изопериметрической задачи на определение нижней грани
находится, как решение изопериметрической задачи на определение нижней грани  на множестве функций f из
на множестве функций f из  подчиненных условиям:
подчиненных условиям:  . Значение
. Значение  при этом оказывается равным
при этом оказывается равным  будет равно
будет равно  если
если  непростое собственное значение, т. е. если кратность
непростое собственное значение, т. е. если кратность  больше единицы). Так подряд находятся все
больше единицы). Так подряд находятся все  и соответствующие им
и соответствующие им  .
.
Для доказательства этих предложений надо учесть, что  . Ввиду этого для любой
. Ввиду этого для любой  из
из 

а для  значение
значение  следовательно, для любой
следовательно, для любой  имеем
имеем

т. е., действительно,  дает решение первой из указанных в теореме вариационных задач. В следующей вариационной задаче мы должны рассмотреть все f из
дает решение первой из указанных в теореме вариационных задач. В следующей вариационной задаче мы должны рассмотреть все f из  удовлетворяющие условиям
удовлетворяющие условиям  . Для них
. Для них  , а, с другой стороны,
, а, с другой стороны,  следовательно,
следовательно,  . Аналогично доказываются и остальные утверждения теоремы.
. Аналогично доказываются и остальные утверждения теоремы.
Полезно отметить, что вариационные задачи, описанные в этой теореме, имеют решения и при значительно меньших предположениях о коэффициентах L и D. Например, достаточно потребовать, чтобы для L выполнялись условия, сформулированные в [144], a D была бы произвольной ограниченной областью. При этом мы получим те же числа  , но относительно соответствующих им функций
, но относительно соответствующих им функций  сможем утверждать лишь, что они суть элементы
сможем утверждать лишь, что они суть элементы  . В соответствии с определением, данным в
. В соответствии с определением, данным в  является обобщенным решением из класса
является обобщенным решением из класса  спектральной задачи (489) при
спектральной задачи (489) при  . Если же L и D удовлетворяют требованиям теоремы 2 из [148], то каждое из этих
. Если же L и D удовлетворяют требованиям теоремы 2 из [148], то каждое из этих  окажется элементом
окажется элементом  и будет удовлетворять уравнениям (489) (см. теорему 2 [149]).
и будет удовлетворять уравнениям (489) (см. теорему 2 [149]).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
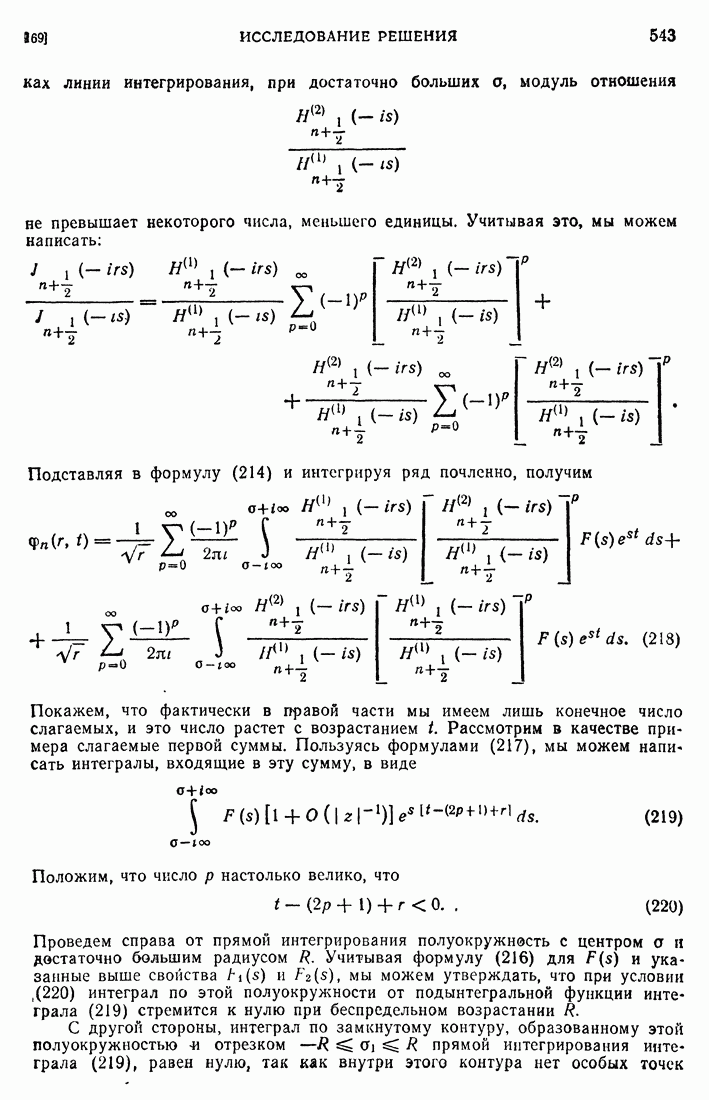
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.