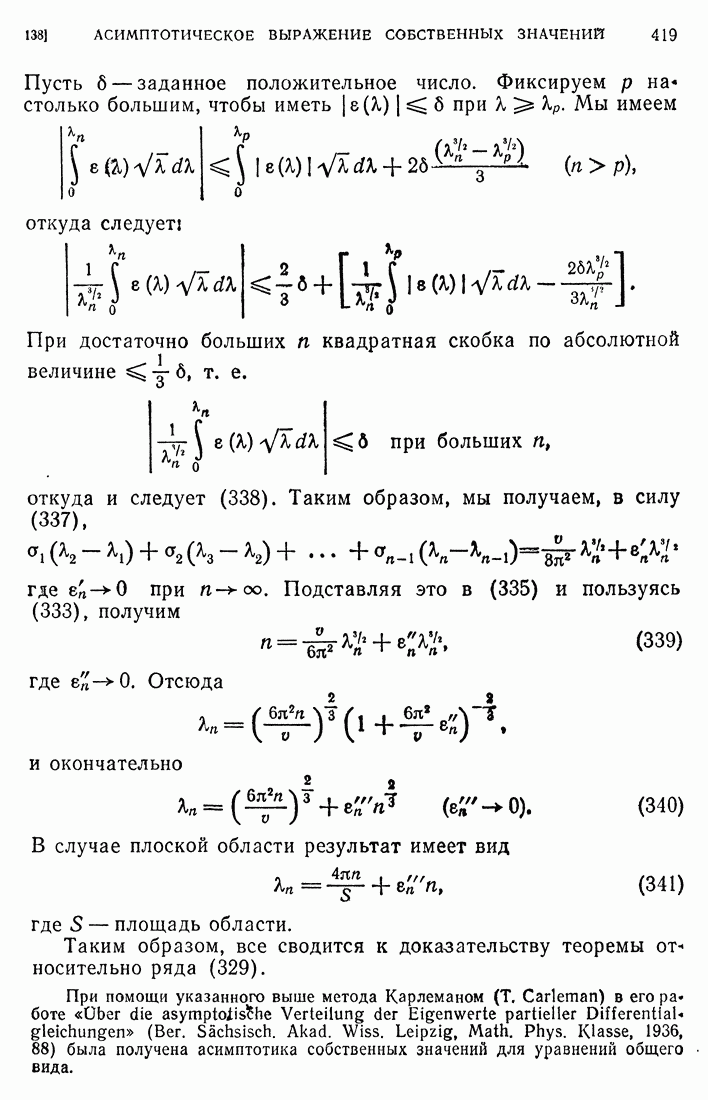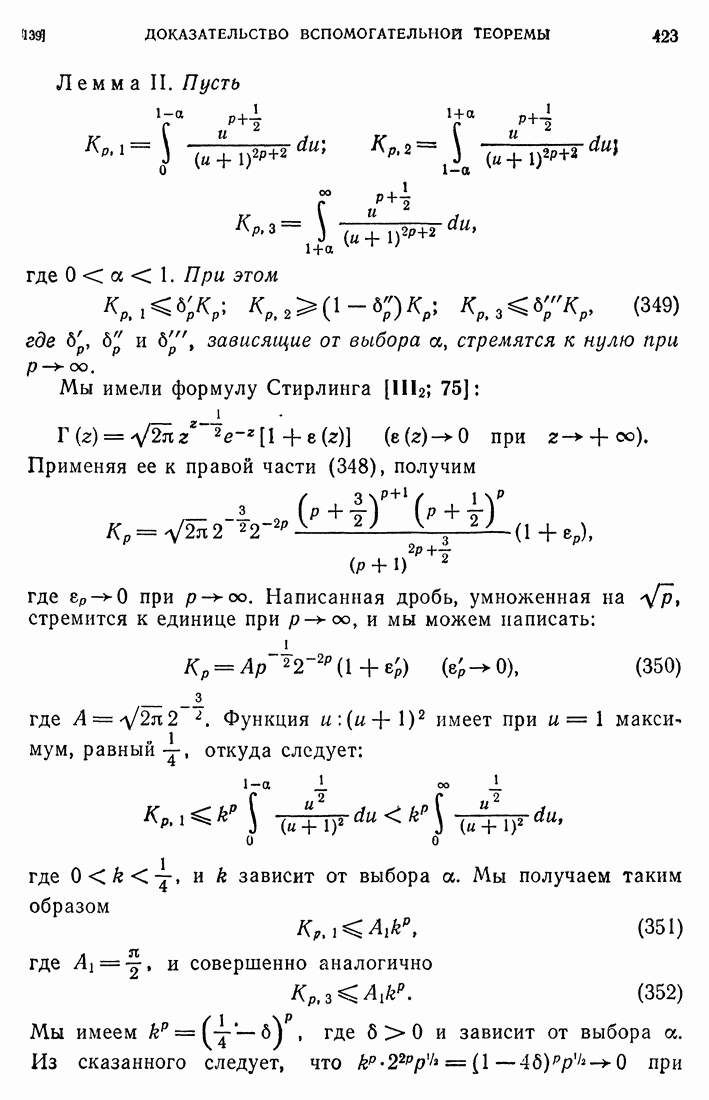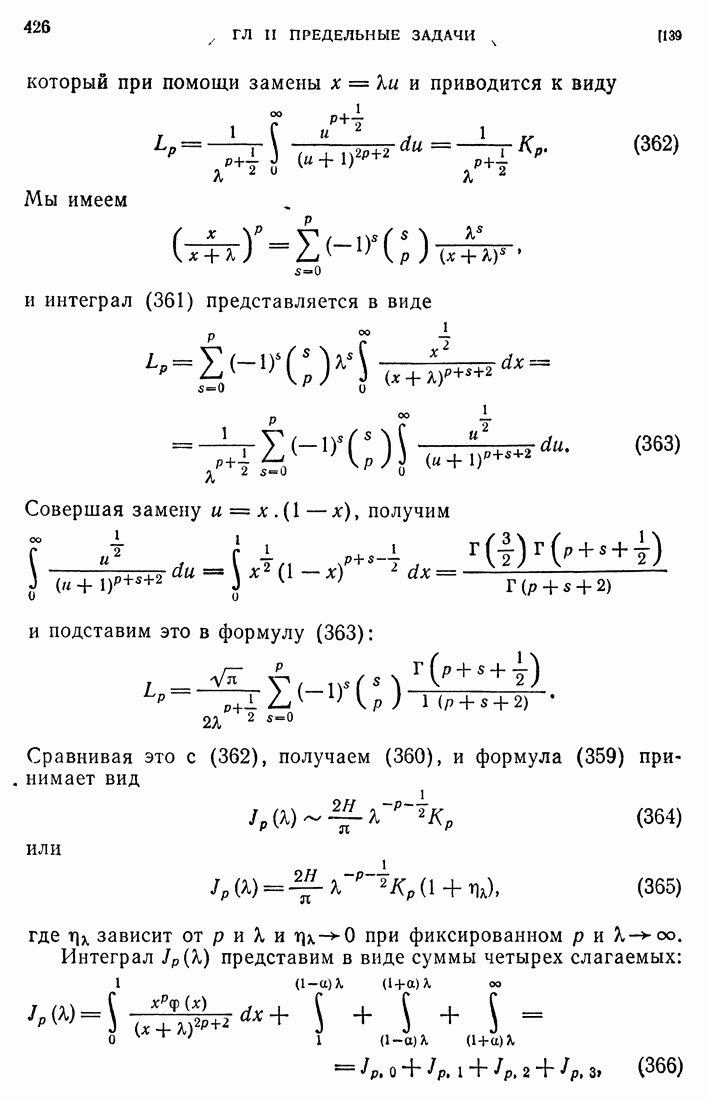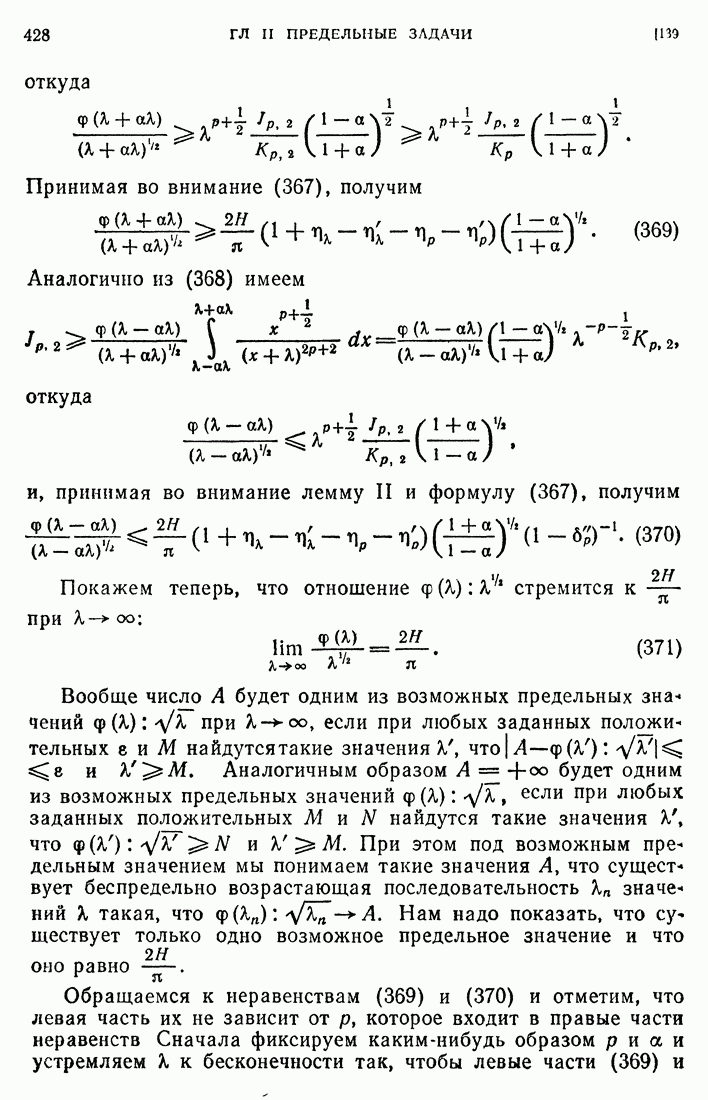| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
120. Исследование граничных значений.
Пока мы не делали никаких предположений о границе области В. Наложим теперь некоторое условие, в формулировке которого будет фигурировать некоторая фиксированная точка  границы области В. Множество граничных точек области В будем обозначать буквой l.
границы области В. Множество граничных точек области В будем обозначать буквой l.
Условие I. Существует непрерывная в В и супергармоническая внутри В функция  такая, что
такая, что  остальных точках S. Докажем теперь следующую теорему:
остальных точках S. Докажем теперь следующую теорему:
Теорема. Если выполнено указанное условие  граничная функция
граничная функция  непрерывна в точке
непрерывна в точке  то
то  стремится к
стремится к  при стремлении М к точке
при стремлении М к точке  изнутри области.
изнутри области.
Обозначим через  множество тех точек области В, расстояние которых до
множество тех точек области В, расстояние которых до  не превышает
не превышает  Пусть е — заданное положительное число. В силу непрерывности
Пусть е — заданное положительное число. В силу непрерывности  в точке
в точке  существует такое положительное число
существует такое положительное число  что для всех точек границы В, принадлежащих
что для всех точек границы В, принадлежащих  выполняется неравенство
выполняется неравенство

Построим непрерывную в Я и субгармоническую внутри В функцию

где С — некоторая положительная постоянная, которую мы сейчас выберем. В силу (180) и  мы имеем
мы имеем  в точках
в точках  принадлежащих
принадлежащих  Выберем С настолько большим, чтобы вне мы имели то же самое неравенство в точках
Выберем С настолько большим, чтобы вне мы имели то же самое неравенство в точках  т. е.
т. е.

Во всех точках S, расстояние которых до  не меньше
не меньше  функция
функция  достигает наименьшего положительного значения, которое мы обозначим через
достигает наименьшего положительного значения, которое мы обозначим через  . Это непосредственно следует из того, что указанные точки образуют замкнутое множество, и функция
. Это непосредственно следует из того, что указанные точки образуют замкнутое множество, и функция  непрерывна и положительна на этом множестве
непрерывна и положительна на этом множестве  Для выполнения неравенства (182) достаточно взять
Для выполнения неравенства (182) достаточно взять

где а — число, фигурирующее в неравенстве (177). При таком выборе С функция (181) будет нижней функцией. Точно так же при достаточно большом С функция

будет верхней функцией. Из  следует:
следует:

и, в силу непрерывности  в Б, найдется такое малое положительное
в Б, найдется такое малое положительное  что в
что в 

Пусть  — любая верхняя функция. Мы имеем для всех точек М, принадлежащих В:
— любая верхняя функция. Мы имеем для всех точек М, принадлежащих В:  и, следовательно, из последнего неравенства следует:
и, следовательно, из последнего неравенства следует:

Точная нижняя граница  также должна удовлетворять этому неравенству, т. е.
также должна удовлетворять этому неравенству, т. е.

Точно так же из (183) следует:

и, следовательно, в силу непрерывности  существует такое малое положительное
существует такое малое положительное  , что в
, что в  мы имеем
мы имеем

и тем более

Пусть  — наименьшее из чисел
— наименьшее из чисел  и
и  . В силу (184) и (185), мы имеем
. В силу (184) и (185), мы имеем

Ввиду произвола в выборе  , отсюда следует, что
, отсюда следует, что  стремится к
стремится к  при
при  изнутри области, и теорема доказана. Доказательство годится как в двумерном, так и в трехмерном случае. Если
изнутри области, и теорема доказана. Доказательство годится как в двумерном, так и в трехмерном случае. Если  непрерывна в каждой точке границы и в каждой точке выполняется условие I, то функция
непрерывна в каждой точке границы и в каждой точке выполняется условие I, то функция  непрерывна в замкнутой области В и принимает в граничных точках значения
непрерывна в замкнутой области В и принимает в граничных точках значения 
Определение. Если при любом выборе непрерывной на I функции  функция
функция  стремится к
стремится к  при
при  то точка
то точка  называется регулярной точкой границы. Точки
называется регулярной точкой границы. Точки
границы, не обладающие этим свойством, называются иррегулярными точками границы.
Из доказанной выше теоремы следует, что условие I есть достаточное условие регулярности точки 
Укажем теперь для трехмерного случая простое достаточное условие геометрического характера регулярности точки границы. Положим, что точка  границы обладает следующим свойством: существует сфера, которая не содержит никаких точек В, кроме точки
границы обладает следующим свойством: существует сфера, которая не содержит никаких точек В, кроме точки  . Пусть
. Пусть  центр этой сферы и R — ее радиус. Обозначая через
центр этой сферы и R — ее радиус. Обозначая через  расстояние
расстояние  построим функцию
построим функцию

Эта функция удовлетворяет, очевидно, всем требованиям условия 1, причем внутри В она — гармоническая.

Рис. 14.
Рассмотрим теперь плоский случай, и пусть граница В состоит из конечного числа простых замкнутых кривых, имеющих уравнения:  где
где  непрерывные периодические функции параметра t (рис. 14). Положим сначала, что точка
непрерывные периодические функции параметра t (рис. 14). Положим сначала, что точка  находится на внешнем контуре
находится на внешнем контуре  (рис. 14). Поместим в нее начало координат
(рис. 14). Поместим в нее начало координат  и выберем масштаб так, чтобы область В помещалась внутри круга
и выберем масштаб так, чтобы область В помещалась внутри круга  Составим функцию
Составим функцию

Когда  двигается в
двигается в  не может обойти вокруг начала, и
не может обойти вокруг начала, и  есть однозначная в В функция, регулярная внутри В и непрерывная в В, причем
есть однозначная в В функция, регулярная внутри В и непрерывная в В, причем  .
.
Полагая  , получим для вещественной части
, получим для вещественной части  выражение
выражение

причем  . Эта гармоническая функция удовлетворяет всем указанным выше условиям.
. Эта гармоническая функция удовлетворяет всем указанным выше условиям.
В частности, вне  мы имеем
мы имеем

где  — наибольшее значение
— наибольшее значение  в В и R — наибольшее расстояние от начала до точек В.
в В и R — наибольшее расстояние от начала до точек В.
Положим теперь, что  лежит на внутреннем контуре
лежит на внутреннем контуре  . Выбираем внутри
. Выбираем внутри  какую-либо точку а и совершаем конформное
какую-либо точку а и совершаем конформное
преобразование плоскости:

Контур  переходит во внешний контур, и мы для рассматриваемой точки
переходит во внешний контур, и мы для рассматриваемой точки  можем построить функцию
можем построить функцию  указанным выше способом. Переходя к прежней переменной z, получаем требуемую функцию. Таким образом, если
указанным выше способом. Переходя к прежней переменной z, получаем требуемую функцию. Таким образом, если  - непрерывна во всех точках рассмотренного контура
- непрерывна во всех точках рассмотренного контура  то
то  будет непрерывна вплоть до контура и на контуре равна
будет непрерывна вплоть до контура и на контуре равна 
Положим теперь, что  есть точка разрыва
есть точка разрыва  причем
причем  при стремлении N к
при стремлении N к  вдоль контура с обеих сторон имеет пределы, но эти пределы различны (разрыв первого рода). Обозначим их через
вдоль контура с обеих сторон имеет пределы, но эти пределы различны (разрыв первого рода). Обозначим их через  и пусть
и пусть  . Рассуждая совершенно так же, как и выше, получим вместо (184)
. Рассуждая совершенно так же, как и выше, получим вместо (184)

и вместо (185)

При стремлении М к  изнутри области В функция
изнутри области В функция  может иметь различные пределы. Но для любого из этих пределов
может иметь различные пределы. Но для любого из этих пределов  мы имеем, в силу предыдущих неравенств и произвольности
мы имеем, в силу предыдущих неравенств и произвольности 

Если  ограниченная функция, т. е. удовлетворяет условиям (177), то и функция
ограниченная функция, т. е. удовлетворяет условиям (177), то и функция  , как мы видели, удовлетворяет этому условию. Таким образом,
, как мы видели, удовлетворяет этому условию. Таким образом,  есть ограниченная гармоническая функция, принимающая предельные значения
есть ограниченная гармоническая функция, принимающая предельные значения  во всех точках непрерывности этой функции.
во всех точках непрерывности этой функции.
Вернемся к трехмерному случаю. Можно построить сравнительно простую замкнутую поверхность, имеющую иррегулярные точки. Это обстоятельство было открыто Лебегом и затем, независимо от него, П. С. Урысоном. Более подробное выяснение вопроса о предельных значениях можно найти в статье М. В. Келдыша (УМН, 1941, 8).
Приведем еще пример в случае плоскости. Пусть В — круг с центром в начале координат и с исключенным центром. Множество  граничных точек состоит из окружности круга и его центра. Пусть
граничных точек состоит из окружности круга и его центра. Пусть  на окружности и
на окружности и  в центре. Такая функция
в центре. Такая функция  непрерывна на
непрерывна на  Гармоническая функция
Гармоническая функция  стремится, очевидно, к нулю при приближении М к точкам окружности. Покажем, что
стремится, очевидно, к нулю при приближении М к точкам окружности. Покажем, что  не может стремиться к единице при приближении к центру. Если бы это было так, то
не может стремиться к единице при приближении к центру. Если бы это было так, то
 была бы гармонической внутри всего круга, если принять ее значение в центре равным единице [105]. Но это противоречит теореме о среднем значении гармонической функции в центре круга. Таким образом, начало координат — иррегулярная точка границы.
была бы гармонической внутри всего круга, если принять ее значение в центре равным единице [105]. Но это противоречит теореме о среднем значении гармонической функции в центре круга. Таким образом, начало координат — иррегулярная точка границы.
Нетрудно показать, что в рассматриваемом случае  . Действительно,
. Действительно,  ограничена, а потому имеет предел при стремлении М к центру [105], и если принять этот предел равным значению
ограничена, а потому имеет предел при стремлении М к центру [105], и если принять этот предел равным значению  в центре, то
в центре, то  гармоническая везде внутри круга [105] и равна нулю на окружности, т. е. и
гармоническая везде внутри круга [105] и равна нулю на окружности, т. е. и 
Отметим еще, что вместо условия I можно поставить условие регулярности, которое касается только окрестности точки  причем можно показать, что это новое условие равносильно условию I.
причем можно показать, что это новое условие равносильно условию I.
Условие II. Для некоторой окрестности  точки
точки  существует функция непрерывная в
существует функция непрерывная в  вплоть до границы, супергармоническая внутри
вплоть до границы, супергармоническая внутри  и такая, что
и такая, что  остальных точках
остальных точках 
Можно показать, что в трехмерном случае точка  удовлетворяет условию II, если эта точка является вершиной кругового конуса, все точки которого, достаточно близкие к
удовлетворяет условию II, если эта точка является вершиной кругового конуса, все точки которого, достаточно близкие к  лежат вне В (кроме точки
лежат вне В (кроме точки  ). Таким образом, такие точки регулярны. (См. Петровский И. Г. Лекции об уравнениях с частными производными. — М.: Физматгиз, 1961.)
). Таким образом, такие точки регулярны. (См. Петровский И. Г. Лекции об уравнениях с частными производными. — М.: Физматгиз, 1961.)
В дальнейшем мы будем всегда считать, если не будет соответствующих оговорок, что контуры или поверхности, ограничивающие области, о которых будет идти речь, таковы, что все их точки суть регулярные точки. Таковыми будут, например, поверхности Ляпунова. Для них мы построили решение задачи Дирихле при помощи теории потенциала и интегральных уравнений.
Если на границе задана непрерывная функция  и все точки границы регулярны, то построенная гармоническая функция
и все точки границы регулярны, то построенная гармоническая функция  непрерывна вплоть до границы и на границе принимает значения
непрерывна вплоть до границы и на границе принимает значения  Мы знаем, что может существовать только одна такая функция. Если на границе имеются нерегулярные точки, то гармоническая функция
Мы знаем, что может существовать только одна такая функция. Если на границе имеются нерегулярные точки, то гармоническая функция  ограничена внутри области и принимает во всех регулярных точках границы значения
ограничена внутри области и принимает во всех регулярных точках границы значения  . Можно показать, что может существовать только одна функция с такими свойствами. Доказательство этого утверждения и ряда других интересных фактов, в том числе критерия регулярности Винера, можно найти в упомянутой выше статье М. В. Келдыша.
. Можно показать, что может существовать только одна функция с такими свойствами. Доказательство этого утверждения и ряда других интересных фактов, в том числе критерия регулярности Винера, можно найти в упомянутой выше статье М. В. Келдыша.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.