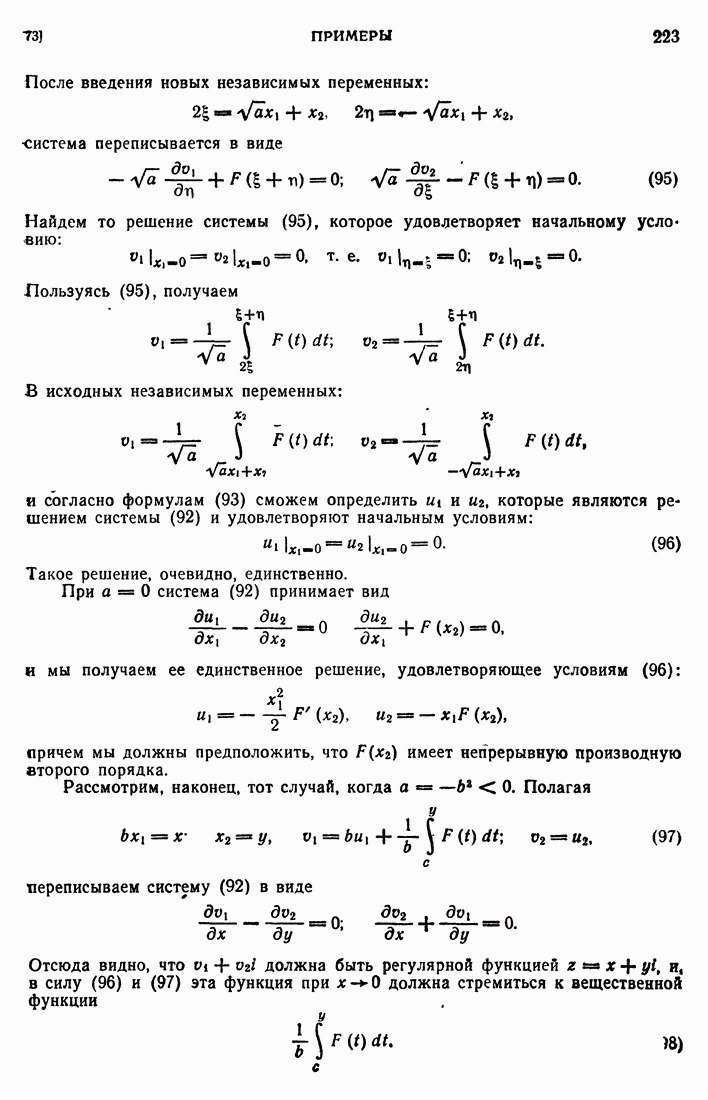
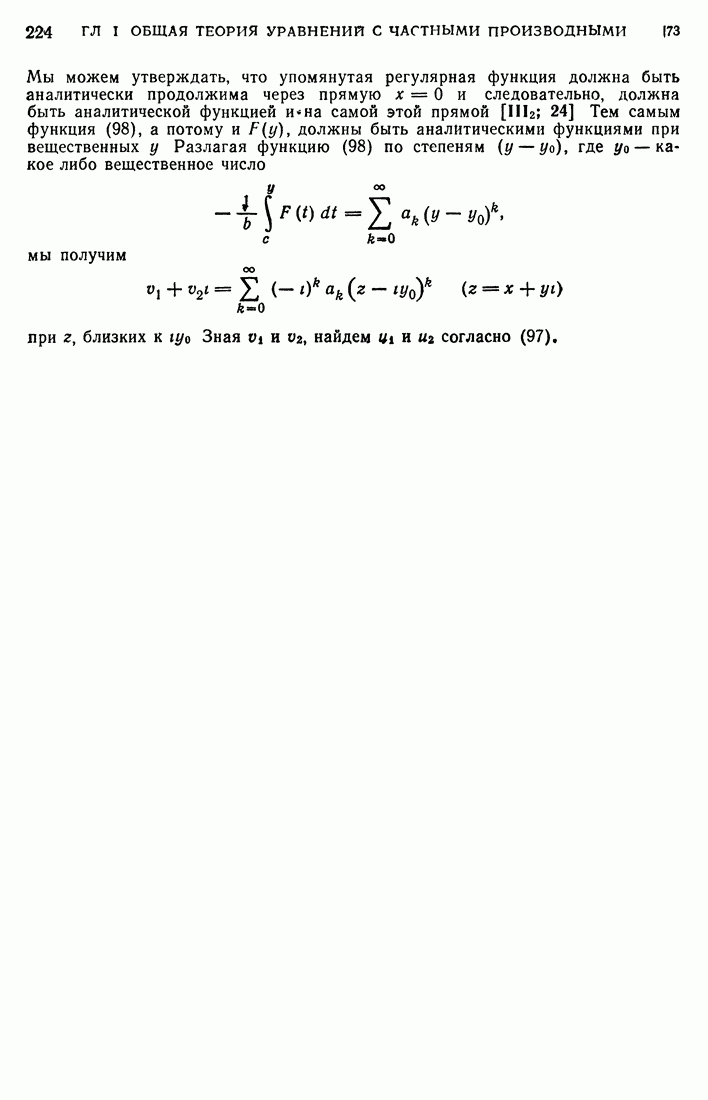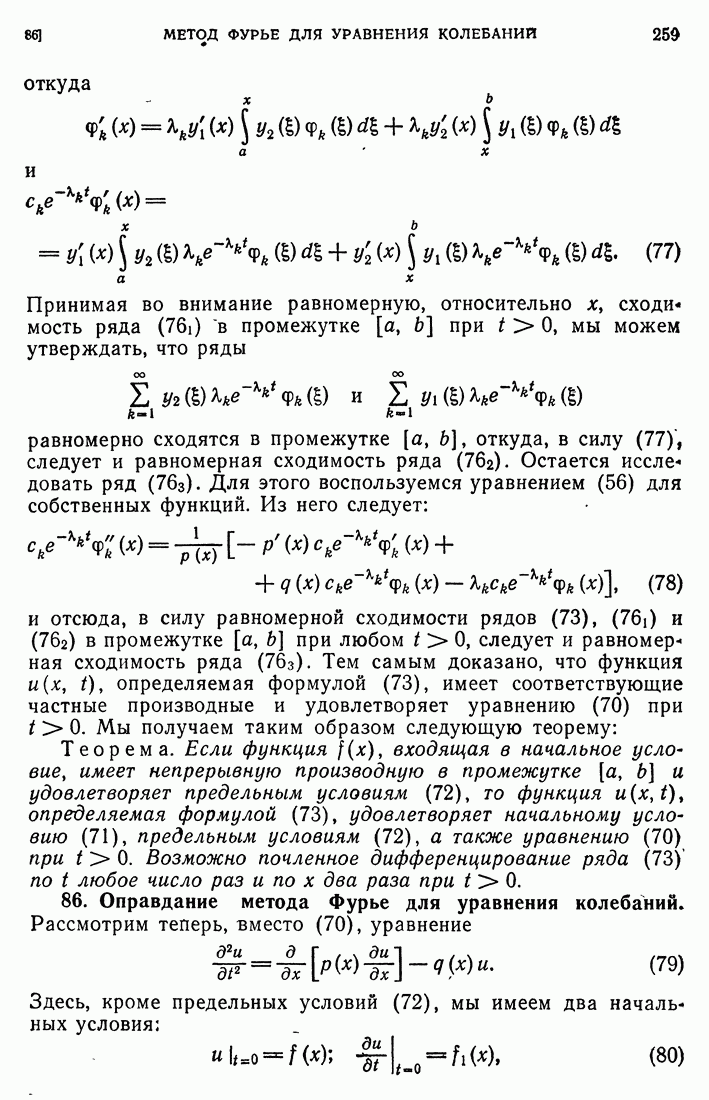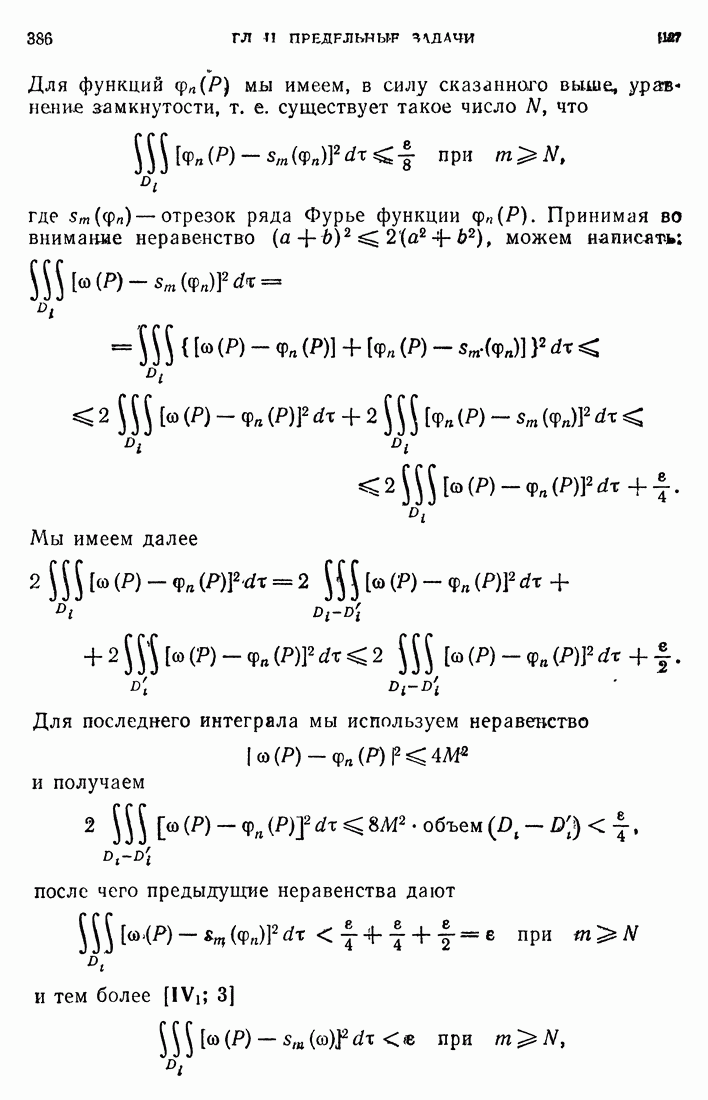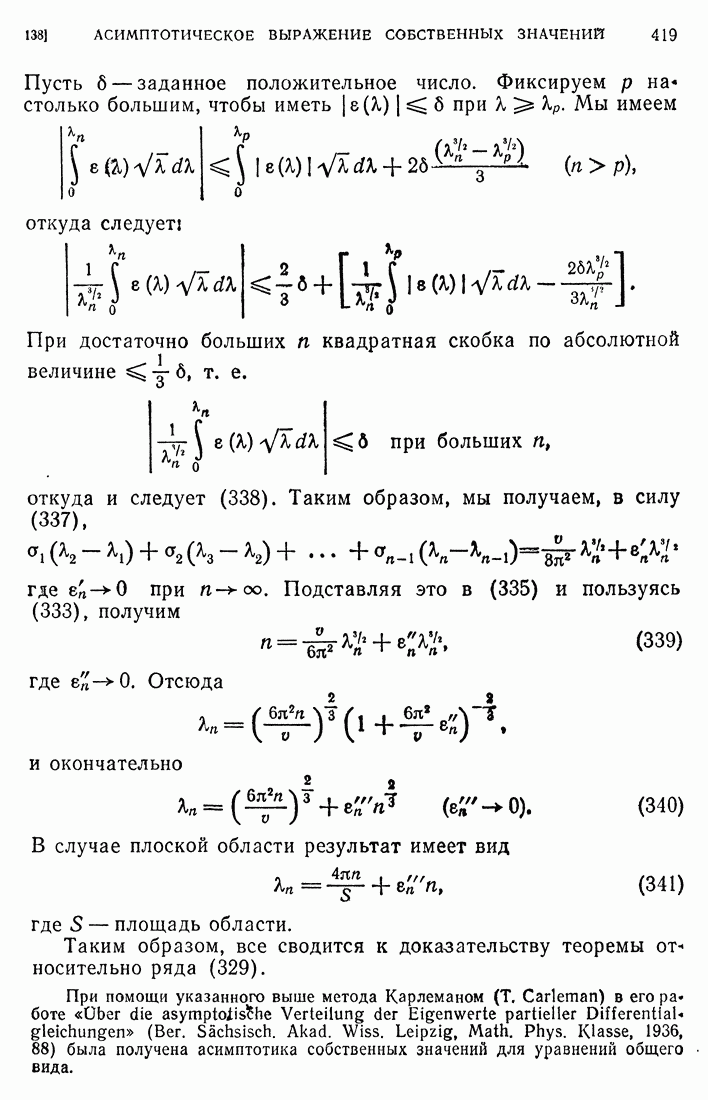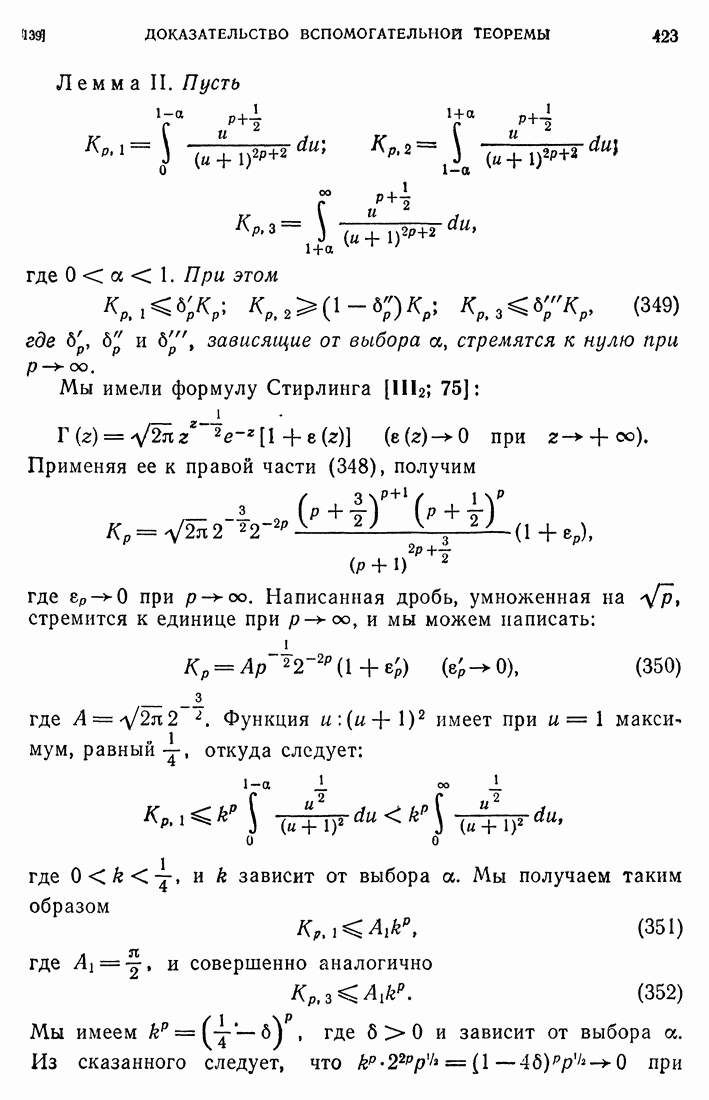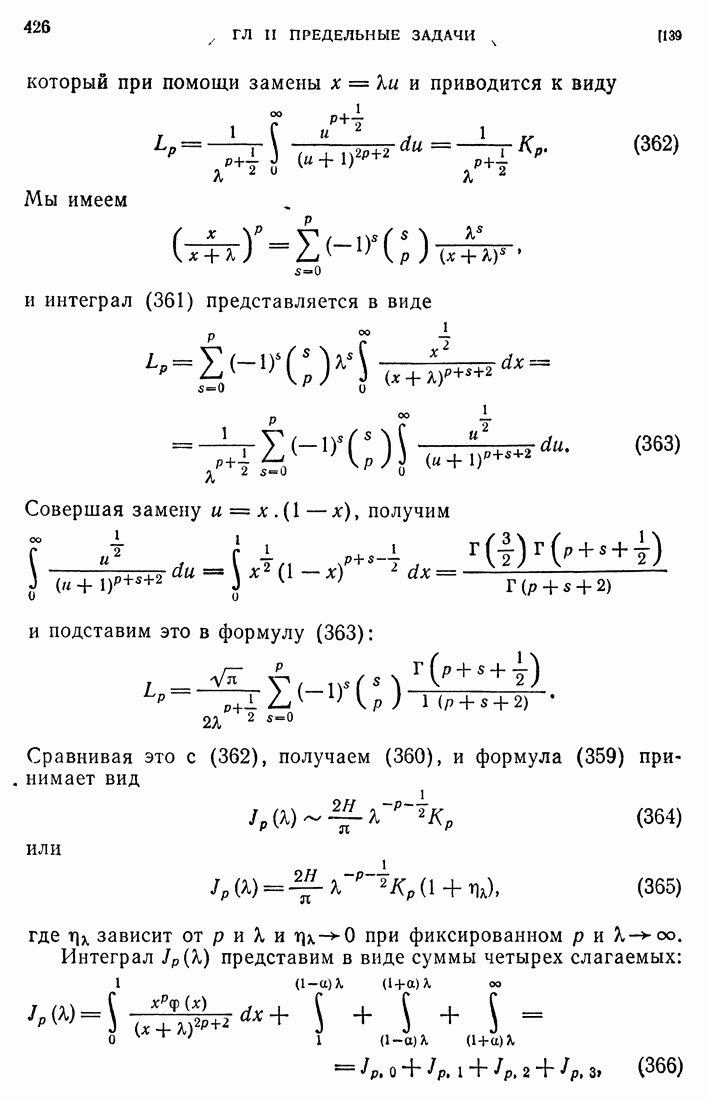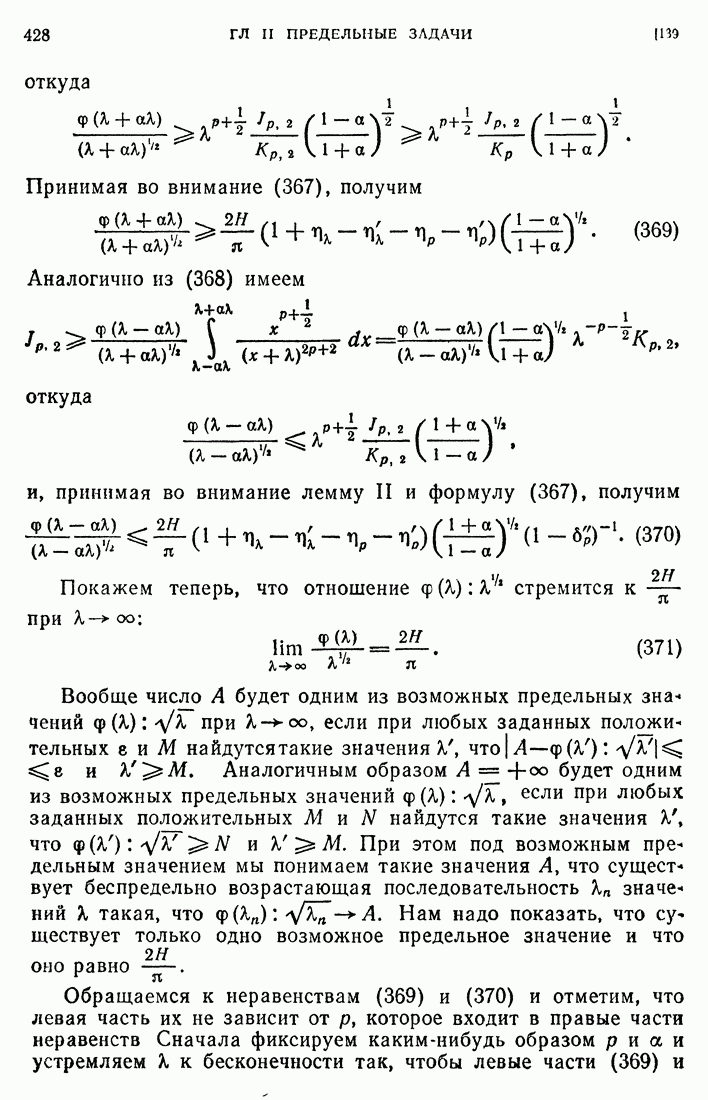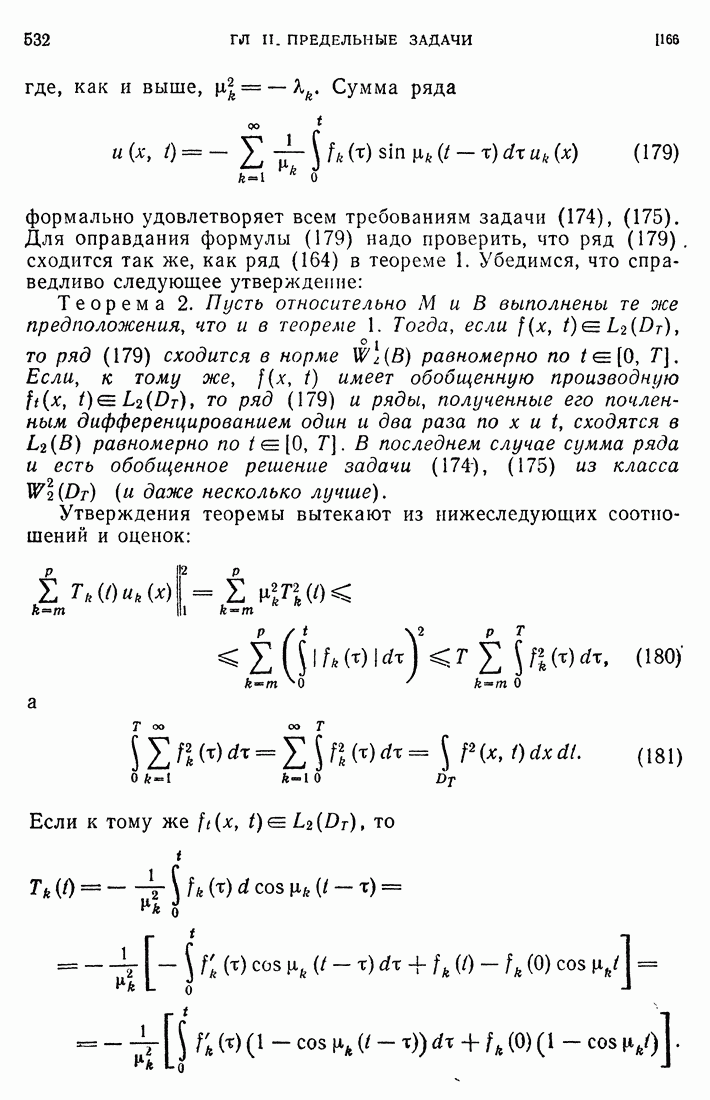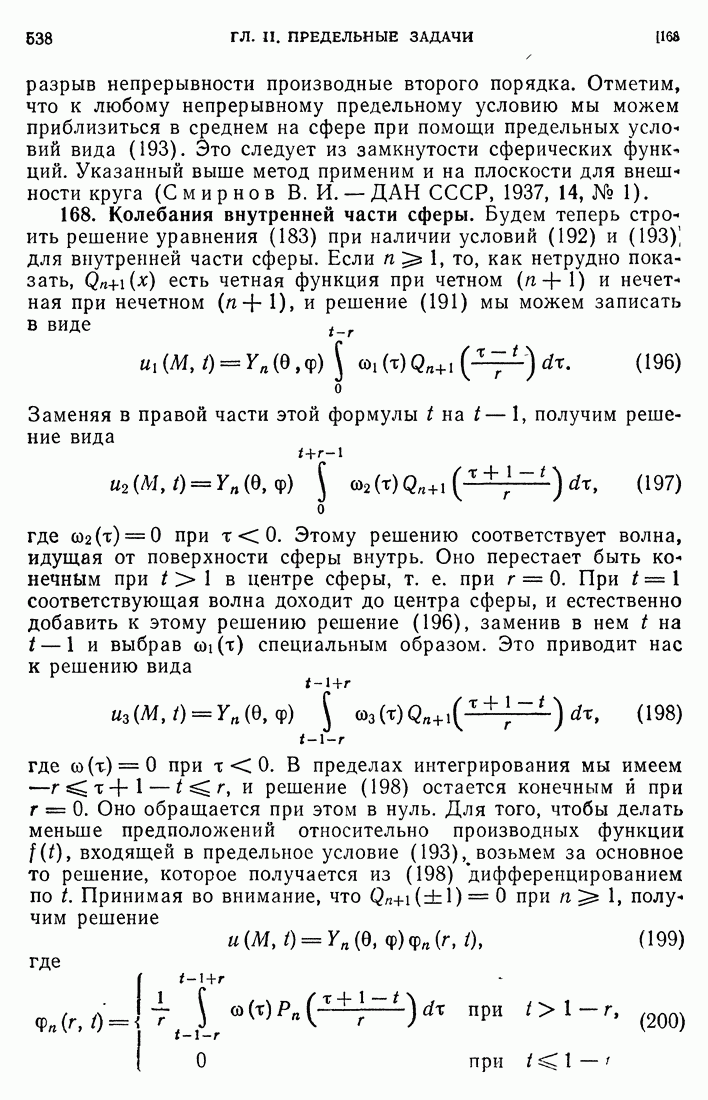| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Задача Коши и характеристики.
Под задачей Коши подразумевают обычно формулированную выше задачу об определении интегральной поверхности уравнения (2), проходящей через заданную линию  Для точного исследования вопроса о существовании и единственности решения этой задачи нам придется пользоваться одной теоремой из теории обыкновенных дифференциальных уравнений, а именно:
Для точного исследования вопроса о существовании и единственности решения этой задачи нам придется пользоваться одной теоремой из теории обыкновенных дифференциальных уравнений, а именно:
Теорема. Если правые части системы дифференциальных уравнений

суть непрерывные функции своих аргументов в некоторой области, определяемой неравенствами

и если, кроме того, в этой области существуют непрерывные частные производные то решение системы (5), определяемое в силу теоремы существования и единственности любыми начальными данными  , находящимися внутри области (6):
, находящимися внутри области (6):

непрерывно по своим аргументам и допускает частные производные  по начальным данным, которые являются непрерывными функциями своих аргументов
по начальным данным, которые являются непрерывными функциями своих аргументов  в некоторой окрестности взятых начальных данных.
в некоторой окрестности взятых начальных данных.
Чтобы не прерывать изложение, мы отложим доказательство этой теоремы до одного из следующих параграфов.
Вернемся к решению задачи Коши. Положим, что уравнение линии l задано в параметрической форме:

и допустим, что правые части уравнений (4) удовлетворяют условиям формулированной выше теоремы в некоторой области пространства  , содержащей внутри себя линию l. Принимая координаты точек l за начальные данные при
, содержащей внутри себя линию l. Принимая координаты точек l за начальные данные при  мы получим решение системы (4):
мы получим решение системы (4):

при s, достаточно близких к нулю, или, в силу (7),

Считая, что правые части уравнений (7) непрерывно дифференцируемы по t, и пользуясь указанной выше теоремой, мы можем утверждать, что функции (8) имеют непрерывные производные не только по s, но и по t. При любом заданном t из промежутка функции (8) определены при всех 
достаточно близких к нулю. Составим функциональный определитель от первых двух из этих функций по s и 

Существенным для дальнейшего будет тот факт, является ли этот определитель отличным от нуля или нет. Мы рассмотрим, во-первых, тот случай, когда  вдоль линии
вдоль линии  и, во-вторых, тот случай, когда
и, во-вторых, тот случай, когда  вдоль линии
вдоль линии  . Начнем с первого случая:
. Начнем с первого случая:

 при
при  но тем самым, в силу непрерывности производных,
но тем самым, в силу непрерывности производных,  и в некоторой окрестности начального значения
и в некоторой окрестности начального значения  и значения
и значения  соответствующего некоторой точке М линии
соответствующего некоторой точке М линии  При этом первые два из уравнений (8) можно решить относительно s и t при всех
При этом первые два из уравнений (8) можно решить относительно s и t при всех  находящихся в окрестности координат
находящихся в окрестности координат  точки М линии
точки М линии  . Это решение — единственно; и полученные функции
. Это решение — единственно; и полученные функции  имеют непрерывные производные первого порядка [III; 19]. Подставляя полученные функции
имеют непрерывные производные первого порядка [III; 19]. Подставляя полученные функции  в третье из уравнений (8), мы и будем иметь в упомянутой окрестности функцию
в третье из уравнений (8), мы и будем иметь в упомянутой окрестности функцию  имеющую непрерывные производные первого порядка, причем поверхность
имеющую непрерывные производные первого порядка, причем поверхность  содержит некоторый участок линии
содержит некоторый участок линии  в окрестности М. Из указанных в предыдущем параграфе геометрических соображений непосредственно следует, что и
в окрестности М. Из указанных в предыдущем параграфе геометрических соображений непосредственно следует, что и  удовлетворяет уравнению (2). Мы это проверим ниже и аналитически.
удовлетворяет уравнению (2). Мы это проверим ниже и аналитически.
Отметим, что мы построили решение  лишь в некоторой окрестности любой заданной точки М линии
лишь в некоторой окрестности любой заданной точки М линии  или, как говорят, получили локальное решение задачи. При некоторых условиях, налагаемых на а,
или, как говорят, получили локальное решение задачи. При некоторых условиях, налагаемых на а,  с и линию
с и линию  можно убедиться в возможности построения интегральной поверхности в некоторой окрестности всей линии
можно убедиться в возможности построения интегральной поверхности в некоторой окрестности всей линии  т. е. при всех х и у, достаточно близких к линии
т. е. при всех х и у, достаточно близких к линии  на плоскости
на плоскости  При этом считается, что производные
При этом считается, что производные  одновременно в нуль не обращаются. Точная формулировка подобных результатов будет указана в следующем параграфе.
одновременно в нуль не обращаются. Точная формулировка подобных результатов будет указана в следующем параграфе.
Вопрос о существовании решения уравнения в некоторой наперед предписанной области плоскости  представляет большие трудности. Можно построить область В плоскости
представляет большие трудности. Можно построить область В плоскости  ней функцию
ней функцию  имеющую производные всех порядков, так, что для уравнения
имеющую производные всех порядков, так, что для уравнения

только  будет решением, имеющим непрерывные производные первого порядка и существующим во всей области В.
будет решением, имеющим непрерывные производные первого порядка и существующим во всей области В.
Проверим теперь, что построенная функция  действительно является решением уравнения (2). Пользуясь правилом
действительно является решением уравнения (2). Пользуясь правилом
дифференцирования сложных функций и уравнениями (4), можем написать:

Это уравнение имеет место для всех s и t, находящихся в окрестности  и значения
и значения  соответствующего некоторой точке
соответствующего некоторой точке  линии l. Но
линии l. Но  , и, следовательно,
, и, следовательно,  удовлетворяет уравнению (2) при всех
удовлетворяет уравнению (2) при всех  лежащих в окрестности
лежащих в окрестности 
Для доказательства единственности достаточно убедиться в том, что всякая гладкая интегральная поверхность и  проходящая через
проходящая через  может быть образована характеристиками. Образуем систему дифференциальных уравнений:
может быть образована характеристиками. Образуем систему дифференциальных уравнений:

В силу сделанных предположений правые части таковы, что имеет место теорема существования и единственности для всех  в окрестности
в окрестности  Из того факта, что интегральная поверхность имеет явное уравнение
Из того факта, что интегральная поверхность имеет явное уравнение  и проходит через участок линии
и проходит через участок линии  в окрестности точки
в окрестности точки  следует, что координаты
следует, что координаты  различных точек линии l в окрестности М различны (мы считаем, что l не пересекает себя). Беря эти координаты за начальные данные при интегрировании системы (11) и подставляя полученные решения в функцию
различных точек линии l в окрестности М различны (мы считаем, что l не пересекает себя). Беря эти координаты за начальные данные при интегрировании системы (11) и подставляя полученные решения в функцию  будем иметь семейство линий на нашей интегральной поверхности. Вдоль этих линий, в силу (11), удовлетворяются первые два из уравнений (4). Нетрудно проверить, что удовлетворяется и третье уравнение. Действительно, пользуясь (11), получаем
будем иметь семейство линий на нашей интегральной поверхности. Вдоль этих линий, в силу (11), удовлетворяются первые два из уравнений (4). Нетрудно проверить, что удовлетворяется и третье уравнение. Действительно, пользуясь (11), получаем

Но  есть интегральная поверхность, т. е.
есть интегральная поверхность, т. е.  откуда
откуда  Таким образом, упомянутые выше линии, покрывающие поверхность и
Таким образом, упомянутые выше линии, покрывающие поверхность и  суть действительно характеристики. Итак, при условии (10) задача Коши имеет единственное решение. Мы еще вернемся к вопросу о единственности при рассмотрении нелинейных уравнений первого порядка.
суть действительно характеристики. Итак, при условии (10) задача Коши имеет единственное решение. Мы еще вернемся к вопросу о единственности при рассмотрении нелинейных уравнений первого порядка.
Положим теперь, что вдоль линии  т. е. при
т. е. при  мы имеем
мы имеем

Покажем, что если в этом случае существует интегральная поверхность  с непрерывными производными первого
с непрерывными производными первого
порядка, проходящая через  то эта линия должна быть характеристикой. Здесь, как и выше, когда мы говорим, что поверхность
то эта линия должна быть характеристикой. Здесь, как и выше, когда мы говорим, что поверхность  проходит через линию l, то понимаем это локально, т. е. рассматриваем лишь некоторый участок
проходит через линию l, то понимаем это локально, т. е. рассматриваем лишь некоторый участок 
Будем считать, что  отличны от нуля вдоль
отличны от нуля вдоль  Принимая во внимание первые два из уравнений (4), мы можем написать условие (12) в виде
Принимая во внимание первые два из уравнений (4), мы можем написать условие (12) в виде

где буквою k мы обозначили общую величину написанных отношений. Пусть  интегральная поверхность, проходящая через l. Подставляя в
интегральная поверхность, проходящая через l. Подставляя в  выражения
выражения  дифференцируя
дифференцируя  пользуясь (13), мы получим
пользуясь (13), мы получим  Принимая во внимание, что и
Принимая во внимание, что и  есть решение уравнения (2), и пользуясь этим уравнением, можем
есть решение уравнения (2), и пользуясь этим уравнением, можем  написать далее
написать далее  что и приведет нас к системе
что и приведет нас к системе

из которой следует, что линия l есть характеристика. Итак, если  то для того, чтобы существовала интегральная поверхность, проходящая через линию
то для того, чтобы существовала интегральная поверхность, проходящая через линию  необходимо, чтобы эта линия была характеристикой. При этом, как мы видели в предыдущем параграфе, через линию I проходит бесчисленное множество интегральных поверхностей. При проведенном выше доказательстве для нас, конечно, было существенным, чтобы интегральная поверхность
необходимо, чтобы эта линия была характеристикой. При этом, как мы видели в предыдущем параграфе, через линию I проходит бесчисленное множество интегральных поверхностей. При проведенном выше доказательстве для нас, конечно, было существенным, чтобы интегральная поверхность  проходящая через
проходящая через  имела в точках этой линии непрерывные производные; может случиться, как это мы увидим на примере, что l не есть характеристика, вдоль нее
имела в точках этой линии непрерывные производные; может случиться, как это мы увидим на примере, что l не есть характеристика, вдоль нее  и все же через
и все же через  проходит интегральная поверхность, но такая, что частные производные от
проходит интегральная поверхность, но такая, что частные производные от  перестают быть непрерывными в точках
перестают быть непрерывными в точках  т. е., иными словами, линия l является особой линией интегральной поверхности. Если
т. е., иными словами, линия l является особой линией интегральной поверхности. Если  характеристика, но вдоль нее
характеристика, но вдоль нее  то это значит, что вдоль линии l
то это значит, что вдоль линии l

Отметим одну особенность системы (4). Вспомогательный параметр s не входит в правую часть уравнений, и одна из произвольных постоянных входит как добавочное слагаемое к s. Эта произвольная постоянная не играет существенной роли и сводится к произвольности выбора начального значения s. Таким образом, мы имеем при интегрировании этой системы две
существенные произвольные постоянные. Этот факт непосредственно очевиден, если записать систему (4) в виде (3).
Напомним, что квазилинейное неоднородное уравнение (2) может быть приведено к чисто линейному однородному уравнению, если искать решение в неявной форме [II, 21].

где С — некоторая произвольная постоянная. Согласно правилу дифференцирования неявных функций, мы имеем

и уравнение (2) порождает линейное однородное уравнение для функции 

Соответствующей ему системой обыкновенных дифференциальных уравнений является система (3). Если

- два независимых интеграла этой системы, то  где F — произвольная функция своих аргументов, будет решением уравнения (15). Мы видели, каким образом из условий задачи Коши можно найти явный вид этой функции [II; 24].
где F — произвольная функция своих аргументов, будет решением уравнения (15). Мы видели, каким образом из условий задачи Коши можно найти явный вид этой функции [II; 24].
Изложенные рассуждения дают повод к следующему вопросу. Мы искали решение уравнения (2) как решение, входящее в целый класс решений, имеющих неявное уравнение (14), содержащее лроизвольную постоянную С. Нетрудно показать, что мы таким путем не потеряем ни одного решения нашего уравнения. Для этого надо принять во внимание то, что, ввиду произвольности начальных данных в задаче Коши, мы можем всякое решение нашего уравнения считать входящим в целое семейство решений, содержащее произвольную постоянную. Решая относительно этой произвольной постоянной, мы и убедимся в том, что всякое решение может быть получено из формулы вида (14). Мы могли бы потерять лишь такие решения (особые решения), которые не могут быть получены указанным выше процессом путем решения задачи Коши Таких решений не может быть, если функции а, b и с удовлетворяют некоторым общим условиям. На подробностях доказательства мы не останавливаемся.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
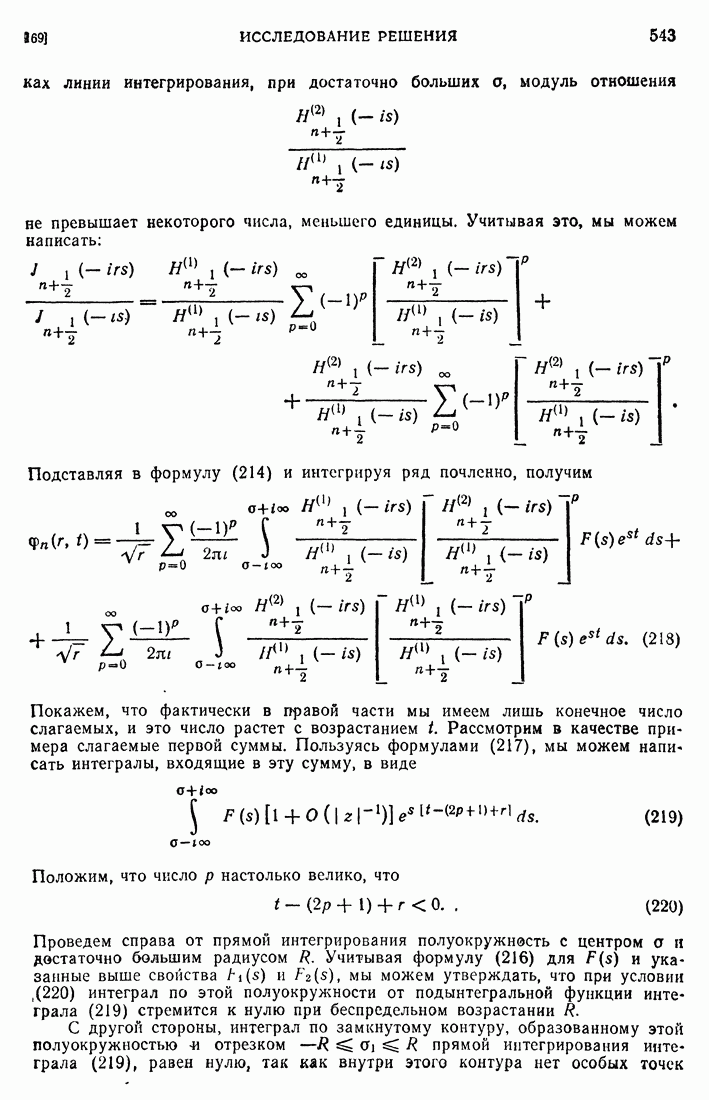
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.