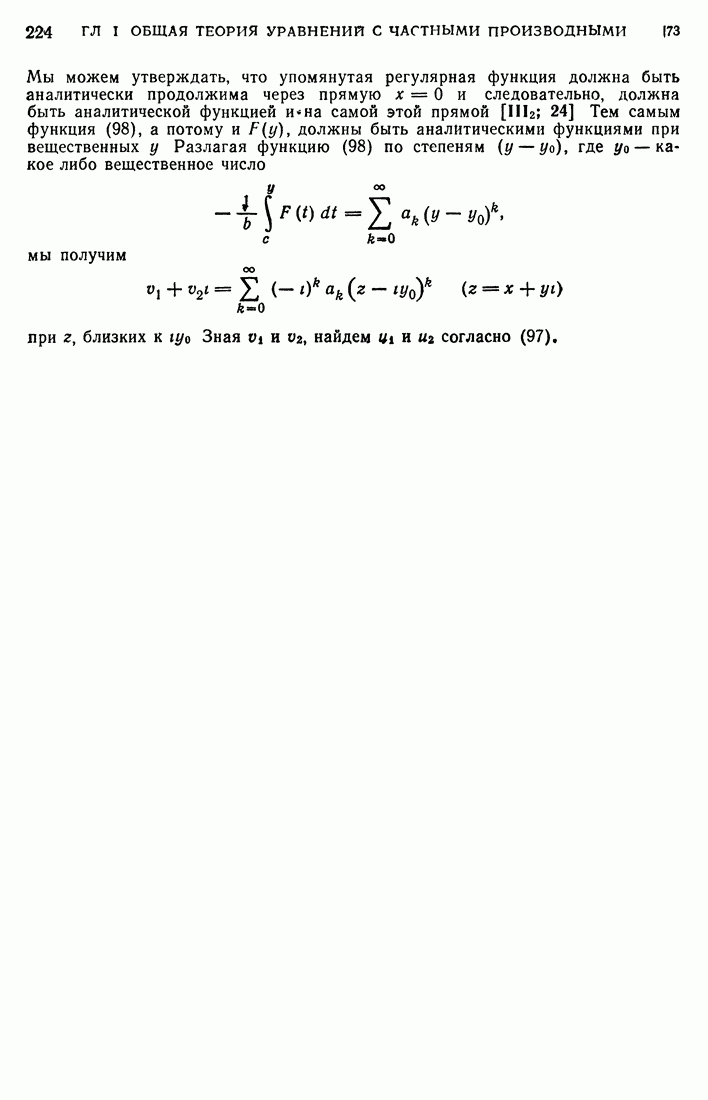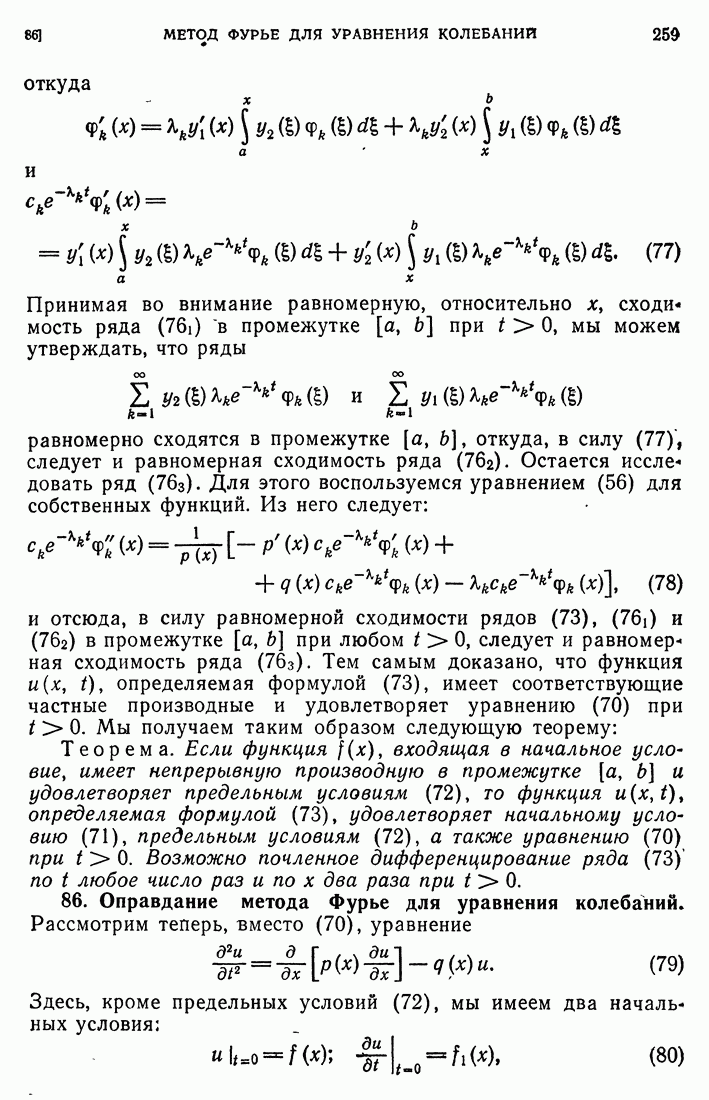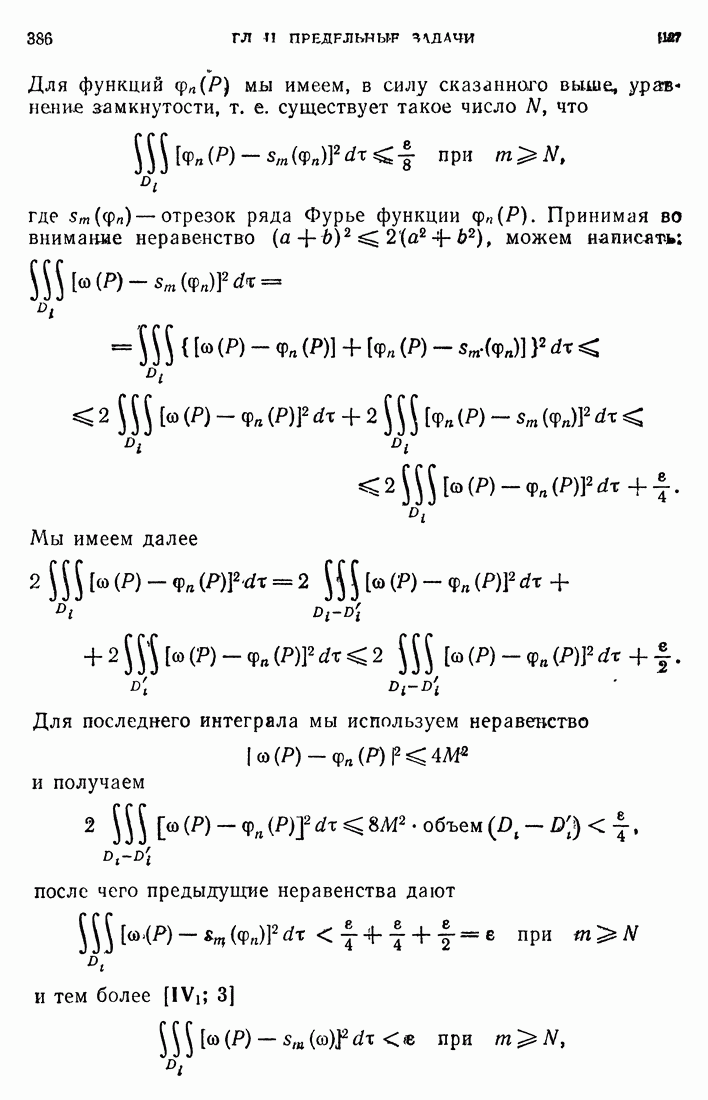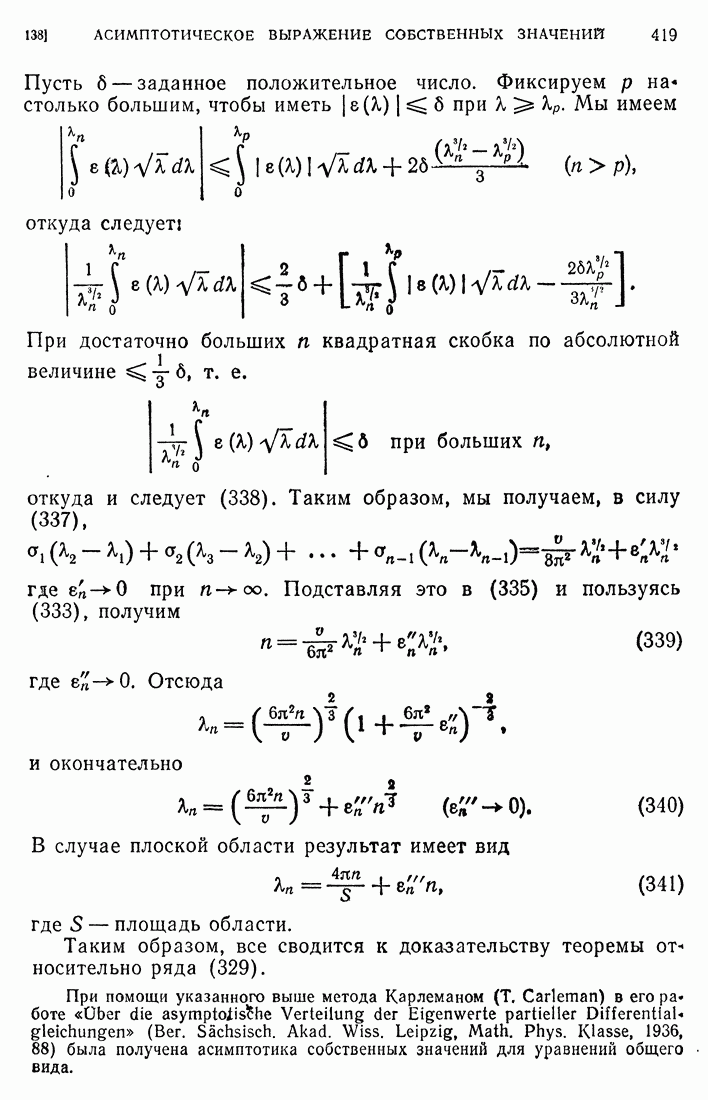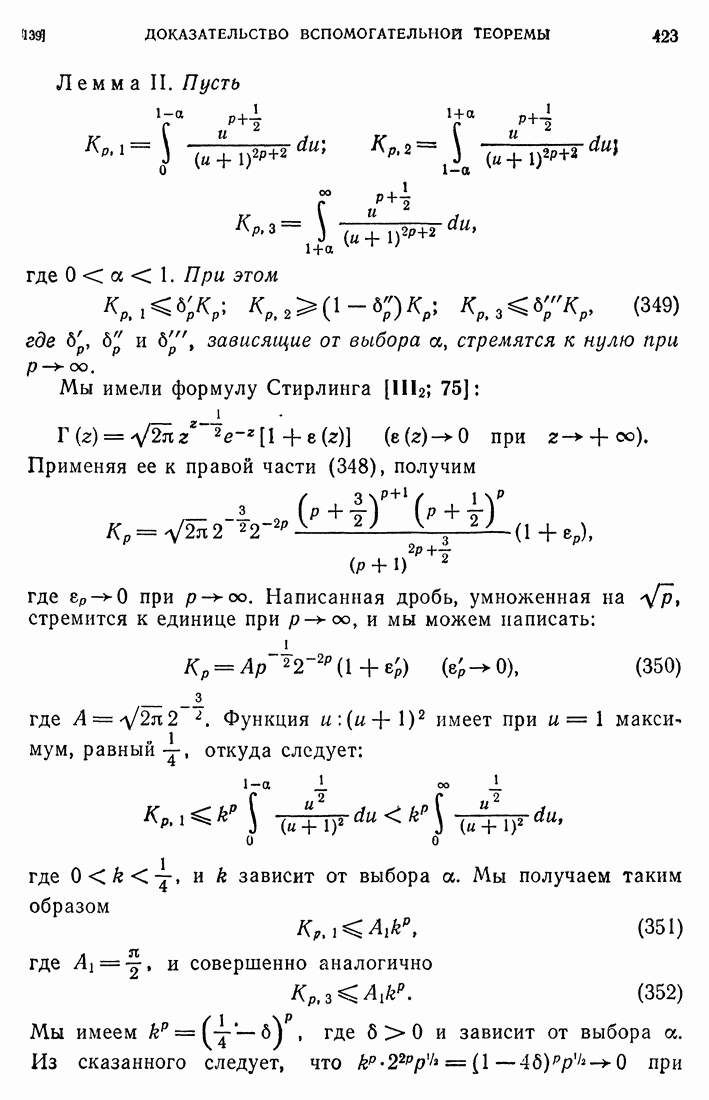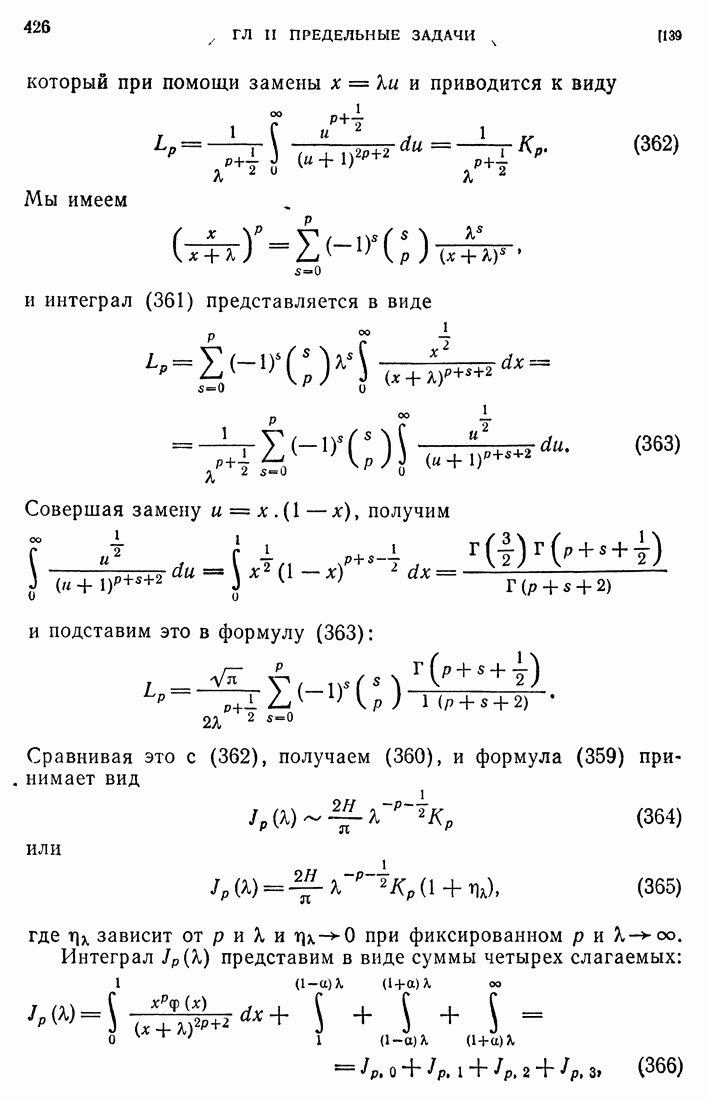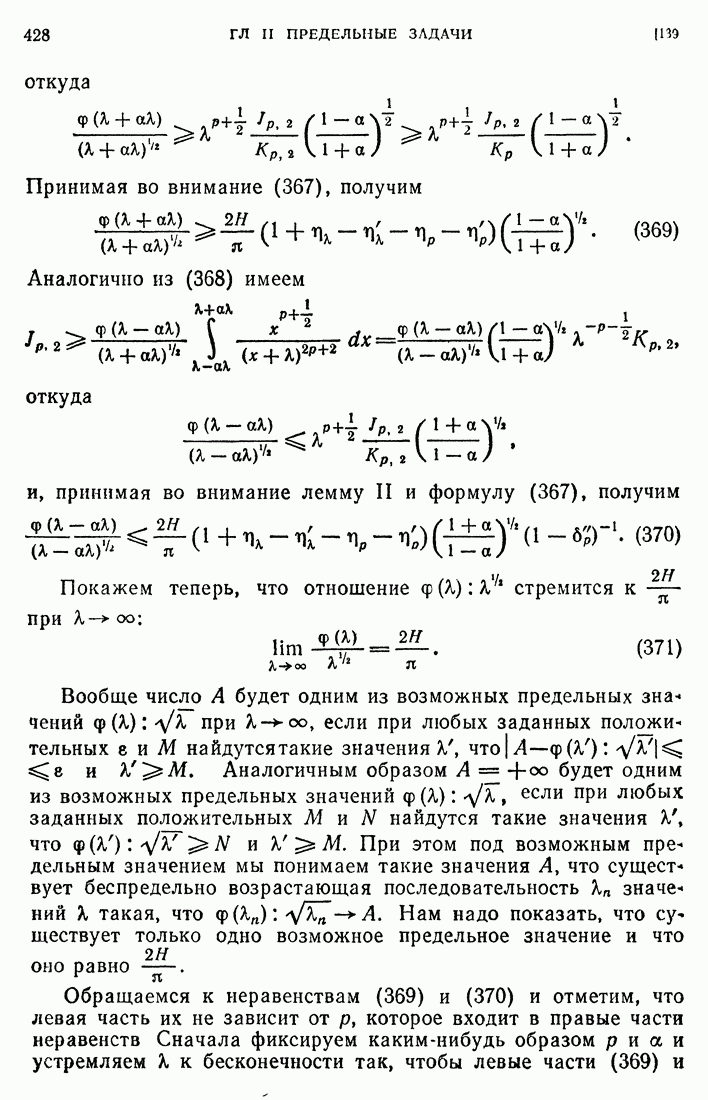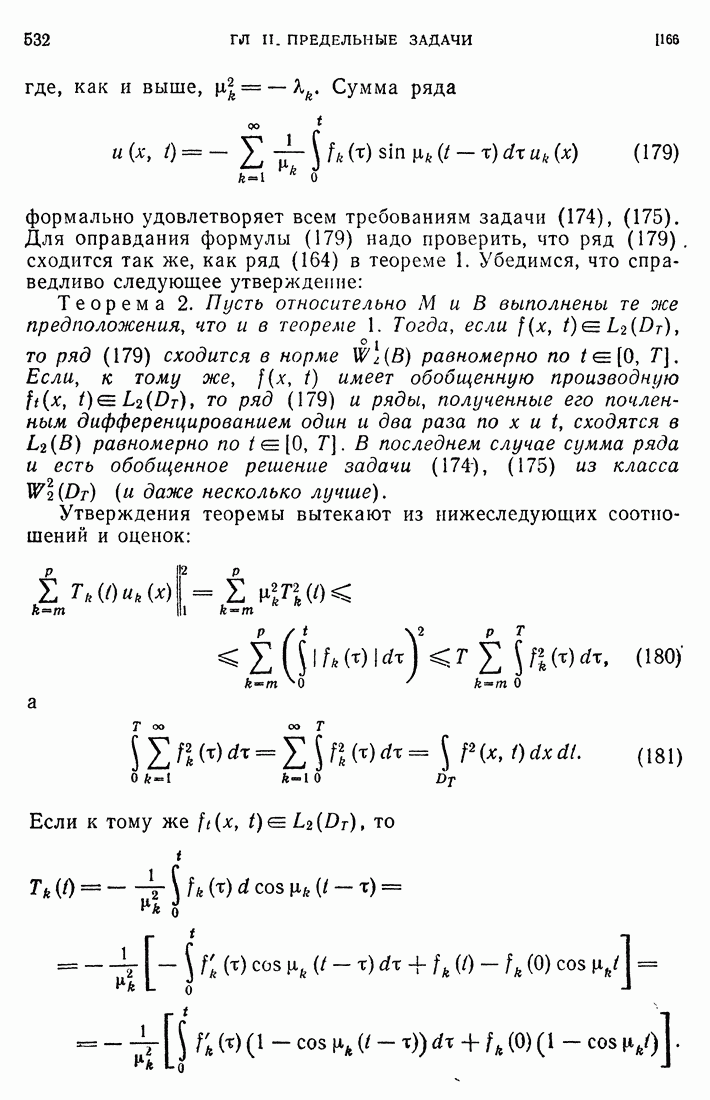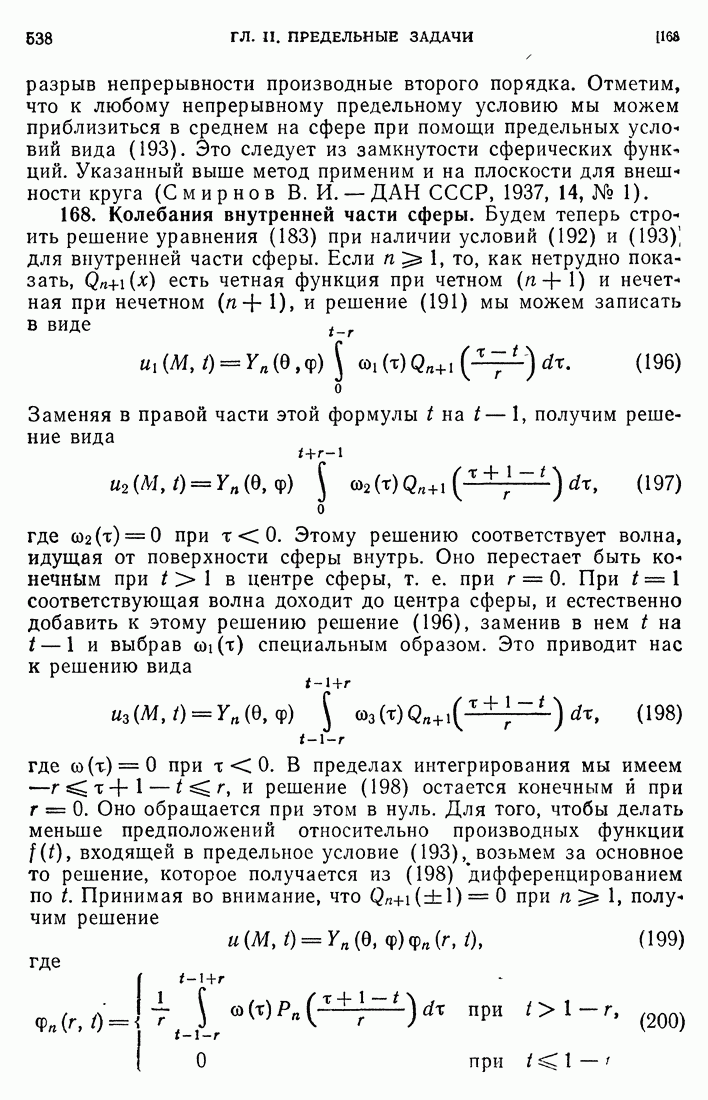| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
84. Уточненные теоремы разложения Стеклова.
В [77] мы получили теорему разложения по собственным функциям  уравнения (16). Предельные условия мы возьмем в виде
уравнения (16). Предельные условия мы возьмем в виде

Теоремы разложения по функциям  при весьма общих условиях, независимо от теории интегральных уравнений, даны в работах В А Стеклова. Относящиеся сюда результаты собраны в его книге «Основные задачи математической физики» т. I (Пгр, 1922). Мы приведем некоторые из полученных им результатов.
при весьма общих условиях, независимо от теории интегральных уравнений, даны в работах В А Стеклова. Относящиеся сюда результаты собраны в его книге «Основные задачи математической физики» т. I (Пгр, 1922). Мы приведем некоторые из полученных им результатов.
Лишь ради упрощения рассуждения будем предполагать, что  Это ограничение можно отбросить во всех пунктах [84] — [91] Пусть
Это ограничение можно отбросить во всех пунктах [84] — [91] Пусть  непрерывная функция, имеющая непрерывную производную в промежутке
непрерывная функция, имеющая непрерывную производную в промежутке  и удовлетворяющая
и удовлетворяющая
предельным условиям (54). Существование производной второго порядка не предполагается. Докажем предварительно формулу

Действительно, производя интегрирование по частям и пользуясь уравнением, которому удовлетворяют собственные функции

получим

Но внеинтегральный член равен нулю в силу  , а последний интеграл равен нулю в силу ортогональности собственных функций Рассмотрим теперь функционал
, а последний интеграл равен нулю в силу ортогональности собственных функций Рассмотрим теперь функционал

и подставим в него

где  — коэффициенты Фурье функции
— коэффициенты Фурье функции  :
:

Раскрывая скобки и принимая во внимание (22) и (55), получим

Производя в последнем интеграле интегрирование по частям и принимая во внимание, что, по условию,  , а также учитывая (56), получим
, а также учитывая (56), получим

Если предположить, что не только  но и
но и  , та из этой формулы непосредственно следует неравенство, аналогичное неравенству Бесселя:
, та из этой формулы непосредственно следует неравенство, аналогичное неравенству Бесселя:

и сходимость ряда, стоящего слева. Все члены этого ряда положительны, ибо  при
при  .
.
Отметим, что доказательство неравенства (61) полностью сохранится, если предположить, что непрерывная функция  имеет производную
имеет производную  везде в
везде в  кроме конечного числа точек
кроме конечного числа точек  причем производная непрерывна везде, кроме упомянутых точек, а в этих точках имеет конечные пределы слева и справа (разрыв первого рода). При интегрировании по частям достаточно интегрировать по промежуткам непрерывности
причем производная непрерывна везде, кроме упомянутых точек, а в этих точках имеет конечные пределы слева и справа (разрыв первого рода). При интегрировании по частям достаточно интегрировать по промежуткам непрерывности  и затем сложить все эти интегралы.
и затем сложить все эти интегралы.
Докажем теперь, что при сделанных выше относительно  предположениях ее ряд Фурье
предположениях ее ряд Фурье

регулярно сходится в промежутке  , т. е. что ряд
, т. е. что ряд

равномерно сходится в этом промежутке. Пользуясь интегральным уравнением

мы можем представить ряд (63) в виде

где

можно рассматривать как коэффициенты Фурье функции  аргумента Пользуясь неравенством (61), можем написать
аргумента Пользуясь неравенством (61), можем написать

где  есть производная
есть производная  по
по  . Все функции, стоящие под знаком интеграла, ограничены, и из (67) следует, что
. Все функции, стоящие под знаком интеграла, ограничены, и из (67) следует, что

где М — некоторая постоянная. Заменим  на и применим к отрезку ряда (65) неравенство Коши
на и применим к отрезку ряда (65) неравенство Коши

или

и из этого неравенства и сходимости ряда с членами непосредственно следует, что ряд (65) сходится равномерно на промежутке  , т. е. ряд (62) сходится регулярно. С другой стороны мы знаем, что его сумма равна
, т. е. ряд (62) сходится регулярно. С другой стороны мы знаем, что его сумма равна 
Приведем еще одно доказательство теоремы разложения без предположения  и при прежних предположениях относительно
и при прежних предположениях относительно  . Оно также принадлежит В. А. Стеклову. Вводя обозначение (58), докажем прежде всего, что существует такая постоянная С (не зависящая от
. Оно также принадлежит В. А. Стеклову. Вводя обозначение (58), докажем прежде всего, что существует такая постоянная С (не зависящая от  ), что
), что

Мы имеем

Интегрируя последний интеграл по частям и принимая во внимание (56), а также ортогональность  к функциям
к функциям  , получим
, получим

откуда, обозначая через  наибольшее значение
наибольшее значение  в промежутке
в промежутке  и применяя неравенство Буняковского, причем в первом интеграле заменяем
и применяя неравенство Буняковского, причем в первом интеграле заменяем  получим
получим

Принимая во внимание, что, в силу уравнения замкнутости,

мы получаем для  неравенство вида
неравенство вида

где  — положительные постоянные. Из этого неравенства видно, что
— положительные постоянные. Из этого неравенства видно, что  при возрастании
при возрастании  остается ограниченной, и мы получаем (69).
остается ограниченной, и мы получаем (69).
Далее из

следует, что

откуда, применяя неравенство Буняковского и считая  получим
получим

В случае  мы должны поменять пределы интегрирования
мы должны поменять пределы интегрирования  . Интегрируя обе части по
. Интегрируя обе части по  на промежутке
на промежутке  получим
получим

Обозначая через  наименьшее значение положительной функции
наименьшее значение положительной функции  в промежутке
в промежутке  можем написать, в силу (69), что
можем написать, в силу (69), что

и предыдущее неравенство дает

Правая часть не зависит от  и при беспредельном возрастании
и при беспредельном возрастании  стремится к нулю, откуда следует, что
стремится к нулю, откуда следует, что  равномерно в промежутке
равномерно в промежутке  т. е. ряд (62) равномерно сходится в этом промежутке и его сумма равна
т. е. ряд (62) равномерно сходится в этом промежутке и его сумма равна  Можно доказать и без предположения
Можно доказать и без предположения  что ряд (62) регулярно сходится.
что ряд (62) регулярно сходится.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
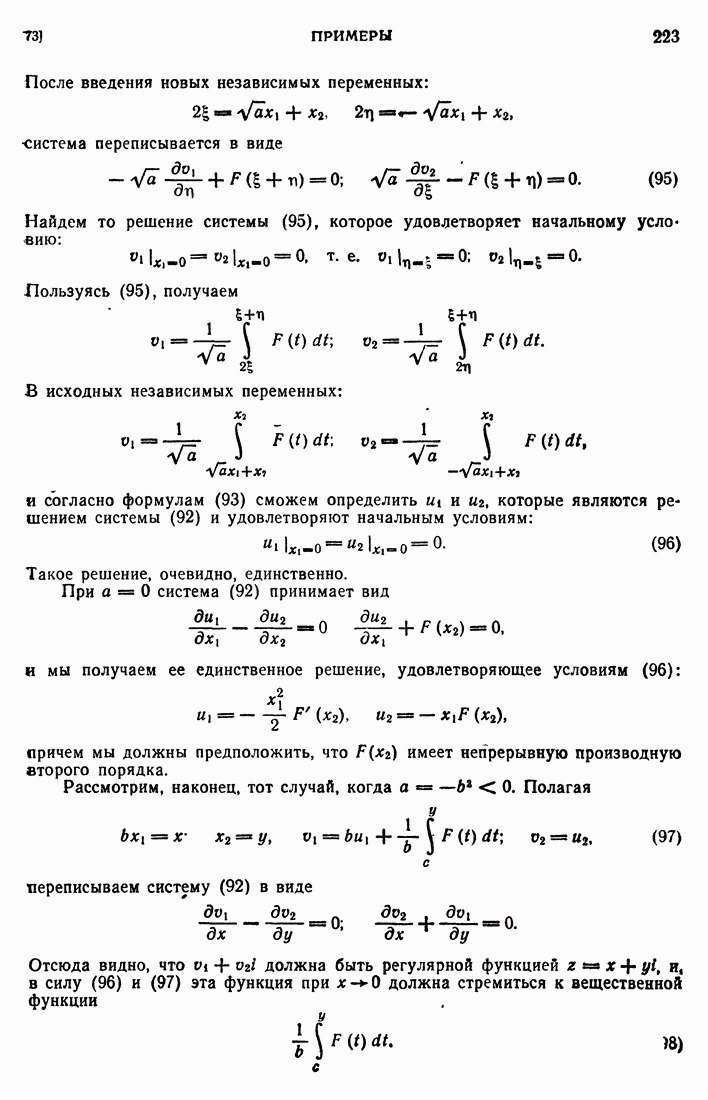
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
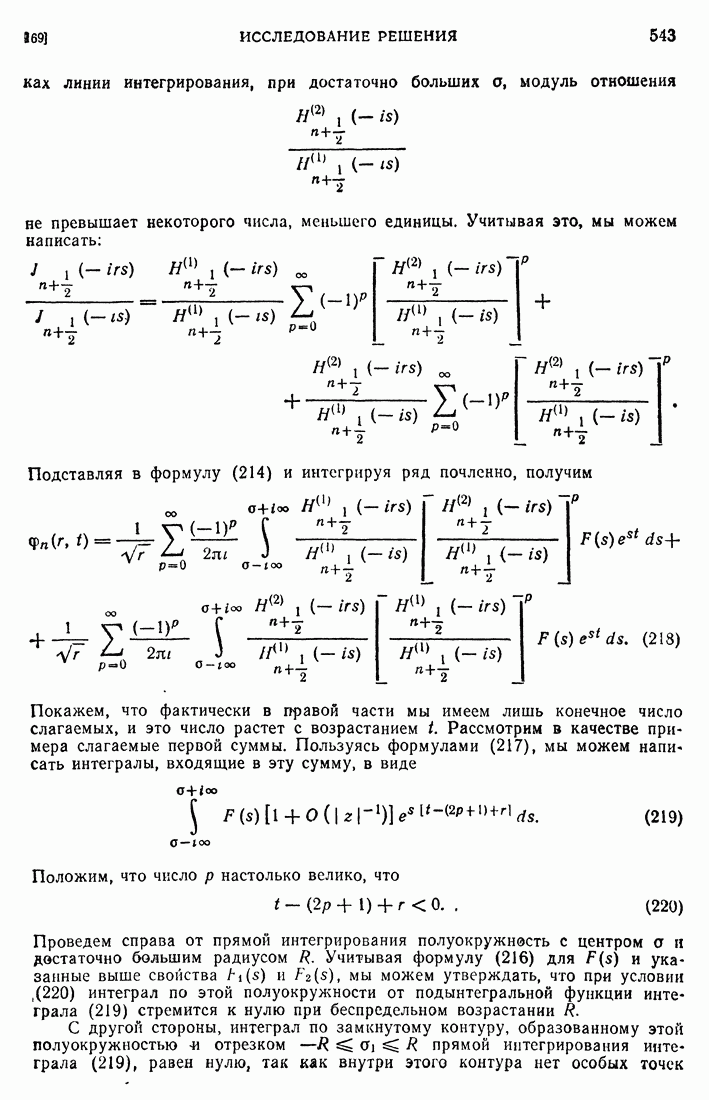
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.