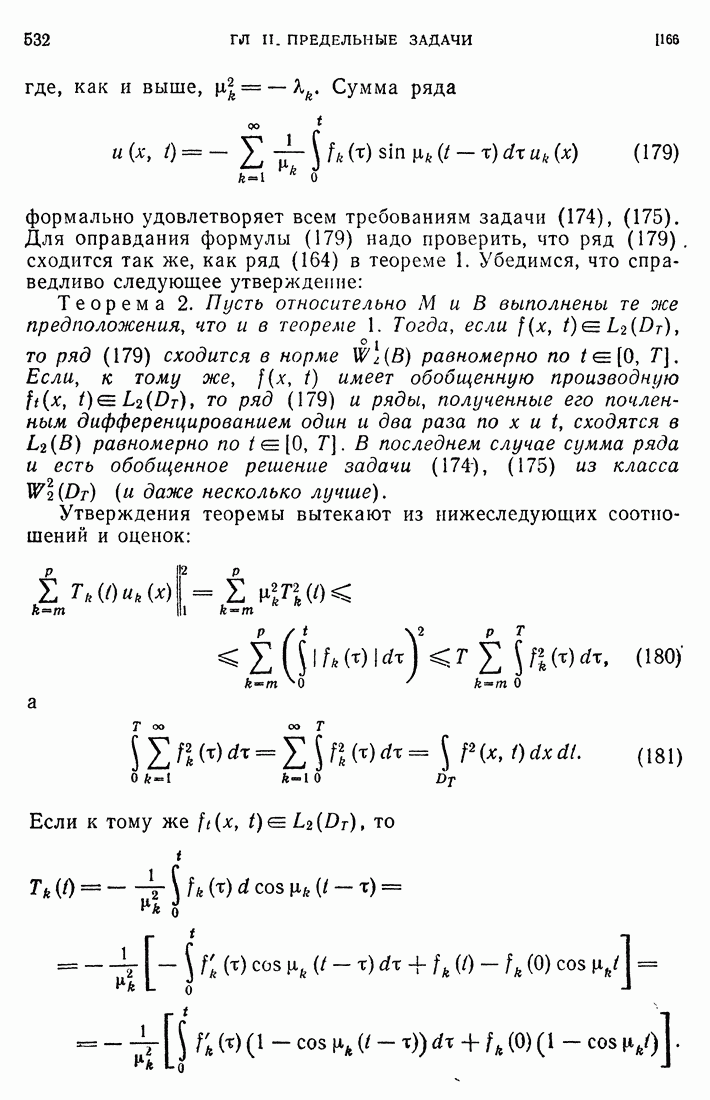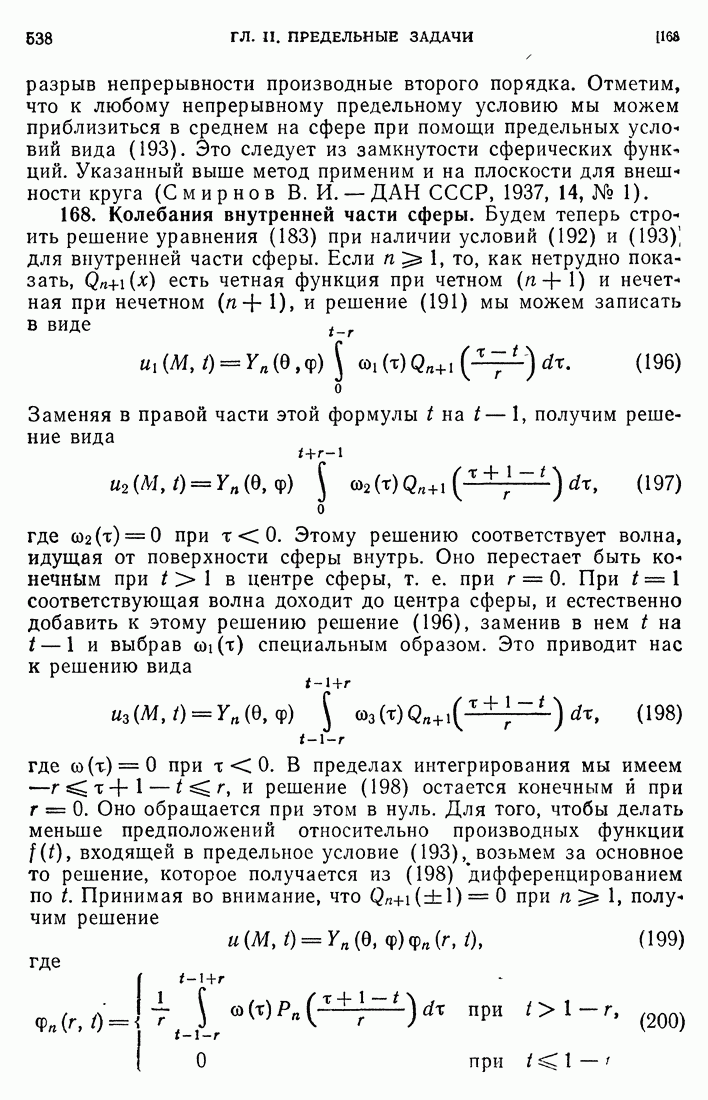| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
28. Теорема Ковалевской.
Указанный выше метод мажорантных рядов или функций применим и для доказательства существования и единственности решения задачи Коши для уравнений с частными производными. При этом мы будем брать всегда дифференциальные уравнения в разрешенной форме. Пусть имеется дифференциальное уравнение первого порядка

где  - регулярная функция в точке
- регулярная функция в точке

причем без ограничения общности мы приняли начальные значения независимых переменных равными нулю. Ищется решение уравнения, удовлетворяющее следующему условию Коши;

При этом мы счйтаем, что функция  регулярна при нулевых значениях своих аргументов и, кроме того,
регулярна при нулевых значениях своих аргументов и, кроме того,

и значок нуль, поставленный снизу, будет указывать всегда на то, что все аргументы функции заменены нулями. Прежде чем переходить к решению этой задачи, мы при помощи элементарной замены искомой функции упростим условия задачи, а именно введем вместо функции и новую искомую функцию  по формуле
по формуле

где постоянная А представляет собою значение правой части уравнения (205) при начальных значениях (206) аргументов, т. е., проще говоря, А есть свободный член в разложении правой части уравнения (205) в соответствующий степенной ряд

Новая искомая функция должна удовлетворять уравнению

и вместо начального условия (207) мы будем иметь начальное условие
Обратим внимание на аргументы функции, стоящей в правой части уравнения (209). Аргумент и  становится равным
становится равным  если положить все
если положить все  . Точно так же каждый из аргументов становится равным
. Точно так же каждый из аргументов становится равным  если
если

положить опять все  . Таким образом, аргументы
. Таким образом, аргументы  упомянутой функции при нулевых значениях
упомянутой функции при нулевых значениях  совпадают как раз с начальными значениями (208), при которых функция
совпадают как раз с начальными значениями (208), при которых функция  регулярна. Мы можем, таким образом, утверждать, что правая часть уравнения (209) есть регулярная функция в точке
регулярна. Мы можем, таким образом, утверждать, что правая часть уравнения (209) есть регулярная функция в точке

Кроме того, принимая во внимание вычитаемое, стоящее в правой части (209), мы можем утверждать, что эта правая часть обращается в нуль при начальных значениях (210) аргументов. Мы привели таким образом начальное значение Коши и все начальные значения аргументов у функции, стоящей в правой части уравнения, к нулю. Удерживая прежнее обозначение, мы получаем, таким образом, следующую задачу; имеется дифференциальное уравнение

где  — регулярная функция в точке
— регулярная функция в точке

равная нулю в этой точке, и ищется решение этого уравнения, удовлетворяющее условию

Заметим, что правая часть уравнения (211) должна разлагаться в ряд вида

сходящийся при всех значениях аргументов, достаточно близких к нулю.
Совершенно так же, как в случае обыкновенного дифференциального уравнения, мы будем, пользуясь уравнением (211) и начальным условием (212), вычислять коэффициенты ряда Маклорена искомой функции  т. е. значение всех частных производных при нулевых значениях аргументов. При дифференцировании по любому аргументу, кроме
т. е. значение всех частных производных при нулевых значениях аргументов. При дифференцировании по любому аргументу, кроме  мы можем предварительно положить
мы можем предварительно положить  .
.
Таким образом, начальное условие (212) показывает нам, что

где  какие угодно целые неотрицательные числа. Будем теперь вычислять начальные значения тех производных, в которые входит дифференцирование по
какие угодно целые неотрицательные числа. Будем теперь вычислять начальные значения тех производных, в которые входит дифференцирование по  Из уравнения (211) следует, что
Из уравнения (211) следует, что

Дифференцируя обе части уравнения (211) любое число раз по переменным  и вводя затем нулевые значения аргументов, мы в правой части будем иметь уже вычисленные значения производных (214) и (215) и таким образом определим
и вводя затем нулевые значения аргументов, мы в правой части будем иметь уже вычисленные значения производных (214) и (215) и таким образом определим

при любых неотрицательных значениях  . Возьмем теперь то уравнение, которое получится
. Возьмем теперь то уравнение, которое получится  уравнения (211) путем дифференцирования по и будем поступать с ним так же, как мы поступали с основным уравнением. Это даст нам вполне определенные значения для производных
уравнения (211) путем дифференцирования по и будем поступать с ним так же, как мы поступали с основным уравнением. Это даст нам вполне определенные значения для производных

Поступая так и дальше, мы можем вычислить любую частную производную искомой функции при начальных значениях аргументов и составить ряд Маклорена

Предыдущие рассуждения так же, как и в случае обыкновенного дифференциального уравнения, доказывают единственность регулярного решения поставленной задачи Коши. Для доказательства существования нам надо обнаружить, что при подстановке полученных начальных значений производных в ряд (216) он сходится в некоторых кругах с центром в начале. Совершенно так же, как и в предыдущем параграфе, можно утверждать, что если мы заменим ряд (213) мажорантным рядом, и если для полученного мажорантного уравнения составленный указанным выше образом ряд (216) будет сходящимся, то тем более он будет сходящимся и для первоначального уравнения. Положим, что ряд (213) абсолютно и равномерно сходится при условии:

и пусть М — наибольшее значение модуля суммы этого ряда при этих условиях. Функция

будет мажорантной для (213), причем мы вычли в правой части предыдущей формулы число М, чтобы избавиться от
свободного члена, который отсутствует и в ряде (213). Тем более мажорантной для ряда (213) будет функция

Если мы разделим переменную  на некоторое число а, удовлетворяющее условию
на некоторое число а, удовлетворяющее условию  , то различные степени этого числа появятся в знаменателях коэффициентов членов, содержащих степени
, то различные степени этого числа появятся в знаменателях коэффициентов членов, содержащих степени  и функция
и функция

будет и подавно мажорантной для (213). Мы имеем, таким образом, мажорантное уравнение

Вычисляя коэффициенты Маклорена для решения этого уравнения, удовлетворяющего начальному условию (212), мы получим степенной ряд, обращающийся в нуль при  и мажорантный для ряда (216), составленного для уравнения (211), Если этот ряд окажется сходящимся, то тем более будет сходиться ряд (216), составленный для уравнения (211). Мы строим сейчас решение уравнения (217), которое удовлетворяет не нулевому начальному условию, а условию
и мажорантный для ряда (216), составленного для уравнения (211), Если этот ряд окажется сходящимся, то тем более будет сходиться ряд (216), составленный для уравнения (211). Мы строим сейчас решение уравнения (217), которое удовлетворяет не нулевому начальному условию, а условию

где  степенной ряд с неотрицательными коэффициентами. Последовательное вычисление коэффициентов Маклорена для такого решения может быть произведено совершенно так же, как и выше, но только начальное условие (218) приведет к тому, что в правой части формул (214) при всех неотрицательных значениях а будут стоять уже не нули, а некоторые неотрицательные числа. Вычисление дальнейших коэффициентов производится, как и выше, и приводит к действиям сложения и умножения над уже полученными неотрицательными коэффициентами и положительными коэффициентами в разложении правой части уравнения (218). Таким образом, если мы для уравнения (217) заменим нулевое начальное условие (212) начальным
степенной ряд с неотрицательными коэффициентами. Последовательное вычисление коэффициентов Маклорена для такого решения может быть произведено совершенно так же, как и выше, но только начальное условие (218) приведет к тому, что в правой части формул (214) при всех неотрицательных значениях а будут стоять уже не нули, а некоторые неотрицательные числа. Вычисление дальнейших коэффициентов производится, как и выше, и приводит к действиям сложения и умножения над уже полученными неотрицательными коэффициентами и положительными коэффициентами в разложении правой части уравнения (218). Таким образом, если мы для уравнения (217) заменим нулевое начальное условие (212) начальным
условием (218), где  разлагается в ряд с вещественными неотрицательными коэффициентами, то ряд (216) для уравнения (217) с начальным условием (218) будет мажорантным по отношению к ряду (216) для уравнения (217) с нулевым начальным условием (212) и тем более мажорантным по отношению к ряду (216) для уравнения (211) с начальным условием (212). Таким образом, все сводится к доказательству того, что ряд (216) для уравнения (217) с каким-либо начальным условием вида (218), где
разлагается в ряд с вещественными неотрицательными коэффициентами, то ряд (216) для уравнения (217) с начальным условием (218) будет мажорантным по отношению к ряду (216) для уравнения (217) с нулевым начальным условием (212) и тем более мажорантным по отношению к ряду (216) для уравнения (211) с начальным условием (212). Таким образом, все сводится к доказательству того, что ряд (216) для уравнения (217) с каким-либо начальным условием вида (218), где  обладает указанным выше свойством, будет сходящимся внутри некоторых кругов с центром в начале.
обладает указанным выше свойством, будет сходящимся внутри некоторых кругов с центром в начале.
Иначе говоря, все дело сводится к построению решения уравнения (217), удовлетворяющего условию вида (218), и к доказательству того, что это решение разлагается в ряд Маклорена, если  достаточно близки к нулю. Будем искать такое решение, как функцию только одного аргумента
достаточно близки к нулю. Будем искать такое решение, как функцию только одного аргумента 

и, следовательно, уравнение (217) примет вид

или

Будем считать, что число а взята настолько близким к нулю, что коэффициент при положителен. В правой части написанного равенства мы получим, разлагая по формуле прогрессии, степенной ряд без свободного члена с положительными коэффициентами. Последнее уравнение может быть записано в виде

где  - степенной ряд без свободного члена с положительными коэффициентами. Решая относительно
- степенной ряд без свободного члена с положительными коэффициентами. Решая относительно  , получим уравнение первого порядка
, получим уравнение первого порядка

причем радикал надо считать равным единице при  Разлагая по биному Ньютона, мы получим
Разлагая по биному Ньютона, мы получим

и все коэффициенты при степенях  оказываются положительными. Переразлагая по степеням z и
оказываются положительными. Переразлагая по степеням z и  мы получим в правой части уравнения (219) степенной ряд
мы получим в правой части уравнения (219) степенной ряд  с положительными коэффициентами и без свободного члена и придем к уравнению первого порядка
с положительными коэффициентами и без свободного члена и придем к уравнению первого порядка

Мы уже имели теорему о существовании регулярного решения такого уравнения, удовлетворяющего начальному условию  . Это решение будет представляться рядом
. Это решение будет представляться рядом

все коэффициенты которого положительны. Если в написанном разложении пбдетавить  то получим решение уравнения (217), представимое степенным рядом с положительными коэффициентами. Это решение будет удовлетворять, при
то получим решение уравнения (217), представимое степенным рядом с положительными коэффициентами. Это решение будет удовлетворять, при  некоторому начальному условию (218), где
некоторому начальному условию (218), где  степенной ряд с положительными коэффициентами. В силу сказанного выше, построение такого решения уравнения (216) доводит до конца доказательство существования решения задачи Коши. Приведенное доказательство принадлежит Гурса. Сама теорема называется обычно теоремой Ковалевской, так как впервые в законченной форме ее доказательство было дано С. В. Ковалевской.
степенной ряд с положительными коэффициентами. В силу сказанного выше, построение такого решения уравнения (216) доводит до конца доказательство существования решения задачи Коши. Приведенное доказательство принадлежит Гурса. Сама теорема называется обычно теоремой Ковалевской, так как впервые в законченной форме ее доказательство было дано С. В. Ковалевской.
Из приведенного выше доказательства следует, что радиусы тех кругов для переменных  , внутри которых установлена сходимость ряда (216), дающего решения задачи (211), (212), зависят лишь от радиусов сходимости правой части уравнения (213) и максимума модуля М этой правой части, но не зависят от конкретного вида функции
, внутри которых установлена сходимость ряда (216), дающего решения задачи (211), (212), зависят лишь от радиусов сходимости правой части уравнения (213) и максимума модуля М этой правой части, но не зависят от конкретного вида функции  Для (205), (207) присоединяется еще зависимость от радиусов сходимости и максимума модуля функции
Для (205), (207) присоединяется еще зависимость от радиусов сходимости и максимума модуля функции  входящей в условие (207). Аналогичное замечание имеет место и для результатов следующего параграфа.
входящей в условие (207). Аналогичное замечание имеет место и для результатов следующего параграфа.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
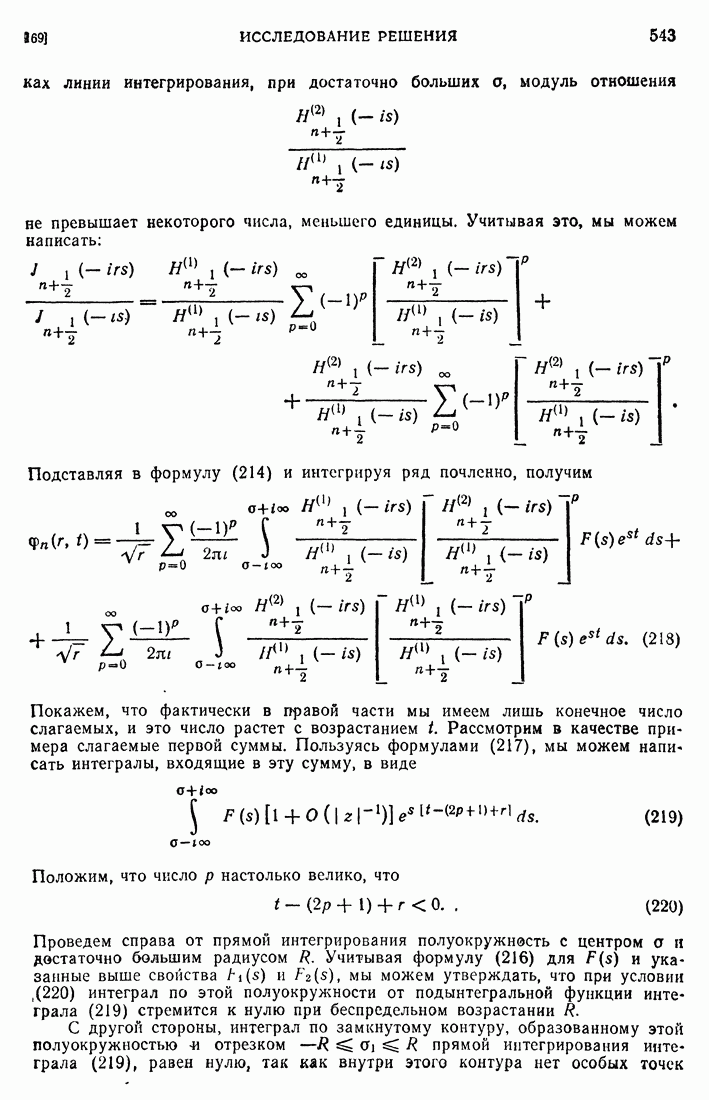
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.