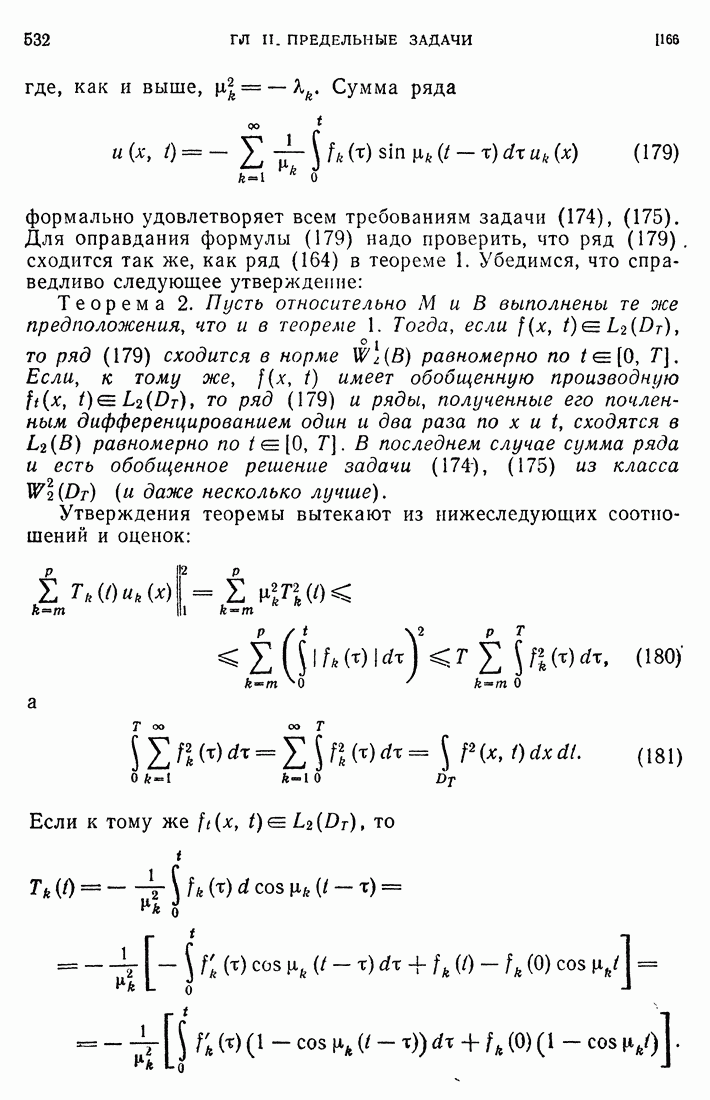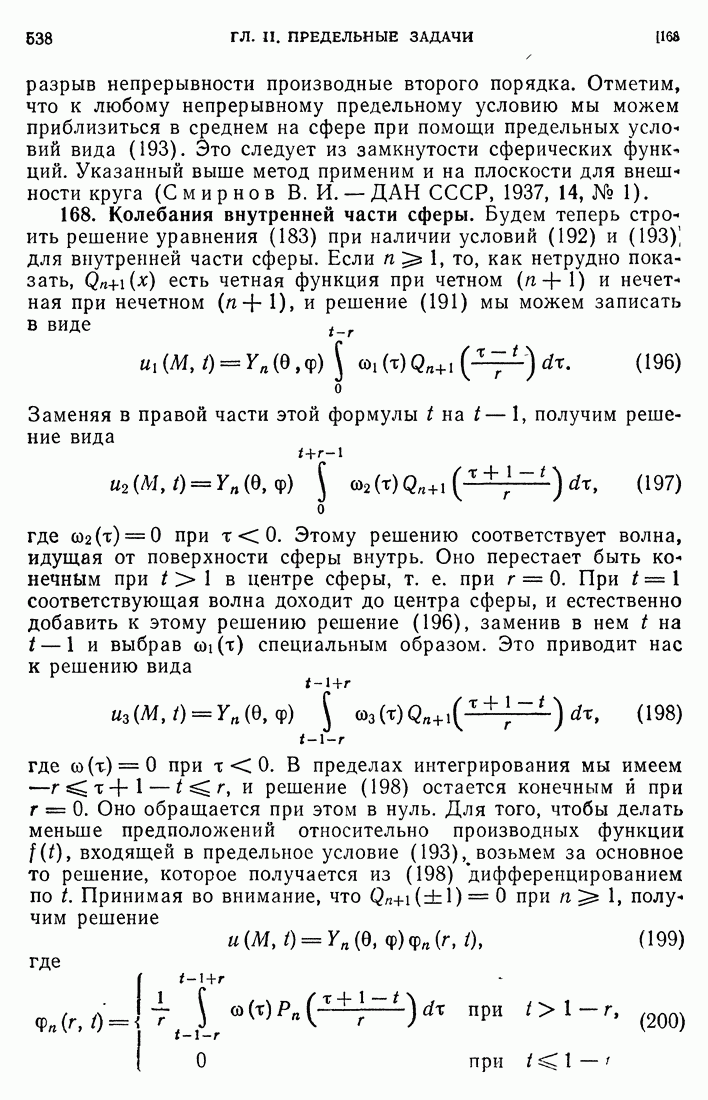| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
В [152] мы изложили решение предельной задачи в полуполосе, ограниченной снизу характеристикой  уравнения (5), а сбоку прямыми
уравнения (5), а сбоку прямыми  Рассмотрим теперь область на плоскости
Рассмотрим теперь область на плоскости  которая ограничена
которая ограничена
снизу характеристикой  , а сбоку — двумя линиями h с явным уравнением (рис. 16):
, а сбоку — двумя линиями h с явным уравнением (рис. 16):

причем  имеют непрерывные производные при
имеют непрерывные производные при  . Для решения задачи в такой области нам надо построить обобщенные потенциалы простого и двойного слоя, которые при
. Для решения задачи в такой области нам надо построить обобщенные потенциалы простого и двойного слоя, которые при  обращаются в потенциалы, указанные в [152]. Эти обобщенные потенциалы имеют вид
обращаются в потенциалы, указанные в [152]. Эти обобщенные потенциалы имеют вид

где  непрерывные функции.
непрерывные функции.
Функции  имеют непрерывные производные и удовлетворяют уравнению (5) везде вне линии
имеют непрерывные производные и удовлетворяют уравнению (5) везде вне линии  Оба потен циала имеют смысл и в том случае, когда точка
Оба потен циала имеют смысл и в том случае, когда точка  находится на линии U. Для потенциала
находится на линии U. Для потенциала  это непосредственно очевидно, так как подынтегральная функция имеет оценку
это непосредственно очевидно, так как подынтегральная функция имеет оценку  где С — постоянная. Для потенциала
где С — постоянная. Для потенциала  если точка
если точка  находится на U, мы можем написать:
находится на U, мы можем написать:

откуда и следует сходимость интеграла (95).

Рис. 16.
Величина интеграла (94) по малому участку:  стремится к нулю при
стремится к нулю при  при любом положении точки
при любом положении точки  и отсюда непосредственно следует, что
и отсюда непосредственно следует, что  непрерывна вплоть до
непрерывна вплоть до  . Для интеграла (95) существуют различные пределы при стремлении
. Для интеграла (95) существуют различные пределы при стремлении  к точке
к точке  лежащей на а именно:
лежащей на а именно:

где  значение интеграла (95) в самой точке
значение интеграла (95) в самой точке  знак
знак  надо брать, если
надо брать, если  справа от и знак
справа от и знак
(—), если  слева от Если
слева от Если  то очевидно, что
то очевидно, что  и мы получаем результат из [152). При доказательстве формулы (96) мы не будем писать знак i. Рассмотрим интеграл (95) при
и мы получаем результат из [152). При доказательстве формулы (96) мы не будем писать знак i. Рассмотрим интеграл (95) при 

и функцию

Вводя вместо новую переменную интегрирования

получим

причем в верхнем пределе надо брать знак  если
если  и знак (—), если
и знак (—), если  . Если точка
. Если точка  лежит на
лежит на  , то
, то

Из определения  непосредственно следует, как и выше, что
непосредственно следует, как и выше, что  непрерывна вплоть до
непрерывна вплоть до  . Из (90) следует
. Из (90) следует

в, вычитая почленно формулу (100) из последней формулы, получим

т. е.

А мы получили формулу (96) при  .
.
Переходим к общему случаю. Перепишем выражение  в виде
в виде

Совершенно так же, как и в [95], достаточно показать, что первое слагаемое сохраняет непрерывность, когда точка  пересекает
пересекает  в точке
в точке  . Пусть
. Пусть  — заданное положительное число. Выберем положительное
— заданное положительное число. Выберем положительное  настолько малым, чтобы имело место неравенство
настолько малым, чтобы имело место неравенство

и разобьем промежуток интегрирования  части
части  Функция, которая выражается интегралом по первому из этих промежутков, непрерывна в точке
Функция, которая выражается интегралом по первому из этих промежутков, непрерывна в точке  и достаточно показать, что интеграл
и достаточно показать, что интеграл

достаточно мал при всех положениях точки  если она достаточно близка к точке
если она достаточно близка к точке  или совпадает с ней. Указанный интеграл по абсолютной величине не превосходит
или совпадает с ней. Указанный интеграл по абсолютной величине не превосходит

Предположим, что разность  меняет знак не больше чем k раз, где k — определенное целое положительное число» при
меняет знак не больше чем k раз, где k — определенное целое положительное число» при  и произвольном положении (х, t) в некоторой окрестности
и произвольном положении (х, t) в некоторой окрестности  При этом интеграл
При этом интеграл

представится как сумма не более чем к интегралов вида

которые отличаются от интегралов 

которая по абсолютной величине не превышает некоторой постоянной. Таким образом, упомянутый выше интеграл остается ограниченным, когда  находится в некоторой окрестности
находится в некоторой окрестности  . Этот интеграл умножается на
. Этот интеграл умножается на  , и тем самым доказательство того, что первое слагаемое правой части формулы (101) непрерывно, когда
, и тем самым доказательство того, что первое слагаемое правой части формулы (101) непрерывно, когда  пересекает l в точке
пересекает l в точке  доводится до конца совершенно так же, как и в [95]. Пользуясь указанными выше потенциалами, можно привести предельную задачу для области, указанной на рис. 16, к интегральному уравнению, как это мы делали в [152]. Положим, что условия таковы:
доводится до конца совершенно так же, как и в [95]. Пользуясь указанными выше потенциалами, можно привести предельную задачу для области, указанной на рис. 16, к интегральному уравнению, как это мы делали в [152]. Положим, что условия таковы:  на характеристике
на характеристике  на
на  Будем искать решение в виде
Будем искать решение в виде

При этом для всяких  удовлетворяется уравнение (5) и предельное условие на характеристике
удовлетворяется уравнение (5) и предельное условие на характеристике  , а из предельных условий на
, а из предельных условий на  получаем систему интегральных уравнений Вольтерра для
получаем систему интегральных уравнений Вольтерра для

Рассмотрим интегралы, входящие в первое уравнение:

В интеграле (104) полярность при  снижается за счет числителя отношения
снижается за счет числителя отношения

совершенно так же, как это было отмечено нами выше. Во втором интеграле показатель  при
при  стремится к
стремится к  и это полностью снимает полярность. Аналогично рассматриваются интегралы и для второго из уравнений (103). Таким образом, система (103) имеет единственное решение и может быть решена методом последовательных приближений.
и это полностью снимает полярность. Аналогично рассматриваются интегралы и для второго из уравнений (103). Таким образом, система (103) имеет единственное решение и может быть решена методом последовательных приближений.
Можно искать решение указанной выше предельной задачи и в виде суммы двух потенциалов простого слоя:

При этом мы приходим к системе интегральных уравнений первого рода:

Умножим обе части на  и проинтегрируем по t от
и проинтегрируем по t от  до
до 

где

причем справа мы изменили порядок интегрирования и воспользовались формулой Дирихле [II; 82]. Система (108) эквивалентна (107) (ср. [II, 82]). Мы
имеем, очевидно,

и, принимая во внимание формулу [II; 79]

мы получаем

Дифференцируец систему (108) по причем мы считаем, что  имеют непрерывны производные, и при этом функции
имеют непрерывны производные, и при этом функции  имеют также непрерывные производные [II; 83]:
имеют также непрерывные производные [II; 83]:

Для вычисления производных представим  в виде
в виде

Интегрируя по частям и дифференцируя по у, получим

При  сходимость интеграла на пределе
сходимость интеграла на пределе  обеспечивается показательной функцией, а при
обеспечивается показательной функцией, а при  дробь, стоящая в фигурных скобках, не имеет полярности и вся фигурная скобка стремится к нулю, как
дробь, стоящая в фигурных скобках, не имеет полярности и вся фигурная скобка стремится к нулю, как  . Учитывая все
. Учитывая все  и производя элементарные оценки подынтегральной функции при
и производя элементарные оценки подынтегральной функции при  нетрудно убедиться, что интегралы мажорируются функцией
нетрудно убедиться, что интегралы мажорируются функцией

где  — некоторая постоянная. Отсюда видно, что
— некоторая постоянная. Отсюда видно, что

где  непрерывные функции
непрерывные функции  и к системе
и к системе  применим метод последовательных приближений
применим метод последовательных приближений  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
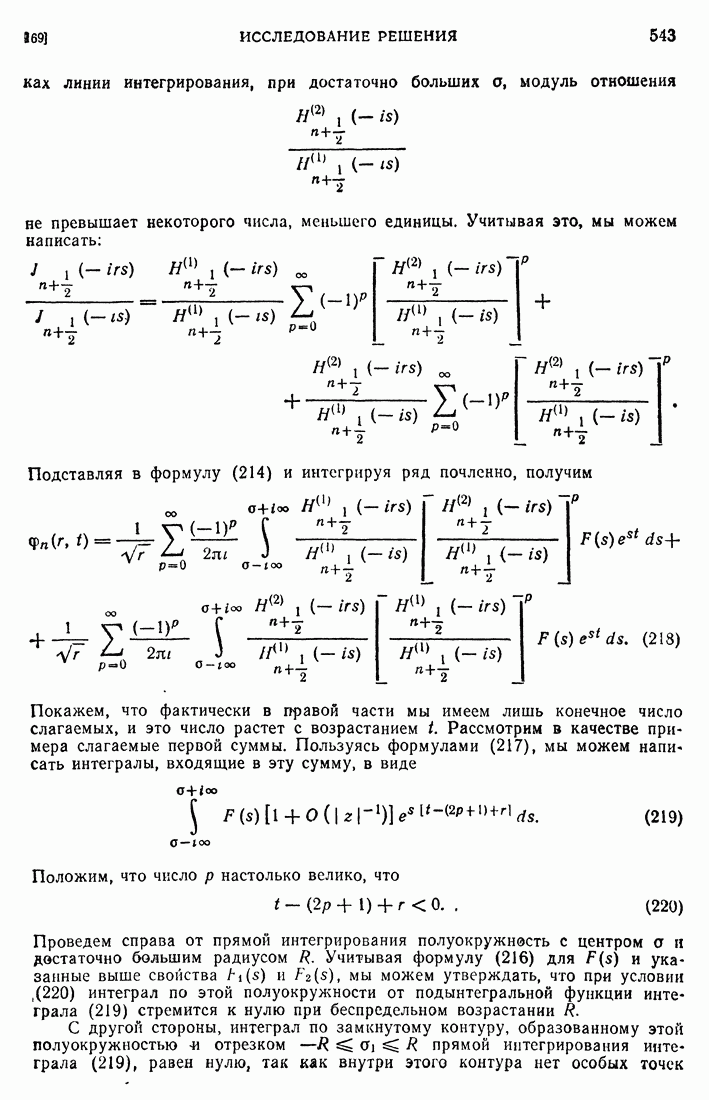
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.