| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
7.3.2. Вакансии, сгруппированные в кластеры
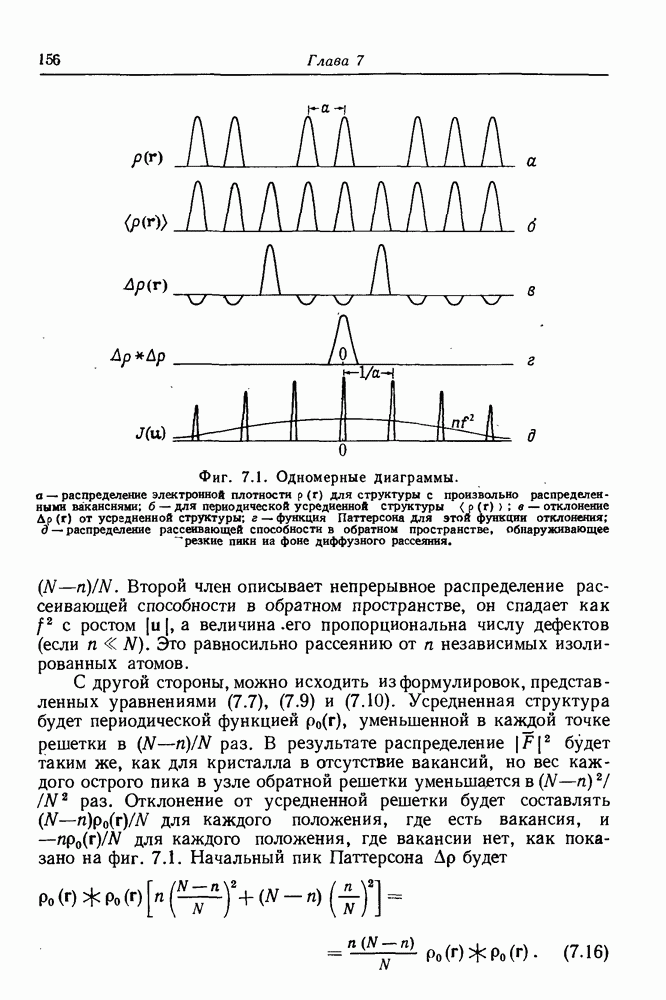
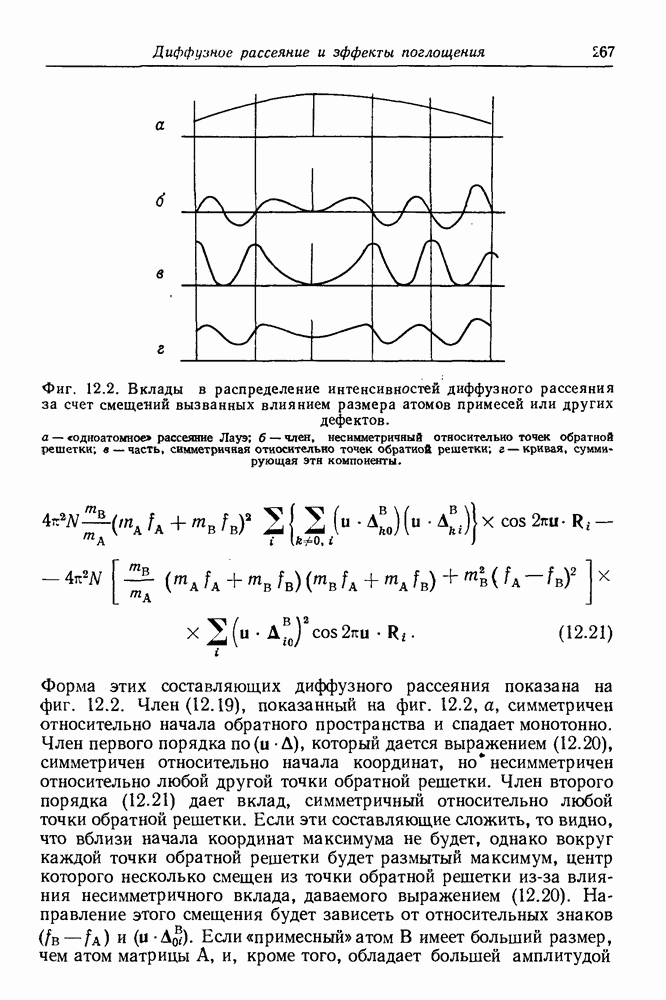
Особым преимуществом рассмотрения рассеяния с помощью функции Паттерсона является возможность немедленной оценки формы диффузного рассеяния для любого вида дефекта и во многих случаях быстрой количественной оценки величины функции рассеивающей способности.
Возьмем, например, случай, подобный рассмотренному в разд. 7.3.1, но с тем отличием, что вакансии распределены не случайно, а до некоторой степени преимущественно и образуют группы — кластеры. Будем считать, что эти вакансии образуют пары, параллельные общей оси. Для такого же общего числа вакансий  усредненная структура, а также
усредненная структура, а также  будут в точности такие же, как в разд. 7.3.1.
будут в точности такие же, как в разд. 7.3.1.
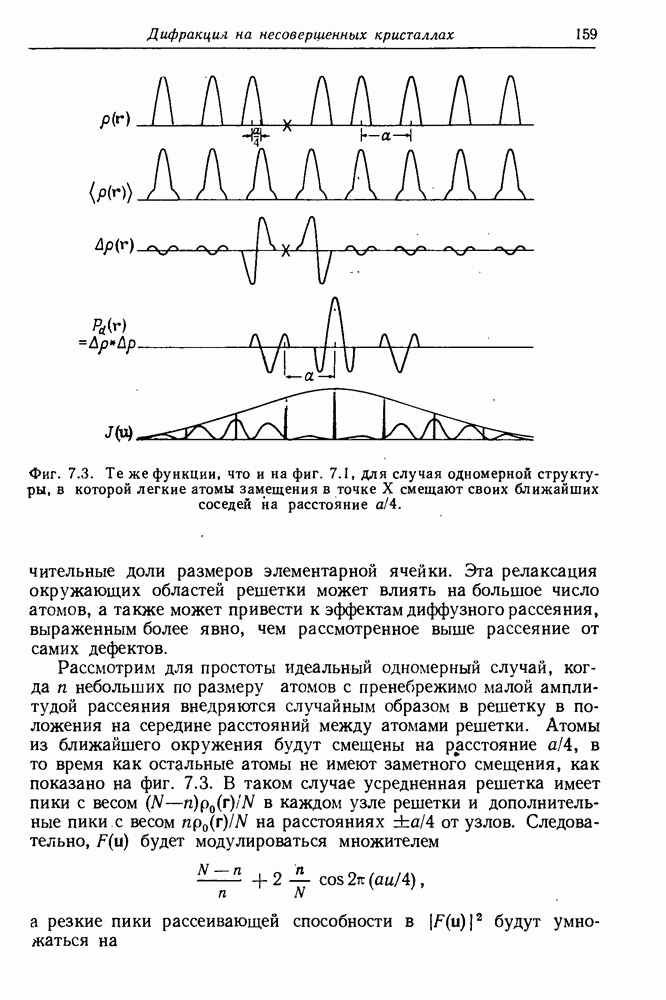
Начальный пик  будет таким же, как и в разд. 7.3.1, и не будет никакой корреляции для межатомных векторов, величина которых превышает расстояние до ближайшего соседа, как показано на фиг. 7.2; на расстояниях, соответствующих расстояниям до ближайших соседей, будут находиться пики с весом
будет таким же, как и в разд. 7.3.1, и не будет никакой корреляции для межатомных векторов, величина которых превышает расстояние до ближайшего соседа, как показано на фиг. 7.2; на расстояниях, соответствующих расстояниям до ближайших соседей, будут находиться пики с весом  поскольку вероятность нахождения какой-либо вакансии на расстоянии а от данной вакансии составляет половину
поскольку вероятность нахождения какой-либо вакансии на расстоянии а от данной вакансии составляет половину

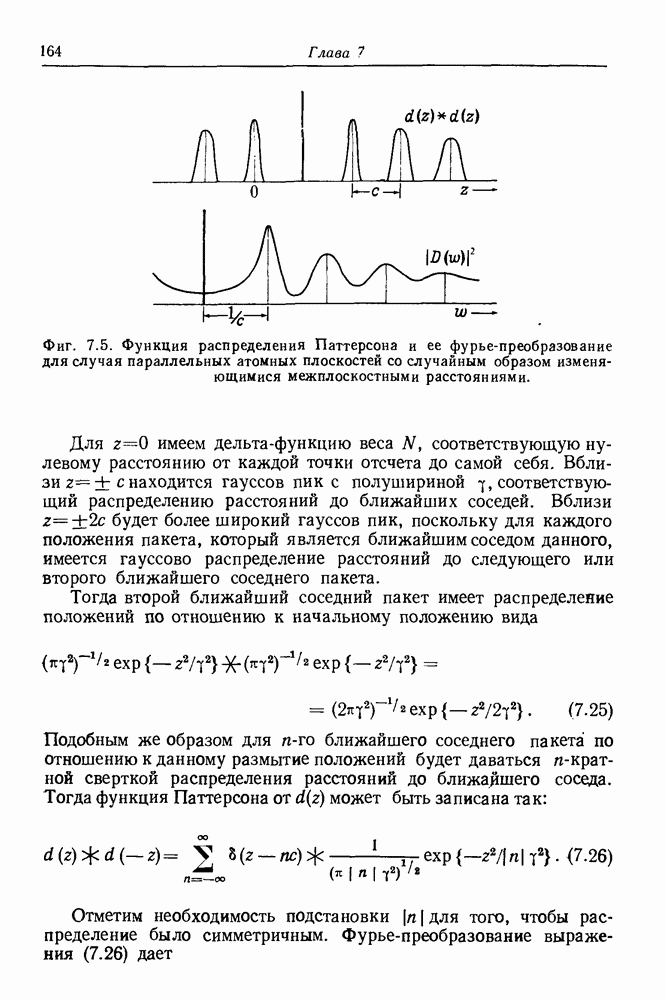
Фиг. 7.2. Отклонение от усредненной структуры, соответствующая функция, Паттерсона и распределение рассеивающей способности для случая, подобного представленному на фиг. 7.1, когда вакансии встречаются парами.
вероятности нахождения вакансии на нулевом расстоянии. Тогда диффузное рассеяние будет модулироваться с периодичностью  и
и

Если в одном направлении попадутся прямые, соединяющие более двух вакансий, то корреляция таких векторов будет давать пики на функции Паттерсона дефектной решетки дальше от начала координат, а модуляция функции диффузного рассеяния будет обладать более резкими пиками вблизи положений в обратной решетке. Подобным же образом при стремлении к образованию трехмерных скоплений вакансий функция Паттерсона будет обнаруживать корреляцию в трех измерениях, а модуляция диффузной части интенсивности будет появляться во всех направлениях.
Эта простая теория с весьма незначительными изменениями применима для определения рассеяния от кристаллов с атомами внедрения, расположенными беспорядочно или кластерами, занимающими правильные атомные положения (твердый раствор замещения).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ГЛАВА 1. Дифракция Френеля и Фраунгофера
- 1.2. Волновые уравнения и волны
- 1.2.2. Электромагнитные волны
- 1.2.3. Волны-частицы
- 1.3. Суперпозиция и когерентность
- 1.3.2. Независимые точенные источники
- 1.4. Принцип Гюйгенса
- 1.4.2. Применение формулы Кирхгофа
- 1.5. Подход с точки зрения теории рассеяния
- 1.5.1. Интегральная форма волнового уравнения
- 1.5.2. Ряд Борна
- 1.6. Принцип взаимности
- 1.7. Дифракция Френеля
- 1.7.2. Интегралы Френеля
- 1.7.3. Периодические объекты — «фурье-изображения»
- 1.8. Дифракция Фраунгофера
- ГЛАВА 2. Фурье-преобразования и свертки
- 2.1.1. Дельта-функция и непрерывность
- 2.1.2. Свертки
- 2.1.3. Примеры сверток
- 2.2. Фурье-преобразования: общее рассмотрение
- 2.2.2. Свойства фурье-преобразований
- 2.2.3. Умножение и свертка
- 2.2.4. Пространство и время
- 2.3. Фурье-преобразования и дифракция: примеры
- 2.3.2. Плоская волна: преобразование, обратное рассмотренному в разд. 2.3.1.
- 2.3.3. Трансляция объекта
- 2.3.4. Функция щели
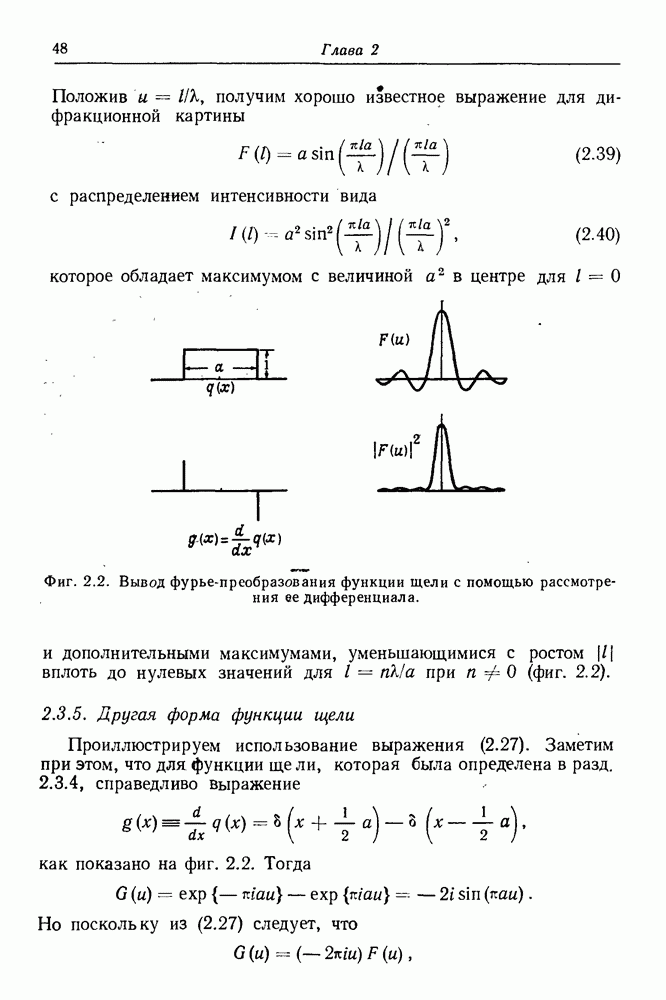
- 2.3.5. Другая форма функции щели
- 2.3.6. Прямолинейный край
- 2.3.7. Прямоугольная апертура
- 2.3.8. Круглая апертура
- 2.3.9. Две очень узкие щели
- 2.3.10. Две щели заметной ширины
- 2.3.11. Конечный цуг волн
- 2.3.12. Периодическая последовательность узких щелей
- 2.3.13. Произвольная периодическая функция
- 2.3.14. Дифракционная решетка: тонкие щели
- 2.3.15. Дифракционная решетка: общее рассмотрение
- 2.3.16. Функция Гаусса
- 2.3.17. Ряд круглых отверстий
- 2.3.18. Дополнительные объекты — теорема Бабине
- 2.3.19. Полные интенсивности: теорема Парсеваля
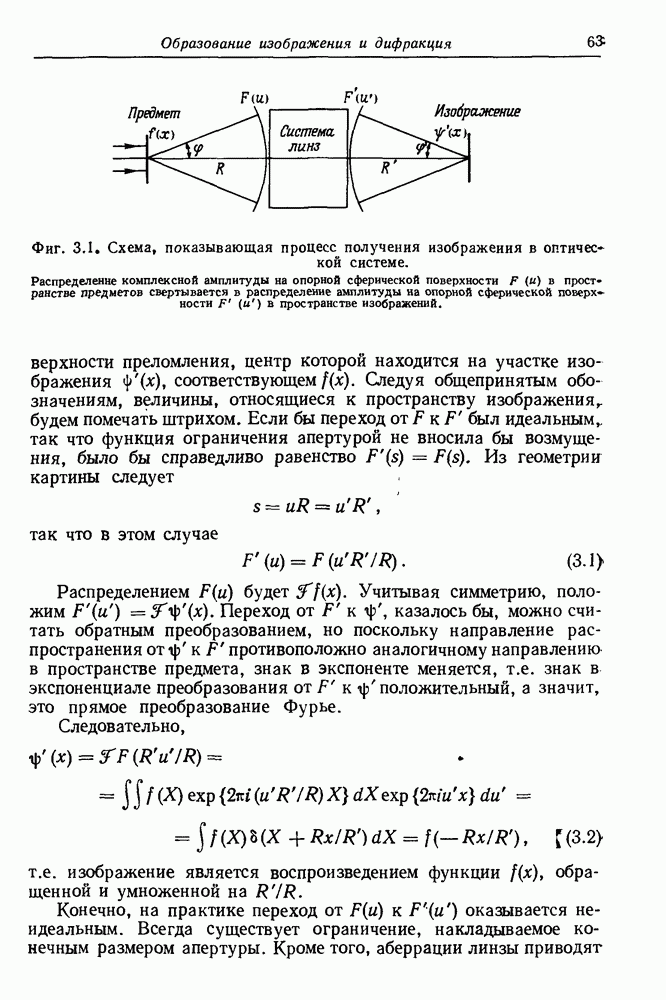
- ГЛАВА 3. Образование изображения и дифракция
- 3.1.1. Когерентная волновая оптика
- 3.1.2. Получение изображения с помощью некогерентных волн
- 3.2. Теория Аббе
- 3.3. Малоугловое приближение
- 3.4. Фазовый контраст
- 3.4.1. Фазовые и амплитудные объекты
- 3.4.2. Контраст при дефокусировке
- 3.4.3. Ограничения, накладываемые апертурой
- 3.4.4. Фазовый контраст Пернике
- 3.5. Многокомпонентные системы
- ГЛАВА 4. Различные виды излучения и рассеяние веществом
- 4.1.1. Источники рентгеновских лучей
- 4.1.2. Рассеяние электронами
- 4.1.3. Рассеяние атомами
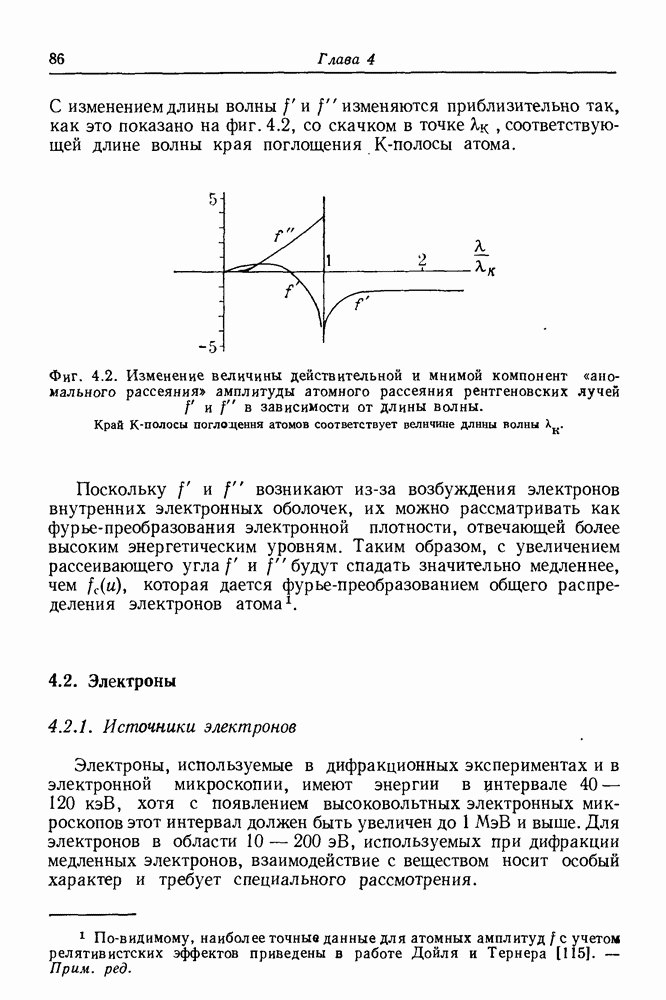
- 4.1.4. Дисперсионные поправки
- 4.2. Электроны
- 4.2.1. Источники электронов
- 4.2.2. Амплитуды атомного рассеяния
- 4.2.3. Приближение фазового объекта
- 4.2.4. Ограниченность первого борновского приближения
- 4.2.5. Эффекты поглощения
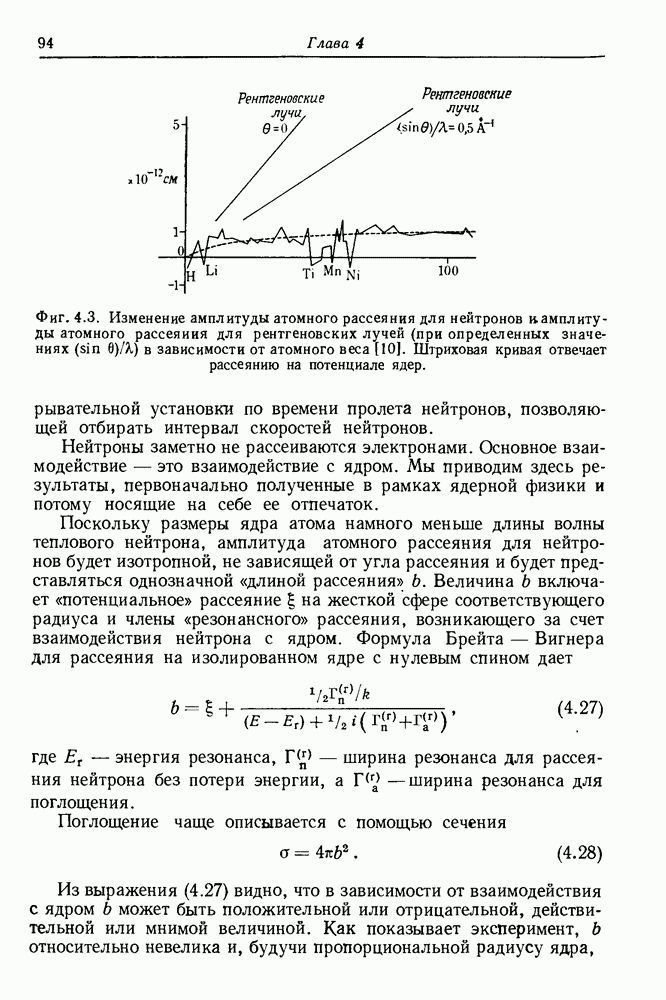
- 4.3. Нейтроны
- 4.3.2. Ядерное спиновое рассеяние
- 4.3.3. Изотопное разупорядочение
- 4.3.4. Тепловое и магнитное рассеяние
- ГЛАВА 5. Рассеяние на совокупности атомов
- 5.2. Прямое и обратное пространства
- 5.2.2. Обратная решетка
- 5.2.3. Закон Фриделя и фазовая задача
- 5.3. Обобщенная функция Паттерсона
- 5.4. Примеры корреляционных функций
- 5.4.1. Ограничения за счет конечных объемов
- 5.4.2. Конечные кристаллы
- 5.5. Корреляция в пространстве и во времени
- 5.5.1. Четырехмерная функция Паттерсона
- 5.5.2. Частные случаи
- 5.5.3. Идеальные одноатомные газы и жидкости
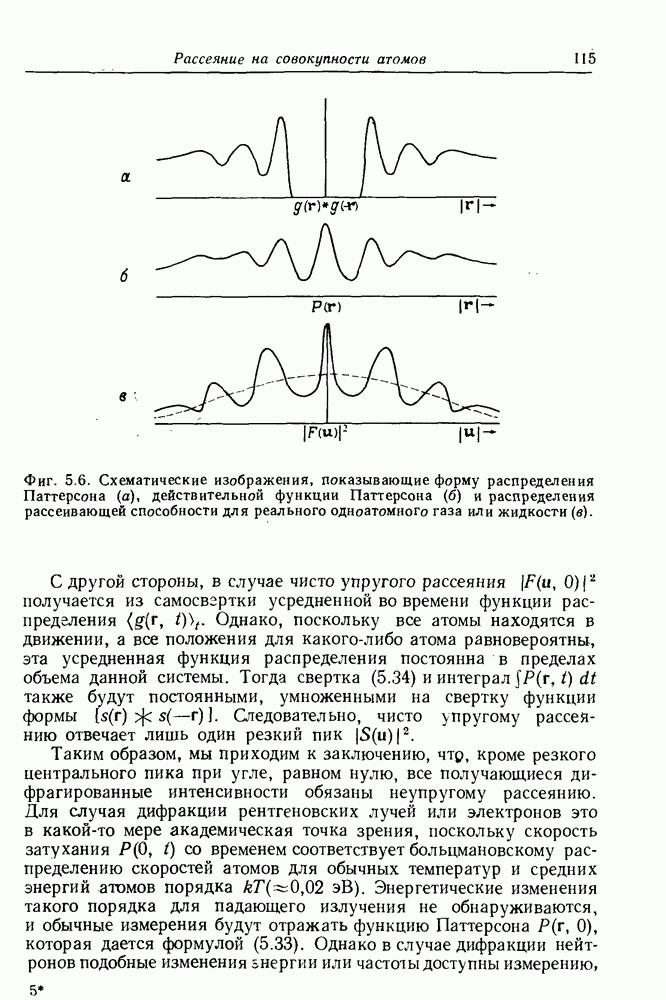
- 5.5.4. Реальные одноатомные газы и жидкости
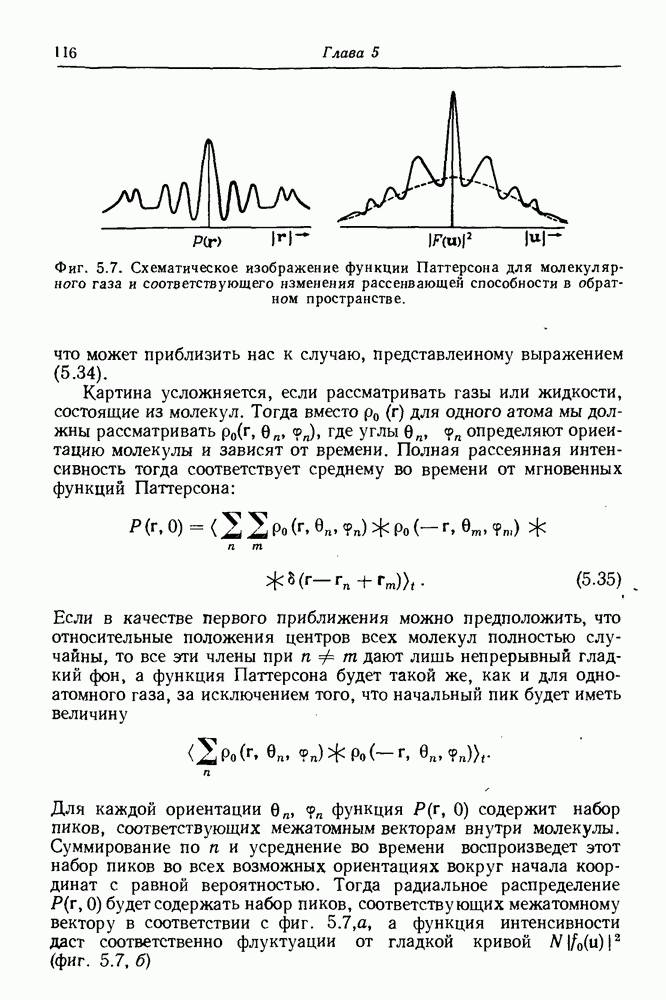
- 5.5.5. Атом водорода
- 5.6. Интенсивности и геометрия дифракции
- 5.7. Практические примеры
- 5.7.1. Конечные источники и детекторы
- 5.7.2. Разброс длин волн
- 5.7.3. Интегральные интенсивности
- 5.8. Сечения и проекции
- ГЛАВА 6. Дифракция на кристаллах
- 6.1. Идеальные кристаллы
- 6.2. Геометрия дифракции
- 6.2.1. Условия дифракции Лауэ и Брэгга
- 6.2.2. Фурье-преобразования функции формы
- 6.2.3. Особые случаи при дифракции электронов
- 6.3. Структурный анализ кристаллов
- 6.3.2. Дополнительная информация
- 6.4. Методы структурного анализа
- 6.4.2. Функция Паттерсона
- 6.4.3. Оптические аналоги
- 6.4.4. Другие методы
- 6.5. Нейтронографический структурный анализ
- 6.5.2. Магнитное рассеяние
- 6.6. Электронографический структурный анализ
- ГЛАВА 7. Дифракция на несовершенных кристаллах
- 7.1. Формулировка дифракционной задачи
- 7.1.2. Общая формулировка дифракционной задачи.
- 7.2. Метод функции Паттерсона
- 7.2.1. Функция Паттерсона для усредненной периодической структуры
- 7.2.2. Функция Паттерсона в отсутствие усредненной структуры
- 7.3. Отклонения от усредненной решетки
- 7.3.1. Распределенные вакансии: отсутствие релаксации
- 7.3.2. Вакансии, сгруппированные в кластеры
- 7.3.3. Релаксация решетки
- 7.3.4. Тепловые колебания — модель Эйнштейна
- 7.4. Несовершенные кристаллы в отсутствие усредненной решетки
- 7.4.2. Разупорядоченные ориентации
- ГЛАВА 8. Дифракция на совершенных кристаллах
- 8.1. Многократное когерентное рассеяние
- 8.2. Теоретические приближения
- 8.3. Теория Бете
- 8.4. Двухволновое приближение
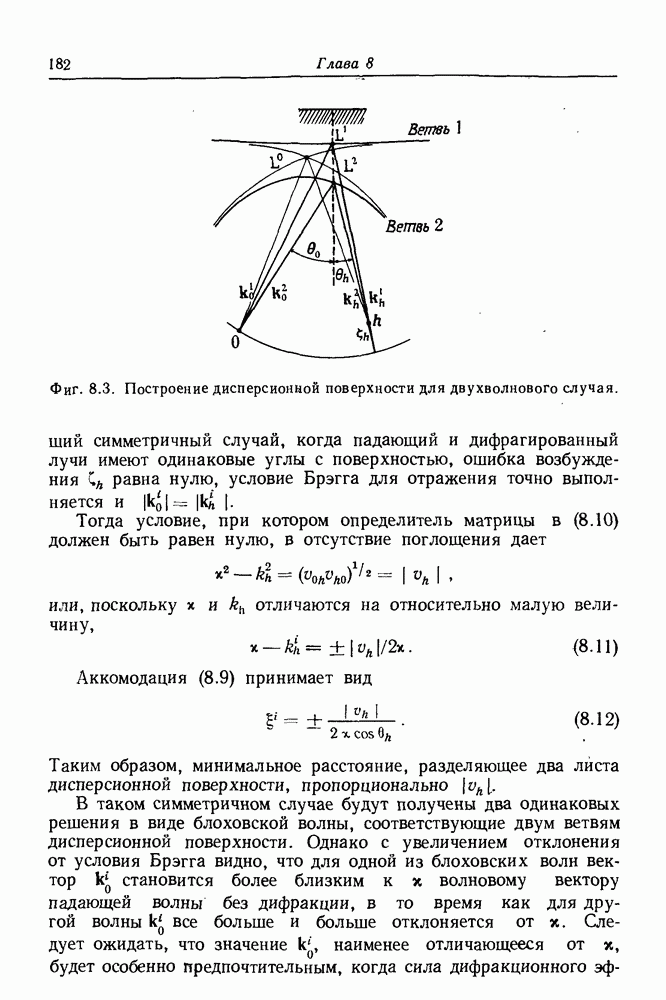
- 8.4.1. Блоховские волны и дисперсионные поверхности
- 8.4.2. Электроны проводимости: энергетическое представление
- 8.4.3. Дифракция рентгеновских лучей; поляризация
- 8.5. Случай Лауэ (прохождение)
- 8.5.1. Дифракция электронов на тонком кристалле
- 8.5.2. Малоугловое приближение
- 8.5.3. Случай Лауэ с поглощением
- 8.6. Потенциалы Бете
- 8.7. Случай Брэгга
- ГЛАВА 9. Динамические дифракционные эффекты
- 9.1. Полосы равной толщины и кривые качания при дифракции электронов
- 9.1.2. Картина процесса в реальном пространстве
- 9.1.3. Кривые качания
- 9.1.4. Экстинкционные контуры
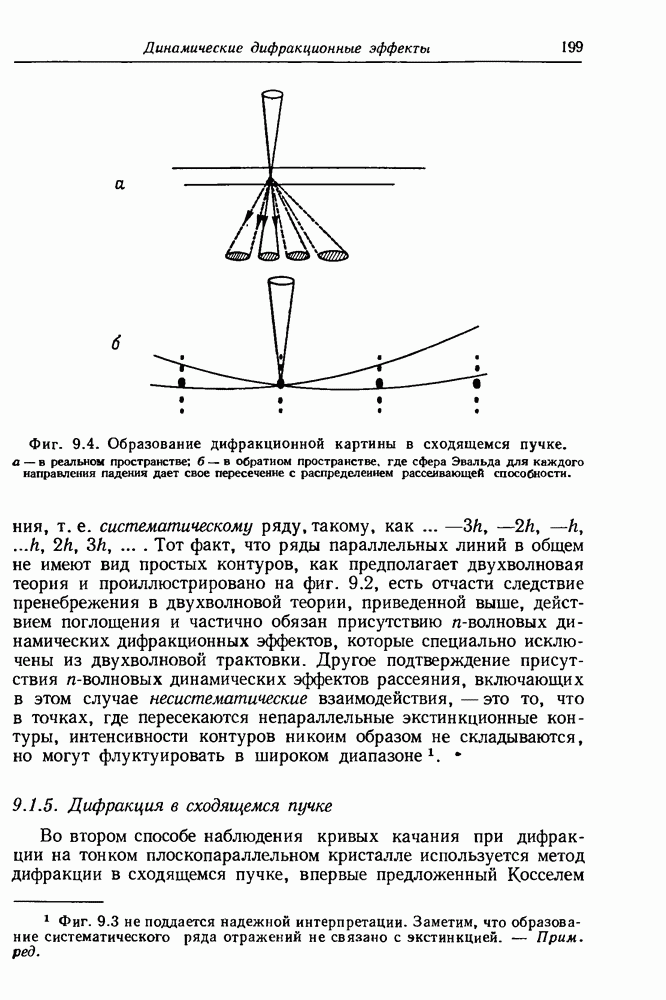
- 9.1.5. Дифракция в сходящемся пучке
- 9.1.6. Дифракция и изображения клиновидных кристаллов
- 9.1.7. Эффекты поглощения для клиньев
- 9.2. Динамические эффекты при дифракции рентгеновских лучей и нейтронов
- 9.2.2. Поток энергии
- 9.2.3. Картина дисперсионной поверхности
- 9.2.4. Дифракция нейтронов
- 9.3. Эффект Боррмана
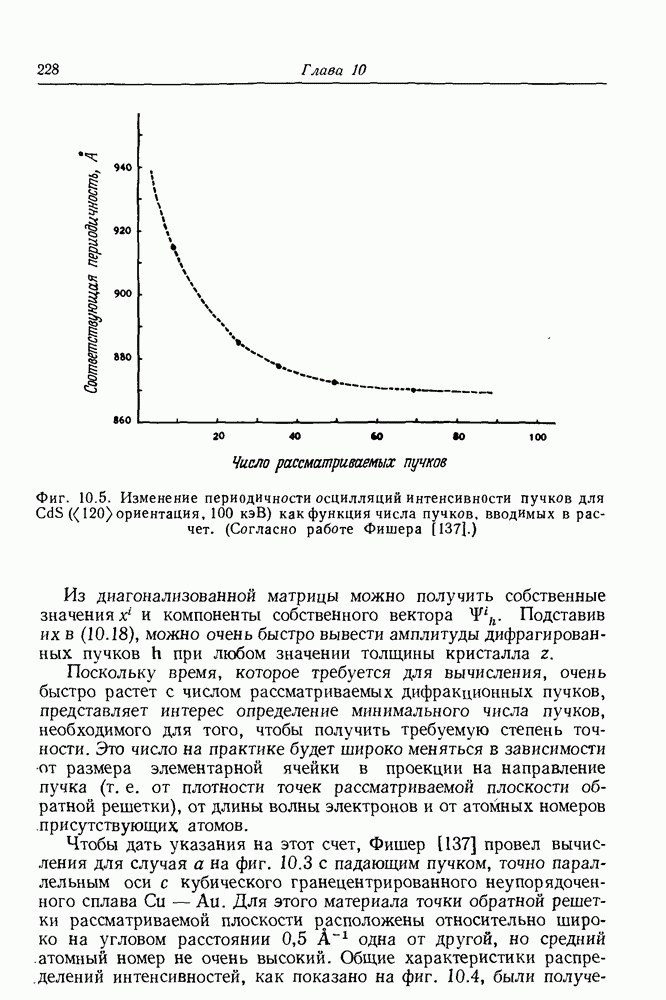
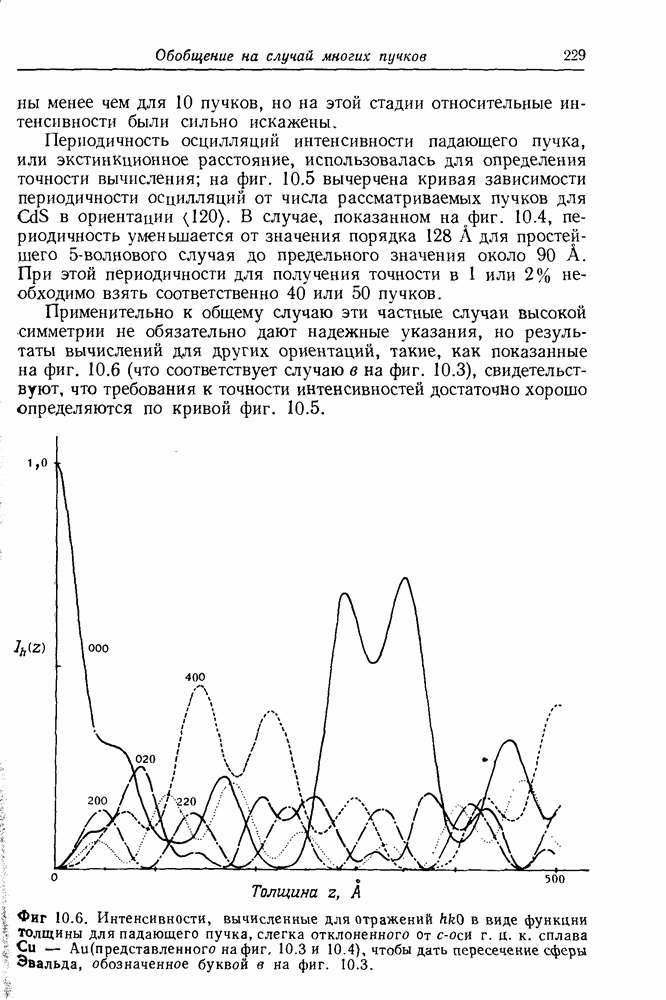
- ГЛАВА 10. Обобщение на случай многих пучков
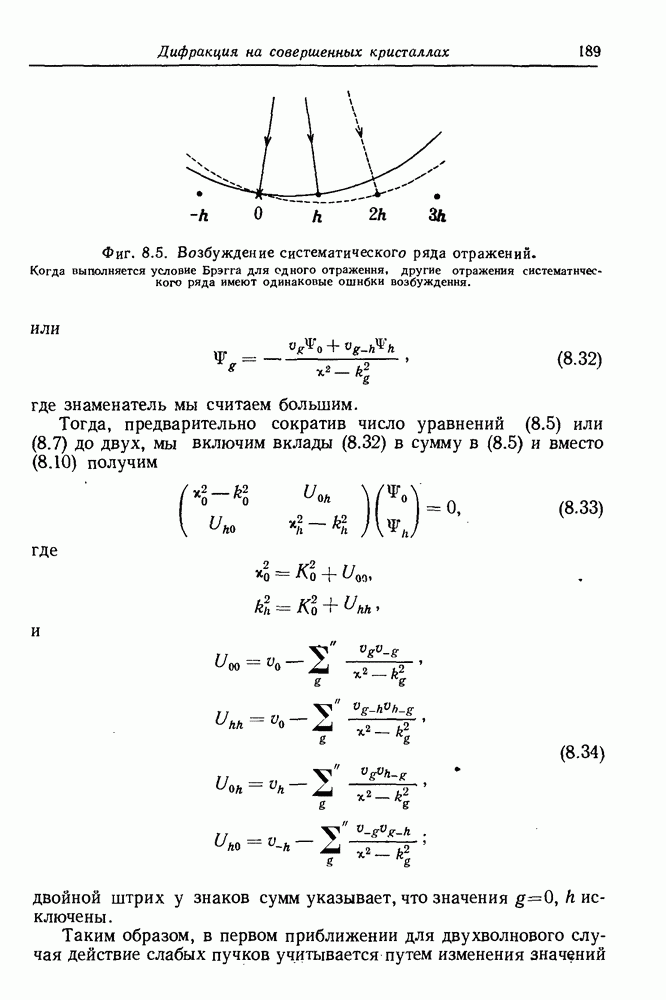
- 10.1. Динамическая n-волновая дифракция
- 10.2. Обобщение теории Бете на случай прохождения
- 10.2.2. Малоугловое приближение
- 10.2.3. Блоховские волны и граничные условия
- 10.2.4. Матрица рассеяния
- 10.3. Подход Дарвина
- 10.4. Специальные случаи — уменьшение числа пучков
- 10.5. Вычислительные методы
- 10.6. Колонковое приближение
- ГЛАВА 11. Метод «физической оптики»
- 11.1 Распространение электронов в кристаллах
- 11.1.3. Дифракция в кристалле
- 11.1.4. Общее выражение в функции от ошибок возбуждения
- 11.2. Ряды многократного рассеяния
- 11.3. Общее решение с двойным суммированием
- 11.3.2. Приближение фазовой решетки
- 11.4. Методы вычислений
- 11.4.1. Вычисления «слоевым методом»
- 11.5. Интенсивности для непериодических объектов
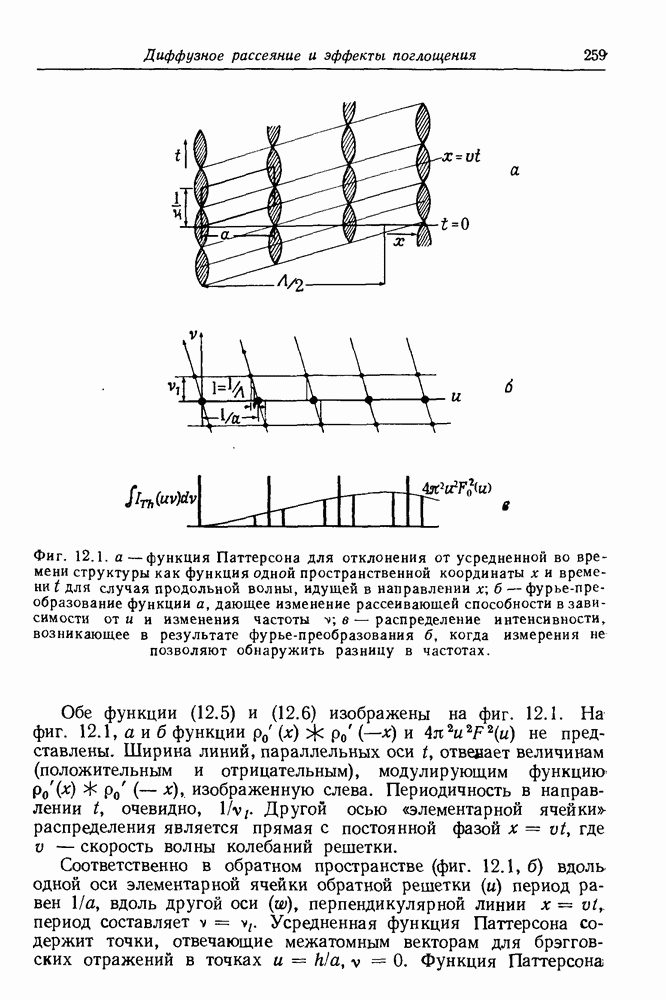
- ГЛАВА 12. Диффузное рассеяние и эффекты поглощения
- 12.1. Тепловое диффузное рассеяние
- 12.1.2. Рассеяние для продольной волны
- 12.1.3. Компонента диффузного рассеяния
- 12.1.4. Дисперсионные кривые
- 12.1.5. Трехмерные обобщения
- 12.2. Статические смещения атомов
- 12.2.2. Дифракционные интенсивности рассеяния на смещенных атомах
- 12.2.3. Брэгговские пики
- 12.2.4. Диффузное рассеяние
- 12.3. Возбуждения электронов
- 12.3.1. Неупругое рентгеновское рассеяние
- 12.3.2. Возбуждение электронов электронами — плазмоны
- 12.3.3. Одноэлектронные возбуждения
- 2.4. Динамические эффекты при диффузном рассеянии
- 12.4.2. Когерентное и некогерентное рассеяние
- 12.4.3. Анализ диффузного рассеяния
- 12.5. Эффекты поглощения
- 12.5.1. Природа параметров поглощения
- 12.5.2. Поглощение рентгеновских лучей и нейтронов
- 12.5.3. «Поглощение» для электронов
- 12.5.4. Поглощение, связанное с тепловыми колебаниями
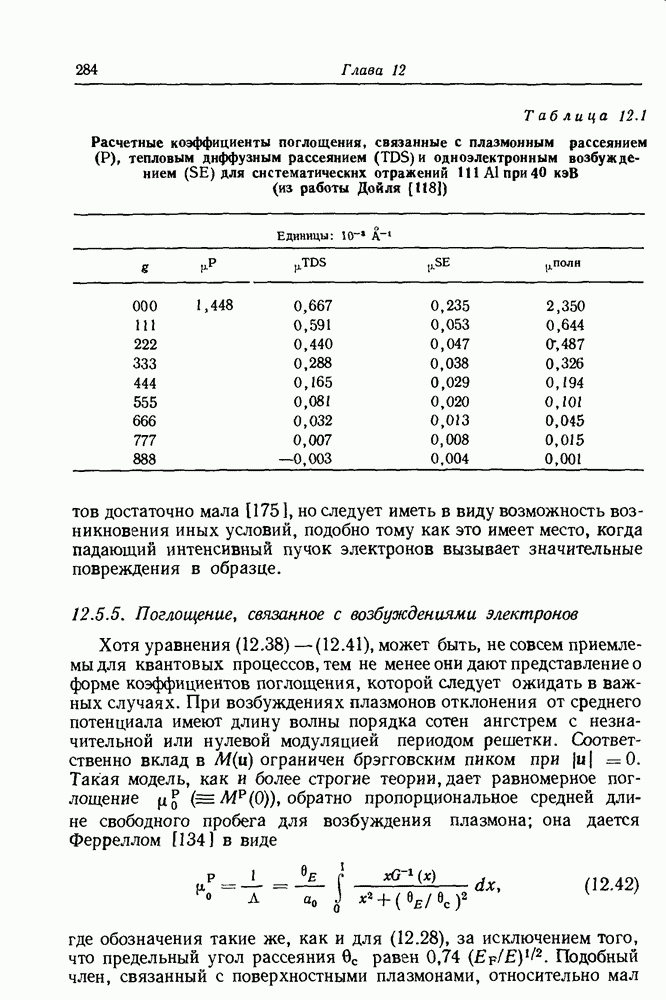
- 12.5.5. Поглощение, связанное с возбуждениями электронов
- 12.5.6. Значения коэффициентов поглощения
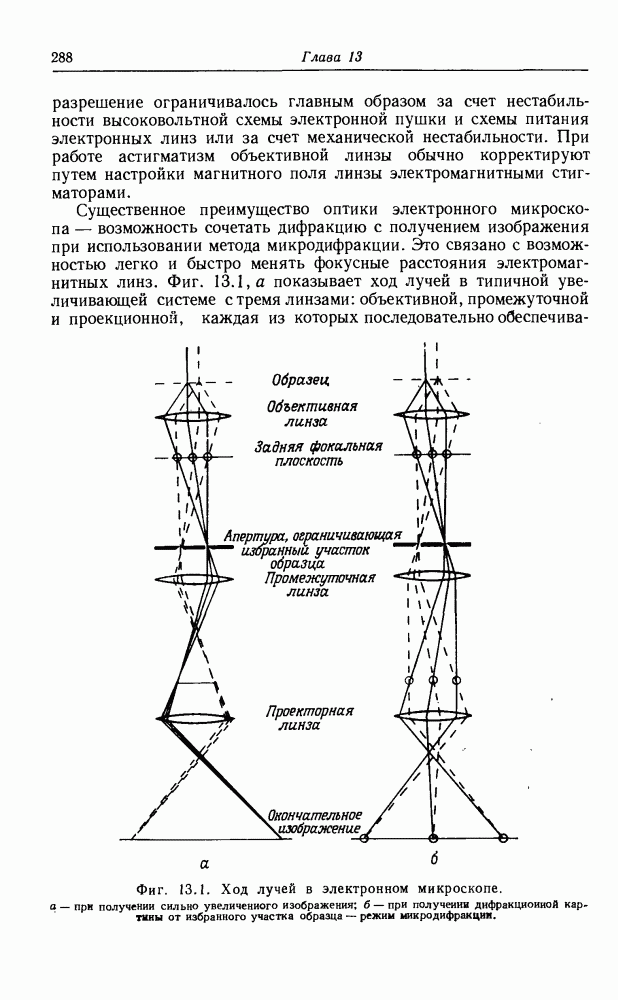
- ГЛАВА 13. Формирование изображения в электронном микроскопе
- 13.1.1. Обычный просвечивающий электронный микроскоп
- 13.1.2. Сканирующий просвечивающий электронный микроскоп
- 13.2. Образование изображения
- 13.3. Контраст для тонких образцов
- 13.3.1. Приближение фазового объекта
- 13.3.2. Функция поглощения
- 13.3.3. Приближение слабофазового объекта
- 13.3.4. Темнопольные изображения
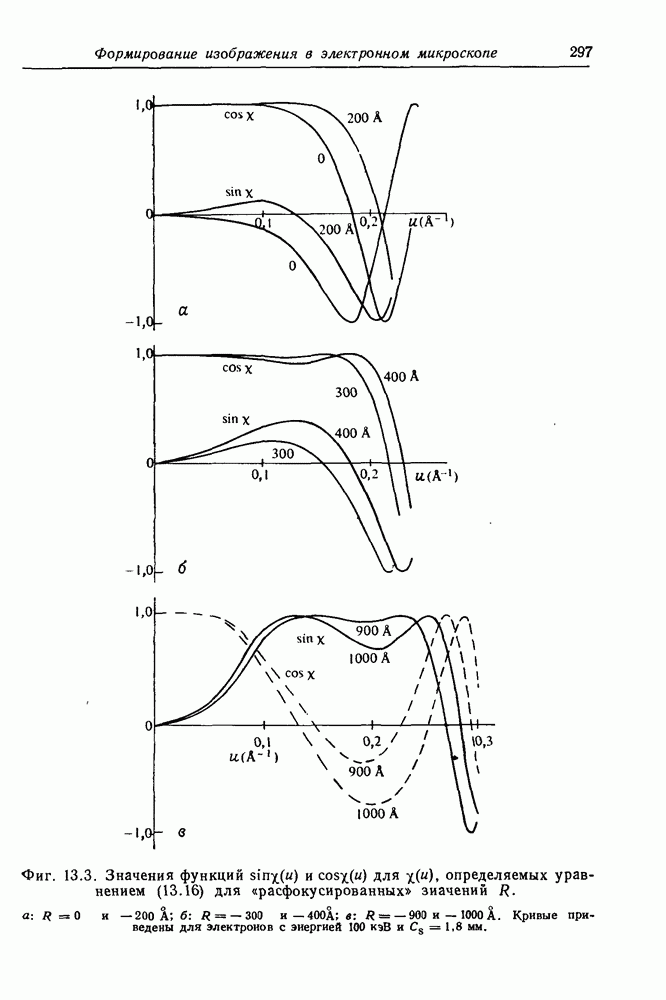
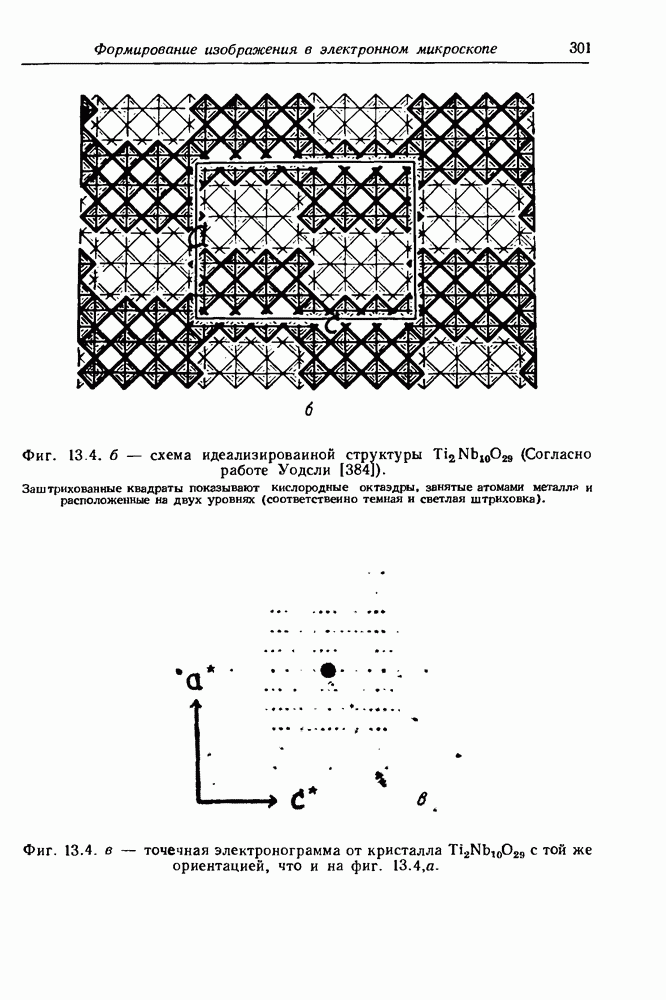
- 13.4. Образование изображения кристаллических структур
- 13.4.1. Образование изображения тонких кристаллов
- 13.4.2. Расчет изображений кристаллов
- 13.4.3. Полосы решетки для толстых кристаллов
- 13.4.4. Получение изображения кристаллов из разрешения решетки
- 13.5. Высоковольтная микроскопия
- ГЛАВА 14. К-линии и каналирование
- 14.1.1. Геометрия линий Косселя
- 14.1.2. Динамическая теория интенсивностей линий Косселя
- 14.1.3. Линии Косселя с ограниченным разрешением
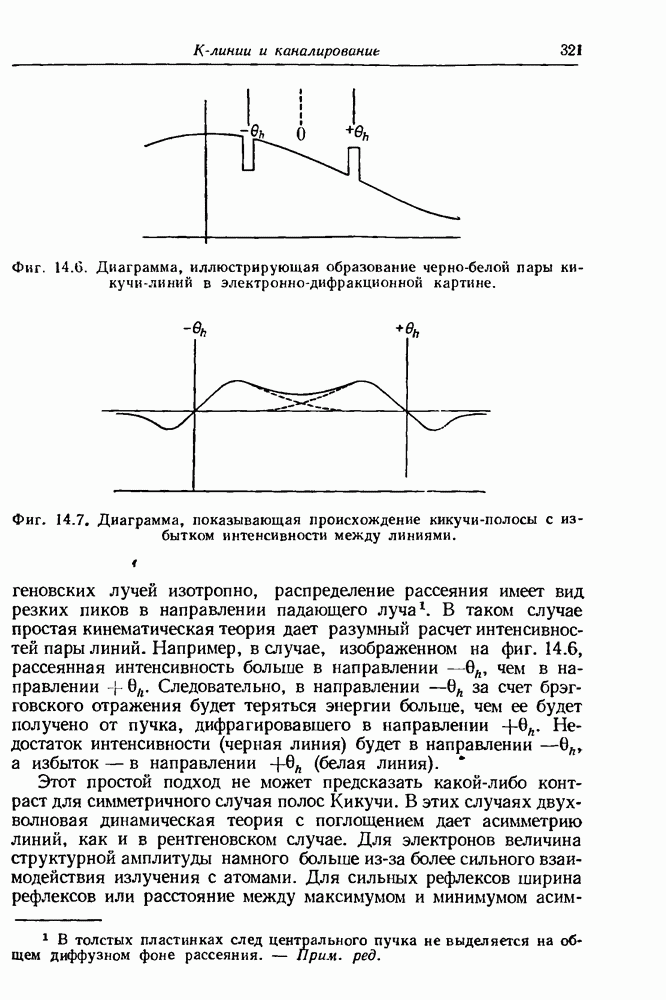
- 14.2. Линии Кикучи
- 14.3. Внешние источники расходящегося излучения
- 14.4. Информация, получаемая из картин К-линий
- 14.5. Каналирование
- 14.6. Вторичные излучения
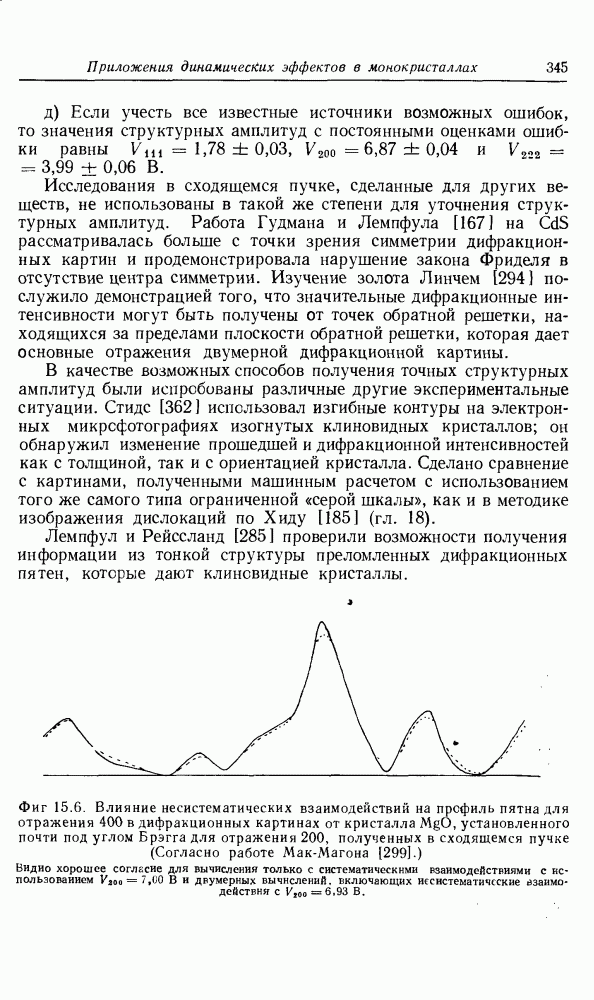
- ГЛАВА 15. Приложения динамических эффектов в монокристаллах
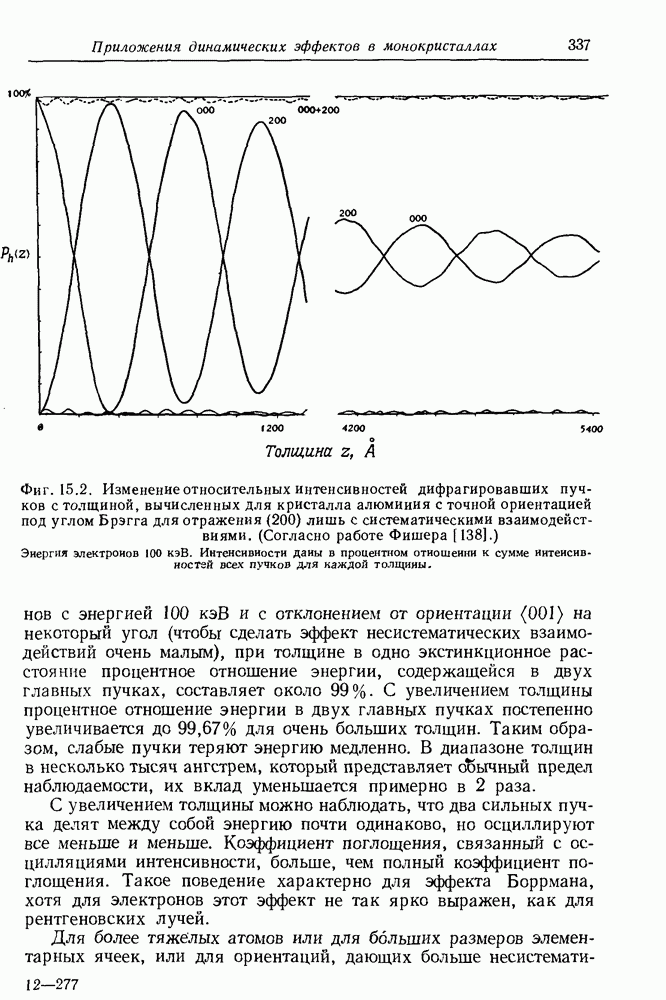
- 15.1. Зависимость динамических эффектов от параметров кристалла
- 15.2. Рентгеновская интерферометрия
- 15.3. n-волновая и двухволновая динамическая дифракция
- 15.4. Определения структурных амплитуд из полос равной толщины
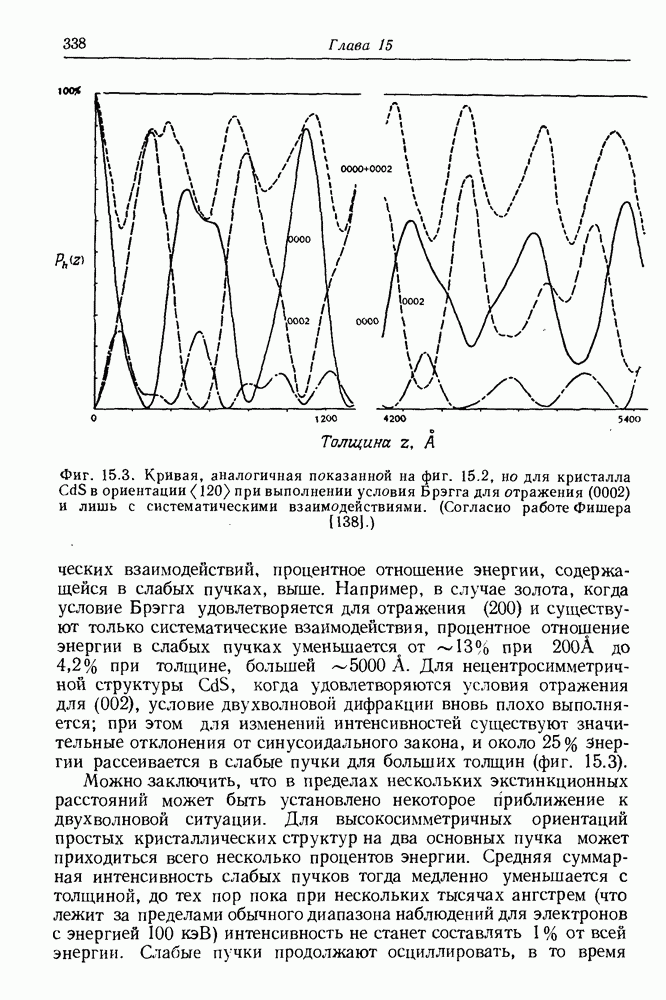
- 15.5. Структурные амплитуды из кривых качания
- 15.6. Релятивистские эффекты
- 15.7. Поглощение и температурные эффекты
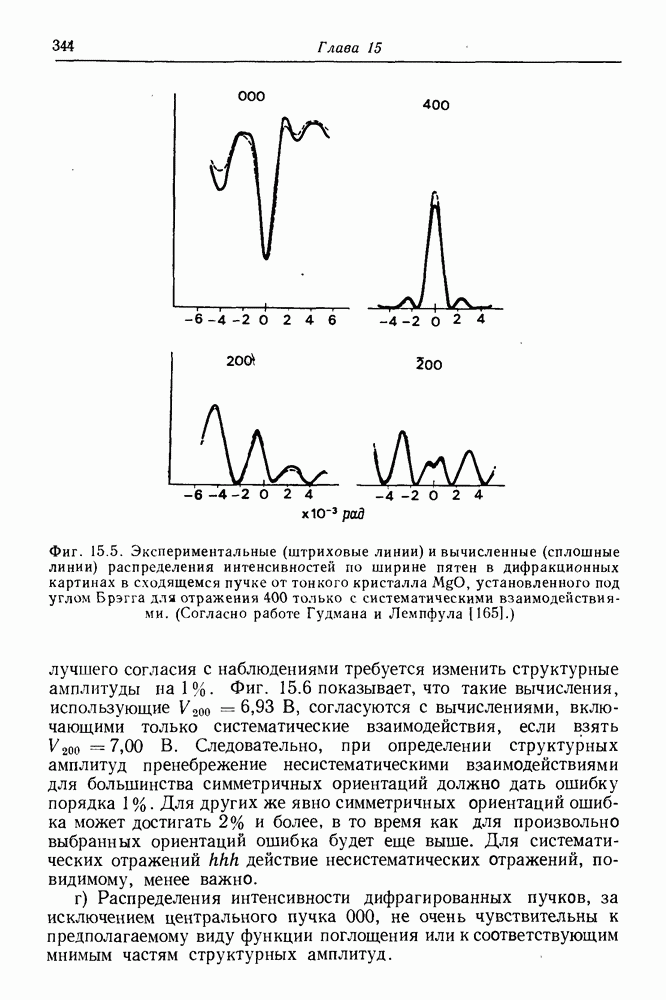
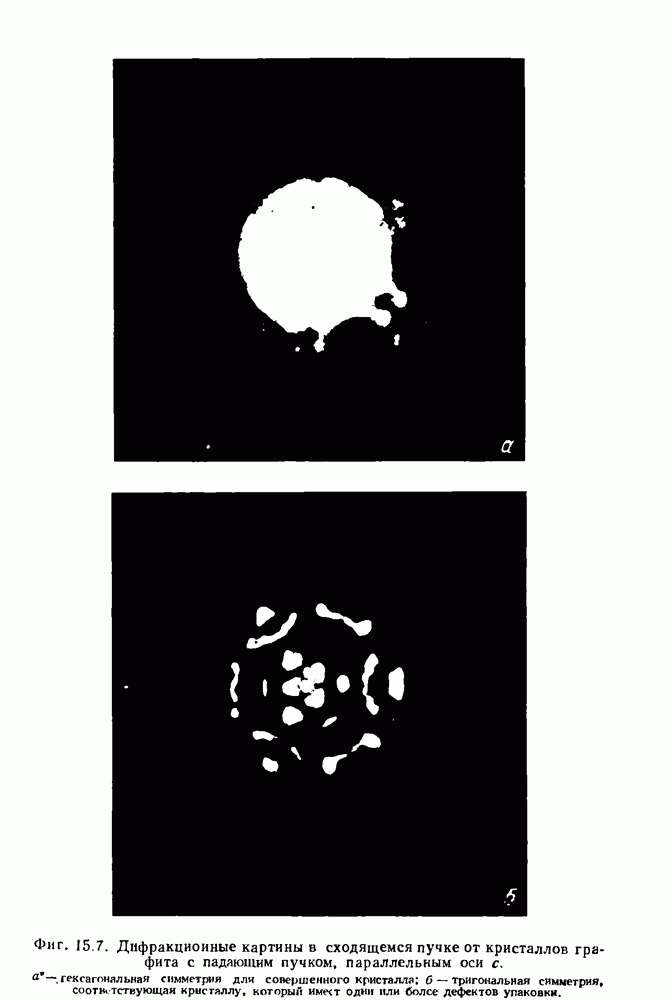
- 15.8. Определение симметрии кристалла
- ГЛАВА 16. Мозаичные кристаллы и поликристаллические материалы
- 16.2. Мозаичные кристаллы
- 16.2.1. Модель мозаичного кристалла
- 16.2.2. Кинематические интегральные интенсивности
- 16.2.3. Экстинкционные эффекты
- 16.2.4. Динамические интенсивности при дифракции электронов
- 16.3. Поликристаллический материал
- 16.3.2. Интенсивности кинематической дифракции
- 16.3.3. Анализ профиля линий
- 16.3.4. Интенсивности динамической дифракции
- 16.3.5. Эффекты n-волновой дифракции
- ГЛАВА 17. Упорядочение атомов в кристаллах
- 17.1. Природа и описание неупорядоченных состояний
- 17.2. Параметры порядка
- 17.3. Функция Паттерсона
- 17.4. Влияние размера атомов
- 17.5. Кинематическая дифракция
- 17.5.1. Дифракция при наличии лишь упорядочения
- 17.5.2. Дифракция и влияние упорядочения и размера атомов
- 17.6. Связь с энергиями упорядочения
- 17.7. Динамическое рассеяние на разупорядоченных кристаллах
- 17.7.2. Расчет диффузного рассеяния
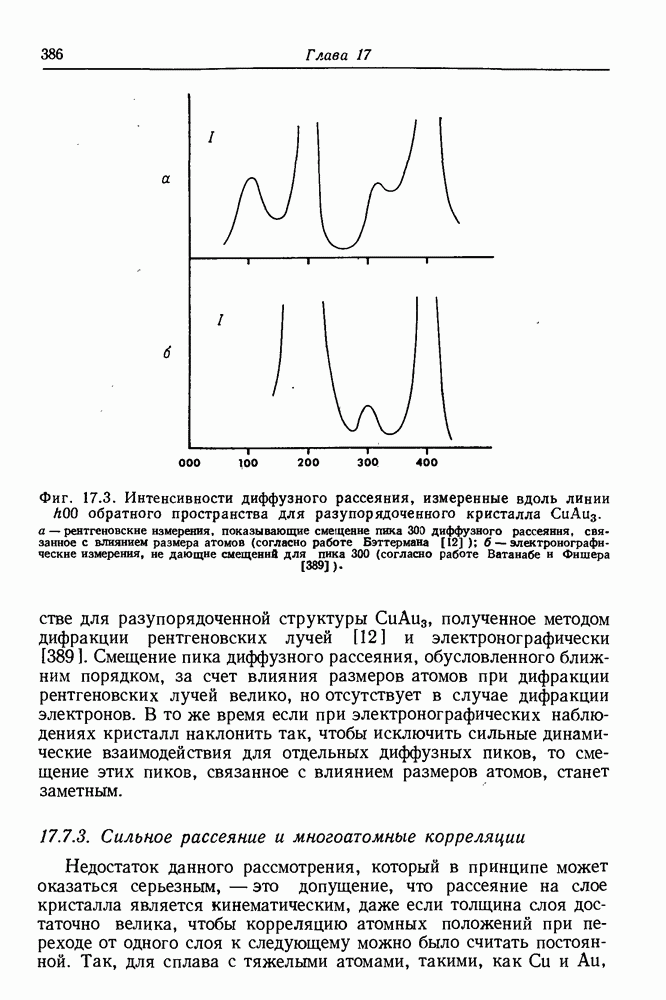
- 17.7.3. Сильное рассеяние и многоатомные корреляции
- 17.8. Некогерентные домены
- 17.8.1. Упорядоченные некогерентные сверхструктуры
- 17.8.2. Некогерентные домены в разупорядоченных сплавах
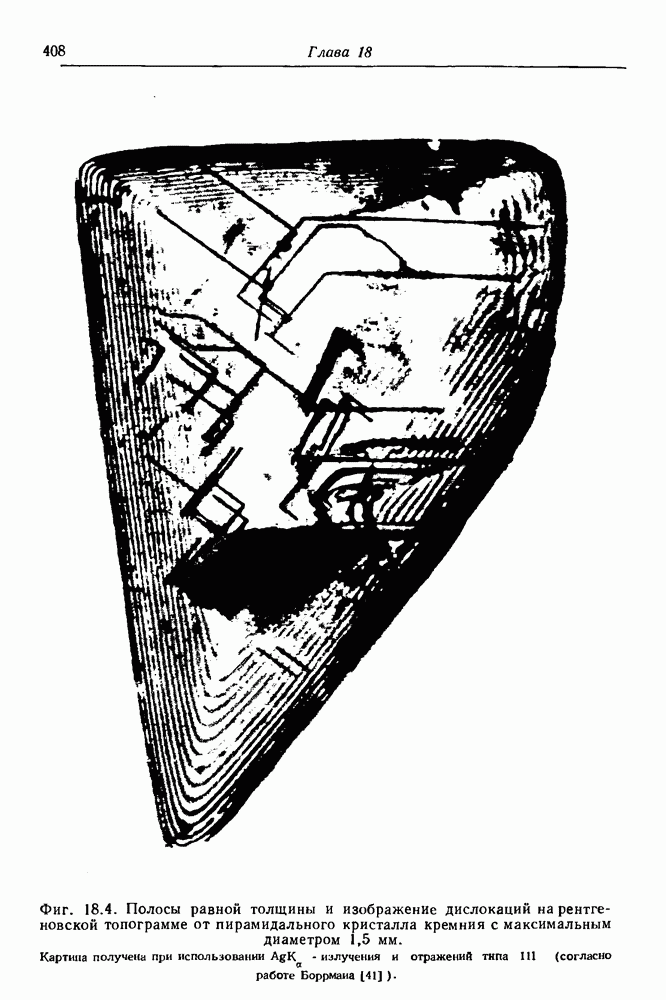
- ГЛАВА 18. Протяженные дефекты
- 18.2. Дефекты упаковки — статистическая кинематическая теория
- 18.2.3. Дефекты в структурах с плотной упаковкой
- 18.3. Динамическая дифракция на дефектах упаковки
- 18.4. Дислокации
- 18.4.1. Дифракционные эффекты.
- 18.4.2. Получение изображений дислокаций
- 18.4.3. Усреднение по углам падения
- 18.4.4. n-волновые дифракционные эффекты