| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 1. Дифракция Френеля и Фраунгофера
1.1. Введение
При построении обобщенной трактовки дифракции рентгеновских лучей, нейтронов и электронов, включая электронную микроскопию и другие методы получения изображений, основанные на явлении дифракции, мы сталкиваемся с задачей объединить многочисленные теории, созданные для более удобного решения частных задач. Часто оказывается, что подход, «популярный» среди экспериментаторов, совсем не является упрощенным вариантом более строгих методов, используемых теоретиками. Его основа может быть совсем другой, более привлекательной умозрительно, хотя и в меньшей степени поддающейся математической трактовке, или более наглядной, как, например, приближение геометрической оптики в теории изображения.
В данной книге мы хотели бы предоставить экспериментатору более последовательное изложение основных теоретических представлений в этой области, используя доводы, для понимания которых достаточно определенного математического минимума. Как теоретику, так и экспериментатору мы надеемся помочь понять, как данные физических наблюдений, в которых используются различные виды излучения и различные типы образцов, можно связать между собой единой нитью теории так, чтобы идеи и понятия, используемые в одной области, можно было связать с другими областями и перенести на них.
Для большинства исследователей, занимающихся рентгеноструктурным анализом кристаллов, дифракция — это обычная теория дифракции Фраунгофера, обобщенная для трех измерений применительно к идеальному случаю бесконечных периодических объектов со строго определенными направлениями дифрагированных пучков и с решеткой, состоящей из взвешенных точек в обратном пространстве. Основной математический инструмент — ряды Фурье. Для случаев конечных или несовершенных кристаллов в том же самом приближении одноволнового кинематического рассеяния используется фурье-преобразование, что, конечно, более сложно.
Такой подход далек от теоретической трактовки дифракции рентгеновских лучей Эвальда [126] или Лауэ [281] или даже от <юлее простого интуитивного подхода Дарвина [108]. И тем не менее именно на эти источники следует опираться, обсуждая допущения теории, простой для использования на практике. Эта же теория дифракции лежит в основе понимания и интерпретации таких важных новых методов, как рентгеновская топография и рентгеновская интерферометрия, и более старых методов, использующих линии Косселя, но упрощения этой теории, созданные для практического использования, развиты в различных направлениях.
Первоначальную теорию дифракции нейтронов создали физики-ядерщики, которые использовали свои профессиональные понятия дифференциальных сечений, а не амплитуды атомного рассеяния. Впоследствии варианты этой теории разработали структурщики, которые внесли в нее понятия, используемые в дифракции рентгеновских лучей, и специалисты по физике твердого тела, описывающие свои эксперименты с помощью волновых векторов к, зон Бриллюэна и т.д. Дополнительное усложнение, которое было связано с изучением неупругого рассеяния в процессах, зависящих от времени и включающих фононы и магноны, привело главным образом к развитию этого, заимствованного из физики твердого тела подхода, а не к обобщению методов фурье-преобразований.
Развитие теории дифракции электронов шло параллельно с развитием теории дифракции рентгеновских лучей. При этом там, где было возможно, использовалось приближение простой кинематической теории дифракции Фраунгофера, а динамическая теория Бете [22] (аналог теории Лауэ для рентгеновских лучей) использовалась лишь по мере необходимости. Отличие от дифракции рентгеновских лучей было связано как с большим вкладом эффектов динамического рассеяния, так и с большей сложностью самих динамических эффектов при дифракции электронов. Соответственно возникла потребность создать относительно простые приближения для практических целей; было разработано несколько таких вариантов для экспериментов различных типов.
Дополнительная трудность в случае дифракции электронов возникала в связи с тем, что факторы атомного рассеяния получали на основе теории рассеяния, т.е. теории, относящейся к ядерной и атомной физике, причем использовали и соответствующую терминологию. Следствием такого «происхождения» является то, что исследователи, работающие в газовой электронографии, рассматривают амплитуды атомного рассеяния (в А) как функцию переменной  а не переменной
а не переменной  (как это принято в дифракции рентгеновских лучей или электронов в твердом теле) или расстояния в обратной решетке
(как это принято в дифракции рентгеновских лучей или электронов в твердом теле) или расстояния в обратной решетке 
Теория образования изображения в электронном микроскопе естественно следует в своем развитии за теорией обычной
микроскопии, но при этом она должна сочетаться с теорией рассеяния или дифракции электронов в объекте. Указанные два аспекта электронной микроскопии естественно объединяются концепцией фурье-преобразования, имеющей первостепенное значение в дифракции электронов и рентгеновских лучей в простом кинематическом приближении и послужившей осноеой для последних достижений теории изображения, впервые предложенной Дюфье [120].
Тогда то, что основные динамические теории дифракции рентгеновских лучей и электронов развиты в терминах дифференциальных уравнений, а не интегралов, таких, как фурье-преобразование предполагает дальнейшее развитие необходимой теории в двух направлениях, связанных лишь формально, а на практике сильно различающихся. Однако по крайней мере для дифракции электронов это препятствие удалось преодолеть благодаря развитию динамических теорий дифракции в интегральной форме, где существенную роль играет фурье-преобразование. Следующий важный компонент теории можно найти в трактовке дифракции Френеля, как она дается в элементарных курсах физики.
Учитывая это, начнем наше рассмотрение дифракции с того, что напомним читателю элементы физической оптики и таким образом введем описание дифракции, рассеяния и получения изображения, используя интеграл фурье-преобразования и важный связанный с ним интеграл-свертку.
Возможно, многим исследователям, занятым практической электронной микроскопией и дифракцией, пришлось бы довольно трудно, если бы мы попытались представить полное рассмотрение дифракции по такой схеме. Поэтому в тех случаях, когда это приемлемо, мы будем переводить нашу трактовку на более привычную почву методов дифференциальных уравнений. Однако мы хотели бы заметить, что рассмотрение в подобных случаях следует считать лишь параллелью основному развитию теории, проведенной либо для удобства, либо в связи с принятыми обозначениями.
Чтобы облегчить понимание, мы избегали чересчур строгой аргументации или сложных выкладок до такой степени, что пурист, разумеется, найдет что критиковать в логике изложения. Во многих случаях математические утверждения мы сопроводили словест ными формулировками, которые часто менее точны, но могут помочь математически более слабо подготовленному читателю.
Будем считать для начала, что читатель знаком с использованием комплексной экспоненты для представления волновой функции, с использованием рядов Фурье для разложения периодической
функции, а также с элементами интегрирования и дифференцирования. Тем, кто не знаком с этими понятиями, мы рекомендуем обратиться К одному из многочисленных учебников по физической оптике, такому, Как учебник Дичберна [114] или Стоуна [363]. Превосходное изложение этих вопросов на несколько более высоком уровне дают С. Липсон и Г. Липсон [292].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ГЛАВА 1. Дифракция Френеля и Фраунгофера
- 1.2. Волновые уравнения и волны
- 1.2.2. Электромагнитные волны
- 1.2.3. Волны-частицы
- 1.3. Суперпозиция и когерентность
- 1.3.2. Независимые точенные источники
- 1.4. Принцип Гюйгенса
- 1.4.2. Применение формулы Кирхгофа
- 1.5. Подход с точки зрения теории рассеяния
- 1.5.1. Интегральная форма волнового уравнения
- 1.5.2. Ряд Борна
- 1.6. Принцип взаимности
- 1.7. Дифракция Френеля
- 1.7.2. Интегралы Френеля
- 1.7.3. Периодические объекты — «фурье-изображения»
- 1.8. Дифракция Фраунгофера
- ГЛАВА 2. Фурье-преобразования и свертки
- 2.1.1. Дельта-функция и непрерывность
- 2.1.2. Свертки
- 2.1.3. Примеры сверток
- 2.2. Фурье-преобразования: общее рассмотрение
- 2.2.2. Свойства фурье-преобразований
- 2.2.3. Умножение и свертка
- 2.2.4. Пространство и время
- 2.3. Фурье-преобразования и дифракция: примеры
- 2.3.2. Плоская волна: преобразование, обратное рассмотренному в разд. 2.3.1.
- 2.3.3. Трансляция объекта
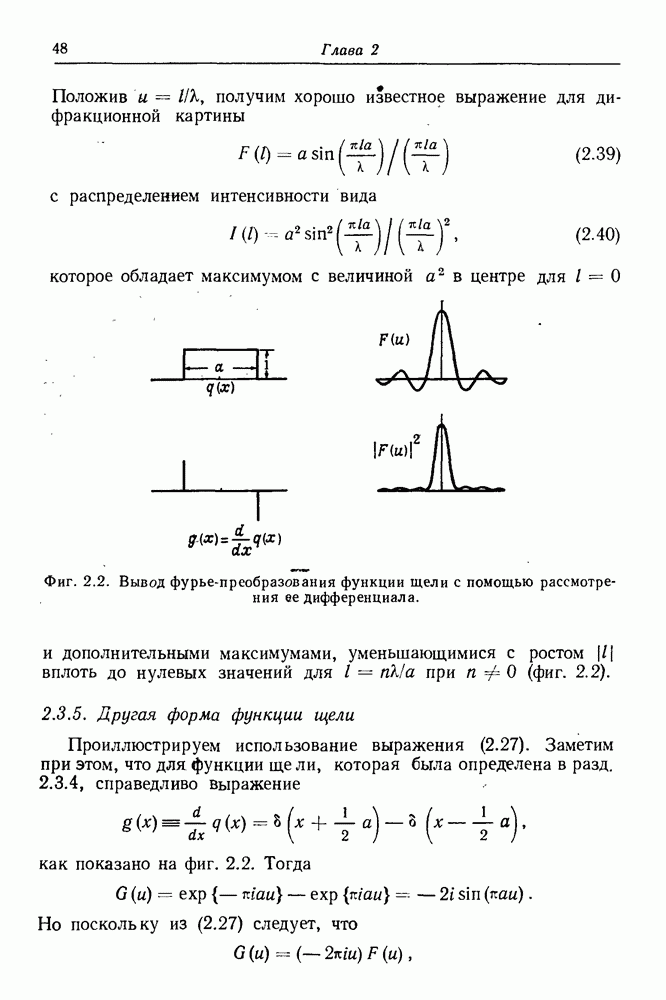
- 2.3.4. Функция щели
- 2.3.5. Другая форма функции щели
- 2.3.6. Прямолинейный край
- 2.3.7. Прямоугольная апертура
- 2.3.8. Круглая апертура
- 2.3.9. Две очень узкие щели
- 2.3.10. Две щели заметной ширины
- 2.3.11. Конечный цуг волн
- 2.3.12. Периодическая последовательность узких щелей
- 2.3.13. Произвольная периодическая функция
- 2.3.14. Дифракционная решетка: тонкие щели
- 2.3.15. Дифракционная решетка: общее рассмотрение
- 2.3.16. Функция Гаусса
- 2.3.17. Ряд круглых отверстий
- 2.3.18. Дополнительные объекты — теорема Бабине
- 2.3.19. Полные интенсивности: теорема Парсеваля
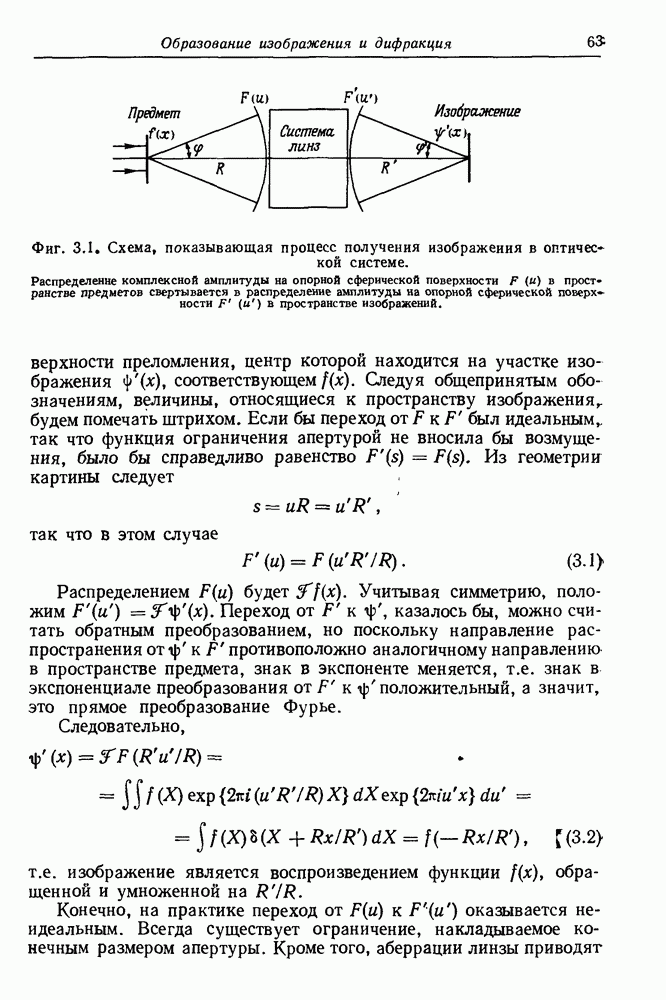
- ГЛАВА 3. Образование изображения и дифракция
- 3.1.1. Когерентная волновая оптика
- 3.1.2. Получение изображения с помощью некогерентных волн
- 3.2. Теория Аббе
- 3.3. Малоугловое приближение
- 3.4. Фазовый контраст
- 3.4.1. Фазовые и амплитудные объекты
- 3.4.2. Контраст при дефокусировке
- 3.4.3. Ограничения, накладываемые апертурой
- 3.4.4. Фазовый контраст Пернике
- 3.5. Многокомпонентные системы
- ГЛАВА 4. Различные виды излучения и рассеяние веществом
- 4.1.1. Источники рентгеновских лучей
- 4.1.2. Рассеяние электронами
- 4.1.3. Рассеяние атомами
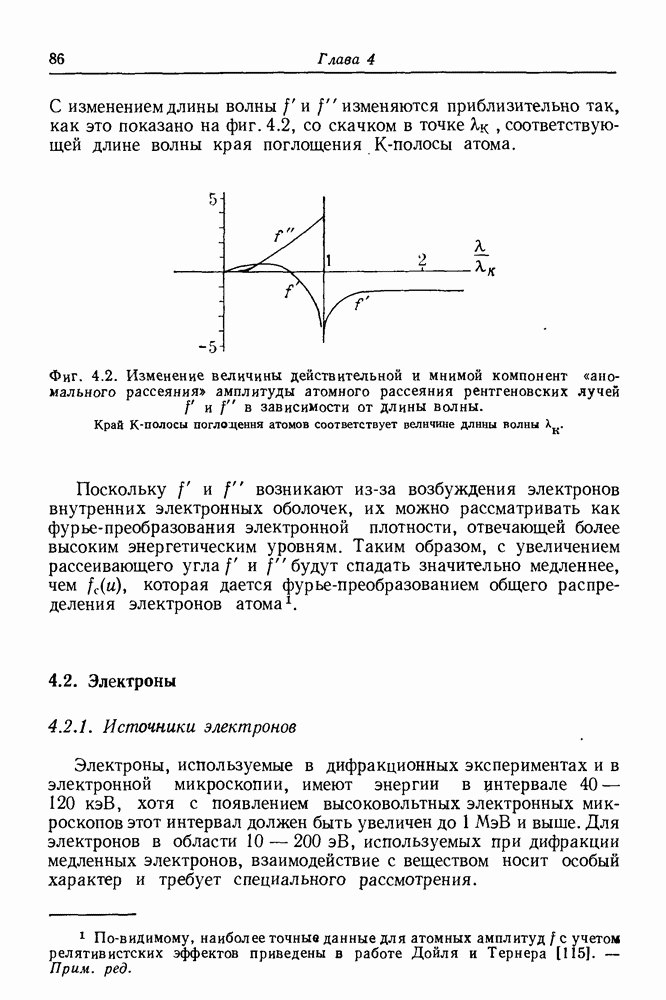
- 4.1.4. Дисперсионные поправки
- 4.2. Электроны
- 4.2.1. Источники электронов
- 4.2.2. Амплитуды атомного рассеяния
- 4.2.3. Приближение фазового объекта
- 4.2.4. Ограниченность первого борновского приближения
- 4.2.5. Эффекты поглощения
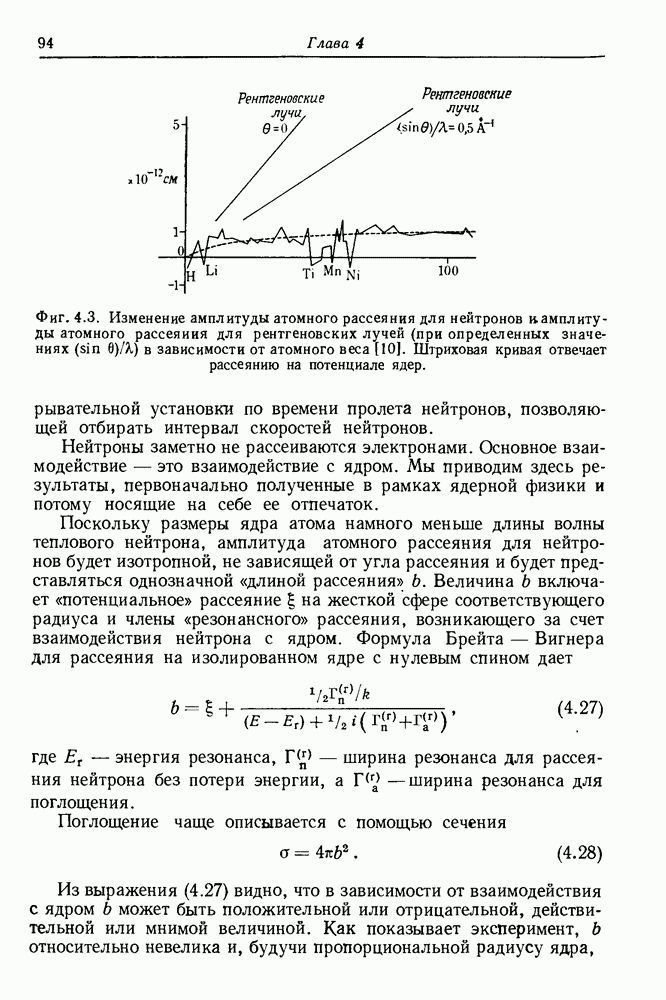
- 4.3. Нейтроны
- 4.3.2. Ядерное спиновое рассеяние
- 4.3.3. Изотопное разупорядочение
- 4.3.4. Тепловое и магнитное рассеяние
- ГЛАВА 5. Рассеяние на совокупности атомов
- 5.2. Прямое и обратное пространства
- 5.2.2. Обратная решетка
- 5.2.3. Закон Фриделя и фазовая задача
- 5.3. Обобщенная функция Паттерсона
- 5.4. Примеры корреляционных функций
- 5.4.1. Ограничения за счет конечных объемов
- 5.4.2. Конечные кристаллы
- 5.5. Корреляция в пространстве и во времени
- 5.5.1. Четырехмерная функция Паттерсона
- 5.5.2. Частные случаи
- 5.5.3. Идеальные одноатомные газы и жидкости
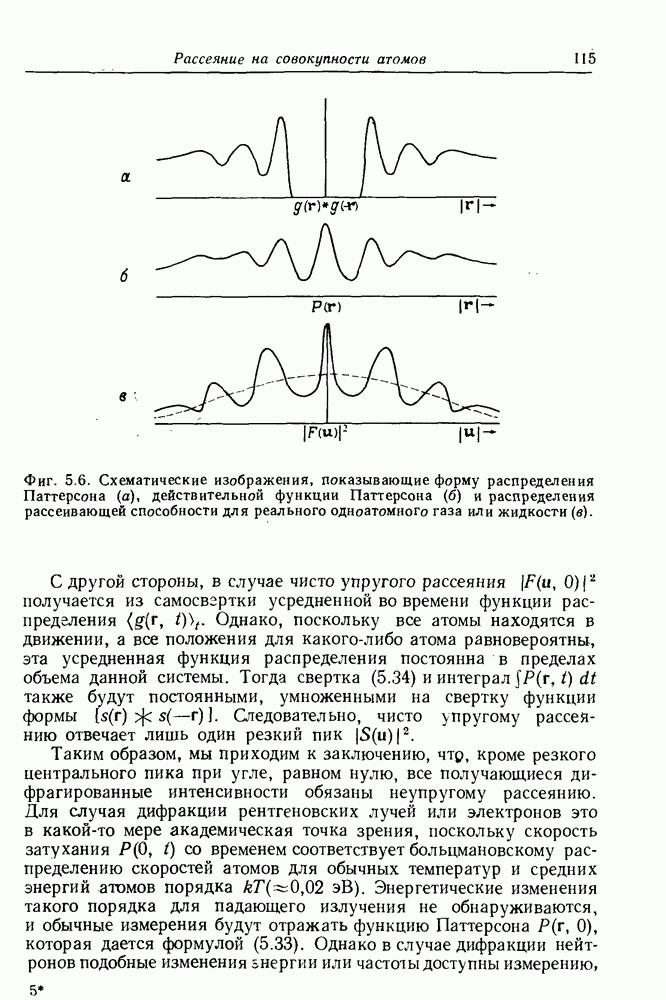
- 5.5.4. Реальные одноатомные газы и жидкости
- 5.5.5. Атом водорода
- 5.6. Интенсивности и геометрия дифракции
- 5.7. Практические примеры
- 5.7.1. Конечные источники и детекторы
- 5.7.2. Разброс длин волн
- 5.7.3. Интегральные интенсивности
- 5.8. Сечения и проекции
- ГЛАВА 6. Дифракция на кристаллах
- 6.1. Идеальные кристаллы
- 6.2. Геометрия дифракции
- 6.2.1. Условия дифракции Лауэ и Брэгга
- 6.2.2. Фурье-преобразования функции формы
- 6.2.3. Особые случаи при дифракции электронов
- 6.3. Структурный анализ кристаллов
- 6.3.2. Дополнительная информация
- 6.4. Методы структурного анализа
- 6.4.2. Функция Паттерсона
- 6.4.3. Оптические аналоги
- 6.4.4. Другие методы
- 6.5. Нейтронографический структурный анализ
- 6.5.2. Магнитное рассеяние
- 6.6. Электронографический структурный анализ
- ГЛАВА 7. Дифракция на несовершенных кристаллах
- 7.1. Формулировка дифракционной задачи
- 7.1.2. Общая формулировка дифракционной задачи.
- 7.2. Метод функции Паттерсона
- 7.2.1. Функция Паттерсона для усредненной периодической структуры
- 7.2.2. Функция Паттерсона в отсутствие усредненной структуры
- 7.3. Отклонения от усредненной решетки
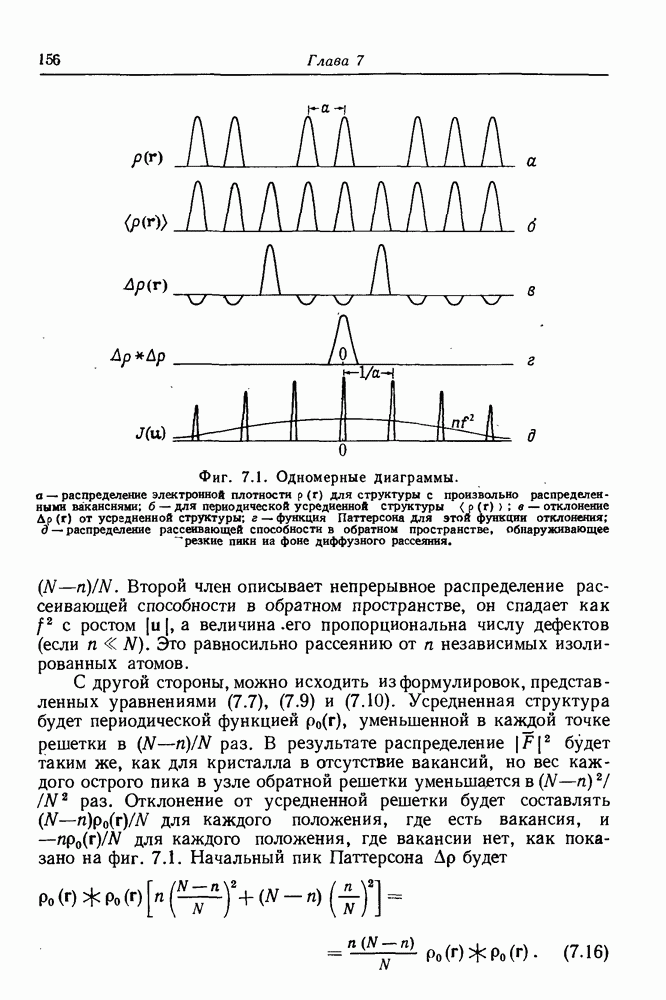
- 7.3.1. Распределенные вакансии: отсутствие релаксации
- 7.3.2. Вакансии, сгруппированные в кластеры
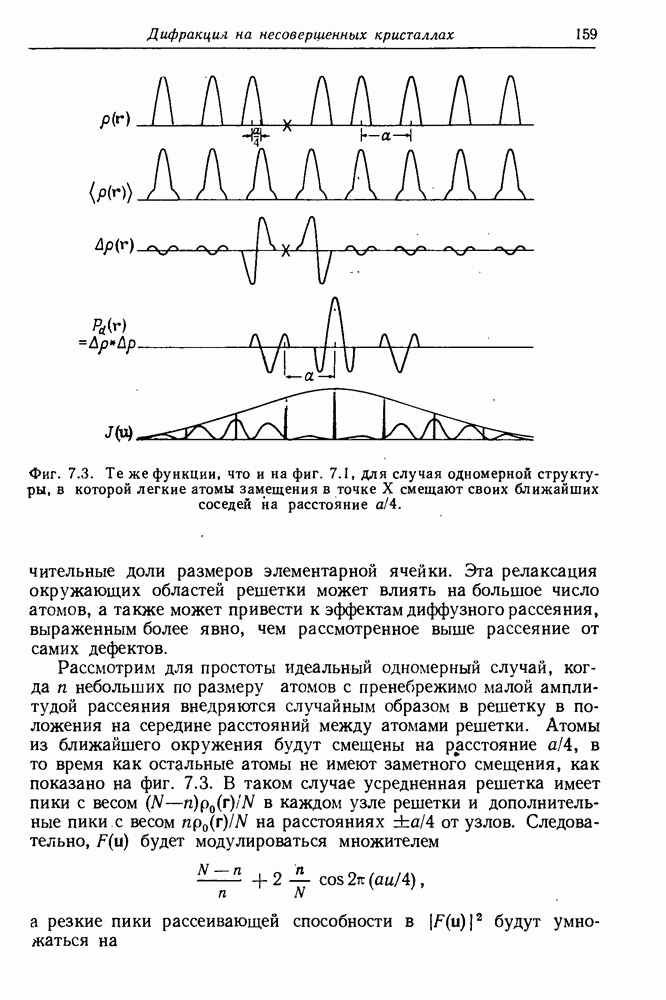
- 7.3.3. Релаксация решетки
- 7.3.4. Тепловые колебания — модель Эйнштейна
- 7.4. Несовершенные кристаллы в отсутствие усредненной решетки
- 7.4.2. Разупорядоченные ориентации
- ГЛАВА 8. Дифракция на совершенных кристаллах
- 8.1. Многократное когерентное рассеяние
- 8.2. Теоретические приближения
- 8.3. Теория Бете
- 8.4. Двухволновое приближение
- 8.4.1. Блоховские волны и дисперсионные поверхности
- 8.4.2. Электроны проводимости: энергетическое представление
- 8.4.3. Дифракция рентгеновских лучей; поляризация
- 8.5. Случай Лауэ (прохождение)
- 8.5.1. Дифракция электронов на тонком кристалле
- 8.5.2. Малоугловое приближение
- 8.5.3. Случай Лауэ с поглощением
- 8.6. Потенциалы Бете
- 8.7. Случай Брэгга
- ГЛАВА 9. Динамические дифракционные эффекты
- 9.1. Полосы равной толщины и кривые качания при дифракции электронов
- 9.1.2. Картина процесса в реальном пространстве
- 9.1.3. Кривые качания
- 9.1.4. Экстинкционные контуры
- 9.1.5. Дифракция в сходящемся пучке
- 9.1.6. Дифракция и изображения клиновидных кристаллов
- 9.1.7. Эффекты поглощения для клиньев
- 9.2. Динамические эффекты при дифракции рентгеновских лучей и нейтронов
- 9.2.2. Поток энергии
- 9.2.3. Картина дисперсионной поверхности
- 9.2.4. Дифракция нейтронов
- 9.3. Эффект Боррмана
- ГЛАВА 10. Обобщение на случай многих пучков
- 10.1. Динамическая n-волновая дифракция
- 10.2. Обобщение теории Бете на случай прохождения
- 10.2.2. Малоугловое приближение
- 10.2.3. Блоховские волны и граничные условия
- 10.2.4. Матрица рассеяния
- 10.3. Подход Дарвина
- 10.4. Специальные случаи — уменьшение числа пучков
- 10.5. Вычислительные методы
- 10.6. Колонковое приближение
- ГЛАВА 11. Метод «физической оптики»
- 11.1 Распространение электронов в кристаллах
- 11.1.3. Дифракция в кристалле
- 11.1.4. Общее выражение в функции от ошибок возбуждения
- 11.2. Ряды многократного рассеяния
- 11.3. Общее решение с двойным суммированием
- 11.3.2. Приближение фазовой решетки
- 11.4. Методы вычислений
- 11.4.1. Вычисления «слоевым методом»
- 11.5. Интенсивности для непериодических объектов
- ГЛАВА 12. Диффузное рассеяние и эффекты поглощения
- 12.1. Тепловое диффузное рассеяние
- 12.1.2. Рассеяние для продольной волны
- 12.1.3. Компонента диффузного рассеяния
- 12.1.4. Дисперсионные кривые
- 12.1.5. Трехмерные обобщения
- 12.2. Статические смещения атомов
- 12.2.2. Дифракционные интенсивности рассеяния на смещенных атомах
- 12.2.3. Брэгговские пики
- 12.2.4. Диффузное рассеяние
- 12.3. Возбуждения электронов
- 12.3.1. Неупругое рентгеновское рассеяние
- 12.3.2. Возбуждение электронов электронами — плазмоны
- 12.3.3. Одноэлектронные возбуждения
- 2.4. Динамические эффекты при диффузном рассеянии
- 12.4.2. Когерентное и некогерентное рассеяние
- 12.4.3. Анализ диффузного рассеяния
- 12.5. Эффекты поглощения
- 12.5.1. Природа параметров поглощения
- 12.5.2. Поглощение рентгеновских лучей и нейтронов
- 12.5.3. «Поглощение» для электронов
- 12.5.4. Поглощение, связанное с тепловыми колебаниями
- 12.5.5. Поглощение, связанное с возбуждениями электронов
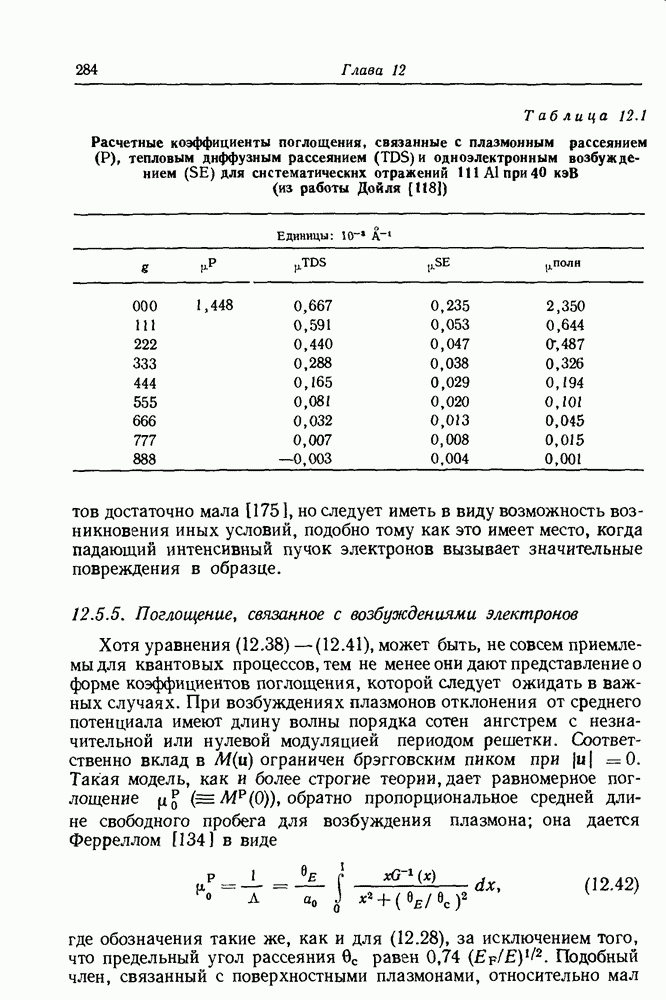
- 12.5.6. Значения коэффициентов поглощения
- ГЛАВА 13. Формирование изображения в электронном микроскопе
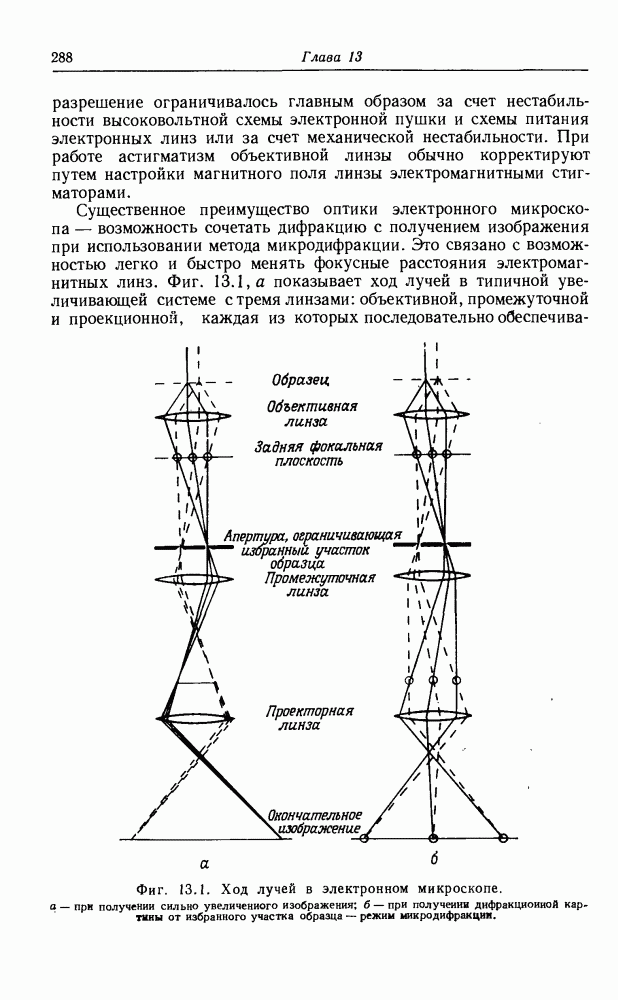
- 13.1.1. Обычный просвечивающий электронный микроскоп
- 13.1.2. Сканирующий просвечивающий электронный микроскоп
- 13.2. Образование изображения
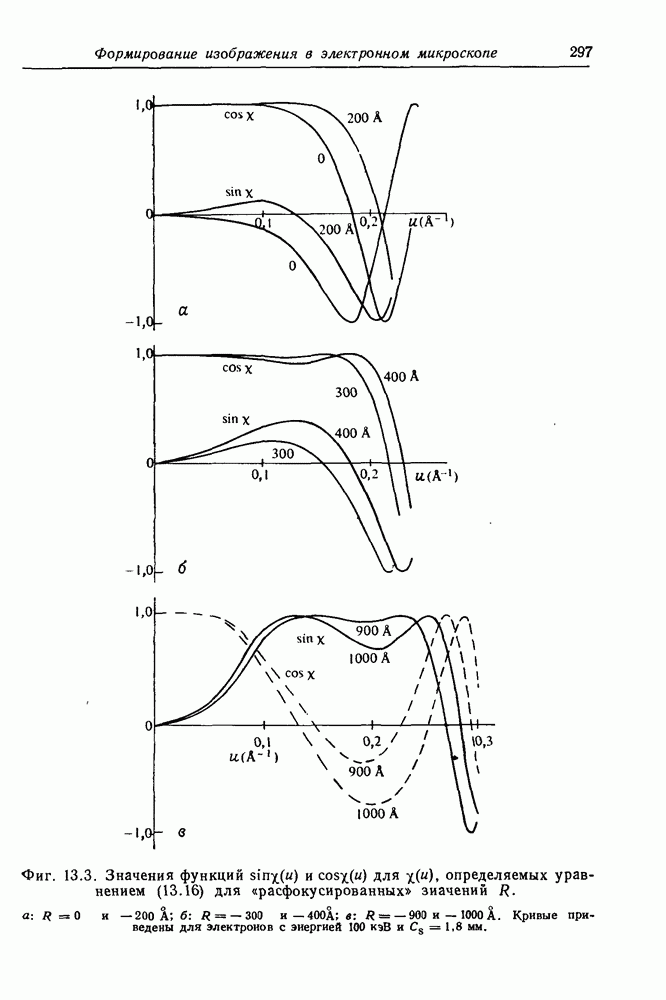
- 13.3. Контраст для тонких образцов
- 13.3.1. Приближение фазового объекта
- 13.3.2. Функция поглощения
- 13.3.3. Приближение слабофазового объекта
- 13.3.4. Темнопольные изображения
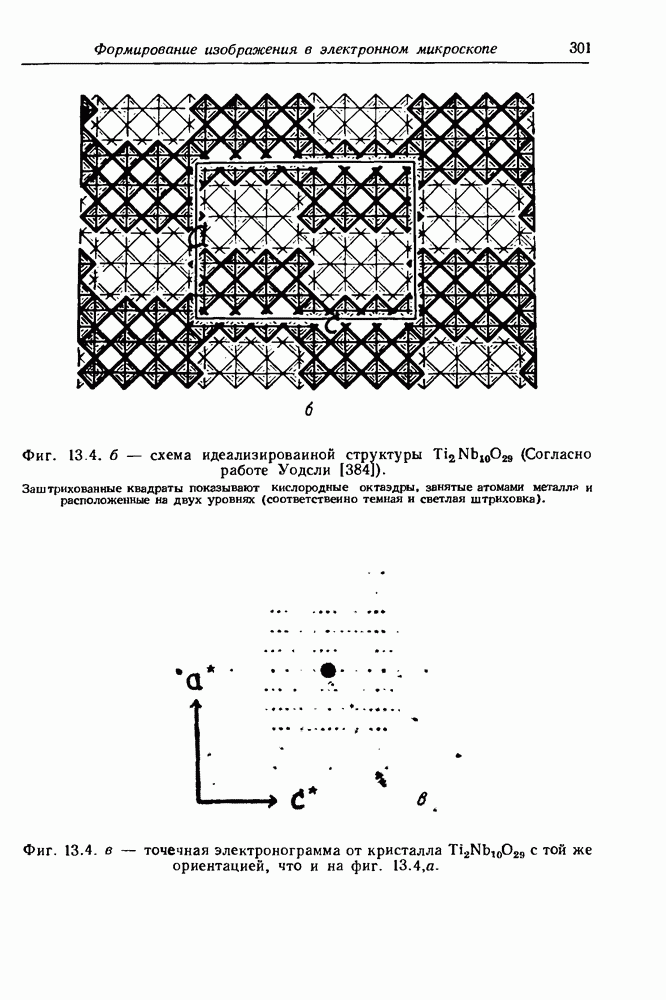
- 13.4. Образование изображения кристаллических структур
- 13.4.1. Образование изображения тонких кристаллов
- 13.4.2. Расчет изображений кристаллов
- 13.4.3. Полосы решетки для толстых кристаллов
- 13.4.4. Получение изображения кристаллов из разрешения решетки
- 13.5. Высоковольтная микроскопия
- ГЛАВА 14. К-линии и каналирование
- 14.1.1. Геометрия линий Косселя
- 14.1.2. Динамическая теория интенсивностей линий Косселя
- 14.1.3. Линии Косселя с ограниченным разрешением
- 14.2. Линии Кикучи
- 14.3. Внешние источники расходящегося излучения
- 14.4. Информация, получаемая из картин К-линий
- 14.5. Каналирование
- 14.6. Вторичные излучения
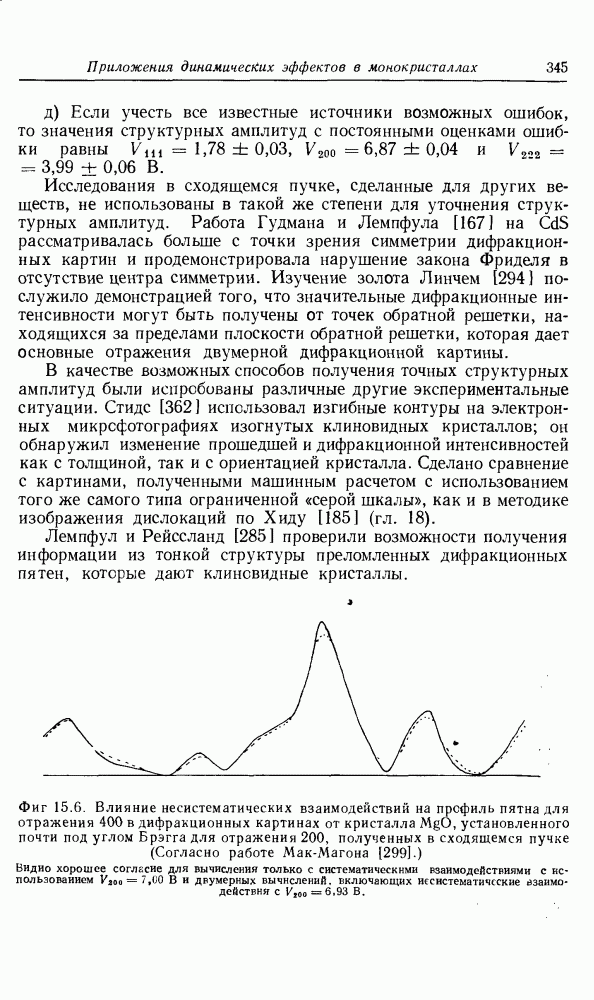
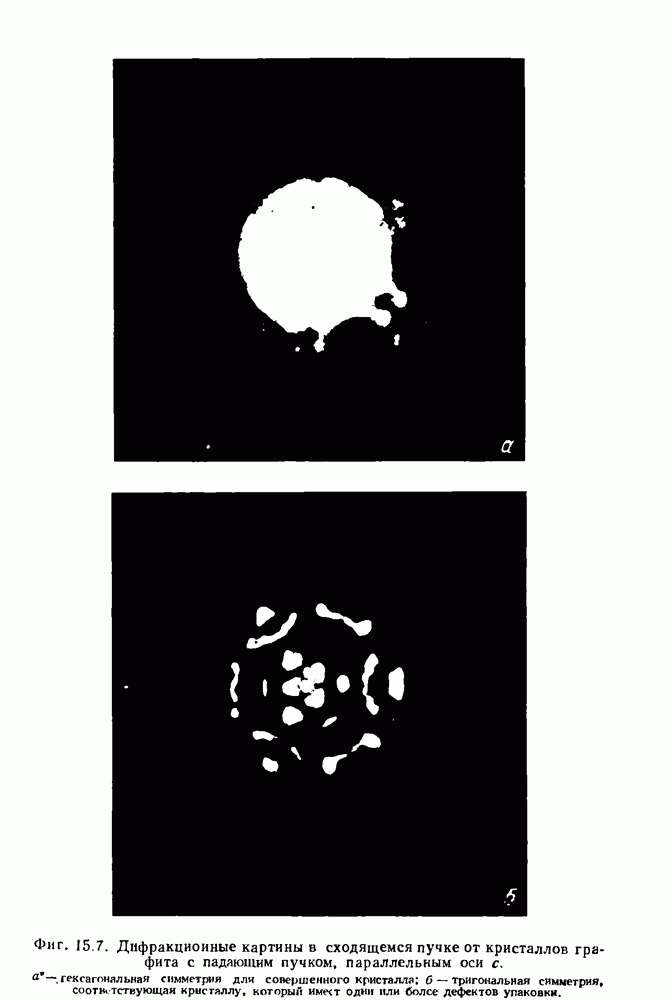
- ГЛАВА 15. Приложения динамических эффектов в монокристаллах
- 15.1. Зависимость динамических эффектов от параметров кристалла
- 15.2. Рентгеновская интерферометрия
- 15.3. n-волновая и двухволновая динамическая дифракция
- 15.4. Определения структурных амплитуд из полос равной толщины
- 15.5. Структурные амплитуды из кривых качания
- 15.6. Релятивистские эффекты
- 15.7. Поглощение и температурные эффекты
- 15.8. Определение симметрии кристалла
- ГЛАВА 16. Мозаичные кристаллы и поликристаллические материалы
- 16.2. Мозаичные кристаллы
- 16.2.1. Модель мозаичного кристалла
- 16.2.2. Кинематические интегральные интенсивности
- 16.2.3. Экстинкционные эффекты
- 16.2.4. Динамические интенсивности при дифракции электронов
- 16.3. Поликристаллический материал
- 16.3.2. Интенсивности кинематической дифракции
- 16.3.3. Анализ профиля линий
- 16.3.4. Интенсивности динамической дифракции
- 16.3.5. Эффекты n-волновой дифракции
- ГЛАВА 17. Упорядочение атомов в кристаллах
- 17.1. Природа и описание неупорядоченных состояний
- 17.2. Параметры порядка
- 17.3. Функция Паттерсона
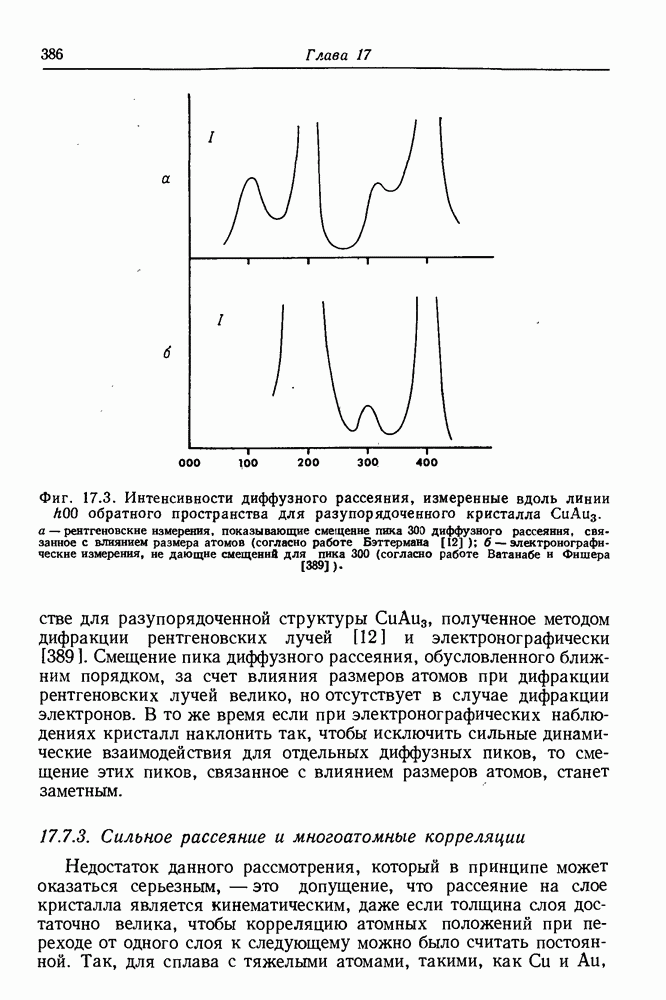
- 17.4. Влияние размера атомов
- 17.5. Кинематическая дифракция
- 17.5.1. Дифракция при наличии лишь упорядочения
- 17.5.2. Дифракция и влияние упорядочения и размера атомов
- 17.6. Связь с энергиями упорядочения
- 17.7. Динамическое рассеяние на разупорядоченных кристаллах
- 17.7.2. Расчет диффузного рассеяния
- 17.7.3. Сильное рассеяние и многоатомные корреляции
- 17.8. Некогерентные домены
- 17.8.1. Упорядоченные некогерентные сверхструктуры
- 17.8.2. Некогерентные домены в разупорядоченных сплавах
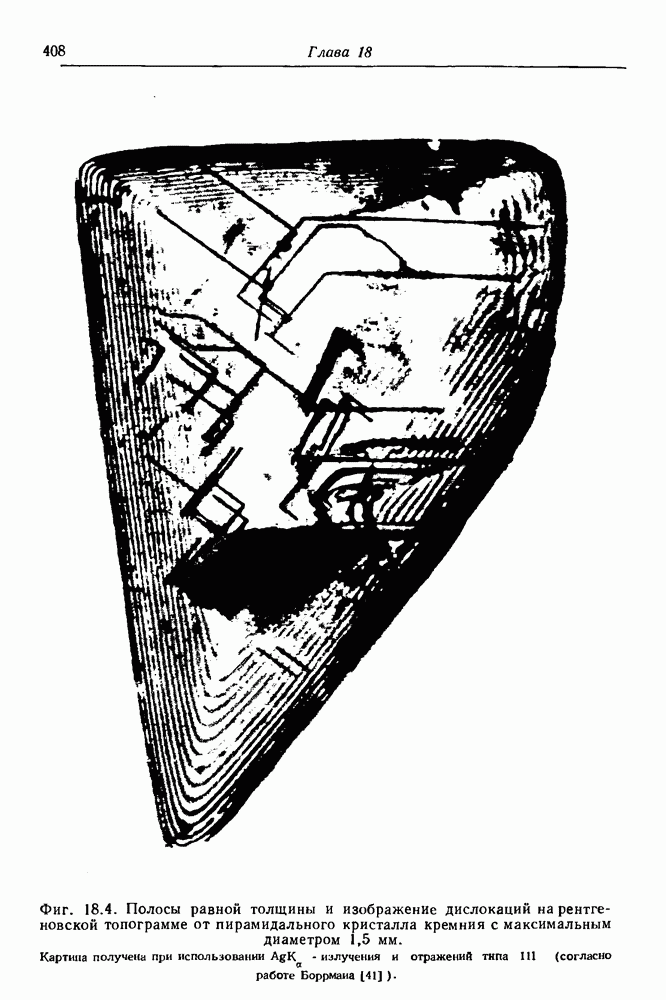
- ГЛАВА 18. Протяженные дефекты
- 18.2. Дефекты упаковки — статистическая кинематическая теория
- 18.2.3. Дефекты в структурах с плотной упаковкой
- 18.3. Динамическая дифракция на дефектах упаковки
- 18.4. Дислокации
- 18.4.1. Дифракционные эффекты.
- 18.4.2. Получение изображений дислокаций
- 18.4.3. Усреднение по углам падения
- 18.4.4. n-волновые дифракционные эффекты