| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5.8. Сечения и проекции
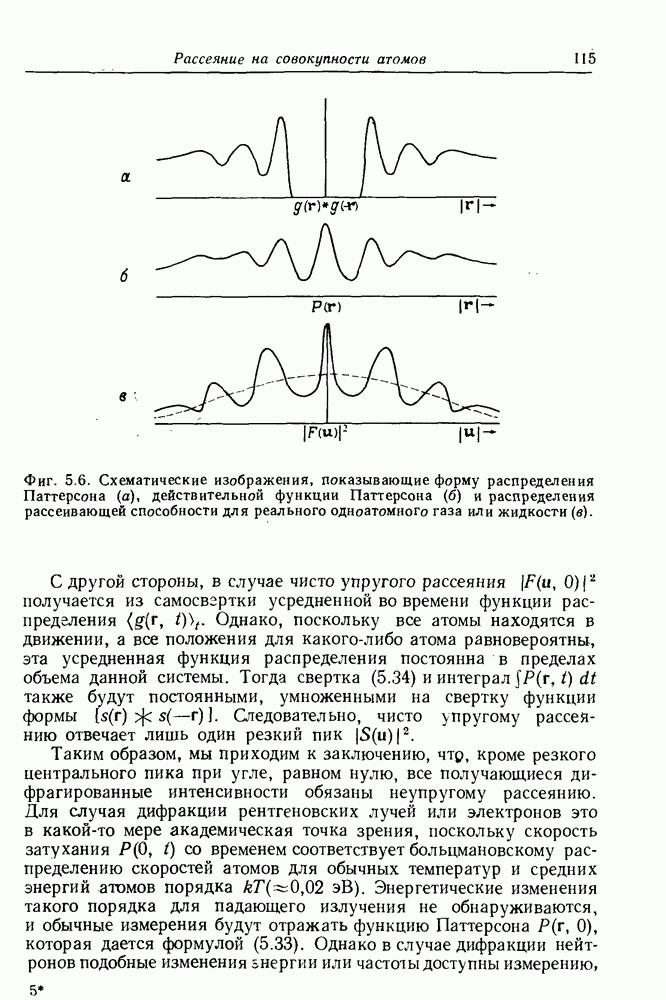
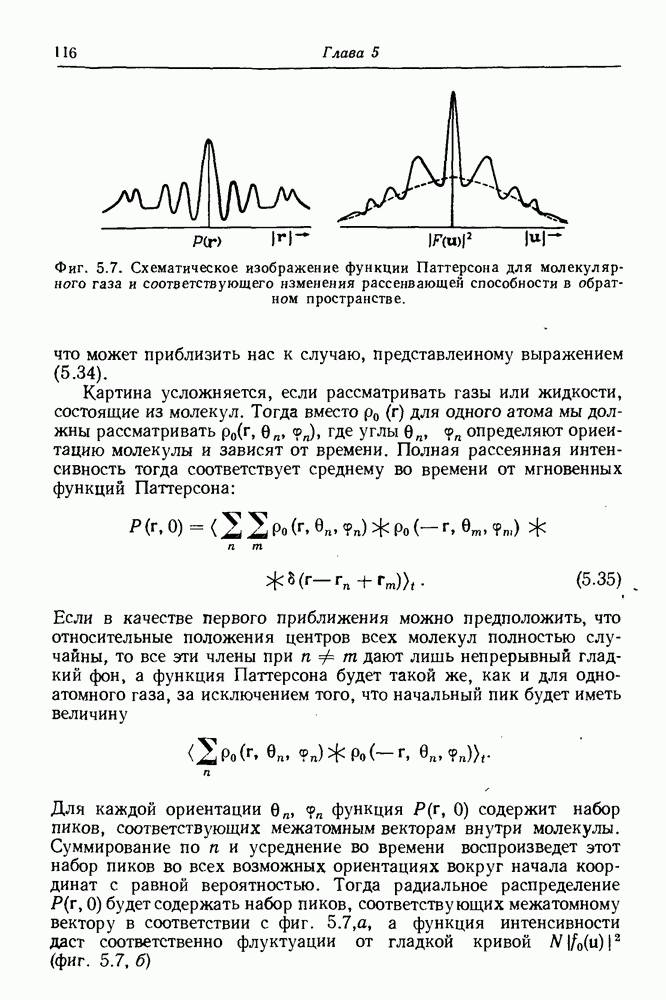
Для многих целей удобно иметь дело с одномерными и двумерными сечениями или проекциями трехмерных функций  Функции, построенные в одном или двух измерениях, значительно легче представлять и оценивать, а для их определения зачастую требуется много меньше данных. Для случая радиально-симметричной функции, такой, как
Функции, построенные в одном или двух измерениях, значительно легче представлять и оценивать, а для их определения зачастую требуется много меньше данных. Для случая радиально-симметричной функции, такой, как  для газа или жидкости, переход к числу измерений, большему единицы, не дает какой-либо новой информации.
для газа или жидкости, переход к числу измерений, большему единицы, не дает какой-либо новой информации.
В первом приближении получаемые экспериментально электронограммы представляют собой плоские сечения обратного пространства. В случае дифракции рентгеновских лучей плоские сечения обратного пространства можно получить, используя прецессионную камеру Бургера или сходные с ней камеры, а простейший режим работы рентгеновского дифрактометра, сканирование  дает сечение вдоль радиальной прямой линии.
дает сечение вдоль радиальной прямой линии.
Следовательно, сейчас будет полезно получить общие соотношения между сечениями и проекциями в реальном и обратном пространствах. Для удобства сделаем это на примере функций  имея в виду также более широкий круг вопросов.
имея в виду также более широкий круг вопросов.
Для проекции функции  в направлении оси
в направлении оси  имеем
имеем

или в зависимости от 

Интеграл по  является дельта-функцией
является дельта-функцией  так что
так что  есть обратное фурье-преобразование
есть обратное фурье-преобразование  сечения
сечения  в плоскости
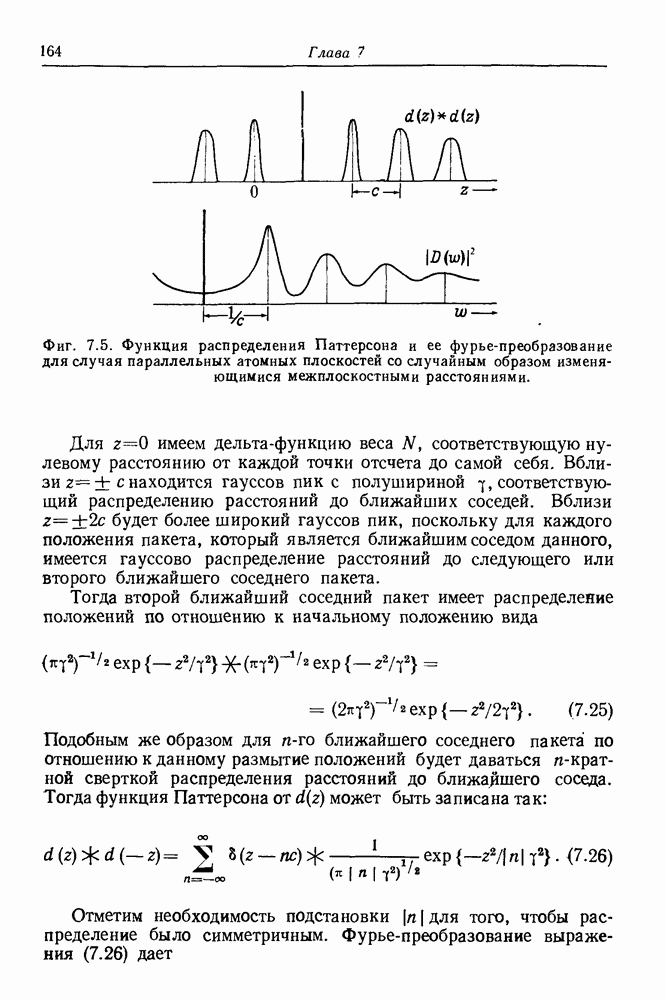
в плоскости 
Подобным же образом плоское сечение  в плоскости
в плоскости  есть
есть

Таким образом, мы получили общее соотношение, показывающее, что плоское сечение, проходящее через начало координат в реальном пространстве, соответствует проекции распределения в обратном пространстве на параллельную плоскость и наоборот.
Например, в первом приближении электронограмма является плоским сечением обратного пространства, так что фурье-преобразование распределения интенсивности электронограммы дает проекцию функции Паттерсона  в направлении пучка. Это является приближением, позволяющем рассматривать объект как двумерный фазовый и амплитудный объект.
в направлении пучка. Это является приближением, позволяющем рассматривать объект как двумерный фазовый и амплитудный объект.
Выше в разд. 5.5 мы видели примеры для случая четырехмерных распределений в пространстве и во времени, когда интенсивность измеряется как функция углов рассеяния и частот. Таким образом, сечение обратного пространства на плоскости  соответствующее чисто упругому рассеянию [см. (5.28)] дает проекцию функции Паттерсона в начальный момент или усредненную во времени корреляционную функцию. Проекция четырехмерного распределения рассеивающей способности в обратном пространстве в направлении
соответствующее чисто упругому рассеянию [см. (5.28)] дает проекцию функции Паттерсона в начальный момент или усредненную во времени корреляционную функцию. Проекция четырехмерного распределения рассеивающей способности в обратном пространстве в направлении  которая дается интегралом по
которая дается интегралом по  в уравнении (5.29), является фурье-преобразованием сечения функции Паттерсона
в уравнении (5.29), является фурье-преобразованием сечения функции Паттерсона  которая является суммой мгновенных пространственных корреляций объекта.
которая является суммой мгновенных пространственных корреляций объекта.
Если сечение в реальном пространстве не проходит через начало координат, то в обратном пространстве вводится соответствующий фазовый множитель. Таким образом, фурье-преобразование сечения р(х, у, с) дает модулированную проекцию

Если это рассмотрение использовать для случая одномерных сечений и проекций, получим

и

Таким образом, значение  вдоль оси
вдоль оси  дается фурье-преобразованием проекции
дается фурье-преобразованием проекции  вдоль обоих направлений
вдоль обоих направлений  на ось
на ось  .
.
Примером четырехмерного случая является случай, описываемый уравнением (5.30), где интересующая нас функция  является корреляцией во времени для положения в центре. Эта функция получается при проектировании функции обратного пространства
является корреляцией во времени для положения в центре. Эта функция получается при проектировании функции обратного пространства  на направления
на направления  т. е. при интегрировании по всем направлениям для каждого изменения частоты
т. е. при интегрировании по всем направлениям для каждого изменения частоты 
ЗАДАЧИ
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ГЛАВА 1. Дифракция Френеля и Фраунгофера
- 1.2. Волновые уравнения и волны
- 1.2.2. Электромагнитные волны
- 1.2.3. Волны-частицы
- 1.3. Суперпозиция и когерентность
- 1.3.2. Независимые точенные источники
- 1.4. Принцип Гюйгенса
- 1.4.2. Применение формулы Кирхгофа
- 1.5. Подход с точки зрения теории рассеяния
- 1.5.1. Интегральная форма волнового уравнения
- 1.5.2. Ряд Борна
- 1.6. Принцип взаимности
- 1.7. Дифракция Френеля
- 1.7.2. Интегралы Френеля
- 1.7.3. Периодические объекты — «фурье-изображения»
- 1.8. Дифракция Фраунгофера
- ГЛАВА 2. Фурье-преобразования и свертки
- 2.1.1. Дельта-функция и непрерывность
- 2.1.2. Свертки
- 2.1.3. Примеры сверток
- 2.2. Фурье-преобразования: общее рассмотрение
- 2.2.2. Свойства фурье-преобразований
- 2.2.3. Умножение и свертка
- 2.2.4. Пространство и время
- 2.3. Фурье-преобразования и дифракция: примеры
- 2.3.2. Плоская волна: преобразование, обратное рассмотренному в разд. 2.3.1.
- 2.3.3. Трансляция объекта
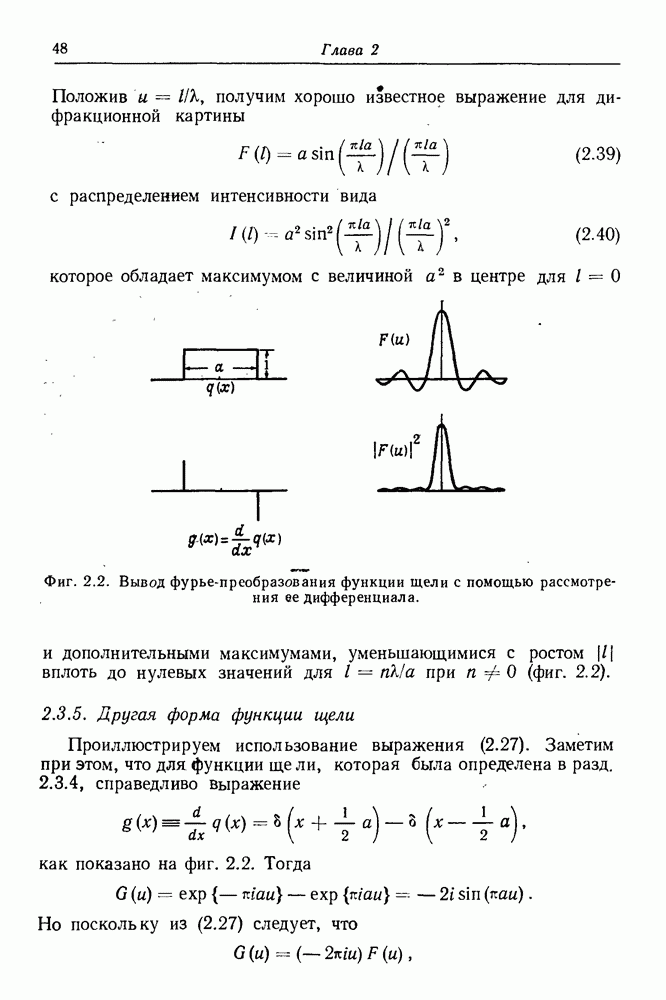
- 2.3.4. Функция щели
- 2.3.5. Другая форма функции щели
- 2.3.6. Прямолинейный край
- 2.3.7. Прямоугольная апертура
- 2.3.8. Круглая апертура
- 2.3.9. Две очень узкие щели
- 2.3.10. Две щели заметной ширины
- 2.3.11. Конечный цуг волн
- 2.3.12. Периодическая последовательность узких щелей
- 2.3.13. Произвольная периодическая функция
- 2.3.14. Дифракционная решетка: тонкие щели
- 2.3.15. Дифракционная решетка: общее рассмотрение
- 2.3.16. Функция Гаусса
- 2.3.17. Ряд круглых отверстий
- 2.3.18. Дополнительные объекты — теорема Бабине
- 2.3.19. Полные интенсивности: теорема Парсеваля
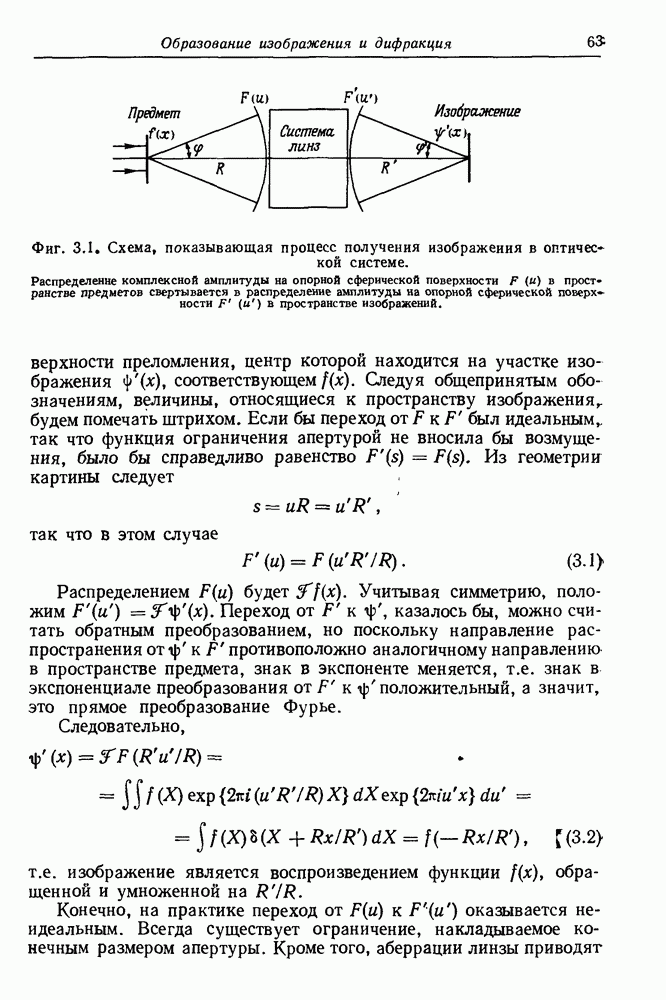
- ГЛАВА 3. Образование изображения и дифракция
- 3.1.1. Когерентная волновая оптика
- 3.1.2. Получение изображения с помощью некогерентных волн
- 3.2. Теория Аббе
- 3.3. Малоугловое приближение
- 3.4. Фазовый контраст
- 3.4.1. Фазовые и амплитудные объекты
- 3.4.2. Контраст при дефокусировке
- 3.4.3. Ограничения, накладываемые апертурой
- 3.4.4. Фазовый контраст Пернике
- 3.5. Многокомпонентные системы
- ГЛАВА 4. Различные виды излучения и рассеяние веществом
- 4.1.1. Источники рентгеновских лучей
- 4.1.2. Рассеяние электронами
- 4.1.3. Рассеяние атомами
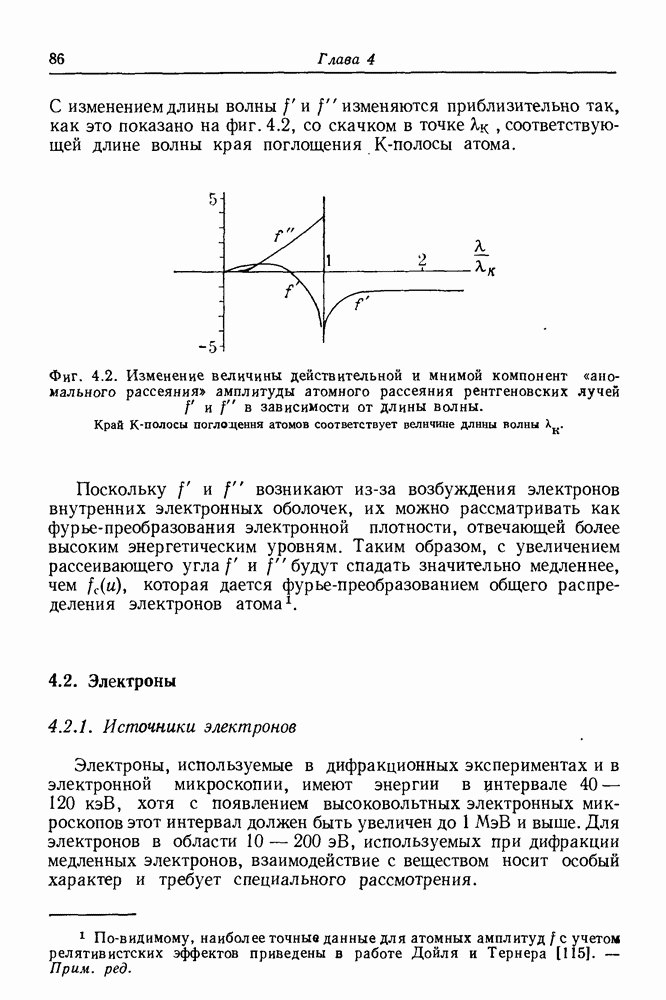
- 4.1.4. Дисперсионные поправки
- 4.2. Электроны
- 4.2.1. Источники электронов
- 4.2.2. Амплитуды атомного рассеяния
- 4.2.3. Приближение фазового объекта
- 4.2.4. Ограниченность первого борновского приближения
- 4.2.5. Эффекты поглощения
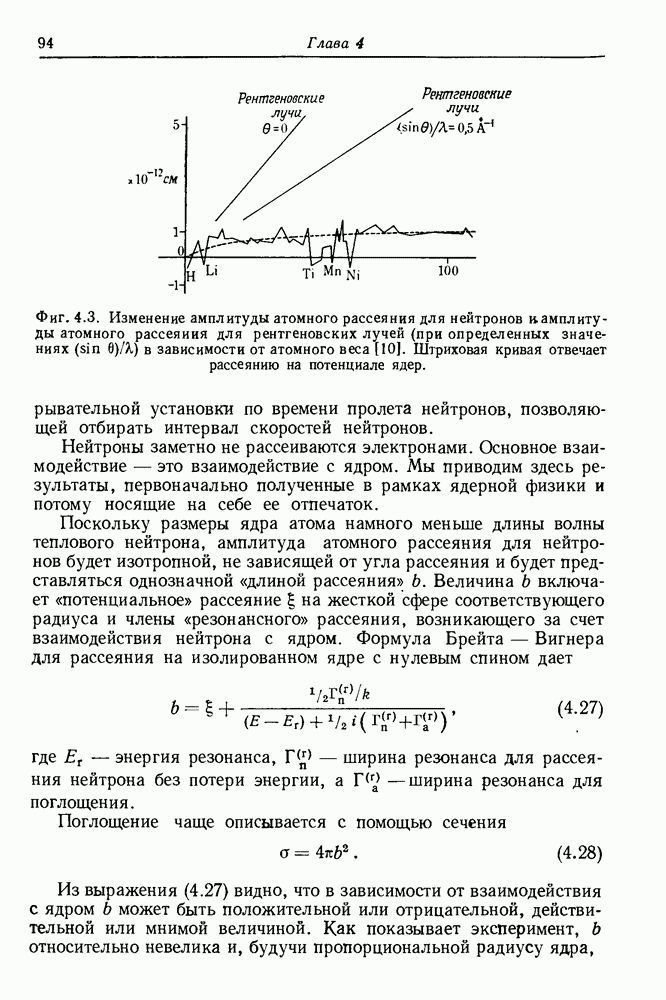
- 4.3. Нейтроны
- 4.3.2. Ядерное спиновое рассеяние
- 4.3.3. Изотопное разупорядочение
- 4.3.4. Тепловое и магнитное рассеяние
- ГЛАВА 5. Рассеяние на совокупности атомов
- 5.2. Прямое и обратное пространства
- 5.2.2. Обратная решетка
- 5.2.3. Закон Фриделя и фазовая задача
- 5.3. Обобщенная функция Паттерсона
- 5.4. Примеры корреляционных функций
- 5.4.1. Ограничения за счет конечных объемов
- 5.4.2. Конечные кристаллы
- 5.5. Корреляция в пространстве и во времени
- 5.5.1. Четырехмерная функция Паттерсона
- 5.5.2. Частные случаи
- 5.5.3. Идеальные одноатомные газы и жидкости
- 5.5.4. Реальные одноатомные газы и жидкости
- 5.5.5. Атом водорода
- 5.6. Интенсивности и геометрия дифракции
- 5.7. Практические примеры
- 5.7.1. Конечные источники и детекторы
- 5.7.2. Разброс длин волн
- 5.7.3. Интегральные интенсивности
- 5.8. Сечения и проекции
- ГЛАВА 6. Дифракция на кристаллах
- 6.1. Идеальные кристаллы
- 6.2. Геометрия дифракции
- 6.2.1. Условия дифракции Лауэ и Брэгга
- 6.2.2. Фурье-преобразования функции формы
- 6.2.3. Особые случаи при дифракции электронов
- 6.3. Структурный анализ кристаллов
- 6.3.2. Дополнительная информация
- 6.4. Методы структурного анализа
- 6.4.2. Функция Паттерсона
- 6.4.3. Оптические аналоги
- 6.4.4. Другие методы
- 6.5. Нейтронографический структурный анализ
- 6.5.2. Магнитное рассеяние
- 6.6. Электронографический структурный анализ
- ГЛАВА 7. Дифракция на несовершенных кристаллах
- 7.1. Формулировка дифракционной задачи
- 7.1.2. Общая формулировка дифракционной задачи.
- 7.2. Метод функции Паттерсона
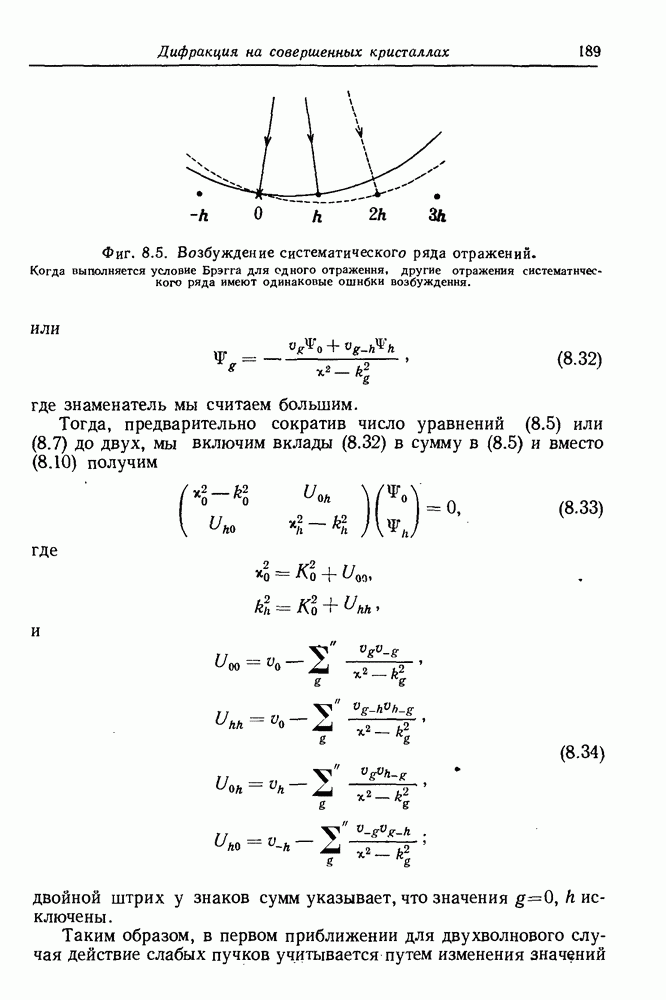
- 7.2.1. Функция Паттерсона для усредненной периодической структуры
- 7.2.2. Функция Паттерсона в отсутствие усредненной структуры
- 7.3. Отклонения от усредненной решетки
- 7.3.1. Распределенные вакансии: отсутствие релаксации
- 7.3.2. Вакансии, сгруппированные в кластеры
- 7.3.3. Релаксация решетки
- 7.3.4. Тепловые колебания — модель Эйнштейна
- 7.4. Несовершенные кристаллы в отсутствие усредненной решетки
- 7.4.2. Разупорядоченные ориентации
- ГЛАВА 8. Дифракция на совершенных кристаллах
- 8.1. Многократное когерентное рассеяние
- 8.2. Теоретические приближения
- 8.3. Теория Бете
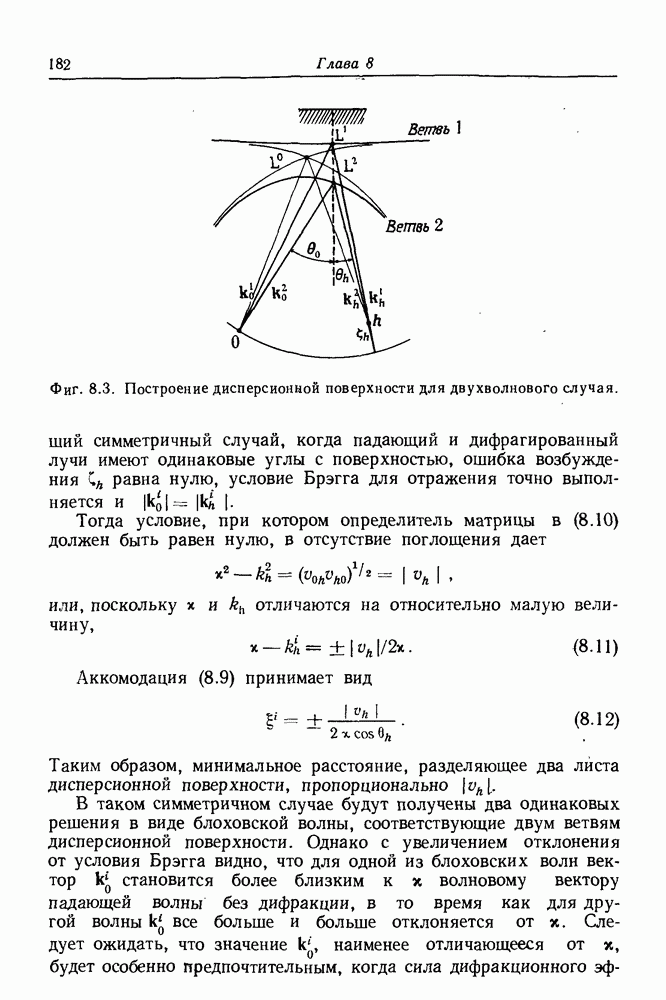
- 8.4. Двухволновое приближение
- 8.4.1. Блоховские волны и дисперсионные поверхности
- 8.4.2. Электроны проводимости: энергетическое представление
- 8.4.3. Дифракция рентгеновских лучей; поляризация
- 8.5. Случай Лауэ (прохождение)
- 8.5.1. Дифракция электронов на тонком кристалле
- 8.5.2. Малоугловое приближение
- 8.5.3. Случай Лауэ с поглощением
- 8.6. Потенциалы Бете
- 8.7. Случай Брэгга
- ГЛАВА 9. Динамические дифракционные эффекты
- 9.1. Полосы равной толщины и кривые качания при дифракции электронов
- 9.1.2. Картина процесса в реальном пространстве
- 9.1.3. Кривые качания
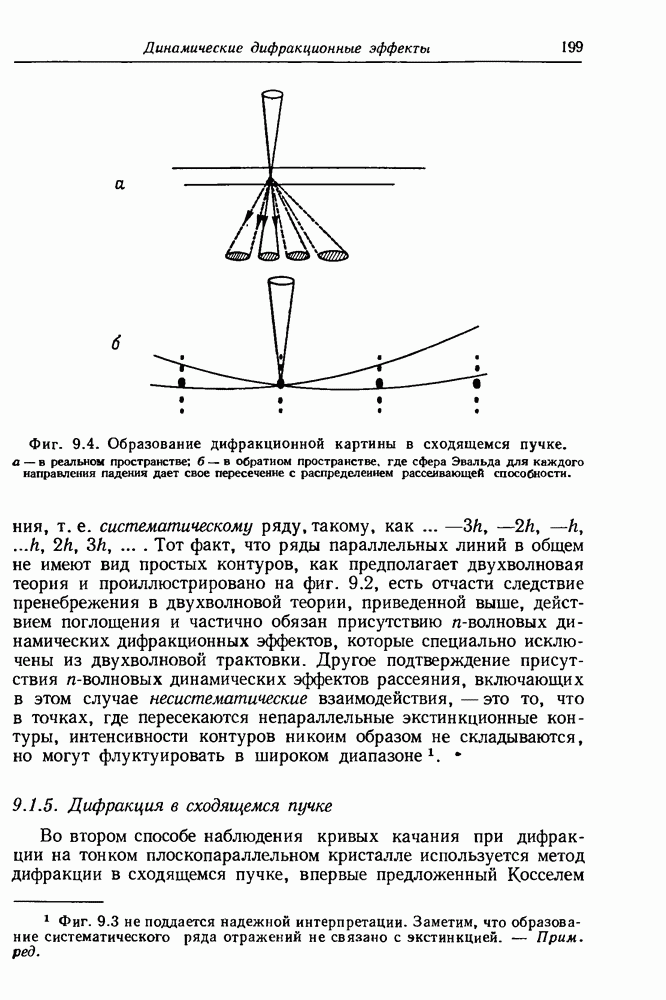
- 9.1.4. Экстинкционные контуры
- 9.1.5. Дифракция в сходящемся пучке
- 9.1.6. Дифракция и изображения клиновидных кристаллов
- 9.1.7. Эффекты поглощения для клиньев
- 9.2. Динамические эффекты при дифракции рентгеновских лучей и нейтронов
- 9.2.2. Поток энергии
- 9.2.3. Картина дисперсионной поверхности
- 9.2.4. Дифракция нейтронов
- 9.3. Эффект Боррмана
- ГЛАВА 10. Обобщение на случай многих пучков
- 10.1. Динамическая n-волновая дифракция
- 10.2. Обобщение теории Бете на случай прохождения
- 10.2.2. Малоугловое приближение
- 10.2.3. Блоховские волны и граничные условия
- 10.2.4. Матрица рассеяния
- 10.3. Подход Дарвина
- 10.4. Специальные случаи — уменьшение числа пучков
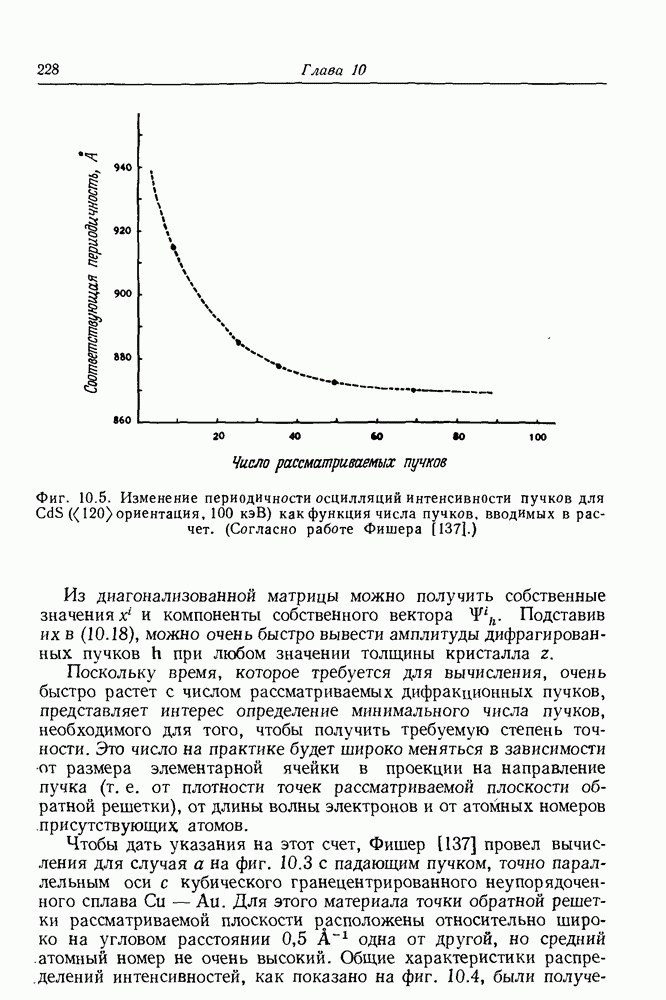
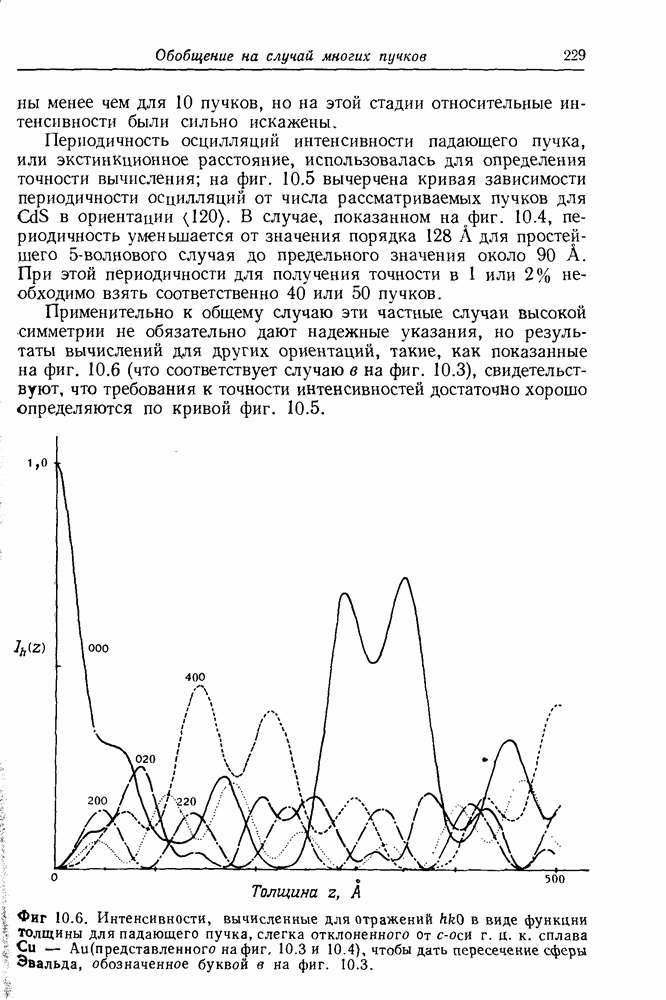
- 10.5. Вычислительные методы
- 10.6. Колонковое приближение
- ГЛАВА 11. Метод «физической оптики»
- 11.1 Распространение электронов в кристаллах
- 11.1.3. Дифракция в кристалле
- 11.1.4. Общее выражение в функции от ошибок возбуждения
- 11.2. Ряды многократного рассеяния
- 11.3. Общее решение с двойным суммированием
- 11.3.2. Приближение фазовой решетки
- 11.4. Методы вычислений
- 11.4.1. Вычисления «слоевым методом»
- 11.5. Интенсивности для непериодических объектов
- ГЛАВА 12. Диффузное рассеяние и эффекты поглощения
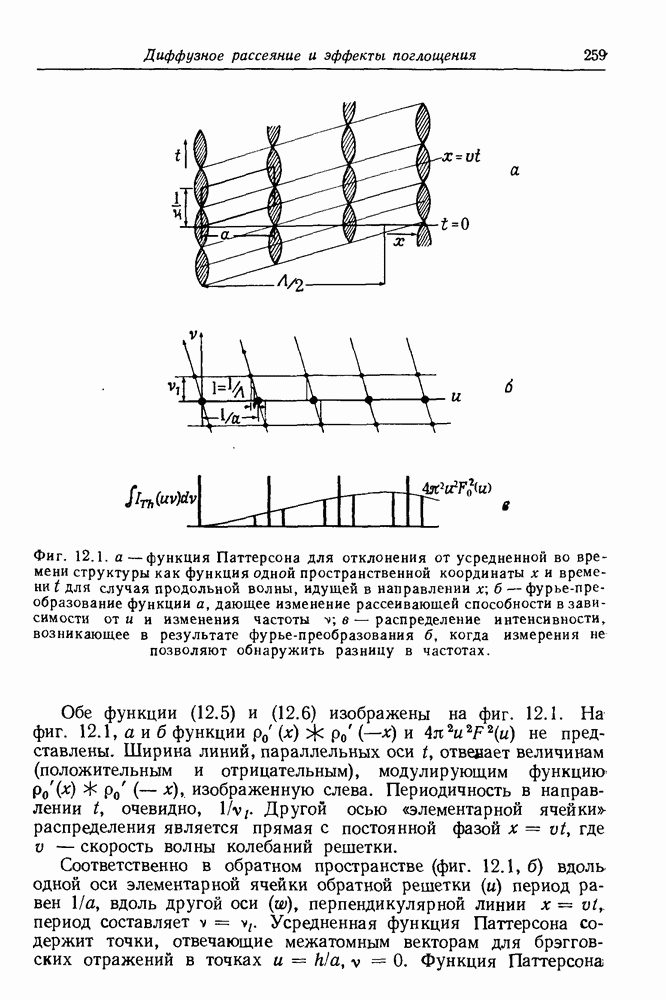
- 12.1. Тепловое диффузное рассеяние
- 12.1.2. Рассеяние для продольной волны
- 12.1.3. Компонента диффузного рассеяния
- 12.1.4. Дисперсионные кривые
- 12.1.5. Трехмерные обобщения
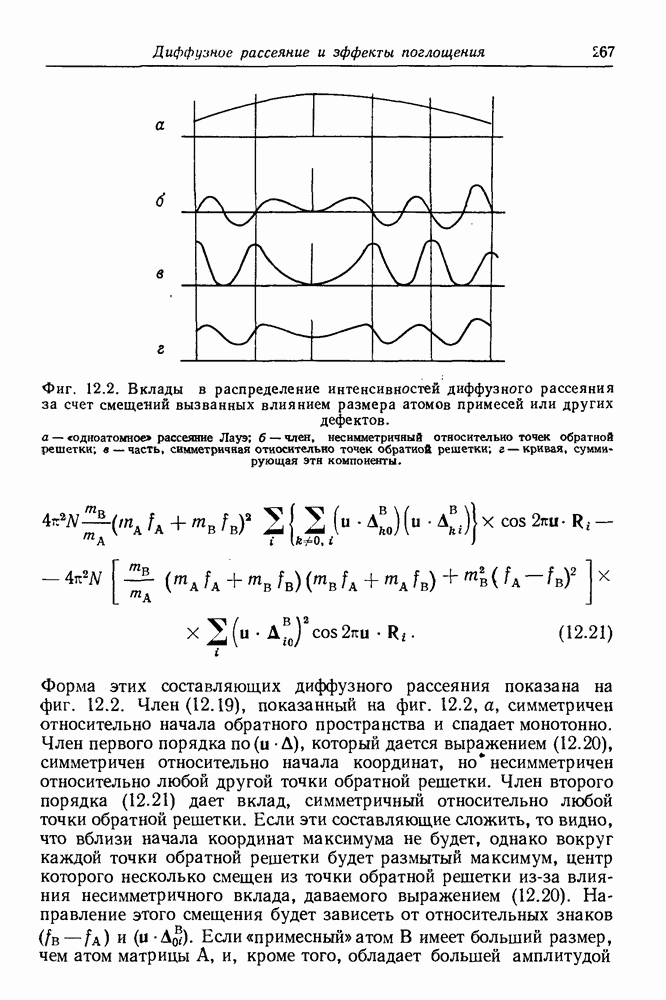
- 12.2. Статические смещения атомов
- 12.2.2. Дифракционные интенсивности рассеяния на смещенных атомах
- 12.2.3. Брэгговские пики
- 12.2.4. Диффузное рассеяние
- 12.3. Возбуждения электронов
- 12.3.1. Неупругое рентгеновское рассеяние
- 12.3.2. Возбуждение электронов электронами — плазмоны
- 12.3.3. Одноэлектронные возбуждения
- 2.4. Динамические эффекты при диффузном рассеянии
- 12.4.2. Когерентное и некогерентное рассеяние
- 12.4.3. Анализ диффузного рассеяния
- 12.5. Эффекты поглощения
- 12.5.1. Природа параметров поглощения
- 12.5.2. Поглощение рентгеновских лучей и нейтронов
- 12.5.3. «Поглощение» для электронов
- 12.5.4. Поглощение, связанное с тепловыми колебаниями
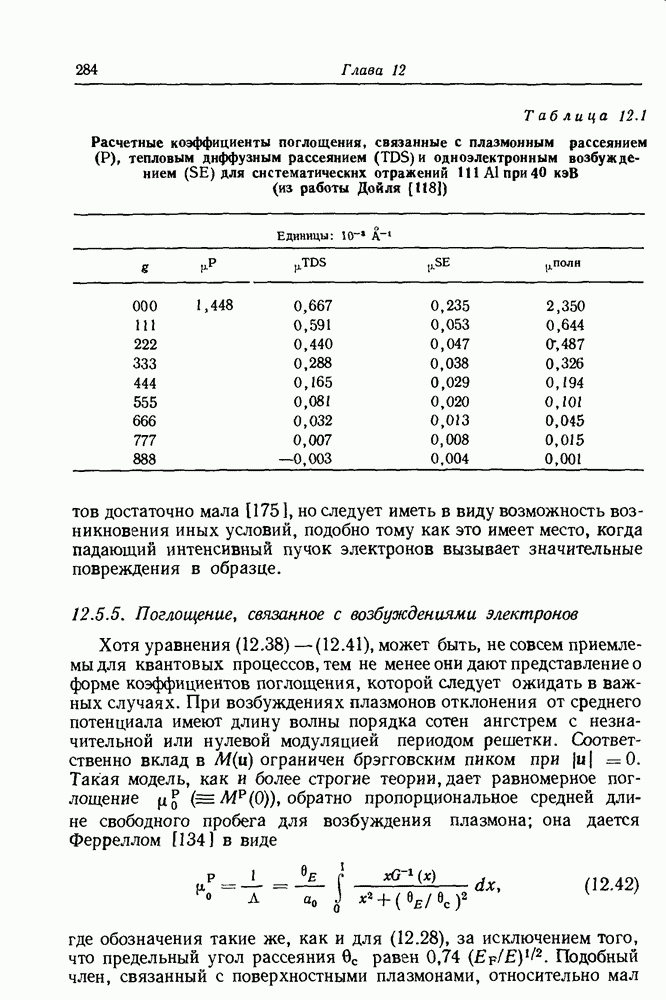
- 12.5.5. Поглощение, связанное с возбуждениями электронов
- 12.5.6. Значения коэффициентов поглощения
- ГЛАВА 13. Формирование изображения в электронном микроскопе
- 13.1.1. Обычный просвечивающий электронный микроскоп
- 13.1.2. Сканирующий просвечивающий электронный микроскоп
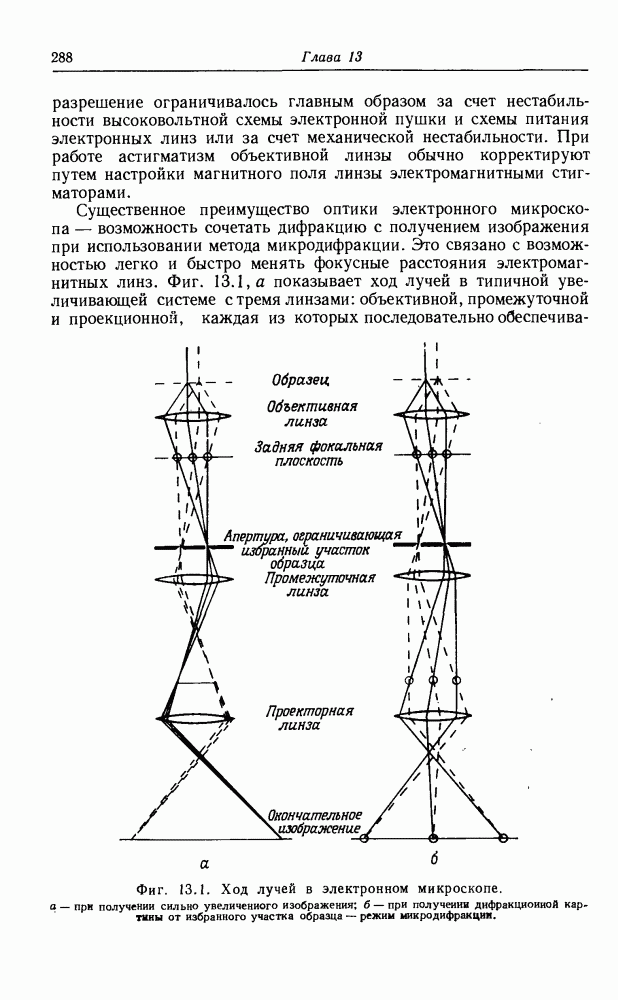
- 13.2. Образование изображения
- 13.3. Контраст для тонких образцов
- 13.3.1. Приближение фазового объекта
- 13.3.2. Функция поглощения
- 13.3.3. Приближение слабофазового объекта
- 13.3.4. Темнопольные изображения
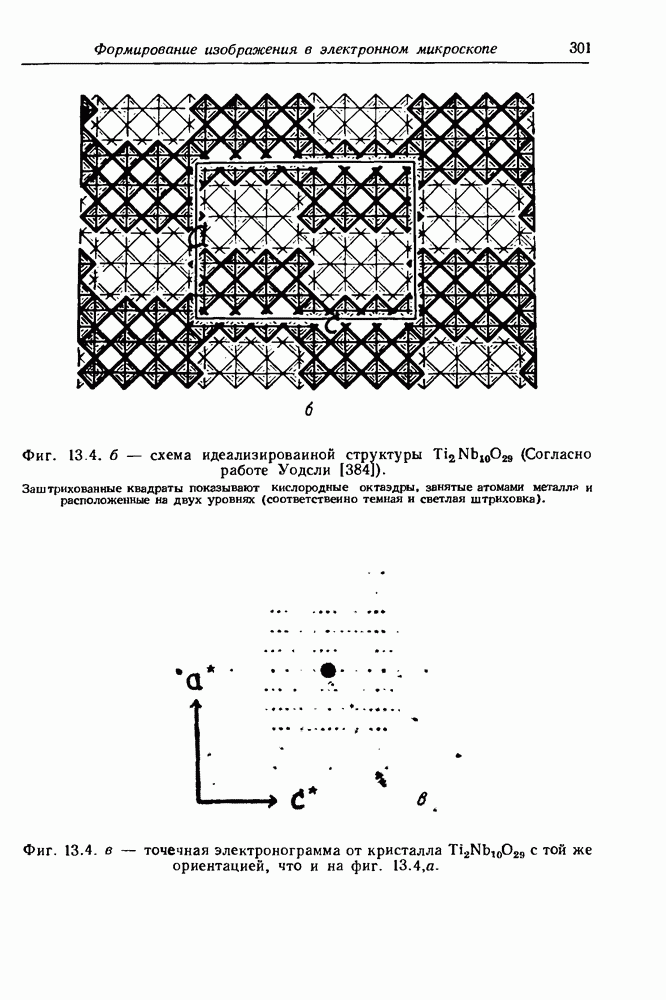
- 13.4. Образование изображения кристаллических структур
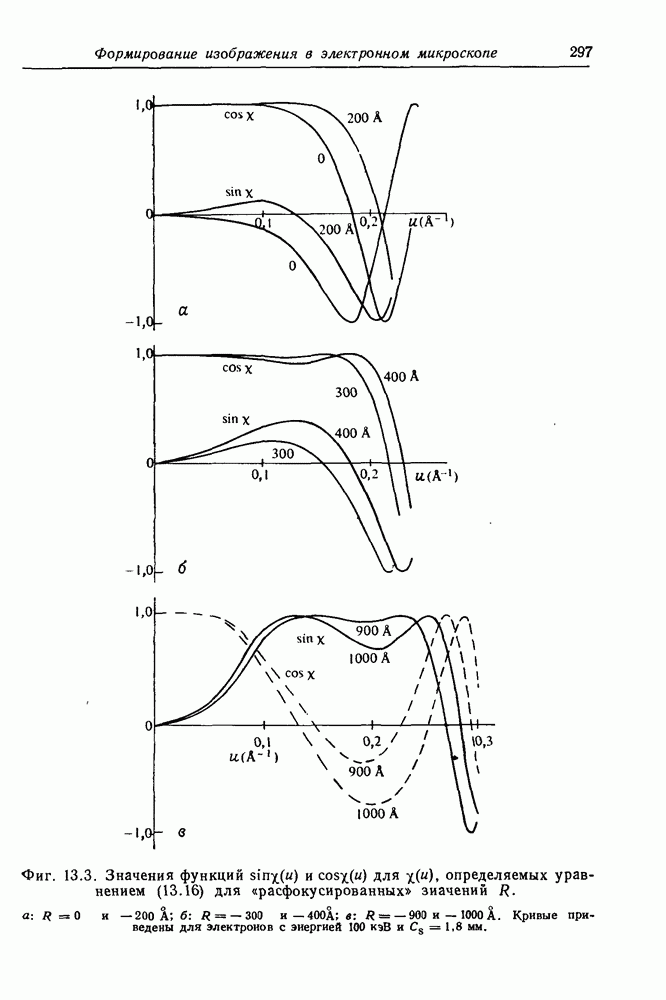
- 13.4.1. Образование изображения тонких кристаллов
- 13.4.2. Расчет изображений кристаллов
- 13.4.3. Полосы решетки для толстых кристаллов
- 13.4.4. Получение изображения кристаллов из разрешения решетки
- 13.5. Высоковольтная микроскопия
- ГЛАВА 14. К-линии и каналирование
- 14.1.1. Геометрия линий Косселя
- 14.1.2. Динамическая теория интенсивностей линий Косселя
- 14.1.3. Линии Косселя с ограниченным разрешением
- 14.2. Линии Кикучи
- 14.3. Внешние источники расходящегося излучения
- 14.4. Информация, получаемая из картин К-линий
- 14.5. Каналирование
- 14.6. Вторичные излучения
- ГЛАВА 15. Приложения динамических эффектов в монокристаллах
- 15.1. Зависимость динамических эффектов от параметров кристалла
- 15.2. Рентгеновская интерферометрия
- 15.3. n-волновая и двухволновая динамическая дифракция
- 15.4. Определения структурных амплитуд из полос равной толщины
- 15.5. Структурные амплитуды из кривых качания
- 15.6. Релятивистские эффекты
- 15.7. Поглощение и температурные эффекты
- 15.8. Определение симметрии кристалла
- ГЛАВА 16. Мозаичные кристаллы и поликристаллические материалы
- 16.2. Мозаичные кристаллы
- 16.2.1. Модель мозаичного кристалла
- 16.2.2. Кинематические интегральные интенсивности
- 16.2.3. Экстинкционные эффекты
- 16.2.4. Динамические интенсивности при дифракции электронов
- 16.3. Поликристаллический материал
- 16.3.2. Интенсивности кинематической дифракции
- 16.3.3. Анализ профиля линий
- 16.3.4. Интенсивности динамической дифракции
- 16.3.5. Эффекты n-волновой дифракции
- ГЛАВА 17. Упорядочение атомов в кристаллах
- 17.1. Природа и описание неупорядоченных состояний
- 17.2. Параметры порядка
- 17.3. Функция Паттерсона
- 17.4. Влияние размера атомов
- 17.5. Кинематическая дифракция
- 17.5.1. Дифракция при наличии лишь упорядочения
- 17.5.2. Дифракция и влияние упорядочения и размера атомов
- 17.6. Связь с энергиями упорядочения
- 17.7. Динамическое рассеяние на разупорядоченных кристаллах
- 17.7.2. Расчет диффузного рассеяния
- 17.7.3. Сильное рассеяние и многоатомные корреляции
- 17.8. Некогерентные домены
- 17.8.1. Упорядоченные некогерентные сверхструктуры
- 17.8.2. Некогерентные домены в разупорядоченных сплавах
- ГЛАВА 18. Протяженные дефекты
- 18.2. Дефекты упаковки — статистическая кинематическая теория
- 18.2.3. Дефекты в структурах с плотной упаковкой
- 18.3. Динамическая дифракция на дефектах упаковки
- 18.4. Дислокации
- 18.4.1. Дифракционные эффекты.
- 18.4.2. Получение изображений дислокаций
- 18.4.3. Усреднение по углам падения
- 18.4.4. n-волновые дифракционные эффекты