| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
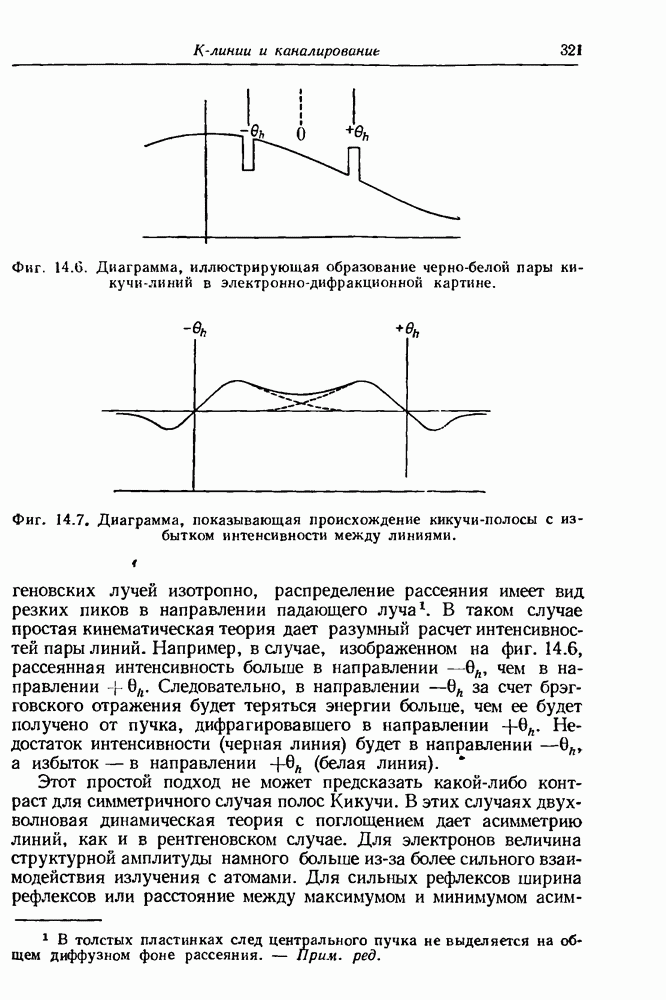
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
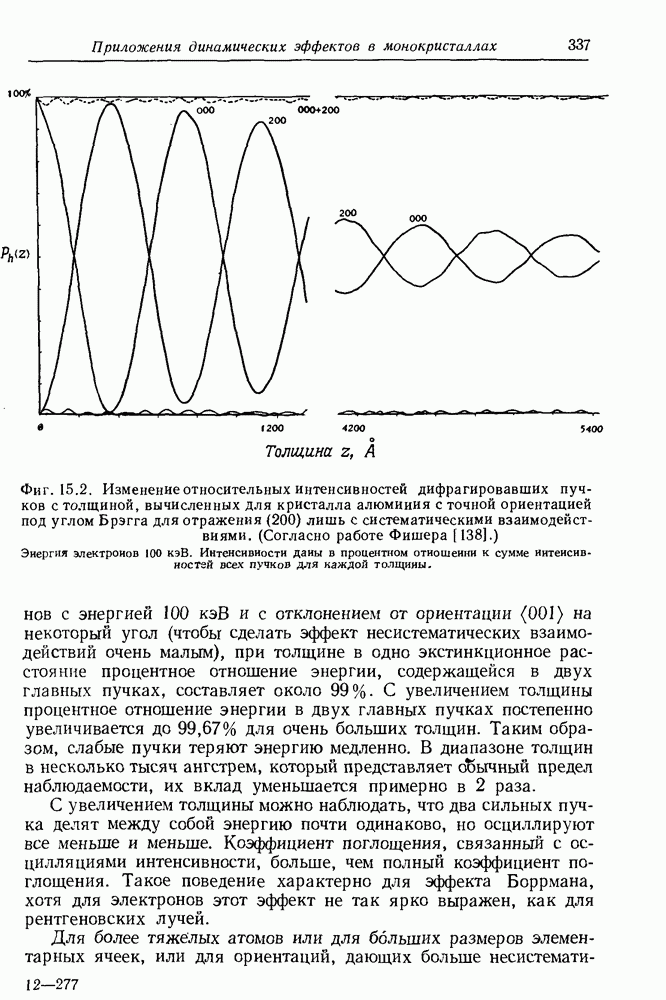
337
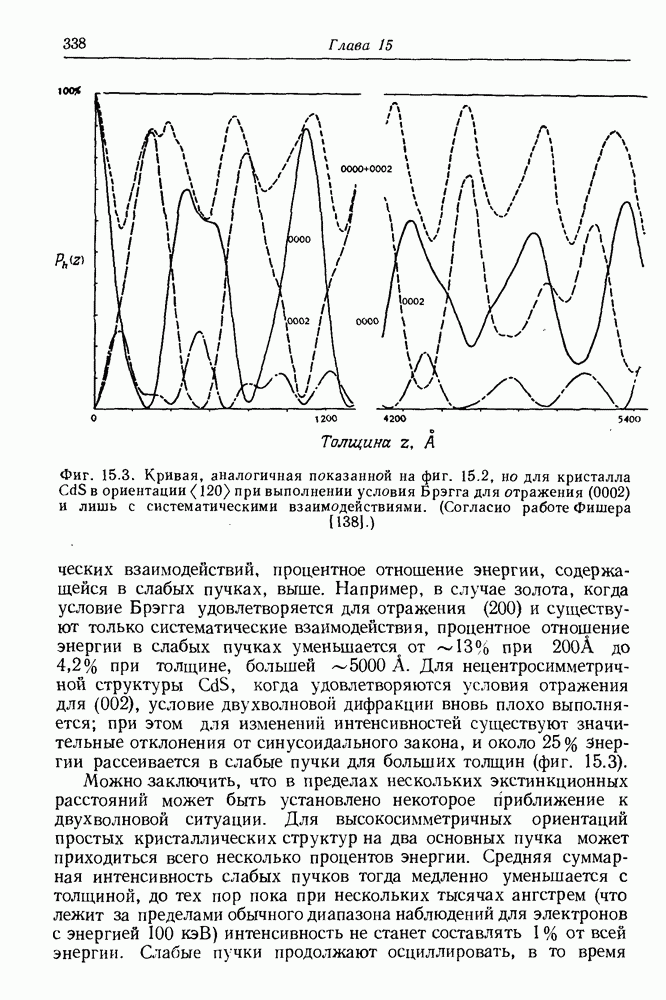
338
339
340
341
342
343
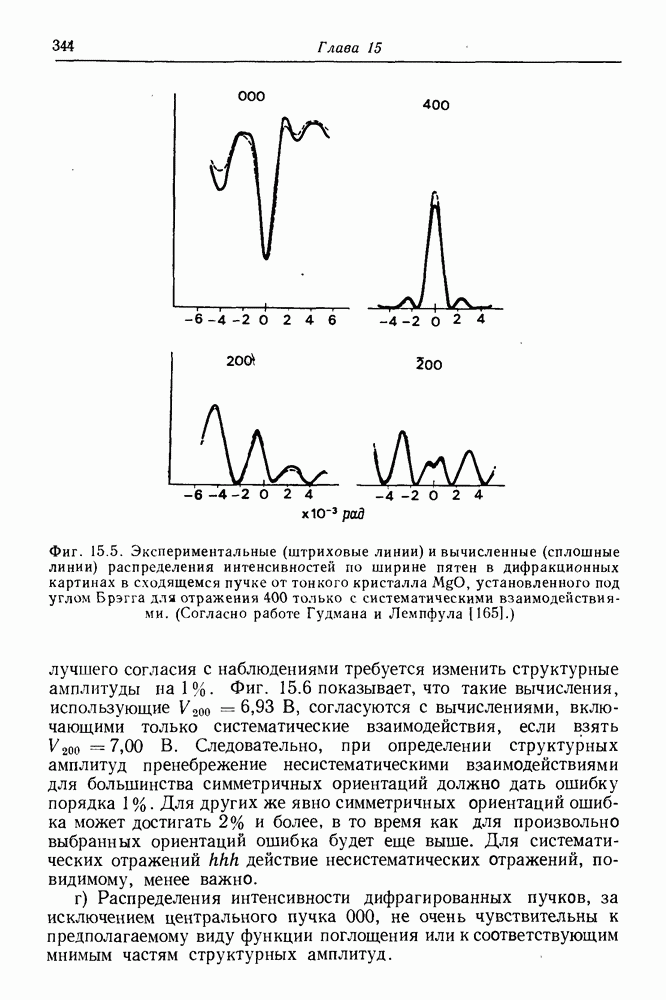
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
След.
Макеты страниц
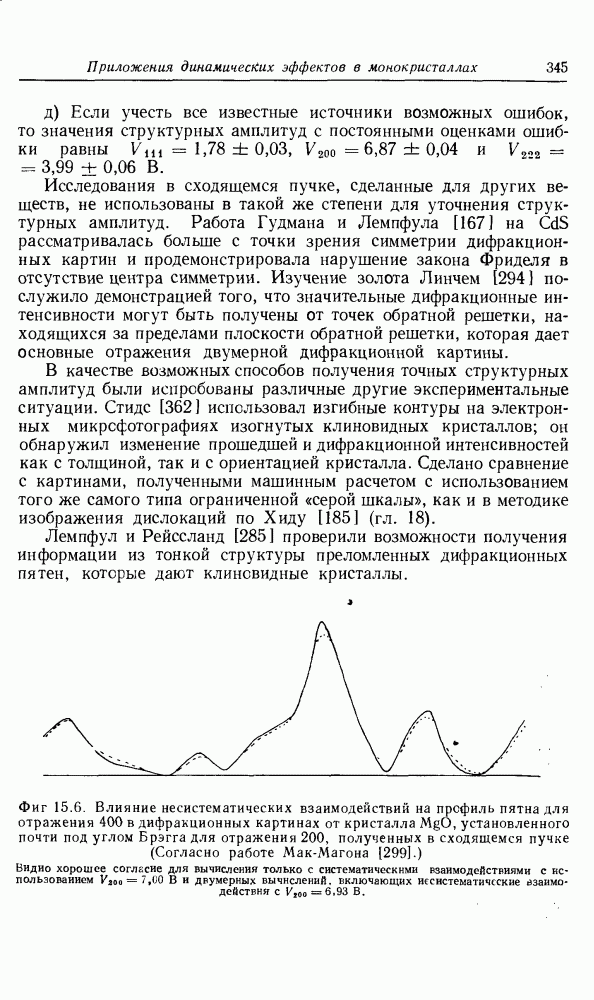
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
11.3.2. Приближение фазовой решетки
Если в (11.43) с соответствующими  -операторами взять члены из столбцов, то получатся ряды для разных значений
-операторами взять члены из столбцов, то получатся ряды для разных значений  Для первого столбца
Для первого столбца

Многократная сумма представляет амплитуду  -члена с
-члена с  -кратной самосверткой
-кратной самосверткой

Следовательно, набор амплитуд дифракционных пучков  представленный функцией
представленный функцией

будет фурье-преобразованием функции

где  и
и  — значения потенциала
— значения потенциала  и функции поглощения
и функции поглощения  в проекции на
в проекции на  -направление.
-направление. 
Таким образом, выражение (11.44), получаемое суммированием первого столбца в (11.43), дает амплитуды дифрагированных пучков, когда все ошибки возбуждения в сумме дают нуль, как если бы сфера Эвальда была плоской или длина волны была равна нулю. То есть выражение (11.44) дает приближение высоких энергий.
В то же время (11.44) это приближение фазовой решетки, которое получается в предположении, что в кристалле суммарное рассеяние и поглощение сконцентрированы в одной плоскости. Проще говоря, считают, что функции  и
и  — это проекции распределения потенциала
— это проекции распределения потенциала  и функции поглощения
и функции поглощения  на направление
на направление  Теперь вместо кристалла мы рассматриваем
Теперь вместо кристалла мы рассматриваем
двумерное распределение, имеющее функцию прохождения

Это приближение фазовой решетки можно рассматривать как первый член ряда — так называемого ряда фазовой решетки, в котором последующие члены включают в себя последовательно другие столбцы членов в (11.43) и, как ожидают, соответствуют учету трехмерных дифракционных эффектов с возрастающей точностью. Однако для членовэтого ряда, за исключением первого, не найдено подходящей формы упрощения. И на самом деле не сразу видно, что члены более высокого порядка могут быть полезны, так как содержат все более высокие положительные степени ошибок возбуждения, а следовательно, выделяют менее важные отражения — те отражения, для которых ошибка возбуждения велика.
Итак, общее выражение (11.40) дает основу для многих рядов разложений, каждый из которых обеспечивает относительно простое приближение к общему результату, справедливое в конкретных условиях. Кинематическое приближение справедливо в пределах небольших структурных факторов для данной толщины. Приближение фазовой решетки применимо в предельных случаях равенств нулю длины волны или толщины кристалла.
Другим простым и, как доказано, весьма полезным является двухволновое приближение. Оно выводится из общего выражения, если допустить, что существуют только два пучка или что  мало и
мало и  для любого другого отражения очень велико. На этой основе Каули и Муди [71] свели такие выражения, как (11.38), к ряду членов, которые после суммирования дают точно такие же амплитуды для падающего и дифрагированных пучков, как и теория Бете.
для любого другого отражения очень велико. На этой основе Каули и Муди [71] свели такие выражения, как (11.38), к ряду членов, которые после суммирования дают точно такие же амплитуды для падающего и дифрагированных пучков, как и теория Бете.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ГЛАВА 1. Дифракция Френеля и Фраунгофера
- 1.2. Волновые уравнения и волны
- 1.2.2. Электромагнитные волны
- 1.2.3. Волны-частицы
- 1.3. Суперпозиция и когерентность
- 1.3.2. Независимые точенные источники
- 1.4. Принцип Гюйгенса
- 1.4.2. Применение формулы Кирхгофа
- 1.5. Подход с точки зрения теории рассеяния
- 1.5.1. Интегральная форма волнового уравнения
- 1.5.2. Ряд Борна
- 1.6. Принцип взаимности
- 1.7. Дифракция Френеля
- 1.7.2. Интегралы Френеля
- 1.7.3. Периодические объекты — «фурье-изображения»
- 1.8. Дифракция Фраунгофера
- ГЛАВА 2. Фурье-преобразования и свертки
- 2.1.1. Дельта-функция и непрерывность
- 2.1.2. Свертки
- 2.1.3. Примеры сверток
- 2.2. Фурье-преобразования: общее рассмотрение
- 2.2.2. Свойства фурье-преобразований
- 2.2.3. Умножение и свертка
- 2.2.4. Пространство и время
- 2.3. Фурье-преобразования и дифракция: примеры
- 2.3.2. Плоская волна: преобразование, обратное рассмотренному в разд. 2.3.1.
- 2.3.3. Трансляция объекта
- 2.3.4. Функция щели
- 2.3.5. Другая форма функции щели
- 2.3.6. Прямолинейный край
- 2.3.7. Прямоугольная апертура
- 2.3.8. Круглая апертура
- 2.3.9. Две очень узкие щели
- 2.3.10. Две щели заметной ширины
- 2.3.11. Конечный цуг волн
- 2.3.12. Периодическая последовательность узких щелей
- 2.3.13. Произвольная периодическая функция
- 2.3.14. Дифракционная решетка: тонкие щели
- 2.3.15. Дифракционная решетка: общее рассмотрение
- 2.3.16. Функция Гаусса
- 2.3.17. Ряд круглых отверстий
- 2.3.18. Дополнительные объекты — теорема Бабине
- 2.3.19. Полные интенсивности: теорема Парсеваля
- ГЛАВА 3. Образование изображения и дифракция
- 3.1.1. Когерентная волновая оптика
- 3.1.2. Получение изображения с помощью некогерентных волн
- 3.2. Теория Аббе
- 3.3. Малоугловое приближение
- 3.4. Фазовый контраст
- 3.4.1. Фазовые и амплитудные объекты
- 3.4.2. Контраст при дефокусировке
- 3.4.3. Ограничения, накладываемые апертурой
- 3.4.4. Фазовый контраст Пернике
- 3.5. Многокомпонентные системы
- ГЛАВА 4. Различные виды излучения и рассеяние веществом
- 4.1.1. Источники рентгеновских лучей
- 4.1.2. Рассеяние электронами
- 4.1.3. Рассеяние атомами
- 4.1.4. Дисперсионные поправки
- 4.2. Электроны
- 4.2.1. Источники электронов
- 4.2.2. Амплитуды атомного рассеяния
- 4.2.3. Приближение фазового объекта
- 4.2.4. Ограниченность первого борновского приближения
- 4.2.5. Эффекты поглощения
- 4.3. Нейтроны
- 4.3.2. Ядерное спиновое рассеяние
- 4.3.3. Изотопное разупорядочение
- 4.3.4. Тепловое и магнитное рассеяние
- ГЛАВА 5. Рассеяние на совокупности атомов
- 5.2. Прямое и обратное пространства
- 5.2.2. Обратная решетка
- 5.2.3. Закон Фриделя и фазовая задача
- 5.3. Обобщенная функция Паттерсона
- 5.4. Примеры корреляционных функций
- 5.4.1. Ограничения за счет конечных объемов
- 5.4.2. Конечные кристаллы
- 5.5. Корреляция в пространстве и во времени
- 5.5.1. Четырехмерная функция Паттерсона
- 5.5.2. Частные случаи
- 5.5.3. Идеальные одноатомные газы и жидкости
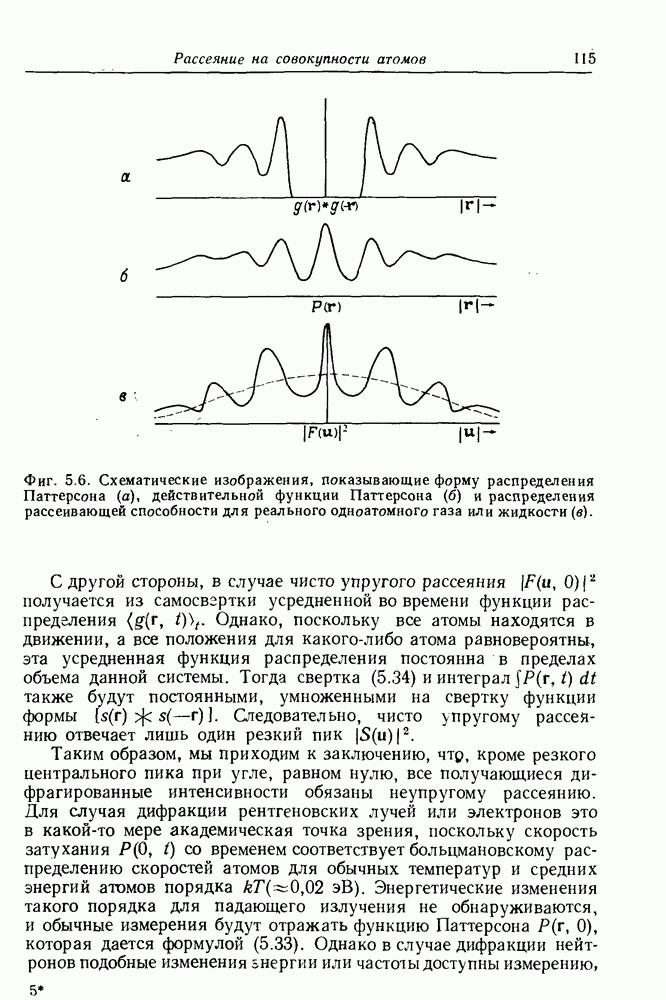
- 5.5.4. Реальные одноатомные газы и жидкости
- 5.5.5. Атом водорода
- 5.6. Интенсивности и геометрия дифракции
- 5.7. Практические примеры
- 5.7.1. Конечные источники и детекторы
- 5.7.2. Разброс длин волн
- 5.7.3. Интегральные интенсивности
- 5.8. Сечения и проекции
- ГЛАВА 6. Дифракция на кристаллах
- 6.1. Идеальные кристаллы
- 6.2. Геометрия дифракции
- 6.2.1. Условия дифракции Лауэ и Брэгга
- 6.2.2. Фурье-преобразования функции формы
- 6.2.3. Особые случаи при дифракции электронов
- 6.3. Структурный анализ кристаллов
- 6.3.2. Дополнительная информация
- 6.4. Методы структурного анализа
- 6.4.2. Функция Паттерсона
- 6.4.3. Оптические аналоги
- 6.4.4. Другие методы
- 6.5. Нейтронографический структурный анализ
- 6.5.2. Магнитное рассеяние
- 6.6. Электронографический структурный анализ
- ГЛАВА 7. Дифракция на несовершенных кристаллах
- 7.1. Формулировка дифракционной задачи
- 7.1.2. Общая формулировка дифракционной задачи.
- 7.2. Метод функции Паттерсона
- 7.2.1. Функция Паттерсона для усредненной периодической структуры
- 7.2.2. Функция Паттерсона в отсутствие усредненной структуры
- 7.3. Отклонения от усредненной решетки
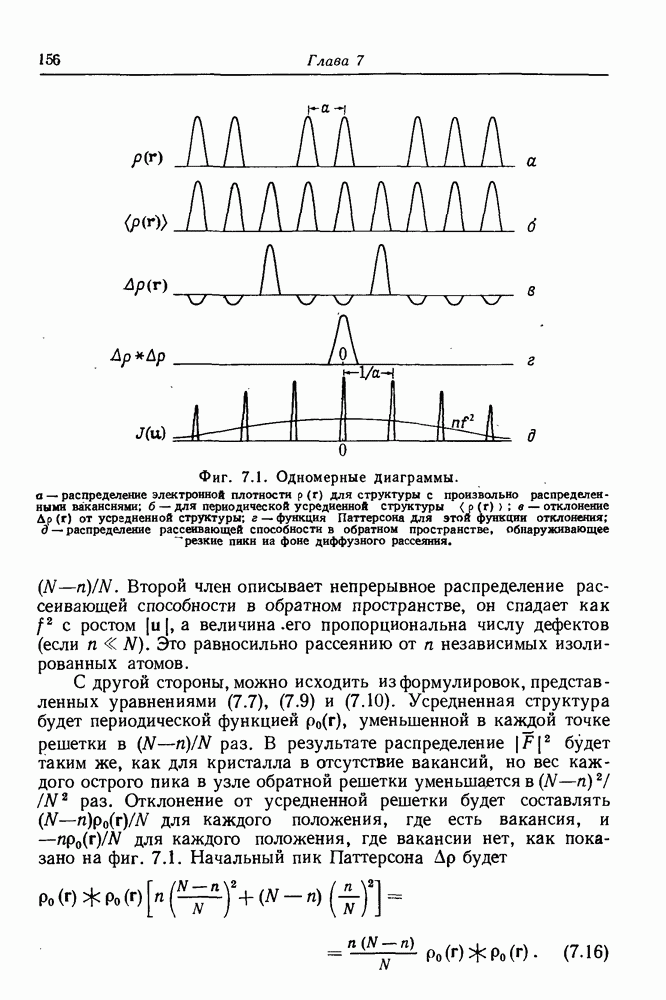
- 7.3.1. Распределенные вакансии: отсутствие релаксации
- 7.3.2. Вакансии, сгруппированные в кластеры
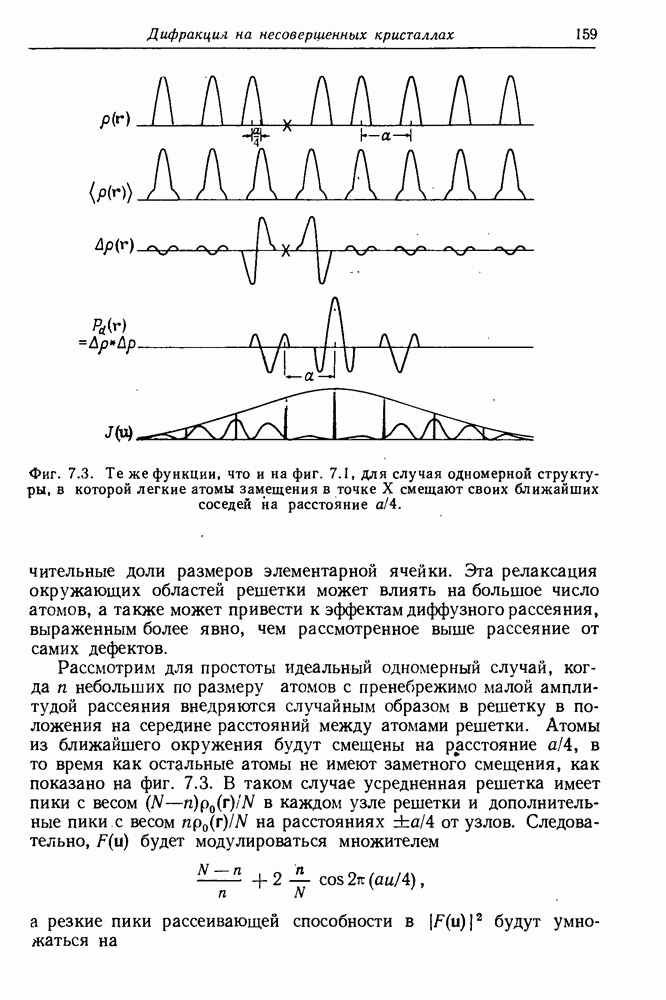
- 7.3.3. Релаксация решетки
- 7.3.4. Тепловые колебания — модель Эйнштейна
- 7.4. Несовершенные кристаллы в отсутствие усредненной решетки
- 7.4.2. Разупорядоченные ориентации
- ГЛАВА 8. Дифракция на совершенных кристаллах
- 8.1. Многократное когерентное рассеяние
- 8.2. Теоретические приближения
- 8.3. Теория Бете
- 8.4. Двухволновое приближение
- 8.4.1. Блоховские волны и дисперсионные поверхности
- 8.4.2. Электроны проводимости: энергетическое представление
- 8.4.3. Дифракция рентгеновских лучей; поляризация
- 8.5. Случай Лауэ (прохождение)
- 8.5.1. Дифракция электронов на тонком кристалле
- 8.5.2. Малоугловое приближение
- 8.5.3. Случай Лауэ с поглощением
- 8.6. Потенциалы Бете
- 8.7. Случай Брэгга
- ГЛАВА 9. Динамические дифракционные эффекты
- 9.1. Полосы равной толщины и кривые качания при дифракции электронов
- 9.1.2. Картина процесса в реальном пространстве
- 9.1.3. Кривые качания
- 9.1.4. Экстинкционные контуры
- 9.1.5. Дифракция в сходящемся пучке
- 9.1.6. Дифракция и изображения клиновидных кристаллов
- 9.1.7. Эффекты поглощения для клиньев
- 9.2. Динамические эффекты при дифракции рентгеновских лучей и нейтронов
- 9.2.2. Поток энергии
- 9.2.3. Картина дисперсионной поверхности
- 9.2.4. Дифракция нейтронов
- 9.3. Эффект Боррмана
- ГЛАВА 10. Обобщение на случай многих пучков
- 10.1. Динамическая n-волновая дифракция
- 10.2. Обобщение теории Бете на случай прохождения
- 10.2.2. Малоугловое приближение
- 10.2.3. Блоховские волны и граничные условия
- 10.2.4. Матрица рассеяния
- 10.3. Подход Дарвина
- 10.4. Специальные случаи — уменьшение числа пучков
- 10.5. Вычислительные методы
- 10.6. Колонковое приближение
- ГЛАВА 11. Метод «физической оптики»
- 11.1 Распространение электронов в кристаллах
- 11.1.3. Дифракция в кристалле
- 11.1.4. Общее выражение в функции от ошибок возбуждения
- 11.2. Ряды многократного рассеяния
- 11.3. Общее решение с двойным суммированием
- 11.3.2. Приближение фазовой решетки
- 11.4. Методы вычислений
- 11.4.1. Вычисления «слоевым методом»
- 11.5. Интенсивности для непериодических объектов
- ГЛАВА 12. Диффузное рассеяние и эффекты поглощения
- 12.1. Тепловое диффузное рассеяние
- 12.1.2. Рассеяние для продольной волны
- 12.1.3. Компонента диффузного рассеяния
- 12.1.4. Дисперсионные кривые
- 12.1.5. Трехмерные обобщения
- 12.2. Статические смещения атомов
- 12.2.2. Дифракционные интенсивности рассеяния на смещенных атомах
- 12.2.3. Брэгговские пики
- 12.2.4. Диффузное рассеяние
- 12.3. Возбуждения электронов
- 12.3.1. Неупругое рентгеновское рассеяние
- 12.3.2. Возбуждение электронов электронами — плазмоны
- 12.3.3. Одноэлектронные возбуждения
- 2.4. Динамические эффекты при диффузном рассеянии
- 12.4.2. Когерентное и некогерентное рассеяние
- 12.4.3. Анализ диффузного рассеяния
- 12.5. Эффекты поглощения
- 12.5.1. Природа параметров поглощения
- 12.5.2. Поглощение рентгеновских лучей и нейтронов
- 12.5.3. «Поглощение» для электронов
- 12.5.4. Поглощение, связанное с тепловыми колебаниями
- 12.5.5. Поглощение, связанное с возбуждениями электронов
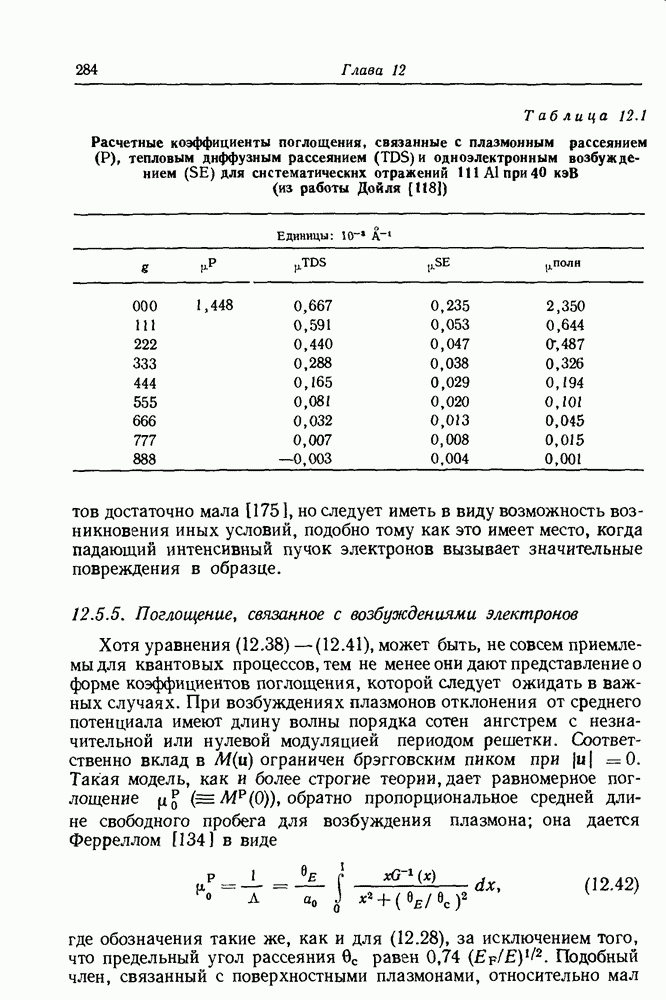
- 12.5.6. Значения коэффициентов поглощения
- ГЛАВА 13. Формирование изображения в электронном микроскопе
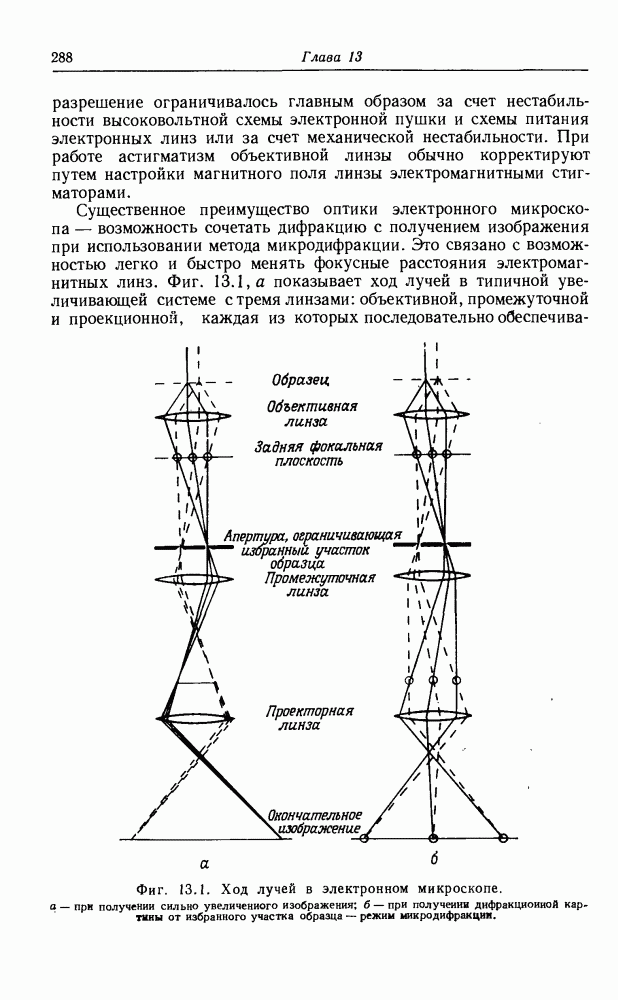
- 13.1.1. Обычный просвечивающий электронный микроскоп
- 13.1.2. Сканирующий просвечивающий электронный микроскоп
- 13.2. Образование изображения
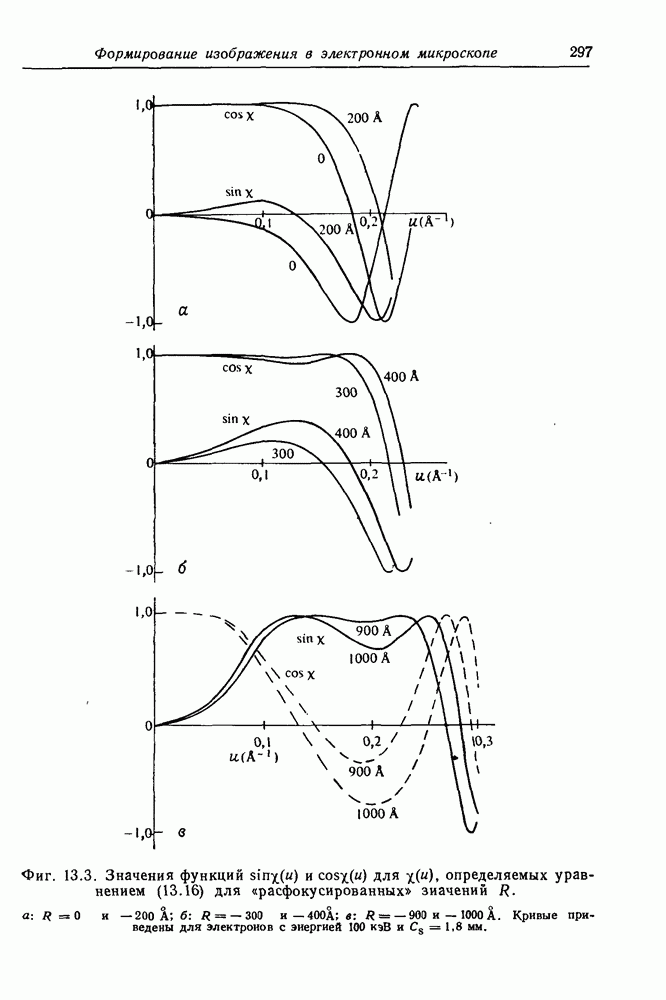
- 13.3. Контраст для тонких образцов
- 13.3.1. Приближение фазового объекта
- 13.3.2. Функция поглощения
- 13.3.3. Приближение слабофазового объекта
- 13.3.4. Темнопольные изображения
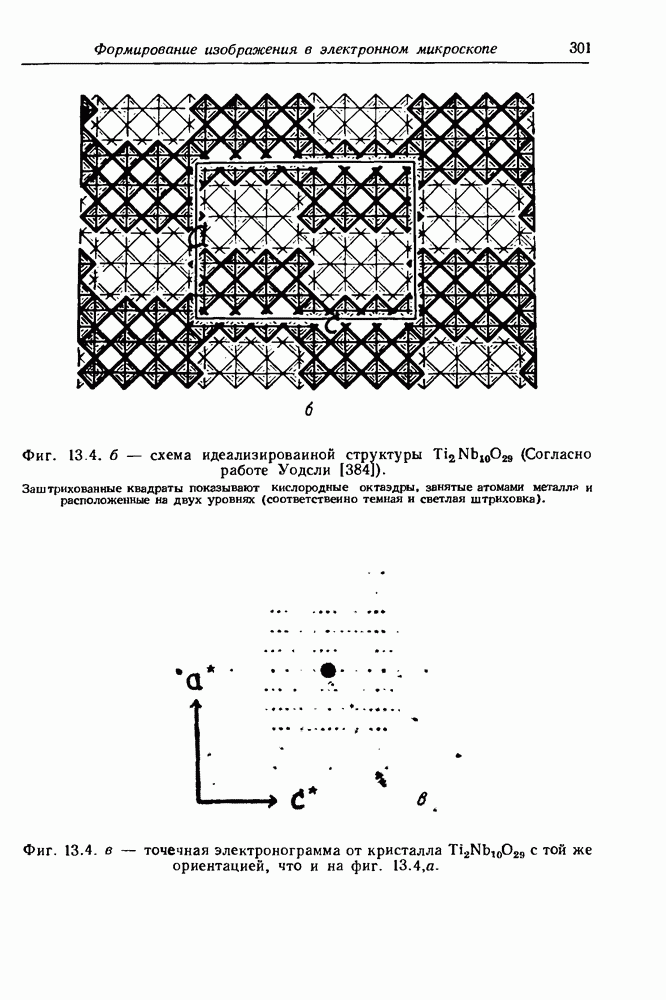
- 13.4. Образование изображения кристаллических структур
- 13.4.1. Образование изображения тонких кристаллов
- 13.4.2. Расчет изображений кристаллов
- 13.4.3. Полосы решетки для толстых кристаллов
- 13.4.4. Получение изображения кристаллов из разрешения решетки
- 13.5. Высоковольтная микроскопия
- ГЛАВА 14. К-линии и каналирование
- 14.1.1. Геометрия линий Косселя
- 14.1.2. Динамическая теория интенсивностей линий Косселя
- 14.1.3. Линии Косселя с ограниченным разрешением
- 14.2. Линии Кикучи
- 14.3. Внешние источники расходящегося излучения
- 14.4. Информация, получаемая из картин К-линий
- 14.5. Каналирование
- 14.6. Вторичные излучения
- ГЛАВА 15. Приложения динамических эффектов в монокристаллах
- 15.1. Зависимость динамических эффектов от параметров кристалла
- 15.2. Рентгеновская интерферометрия
- 15.3. n-волновая и двухволновая динамическая дифракция
- 15.4. Определения структурных амплитуд из полос равной толщины
- 15.5. Структурные амплитуды из кривых качания
- 15.6. Релятивистские эффекты
- 15.7. Поглощение и температурные эффекты
- 15.8. Определение симметрии кристалла
- ГЛАВА 16. Мозаичные кристаллы и поликристаллические материалы
- 16.2. Мозаичные кристаллы
- 16.2.1. Модель мозаичного кристалла
- 16.2.2. Кинематические интегральные интенсивности
- 16.2.3. Экстинкционные эффекты
- 16.2.4. Динамические интенсивности при дифракции электронов
- 16.3. Поликристаллический материал
- 16.3.2. Интенсивности кинематической дифракции
- 16.3.3. Анализ профиля линий
- 16.3.4. Интенсивности динамической дифракции
- 16.3.5. Эффекты n-волновой дифракции
- ГЛАВА 17. Упорядочение атомов в кристаллах
- 17.1. Природа и описание неупорядоченных состояний
- 17.2. Параметры порядка
- 17.3. Функция Паттерсона
- 17.4. Влияние размера атомов
- 17.5. Кинематическая дифракция
- 17.5.1. Дифракция при наличии лишь упорядочения
- 17.5.2. Дифракция и влияние упорядочения и размера атомов
- 17.6. Связь с энергиями упорядочения
- 17.7. Динамическое рассеяние на разупорядоченных кристаллах
- 17.7.2. Расчет диффузного рассеяния
- 17.7.3. Сильное рассеяние и многоатомные корреляции
- 17.8. Некогерентные домены
- 17.8.1. Упорядоченные некогерентные сверхструктуры
- 17.8.2. Некогерентные домены в разупорядоченных сплавах
- ГЛАВА 18. Протяженные дефекты
- 18.2. Дефекты упаковки — статистическая кинематическая теория
- 18.2.3. Дефекты в структурах с плотной упаковкой
- 18.3. Динамическая дифракция на дефектах упаковки
- 18.4. Дислокации
- 18.4.1. Дифракционные эффекты.
- 18.4.2. Получение изображений дислокаций
- 18.4.3. Усреднение по углам падения
- 18.4.4. n-волновые дифракционные эффекты