11.4. Методы вычислений

11.4.1. Вычисления «слоевым методом»

На основе данного подхода физической оптики в задачам дифракции Гудман и Муди [164, 169] (см. также работу Динча [294]) разработали программу расчета, позволяющую с любой заданной точностью вычислять интенсивности дифракционных картин или электронно-микроскопических изображений путем интегрирования элементарных эффектов, действующих на волну, прошедшую через кристалл. Конечно, невозможно аналитически рассмотреть предельный случай бесконечного числа слоев нулевой толщины. Вместо этого используют конечное число слоев и устанавливают четкий критерий проверки того, является ли толщина слоя достаточно малой, чтобы не привести к заметным ошибкам.

Для слоя конечной толщины уравнение (11. 4), или приближение однократного рассеяния, использовать нельзя, потому что, как мы уже видели раньше, многократное рассеяние может быть существенным даже для одного тяжелого атома. Поэтому функцию прохождения для слоя следует записывать в приближении фазовой решетки как

В большинстве случаев функцию распространения рп(х, у), используемую для передачи волны из одной плоскости в другую, можно без заметной ошибки записать в малоугловом приближении (11.10). Обычно для периодических объектов предпочитают формулу для обратного пространства.

Результирующее действие кристалла на падающую волну дается тогда -кратным повторением единичного процесса, который преобразует волну, выходящую из -слоя, в волну, покидающую слой, а именно

или для периодического объекта

Процесс умножения и суммирования набора (комплексных) чисел в формуле (11.50) быстро осуществляется на цифровой Тогда, начиная с известной падающей волны повторение этого процесса дает дифракционные амплитуды после прохождения через любое число слоев кристалла. Амплитуду в реальном пространстве на выходной поверхности кристалла получают суммированием рядов Фурье с коэффициентами и отсюда получают сфокусированное изображение. Несфокусированное изображение получают умножением на соответствующие измененные значения функции распространения

Для вычисления удобно, если имеют одинаковые значения для каждого слоя. Это возможно для совершенного кристалла, если размеры элементарной ячейки в направлении пучка достаточно малы, как обычно бывает в случае относительно простых структур. Однако это не является необходимым в общем случае. Если периодичность в направлении пучка велика, содержимое элементарной ячейки можно разделить на ряд слоев, которые затем периодически повторяются в вычислениях. Изменения периодичности или структуры кристалла в больших или небольших

пределах, которые не включают в себя изменений периодичностей в поперечных направлениях, могут быть учтены путем изменения значений или межслоевых расстояний, входящих в для отдельных слоев или для любого числа слоев. Таким образом, влияние различных нарушений структуры кристалла могут быть учтены без существенного изменения программы вычислений. Вместе с колонковым приближением программу можно применять к вычислению действий на дифракционные картины или электронно-микроскопические изображения локализованных дефектов кристаллической решетки (например, изображений дислокаций).

Поперечные смещения атомов в пределах каждой колонки предполагают постоянными и учитывают, умножая на фазовый множитель. Смещения вдоль направления пучка могут быть учтены варьированием значений Нарушения кристаллической решетки, для которой колонковое приближение неприемлемо, можно учесть с помощью специальных методов; мы их опишем ниже.

11.4.2. Этапы вычисления

Для того чтобы сделать ясным ход расчета, мы выпишем этапы вычислений, используемых в простейшем случае, когда падающий пучок параллелен оси с центросимметричного ромбического кристалла в отсутствие поглощения. Размер вдоль оси с возьмем в качестве толщины кристалла. Программа записывается в следующем порядке:

A. Вычисление амплитуд фазовой решетки для слоев.

а) Из атомных амплитуд рассеяния и положений атомов вычисляют структурные амплитуды

б) Проекцию элементарной ячейки получают, суммируя ряды Фурье с коэффициентами

в) Вычисляют действительные и мнимые части

г) Преобразования Фурье и дают действительную и мнимую части

Б. Функция распространения.

а) Для требуемого диапазона индексов находят ошибки возбуждения Для этого обычно достаточно параболической аппроксимации сферы Эвальда.

б) Вычисляют фазовые множители .

B. Итерационное вычисление.

а) Для первого слоя амплитуды волны, покидающей слой, есть

б) Для второго слоя значения вычисляют, выполняя суммирование (11.50).

в) Суммирование (11.50) повторяют для каждого последующего слоя.

Г. Результат вычислений.

а) Интенсивности дифрагированных пучков в виде функций толщины кристалла даются вычислением после каждого слоя.

б) Изображения в фокусе находят, суммируя ряды Фурье, чтобы получить и затем вычисляя .

в) Для несфокусированных изображений и учета аберраций эффект дефокусировки дается умножением амплитуд на перед тем, как суммировать ряды Фурье в Действие аберраций линз учитывают добавлением сдвига фазы, зависящего от более высоких порядков

При учете поглощения амплитуды становятся комплексными, но, поскольку заключительные вычисления в любом случае производят с комплексными числами, это вносит в дальнейшем лишь незначительное усложнение. Если падающий пучок не точно параллелен оси кристалла, то угол наклона с компонентами можно учесть, добавляя трансляции на величины и к функции распространения, которая теперь примет вид

Можно сделать и по-другому. Иногда бывает удобно предположить, что направление падающего пучка неизменно, но последующие слои кристалла транслированы так, что дают эквивалентное изменение дифракционных условий, и тогда

Точнее говоря, повторяющиеся расстояния должны быть умножены на а расстояние с должно быть немного увеличено. Эти приближения наклонного пучка пригодны только для углов наклона в несколько градусов. Для больших углов необходимо рассматривать различные проекции структуры.

11.4.3. Возможные ошибки

Одним из наиболее важных допущений в этом методе расчета является то, что берется конечная толщина слоя. Чтобы проверить, является ли некоторая предположенная толщина слоя достаточно малой, вычисления повторяют для слоя с меньшей толщиной и результаты сравнивают. Таким путем было найдено, что для электронов с энергией порядка и для структуры средней сложности

с атомами элементов средних порядковых номеров ошибка в результатах незначительна для слоя толщиной до 4 А. Для слоя толщиной 8—10 А ошибки достигают нескольких процентов, в особенности для слабых пучков. Слои толщиной 12—15 А дают большие ошибки, так что хотя бы качественно правильные результаты получаются лишь для самых сильных пучков.

Другой важный источник ошибок — неправильный выбор числа дифракционных пучков, принимаемых в расчет. В вычислениях матричным методом мы видели, что исключение сильных пучков искажает изменения интенсивностей рассматриваемых пучков, так как структуре кристалла приписывается неверная модель. Однако для вычислений слоевым методом неучет некоторых сильных пучков означает, что будет исключено взаимодействие этих пучков с другими пучками. Энергия рассеивается в эти пучки, но не может рассеиваться обратно и поэтому теряется для системы.

11.4.4. Проверки на совместимость

Проверка, к которой прибегают, чтобы определить, достаточное ли количество пучков включено в рассмотрение, состоит в суммировании интенсивностей всех дифракционных пучков, рассматриваемых на каждом этапе вычислений. В отсутствие поглощения эта сумма должна быть постоянной и равной интенсивности падающего пучка с точностью лучше чем Как и в вычислениях матричным методом, найдено, что для двумерной дифракционной картины, например от простого металла с г. ц. к. решеткой, должно быть учтено по крайней мере 50 и даже более пучков, и это число должно увеличиваться для веществ с большими элементарными ячейками или для более высоких ускоряющих напряжений электронов.

Требование сохранения энергии есть часть более общего условия, которое должно выполняться для каждого слоя фазовой решетки. В отсутствие поглощения

Соответствующее соотношение в обратном пространстве

Набор значений может считаться удовлетворительным, если это соотношение удовлетворяется с точностью, как это принято, одна миллионная.

11.4.5. Одномерные вычисления

Чтобы уменьшить число требуемых вычислений, часто рассматривают такие особые ориентации, для которых в дифракционной картине сильной оказывается только одна линия рефлексов, т.е. систематический ряд пучков, соответствующий линии точек обратной решетки, проходящей через ее начало. Тогда мы имеем дело с функцией одной переменной

где представляют собой проекции в направлениях Суммирование теперь производится только по одному индексу число рассматриваемых пучков уменьшается до 7—15 для простых структур, и объем вычислений становится намного меньше.

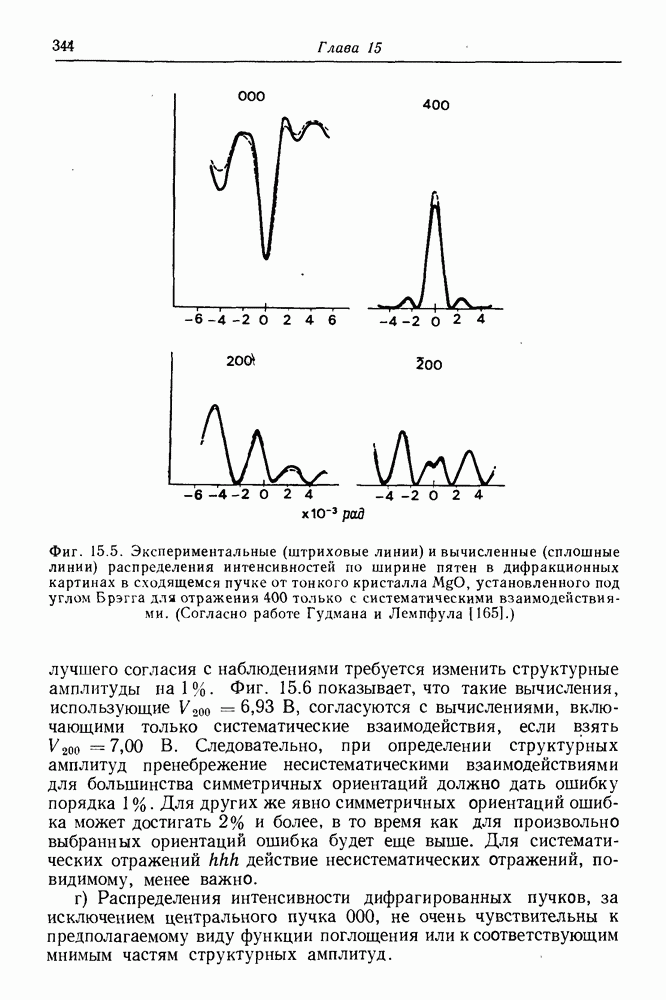
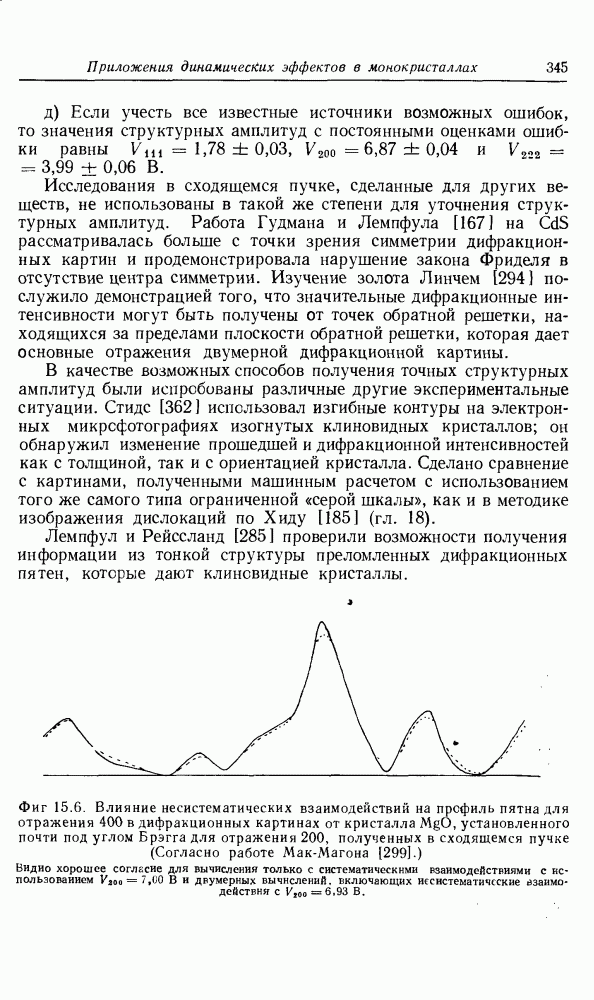
Строгое обоснование использования одномерных вычислений неочевидно, но их точность по сравнению с полными двумерными вычислениями была всестороне проверена для кристаллов в некоторых ориентациях. Например, в случае MgO Мак-Магон [299] сравнил одномерные систематические вычисления для отражений с двумерными вычислениями для ориентаций, выбранных так, чтобы свести к минимуму число и силу несистематических отражений. Для большинства благоприятных случаев, проиллюстрированных на фиг. 15.7, профили интенсивностей, вычисленные для дифракционных пятен в сходящемся пучке, в двумерном и систематическом случаях согласуются очень хорошо только тогда, когда значения использованных структурных амплитуд для систематического ряда отражений взяты примерно на выше точных значений. Для других несколько менее благоприятных ориентаций использование одномерных вычислений дает большие отклонения, соответствующие ошибки в структурных амплитудах, и для произвольной ориентации, которой соответствует в основном систематический ряд отражений, ошибки могут быть значительно выше. Одна ко точность в 1 или 2% требуется только для таких экспериментов, в которых хотят получить очень точные значения структурных амплитуд, а для многих целей можно предположить, что одномерные вычисления достаточно хорошо определяют интенсивности, если не существует очевидных нарушений, возможных в случае несистематических взаимодействий.

Сравнение этого слоевого метода вычисления с матричным методом, описанным в предыдущей главе, показывает, что для большинства задач преимущество одного метода перед другим во

времени счета невелико. В ряде проверочных расчетов, выполненных П. М. Дж. Фишером, П. С. Тернером и П. М. Варбуртоном в Мельбурне в 1968 г., сравнивались результаты вычислений с помощью обоих методов с использованием в каждом случае 49 пучков для кристалла меди в ориентации [100] и расчетом интенсивностей для толщин от 0 до 2000 А с интервалом в 4 А. Оба метода дают интенсивности, согласующиеся с точностью до от суммарной интенсивности, и в каждом случае время счета равно примерно 7 мин для ЭВМ средней мощности (IBM 7044). Для других типов вычислений или других типов ЭВМ может иметь преимущество либо один, либо другой метод. Слоевой метод может быть лучшим для тонких кристаллов и для более высоких ускоряющих напряжений и будет иметь определенные преимущества для непериодических объектов, рассматриваемых ниже.