| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
УПРАЖНЕНИЯ
1. Пусть k — поле, X — переменная над k и

— рациональная функция из k (X), представленная в виде отношения двух взаимно простых многочленов  Определим степень
Определим степень  как
как  и положим
и положим 
(а) Показать, что степень  равна степени расширения k(X) над k(Y) (в предположении, что
равна степени расширения k(X) над k(Y) (в предположении, что  ).
).
(б) Показать, что всякий автоморфизм поля k(X) над k может быть представлен рациональной функцией  степени 1 и, обратно, что всякая такая функция
степени 1 и, обратно, что всякая такая функция  определяет некоторый автоморфизм, (в) Показать, что эта группа автоморфизмов порождается следующими отображениями
определяет некоторый автоморфизм, (в) Показать, что эта группа автоморфизмов порождается следующими отображениями 

2. Пусть k — поле из q элементов и  — поле рациональных функций от одной переменной над k. Пусть G — группа автоморфизмов поля К, задаваемых отображениями
— поле рациональных функций от одной переменной над k. Пусть G — группа автоморфизмов поля К, задаваемых отображениями

где а, b, с, d лежат в  . Доказать следующие утверждения:
. Доказать следующие утверждения:
(i) Порядок G равен 
(ii) Неподвижное поле группы G равно k (К), где

(iii) Пусть  — подгруппа в G, состоящая из отображений
— подгруппа в G, состоящая из отображений  Неподвижное поле группы
Неподвижное поле группы  , совпадает с
, совпадает с  , где
, где  .
.
(iv) Пусть  — подгруппа в Ни состоящая из отображений
— подгруппа в Ни состоящая из отображений  Неподвижное поле группы
Неподвижное поле группы  равно k (Z), где
равно k (Z), где 
3. Пусть Q — фиксированное алгебраическое замыкание поля Q, Е — максимальное подполе в Q, не содержащее  (такое подполе существует в силу леммы Цорна). Показать, что всякое конечное расширение поля Е — циклическое. (Ваше доказательство должно остаться пригодным, если вместо
(такое подполе существует в силу леммы Цорна). Показать, что всякое конечное расширение поля Е — циклическое. (Ваше доказательство должно остаться пригодным, если вместо  взять любое алгебраическое иррациональное число.)
взять любое алгебраическое иррациональное число.)
4. Пусть k — поле, k — его алгебраическое замыкание, а — автоморфизм k, оставляющий k неподвижным, и  - неподвижное поле относительно а. Показать, что всякое конечное расширение поля F — циклическое.
- неподвижное поле относительно а. Показать, что всякое конечное расширение поля F — циклическое.
(Две предыдущие задачи — это примеры Артина, показывающие, как выкапывать ямы в алгебраически замкнутом поле.)
5. (i) Пусть К — циклическое расширение поля F с группой Галуа G, порожденной  Предположим, что характеристика равна
Предположим, что характеристика равна  и что
и что  где m — некоторое целое число 2. Пусть (3 — элемент поля К, для которого
где m — некоторое целое число 2. Пусть (3 — элемент поля К, для которого  )
)  . Показать, что в К существует элемент а, такой, что
. Показать, что в К существует элемент а, такой, что

(ii) Доказать, что многочлен  неприводим в
неприводим в  .
.
Доказать, что если  — корень этого многочлена, то
— корень этого многочлена, то  — расширение Галуа поля F, циклическое и имеющее степень
— расширение Галуа поля F, циклическое и имеющее степень  и что его группа Галуа порождается продолжением а автоморфизма
и что его группа Галуа порождается продолжением а автоморфизма  для которого
для которого

6. Пусть Е — алгебраическое расширение поля  , такое, что всякий многочлен
, такое, что всякий многочлен  из
из  степени -1 имеет хотя бы один корень в Е. Доказать, что Е алгебраически замкнуто.
степени -1 имеет хотя бы один корень в Е. Доказать, что Е алгебраически замкнуто.
[Указание: рассмотреть отдельно сепарабельный и чисто несепарабельный случай и воспользоваться теоремой о примитивном элементе.]
7. Относительные инварианты (Сато). Пусть  — поле, К — его расширение и G — группа автоморфизмов К над k, причем k совпадает с неподвижным полем группы G. (Мы не предполагаем, что К алгебраично над k.) Под относительным инвариантом группы G в К мы будем понимать элемент
— поле, К — его расширение и G — группа автоморфизмов К над k, причем k совпадает с неподвижным полем группы G. (Мы не предполагаем, что К алгебраично над k.) Под относительным инвариантом группы G в К мы будем понимать элемент  такой, что для всякого существует элемент
такой, что для всякого существует элемент  для которого
для которого  Так как
Так как  — автоморфизм, то
— автоморфизм, то  . Мы будем говорить, что отображение
. Мы будем говорить, что отображение  принадлежит Р, и будем называть его характером. Доказать следующие утверждения:
принадлежит Р, и будем называть его характером. Доказать следующие утверждения:
(а) Определенное выше отображение  — гомоморфизм.
— гомоморфизм.
(б) Если один и тот же характер  принадлежит относительным инвариантам Р и Q, то существует такой элемент
принадлежит относительным инвариантам Р и Q, то существует такой элемент  что
что 
(в) Относительные инварианты образуют мультипликативную группу, которую мы обозначаем через 
Элементы  из
из  называются мультипликативно независимыми по модулю k, если их образы в факторгруппе
называются мультипликативно независимыми по модулю k, если их образы в факторгруппе  мультипликативно независимы, т. е. если из соотношения
мультипликативно независимы, т. е. если из соотношения

где  — целые числа, следует, что
— целые числа, следует, что 
(г) Доказать, что если  мультипликативно независимы по модулю k, то они алгебраически независимы над k. [Указание: воспользоваться теоремой Артина о характерах.]
мультипликативно независимы по модулю k, то они алгебраически независимы над k. [Указание: воспользоваться теоремой Артина о характерах.]
(д) Пусть  — поле частных кольца многочленов
— поле частных кольца многочленов  причем G индуцирует автоморфизмы этого кольца многочленов.
причем G индуцирует автоморфизмы этого кольца многочленов.  если
если  — относительно инвариантные многочлены, то их н. о. д. является относительным инвариантом; если
— относительно инвариантные многочлены, то их н. о. д. является относительным инвариантом; если  — относительный инвариант, являющийся отношением двух взаимно простых многочленов, то
— относительный инвариант, являющийся отношением двух взаимно простых многочленов, то  — относительные инварианты. Доказать, что относительно инвариантные многочлены порождают
— относительные инварианты. Доказать, что относительно инвариантные многочлены порождают  Пусть S — множество относительно инвариантных многочленов, которые не могут быть разложены в произведение двух относительно инвариантных многочленов степени
Пусть S — множество относительно инвариантных многочленов, которые не могут быть разложены в произведение двух относительно инвариантных многочленов степени  Показать, что элементы из
Показать, что элементы из  мультипликативно независимы и что, следовательно,
мультипликативно независимы и что, следовательно,  — свободная абелева группа. (Если вы знакомы с понятием степени трансцендентности, то, используя
— свободная абелева группа. (Если вы знакомы с понятием степени трансцендентности, то, используя  , вы сможете заключить, что эта группа — конечно порожденная.]
, вы сможете заключить, что эта группа — конечно порожденная.]
8. Пусть Е — конечное сепарабельное расширение над k степени  — система элементов из
— система элементов из  — различные вложения Е в k над k. Определим дискриминант системы W, положив
— различные вложения Е в k над k. Определим дискриминант системы W, положив

Доказать: (а) Если  — какая-нибудь другая система (столбец) элементов из Е и
— какая-нибудь другая система (столбец) элементов из Е и  — матрица из элементов поля k, такая, что
— матрица из элементов поля k, такая, что  то
то

(б) Дискриминант является элементом из 
(в) Пусть  . Пусть
. Пусть  — корни
— корни  скажем,
скажем,  Тогда
Тогда

Показать, что

(г) Пусть обозначения те же, что и в (а). Показать, что

[Указание: пусть А — матрица  Показать, что
Показать, что  есть матрица
есть матрица  .]
.]
9. Пусть F — конечное поле и К — его конечное расширение. Показать, что норма  и след
и след  сюръективны (как отображения К в
сюръективны (как отображения К в  ).
).
10. Пусть  - целое число, свободное от квадратов. Для каждого простого числа
- целое число, свободное от квадратов. Для каждого простого числа  пусть
пусть  — поле разложения многочлена
— поле разложения многочлена  над Q. Показать, что
над Q. Показать, что  . Для всякого целого числа
. Для всякого целого числа  свободного от квадратов, пусть
свободного от квадратов, пусть

— композит всех полей  , и пусть
, и пусть  — степень
— степень  над Q. Показать, что если
над Q. Показать, что если  нечетно, то
нечетно, то  а если
а если  четно,
четно,  то
то  или
или  в зависимости от того, содержится или нет
в зависимости от того, содержится или нет  а в поле корней
а в поле корней  степени из единицы
степени из единицы 
11. Пусть А — абелева группа и G — конечная циклическая группа с образующей о, действующая на А [посредством гомоморфизма  . Определим след
. Определим след  на А, положив
на А, положив  )
)  Обозначим через
Обозначим через  ядро следа и рассмотрим
ядро следа и рассмотрим  — подгруппу в А, состоящую из всех элементов вида
— подгруппу в А, состоящую из всех элементов вида  Показать, что
Показать, что  .
.
12. Какова группа Галуа следующих многочленов: (а)  над (б)
над (б)  над Q. (в)
над Q. (в)  над
над  над
над  над
над  над
над  над Q, где а — любое целое число
над Q, где а — любое целое число  и свободное от квадратов,
и свободное от квадратов,  — а над Q, где
— а над Q, где  нечетное
нечетное  а — любое свободное от квадратов целое положительное число,
а — любое свободное от квадратов целое положительное число,  над
над  над
над  над
над  — различные простые числа),
— различные простые числа),  над
над  над С (t), где t трансцендентно над полем комплексных чисел С, а и — целое положительное число,
над С (t), где t трансцендентно над полем комплексных чисел С, а и — целое положительное число,  над R (t), где t такое же, как и выше.
над R (t), где t такое же, как и выше.
13. Пусть k — поле,  — нечетное целое число
— нечетное целое число  и J — примитивный корень
и J — примитивный корень  степени из единицы, лежащий в k. Показать, что k содержит также примитивный корень
степени из единицы, лежащий в k. Показать, что k содержит также примитивный корень  степени из единицы.
степени из единицы.
14. Пусть k — конечное расширение поля рациональных чисел. Показать, что в k имеется только конечное число корней из единицы.
1S. Определить, какие корни из единицы имеются в следующих полях: 
16. Для каких целых чисел  примитивный корень
примитивный корень  степени из единицы имеет степень 2 над
степени из единицы имеет степень 2 над 
17. Пусть k — поле характеристики 0, причем для всякого конечного расширения Е поля k индекс  конечен, каково бы ни было целое положительное
конечен, каково бы ни было целое положительное  . Доказать, что для всякого такого
. Доказать, что для всякого такого  существует только конечное число абелевых расширений над k степени
существует только конечное число абелевых расширений над k степени  .
.
18. Пусть  — рациональная функция с коэффициентами в конечном расширении поля рациональных чисел, причем существует бесконечно много корней из единицы ?, для которых
— рациональная функция с коэффициентами в конечном расширении поля рациональных чисел, причем существует бесконечно много корней из единицы ?, для которых  есть корень из единицы. Показать, что существует такое целое число
есть корень из единицы. Показать, что существует такое целое число  , что
, что  где с — некоторая константа (являющаяся на самом деле корнем из единицы).
где с — некоторая константа (являющаяся на самом деле корнем из единицы).
Это упражнение может быть обобщено следующим образом. Пусть  — конечно порожденная мультипликативная группа комплексных чисел и Г — группа всех комплексных чисел у, таких, что
— конечно порожденная мультипликативная группа комплексных чисел и Г — группа всех комплексных чисел у, таких, что  лежит в
лежит в  для некоторого целого
для некоторого целого  . Пусть
. Пусть  — рациональная функция с комплексными коэффициентами, такая, что существует бесконечно много
— рациональная функция с комплексными коэффициентами, такая, что существует бесконечно много  , для которых
, для которых  лежит в Г. Тогда снова
лежит в Г. Тогда снова  для некоторых
для некоторых 
Мною дано доказательство соответствующего утверждения для случая, когда значения  берутся в
берутся в  а не в Г (см. «Diophantine Geometry», гл. VII, теорема 7).
а не в Г (см. «Diophantine Geometry», гл. VII, теорема 7).
19. Пусть  — расширение Галуа. На группе
— расширение Галуа. На группе  определяем топологию Крулля, беря в качестве фундаментальной системы открытых окрестностей единицы множество подгрупп, которые принадлежат конечным расширениям Е поля k, содержащимся в К. Используя представление на левых смежных классах, находим, что нормальные подгруппы кофинальны в этом семействе и что, следовательно, семейство нормальных подгрупп, принадлежащих конечным нормальным расширениям, определяет ту же самую топологию. Показать, что группа G алгебраически и топологически изоморфна проективному пределу конечных факторгрупп
определяем топологию Крулля, беря в качестве фундаментальной системы открытых окрестностей единицы множество подгрупп, которые принадлежат конечным расширениям Е поля k, содержащимся в К. Используя представление на левых смежных классах, находим, что нормальные подгруппы кофинальны в этом семействе и что, следовательно, семейство нормальных подгрупп, принадлежащих конечным нормальным расширениям, определяет ту же самую топологию. Показать, что группа G алгебраически и топологически изоморфна проективному пределу конечных факторгрупп  , где U пробегает все такие нормальные подгруппы. Вывести отсюда, что G компактна и вполне несвязна. Такие группы называются проконечными. Показано, что всякая замкнутая подгруппа конечного индекса открыта. Показать, что замкнутые подгруппы — это в точности те подгруппы, которые принадлежат промежуточным подполям
, где U пробегает все такие нормальные подгруппы. Вывести отсюда, что G компактна и вполне несвязна. Такие группы называются проконечными. Показано, что всякая замкнутая подгруппа конечного индекса открыта. Показать, что замкнутые подгруппы — это в точности те подгруппы, которые принадлежат промежуточным подполям  с К. Показать, что если Н — произвольная подгруппа в G и
с К. Показать, что если Н — произвольная подгруппа в G и  неподвижное поле, то подгруппа в G, принадлежащая F, совпадает с замыканием Н в
неподвижное поле, то подгруппа в G, принадлежащая F, совпадает с замыканием Н в 
20. Пусть k — такое поле, что всякое его конечное расширение — циклическое и что для всякого целого  оно имеет одно расширение степени
оно имеет одно расширение степени  . Показать, что группа Галуа
. Показать, что группа Галуа  есть обратный предел
есть обратный предел  где
где  пробегает все подгруппы в Z, упорядоченные по включению. Показать, что этот предел изоморфен прямому произведению пределов
пробегает все подгруппы в Z, упорядоченные по включению. Показать, что этот предел изоморфен прямому произведению пределов

взятому по всем простым числам  , другим» словами, он изоморфен произведению всех аддитивных групп целых
, другим» словами, он изоморфен произведению всех аддитивных групп целых  -адических чисел.
-адических чисел.
21. Векторы Витта. Пусть  — последовательность алгебраически независимых элементов над кольцом целых чисел Z. Для всякого
— последовательность алгебраически независимых элементов над кольцом целых чисел Z. Для всякого  положим
положим

Показать, что  может быть выражено черзз
может быть выражено черзз  где
где  с рациональными коэффициентами.
с рациональными коэффициентами.
Используя векторную терминологию, мы называем  компонентами Витта вектора
компонентами Витта вектора  — его призрачными компонентами. Сам
— его призрачными компонентами. Сам  мы называем вектором Витта-Рассмотрим степенной ряд
мы называем вектором Витта-Рассмотрим степенной ряд

Показать, что

[Под  мы понимаем
мы понимаем  , где
, где  степенной ряд, производная которого
степенной ряд, производная которого  берется формально.]
берется формально.]
Если х, у — два вектора Витта, то их сумму и произведение определяем покомпонентно относительно призрачных компонент, т. е. полагаем

Каковы  Показать, что
Показать, что

Стало быть,  — многочлен с целочисленными коэффициентами от
— многочлен с целочисленными коэффициентами от  . Показать также, что
. Показать также, что

где  — наименьшее общее кратное
— наименьшее общее кратное  пробегают все целые числа 1. Таким образом,
пробегают все целые числа 1. Таким образом,  также есть многочлен от
также есть многочлен от  с целочисленными коэффициентами.
с целочисленными коэффициентами.
Предыдущие соображения принадлежат Витту (устное сообщение) и отличаются от приведенных в его первоначальной работе.
Проверить, что формулы, выражающие компоненты  зависят только от компонент х и у где
зависят только от компонент х и у где  .
.
Если А — коммутативное кольцо, то, взяв гомоморфный образ кольца многочленов над Z в А, мы увидим, что можно определить сложение и умножение векторов Витта с компонентами в А и что эти векторы Витта образуют кольцо W (А). Показать, что W есть функтор, т. е. что любой гомоморфизм  кольца А в коммутативное кольцо А индуцирует гомоморфизм
кольца А в коммутативное кольцо А индуцирует гомоморфизм  .
.
22. Пусть  — простое число. Рассмотрим векторы Витта с компонентами, равными 0, за исключением тех, которые занумерованы степенями
— простое число. Рассмотрим векторы Витта с компонентами, равными 0, за исключением тех, которые занумерованы степенями  . Применим
. Применим  по основанию
по основанию  к номерам этих компонент, — так что мы будем писать
к номерам этих компонент, — так что мы будем писать  нчесто
нчесто  . Например,
. Например,  теперь обозначает то, что раньше было
теперь обозначает то, что раньше было  Если k — поле характеристики
Если k — поле характеристики  , то тем же символом
, то тем же символом  обозначается совокупность векторов Витта только что указанного вида. В силу упражнения
обозначается совокупность векторов Витта только что указанного вида. В силу упражнения  является кольцом. Для вектора Витта
является кольцом. Для вектора Витта  положим
положим

Таким образом, V есть оператор сдвига. Очевидно,  Показать, что
Показать, что

Кроме того, по определению имеем

23. Рассмотрим снова W(k), где k — поле характеристики  . Тогда V — аддитивный эндоморфизм кольца
. Тогда V — аддитивный эндоморфизм кольца  и F — кольцевой гомоморфизм
и F — кольцевой гомоморфизм  в себя. Кроме того, для всякого
в себя. Кроме того, для всякого  имеем
имеем

Если  то
то  Обозначая для
Обозначая для  через
через  вектор Витта
вектор Витта  мы можем символически записать
мы можем символически записать

Показать, что если  , то
, то  есть единица в W(k). [Указание: имеем
есть единица в W(k). [Указание: имеем  и затем
и затем

24. Пусть  — целое число
— целое число  , как обычно, — простое число и k — поле характеристики
, как обычно, — простое число и k — поле характеристики  . Обозначим символом
. Обозначим символом  кольцо усеченных векторов Витта
кольцо усеченных векторов Витта  с компонентами в k. Мы рассматриваем
с компонентами в k. Мы рассматриваем  как аддитивную группу. Для
как аддитивную группу. Для  положим
положим  Очевидно, Р — гомоморфизм. Если К — расширение Галуа поля
Очевидно, Р — гомоморфизм. Если К — расширение Галуа поля  то мы можем определить
то мы можем определить  как вектор с компонентами
как вектор с компонентами  . Доказать аналог теоремы 90 Гильберта для векторов Витта и показать, что первая группа когомологий тривиальна. [Берем вектор, след которого является единицей в
. Доказать аналог теоремы 90 Гильберта для векторов Витта и показать, что первая группа когомологий тривиальна. [Берем вектор, след которого является единицей в  (к), и тем же путем, что и в доказательстве теоремы 17, § 10, устанавливаем, что цикл является кограницей.]
(к), и тем же путем, что и в доказательстве теоремы 17, § 10, устанавливаем, что цикл является кограницей.]
25. Показать, что если  то существует вектор
то существует вектор  , для которого
, для которого  . Сделать это по индукции сначала для первой компоненты, а затем показать, что вектор
. Сделать это по индукции сначала для первой компоненты, а затем показать, что вектор  лежит в образе
лежит в образе  тогда и только тогда, когда
тогда и только тогда, когда  лежит в образе
лежит в образе  . Доказать по индукции, что если
. Доказать по индукции, что если  для некоторого расширения к поля к и если
для некоторого расширения к поля к и если  то
то  — вектор, компоненты которого лежат в простом поле. Следовательно, решения уравнения
— вектор, компоненты которого лежат в простом поле. Следовательно, решения уравнения  для заданного
для заданного  отличаются все между собой на векторы с компонентами из простого поля, а таких векторов имеется
отличаются все между собой на векторы с компонентами из простого поля, а таких векторов имеется  штук. Полагаем
штук. Полагаем

или символически

Доказать, что это расширение Галуа поля k, и показать, что циклические расширения поля k, имеющие степень  — это в точности расширения типа
— это в точности расширения типа  где вектор
где вектор  таков, что
таков, что 
26. Развить теорию Куммера для абелевых расширений показателя  поля к, используя
поля к, используя 
Другими словами, показать, что между подгруппами В в  содержащими
содержащими  и абелевыми расширениями указанного выше типа имеется биективное соответствие
и абелевыми расширениями указанного выше типа имеется биективное соответствие

где  . Все это принадлежит Витту (см. Witt Е., Journal fiir die reine und angewandte Mathematik, 1935 и 1936 гг.). Доказательства, с небольшими изменениями, те же самые, что и данные в тексте для теории Куммера.
. Все это принадлежит Витту (см. Witt Е., Journal fiir die reine und angewandte Mathematik, 1935 и 1936 гг.). Доказательства, с небольшими изменениями, те же самые, что и данные в тексте для теории Куммера.
27. Дать пример поля К, имеющего степень 2 над двумя различными подполями Е и F соответственно, но такого, что К не алгебраично над 
28. Пусть  -простое поле характеристики
-простое поле характеристики  — поле, полученное из F присоединением всех примитивных корней
— поле, полученное из F присоединением всех примитивных корней  степени из единицы для всех простых чисел
степени из единицы для всех простых чисел  . Показать, что К алгебраически замкнуто. [Указание: показать, что если q — простое число и
. Показать, что К алгебраически замкнуто. [Указание: показать, что если q — простое число и  — целое число
— целое число  то существует простое число I, такое, что период
то существует простое число I, такое, что период  равен
равен  Для этого используется старый прием Ван дер Вардена. Пусть I — простое число, делящее целое число
Для этого используется старый прием Ван дер Вардена. Пусть I — простое число, делящее целое число

Если I не делит  то все готово. В противном случае
то все готово. В противном случае 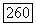 Но при этом
Но при этом 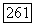 не делит b и, следовательно, существует простое число
не делит b и, следовательно, существует простое число 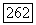 , делящее b. Тогда степень
, делящее b. Тогда степень 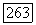 над F есть
над F есть 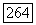 так что К содержит подполя произвольной степени над
так что К содержит подполя произвольной степени над 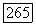
| << Предыдущий параграф | Следующий параграф >> |
- От редактора перевода
- Предисловие
- Предварительные сведения
- Литература
- Часть первая. ГРУППЫ, КОЛЬЦА И МОДУЛИ
- § 1. Моноиды
- § 2. Группы
- § 3. Циклические группы
- § 4. Нормальные подгруппы
- § 5. Действие группы на множестве
- § 6. Силовские подгруппы
- § 7. Категории и функторы
- Произведения и копроизведения
- § 8. Свободные группы
- § 9. Прямые суммы и свободные абелевы группы
- § 10. Конечно порожденные абелевы группы
- § 11. Дуальная группа
- УПРАЖНЕНИЯ
- Глава II. Кольца
- § 1. Кольца и гомоморфизмы
- § 2. Коммутативные кольца
- § 3. Локализация
- § 4. Кольца главных идеалов
- УПРАЖНЕНИЯ
- Глава III. Модули
- § 2. Группа гомоморфизмов
- § 3. Прямые произведения и суммы модулей
- § 4. Свободные модули
- § 5. Векторные пространства
- § 6. Дуальное пространство
- УПРАЖНЕНИЯ
- Глава IV. Гомологии
- § 1. Комплексы
- § 2. Гомологическая последовательность
- § 3. Эйлерова характеристика
- § 4. Теорема Жордана — Гёльдера
- УПРАЖНЕНИЯ
- Глава V. Многочлены
- § 1. Свободные алгебры
- § 2. Определение многочленов
- § 3. Элементарные свойства многочленов
- § 4. Алгоритм Евклида
- § 5. Простейшие дроби
- § 6. Однозначность разложения на простые множители многочленов от нескольких переменных
- § 7. Критерии неприводимости
- § 8. Производная и кратные корни
- § 9. Симметрические многочлены
- § 10. Результант
- УПРАЖНЕНИЯ
- Глава VI. Нётеровы кольца и модули
- § 1. Основные критерии.
- § 2. Теорема Гильберта
- § 3. Степенные ряды
- § 4. Ассоциированные простые идеалы
- § 5. Примарное разложение
- УПРАЖНЕНИЯ
- Часть вторая. ТЕОРИЯ ПОЛЕЙ
- § 1. Конечные и алгебраические расширения
- § 2. Алгебраическое замыкание
- § 3. Поля разложения и нормальные расширения
- § 4. Сепарабельные расширения
- § 5. Конечные поля
- § 6. Примитивные элементы
- § 7. Чисто несепарабельные расширения
- УПРАЖНЕНИЯ
- Глава VIII. Теория Галуа
- § 1. Расширения Галуа
- § 2. Примеры и приложения
- § 3. Корни из единицы
- § 4. Линейная независимость характеров
- § 5. Норма и след
- § 6. Циклические расширения
- § 7. Разрешимые и радикальные расширения
- § 8. Теория Куммера
- § 9. Уравнение X^n — a = 0
- § 10. Когомологии Галуа
- § 11. Алгебраическая независимость гомоморфизмов
- § 12. Теорема о нормальном базисе
- УПРАЖНЕНИЯ
- Глава IX. Расширения колец
- § 1. Целые расширения колец
- 2. Целые расширения Галуа
- § 3. Продолжение гомоморфизмов
- УПРАЖНЕНИЯ
- Глава X. Трансцендентные расширения
- § 1. Базисы трансцендентности
- § 2. Теорема Гильберта о нулях
- § 3. Алгебраические множества
- § 4. Теорема Нётера о нормализации
- § 5. Линейно свободные расширения
- § 6. Сепарабельные расширения
- § 7. Дифференцирования
- УПРАЖНЕНИЯ
- Глава XI. Вещественные поля
- § 1. Упорядоченные поля
- § 2. Вещественные поля
- § 3. Вещественные нули и гомоморфизмы
- УПРАЖНЕНИЯ
- Глава XII. Абсолютные значения
- § 1. Определения, зависимость и независимость
- § 2. Пополнения
- § 3. Конечные расширения
- § 4. Нормирования
- § 5. Пополнения и нормирования
- § 6. Дискретные нормирования
- § 7. Нули многочленов в полных полях
- УПРАЖНЕНИЯ
- Часть третья. ЛИНЕИНАЯ АЛГЕБРА И ПРЕДСТАВЛЕНИЯ
- § 1. Матрицы
- § 2. Ранг матрицы
- § 3. Матрицы и линейные отображения
- § 4. Определители
- § 5. Двойственность
- § 6. Матрицы и билинейные формы
- § 7. Полуторалинейная двойственность
- Терминология
- УПРАЖНЕНИЯ
- Глава XIV. Структура билинейных форм
- § 1. Предварительные сведения, ортогональные суммы
- § 2. Квадратичные отображения
- § 3. Симметрические формы, ортогональные базисы
- § 4. Гиперболические пространства
- § 5. Теорема Витта
- § 6. Группа Витта
- § 7. Симметрические формы над упорядоченными полями
- § 8. Алгебра Клиффорда
- § 9. Знакопеременные формы
- § 10. Пфаффиан
- § 11. Эрмитовы формы
- § 12. Спектральная теорема (эрмитов случай)
- § 13. Спектральная теорема (симметрический случай)
- УПРАЖНЕНИЯ
- Глава XV. Представление одного эндоморфизма
- § 2. Модули над кольцами главных идеалов
- § 3. Разложение над одним эндоморфизмом
- § 4. Характеристический многочлен
- УПРАЖНЕНИЯ
- Глава XVI. Полилинейные произведения
- § 1. Тензорное произведение
- § 2. Основные свойства
- § 3. Расширение основного кольца
- § 4. Тензорное произведение алгебр
- § 5. Тензорная алгебра модуля
- § 6. Знакопеременные произведения
- § 7. Симметрические произведения
- § 8. Кольцо Эйлера — Гротендика
- § 9. Некоторые функториальные изоморфизмы
- УПРАЖНЕНИЯ
- Глава XVII. Полупростота
- § 1. Матрицы и линейные отображения над некоммутативными кольцами
- § 2. Условия, определяющие полупростоту
- § 3. Теорема плотности
- § 4. Полупростые кольца
- § 5. Простые кольца
- § 6. Сбалансированные модули
- УПРАЖНЕНИЯ
- Глава XVIII. Представления конечных групп
- § 1. Полупростота групповой алгебры
- § 2. Характеры
- § 3. Одномерные представления
- § 4. Пространство функций классов
- § 5. Соотношения ортогональности
- § 6. Индуцированные характеры
- § 7. Индуцированные представления
- § 8. Положительное разложение регулярного характера
- § 9. Сверхразрешимые группы
- § 10. Теорема Брауэра
- § 11. Поле определения представления
- УПРАЖНЕНИЯ
- Добавление































































































































































































































































































































































































































































































































































