§ 4.7. Запаздывающее взаимодействие зарядов

4.7.1. Функция взаимодействия двух зарядов.

предыдущем параграфе мы определили матричный элемент рассеяния электрона электроном и вычислили сечение этого процесса. С другой стороны, в § 1.7 мы определили матричный элемент рассеяния электрона во внешнем поле, в частности в кулоновском поле точечного заряда, и с помощью этого матричного элемента нашли сечение рассеяния электрона. Но как видно из (1.7.50) и (4.6.4), сечения в обоих случаях получаются различными. Это значит, что рассеяние электрона электроном нельзя трактовать как рассеяние одного электрона в кулоновском поле, создаваемом другим электроном. Причина этого заключается в том, что взаимодействие двух электронов является запаздывающим и не сводится к мгновенному кулоновскому взаимодействию. Действительно, в электродинамике не существует потенциальной энергии взаимодействия, зависящей от координат взаимодействующих частиц, взятых в один и тот же момент времени, так как электроны взаимодействуют посредством электромагнитного поля.

Оператор энергии взаимодействия заменяет в первом приближении играющая аналогичную роль матрица рассеяния

    (4.7.1)

Она представляет собой первый член разложения матрицы, рассеяния (3.2.26), описывающей процесс рассеяния без участия фотонов,

Подынтегральное выражение в (4.7.1) содержит координаты (включая однако и временную координату) только зарядов, электромагнитное же поле в этой формуле исключено. Поэтому функцию можно назвать функцией взаимодействия двух зарядов. Как мы увидим далее, в нерелятивистском приближении функция взаимодействия приводит к энергии взаимодействия двух зарядов, т. е. к закону Кулона и к поправкам к нему.

Два оператора тока, входящие в (4.7.1), могут относиться либо к различным полям (например, один к электронному, другой к мюонному или адронному), либо к одинаковым (например, к электронному). В первом случае токи, очевидно, коммутируют между собой, и оператор может считаться равным единице. Аналогичная ситуация имеет место и в случае одинаковых полей. Действительно, оператор содержит произведения четырех операторов испускания или поглощения электронов (позитронов), но мы будем интересоваться теми матричными элементами которым соответствуют две частицы в начальном и две частицы в конечном состояниях. В этом случае вклад в матричный элемент будут вносить только те члены оператора которые содержат два оператора испускания и два оператора поглощения, причем все они будут относиться к различным индивидуальным состояниям электронов. Поэтому все четыре сомножителя антикоммутируют друг с другом, а их попарные произведения коммутируют. Следовательно, символ может быть опущен и в этом случае.

Интересуясь возможностью введения энергии взаимодействия частиц, напишем выражение для матричного элемента оператора в координатном представлении. Пусть сначала обе частицы являются электронами. Если 1 и 2 обозначают совокупности квантовых чисел начальных состояний, 1 и 2 — конечных состояний электронов, то в операторе отличные от нуля значения дадут лишь следующие члены:

где — операторы испускания и поглощения электрона в состоянии — плотность тока перехода электрона из состояния 1 в состояние — соответствующие решения уравнения Дирака. Используя антикоммутативность получим следующее выражение для матричного элемента:

    (4.7.2)

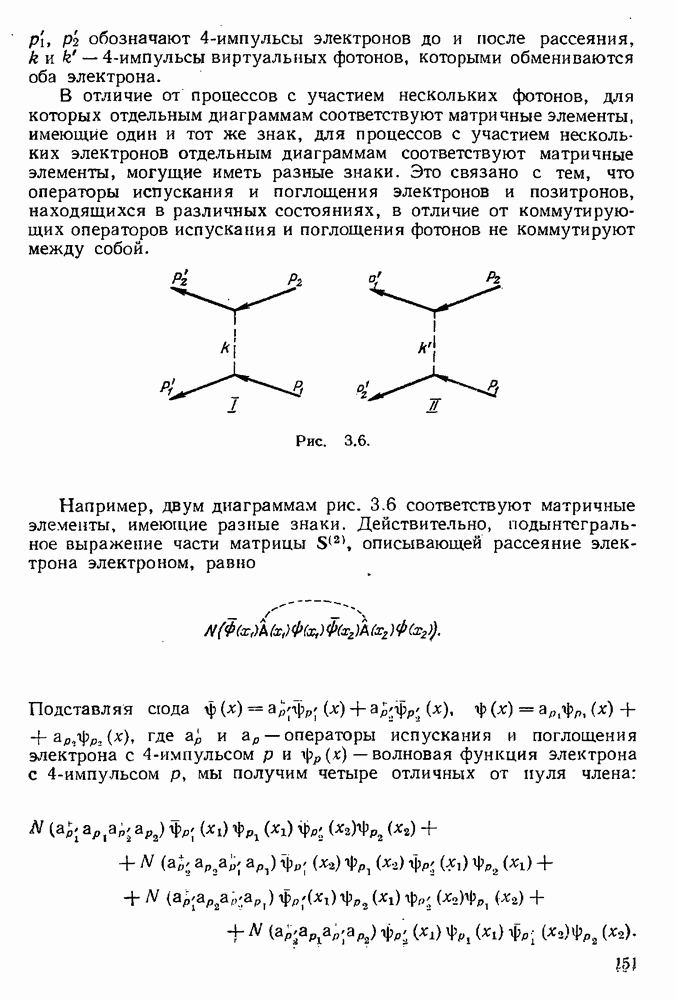
Двум слагаемым здесь соответствуют две диаграммы на рис. 4.23: они различаются местами индексов конечных состояний.

Поэтому второй член в (4.7.2) и вторая диаграмма называются обменными по отношению к первым. Знак минус у обменного члена в (4.7.2) соответствует тому, что волновая функция двух электронов в конфигурационном пространстве является антисимметричной.

Эти же диаграммы описывают взаимодействие двух позитронов. Если начальные состояния позитронов обозначить через 1 и 2, а конечные состояния позитронов через 1 и 2, то матричный элемент будет иметь вид

где ток перехода позитрона из состояния Г в состояние — волновые функции позитрона.

Наконец, матричный элемент взаимодействия электрона с позитроном определяется формулой

    (4.7.4)

Первые члены в (4.7.4) и (4.7.2) различаются знаком, что соответствует противоположным знакам зарядов электрона и позитрона.

Обменный член в (4.7.4) (вторая диаграмма на рис. 4.23 с начальным состоянием 1 2) теперь соответствует виртуальному поглощению и образованию вновь электронно-позитронной пары.

Рис. 4.23.

Как уже указывалось, (4.7.1) можно применять для описания взаимодействия электрона с другой частицей, например, мюоном. В этом случае под следует понимать электронный ток, а под — мюонный. В матричных элементах будут теперь отсутствовать обменные члены. Если. состояния относятся к одной частице, а — к другой, то матричный элемент будет иметь вид

    (4.7.5)

Этот матричный элемент можно представить в виде, допускающем простое физическое истолкование, если ввести запаздывающие потенциалы частиц. Будем рассматривать с этой целью стационарные состояния ; тогда где -

Используя формулу

получим

    (4.7.6)

От матрицы рассеяния удобно перейти к матрице эффективной энергии взаимодействия V, согласно формуле

откуда

Эту формулу можно записать также в виде

где

Последняя величина представляет собой запаздывающий потенциал, создаваемый током перехода . Действительно, удовлетворяет уравнению классической электродинамики для монохроматических полей

Если учесть зависимости от и от t, то мы получим

или

    (4.7.8)

Таким образом, матрица V определяется взаимодействием тока перехода одной частицы с потенциалом, порождаемым током перехода другой частицы.

4.7.2. Энергия взаимодействия двух электронов с точностью до . В (4.7.7) токи переходов можно выразить через волновые функции электронов

    (4.7.9)

где — матрицы Дирака, действующие соответственно на . В подынтегральное выражение входит наряду с

оператором зависящим от координат и спиновых переменных обеих частиц, также и фактор запаздывания Наличие этого фактора, зависящего явно от начальной и конечной энергий системы, не позволяет в общем случае ввести гамильтониан взаимодействия двух электронов, т. е. оператор V, для которого выполнялось бы соотношение

    (4.7.10)

Однако при малых скоростях, такой оператор можно построить. С этой целью разложим матричный элемент по степеням с точностью до введя предварительно явно скорость света. Для фактора запаздывания такое разложение с точностью до членов порядка имеет вид

Матричные элементы, содержащие а, по порядку величины равны Поэтому в членах, содержащих агаг, достаточно сохранить лишь первый член в разложении (4.7.11). Второй член в (4.7.11) после подстановки в интеграл (4.7.9) обратится в нуль в силу ортогональности функций Третий член можно преобразовать к симметричному виду, воспользовавшись тем, что — и поэтому

Далее можно исключить из выражения для матричного элемента частоты, используя уравнение Дирака Имея в виду, что выражение (4.7.11) умножается справа на а слева на и интегрируется по мы можем заменить в нем частоты операторами расположенными справа от , а частоты - операторами расположенными слева от

(квадратные скобки обозначают коммутаторы соответствующих величин). Так как оператор Гамильтона электрона имеет вид , где — внешнее поле, то не коммутирующим с является только однн член в Н, а именно Вычислив коммутатор легко убедиться, что после подстановки (4.7.11) в (4.7.9) можно произвести замену

где

Таким образом, величина действительно может быть представлена в виде (4.7.10), где оператор V определяется формулой [36]

Первый член в этой формуле определяет кулоновское взаимодействие зарядов, а второе слагаемое — поправки к кулоновскому взаимодействию, обусловленные наличием спинов.

Так как выражение для V имеет смысл только с точностью до членов порядка то волновые функции электронов следует брать с той же точностью. Обозначим соответствующие двухкомпонентные волновые функции, нормированные на единицу, через . Тогда

При этом матричный элемент приобретает вид

    (4.7.13)

где — некоторый оператор, который может быть назван оператором энергии взаимодействия двух электронов с точностью до Выражение для него можно получить из (4.7.12):

    (4.7.14)

Заметим, что наличие здесь -функций не означает сильного взаимодействия. Те члены, в которые входят S-функции, содержат в коэффициентах и поэтому должны по смыслу проводившегося разложения рассматриваться как малые по сравнению с первым членом, соответствующим кулоновскому взаимодействию.

Выражение для оператора энергии взаимодействия двух электронов можно получить также иначе, если воспользоваться выражением для матричного элемента энергии взаимодействия в импульсном представлении. Запишем с этой целью в виде

где М — амплитуда, соответствующая первой диаграмме на рис. 4.23:

В нерелятивистском приближении биспинор и можно записать в виде (включая члены порядка )

При этом матричный элемент будет иметь следующую структуру:

    (4.7.15)

где — импульсное представление энергии взаимодействия двух электронов. Действительно, эта формула может быть получена путем преобразования Фурье из формулы (4.7.13), если в последней перейти к нормированным плоским волнам (нормировочный объем принят равным единице) и учесть, что энергия взаимодействия двух частиц является функцией разности их координат. Замечая еще, что в нерелятивистском приближении

легко убедиться, что

Эта величина, как и следовало ожидать, является (-представлением энергии взаимодействия (4.7.14):

В задаче о взаимодействии двух электронов необходимо естественно рассматривать кроме матричного элемента (4.7.13) еще обменный матричный элемент

где — тот же оператор (4.7.14). Вводя антисимметризованные волновые функции двух электронов

( — спиновые переменные частиц) и аналогичные функции для других пар состояний, можно представить суммарный матричный элемент в виде

    (4.7.17)

Если 1 и 2 — произвольные стационарные состояния электрона во внешнем поле, то волновые функции будут образовывать полную систему антисимметризованных собственных функций оператора , где — оператор Гамильтона электрона во внешнем поле.