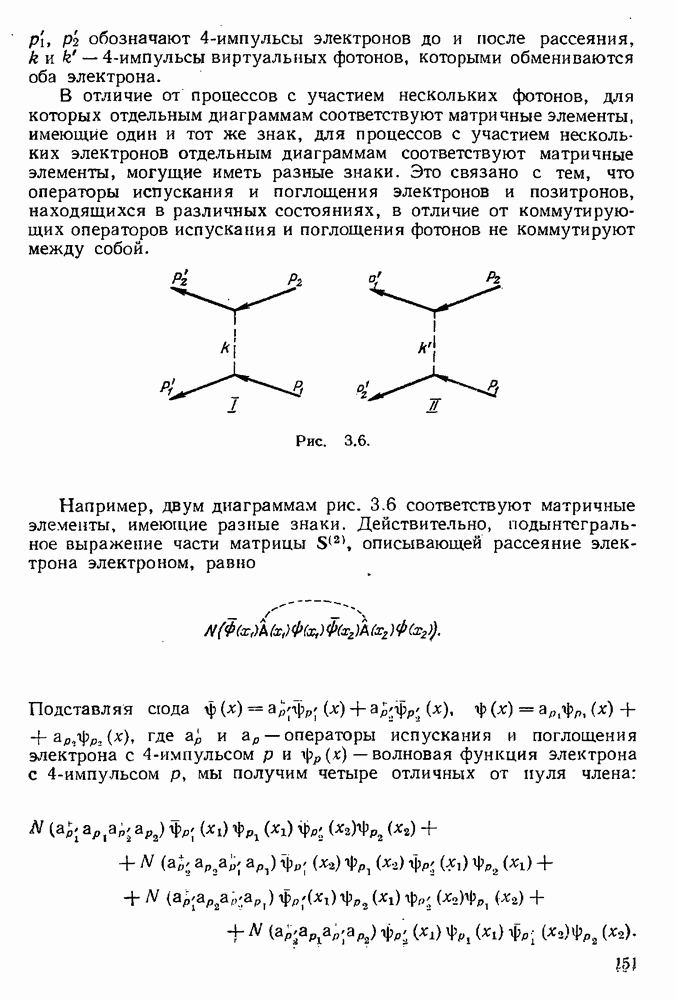
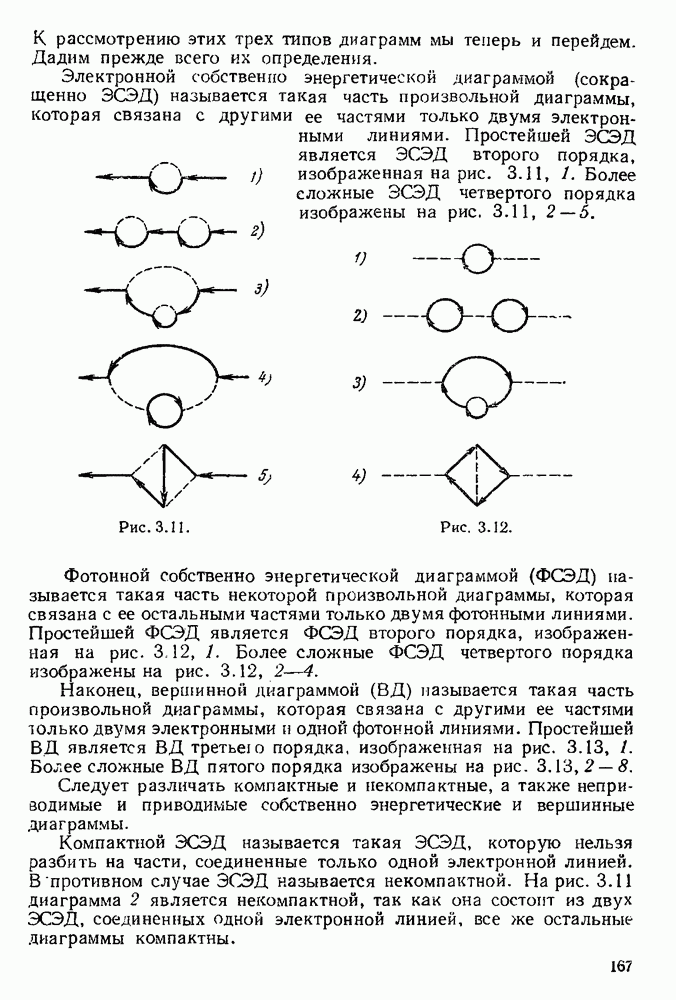
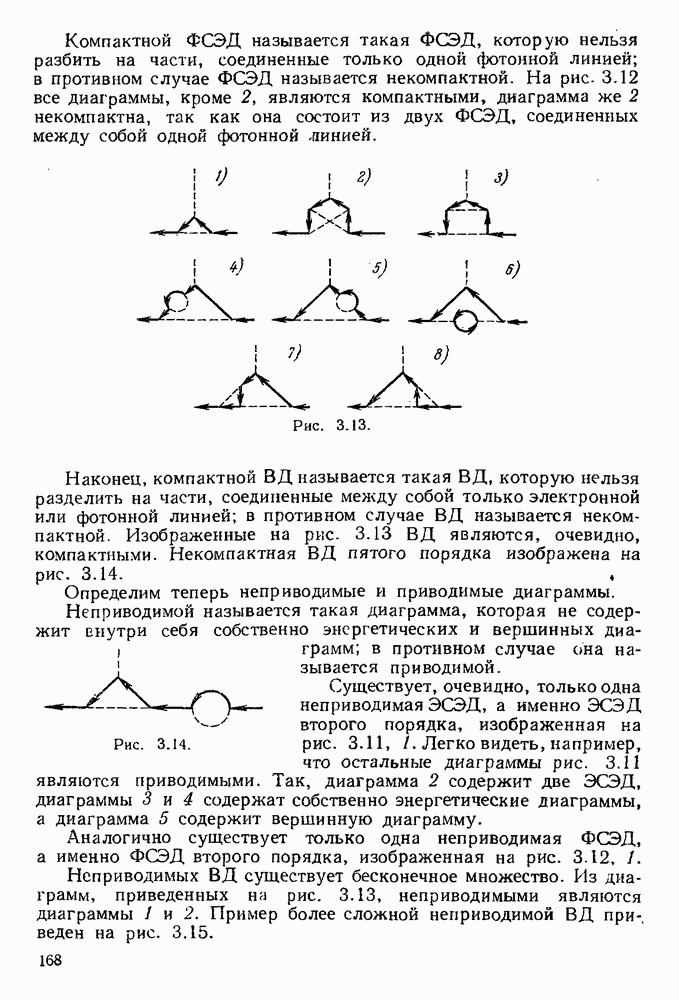
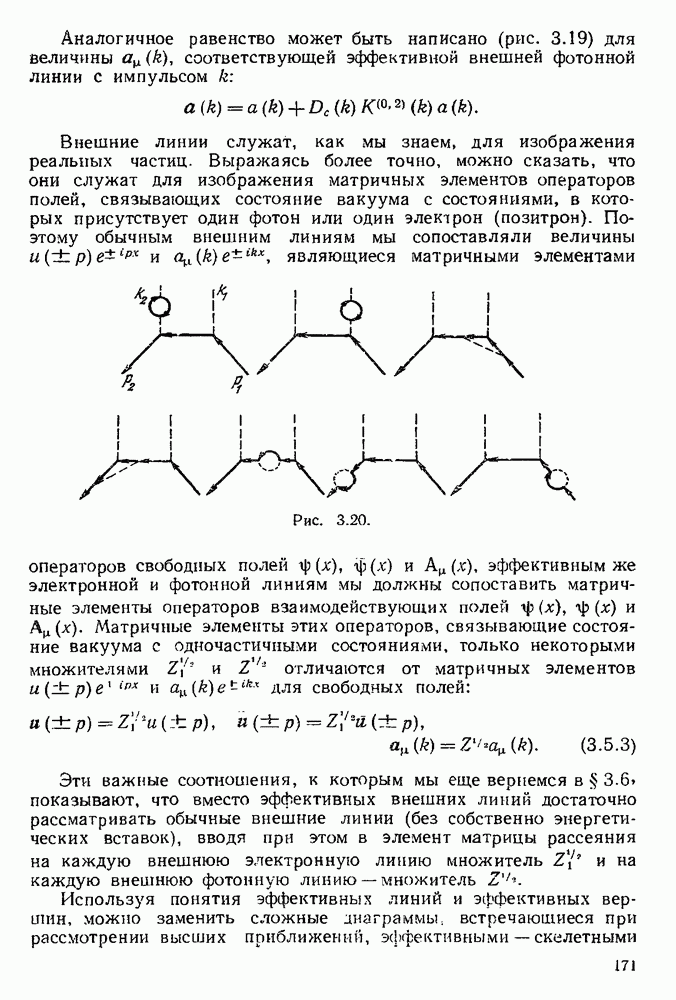
3.8.3. Асимптотический характер регулярнзованных разложений матрицы рассеяния и проблема замкнутости квантовой электродинамики.

Изложенный в § 3.7 метод регуляризации устраняет расходимости, в отдельных матричных элементах, т. е. в отдельных членах разложения матрицы рассеяния в ряд по степеням заряда

электрона, a не сразу во всей матрице рассеяния. Возникает поэтому вопрос, будет ли сходящимся полученный таким образом ряд теории возмущений, состоящий из регуляризованных слагаемых.

Можно высказать соображения, указывающие на расходимость этого ряда, который является, по-видимому, асимптотическим. Эти соображения заключаются в следующем [22].

Взаимодействие между двумя электронами, не связанное с процессами излучения и поглощения фотонов, определяется функцией . Вычислив с помощью этой функции некоторую физическую величину мы получим бесконечный ряд по степеням

    (3.8.26)

где — некоторые функции -импульсов частиц. Допустим, что этот ряд, отдельные члены которого регуляризованы, согласно методу § 3.7 сходится при некотором значении . Тогда будет аналитической функцией при , а следовательно, и при достаточно малых значениях заряда также будет аналитической функцией, представимой в виде степенного ряда. Но допускает простую физическую интерпретацию. Именно, представляла бы собой изучаемую нами величину F в том случае, если бы взаимодействие двух зарядов определялось функцией — , а не иными словами, если бы одноименные заряды притягивались, а не отталкивались.

Легко видеть, что при этом обычное определение вакуума не соответствует состоянию с наименьшей энергией. Действительно, представим себе, что образовано электронно-позитронных пар и что все электроны сосредоточены в одной области пространства, а позитроны — в другой. Если эти области достаточно малы и достаточно отдалены друг от друга, то при большом N отрицательная кулоновская энергия притягивающихся одноименных зарядов будет больше энергии покоя частиц и их кинетической энергии. Назовем такие состояния «патологическими».

Предполагая, что взаимодействие между зарядами определяется функцией — рассмотрим некоторое обычное состояние, характеризующееся наличием нескольких частиц. Это состояние отделено потенциальным барьером от «патологического» состояния с такой же энергией, причем высота барьера определяется энергией, необходимой для создания N пар, т. е. энергией покоя частиц.

В силу туннельного эффекта существует конечная вероятность перехода из обычного в «патологическое» состояние. Это значит, что каждое физическое состояние является неустойчивым по отношению к спонтанному рождению большого числа частиц.

«Патологическое» состояние, в которое перейдет система, не будет стационарным, так как в нем будет образовываться все большее и большее число частиц, т. е. будет происходить как бы дезинтеграция вакуума. В силу этих эффектов нельзя предполагать, чтобы квантовая электродинамика с функцией взаимодействия приводила к вполне определенным аналитическим функциям. Скорее следует считать, что функция не может быть аналитической и что поэтому ряд (3.8.26) не сходится при .

В связи с этим возникает естественный вопрос — какой же смысл имеет ряд (3.8.26) и почему квантовая электродинамика, оперирующая с такими рядами, находится в соответствии с экспериментальными данными? Ответ на этот вопрос заключается в том, что ряд (3.8.26) является асимптотическим рядом. Как известно, такие ряды в некоторых условиях могут быть использованы для описания поведения функций, которые они представляют, с очень большой, но всегда конечной точностью. В отличие от сходящихся рядов члены асимптотического ряда сначала с ростом номера падают, а затем, начиная с некоторого значения , которое мы обозначим через начинают расти и, вообще говоря, расти неограниченно. При этом максимальная точность, с которой асимптотический ряд может аппроксимировать функцию F, определяется величиной Чем величина меньше, тем точность больше. В случае квантовой электродинамики есть основания предполагать, что в ряде (3.8.26) величины будут падать вплоть до порядка Так как это значение велико, то точность, с которой в квантовой электродинамике ряд (3.8.26) должен соответствовать реальности, очень велика. По всей вероятности, неточность ряда (3.8.26) порядка что является ничтожно малой величиной. Для практических целей квантовой электродинамики такая точность более чем достаточна. Для устранения расходимостей в матрице рассеяния мы вводили граничный импульс L и предполагали, что область импульсов не играет роли, если изменения импульсов реальных частиц малы по сравнению с L. Получаемые при этом выводы и предсказания квантовой электродинамики находятся в прекрасном согласии с экспериментальными данными.

Однако ясно, что строгий смысл имеет лишь предельный случай , который не может быть рассмотрен в рамках квантовой электродинамики.