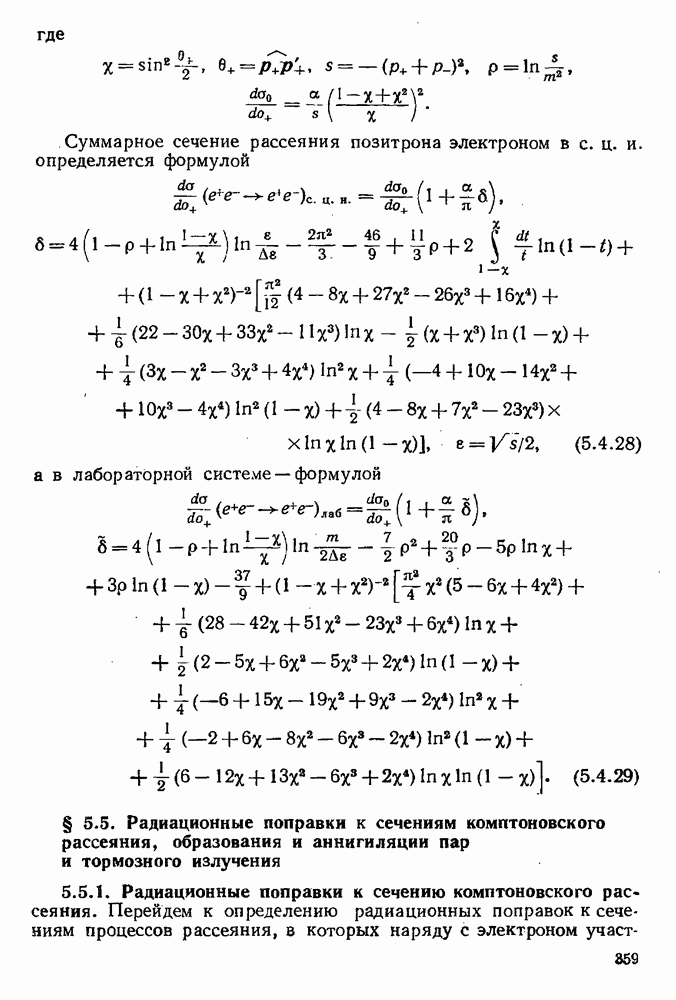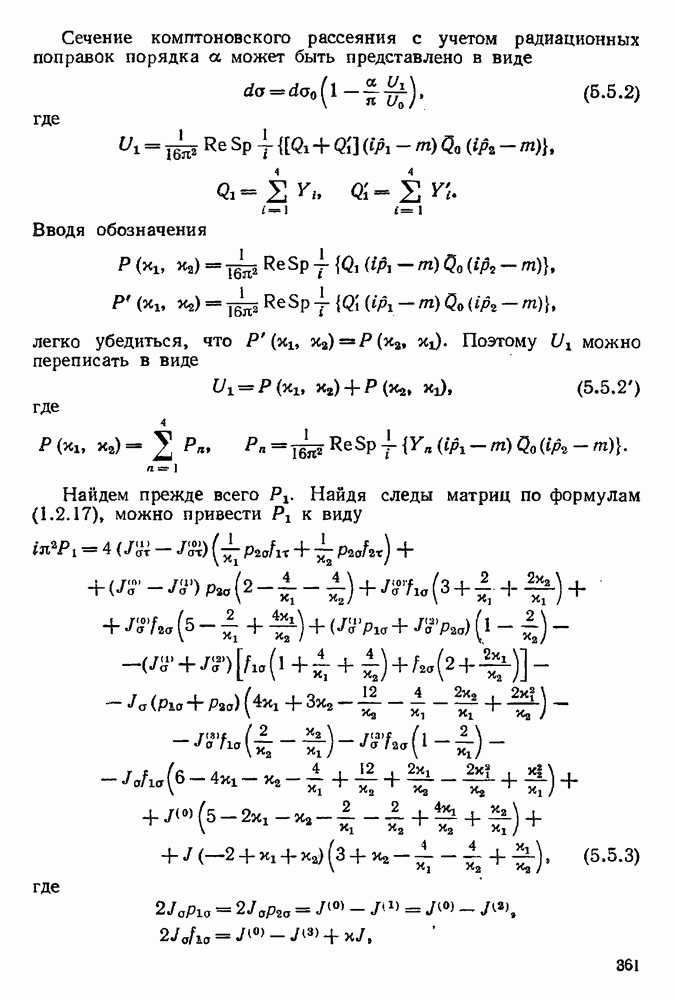| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ПРИЛОЖЕНИЕ
А.1. Вычисление интегралов по инвариантному объему в 4-импульсном пространстве.
Мы разъясним здесь технику вычисления встречающихся в квантовой электродинамике интегралов.
Интегральные выражения, сопоставляемые, согласно правилам Фейнмана, различным диаграммам, имеют следующую структуру:

где F — некоторый полином относительно 4-нмпульсов  — полиномы второй степени относительно
— полиномы второй степени относительно  Вычисление таких интегралов удобно производить, воспользовавшись предварительно тождеством
Вычисление таких интегралов удобно производить, воспользовавшись предварительно тождеством

При  это тождество очевидно, так как
это тождество очевидно, так как

Но его легко доказать и в общем виде.
Используя тождество  получим интеграл в
получим интеграл в  -пространстве вида
-пространстве вида

где а и I зависят от параметров  . Искомый интеграл I получается из
. Искомый интеграл I получается из  интегрированием по
интегрированием по  (Этот метод вычисления интегралов
(Этот метод вычисления интегралов  мы будем называть методом параметризации
мы будем называть методом параметризации 
Перейдем к вычислению интеграла  Предположим сначала, что интеграл сходится. В этом случае можно сделать преобразование
Предположим сначала, что интеграл сходится. В этом случае можно сделать преобразование  , после чего интеграл приобретает вид
, после чего интеграл приобретает вид

Достаточно, очевидно, ограничиться рассмотрением случая, когда  представляет собой некоторую скалярную функцию от
представляет собой некоторую скалярную функцию от  Действительно, если
Действительно, если  то
то  если
если  то
то

В интеграле  интегрирование по
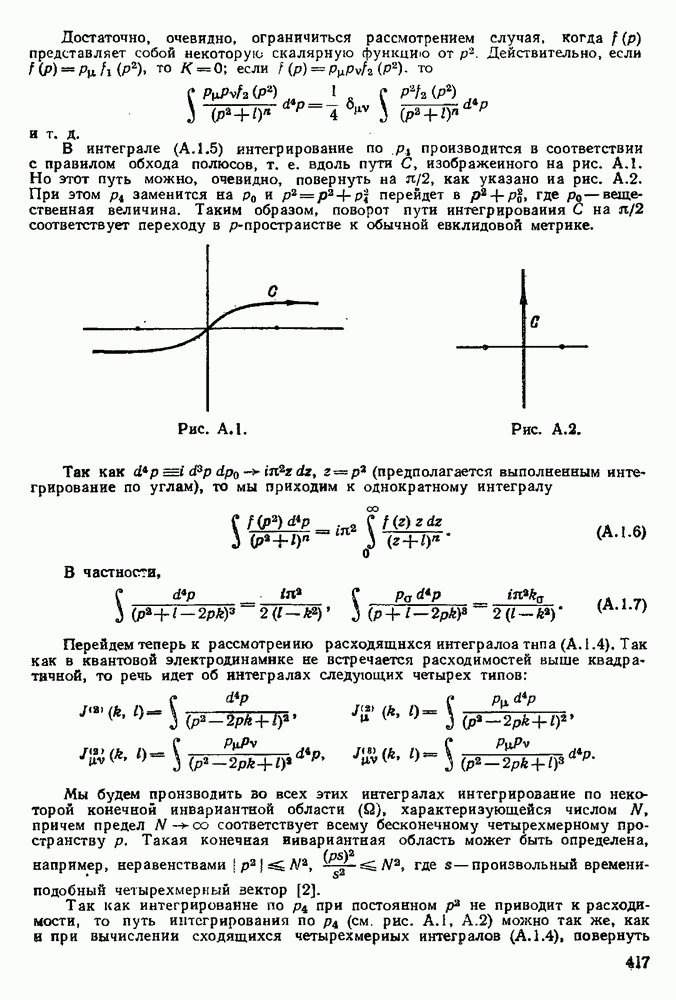
интегрирование по  производится в соответствии с правилом обхода полюсов, т. е. вдоль пути С, изображенного на рис. А.1. Но этот путь можно, очевидно, повернуть на
производится в соответствии с правилом обхода полюсов, т. е. вдоль пути С, изображенного на рис. А.1. Но этот путь можно, очевидно, повернуть на  как указано на рис. А.2. При этом
как указано на рис. А.2. При этом  заменится на
заменится на  перейдет в
перейдет в  где
где  -вещественная величина. Таким образом, поворот пути интегрирования С на
-вещественная величина. Таким образом, поворот пути интегрирования С на  соответствует переходу в
соответствует переходу в  -простраистве к обычной евклидовой метрике.
-простраистве к обычной евклидовой метрике.

Рис. А.1

Рис. А.2
Так как  (предполагается выполненным интегрирование по углам), то мы приходим к однократному интегралу
(предполагается выполненным интегрирование по углам), то мы приходим к однократному интегралу

В частности,

Перейдем теперь к рассмотрению расходящихся интегралоа типа  Так как в квантовой электродинамике не встречается расходимостей выше квадратичной, то речь идет об интегралах следующих четырех типов:
Так как в квантовой электродинамике не встречается расходимостей выше квадратичной, то речь идет об интегралах следующих четырех типов:

Мы будем производить во всех этих интегралах интегрирование по некоторой конечной инвариантной области (Q), характеризующейся числом N, причем предел  соответствует всему бесконечному четырехмерному пространству
соответствует всему бесконечному четырехмерному пространству  . Такая конечная инвариантная область может быть определена, например, неравенствами
. Такая конечная инвариантная область может быть определена, например, неравенствами  где
где  -произвольный времени-подобный четырехмерный зектор [2].
-произвольный времени-подобный четырехмерный зектор [2].
Так как интегрирование по  при постоянном
при постоянном  не приводит к расходимости, то путь интегрирования по
не приводит к расходимости, то путь интегрирования по  (см. рис. А.1, А.2) можно так же, как Н при вычислении сходящихся четырехмериых интегралов
(см. рис. А.1, А.2) можно так же, как Н при вычислении сходящихся четырехмериых интегралов  повернуть
повернуть
на  . После такого поворота мы полупим четырехмерное евклидово
. После такого поворота мы полупим четырехмерное евклидово  -пространство с вещественной четвертой координатой, и область интегрирования станет четырехмерной сферой, радиус которой мы обозначим через L и отождествим с введенным в § 3.7 предельным импульсом.
-пространство с вещественной четвертой координатой, и область интегрирования станет четырехмерной сферой, радиус которой мы обозначим через L и отождествим с введенным в § 3.7 предельным импульсом.
Переходя к вычислению интересующих нас расходящихся интегралов, качнем с логарифмически расходящегося интеграла

Повернув путь интегрирования по  на
на  и воспользовавшись формулой (А. 1.6), имеем
и воспользовавшись формулой (А. 1.6), имеем

Вычислив последний интеграл и отбросив члены порядка  получим
получим

Рассмотрим далее интеграл  , который так же как и интеграл
, который так же как и интеграл  расходится логарифмически. Переписав тот интеграл в виде
расходится логарифмически. Переписав тот интеграл в виде

сделаем замену переменных  Тогда интеграл приобретет вид (А.1.8) с измененной, однако, областью интегрирования, которую мы обозначим через
Тогда интеграл приобретет вид (А.1.8) с измененной, однако, областью интегрирования, которую мы обозначим через  Согласно
Согласно  интеграл
интеграл  будет равен
будет равен  отличается от L на конечную величину, поэтому если L достаточно велико, то
отличается от L на конечную величину, поэтому если L достаточно велико, то  отличается от
отличается от  на малую величину порядка
на малую величину порядка  и окончательйо мы получим
и окончательйо мы получим

Вычислим теперь логарифмически расходящийся интеграл I). Так же, как и при вычислении интеграла  мы можем сделать смещение начала координат, введя новую переменную интегрирования
мы можем сделать смещение начала координат, введя новую переменную интегрирования 

Замечай, что

получим окончательно

Переходя к вычислению интеграла  заметим, что
заметим, что

и что 4-вектор  должен быть направлен вдоль
должен быть направлен вдоль  Отсюда и из
Отсюда и из  следует:
следует:

Обратим внимание на то, что если бы мы вычисляли этот интеграл, сделав замену переменной (при той же области интегрирования  то получили бы в результате
то получили бы в результате  Таким образом, при преобразовании
Таким образом, при преобразовании  , т. е. смещении начала координат на к, расходящийся интеграл
, т. е. смещении начала координат на к, расходящийся интеграл  получает добавку
получает добавку 
Рассмотрим, наконец, квадратично расходящийся интеграл  . Проинтегрировав выражение
. Проинтегрировав выражение  по
по  получим
получим

где g — некоторая функция от N и  содержащая квадратично расходящуюся при
содержащая квадратично расходящуюся при  константу. Легко видеть, что g представляет собой линейную функцию от
константу. Легко видеть, что g представляет собой линейную функцию от  Действительно, левая часть
Действительно, левая часть  при преобразовании
при преобразовании  где
где  — произвольное число, приобретает множитель
— произвольное число, приобретает множитель  что возможно только в том случае, если
что возможно только в том случае, если

где  — квадратично расходящаяся константа, а а и b — некоторые числа
— квадратично расходящаяся константа, а а и b — некоторые числа  умножается на логарифмически расходящуюся константу
умножается на логарифмически расходящуюся константу  а не на
а не на  так как только при этом оба слагаемых в g будут иметь одинаковую размерность).
так как только при этом оба слагаемых в g будут иметь одинаковую размерность).
Продифференцировав  по
по  получим интересующий нас интеграл
получим интересующий нас интеграл 

Для того чтобы найти а и b и выразить  через L, можно поступит следующим образом. Представим
через L, можно поступит следующим образом. Представим  в виде
в виде

Второй интеграл в (А.1.14) может быть немедленно вычислен:

Интеграл же  с помощью формулы
с помощью формулы

приводится к виду

Так как

то, применяя еще раз формулу (А.1.15), получим

Входящий сюда интеграл по  расходится логарифмически и может быть вычислен так же, как и интегралы
расходится логарифмически и может быть вычислен так же, как и интегралы  Поступая таким образом, найдем
Поступая таким образом, найдем

Приведем в заключение сводку вычисленных интегралов:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА ЭЛЕКТРОНА
- 1.1.2. Симметричная форма уравнения Дирака.
- 1.1.3. Решения с положительными и отрицательными частотами.
- 1.1.4. Плоские волны.
- 1.1.5. Поляризационные состояния электрона.
- 1.1.6. Поляризационная матрица плотности электрона.
- 1.1.7. Поляризационные состояния электрона в ультрарелятизистском пределе.
- § 1.2. Уравнение Дирака для электрона в электромагнитном поле и свойства инвариантности уравнения Дирака
- 1.2.1. Уравнение Дирака для электрона во внешнем электромагнитном поле.
- 1.2.2. Уравнение непрерывности.
- 1.2.3. Различные представления уравнения Дирака.
- 1.2.4. Алгебра матриц Дирака.
- 1.2.5. Релятивистская инвариантность уравнения Дирака.
- 1.2.6. Пространственное отражение, обращение времени и зарядовое сопряжение.
- 1.2.7. Ковариантные билинейные формы.
- 1.2.8. Использование обозначений, соответствующих псевдоевклидовой метрике.
- § 1.3. Предельные переходы к нерелятивистской квантовой механике и релятивистской классической механике
- 1.3.2. Второе приближение.
- 1.3.3. Переход к релятивистской классической механике.
- 1.3.4. Высокоэнергетическое приближение.
- 1.3.5. Борновское приближение.
- § 1.4. Момент импульса электрона
- 1.4.2. Волновая функция свободного электрона с определенным моментом.
- 1.4.3. Четность состояния.
- 1.4.4. Разложение по сферическим волнам.
- § 1.5. Движение электрона в центральном поле
- 1.5.2. Сферически-симметричная потенциальная яма.
- 1.5.3. Движение электрона в кулоновском поле ядра.
- 1.5.4. Волновые функции непрерывного спектра в кулоновском поле ядра.
- 1.5.5. Критический заряд ядра.
- § 1.6. Движение в однородных полях
- 1.6.2. Электрон в постоянном и однородном магнитном поле.
- 1.6.3. Электрон в постоянном и однородном электрическом поле.
- 1.6.4. Парадокс Клейна.
- § 1.7. Рассеяние электронов
- 1.7.2. Амплитуда и сечение рассеяния.
- 1.7.3. Поляризация и азимутальная асимметрия.
- 1.7.4. Упругое рассеяние в борцовском приближении.
- 1.7.5. Упругое рассеяние в эйкональном приближении.
- 1.7.6. Рассеяние в кулоновском поле ядра.
- ГЛАВА 2. КВАНТОВАНИЕ ПОЛЕЙ
- § 2.1. Квантовая механика фотона
- 2.1.2. Волновая функция фотона.
- 2.1.3. Плоские волны.
- § 2.2. Момент импульса фотона
- 2.2.2. Собственные функции оператора момента фотона.
- 2.2.3. Продольный и поперечные шаровые векторы.
- 2.2.4. Четность состоянии фотона.
- 2.2.5. Сферические электромагнитные волны.
- § 2.3. Квантование электромагнитного поля
- 2.3.2. Перестановочные соотношения для потенциалов электромагнитного поля.
- 2.3.3. Хронологическое и нормальное произведения операторов электромагнитных потенциалов.
- § 2.4. Корреляционные функции электромагнитного поля
- 2.4.2. Когерентные состояния.
- 2.4.3. Корреляционные функции и когерентность высших порядков.
- 2.4.4. Поляризационная матрица плотности.
- § 2.5. Квантование электронно-позитронного поля
- 2.5.2. Операторы испускания и поглощения электронов и позитронов.
- 2.5.3. Антикоммутаторы электронного поля.
- 2.5.4. Хронологическое и нормальное произведения операторов электронного поля.
- ГЛАВА 3. ЭЛЕКТРОМАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ
- § 3.1. Основные уравнения квантовой электродинамики
- 3.1.2. Лагранжиан и гамильтониан взаимодействующих полей.
- 3.1.3. Представление взаимодействия.
- § 3.2. Матрица рассеяния
- 3.2.2. Инвариантная теория возмущений.
- 3.2.3. Представление матрицы рассеяния в виде суммы нормальных произведений.
- 3.2.4. Функциональная форма представления матрицы рассеяния в виде N-упорядоченного оператора.
- § 3.3. Графическое представление элементов матрицы рассеяния
- 3.3.2. Импульсное представление.
- 3.3.3. Правила Фейнмана.
- § 3.4. Вероятность и эффективное сечение
- 3.4.2. Суммирование по состояниям поляризации электронов и фотонов.
- 3.4.3. Эффективное сечение.
- 3.4.4. Вероятность процессов рассеяния поляризованных частиц.
- § 3.5. Структура диаграмм матрицы рассеяния
- 3.5.2. Эффективные линии.
- 3.5.3. Уравнения Дайсона для функций Грина и графическое уравнение для вершинной функции.
- 3.5.4. Функции Грина как вакуумные средние.
- § 3.6. Перенормировка массы и заряда электрона
- 3.6.2. Физический заряд электрона.
- 3.6.3. Перенормировка функций Грина и вершинной функции.
- 3.6.4. Перенормировка элементов матрицы рассеяния.
- § 3.7. Расходимости в матрице рассеяния и их устранение
- 3.7.2. Введение граничного импульса.
- 3.7.3. Регуляризация функций, соответствующих неприводимым диаграммам.
- 3.7.4. Регуляризация функций, соответствующих приводимым диаграммам.
- § 3.8. Асимптотические свойства функций Грина
- 3.8.2. Асимптотические выражения для функций Грина.
- 3.8.3. Асимптотический характер регулярнзованных разложений матрицы рассеяния и проблема замкнутости квантовой электродинамики.
- ГЛАВА 4. ОСНОВНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ЯВЛЕНИЯ
- § 4.1. Излучение фотона
- 4.1.2. Излучение электрического и магнитного мультиполей.
- 4.1.3. Излучение ядер. Правила отбора.
- 4.1.4. Фотоэффект.
- § 4.2. Рассеяние фотона электроном
- 4.2.2. Дифференциальное сечение рассеяния неполяризованных частиц.
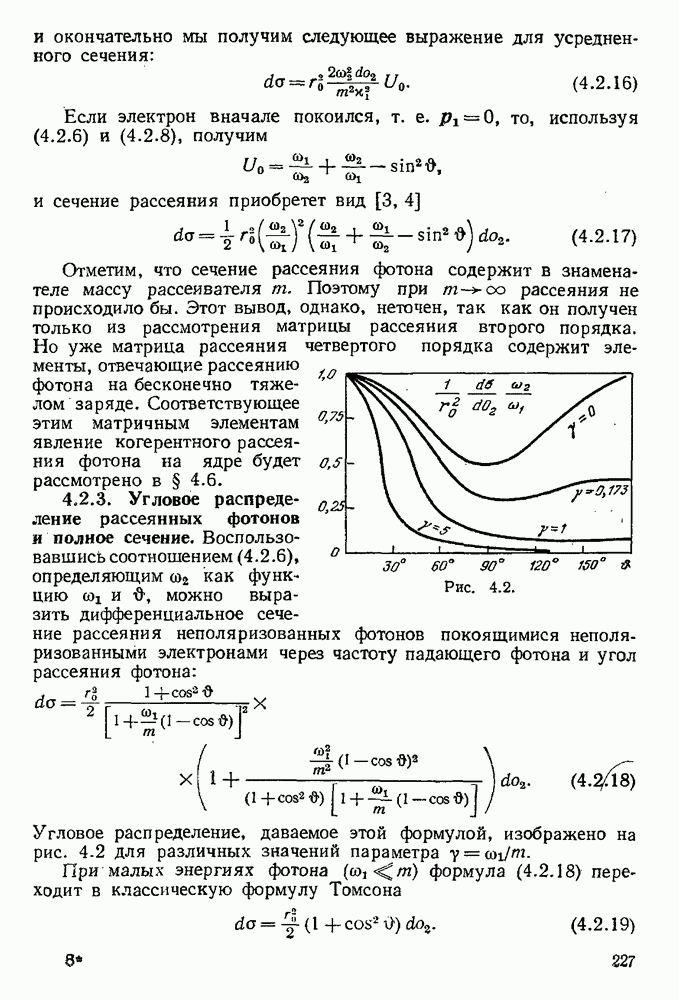
- 4.2.3. Угловое распределение рассеянных фотонов и полное сечение.
- 4.2.4. Поляризационные эффекты.
- 4.2.5. Рассеяние поляризованных фотонов неполяризованными электронами.
- 4.2.6. Дисперсионная формула.
- § 4.3. Тормозное излучение
- 4.3.2. Тормозное излучение в высокоэнергетическом приближении.
- 4.3.3. Сечение тормозного излучения в кулоновском поле ядра в борновском приближении.
- 4.3.4. Экранирование.
- 4.3.5. Потеря энергии на излучение.
- 4.3.6. Тормозное излучение в кулоновском поле ядра в высокоэнергетическом приближении.
- 4.3.7. Точная теория тормозного излучения в нерелятивистской области.
- § 4.4. Излучение длинноволновых фотонов
- 4.4.2. Сечение рассеяния электрона с излучением мягкого фотона.
- 4.4.3. Исследование расходимости в области малых частот.
- 4.4.4. Излучение мягких фотонов при произвольных столкновениях.
- § 4.5. Образование и аннигиляция электронно-позитронных пар
- 4.5.2. Точная теория образования пары фотоном в поле ядра вблизи порога.
- 4.5.3. Образование пары двзмя фотонами.
- 4.5.4. Аннигиляция пары в два и три фотона.
- 4.5.5. Поляризационные эффекты при двухфотонной аннигиляции пар.
- 4.5.6. Распад позитрония.
- 4.5.7. Превращение пары в один фотон.
- § 4.6. Рассеяние электрона и позитрона электроном
- 4.6.2. Сечение рассеяния позитрона электроном.
- 4.6.3. Рассеяние поляризованных электронов.
- 4.6.4. Рассеяние мюона электроном.
- 4.6.5. Излучение фотона при рассеянии электрона электроном и электрона позитроном и при превращении …
- § 4.7. Запаздывающее взаимодействие зарядов
- 4.7.3. Взаимодействие электрона с позитроном и позитроний.
- § 4.8. Метод эквивалентных фотонов
- 4.8.2. Тормозное излучение в процессах рассеяния электрона ядром и электрона электроном.
- 4.8.3. Образование пар фотоном в поле ядра и при столкно вении двух быстрых заряженных частиц.
- 4.8.4. Сечение двуструйного процесса.
- ГЛАВА 5. КВАНТОВОЭЛЕКТРОДИНАМИЧЕСКИЕ ЭФФЕКТЫ В ВЫСШИХ ПРИБЛИЖЕНИЯХ ТЕОРИИ ВОЗМУЩЕНИЙ
- § 5.1. Радиационные поправки к электродинамическим функциям Грина
- 5.1.2. Поляризационный оператор второго порядка.
- 5.1.3. Вершинная функция третьего порядка.
- § 5.2. Модификация закона Кулона. Аномальный магнитный момент электрона
- 5.2.2. Аномальный магнитный момент электрона и мюона.
- § 5.3. Радиационное смещение атомных уровней
- 5.3.2. Радиационное смещение и естественная ширина атомных уровней.
- 5.3.3. Радиационное смещение уровней атома водорода.
- 5.3.4. Рассеяние фотона вблизи резонанса.
- § 5.4. Радиационные поправки к сечениям рассеяния электрона во внешнем поле и рассеяния электрона электроном
- 5.4.2. Исключение «массы» фотона из сечения рассеяния.
- 5.4.3. Устранение инфракрасной расходимости в случае произвольного процесса рассеяния.
- 5.4.4. Радиационные поправки к сечению рассеяния электрона электроном и электрона позитроном.
- § 5.5. Радиационные поправки к сечениям комптоновского рассеяния, образования и аннигиляции пар и тормозного излучения
- 5.5.1. Радиационные поправки к сечению комптоновского рассеяния.
- 5.5.2. Рассеяние электроном фотонов малой частоты.
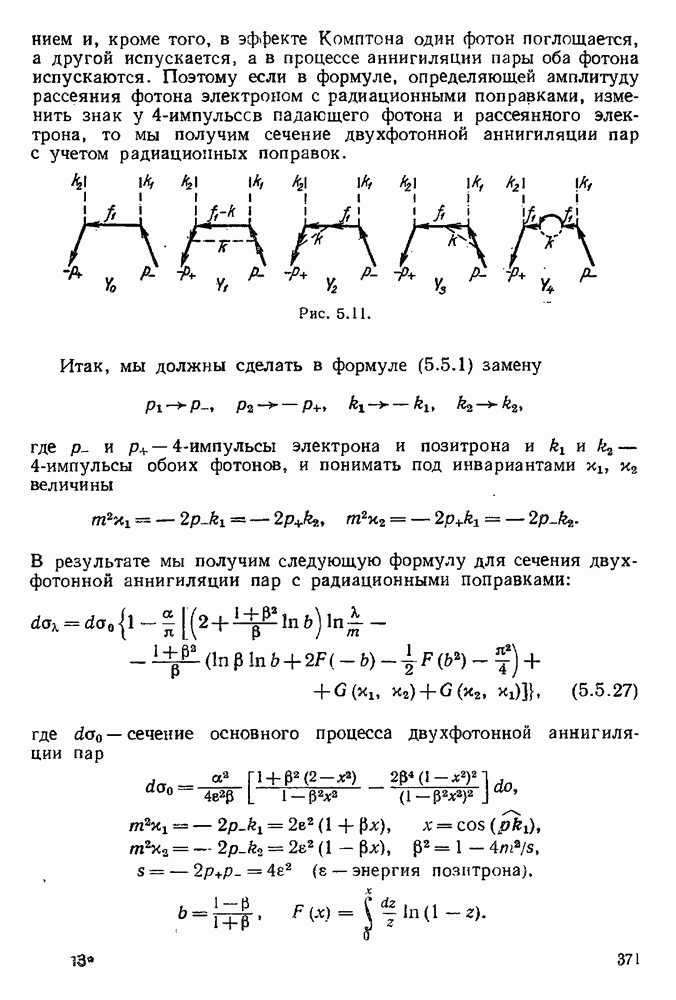
- 5.5.3. Радиационные поправки к сечению двухфотонной аннигиляции пар.
- 5.5.4. Радиационные поправки к сечению тормозного излучения.
- 5.5.4. Радиационные поправки к сечению тормозного излучения.
- 5.5.5. Радиационные поправки к сечению превращения электронно-позитронной пары в мюонную пару.
- § 5.6. Нелинейная электродинамика вакуума
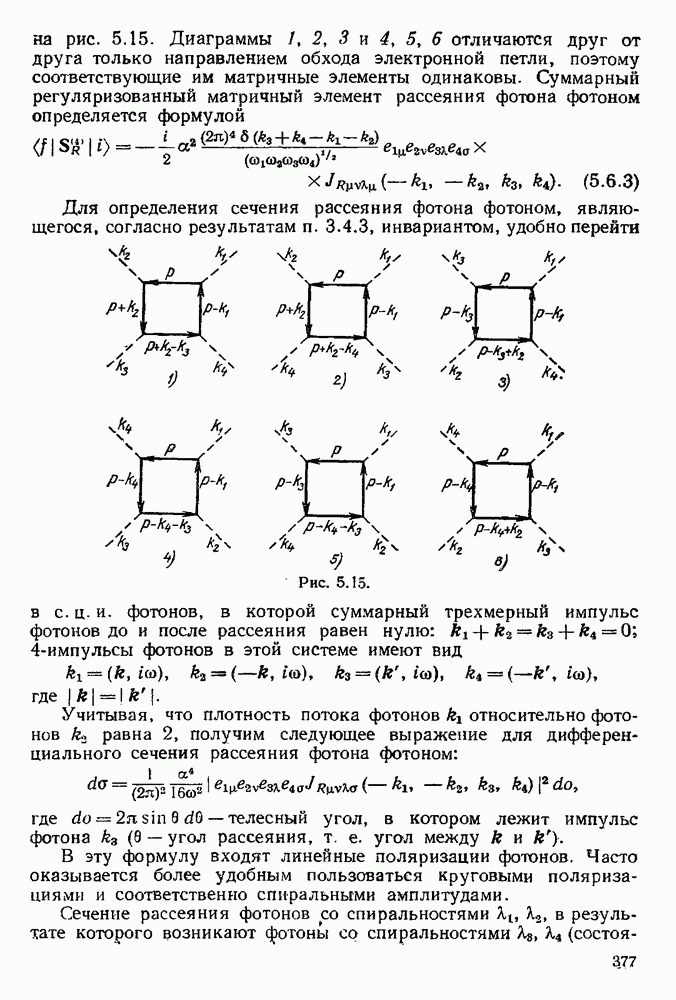
- 5.6.1. Тензор рассеяния фотона фотоном четвертого ранга.
- 5.6.2. Сечение рассеяния фотона фотоном.
- 5.6.3. Радиационные поправки к функции Лагранжа электромагнитного поля в вакууме.
- 5.6.4. Точное выражение для лагранжиана произвольного медленно меняющегося электромагнитного поля.
- 5.6.5. Сечение рассеяния фэтэна в постоянном электромагнитном поле.
- 5.6.6. Связь между амплитудой рассеяния фотона на нулевой угол и сечением образования пар.
- 5.6.7. Импульсное и угловое распределения ядер отдачи при образовании пар фотоном в поле ядра.
- § 5.7. Дважды логарифмическая асимптотика сечений квантовоэлектродинамических процессов
- 5.7.2. Дважды логарифмическая асимптотика сечения рассеяния электрона во внешнем поле.
- 5.7.3. Дважды логарифмическая асимптотика сечения процесса …
- 5.7.4. Сводка формул для сечений квантовоэлектродинамических процессов в дважды логарифмическом приближении.
- ПРИЛОЖЕНИЕ
- А.1. Вычисление интегралов по инвариантному объему в 4-импульсном пространстве.
- A.2. Метод размерной регуляризации.
- ЛИТЕРАТУРА