§ 5.7. Дважды логарифмическая асимптотика сечений квантовоэлектродинамических процессов

5.7.1. Дважды логарифмическая асимптотика вершинной функции.

В предыдущих параграфах мы определили радиационные поправки к сечениям рассеяния различных процессов в наинизшем приближении теории возмущений. Общей особенностью этих поправок является то, что они становятся сравнимыми и могут даже превосходить сечение основного процесса в области больших энергий. Например, величина определяющая радиационные поправки к сечению рассеяния электрона во внешнем поле, ведет себя при больших переданных импульсах q как и достигает значения порядка единицы при Ясно, что при таких и больших значениях q формула (5.4.12) для теряет смысл, так как она выведена в предположении о малости радиационных поправок. Аналогичная ситуация имеет место и для других квантовоэлектродинамических процессов.

Мы видим, таким образом, что для получения правильных выражений для сечений различных процессов в области больших значений энергии и переданного импульса необходимо учитывать радиационные поправки к сечениям не только в наинизшем, но и во всех последующих порядках теории возмущений. Получающиеся бесконечные ряды (состоящие из регуляризоваиных слагаемых) мы не умеем суммировать и, строго говоря, вообще не знаем, сходятся ли они (см. в связи с этим п. 3.8.3). Но если считать,

Что эти ряды являются асимптотическими рядами, описывающими соответствующие квантовоэлектродинамические величины, то в них могут быть выделены главные последовательности членов, которые могут быть просуммированы.

Если рассматривать рассеяние ультрарелятивистского электрона во внешнем поле, то главным в приближении теории возмущении оказывается член вида

Аналогичная ситуация имеет место и для других квантово-электродинамических процессов: всегда в области больших значений энергии и переданного импульса главным в каждом приближении теории возмущений оказывается член, в котором на каждый множитель а приходится произведение двух логарифмов от больших аргументов. Такие члены (мы будем называть их дважды логарифмическими) можно просуммировать и найти таким образом асимптотику сечений различных квантовоэлектродинамических процессов в области больших значений энергии и переданного импульса. Эту асимитотику называют обычно дважды логарифмической.

Покажем, как производится выделение дважды логарифмических членов. Рассмотрим сначала простейшую задачу этого типа — выделение дважды логарифмических членов в радиационных поправках к вершинной функции в области 4-импульсов

    (5.7.1)

Начнем с радиационной поправки порядка

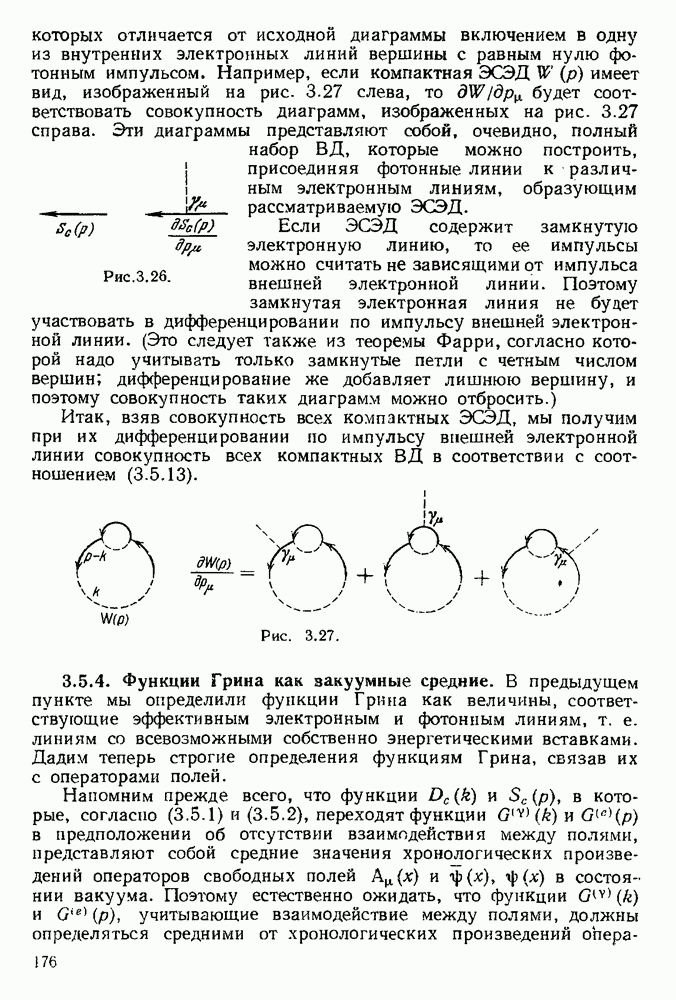
которой соответствует диаграмма 1 рис. 5.18. (Мы пренебрегли всюду в соответствии с неравенствами величиной )

Для нахождения асимптотики функции в области (5.7.1) удобно перейти от k к новым переменным интегрирования и, определенным в § 4.9 формулой (4.9.4):

    (5.7.3)

Легко видеть, что 4-вектор является пространственноподобным, элемент объема в -пространстве, проинтегрированный по углу равен

    (5.7.4)

где

Наконец, выразим в новых переменных множители, входящие в знаменатель подынтегрального выражения для

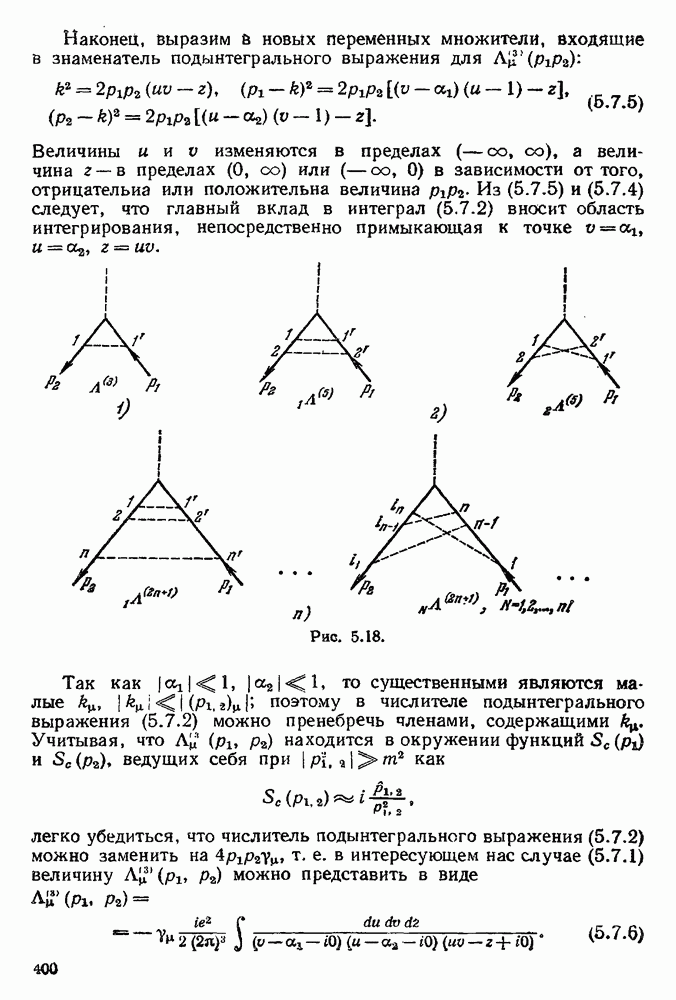
Величины изменяются в пределах , а величина — в пределах или в зависимости оттого, отрицательна или положительна величина Из (5.7.5) и (5.7.4) следует, что главный вклад в интеграл (5.7.2) вносит область интегрирования, непосредственно примыкающая к точке

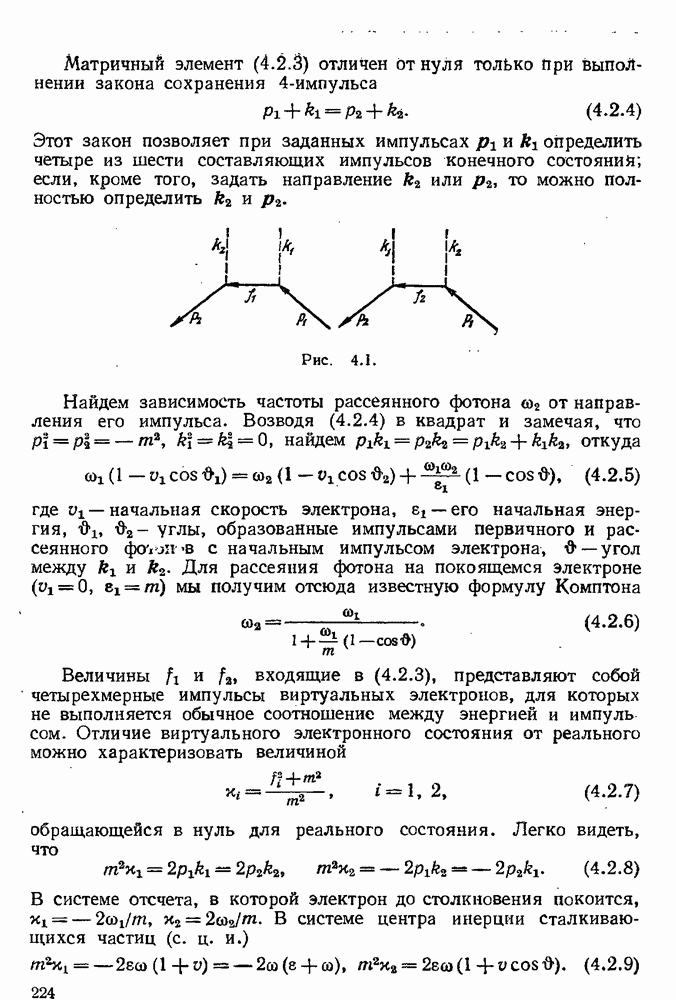
Рис. 5.18.

Так как то существенными являются малые поэтому в числителе подынтегрального выражения (5.7.2) можно пренебречь членами, содержащими k. Учитывая, что находится в окружении функций ведущих себя при как

легко убедиться, что числитель подынтегрального выражения (5.7.2) можно заменить на , т. е. в интересующем нас случае (5.7.1) величину можно представить в виде

Точные значения пределов здесь несущественны, и мы можем их взять равными —1 и +1 при интегрировании по и равными 0 и +1 при интегрировании по .

Выполним сначала интегрирование по . Используя формулу

    (5.7.7)

имеем

Подставляя далее это выражение в (6.7.6) и опуская член с логарифмом, получим

Таким образом, мы видим, что при вершинная функция содержит дважды логарифмическое слагаемое, пропорциональное произведению а и двух больших логарифмов. Это слагаемое, являющееся главным членом в возникает, как мы видим, при интегрировании по двум переменным х и у. Логарифмическое же слагаемое, возникающее при интегрировании по третьей переменной , не вносит вклада в главный член, который связан только с мнимой частью интеграла по .

Прежде чем переходить к вычислению следующих радиационных поправок к вершинной функции, убедимся, что если невелико по сравнению с , то радиационная поправка к вершинной функции не будет содержать дважды логарифмических членов. Рассмотрим, например, в предположении, что

В этом случае, в отличие от случая (6.7.1), в знаменатель подынтегрального выражения (5.7.2) будет входить 4-вектор с большим квадратом, благодаря чему непосредственно нельзя использовать примененную нами только что методику вычисления интеграла (5.7.2). Однако можно добиться того, чтобы в знаменатель входили векторы с малым квадратом, если предварительно произвести замену переменных интегрирования после которой интеграл (5.7.2) примет вид

где . Применяя теперь преобразование (5.7.3) с вектором — q вместо вектора легко убедиться, что главный вклад в интеграл (5.7.10) вносит область интегрирования в которой интеграл (5.7.10) принимает вид

В этом выражении, в отличие от выражения для в случае (5.7.1), нельзя пренебрегать в числителе под знаком интеграла членами, содержащими , так как они умножаются на малые величины и q. Благодаря этому интеграл (5.7.11) не будет содержать дважды логарифмических членов.

Легко убедиться, что регуляризованное значение в рассматриваемом случае равно

    (5.7.12)

Это выражение содержит, как мы видим, только однологарифмические члены.

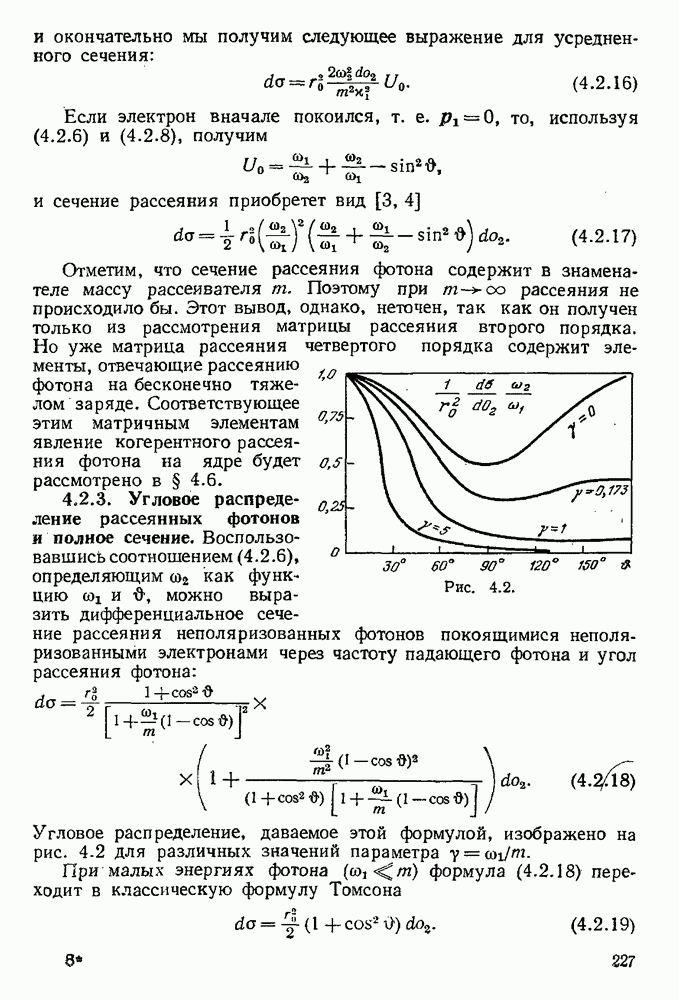
Рис. 5.19.

Таким образом, действительно, вершинная функция при будет содержать дважды логарифмические члены только в том случае, если . Далее мы увидим, что дважды логарифмические члены возникают и при если выполняется условие . Этот случай будет играть особенно важную роль в дальнейшем, так как именно он соответствует рассеянию с большим переданным импульсом.

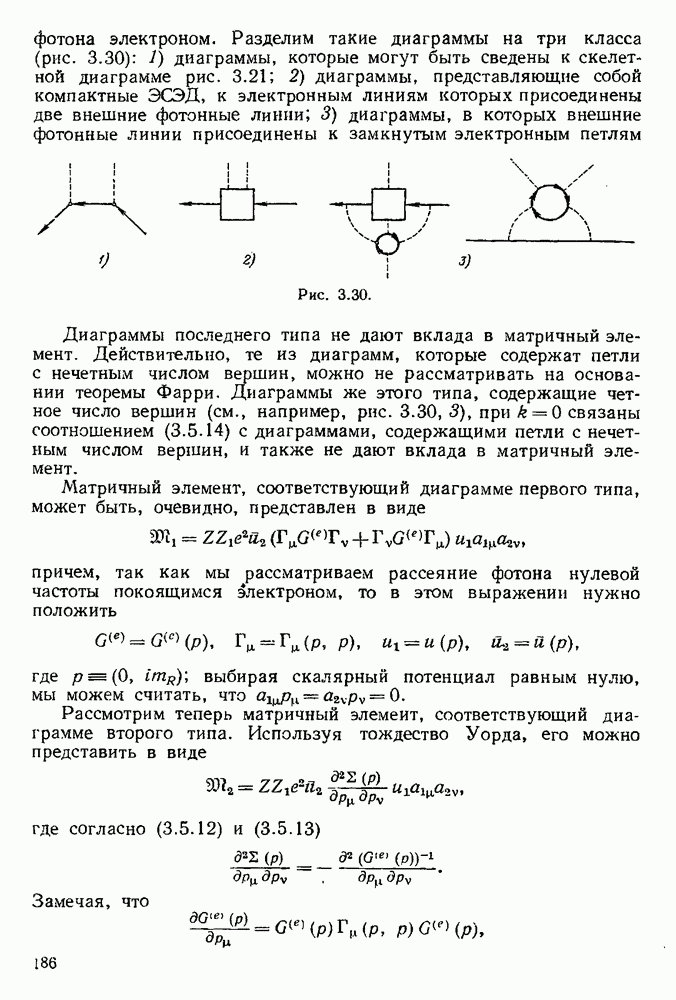
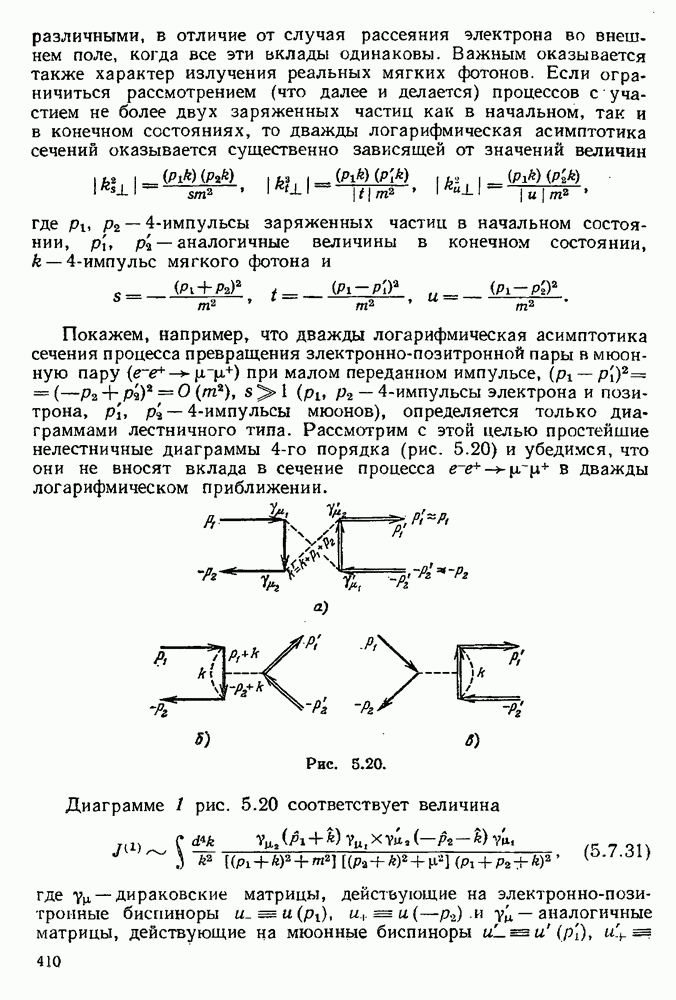
Вернемся теперь к определению следующих радиационных поправок к вершинной функции в случае (5.7.1). Выясним прежде всего, какие диаграммы приводят к дважды логарифмическим членам. Легко видеть, что замкнутые электронные линии не приводят

к дважды логарифмическим членам: для таких диаграмм степени больших логарифмов оказываются всегда меньшими, чем степень квадрата заряда. Рассмотрим, например, диаграмму рис. 5.19. Внутренней электронной петле соответствует, согласно (5.1.16), функция

откуда с логарифмической точностью

Поэтому всей диаграмме I в целом будет соответствовать величина

Переходя к переменным , согласно (5.7.3), и делая необходимые пренебрежения, получим

    (5.7.13)

где . Мы видим, как и утверждалось выше, что эта величина содержит большой логарифм в третьей степени, а заряд — в четвертой.

Таким образом, мы должны рассматривать только диаграммы с внутренними фотонными линиями. Однако и они не все будут приводить к дважды логарифмическим членам. Легко видеть, что только те из диаграмм, в которых все линии виртуальных фотонов охватывают точку испускания внешнего фотона, приводят к дважды логарифмическим членам. Рассмотрим, например, диаграммы 2 и 3

на рис. 5.19. Используя вытекающую из (5.1.12) формулу для массового оператора

справедливую при и аналогичную формулу для вершинной функции

справедливую при получим следующие выражения для величин, соответствующих диаграммам 2 и 3:

Поступая так же, как и при выводе формулы (5.7.13), получим

    (5.7.14)

Эти величины, как мы видим, не содержат дважды логарифмических членов.

Перейдем теперь к рассмотрению диаграмм, содержащих только внутренние фотонные линии, охватывающие точку испускания внешнего фотона. В приближении содержится, очевидно, таких диаграмм, которые отличаются друг от друга только - перестановкой концов виртуальных фотонных линий (см. диаграммы рис. 5.18). Вклад, вносимый этими диаграммами в вершинную функцию, будет равен, очевидно,

где обозначает суммирование по всем перестановкам то фотонные линии не пересекаются; диаграмма в этом случае называется лестничной.)

Предполагая выполненными условия (5.7.1), можно в числителе подынтегрального выражения (5.7.15) пренебречь величинами по сравнению с и заменить числитель на

Для вычисления этого интеграла перейдем вместо к новым переменным интегрирования согласно (5.7.3),

Вспоминая, что при интегрировании по должна быть взята в соответствии с (5.7.7) только мнимая часть интеграла, мы получим следующее выражение для

Главный вклад во входящие сюда интегралы вносит область интегрирования

Каждый из интегралов равен, как легко видеть,

Поэтому для мы получим выражение

    (5.7.16)

Обратим внимание на то обстоятельство, что все диаграммы, отличающиеся лишь перестановкой концов виртуальных фотонных линий, вносят одинаковый вклад в Суммируя выражение (5.7.16) по , найдем вершинную функцию

и случае

    (5.7.17)

Эта важная формула [29] справедлива при выполнении следующих условий:

    (5.7.18)

где