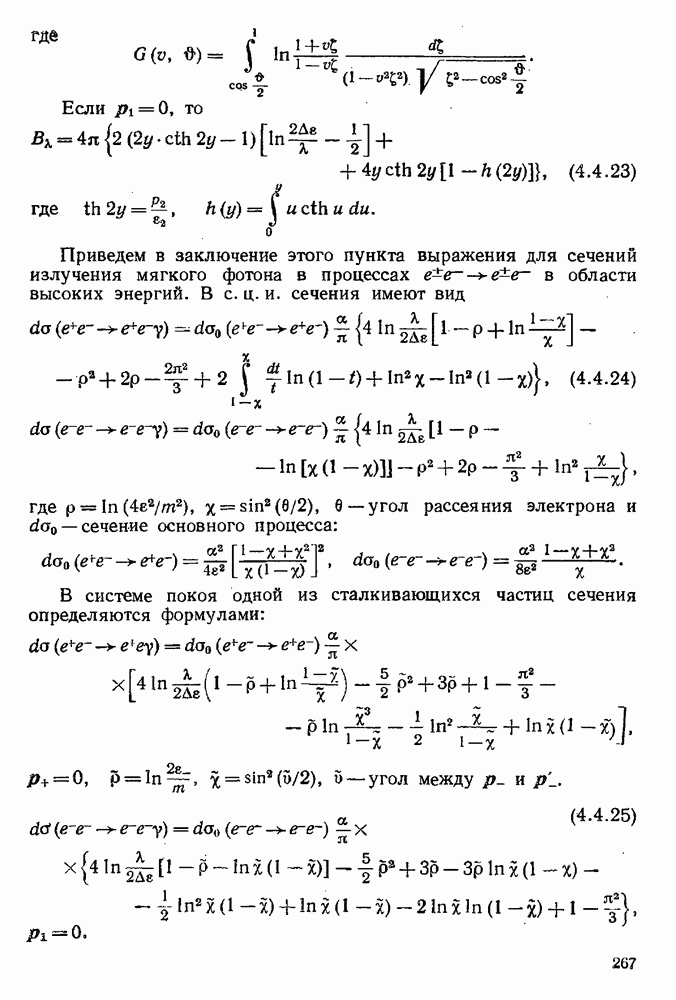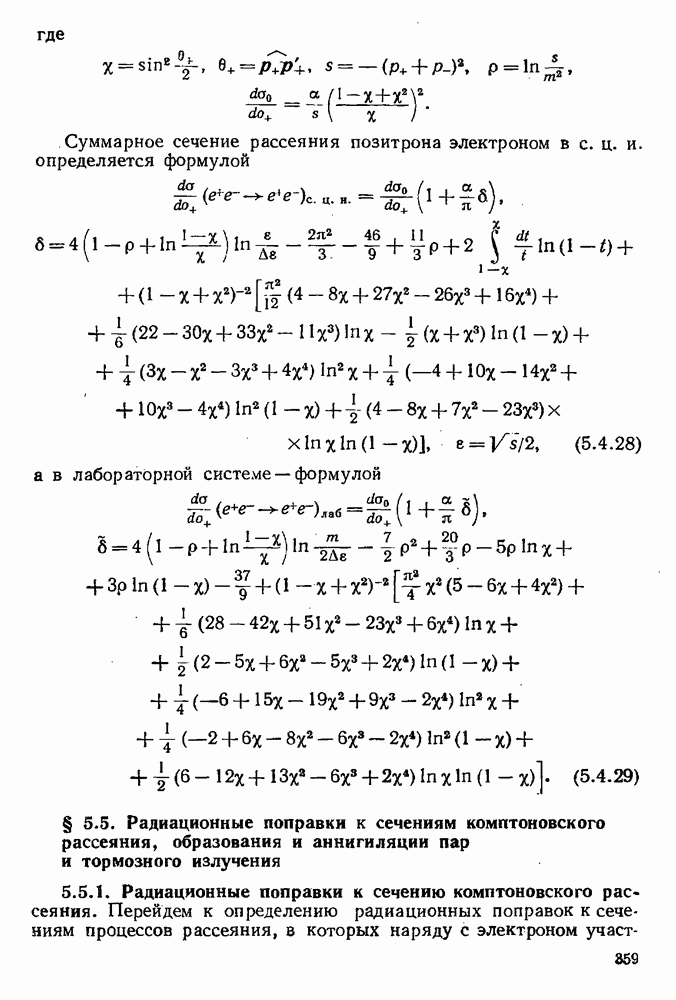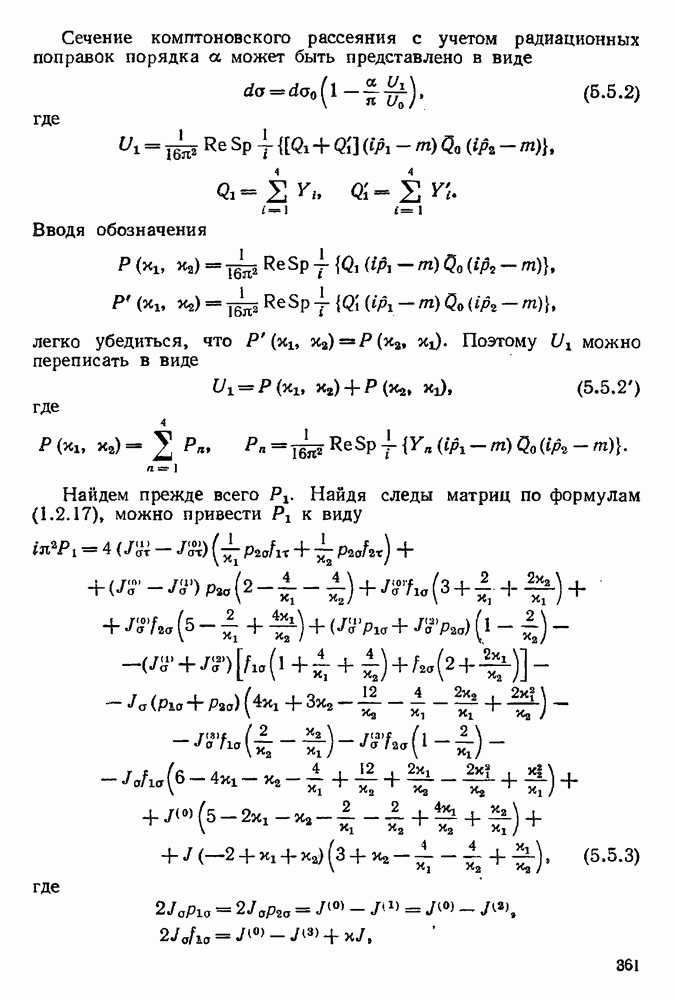| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.2.8. Использование обозначений, соответствующих псевдоевклидовой метрике.
Наряду с принятыми нами обозначениями, соответствующими евклидовой метрике 4-пространства (с мнимой четвертой компонентой 4-векторов), часто используются также обозначения, соответствующие псевдоевклидовой метрике с вещественной четвертой компонентой 4-векторов [10,11]. При этом скалярное произведение двух 4-векторов а и b определяется не как

а как

где 
При таком определении скалярного произведения удобно вместо матриц  применять другие матрицы,
применять другие матрицы,
которые мы будем обозначать через  и которые связаны с матрицами
и которые связаны с матрицами  соотношениями
соотношениями

Ясно, что матрица  эрмитова, а матрицы
эрмитова, а матрицы  антиэрмитовы:
антиэрмитовы:

Матрицы 7 удовлетворяют, очевидно, соотношениям
 (1.2.41)
(1.2.41)
По аналогии с величиной

теперь вводится величина
 (1.2.42)
(1.2.42)
Используя (1.2.41), легко убедиться, что
 (1.2.43)
(1.2.43)
Уравнения Дирака в новых обозначениях имеют вид
 (1.2.44)
(1.2.44)
где

Легко видеть, что матрица зарядового сопряжения С связана с матрицами  такими же соотношениями, как и с матрицами
такими же соотношениями, как и с матрицами 

Прежний вид имеют определение 4-вектора плотности тока

а также определения других билинейных форм; в них нужно лишь заменить на  на
на

При вычислении вероятностей процессов с участием поляризованных электронов нужно в формулах (1.1.40) и (1.1.47) произвести замену

Матрица плотности электрона, определяемая формулой (1.1.40), в новых обозначениях имеет вид

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА ЭЛЕКТРОНА
- 1.1.2. Симметричная форма уравнения Дирака.
- 1.1.3. Решения с положительными и отрицательными частотами.
- 1.1.4. Плоские волны.
- 1.1.5. Поляризационные состояния электрона.
- 1.1.6. Поляризационная матрица плотности электрона.
- 1.1.7. Поляризационные состояния электрона в ультрарелятизистском пределе.
- § 1.2. Уравнение Дирака для электрона в электромагнитном поле и свойства инвариантности уравнения Дирака
- 1.2.1. Уравнение Дирака для электрона во внешнем электромагнитном поле.
- 1.2.2. Уравнение непрерывности.
- 1.2.3. Различные представления уравнения Дирака.
- 1.2.4. Алгебра матриц Дирака.
- 1.2.5. Релятивистская инвариантность уравнения Дирака.
- 1.2.6. Пространственное отражение, обращение времени и зарядовое сопряжение.
- 1.2.7. Ковариантные билинейные формы.
- 1.2.8. Использование обозначений, соответствующих псевдоевклидовой метрике.
- § 1.3. Предельные переходы к нерелятивистской квантовой механике и релятивистской классической механике
- 1.3.2. Второе приближение.
- 1.3.3. Переход к релятивистской классической механике.
- 1.3.4. Высокоэнергетическое приближение.
- 1.3.5. Борновское приближение.
- § 1.4. Момент импульса электрона
- 1.4.2. Волновая функция свободного электрона с определенным моментом.
- 1.4.3. Четность состояния.
- 1.4.4. Разложение по сферическим волнам.
- § 1.5. Движение электрона в центральном поле
- 1.5.2. Сферически-симметричная потенциальная яма.
- 1.5.3. Движение электрона в кулоновском поле ядра.
- 1.5.4. Волновые функции непрерывного спектра в кулоновском поле ядра.
- 1.5.5. Критический заряд ядра.
- § 1.6. Движение в однородных полях
- 1.6.2. Электрон в постоянном и однородном магнитном поле.
- 1.6.3. Электрон в постоянном и однородном электрическом поле.
- 1.6.4. Парадокс Клейна.
- § 1.7. Рассеяние электронов
- 1.7.2. Амплитуда и сечение рассеяния.
- 1.7.3. Поляризация и азимутальная асимметрия.
- 1.7.4. Упругое рассеяние в борцовском приближении.
- 1.7.5. Упругое рассеяние в эйкональном приближении.
- 1.7.6. Рассеяние в кулоновском поле ядра.
- ГЛАВА 2. КВАНТОВАНИЕ ПОЛЕЙ
- § 2.1. Квантовая механика фотона
- 2.1.2. Волновая функция фотона.
- 2.1.3. Плоские волны.
- § 2.2. Момент импульса фотона
- 2.2.2. Собственные функции оператора момента фотона.
- 2.2.3. Продольный и поперечные шаровые векторы.
- 2.2.4. Четность состоянии фотона.
- 2.2.5. Сферические электромагнитные волны.
- § 2.3. Квантование электромагнитного поля
- 2.3.2. Перестановочные соотношения для потенциалов электромагнитного поля.
- 2.3.3. Хронологическое и нормальное произведения операторов электромагнитных потенциалов.
- § 2.4. Корреляционные функции электромагнитного поля
- 2.4.2. Когерентные состояния.
- 2.4.3. Корреляционные функции и когерентность высших порядков.
- 2.4.4. Поляризационная матрица плотности.
- § 2.5. Квантование электронно-позитронного поля
- 2.5.2. Операторы испускания и поглощения электронов и позитронов.
- 2.5.3. Антикоммутаторы электронного поля.
- 2.5.4. Хронологическое и нормальное произведения операторов электронного поля.
- ГЛАВА 3. ЭЛЕКТРОМАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ
- § 3.1. Основные уравнения квантовой электродинамики
- 3.1.2. Лагранжиан и гамильтониан взаимодействующих полей.
- 3.1.3. Представление взаимодействия.
- § 3.2. Матрица рассеяния
- 3.2.2. Инвариантная теория возмущений.
- 3.2.3. Представление матрицы рассеяния в виде суммы нормальных произведений.
- 3.2.4. Функциональная форма представления матрицы рассеяния в виде N-упорядоченного оператора.
- § 3.3. Графическое представление элементов матрицы рассеяния
- 3.3.2. Импульсное представление.
- 3.3.3. Правила Фейнмана.
- § 3.4. Вероятность и эффективное сечение
- 3.4.2. Суммирование по состояниям поляризации электронов и фотонов.
- 3.4.3. Эффективное сечение.
- 3.4.4. Вероятность процессов рассеяния поляризованных частиц.
- § 3.5. Структура диаграмм матрицы рассеяния
- 3.5.2. Эффективные линии.
- 3.5.3. Уравнения Дайсона для функций Грина и графическое уравнение для вершинной функции.
- 3.5.4. Функции Грина как вакуумные средние.
- § 3.6. Перенормировка массы и заряда электрона
- 3.6.2. Физический заряд электрона.
- 3.6.3. Перенормировка функций Грина и вершинной функции.
- 3.6.4. Перенормировка элементов матрицы рассеяния.
- § 3.7. Расходимости в матрице рассеяния и их устранение
- 3.7.2. Введение граничного импульса.
- 3.7.3. Регуляризация функций, соответствующих неприводимым диаграммам.
- 3.7.4. Регуляризация функций, соответствующих приводимым диаграммам.
- § 3.8. Асимптотические свойства функций Грина
- 3.8.2. Асимптотические выражения для функций Грина.
- 3.8.3. Асимптотический характер регулярнзованных разложений матрицы рассеяния и проблема замкнутости квантовой электродинамики.
- ГЛАВА 4. ОСНОВНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ЯВЛЕНИЯ
- § 4.1. Излучение фотона
- 4.1.2. Излучение электрического и магнитного мультиполей.
- 4.1.3. Излучение ядер. Правила отбора.
- 4.1.4. Фотоэффект.
- § 4.2. Рассеяние фотона электроном
- 4.2.2. Дифференциальное сечение рассеяния неполяризованных частиц.
- 4.2.3. Угловое распределение рассеянных фотонов и полное сечение.
- 4.2.4. Поляризационные эффекты.
- 4.2.5. Рассеяние поляризованных фотонов неполяризованными электронами.
- 4.2.6. Дисперсионная формула.
- § 4.3. Тормозное излучение
- 4.3.2. Тормозное излучение в высокоэнергетическом приближении.
- 4.3.3. Сечение тормозного излучения в кулоновском поле ядра в борновском приближении.
- 4.3.4. Экранирование.
- 4.3.5. Потеря энергии на излучение.
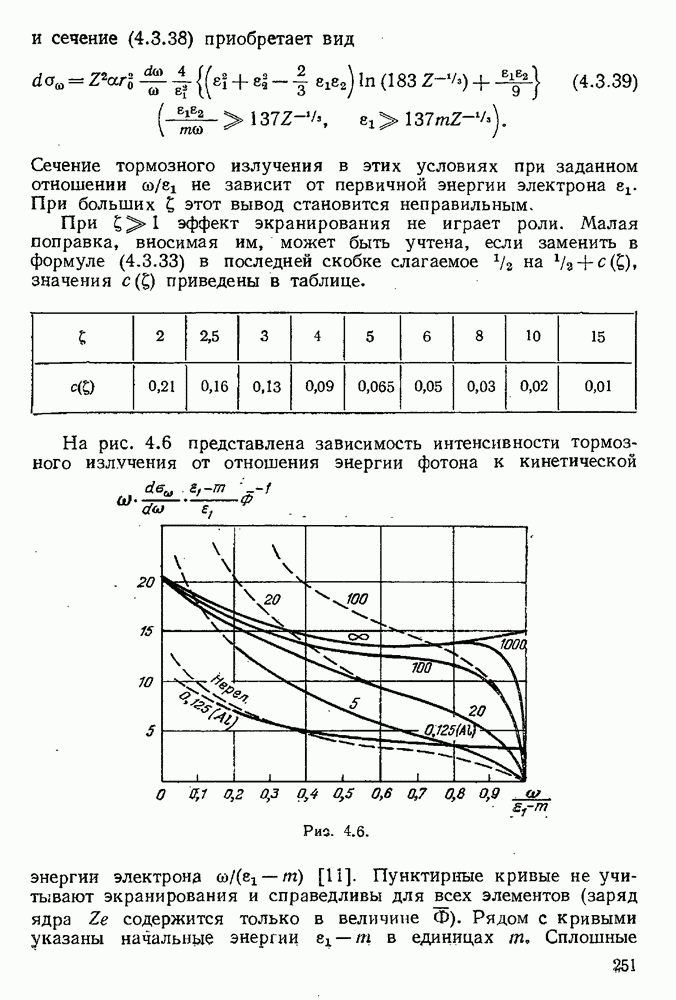
- 4.3.6. Тормозное излучение в кулоновском поле ядра в высокоэнергетическом приближении.
- 4.3.7. Точная теория тормозного излучения в нерелятивистской области.
- § 4.4. Излучение длинноволновых фотонов
- 4.4.2. Сечение рассеяния электрона с излучением мягкого фотона.
- 4.4.3. Исследование расходимости в области малых частот.
- 4.4.4. Излучение мягких фотонов при произвольных столкновениях.
- § 4.5. Образование и аннигиляция электронно-позитронных пар
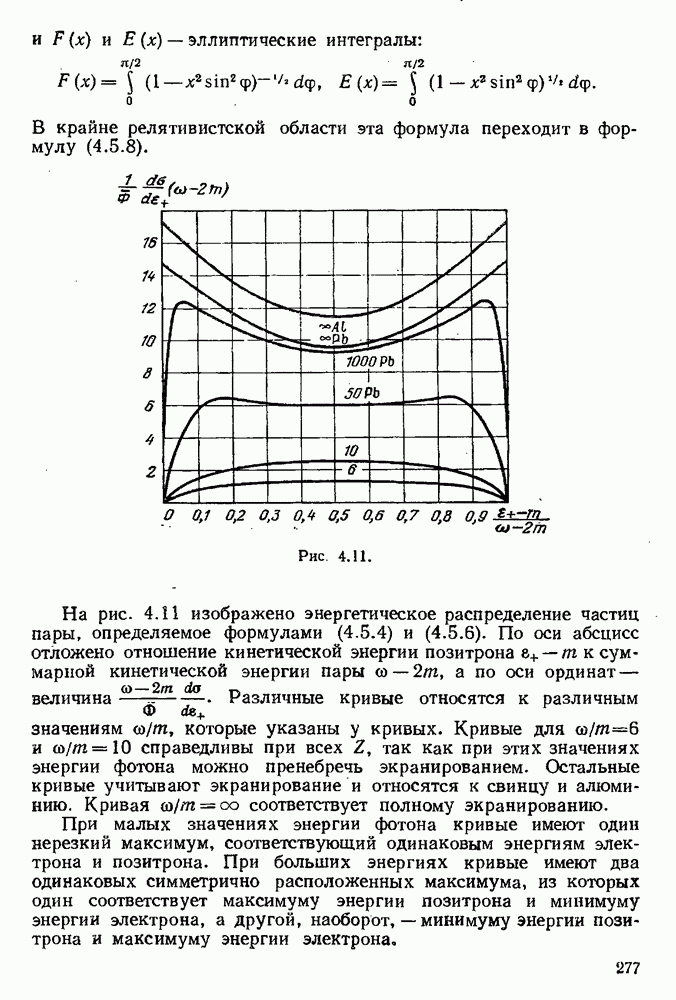
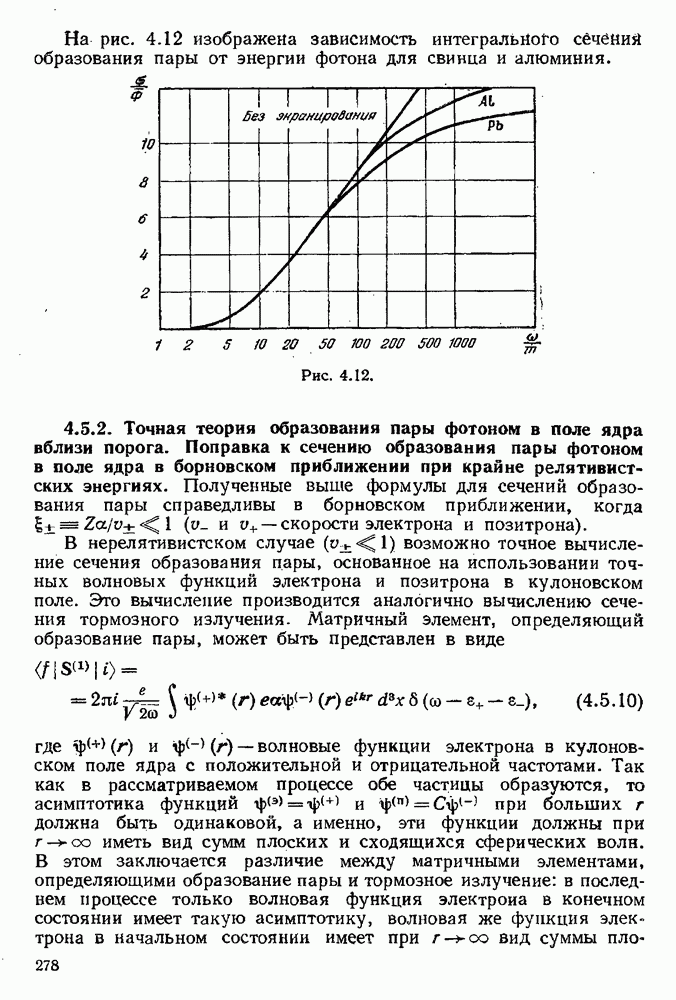
- 4.5.2. Точная теория образования пары фотоном в поле ядра вблизи порога.
- 4.5.3. Образование пары двзмя фотонами.
- 4.5.4. Аннигиляция пары в два и три фотона.
- 4.5.5. Поляризационные эффекты при двухфотонной аннигиляции пар.
- 4.5.6. Распад позитрония.
- 4.5.7. Превращение пары в один фотон.
- § 4.6. Рассеяние электрона и позитрона электроном
- 4.6.2. Сечение рассеяния позитрона электроном.
- 4.6.3. Рассеяние поляризованных электронов.
- 4.6.4. Рассеяние мюона электроном.
- 4.6.5. Излучение фотона при рассеянии электрона электроном и электрона позитроном и при превращении …
- § 4.7. Запаздывающее взаимодействие зарядов
- 4.7.3. Взаимодействие электрона с позитроном и позитроний.
- § 4.8. Метод эквивалентных фотонов
- 4.8.2. Тормозное излучение в процессах рассеяния электрона ядром и электрона электроном.
- 4.8.3. Образование пар фотоном в поле ядра и при столкно вении двух быстрых заряженных частиц.
- 4.8.4. Сечение двуструйного процесса.
- ГЛАВА 5. КВАНТОВОЭЛЕКТРОДИНАМИЧЕСКИЕ ЭФФЕКТЫ В ВЫСШИХ ПРИБЛИЖЕНИЯХ ТЕОРИИ ВОЗМУЩЕНИЙ
- § 5.1. Радиационные поправки к электродинамическим функциям Грина
- 5.1.2. Поляризационный оператор второго порядка.
- 5.1.3. Вершинная функция третьего порядка.
- § 5.2. Модификация закона Кулона. Аномальный магнитный момент электрона
- 5.2.2. Аномальный магнитный момент электрона и мюона.
- § 5.3. Радиационное смещение атомных уровней
- 5.3.2. Радиационное смещение и естественная ширина атомных уровней.
- 5.3.3. Радиационное смещение уровней атома водорода.
- 5.3.4. Рассеяние фотона вблизи резонанса.
- § 5.4. Радиационные поправки к сечениям рассеяния электрона во внешнем поле и рассеяния электрона электроном
- 5.4.2. Исключение «массы» фотона из сечения рассеяния.
- 5.4.3. Устранение инфракрасной расходимости в случае произвольного процесса рассеяния.
- 5.4.4. Радиационные поправки к сечению рассеяния электрона электроном и электрона позитроном.
- § 5.5. Радиационные поправки к сечениям комптоновского рассеяния, образования и аннигиляции пар и тормозного излучения
- 5.5.1. Радиационные поправки к сечению комптоновского рассеяния.
- 5.5.2. Рассеяние электроном фотонов малой частоты.
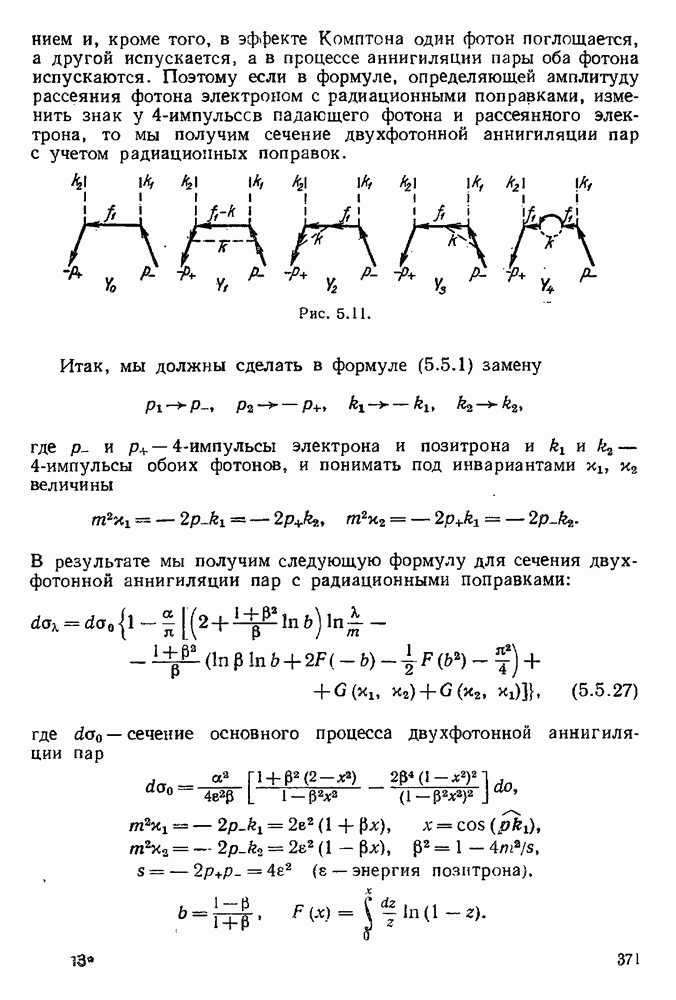
- 5.5.3. Радиационные поправки к сечению двухфотонной аннигиляции пар.
- 5.5.4. Радиационные поправки к сечению тормозного излучения.
- 5.5.4. Радиационные поправки к сечению тормозного излучения.
- 5.5.5. Радиационные поправки к сечению превращения электронно-позитронной пары в мюонную пару.
- § 5.6. Нелинейная электродинамика вакуума
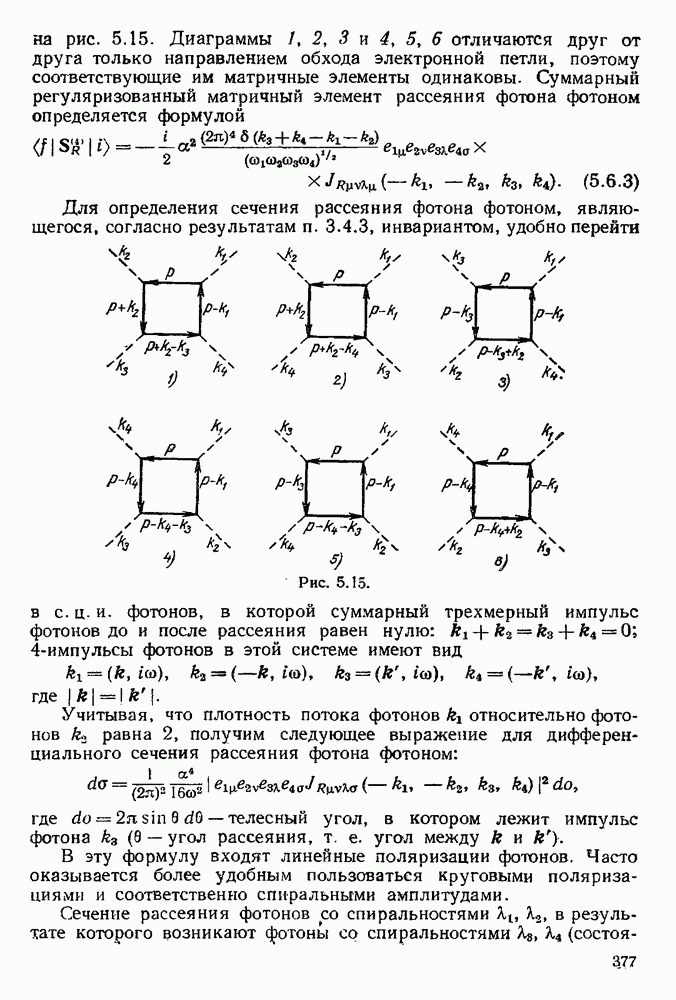
- 5.6.1. Тензор рассеяния фотона фотоном четвертого ранга.
- 5.6.2. Сечение рассеяния фотона фотоном.
- 5.6.3. Радиационные поправки к функции Лагранжа электромагнитного поля в вакууме.
- 5.6.4. Точное выражение для лагранжиана произвольного медленно меняющегося электромагнитного поля.
- 5.6.5. Сечение рассеяния фэтэна в постоянном электромагнитном поле.
- 5.6.6. Связь между амплитудой рассеяния фотона на нулевой угол и сечением образования пар.
- 5.6.7. Импульсное и угловое распределения ядер отдачи при образовании пар фотоном в поле ядра.
- § 5.7. Дважды логарифмическая асимптотика сечений квантовоэлектродинамических процессов
- 5.7.2. Дважды логарифмическая асимптотика сечения рассеяния электрона во внешнем поле.
- 5.7.3. Дважды логарифмическая асимптотика сечения процесса …
- 5.7.4. Сводка формул для сечений квантовоэлектродинамических процессов в дважды логарифмическом приближении.
- ПРИЛОЖЕНИЕ
- А.1. Вычисление интегралов по инвариантному объему в 4-импульсном пространстве.
- A.2. Метод размерной регуляризации.
- ЛИТЕРАТУРА