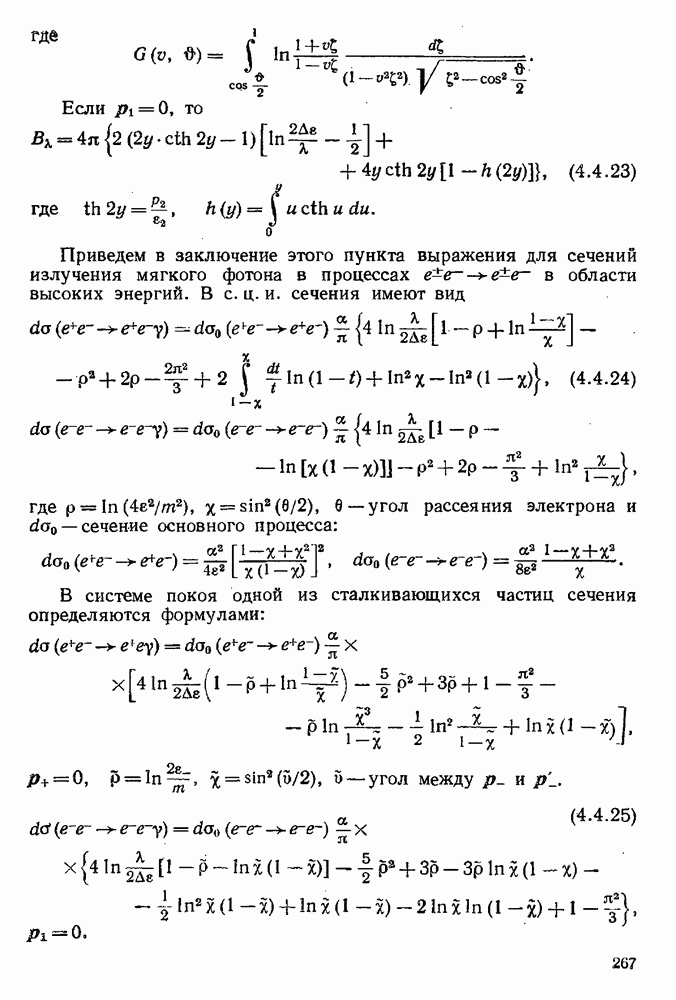| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3.2.4. Функциональная форма представления матрицы рассеяния в виде N-упорядоченного оператора.
Покажем, что не только отдельные члены разложения матрицы рассеяния, но и вся она в целом может быть представлена в виде  -упорядоченного оператора [5]. Рассмотрим прежде всего функционал от операторов электромагнитного поля
-упорядоченного оператора [5]. Рассмотрим прежде всего функционал от операторов электромагнитного поля
 (3.2.20)
(3.2.20)
где  — некоторые с-функции от
— некоторые с-функции от  и суммирование производится, помимо
и суммирование производится, помимо  , также по всем
, также по всем  пробегающим значения
пробегающим значения  ; тогда нетрудно убедиться, что
; тогда нетрудно убедиться, что
 (3.2.21)
(3.2.21)
где

Формула, аналогичная (3.2.21), справедлива и для электронно-позитронных операторов, а именно если  — функционал от операторов
— функционал от операторов  вида
вида

где суммирование производится, помимо  и по спинорным индексам, от которых зависит
и по спинорным индексам, от которых зависит  , то
, то
 (3.2.22)
(3.2.22)
где

Из (3.2.21) и (3.2.22) следует, что если мы имеем общий функционал  операторов
операторов  то
то
 (3.2.23)
(3.2.23)
Полагая

и вспоминая, что

( и
и  обозначают
обозначают  -упорядочения операторов
-упорядочения операторов  ), получим следующее общее выражение для матрицы рассеяния в виде
), получим следующее общее выражение для матрицы рассеяния в виде  -упорядоченного оператора:
-упорядоченного оператора:
 (3.2.24)
(3.2.24)
Используя соотношение

( обозначает
обозначает  -упорядочение операторов
-упорядочение операторов  ) и замечая, что
) и замечая, что

легко убедиться, что

Поэтому

Отсюда следует:
 (3.2.25)
(3.2.25)
Для процессов без участия фотонов последний множитель в (3.2.25) равен единице, и матрица рассеяния приобретает вид

Если движение электронов можно считать заданным, то плотность тока можно рассматривать как заданную с-функцию 
Из (3.2.25) следует, что в таком приближении матрица рассеяния приобретает вид

где операторами являются только электромагнитные потенциалы  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА ЭЛЕКТРОНА
- 1.1.2. Симметричная форма уравнения Дирака.
- 1.1.3. Решения с положительными и отрицательными частотами.
- 1.1.4. Плоские волны.
- 1.1.5. Поляризационные состояния электрона.
- 1.1.6. Поляризационная матрица плотности электрона.
- 1.1.7. Поляризационные состояния электрона в ультрарелятизистском пределе.
- § 1.2. Уравнение Дирака для электрона в электромагнитном поле и свойства инвариантности уравнения Дирака
- 1.2.1. Уравнение Дирака для электрона во внешнем электромагнитном поле.
- 1.2.2. Уравнение непрерывности.
- 1.2.3. Различные представления уравнения Дирака.
- 1.2.4. Алгебра матриц Дирака.
- 1.2.5. Релятивистская инвариантность уравнения Дирака.
- 1.2.6. Пространственное отражение, обращение времени и зарядовое сопряжение.
- 1.2.7. Ковариантные билинейные формы.
- 1.2.8. Использование обозначений, соответствующих псевдоевклидовой метрике.
- § 1.3. Предельные переходы к нерелятивистской квантовой механике и релятивистской классической механике
- 1.3.2. Второе приближение.
- 1.3.3. Переход к релятивистской классической механике.
- 1.3.4. Высокоэнергетическое приближение.
- 1.3.5. Борновское приближение.
- § 1.4. Момент импульса электрона
- 1.4.2. Волновая функция свободного электрона с определенным моментом.
- 1.4.3. Четность состояния.
- 1.4.4. Разложение по сферическим волнам.
- § 1.5. Движение электрона в центральном поле
- 1.5.2. Сферически-симметричная потенциальная яма.
- 1.5.3. Движение электрона в кулоновском поле ядра.
- 1.5.4. Волновые функции непрерывного спектра в кулоновском поле ядра.
- 1.5.5. Критический заряд ядра.
- § 1.6. Движение в однородных полях
- 1.6.2. Электрон в постоянном и однородном магнитном поле.
- 1.6.3. Электрон в постоянном и однородном электрическом поле.
- 1.6.4. Парадокс Клейна.
- § 1.7. Рассеяние электронов
- 1.7.2. Амплитуда и сечение рассеяния.
- 1.7.3. Поляризация и азимутальная асимметрия.
- 1.7.4. Упругое рассеяние в борцовском приближении.
- 1.7.5. Упругое рассеяние в эйкональном приближении.
- 1.7.6. Рассеяние в кулоновском поле ядра.
- ГЛАВА 2. КВАНТОВАНИЕ ПОЛЕЙ
- § 2.1. Квантовая механика фотона
- 2.1.2. Волновая функция фотона.
- 2.1.3. Плоские волны.
- § 2.2. Момент импульса фотона
- 2.2.2. Собственные функции оператора момента фотона.
- 2.2.3. Продольный и поперечные шаровые векторы.
- 2.2.4. Четность состоянии фотона.
- 2.2.5. Сферические электромагнитные волны.
- § 2.3. Квантование электромагнитного поля
- 2.3.2. Перестановочные соотношения для потенциалов электромагнитного поля.
- 2.3.3. Хронологическое и нормальное произведения операторов электромагнитных потенциалов.
- § 2.4. Корреляционные функции электромагнитного поля
- 2.4.2. Когерентные состояния.
- 2.4.3. Корреляционные функции и когерентность высших порядков.
- 2.4.4. Поляризационная матрица плотности.
- § 2.5. Квантование электронно-позитронного поля
- 2.5.2. Операторы испускания и поглощения электронов и позитронов.
- 2.5.3. Антикоммутаторы электронного поля.
- 2.5.4. Хронологическое и нормальное произведения операторов электронного поля.
- ГЛАВА 3. ЭЛЕКТРОМАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ
- § 3.1. Основные уравнения квантовой электродинамики
- 3.1.2. Лагранжиан и гамильтониан взаимодействующих полей.
- 3.1.3. Представление взаимодействия.
- § 3.2. Матрица рассеяния
- 3.2.2. Инвариантная теория возмущений.
- 3.2.3. Представление матрицы рассеяния в виде суммы нормальных произведений.
- 3.2.4. Функциональная форма представления матрицы рассеяния в виде N-упорядоченного оператора.
- § 3.3. Графическое представление элементов матрицы рассеяния
- 3.3.2. Импульсное представление.
- 3.3.3. Правила Фейнмана.
- § 3.4. Вероятность и эффективное сечение
- 3.4.2. Суммирование по состояниям поляризации электронов и фотонов.
- 3.4.3. Эффективное сечение.
- 3.4.4. Вероятность процессов рассеяния поляризованных частиц.
- § 3.5. Структура диаграмм матрицы рассеяния
- 3.5.2. Эффективные линии.
- 3.5.3. Уравнения Дайсона для функций Грина и графическое уравнение для вершинной функции.
- 3.5.4. Функции Грина как вакуумные средние.
- § 3.6. Перенормировка массы и заряда электрона
- 3.6.2. Физический заряд электрона.
- 3.6.3. Перенормировка функций Грина и вершинной функции.
- 3.6.4. Перенормировка элементов матрицы рассеяния.
- § 3.7. Расходимости в матрице рассеяния и их устранение
- 3.7.2. Введение граничного импульса.
- 3.7.3. Регуляризация функций, соответствующих неприводимым диаграммам.
- 3.7.4. Регуляризация функций, соответствующих приводимым диаграммам.
- § 3.8. Асимптотические свойства функций Грина
- 3.8.2. Асимптотические выражения для функций Грина.
- 3.8.3. Асимптотический характер регулярнзованных разложений матрицы рассеяния и проблема замкнутости квантовой электродинамики.
- ГЛАВА 4. ОСНОВНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ЯВЛЕНИЯ
- § 4.1. Излучение фотона
- 4.1.2. Излучение электрического и магнитного мультиполей.
- 4.1.3. Излучение ядер. Правила отбора.
- 4.1.4. Фотоэффект.
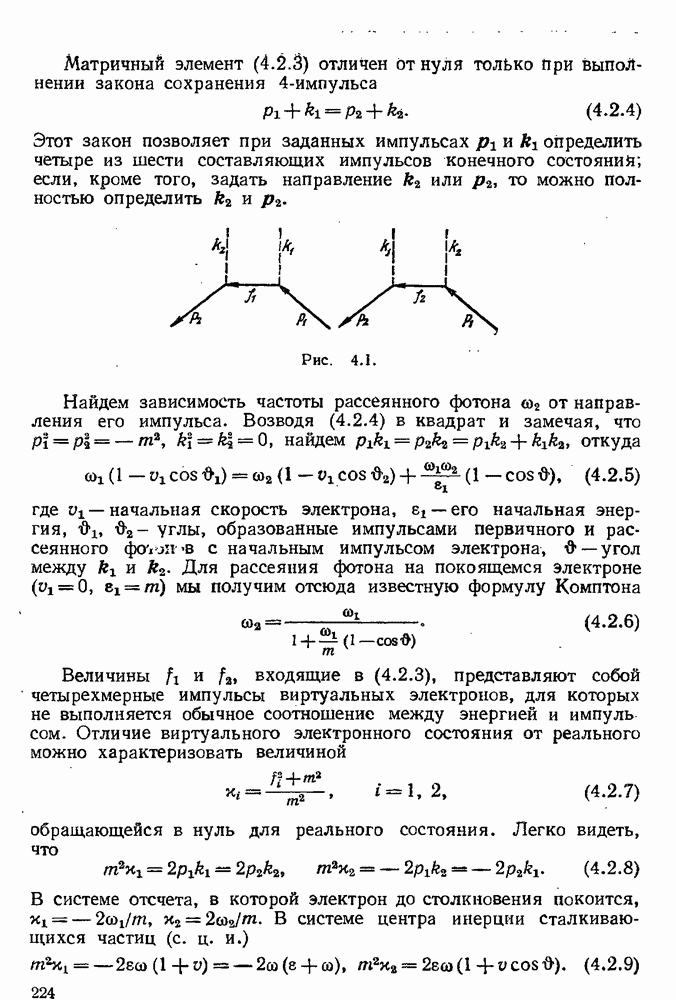
- § 4.2. Рассеяние фотона электроном
- 4.2.2. Дифференциальное сечение рассеяния неполяризованных частиц.
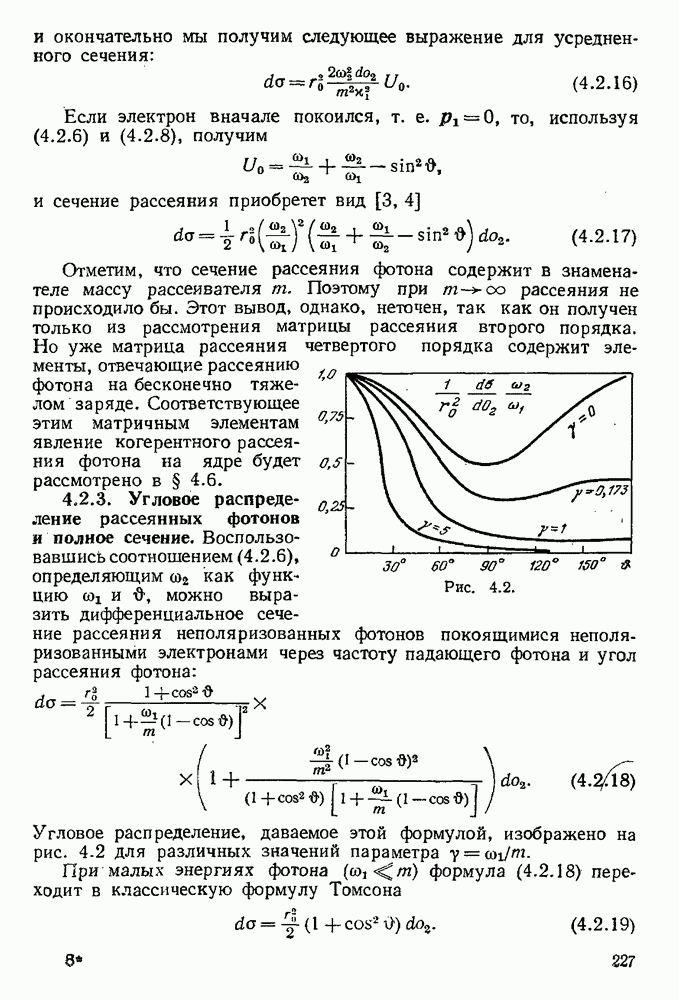
- 4.2.3. Угловое распределение рассеянных фотонов и полное сечение.
- 4.2.4. Поляризационные эффекты.
- 4.2.5. Рассеяние поляризованных фотонов неполяризованными электронами.
- 4.2.6. Дисперсионная формула.
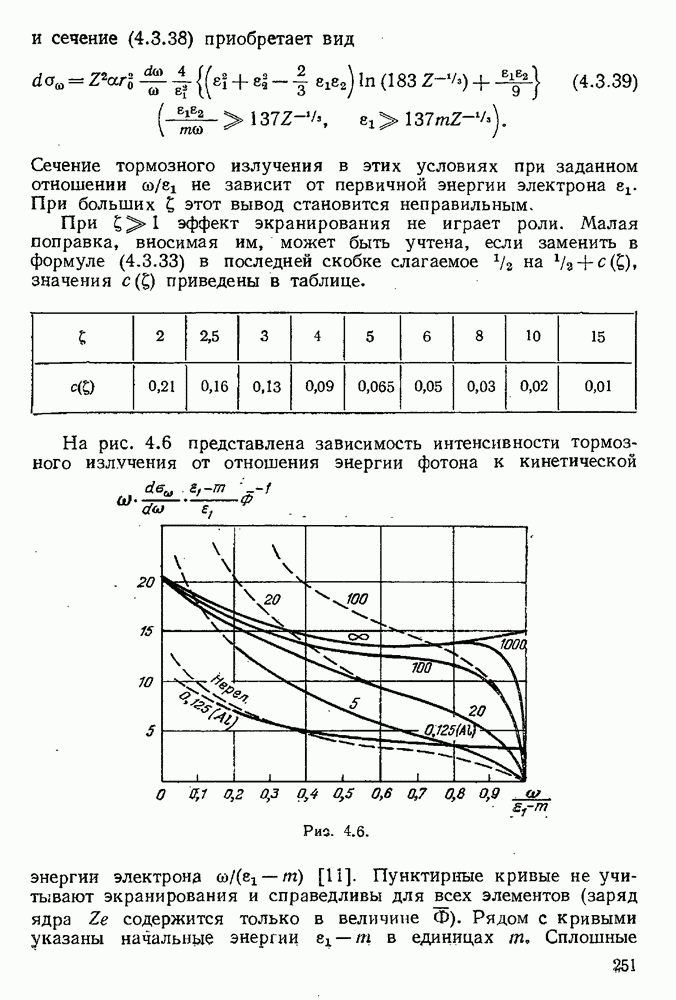
- § 4.3. Тормозное излучение
- 4.3.2. Тормозное излучение в высокоэнергетическом приближении.
- 4.3.3. Сечение тормозного излучения в кулоновском поле ядра в борновском приближении.
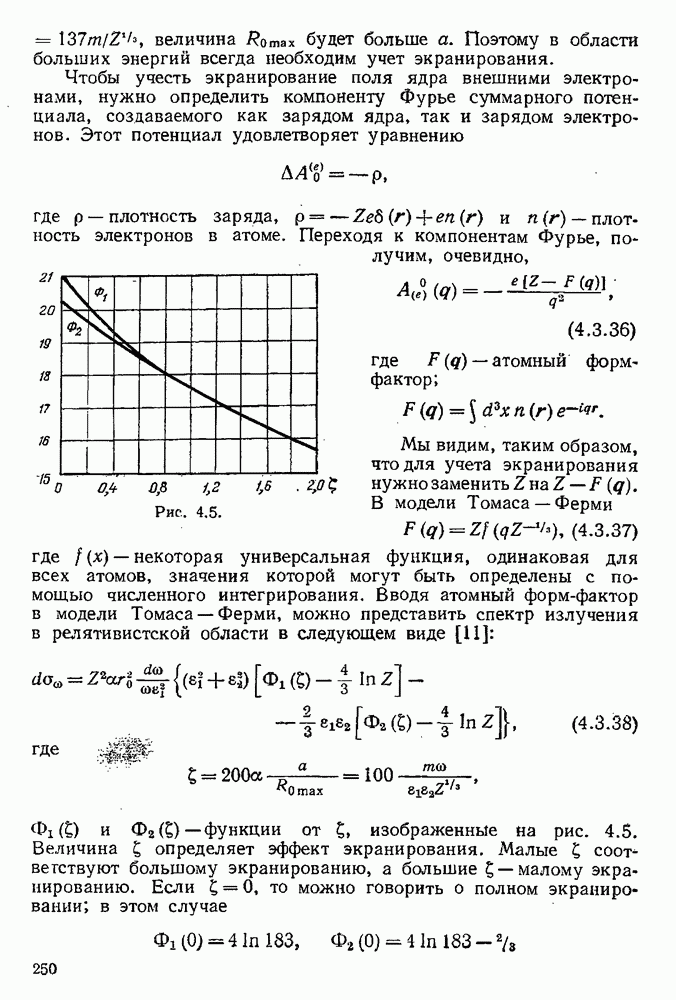
- 4.3.4. Экранирование.
- 4.3.5. Потеря энергии на излучение.
- 4.3.6. Тормозное излучение в кулоновском поле ядра в высокоэнергетическом приближении.
- 4.3.7. Точная теория тормозного излучения в нерелятивистской области.
- § 4.4. Излучение длинноволновых фотонов
- 4.4.2. Сечение рассеяния электрона с излучением мягкого фотона.
- 4.4.3. Исследование расходимости в области малых частот.
- 4.4.4. Излучение мягких фотонов при произвольных столкновениях.
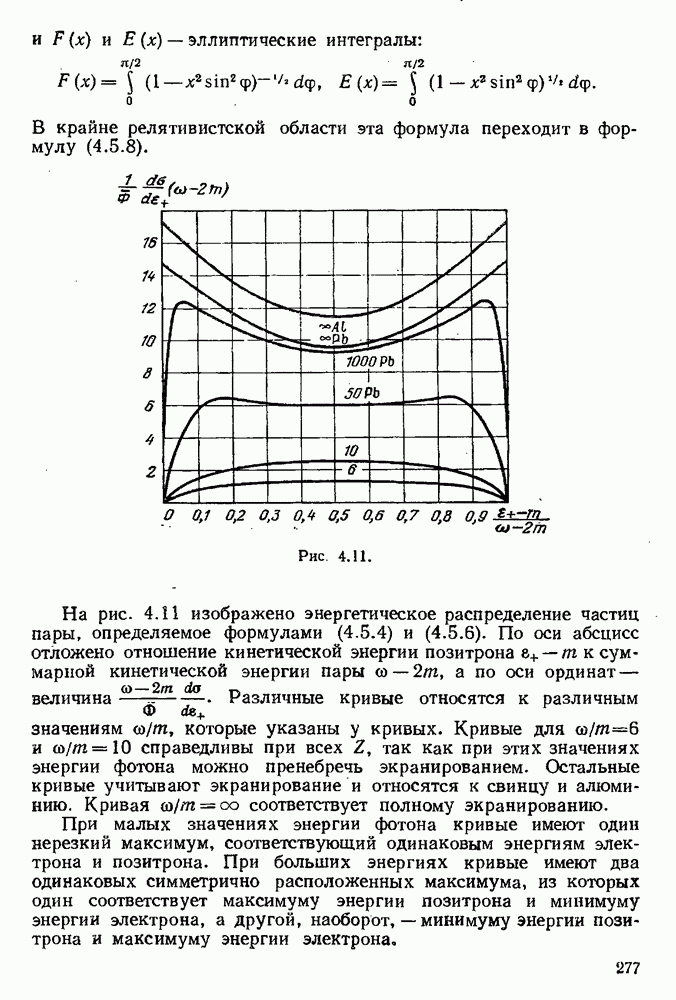
- § 4.5. Образование и аннигиляция электронно-позитронных пар
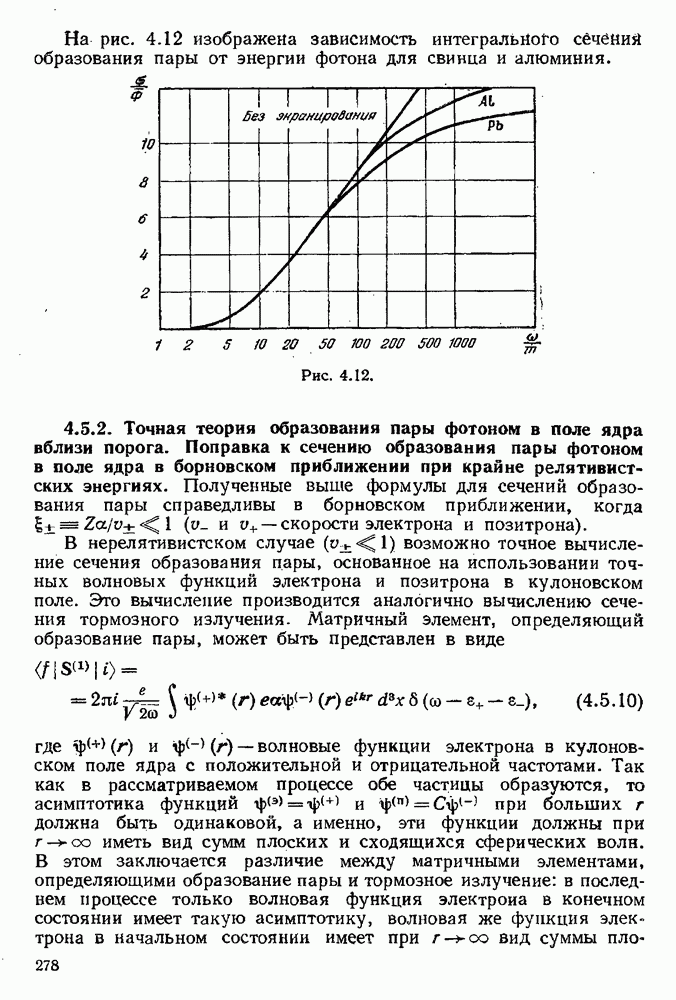
- 4.5.2. Точная теория образования пары фотоном в поле ядра вблизи порога.
- 4.5.3. Образование пары двзмя фотонами.
- 4.5.4. Аннигиляция пары в два и три фотона.
- 4.5.5. Поляризационные эффекты при двухфотонной аннигиляции пар.
- 4.5.6. Распад позитрония.
- 4.5.7. Превращение пары в один фотон.
- § 4.6. Рассеяние электрона и позитрона электроном
- 4.6.2. Сечение рассеяния позитрона электроном.
- 4.6.3. Рассеяние поляризованных электронов.
- 4.6.4. Рассеяние мюона электроном.
- 4.6.5. Излучение фотона при рассеянии электрона электроном и электрона позитроном и при превращении …
- § 4.7. Запаздывающее взаимодействие зарядов
- 4.7.3. Взаимодействие электрона с позитроном и позитроний.
- § 4.8. Метод эквивалентных фотонов
- 4.8.2. Тормозное излучение в процессах рассеяния электрона ядром и электрона электроном.
- 4.8.3. Образование пар фотоном в поле ядра и при столкно вении двух быстрых заряженных частиц.
- 4.8.4. Сечение двуструйного процесса.
- ГЛАВА 5. КВАНТОВОЭЛЕКТРОДИНАМИЧЕСКИЕ ЭФФЕКТЫ В ВЫСШИХ ПРИБЛИЖЕНИЯХ ТЕОРИИ ВОЗМУЩЕНИЙ
- § 5.1. Радиационные поправки к электродинамическим функциям Грина
- 5.1.2. Поляризационный оператор второго порядка.
- 5.1.3. Вершинная функция третьего порядка.
- § 5.2. Модификация закона Кулона. Аномальный магнитный момент электрона
- 5.2.2. Аномальный магнитный момент электрона и мюона.
- § 5.3. Радиационное смещение атомных уровней
- 5.3.2. Радиационное смещение и естественная ширина атомных уровней.
- 5.3.3. Радиационное смещение уровней атома водорода.
- 5.3.4. Рассеяние фотона вблизи резонанса.
- § 5.4. Радиационные поправки к сечениям рассеяния электрона во внешнем поле и рассеяния электрона электроном
- 5.4.2. Исключение «массы» фотона из сечения рассеяния.
- 5.4.3. Устранение инфракрасной расходимости в случае произвольного процесса рассеяния.
- 5.4.4. Радиационные поправки к сечению рассеяния электрона электроном и электрона позитроном.
- § 5.5. Радиационные поправки к сечениям комптоновского рассеяния, образования и аннигиляции пар и тормозного излучения
- 5.5.1. Радиационные поправки к сечению комптоновского рассеяния.
- 5.5.2. Рассеяние электроном фотонов малой частоты.
- 5.5.3. Радиационные поправки к сечению двухфотонной аннигиляции пар.
- 5.5.4. Радиационные поправки к сечению тормозного излучения.
- 5.5.4. Радиационные поправки к сечению тормозного излучения.
- 5.5.5. Радиационные поправки к сечению превращения электронно-позитронной пары в мюонную пару.
- § 5.6. Нелинейная электродинамика вакуума
- 5.6.1. Тензор рассеяния фотона фотоном четвертого ранга.
- 5.6.2. Сечение рассеяния фотона фотоном.
- 5.6.3. Радиационные поправки к функции Лагранжа электромагнитного поля в вакууме.
- 5.6.4. Точное выражение для лагранжиана произвольного медленно меняющегося электромагнитного поля.
- 5.6.5. Сечение рассеяния фэтэна в постоянном электромагнитном поле.
- 5.6.6. Связь между амплитудой рассеяния фотона на нулевой угол и сечением образования пар.
- 5.6.7. Импульсное и угловое распределения ядер отдачи при образовании пар фотоном в поле ядра.
- § 5.7. Дважды логарифмическая асимптотика сечений квантовоэлектродинамических процессов
- 5.7.2. Дважды логарифмическая асимптотика сечения рассеяния электрона во внешнем поле.
- 5.7.3. Дважды логарифмическая асимптотика сечения процесса …
- 5.7.4. Сводка формул для сечений квантовоэлектродинамических процессов в дважды логарифмическом приближении.
- ПРИЛОЖЕНИЕ
- А.1. Вычисление интегралов по инвариантному объему в 4-импульсном пространстве.
- A.2. Метод размерной регуляризации.
- ЛИТЕРАТУРА