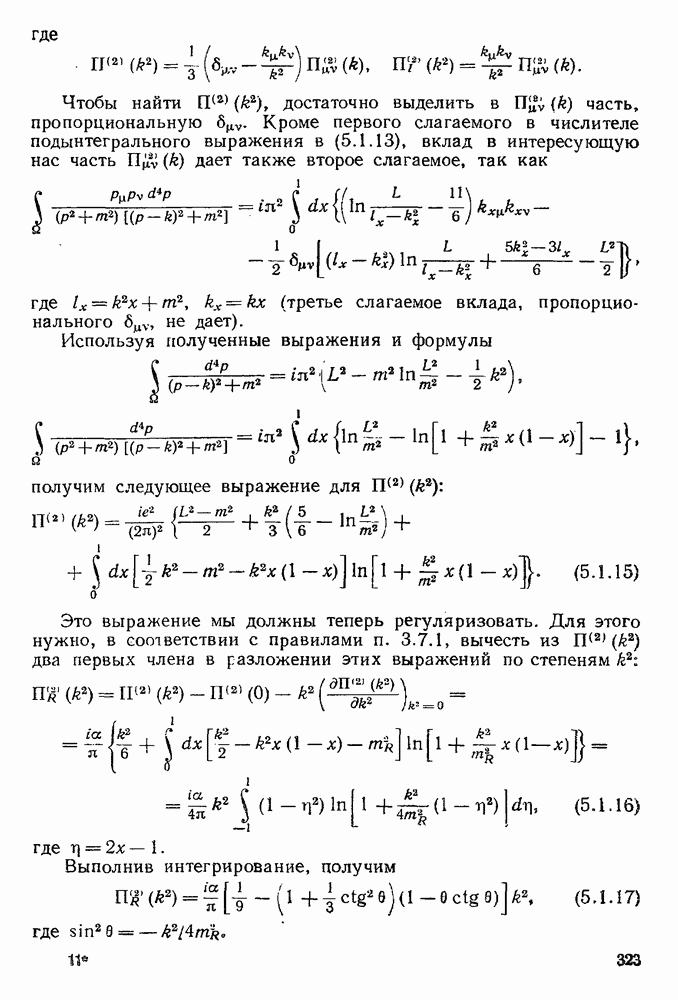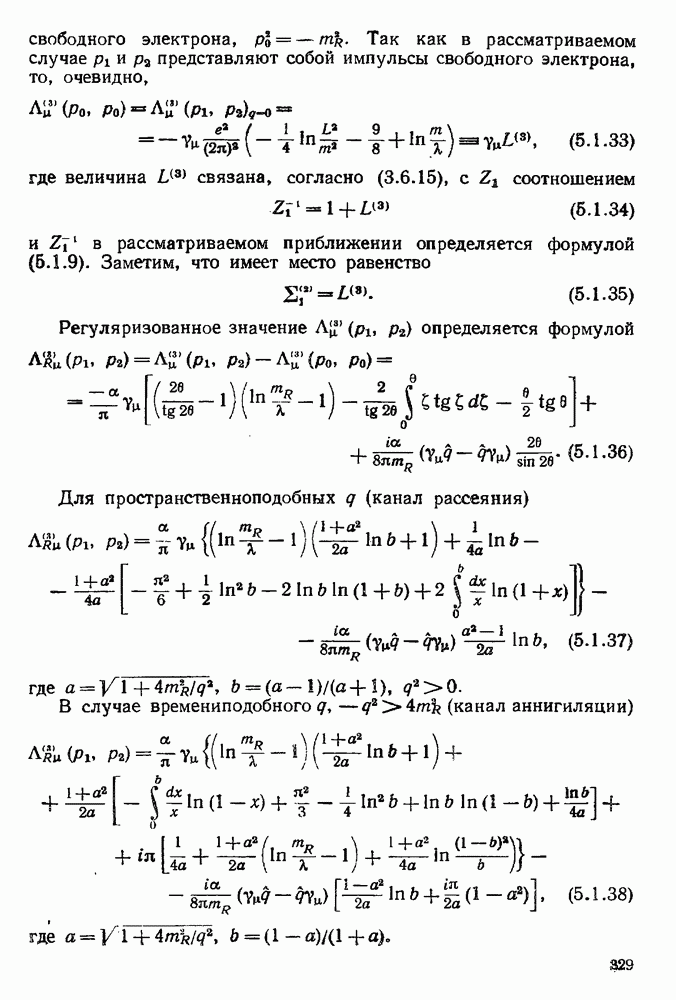| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.4.3. Устранение инфракрасной расходимости в случае произвольного процесса рассеяния.
Мы видели выше, что радиационные поправки к сечению рассеяния электрона во внешнем поле содержат «массу» фотона. Проследим, как формально возникает в матричных элементах инфракрасная расходимость. До регуляризации ни электронная собственно энергетическая функция, ни вершинная функция (с внутренними электронными линиями) не содержат расходящихся величин в области малых частот виртуальных фотонов, вершинная же и собственно энергетическая электронная функции в случае свободных электронных линий содержат такие величины.
При регуляризации внутренней вершинной функции  мы отнимаем от нее величину
мы отнимаем от нее величину  соответствующую свободным электронным линиям. Эта величина содержит интеграл, который расходится в области малых импульсов виртуальных фотонов. Чтобы обеспечить сходимость интеграла, мы вводим отличную от нуля «массу» фотона X, которая таким образом появляется в регуляризованной вершинной функции.
соответствующую свободным электронным линиям. Эта величина содержит интеграл, который расходится в области малых импульсов виртуальных фотонов. Чтобы обеспечить сходимость интеграла, мы вводим отличную от нуля «массу» фотона X, которая таким образом появляется в регуляризованной вершинной функции.
Аналогичным образом возникает I и в выражении для регуляризованной электронной собственно энергетической функции. По этой причине «масса» фотона начинает входить в радиационные поправки к сечениям самых различных процессов рассеяния.
Мы покажем теперь, обобщая результат, полученный для радиационных поправок к сечению рассеяния электрона в кулоновском поле ядра, что если для любого сколь угодно сложного процесса рассеяния, являющегося эффектом  порядка теории возмущений, наряду с радиационными поправками к нему, соответствующими
порядка теории возмущений, наряду с радиационными поправками к нему, соответствующими  порядку теории возмущений, рассматривать также излучение реального мягкого фотона, то суммарное сечение рассеяния, учитывающее как радиационные поправки, так и дополнительное излучение мягкого фотона, не будет содержать «массу» фотона.
порядку теории возмущений, рассматривать также излучение реального мягкого фотона, то суммарное сечение рассеяния, учитывающее как радиационные поправки, так и дополнительное излучение мягкого фотона, не будет содержать «массу» фотона.
Так как инфракрасная расходимость возникает при интегрировании в области малых импульсов виртуальных и реальных
фотонов, а «Мягкость» и «жесткость» фотона не являются, вообще говоря, инвариантными понятиями, то мы будем пользоваться определенной системой отсчета, а именно системой, в которой потеря энергии каждой заряженной частицей, обусловленная испусканием «мягких» фотонов, не превосходит некоторой величины s, малой по сравнению с энергиями всех заряженных частиц, участвующих в процессе.
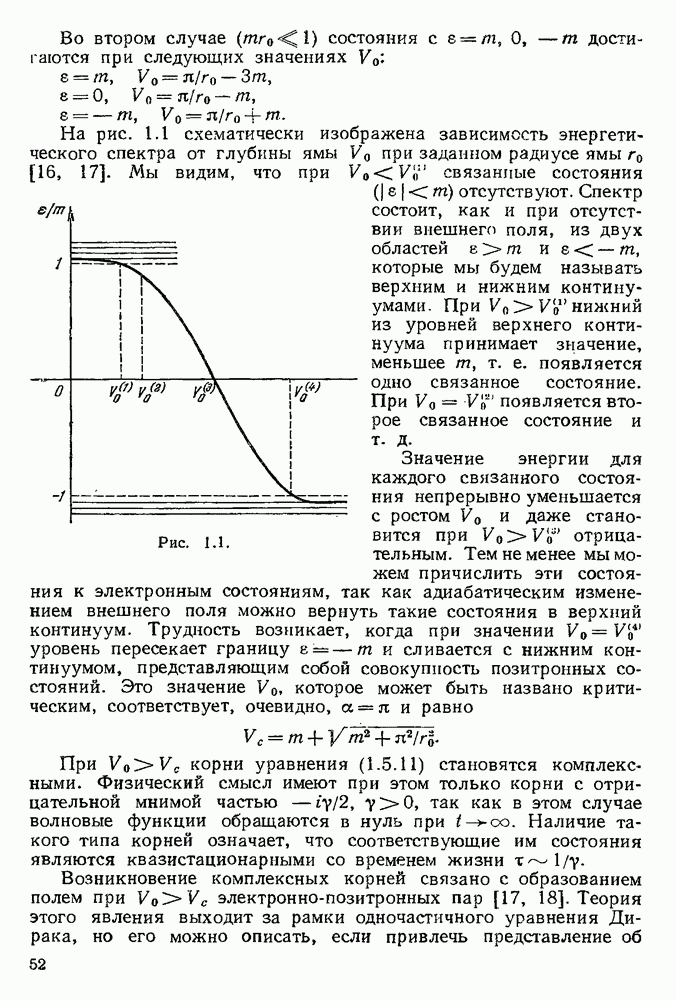
Пользуясь этой системой отсчета, мы выделим в пространстве 4-импульсов фотона k область  , в которой
, в которой  , где е — некоторая малая величина (она может быть выбрана, например, таким образом, чтобы выполнялось неравенство
, где е — некоторая малая величина (она может быть выбрана, например, таким образом, чтобы выполнялось неравенство  ), и будем называть мягкими те фотоны,
), и будем называть мягкими те фотоны,  -импульсы которых лежат в
-импульсы которых лежат в  остальные фотоны будем называть жесткими.
остальные фотоны будем называть жесткими.

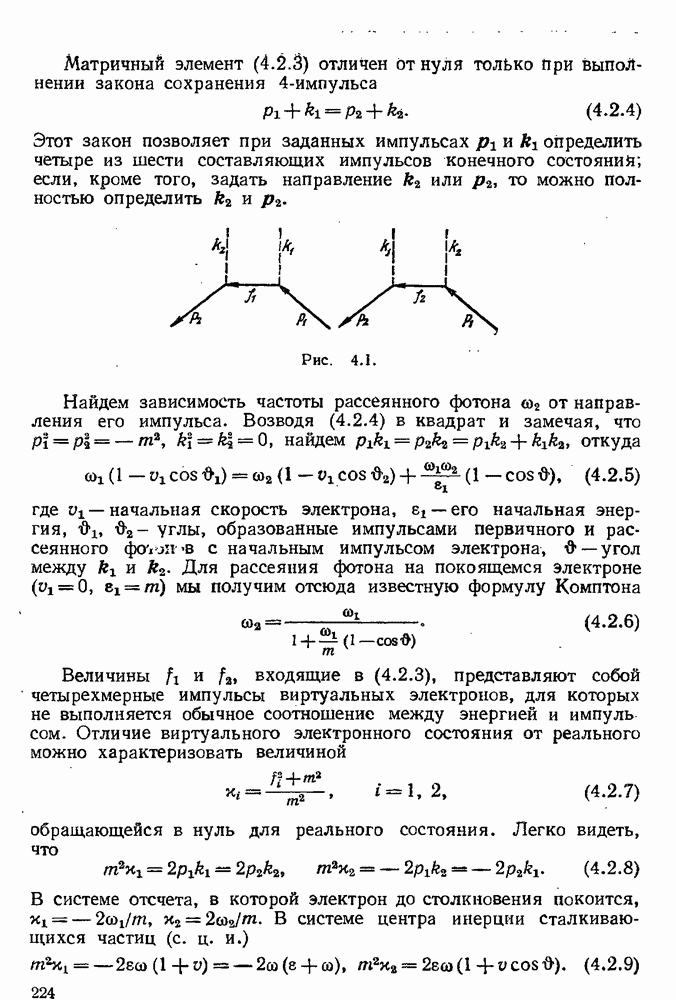
Рис. 5.5.
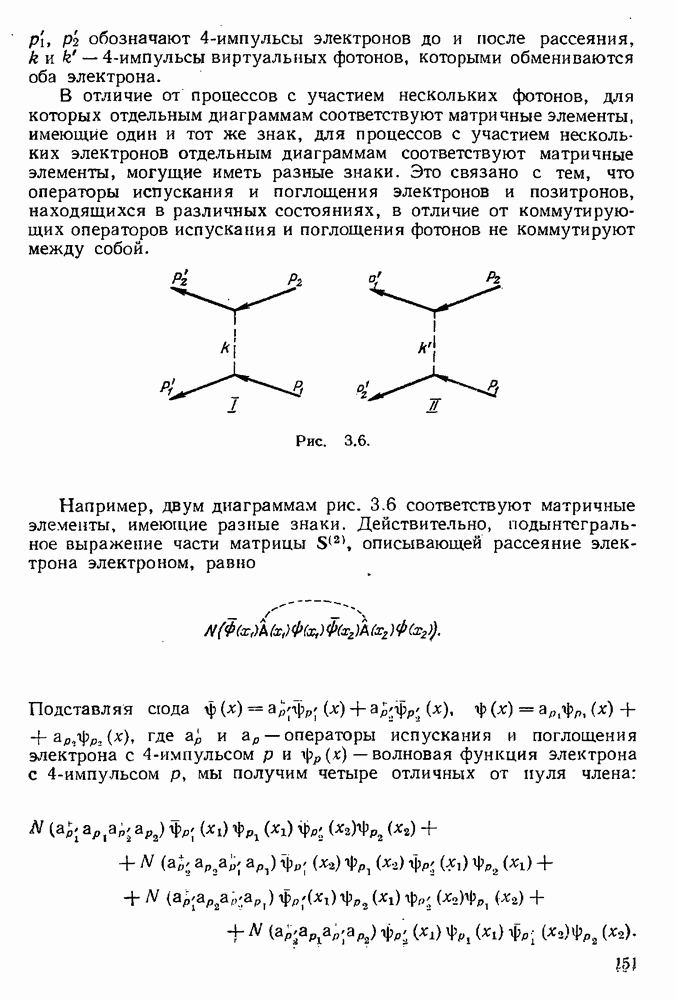
Будем для простоты предполагать, что в процессе рассеяния участвует только один электрон. Матричный элемент такого процесса можно записать в виде  где
где  — 4-импульсы электрона до и после рассеяния, и
— 4-импульсы электрона до и после рассеяния, и  — соответствующие им биспинорные амплитуды и
— соответствующие им биспинорные амплитуды и  — некоторая матрица.
— некоторая матрица.
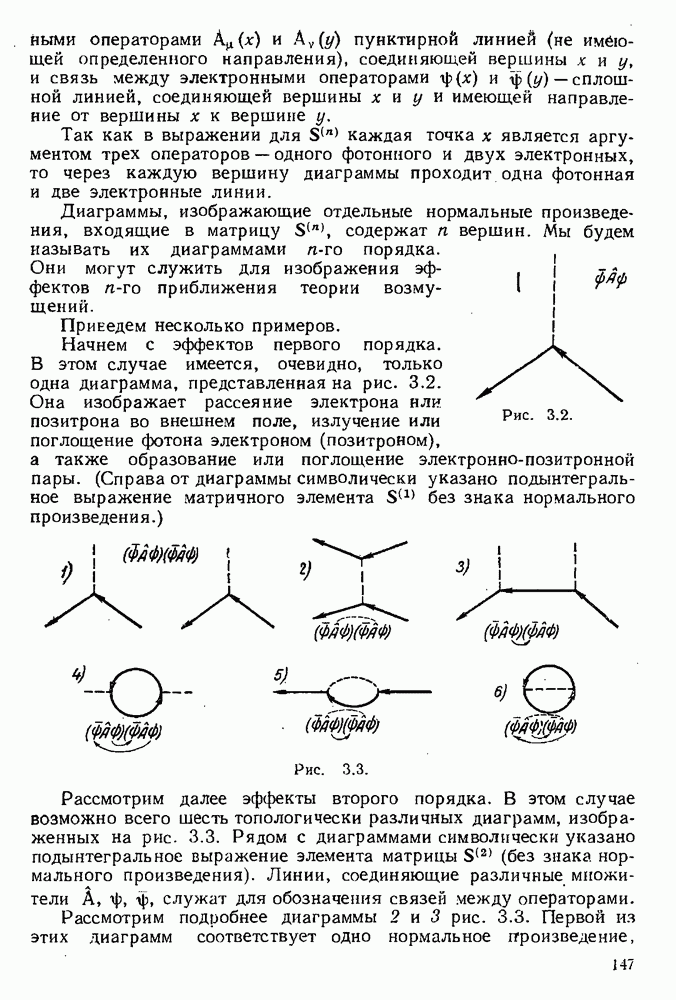
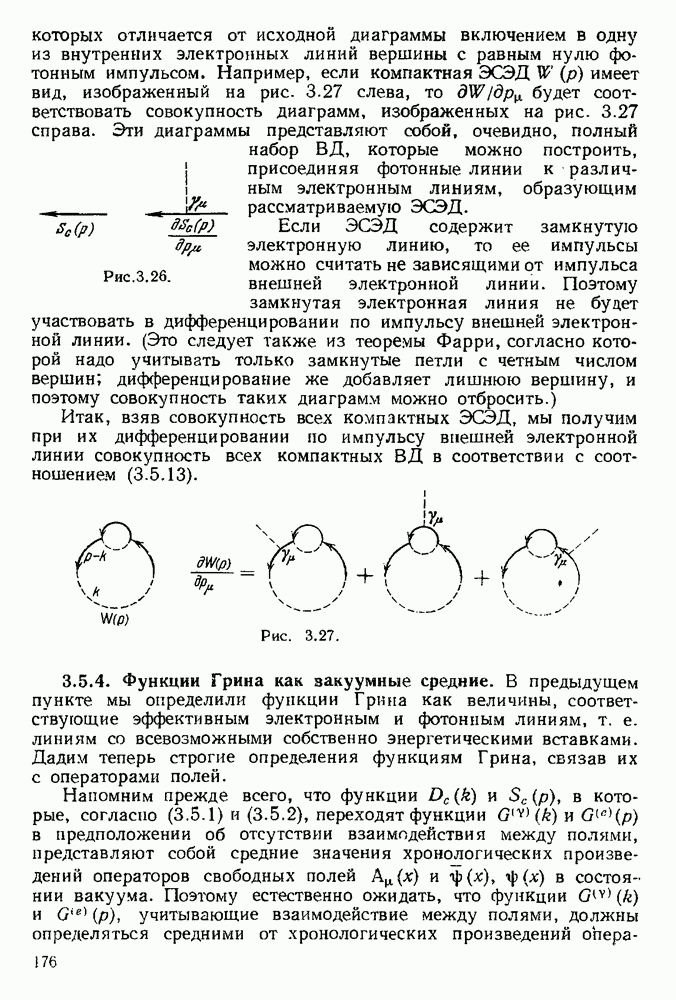
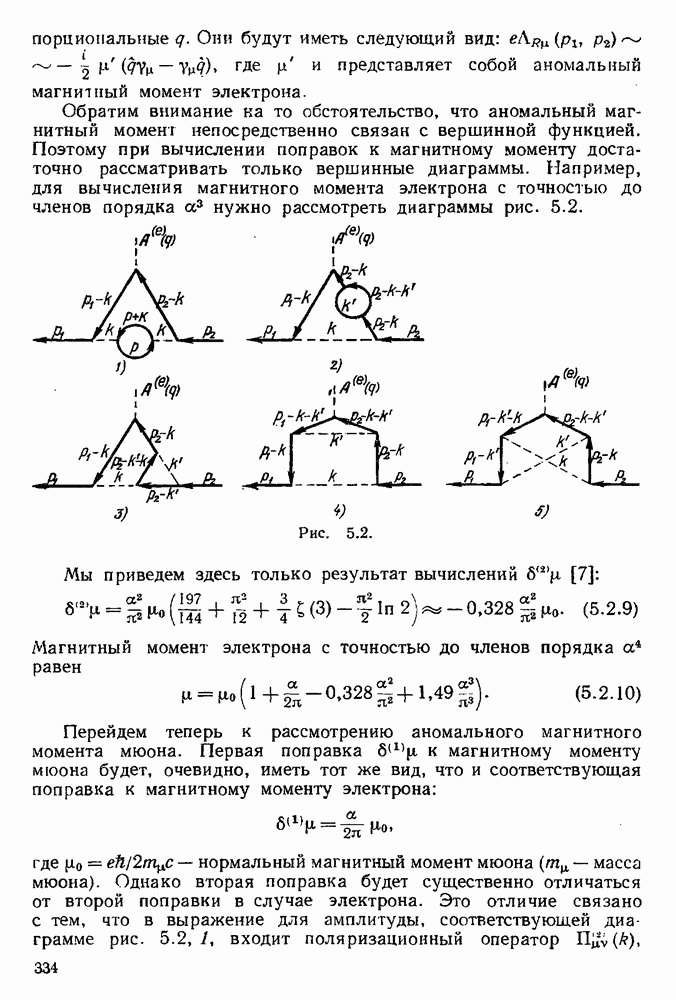
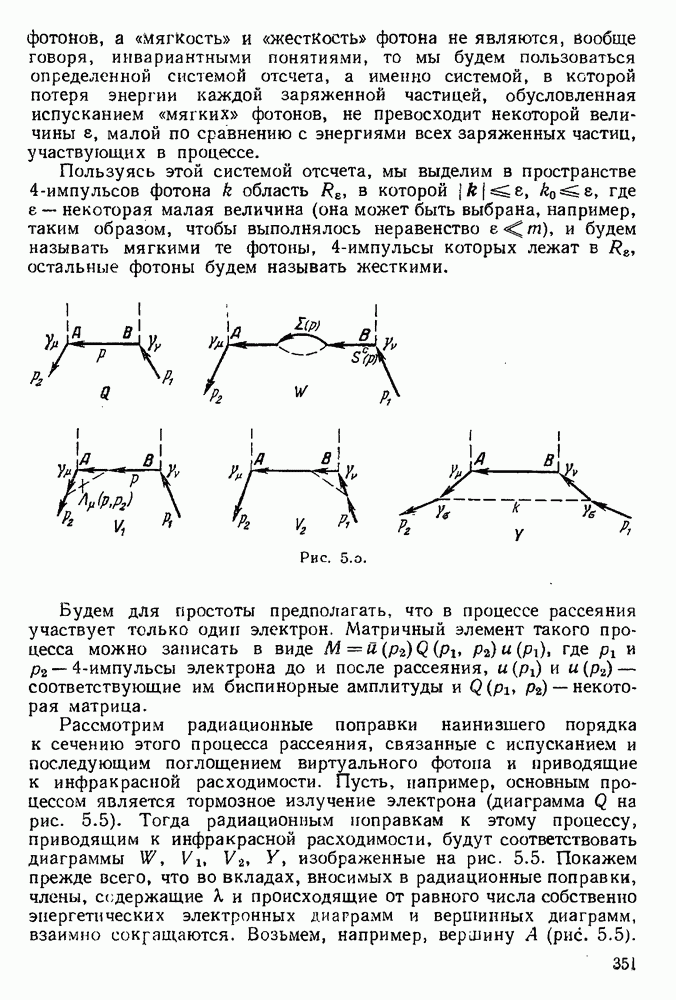
Рассмотрим радиационные поправки наинизшего порядка к сечению этого процесса рассеяния, связанные с испусканием и последующим поглощением виртуального фотона и приводящие к инфракрасной расходимости. Пусть, например, основным процессом является тормозное излучение электрона (диаграмма Q на рис. 5.5). Тогда радиационным поправкам к этому процессу, приводящим к инфракрасной расходимости, будут соответствовать диаграммы  , изображенные на рис. 5.5. Покажем прежде всего, что во вкладах, вносимых в радиационные поправки, члены, содержащие к и происходящие от равного числа собственно энергетических электронных диаграмм и вершинных диаграмм, взаимно сокращаются. Возьмем, например, вершину А (рис. 5.5).
, изображенные на рис. 5.5. Покажем прежде всего, что во вкладах, вносимых в радиационные поправки, члены, содержащие к и происходящие от равного числа собственно энергетических электронных диаграмм и вершинных диаграмм, взаимно сокращаются. Возьмем, например, вершину А (рис. 5.5).
Матрице  в основном процессе Q соответствует следующий вклад от диаграмм радиационных поправок ИР и
в основном процессе Q соответствует следующий вклад от диаграмм радиационных поправок ИР и 

где  Левая часть этого равенства не содержит инфракрасной расходимости, которая появляется в константах
Левая часть этого равенства не содержит инфракрасной расходимости, которая появляется в константах  . Но, согласно (5.1.36), эти константы равны
. Но, согласно (5.1.36), эти константы равны  и, следовательно, члены, содержащие их, сокращаются. По этой причине регуляризованное значение написанного выражения
и, следовательно, члены, содержащие их, сокращаются. По этой причине регуляризованное значение написанного выражения  не будет, как и утверждалось, содержать инфракрасной расходимости.
не будет, как и утверждалось, содержать инфракрасной расходимости.
Если основная диаграмма Q содержит  внутренних электронных линий, то в диаграммах радиационных поправок типов W и V будет
внутренних электронных линий, то в диаграммах радиационных поправок типов W и V будет  внутренних ЭСЭД и
внутренних ЭСЭД и  внутренних ВД. От этих диаграмм останется одна нескомпенсированная «масса» фотона к, соответствующая одной ЗСЭД. Учитывая наличие двух свободных электронных линий, с которыми связаны две ВД, мы окончательно получим от всех диаграмм W и V одну «нескомпенсированную» Я от одной ВД. Согласно (5.1.36) величина к входит в вершинную функцию в виде
внутренних ВД. От этих диаграмм останется одна нескомпенсированная «масса» фотона к, соответствующая одной ЗСЭД. Учитывая наличие двух свободных электронных линий, с которыми связаны две ВД, мы окончательно получим от всех диаграмм W и V одну «нескомпенсированную» Я от одной ВД. Согласно (5.1.36) величина к входит в вершинную функцию в виде  Считая
Считая  мы можем поэтому написать следующее выражение для главной относительно
мы можем поэтому написать следующее выражение для главной относительно  части матричного элемента, соответствующего диаграммам типов W и V:
части матричного элемента, соответствующего диаграммам типов W и V:
 (5.4.13)
(5.4.13)
Этот результат можно сформулировать и иначе, сказав, что с каждой свободной электронной линиейсвязана инфракрасная расходимость, причем вклад от каждой из этих лннрй в матричный элемент, соответствующий диаграммам тинов w и V, равен

Рассмотрим теперь последнюю диаграмму радиационный поправок У. Соответствующий ей матричный элемент  при малых k имеет вид
при малых k имеет вид

Легко показать, что к входит в  в виде слагаемого
в виде слагаемого

( — скорость электрона после рассеяния
— скорость электрона после рассеяния  ).
).
В суммарный матричный элемент радиационных поправок «масса» фотона будет входить в виде  а в сечение рассеяния с учетом радиационных поправок — в виде
а в сечение рассеяния с учетом радиационных поправок — в виде

Поэтому сечение рассеяния с учетом радиационных поправок  будет содержать к в виде слагаемого
будет содержать к в виде слагаемого
 (5.4.14)
(5.4.14)
 — сечение основного процесса).
— сечение основного процесса).

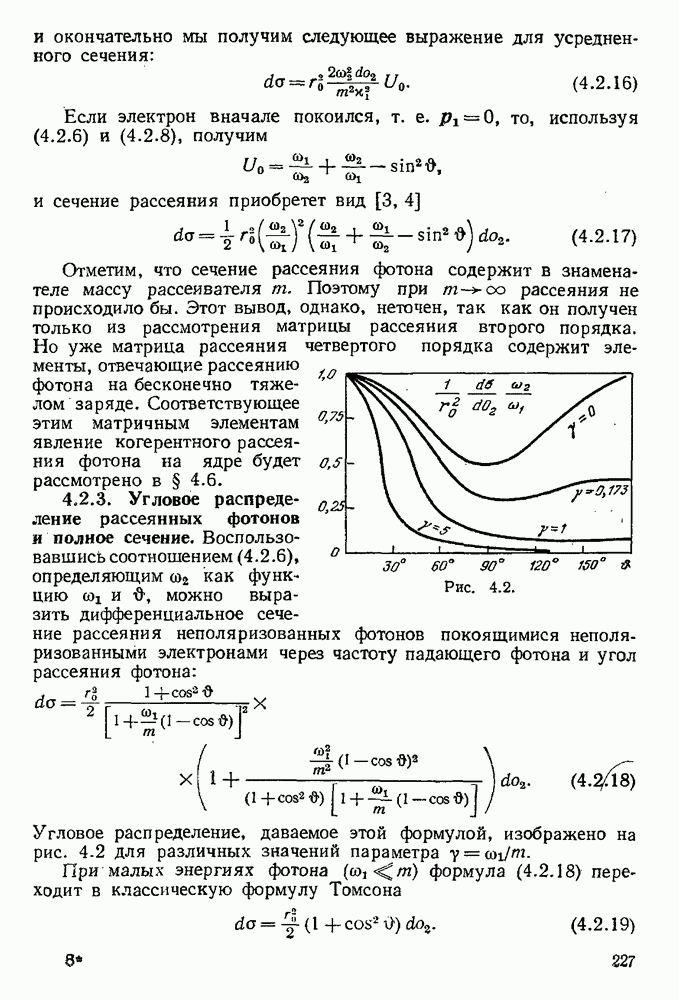
Рис. 5.6.
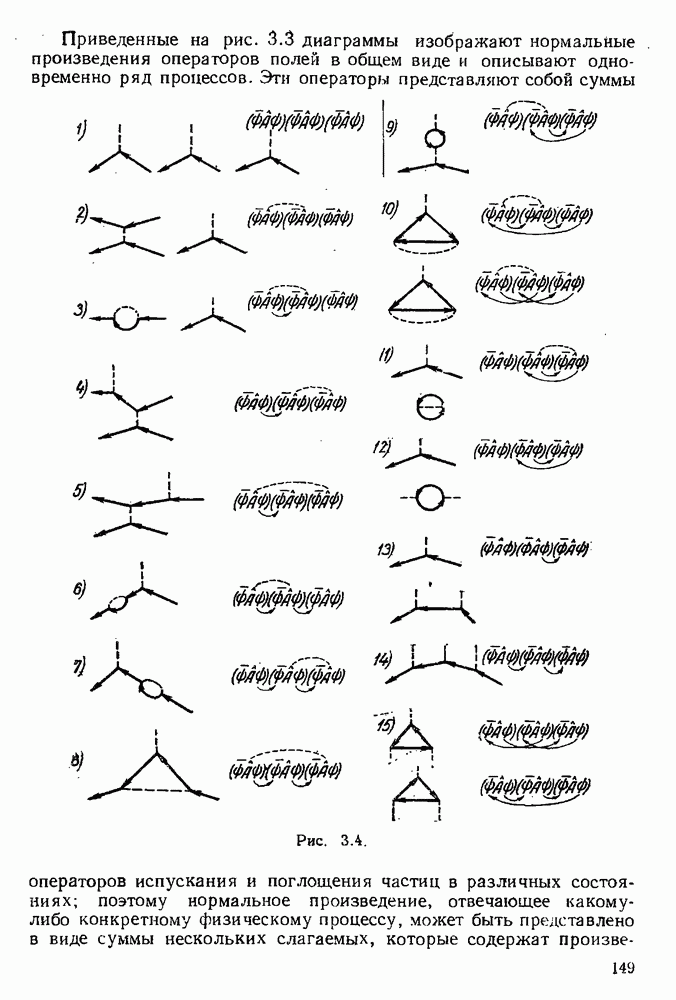
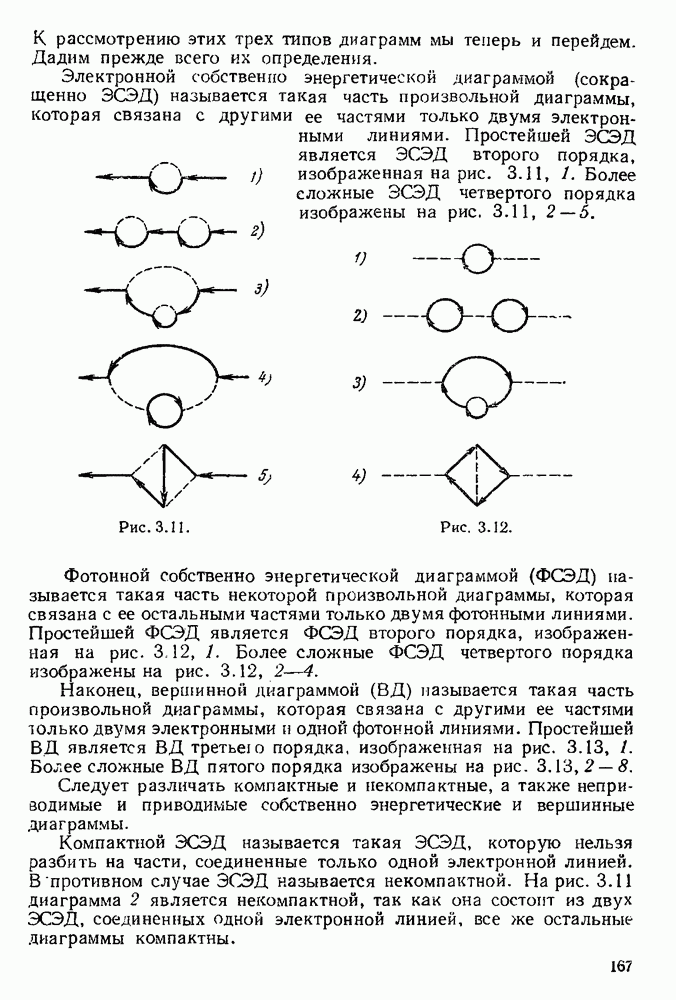
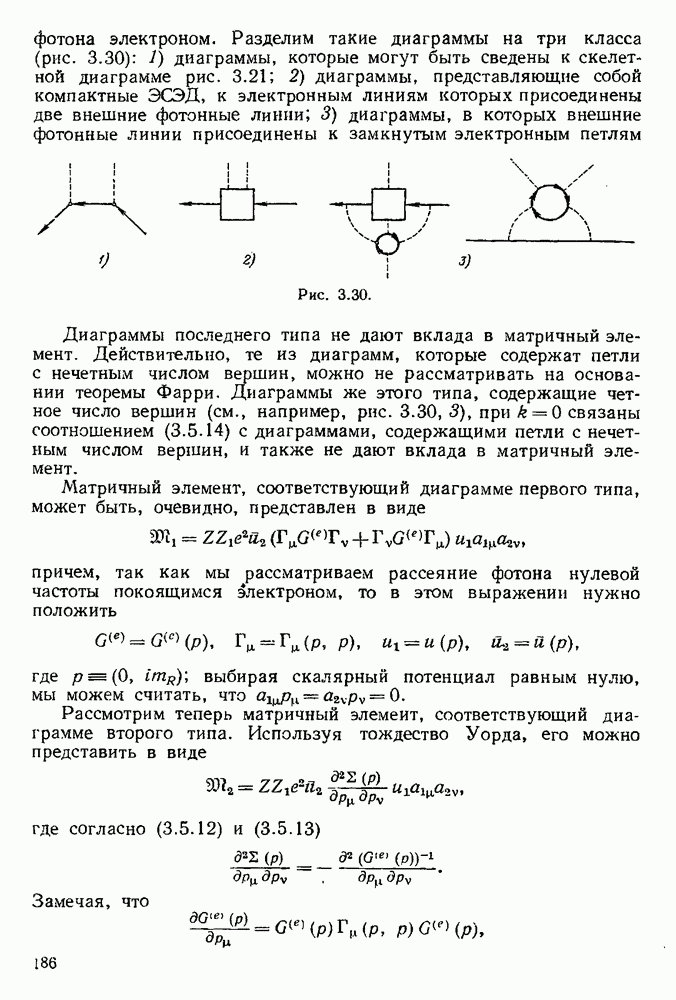
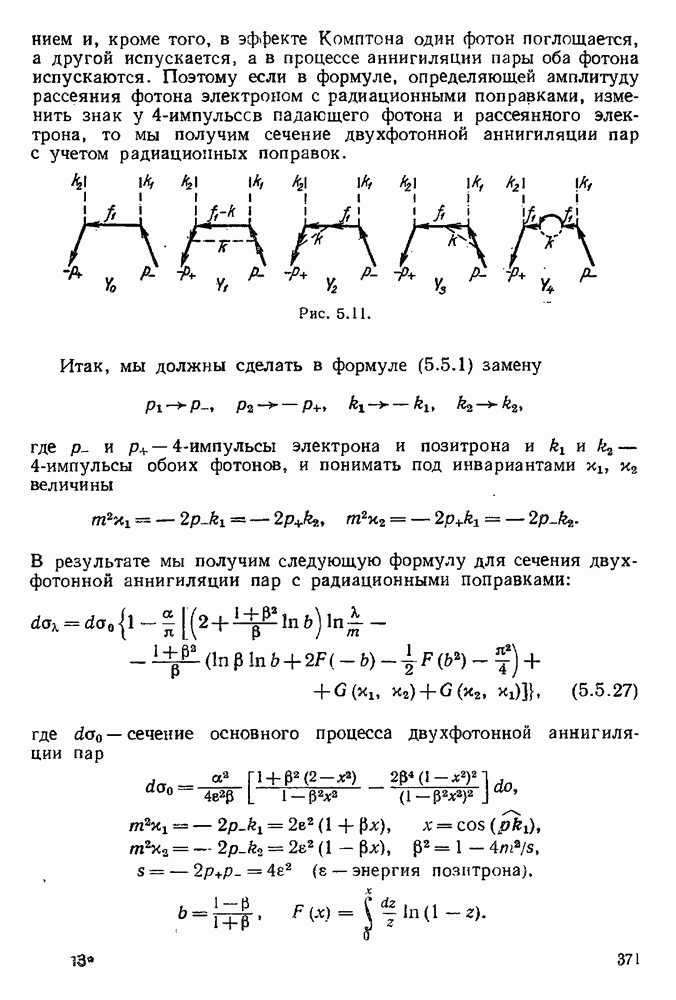
Рассмотрим теперь наряду с радиационными поправками излучение реального мягкого фотона с импульсом k и поляризацией е. Диаграммы, изображающие излучение фотона к, представлены на рис. 5.6. Матричный элемент, соответствующий этим диаграммам, равен
 (5.4.15)
(5.4.15)
Сечение рассеяния с излучением мягкого фотона с энергией, не превосходящей  , будет, очевидно,
, будет, очевидно,
 (5.4.16)
(5.4.16)
Считая, так же как и выше, что  , получим согласно § 4.2:
, получим согласно § 4.2:

Формула (5.4.16) показывает, что сечение рассеяния с излучением мягкого фотона представляет собой произведение сечения гроцесса без излучения фотона на вероятность излучения мягкого фотона. Такая факторизация является характерной чертой сечений рассеяния с излучением произвольного числа мягких фотонов.
Найдем, наконец, суммарное сечение рассеяния, учитывающее как радиационные поправки, так и излучение мягкого фотона:  .
.
Часть  содержащая
содержащая  , имеет вид
, имеет вид

Но эта величина, согласно (5.4.14) и (5.4.17), не содержит массе фотона, поэтому X, как и утверждалось, не входит в суммарное сечение рассеяния [15].
Мы показали, как устраняется инфракрасная расходимость в случае произвольного процесса рассеяния в наинизшем приближении теории возмущений. Но полученные результаты могут быть обобщены на все порядки теории возмущений.

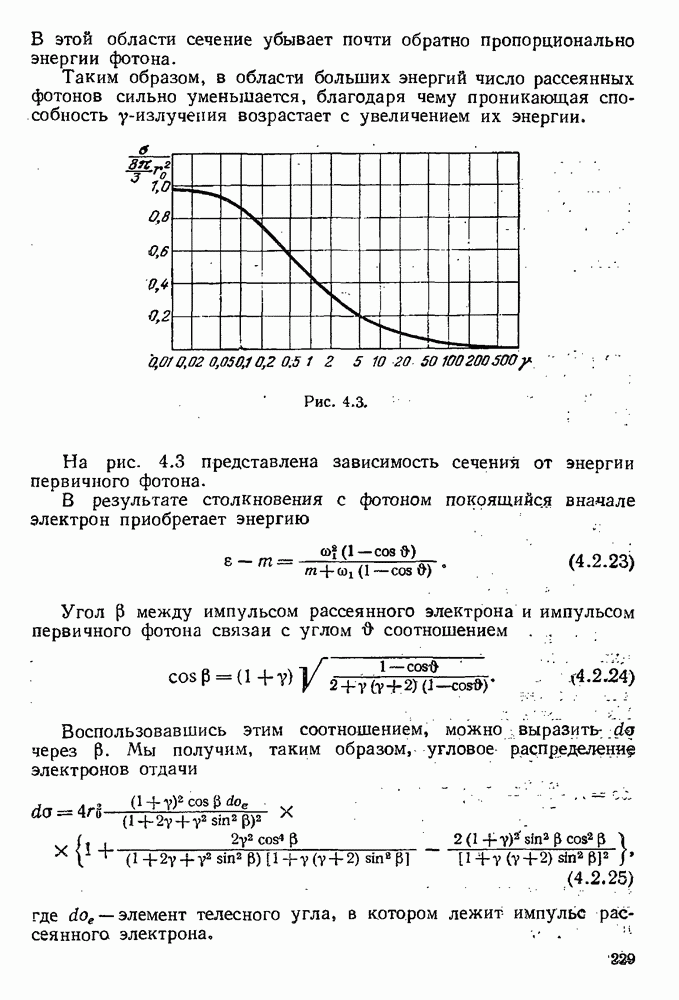
Рис. 5.7.
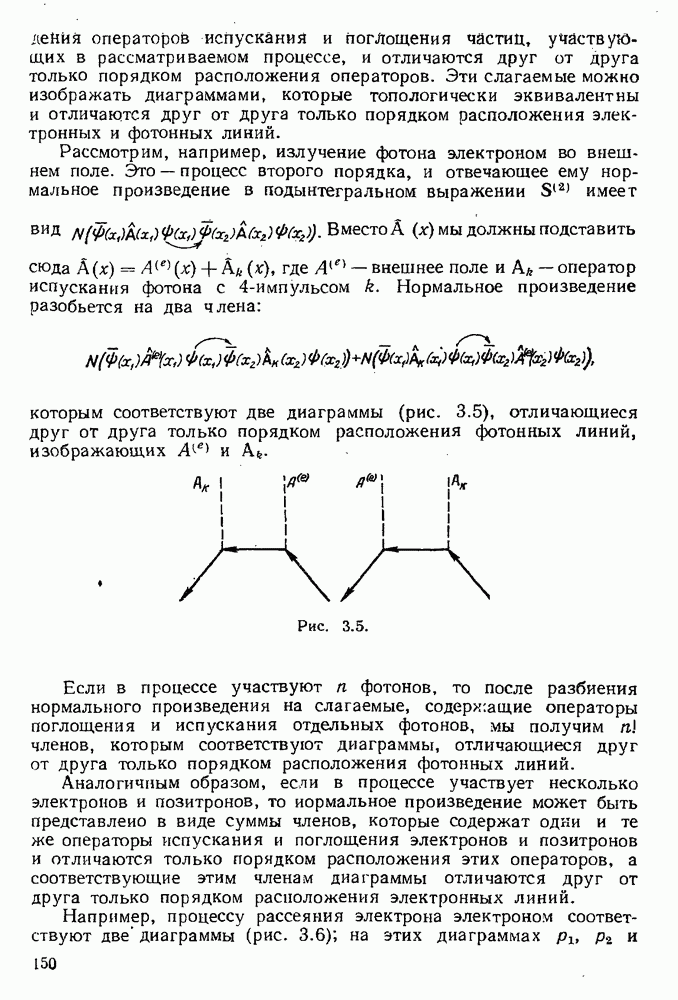
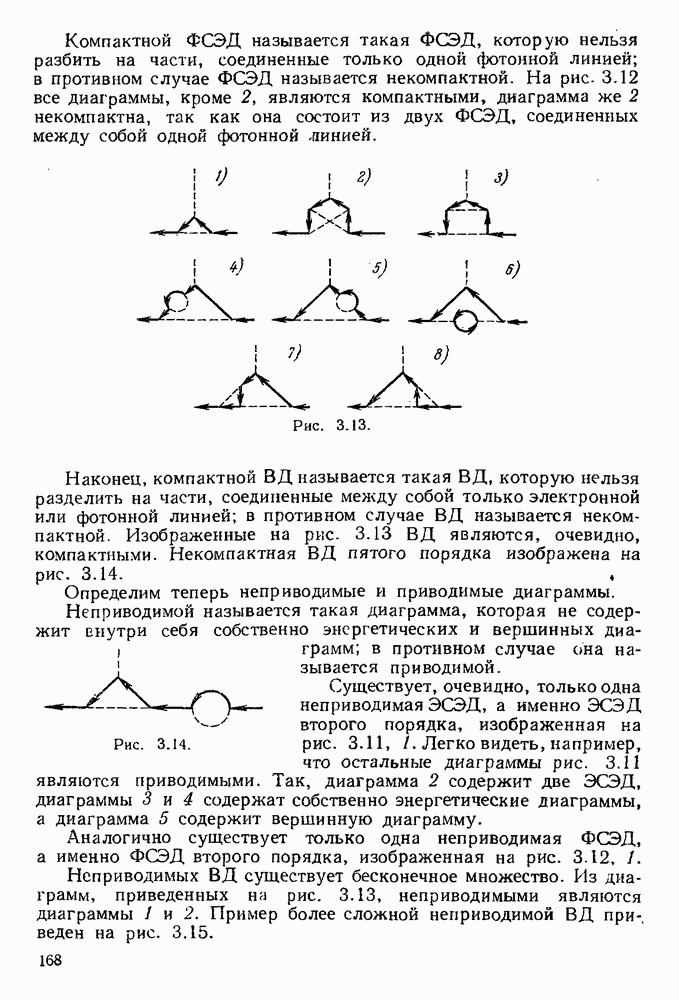
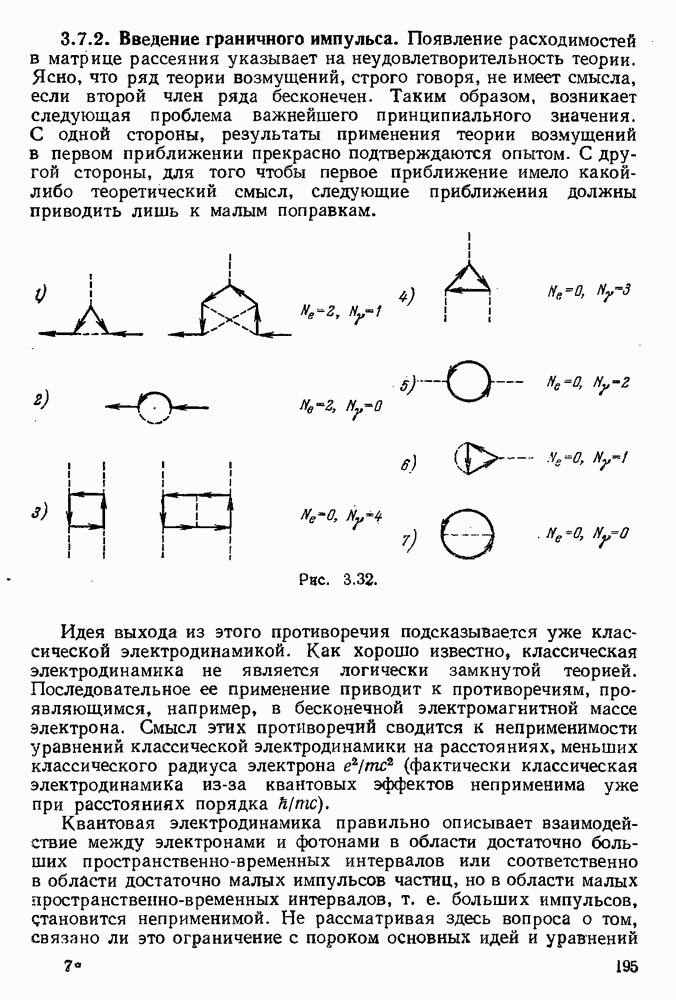
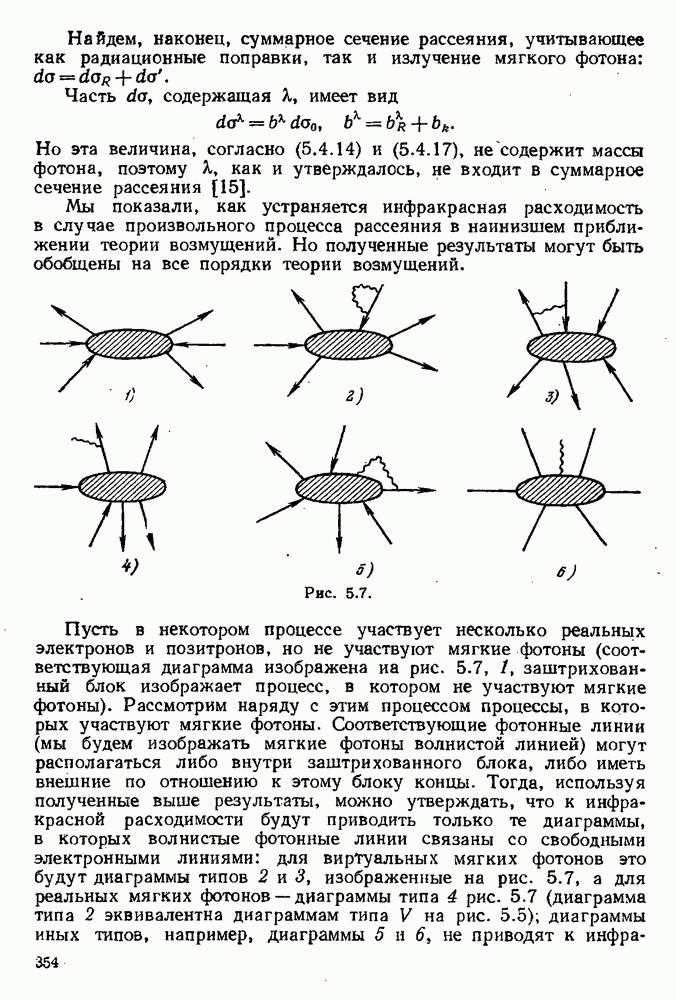
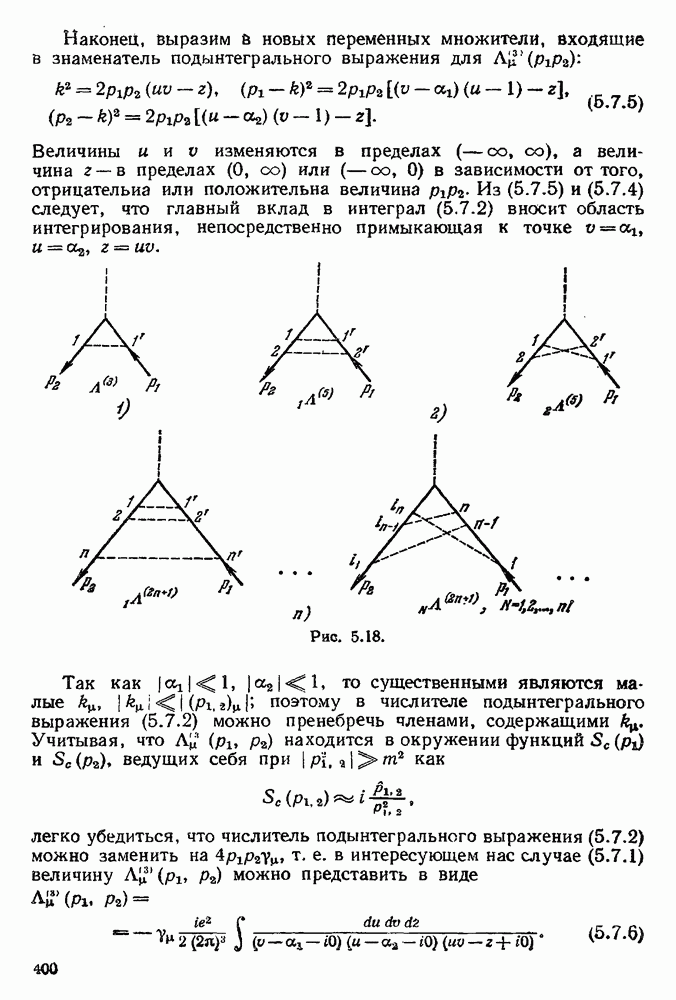
Пусть в некотором процессе участвует несколько реальных электронов и позитронов, но не участвуют мягкие фотоны (соответствующая диаграмма изображена на рис. 5.7, l, заштрихованный блок изображает процесс, в котором не участвуют мягкие фотоны). Рассмотрим наряду с этим процессом процессы, в которых участвуют мягкие фотоны. Соответствующие фотонные линии (мы будем изображать мягкие фотоны волнистой линией) могут располагаться либо внутри заштрихованного блока, либо иметь внешние по отношению к этому блоку концы. Тогда, используя полученные выше результаты, можно утверждать, что к инфракрасной расходимости будут приводить только те диаграммы, в которых волнистые фотонные линии связаны со свободными электронными линиями: для виртуальных мягких фотонов это будут диаграммы типов 2 и 3, изображенные на рис. 5.7, а для реальных мягких фотонов — диаграммы типа 4 рис. 5.7 (диаграмма типа 2 эквивалентна диаграммам типа V на рис. 5.5); диаграммы иных типов, например, диаграммы 5 и 6, не приводят к инфракрасной
красной расходимости. Мы не будем приводить здесь вычисления соответствующих матричных элементов и приведем только окончательные результаты [15].
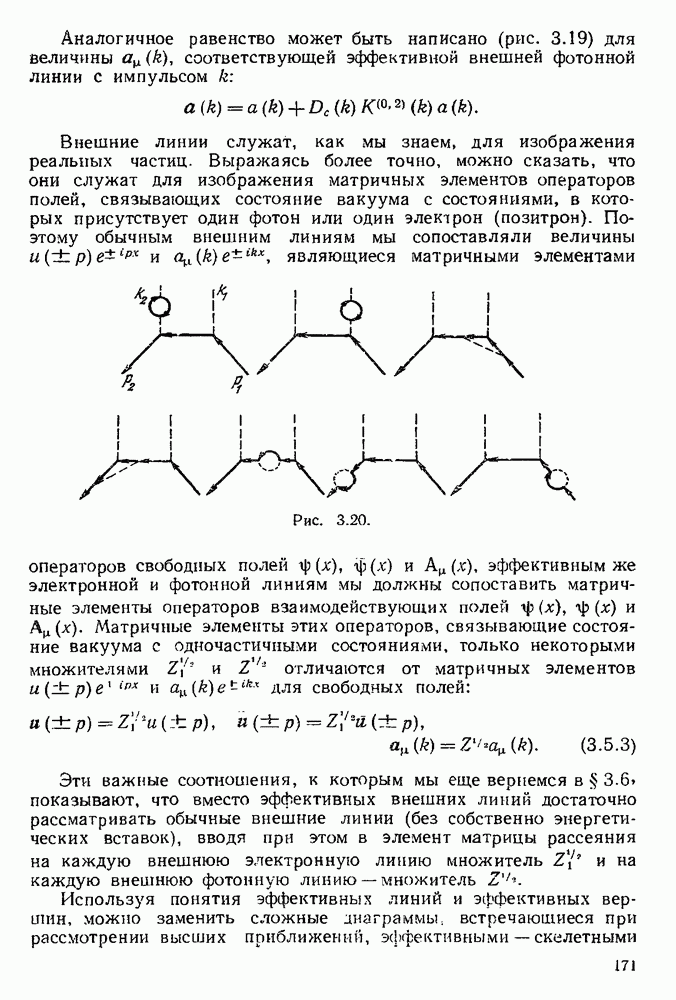
Рассмотрим сначала некоторый процесс, в котором участвуют два свободных электрона. Тогда матричный элемент, соответствующий этому процессу с учетом всех радиационных поправок к нему, будет иметь следующую структуру:
 (5.4.18)
(5.4.18)
где

 — 4-импульсы электронов и
— 4-импульсы электронов и  — некоторая величина, не содержащая инфракрасной расходимости, т. е. остающаяся конечной при
— некоторая величина, не содержащая инфракрасной расходимости, т. е. остающаяся конечной при  Величина, стоящая в скобках под знаком интеграла В, представляет собой, с точностью до множителя
Величина, стоящая в скобках под знаком интеграла В, представляет собой, с точностью до множителя  - ток «перехода»
- ток «перехода»

удовлетворяющий уравнению непрерывности 
Если наряду с радиационными поправками учитывать также излучение электронами реальных «мягких» фотонов, то суммарное сечение основного процесса вместе с радиационными поправками и излучением «мягких» фотонов будет иметь вид
 (5.4.19)
(5.4.19)
где

 — максимальная энергия фотонов и
— максимальная энергия фотонов и  — величина, пропорциональная
— величина, пропорциональная  и не содержащая инфракрасной расходимости. Легко видеть, что
и не содержащая инфракрасной расходимости. Легко видеть, что  остается конечным при
остается конечным при  . Считая, что
. Считая, что  получим
получим

Эти формулы могут быть обобщены на тот случай, когда в процессе участвуют не два, а произвольное число электронов, а также позитронов и других заряженных частиц. В этом случае величины В и В имеют следующий вид:
 (5.4.21)
(5.4.21)
где  для частицы в конечном состоянии,
для частицы в конечном состоянии,  для частицы в начальном состоянии и да — заряд частицы.
для частицы в начальном состоянии и да — заряд частицы.
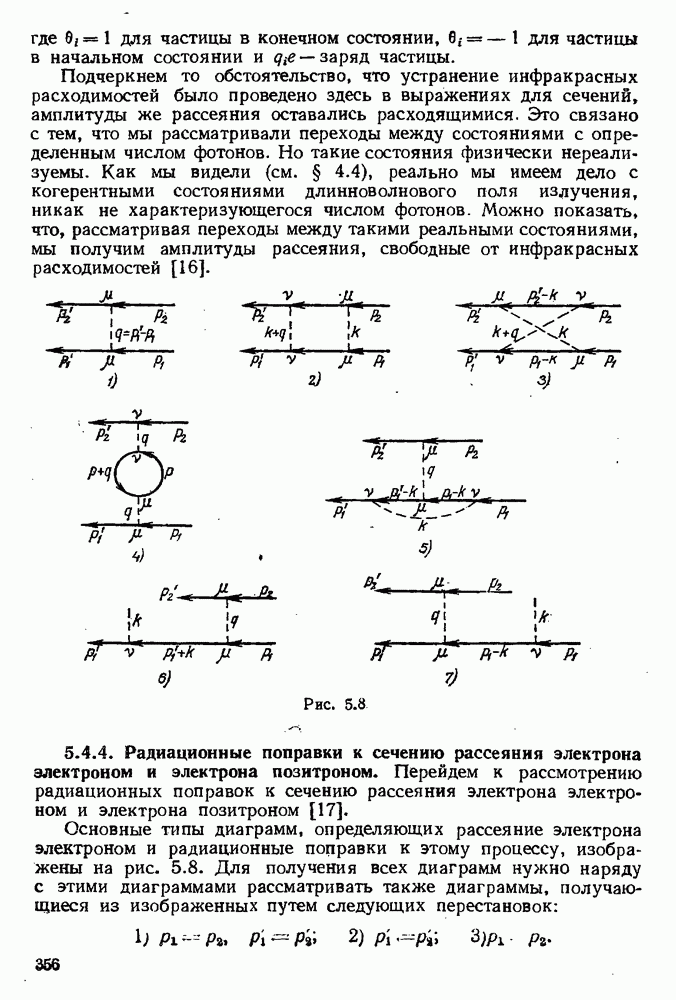
Подчеркнем то обстоятельство, что устранение инфракрасных расходимостей было проведено здесь в выражениях для сечений, амплитуды же рассеяния оставались расходящимися. Это связано с тем, что мы рассматривали переходы между состояниями с определенным числом фотонов. Но такие состояния физически нереализуемы. Как мы видели (см. § 4.4), реально мы имеем дело с когерентными состояниями длинноволнового поля излучения, никак не характеризующегося числом фотонов. Можно показать, что, рассматривая переходы между такими реальными состояниями, мы получим амплитуды рассеяния, свободные от инфракрасных расходимостей [16].

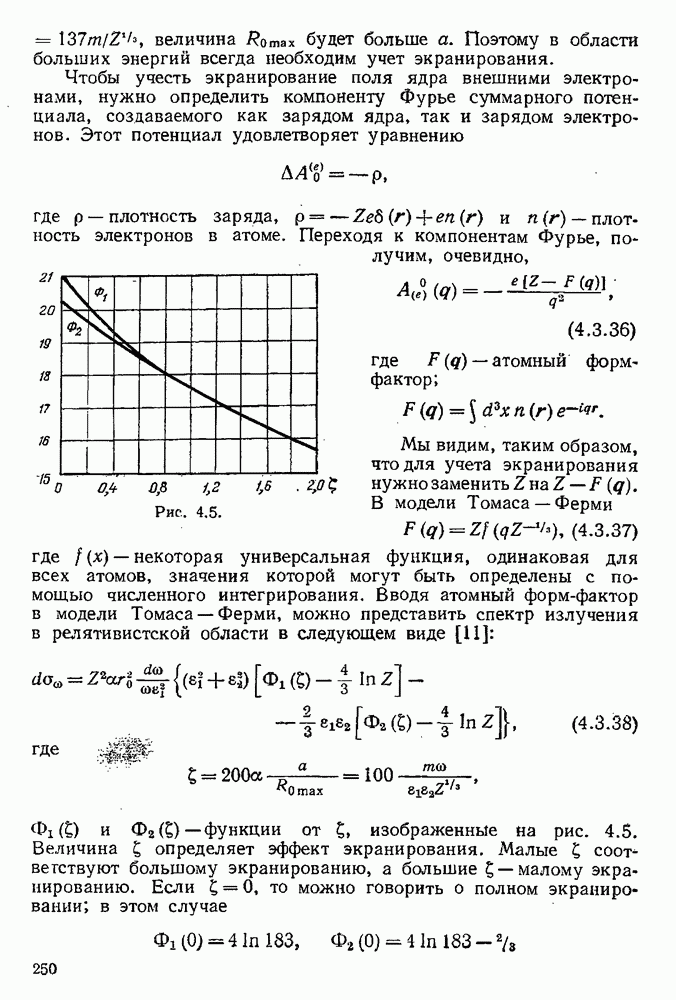
Рис. 5.8
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА ЭЛЕКТРОНА
- 1.1.2. Симметричная форма уравнения Дирака.
- 1.1.3. Решения с положительными и отрицательными частотами.
- 1.1.4. Плоские волны.
- 1.1.5. Поляризационные состояния электрона.
- 1.1.6. Поляризационная матрица плотности электрона.
- 1.1.7. Поляризационные состояния электрона в ультрарелятизистском пределе.
- § 1.2. Уравнение Дирака для электрона в электромагнитном поле и свойства инвариантности уравнения Дирака
- 1.2.1. Уравнение Дирака для электрона во внешнем электромагнитном поле.
- 1.2.2. Уравнение непрерывности.
- 1.2.3. Различные представления уравнения Дирака.
- 1.2.4. Алгебра матриц Дирака.
- 1.2.5. Релятивистская инвариантность уравнения Дирака.
- 1.2.6. Пространственное отражение, обращение времени и зарядовое сопряжение.
- 1.2.7. Ковариантные билинейные формы.
- 1.2.8. Использование обозначений, соответствующих псевдоевклидовой метрике.
- § 1.3. Предельные переходы к нерелятивистской квантовой механике и релятивистской классической механике
- 1.3.2. Второе приближение.
- 1.3.3. Переход к релятивистской классической механике.
- 1.3.4. Высокоэнергетическое приближение.
- 1.3.5. Борновское приближение.
- § 1.4. Момент импульса электрона
- 1.4.2. Волновая функция свободного электрона с определенным моментом.
- 1.4.3. Четность состояния.
- 1.4.4. Разложение по сферическим волнам.
- § 1.5. Движение электрона в центральном поле
- 1.5.2. Сферически-симметричная потенциальная яма.
- 1.5.3. Движение электрона в кулоновском поле ядра.
- 1.5.4. Волновые функции непрерывного спектра в кулоновском поле ядра.
- 1.5.5. Критический заряд ядра.
- § 1.6. Движение в однородных полях
- 1.6.2. Электрон в постоянном и однородном магнитном поле.
- 1.6.3. Электрон в постоянном и однородном электрическом поле.
- 1.6.4. Парадокс Клейна.
- § 1.7. Рассеяние электронов
- 1.7.2. Амплитуда и сечение рассеяния.
- 1.7.3. Поляризация и азимутальная асимметрия.
- 1.7.4. Упругое рассеяние в борцовском приближении.
- 1.7.5. Упругое рассеяние в эйкональном приближении.
- 1.7.6. Рассеяние в кулоновском поле ядра.
- ГЛАВА 2. КВАНТОВАНИЕ ПОЛЕЙ
- § 2.1. Квантовая механика фотона
- 2.1.2. Волновая функция фотона.
- 2.1.3. Плоские волны.
- § 2.2. Момент импульса фотона
- 2.2.2. Собственные функции оператора момента фотона.
- 2.2.3. Продольный и поперечные шаровые векторы.
- 2.2.4. Четность состоянии фотона.
- 2.2.5. Сферические электромагнитные волны.
- § 2.3. Квантование электромагнитного поля
- 2.3.2. Перестановочные соотношения для потенциалов электромагнитного поля.
- 2.3.3. Хронологическое и нормальное произведения операторов электромагнитных потенциалов.
- § 2.4. Корреляционные функции электромагнитного поля
- 2.4.2. Когерентные состояния.
- 2.4.3. Корреляционные функции и когерентность высших порядков.
- 2.4.4. Поляризационная матрица плотности.
- § 2.5. Квантование электронно-позитронного поля
- 2.5.2. Операторы испускания и поглощения электронов и позитронов.
- 2.5.3. Антикоммутаторы электронного поля.
- 2.5.4. Хронологическое и нормальное произведения операторов электронного поля.
- ГЛАВА 3. ЭЛЕКТРОМАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ
- § 3.1. Основные уравнения квантовой электродинамики
- 3.1.2. Лагранжиан и гамильтониан взаимодействующих полей.
- 3.1.3. Представление взаимодействия.
- § 3.2. Матрица рассеяния
- 3.2.2. Инвариантная теория возмущений.
- 3.2.3. Представление матрицы рассеяния в виде суммы нормальных произведений.
- 3.2.4. Функциональная форма представления матрицы рассеяния в виде N-упорядоченного оператора.
- § 3.3. Графическое представление элементов матрицы рассеяния
- 3.3.2. Импульсное представление.
- 3.3.3. Правила Фейнмана.
- § 3.4. Вероятность и эффективное сечение
- 3.4.2. Суммирование по состояниям поляризации электронов и фотонов.
- 3.4.3. Эффективное сечение.
- 3.4.4. Вероятность процессов рассеяния поляризованных частиц.
- § 3.5. Структура диаграмм матрицы рассеяния
- 3.5.2. Эффективные линии.
- 3.5.3. Уравнения Дайсона для функций Грина и графическое уравнение для вершинной функции.
- 3.5.4. Функции Грина как вакуумные средние.
- § 3.6. Перенормировка массы и заряда электрона
- 3.6.2. Физический заряд электрона.
- 3.6.3. Перенормировка функций Грина и вершинной функции.
- 3.6.4. Перенормировка элементов матрицы рассеяния.
- § 3.7. Расходимости в матрице рассеяния и их устранение
- 3.7.2. Введение граничного импульса.
- 3.7.3. Регуляризация функций, соответствующих неприводимым диаграммам.
- 3.7.4. Регуляризация функций, соответствующих приводимым диаграммам.
- § 3.8. Асимптотические свойства функций Грина
- 3.8.2. Асимптотические выражения для функций Грина.
- 3.8.3. Асимптотический характер регулярнзованных разложений матрицы рассеяния и проблема замкнутости квантовой электродинамики.
- ГЛАВА 4. ОСНОВНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ЯВЛЕНИЯ
- § 4.1. Излучение фотона
- 4.1.2. Излучение электрического и магнитного мультиполей.
- 4.1.3. Излучение ядер. Правила отбора.
- 4.1.4. Фотоэффект.
- § 4.2. Рассеяние фотона электроном
- 4.2.2. Дифференциальное сечение рассеяния неполяризованных частиц.
- 4.2.3. Угловое распределение рассеянных фотонов и полное сечение.
- 4.2.4. Поляризационные эффекты.
- 4.2.5. Рассеяние поляризованных фотонов неполяризованными электронами.
- 4.2.6. Дисперсионная формула.
- § 4.3. Тормозное излучение
- 4.3.2. Тормозное излучение в высокоэнергетическом приближении.
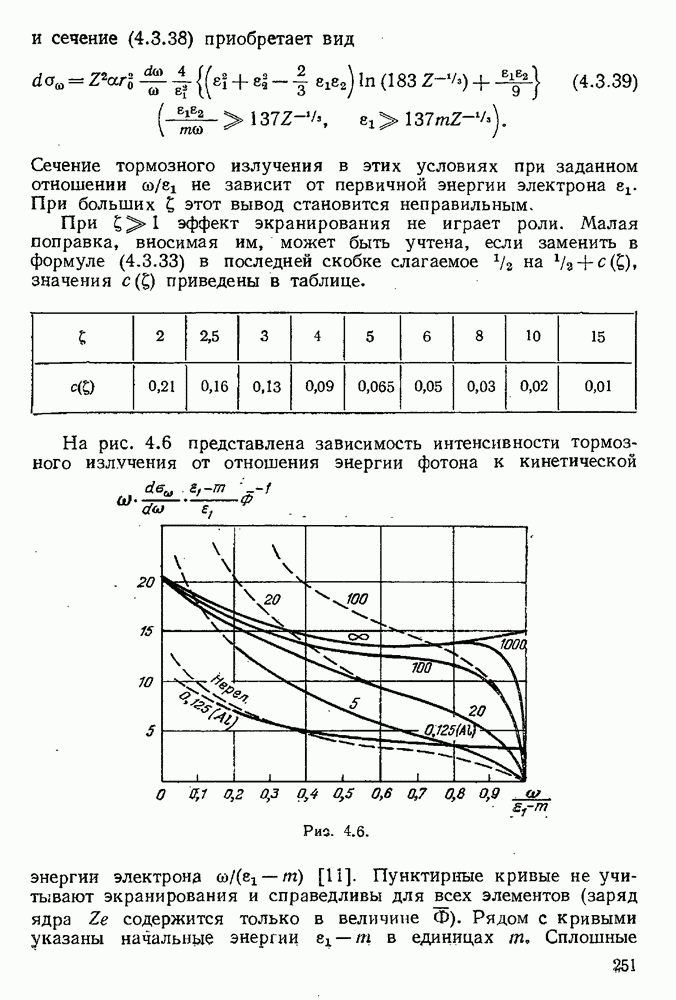
- 4.3.3. Сечение тормозного излучения в кулоновском поле ядра в борновском приближении.
- 4.3.4. Экранирование.
- 4.3.5. Потеря энергии на излучение.
- 4.3.6. Тормозное излучение в кулоновском поле ядра в высокоэнергетическом приближении.
- 4.3.7. Точная теория тормозного излучения в нерелятивистской области.
- § 4.4. Излучение длинноволновых фотонов
- 4.4.2. Сечение рассеяния электрона с излучением мягкого фотона.
- 4.4.3. Исследование расходимости в области малых частот.
- 4.4.4. Излучение мягких фотонов при произвольных столкновениях.
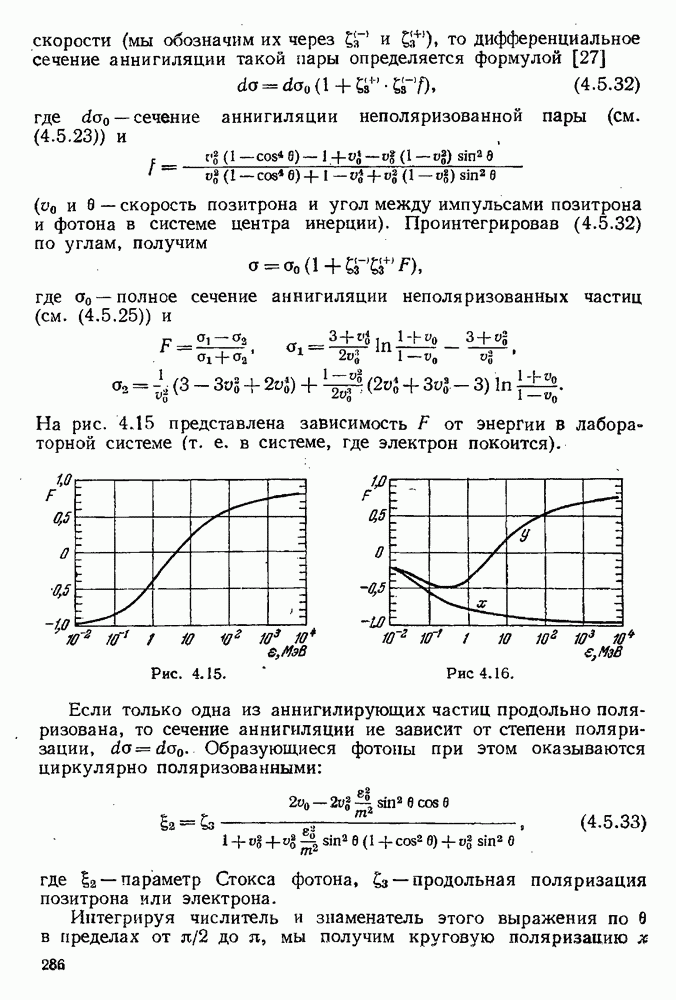
- § 4.5. Образование и аннигиляция электронно-позитронных пар
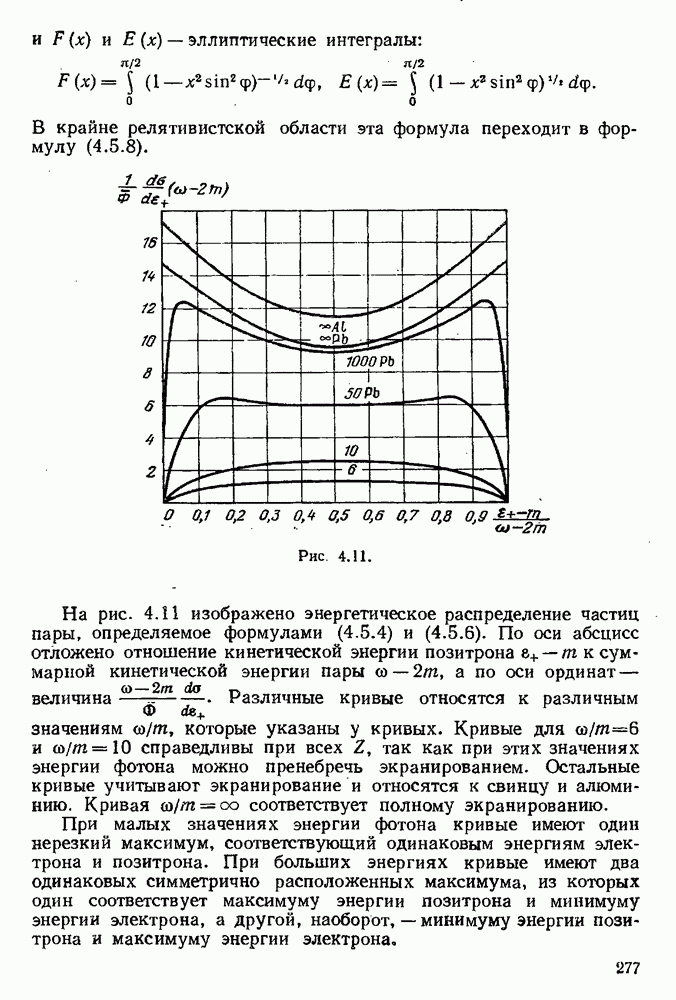
- 4.5.2. Точная теория образования пары фотоном в поле ядра вблизи порога.
- 4.5.3. Образование пары двзмя фотонами.
- 4.5.4. Аннигиляция пары в два и три фотона.
- 4.5.5. Поляризационные эффекты при двухфотонной аннигиляции пар.
- 4.5.6. Распад позитрония.
- 4.5.7. Превращение пары в один фотон.
- § 4.6. Рассеяние электрона и позитрона электроном
- 4.6.2. Сечение рассеяния позитрона электроном.
- 4.6.3. Рассеяние поляризованных электронов.
- 4.6.4. Рассеяние мюона электроном.
- 4.6.5. Излучение фотона при рассеянии электрона электроном и электрона позитроном и при превращении …
- § 4.7. Запаздывающее взаимодействие зарядов
- 4.7.3. Взаимодействие электрона с позитроном и позитроний.
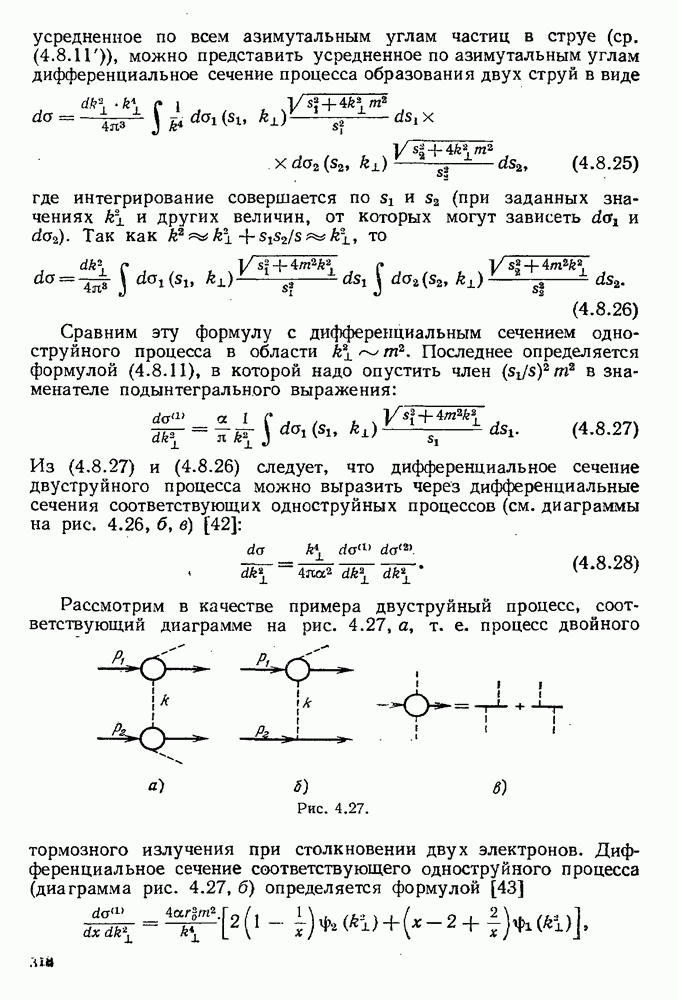
- § 4.8. Метод эквивалентных фотонов
- 4.8.2. Тормозное излучение в процессах рассеяния электрона ядром и электрона электроном.
- 4.8.3. Образование пар фотоном в поле ядра и при столкно вении двух быстрых заряженных частиц.
- 4.8.4. Сечение двуструйного процесса.
- ГЛАВА 5. КВАНТОВОЭЛЕКТРОДИНАМИЧЕСКИЕ ЭФФЕКТЫ В ВЫСШИХ ПРИБЛИЖЕНИЯХ ТЕОРИИ ВОЗМУЩЕНИЙ
- § 5.1. Радиационные поправки к электродинамическим функциям Грина
- 5.1.2. Поляризационный оператор второго порядка.
- 5.1.3. Вершинная функция третьего порядка.
- § 5.2. Модификация закона Кулона. Аномальный магнитный момент электрона
- 5.2.2. Аномальный магнитный момент электрона и мюона.
- § 5.3. Радиационное смещение атомных уровней
- 5.3.2. Радиационное смещение и естественная ширина атомных уровней.
- 5.3.3. Радиационное смещение уровней атома водорода.
- 5.3.4. Рассеяние фотона вблизи резонанса.
- § 5.4. Радиационные поправки к сечениям рассеяния электрона во внешнем поле и рассеяния электрона электроном
- 5.4.2. Исключение «массы» фотона из сечения рассеяния.
- 5.4.3. Устранение инфракрасной расходимости в случае произвольного процесса рассеяния.
- 5.4.4. Радиационные поправки к сечению рассеяния электрона электроном и электрона позитроном.
- § 5.5. Радиационные поправки к сечениям комптоновского рассеяния, образования и аннигиляции пар и тормозного излучения
- 5.5.1. Радиационные поправки к сечению комптоновского рассеяния.
- 5.5.2. Рассеяние электроном фотонов малой частоты.
- 5.5.3. Радиационные поправки к сечению двухфотонной аннигиляции пар.
- 5.5.4. Радиационные поправки к сечению тормозного излучения.
- 5.5.4. Радиационные поправки к сечению тормозного излучения.
- 5.5.5. Радиационные поправки к сечению превращения электронно-позитронной пары в мюонную пару.
- § 5.6. Нелинейная электродинамика вакуума
- 5.6.1. Тензор рассеяния фотона фотоном четвертого ранга.
- 5.6.2. Сечение рассеяния фотона фотоном.
- 5.6.3. Радиационные поправки к функции Лагранжа электромагнитного поля в вакууме.
- 5.6.4. Точное выражение для лагранжиана произвольного медленно меняющегося электромагнитного поля.
- 5.6.5. Сечение рассеяния фэтэна в постоянном электромагнитном поле.
- 5.6.6. Связь между амплитудой рассеяния фотона на нулевой угол и сечением образования пар.
- 5.6.7. Импульсное и угловое распределения ядер отдачи при образовании пар фотоном в поле ядра.
- § 5.7. Дважды логарифмическая асимптотика сечений квантовоэлектродинамических процессов
- 5.7.2. Дважды логарифмическая асимптотика сечения рассеяния электрона во внешнем поле.
- 5.7.3. Дважды логарифмическая асимптотика сечения процесса …
- 5.7.4. Сводка формул для сечений квантовоэлектродинамических процессов в дважды логарифмическом приближении.
- ПРИЛОЖЕНИЕ
- А.1. Вычисление интегралов по инвариантному объему в 4-импульсном пространстве.
- A.2. Метод размерной регуляризации.
- ЛИТЕРАТУРА