| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 36. Итерации с переменным шагом
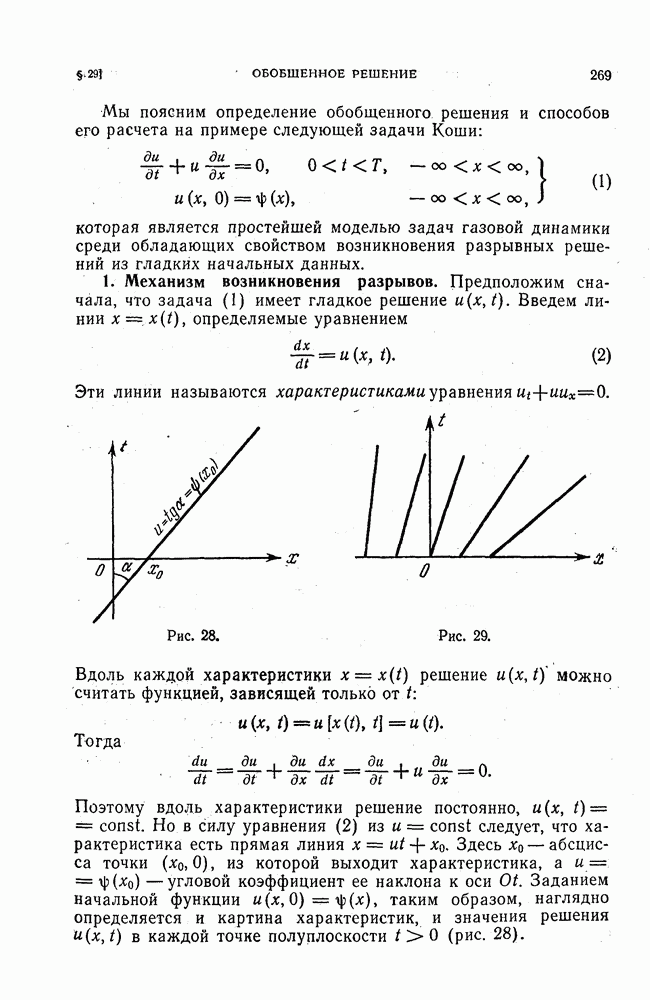
1. Идея Ричардсона.
Механизм сходимости простейшей схемы установления (4) § 35

состоит, как мы видели, в погашении каждой из гармоник  по которым разлагается погрешность
по которым разлагается погрешность  нулевого приближения в конечный ряд Фурье. Если
нулевого приближения в конечный ряд Фурье. Если

то коэффициенты Фурье погрешности следующего приближения

выражаются через  по формулам (см. (10), (11), § 35):
по формулам (см. (10), (11), § 35):

При фиксированном выборе  не все гармоники погашаются одинаково быстро. Более сильно погашаются те гармоники
не все гармоники погашаются одинаково быстро. Более сильно погашаются те гармоники  для которых множитель погашения
для которых множитель погашения  ближе к нулю, т. е. те, для которых
ближе к нулю, т. е. те, для которых  . Это наводит на мысль от шага к шагу менять параметр
. Это наводит на мысль от шага к шагу менять параметр  , чтобы поочередно хорошо гасились все гармоники
, чтобы поочередно хорошо гасились все гармоники  и в результате за несколько шагов все гармоники гасились бы более или менее равномерно.
и в результате за несколько шагов все гармоники гасились бы более или менее равномерно.
В этом состоит идея Ричардсона для решения самосопряженных линейных систем уравнений с матрицей, все собственные значения которой имеют одинаковый знак.
2. Чебышевский набор параметров.
Итерационный процесс Ричардсона задается формулами

с итерационным параметром  зависящим от номера итера
зависящим от номера итера  Ричардсон указал приемлемый, но не оптимальный набор параметров
Ричардсон указал приемлемый, но не оптимальный набор параметров  Изложим результаты об оптимальном наборе итерационных параметров
Изложим результаты об оптимальном наборе итерационных параметров  и оценке скорости убывания нормы погрешности
и оценке скорости убывания нормы погрешности  . В силу формулы (3) очевидно, что коэффициенты Фурье
. В силу формулы (3) очевидно, что коэффициенты Фурье  погрешности
погрешности  шаге выражаются через коэффициенты Фурье
шаге выражаются через коэффициенты Фурье  начальной погрешности
начальной погрешности  по формулам
по формулам

Введем обозначение  , положив
, положив

Тогда

Очевидно, что неравенство

при некоторых  становится точным равенством. Числа
становится точным равенством. Числа  задаваемые формулой (3), разбросаны по отрезку
задаваемые формулой (3), разбросаны по отрезку

где

Мы не будем опираться на фактическое знание чисел  так как это — случайное обстоятельство, имеющее место только для нашего примера. Будем пользоваться лишь тем, что известны границы а и b отрезка (6), на котором они лежат. Поэтому, задай k, поставим задачу такого определения итерационных параметров
так как это — случайное обстоятельство, имеющее место только для нашего примера. Будем пользоваться лишь тем, что известны границы а и b отрезка (6), на котором они лежат. Поэтому, задай k, поставим задачу такого определения итерационных параметров  чтобы среди всех многочленов
чтобы среди всех многочленов  степени k, удовлетворяющих условию
степени k, удовлетворяющих условию

многочлен (5) на отрезке  наименее уклонялся от нуля:
наименее уклонялся от нуля:  минимально. (8)
минимально. (8)

Эта задача теории аппроксимации функций решена в 1892 году А. А. Марковым. Искомый многочлен  выражается через многочлен Чебышева (см., например, В. Л. Гончаров, Теория интерполирования и приближения функций, М., 1954)
выражается через многочлен Чебышева (см., например, В. Л. Гончаров, Теория интерполирования и приближения функций, М., 1954)

наименее уклоняющийся от нуля на отрезке  среди всех многочленов степени k, с коэффициентом единица при
среди всех многочленов степени k, с коэффициентом единица при  Именно, если сделать линейное преобразование
Именно, если сделать линейное преобразование

переводящее отрезок  в отрезок
в отрезок  , а точку
, а точку  в точку
в точку  , то
, то

 итерационных параметров
итерационных параметров  , при которых возникает многочлен (10), определяется из условия, чтобы нули
, при которых возникает многочлен (10), определяется из условия, чтобы нули  многочлена
многочлена  при преобразовании. (9) переходили в нули
при преобразовании. (9) переходили в нули  многочлена Чебышева
многочлена Чебышева  :
:

Оценим наибольшее отклонение Q многочлена  от нуля на отрезке
от нуля на отрезке  . Как известно из теории аппроксимации функций, многочлен Чебышева
. Как известно из теории аппроксимации функций, многочлен Чебышева  принимает наибольшее по модулю значение на отрезке
принимает наибольшее по модулю значение на отрезке  в
в  точках, к числу которых принадлежат концы этого отрезка. Поэтому из (10) следует, что
точках, к числу которых принадлежат концы этого отрезка. Поэтому из (10) следует, что

Далее, из (9) получаем

Поэтому при больших М

откуда, с учетом (13), следует

Считая, что норма первоначальной ошибки  порядка единицы,
порядка единицы,  в силу замечания п. 4 § 35 о разумном порядке
в силу замечания п. 4 § 35 о разумном порядке
точности, которого следует добиваться, решая задачу итерациями, надо выбрать k из условия  т. е.
т. е.

Для погашения первоначальной погрешности в  раз надо выбрать k из условия
раз надо выбрать k из условия  т. е.
т. е.

Выбрав k из этого условия, можно затем первые k шагов итерации принять за первый цикл итераций и повторять весь цикл с тем же набором параметров  Для уменьшения нормы погрешности в
Для уменьшения нормы погрешности в  раз потребуется такое число v циклов, чтобы
раз потребуется такое число v циклов, чтобы  Общее число элементарных шагов итерационного процесса за v циклов будет
Общее число элементарных шагов итерационного процесса за v циклов будет

Оно лишь в конечное число раз

превосходит число (14) элементарных шагов итерационного процесса, не использующего зацикливание. Таким образом, использование цикла с  дает упрощение без существенного увеличения числа итераций.
дает упрощение без существенного увеличения числа итераций.
Использовать циклы длины  нецелесообразно. Например, при
нецелесообразно. Например, при  процесс Ричардсона (4) превратится в процесс простых итераций (1) с оптимальным выбором т. Число шагов процесса для уменьшения нормы первоначальной ошибки
процесс Ричардсона (4) превратится в процесс простых итераций (1) с оптимальным выбором т. Число шагов процесса для уменьшения нормы первоначальной ошибки  в
в  раз будет
раз будет  как показано в п. 2 § 35. Это число в
как показано в п. 2 § 35. Это число в  раз превышает число шагов, необходимых для этой же цели при выборе длины k цикла в соответствии с (15).
раз превышает число шагов, необходимых для этой же цели при выборе длины k цикла в соответствии с (15).
3. Нумерация итерационных параметров.
Формулы (11) задают оптимальный набор итерационных параметров  (при заданном фиксированном k). Переставим как-либо члены последовательности
(при заданном фиксированном k). Переставим как-либо члены последовательности  , расположив их в некоторой очередности
, расположив их в некоторой очередности  и будем вести итерации по формулам
и будем вести итерации по формулам

При идеальной реализации алгоритма (16) результат финальной,  итерации
итерации  зависит от выбранной очередности
зависит от выбранной очередности  . Но при реальном расчете, который ведется на машине с конечным числом знаков, этот порядок крайне важен. От него при больших k резко зависит чувствительность результата к ошибкам округления, допускаемым на промежуточных шагах процесса, т. е. вычислительная устойчивость алгоритма. Прежде чем приводить приемлемые порядки
. Но при реальном расчете, который ведется на машине с конечным числом знаков, этот порядок крайне важен. От него при больших k резко зависит чувствительность результата к ошибкам округления, допускаемым на промежуточных шагах процесса, т. е. вычислительная устойчивость алгоритма. Прежде чем приводить приемлемые порядки  заметим, что исходный алгоритм (4), отвечающий
заметим, что исходный алгоритм (4), отвечающий  практически непригоден.
практически непригоден.

Рис. 45.
Разберемся в механизме возникновения неустойчивости в этом случае. Пусть начальная погрешность  имеет вид
имеет вид  и расчет ведется точно, без ошибок округления. Тогда коэффициенты погрешности
и расчет ведется точно, без ошибок округления. Тогда коэффициенты погрешности  приближения
приближения  выражаются формулой
выражаются формулой

Проследим за эволюцией  с ростом l при
с ростом l при  . В этом случае
. В этом случае

Рассмотрим линейные функции  нули которых
нули которых  определяются формулами (11). Из этих формул видно, что при
определяются формулами (11). Из этих формул видно, что при  или
или  справедливо неравенство
справедливо неравенство  и поэтому (рис. 45)
и поэтому (рис. 45)

Если  то
то  и поэтому
и поэтому

Таким образом, величина определенная формулой (17), увеличивается сначала примерно в  раз за один шаг, а потом медленнее. В силу (18) этот рост продолжается во всяком случае до тех пор, пока
раз за один шаг, а потом медленнее. В силу (18) этот рост продолжается во всяком случае до тех пор, пока  так что при
так что при  величина
величина  а вместе с ней и
а вместе с ней и  окажется очень большой и тем большей, чем больше число k. При этом порядки величин значений приближения
окажется очень большой и тем большей, чем больше число k. При этом порядки величин значений приближения  могут выйти за пределы допустимых для данной машины уже при умеренных
могут выйти за пределы допустимых для данной машины уже при умеренных  .
.
Если гипотетически считать, что этого не произошло и что счет продолжается точно, то к шагу  величина
величина  вновь уменьшится, так что
вновь уменьшится, так что
Но дело в том, что даже если и не произошло переполнения ячеек машинной памяти при  неизбежные малые относительные ошибки округления при
неизбежные малые относительные ошибки округления при  велики по абсолют ной величине. Они носят случайный характер, так что в их разложении в конечный ряд Фурье будут присутствовать все члены, в частности член вида
велики по абсолют ной величине. Они носят случайный характер, так что в их разложении в конечный ряд Фурье будут присутствовать все члены, в частности член вида

причем  величина не малая по абсолютной величине.
величина не малая по абсолютной величине.
Покажем, что при дальнейших шагах итерации ошибка  внесенная на гармонику
внесенная на гармонику  в результате округления на шаге
в результате округления на шаге  не претерпевает существенного погашения и недопустимо искажает результат. Вызванный ею вклад с
не претерпевает существенного погашения и недопустимо искажает результат. Вызванный ею вклад с  в приближение
в приближение  полученное на последнем,
полученное на последнем,  шаге, выражается формулой
шаге, выражается формулой

Но при  , очевидно,
, очевидно,

Поэтому

так что  и погашения погрешности округления не произошло. Практическая непригодность нумерации параметров
и погашения погрешности округления не произошло. Практическая непригодность нумерации параметров  показана.
показана.
Если на  шаге процесса (13) внесена погрешность округления
шаге процесса (13) внесена погрешность округления

то на  шаге она разовьется в
шаге она разовьется в

Поэтому целесообразно стремиться к такому выбору  при котором имеет место оценка
при котором имеет место оценка

при умеренном значении А.
Пусть  компонента погрешности
компонента погрешности  нулевого приближения. К l-му шагу она разовьется в
нулевого приближения. К l-му шагу она разовьется в

Если норма этой функции велика, то ее округление дает значительный по абсолютной величине вклад во все гармоники. Может оказаться, что вклад, полученный некоторыми гармониками, при дальнейших итерациях не погашается и сильно искажает результат. Поэтому естественно стремиться к такому выбору  при котором выполнено неравенство
при котором выполнено неравенство

при умеренном значении В.
В работе В. И. Лебедева и С. А. Финогенова, ЖВМ и МФ 11, № 2, (1971), и в работе А. А. Самарского [23] указаны различные целесообразные способы нумерации параметров и освещена история вопроса. Приведем результаты работы В. И. Лебедева и С. А. Финогенова. В ней предполагается, что k является степенью числа 2, т. е.  и указаны реккурентные формулы для построения
и указаны реккурентные формулы для построения 
Именно, при 

Если при  порядок уже определен:
порядок уже определен:

то полагаем

В частности, при  последовательно получаем
последовательно получаем

При указанном способе (21) упорядочения итерационных параметров числа А и В в неравенствах (19) и (20) можно выбрать независимыми от k и от
Алгоритм упорядочения параметров, указанный А. А. Самарским, формулируется несколько сложнее, но при этом k не обязательно степень двойки. Число k может иметь вид  . Вместо (19), (20) установлены другие оценки, гарантирующие устойчивость в некотором смысле.
. Вместо (19), (20) установлены другие оценки, гарантирующие устойчивость в некотором смысле.
4. Метод Дугласа Рэкфорда.
В схеме переменных направлений (6) § 35 будем считать итерационный параметр  зависящим от номера шага, положив
зависящим от номера шага, положив

Для погрешности  и получим выражение
и получим выражение

где

При заданном k оптимальным является такой выбор чисел  при котором величина
при котором величина

принимает наименьшее значение. Если не пользоваться точным знанием чисел  а лишь границами, где они лежат, возникает задача чебышевского типа для произведения дробнолинейных функций, подобная рассмотренной в п. 2 для многочленов.
а лишь границами, где они лежат, возникает задача чебышевского типа для произведения дробнолинейных функций, подобная рассмотренной в п. 2 для многочленов.
Постановка этой задачи, как впрочем и предложение использовать для решения уравнения Пуассона процесс установления
со схемой переменных направлений, принадлежит Дугласу, Писману и Рэкфорду. В работе Дугласа и Рэкфорда 1956 года, которую мы здесь изложим, было дано приближенное решение этой задачи. При их выборе итерационных параметров число шагов итерационного процесса, нужное для уменьшения ошибки в  раз, есть
раз, есть  , а число арифметических действий есть
, а число арифметических действий есть  .
.
Покажем, что, задав произвольно положительное  можно так выбрать итерационные параметры
можно так выбрать итерационные параметры  в количестве
в количестве  чтобы выполнялись неравенства
чтобы выполнялись неравенства

Тогда  . Если производить первые k итераций с итерационными параметрами
. Если производить первые k итераций с итерационными параметрами  затем следующие k итераций, снова используя
затем следующие k итераций, снова используя  то для уменьшения нормы погрешности в
то для уменьшения нормы погрешности в  раз потребуется, очевидно, некоторое не зависящее от М число таких циклов, содержащих по
раз потребуется, очевидно, некоторое не зависящее от М число таких циклов, содержащих по  итераций каждый.
итераций каждый.
Обоснуем равенство (22) и при этом объясним, как можно выбрать параметры  . Очевидно, что
. Очевидно, что

Поэтому для выполнения при любых  неравенства (22) достаточно, чтобы при любом
неравенства (22) достаточно, чтобы при любом  хотя бы один из k сомножителей
хотя бы один из k сомножителей  удовлетворял неравенству
удовлетворял неравенству

Все числа  принадлежат отрезку
принадлежат отрезку

Итак, для выполнения (22) достаточно ввиду (23), чтобы для каждого значения  из отрезка (24) хотя бы при одном
из отрезка (24) хотя бы при одном  выполнялись неравенства
выполнялись неравенства

и тем более достаточно, чтобы выполнялись неравенства

Для этого нужно, чтобы для каждого  из отрезка (24) при некотором
из отрезка (24) при некотором  , выполнялись неравенства
, выполнялись неравенства

Зададим  соответственно формулами
соответственно формулами

Тогда при возрастании  от
от  до
до  число
число  пробегает отрезок (25).
пробегает отрезок (25).
Очевидно, что, выбрав k из условия 

мы и получим по формуле (26) интересующую нас последовательность 
ЗАДАЧИ
1. Можно ли выбрать итерационные параметры  та так, чтобы за конечное число шагов итерационного процесса (4) получилось точное решение разностной задачи Дирихле?
та так, чтобы за конечное число шагов итерационного процесса (4) получилось точное решение разностной задачи Дирихле?
Сколько для этого надо сделать итераций? Выдерживает ли такой прием решения обобщение на случай, когда точные значения собственных чисел  неизвестны?
неизвестны?
2. Объяснить механизм вычислительной неустойчивости, развивающейся при расчете по формулам (16) при

и больших значениях k и М.
Какие гармоники  будут преобладать в ряде Фурье для погрешности
будут преобладать в ряде Фурье для погрешности  , полученной в результате расчета при
, полученной в результате расчета при  с ошибками округления?
с ошибками округления?
3. Пусть А — самосопряженный оператор, собственные значения которого лежат на отрезке  Какому условию должно удовлетворять число обусловленности
Какому условию должно удовлетворять число обусловленности  чтобы для решения уравнения
чтобы для решения уравнения  сходился и был вычислительно устойчив процесс Ричардсона
сходился и был вычислительно устойчив процесс Ричардсона

при произвольном выборе  произвольно?
произвольно?
4. Почему при использовании схемы Дугласа — Рэкфорда очередность использования параметров  не влияет существенным образом на вычислительную устойчивость итерационного процесса?
не влияет существенным образом на вычислительную устойчивость итерационного процесса?
5. Считая, что затраты машинного времени на один шаг итерационного процесса Дугласа — Рэкфорда в двадцать раз больше, чем на один шаг процесса Ричардсона, прикинуть по формулам (15) и (27), при каких М преимущества метода Дугласа — Рэкфорда начинают проявляться.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
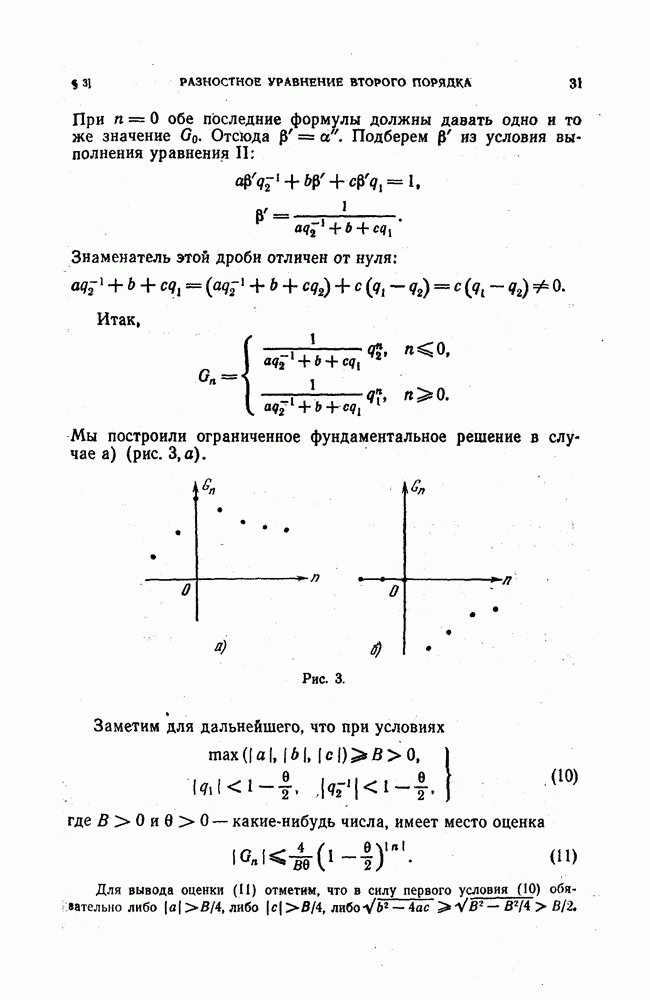
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
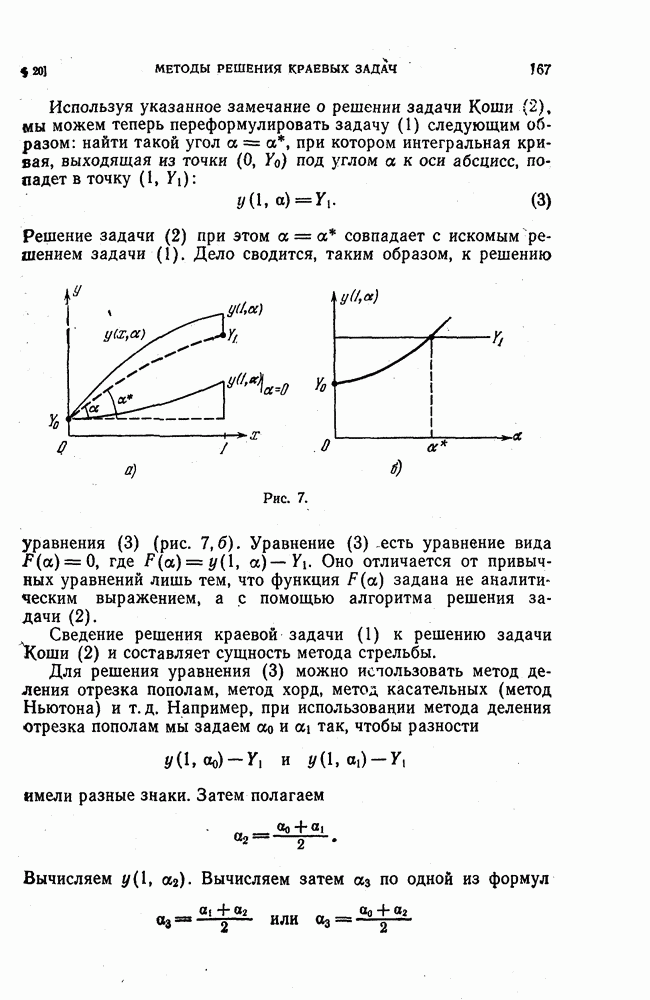
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА