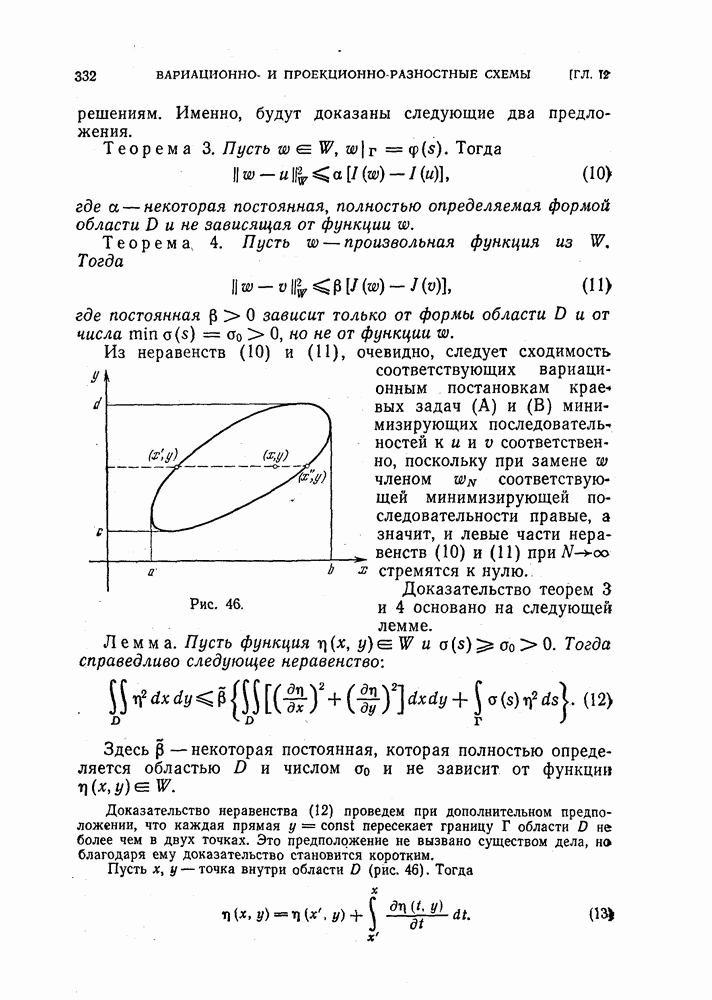
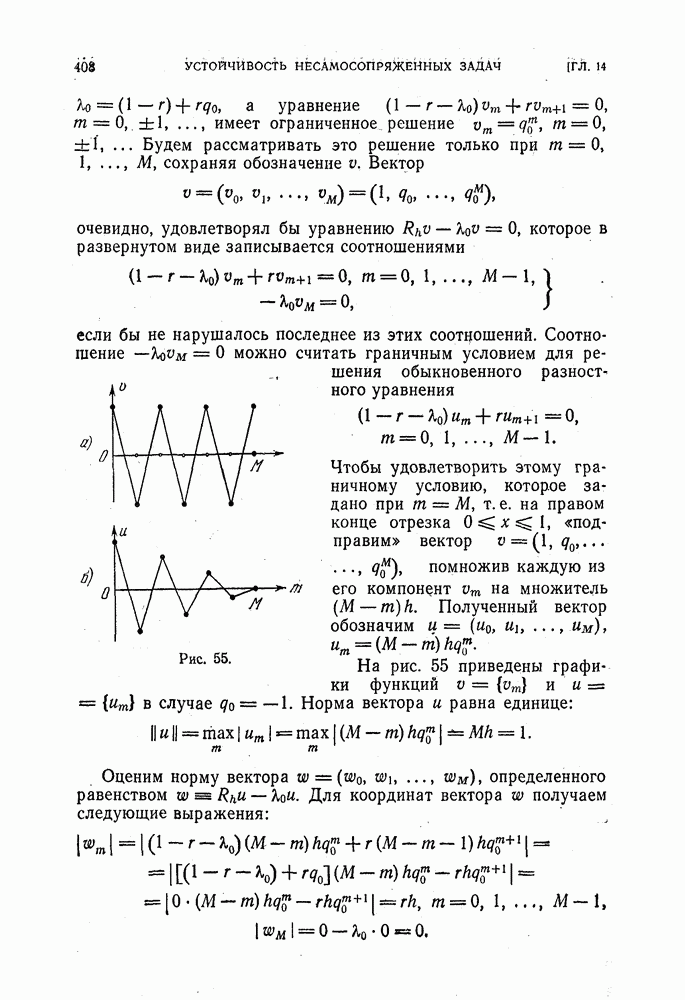
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
В гл. 4 мы на примерах выяснили, что такое аппроксимация дифференциальной задачи разностной задачей и в чем состоит сходимость, благодаря которой решение дифференциальной задачи можно приближенно вычислять по разностной схеме. Мы познакомились с явлением неустойчивости, которое может сделать разностную схему расходящейся и непригодной для вычислений. Анализ поведения решений в этих элементарных вводных примерах, предназначенных только для предварительного знакомства с основными понятиями, был основан на записи решений в виде формул. Такая запись оказалась возможной лишь благодаря специальному подбору примеров.
В этой главе мы дадим строгие определения понятий сходимости, аппроксимации и устойчивости. Мы покажем, что доказательство сходимости не обязательно основывать на анализе формул для решений. Это доказательство можно разбить на проверку аппроксимации дифференциальной задачи разностной и проверку устойчивости разностной задачи.
§ 10. Сходимость разностной схемы
1. Понятие о сетке и сеточной функции.
Пусть на некотором отрезке D поставлена некоторая дифференциальная краевая задача. Это значит, что задано дифференциальное уравнение (или система), которому должно удовлетворять решение и на отрезке D и дополнительные условия для и на одном или на обоих концах отрезка. Дифференциальную краевую задачу будем записывать в виде символического равенства

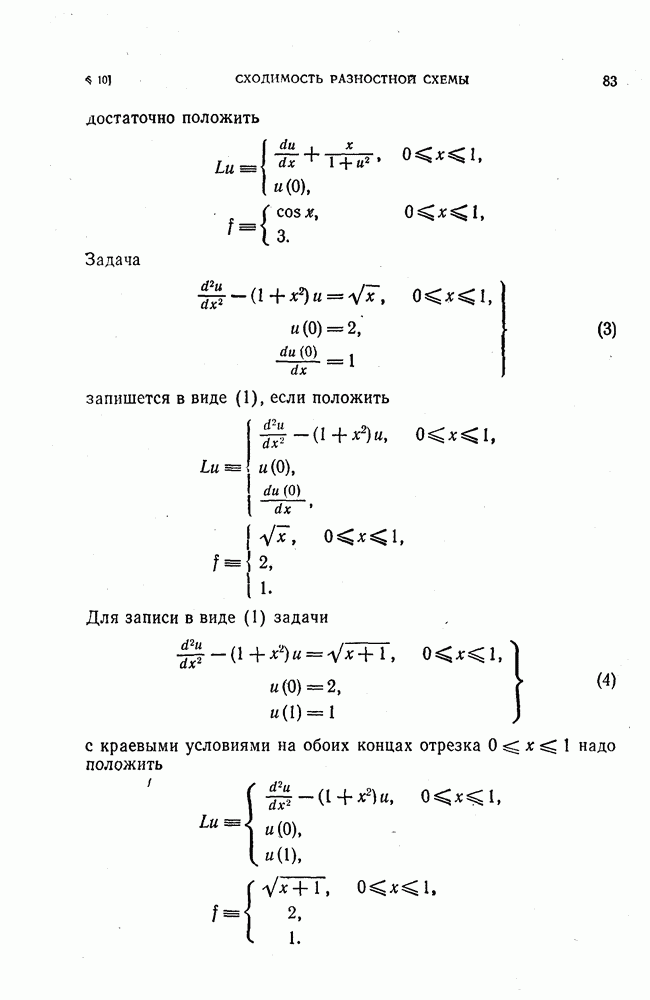
где L — заданный дифференциальный оператор,  — заданная правая часть. Так, например, чтобы записать в виде (1) задачу
— заданная правая часть. Так, например, чтобы записать в виде (1) задачу

достаточно положить

Задача

запишется в виде (1), если положить

Для записи в виде (1) задачи

с краевыми условиями на обоих концах отрезка  надо положить
надо положить

Краевая задача для системы дифференциальных уравнений

будет записана в форме (1), если считать и вектор-функцией  и положить
и положить

Во всех примерах мы рассматриваем задачу на отрезке  не на каком-либо другом, только для определенности.
не на каком-либо другом, только для определенности.
Будем предполагать, что решение  задачи (1) на отрезке существует. Для вычисления этого решения с помощью метода конечных разностей, или метода сеток, надо прежде всего выбрать на отрезке D конечное число точек, совокупность которых будем называть сеткой и обозначать через
задачи (1) на отрезке существует. Для вычисления этого решения с помощью метода конечных разностей, или метода сеток, надо прежде всего выбрать на отрезке D конечное число точек, совокупность которых будем называть сеткой и обозначать через  , а затем считать искомым не решение
, а затем считать искомым не решение  задачи (1), а таблицу
задачи (1), а таблицу  значений этого решения в точках сетки
значений этого решения в точках сетки  . Предполагается, что сетка
. Предполагается, что сетка  зависит от параметра
зависит от параметра  который может принимать сколь угодно малые положительные значения. При стремлении «шага сетки» h к нулю сетка должна становиться все «гуще». Например, можно положить
который может принимать сколь угодно малые положительные значения. При стремлении «шага сетки» h к нулю сетка должна становиться все «гуще». Например, можно положить  , где N — какое-нибудь натуральное число, и принять за сетку
, где N — какое-нибудь натуральное число, и принять за сетку  совокупность точек
совокупность точек  . Искомая сеточная функция
. Искомая сеточная функция  в этом случае в точке
в этом случае в точке  сетки
сетки  принимает значение
принимает значение  которое для краткости будем обозначать
которое для краткости будем обозначать  .
.
Для приближенного вычисления таблицы значений решения  в случае задачи (2) можно воспользоваться, например, системой уравнений
в случае задачи (2) можно воспользоваться, например, системой уравнений

полученной в результате замены производной  в точках сетки разностным отношением по приближенной формуле
в точках сетки разностным отношением по приближенной формуле

Решение  системы (6) определено на той же сетке
системы (6) определено на той же сетке  что и искомая сеточная функция
что и искомая сеточная функция  . Его значения
. Его значения  в точках
в точках  последовательно вычисляются из (6) при
последовательно вычисляются из (6) при  Для краткости в уравнении (6) мы не пишем значок h при
Для краткости в уравнении (6) мы не пишем значок h при  . Как правило, мы будем так же поступать в аналогичных случаях и в дальнейшем.
. Как правило, мы будем так же поступать в аналогичных случаях и в дальнейшем.
В случае задачи (4) для отыскания сеточной функции  приближенно совпадающей с искомой таблицей решения
приближенно совпадающей с искомой таблицей решения  можно воспользоваться разностной схемой
можно воспользоваться разностной схемой

Эта схема возникает в результате замены в точках сетки производной  входящей в дифференциальное уравнение, по приближенной формуле
входящей в дифференциальное уравнение, по приближенной формуле

Для вычисления решения  задачи (7) можно воспользоваться алгоритмом исключения — прогонки, описанным в § 5.
задачи (7) можно воспользоваться алгоритмом исключения — прогонки, описанным в § 5.
Выпишем еще разностную схему, пригодную для вычисления решения задачи (5):

Здесь  задано. При
задано. При  из уравнений (9) можно найти
из уравнений (9) можно найти  Вообще, зная
Вообще, зная  , можно при
, можно при  вычислить
вычислить 
В рассмотренных примерах сетка  состоит из удаленных друг от друга на расстояние h точек. Ясно, что можно было бы расположить
состоит из удаленных друг от друга на расстояние h точек. Ясно, что можно было бы расположить  точек сетки
точек сетки  на отрезке [0, 1] не равномерно, а так, чтобы
на отрезке [0, 1] не равномерно, а так, чтобы  где
где  не равные между собой числа, однако такие, что
не равные между собой числа, однако такие, что  при
при  Выбором расположения узлов сетки
Выбором расположения узлов сетки  можно добиться того, чтобы искомая таблица
можно добиться того, чтобы искомая таблица  решения
решения  была подробнее при данном фиксированном
была подробнее при данном фиксированном  на тех участках, где
на тех участках, где  более быстро изменяется. Такие участки иногда бывают заранее известны из физики или из предвари тельных грубых расчетов. Информация о скорости изменения
более быстро изменяется. Такие участки иногда бывают заранее известны из физики или из предвари тельных грубых расчетов. Информация о скорости изменения  выявляется также в ходе последовательного вычисления
выявляется также в ходе последовательного вычисления  и может быть учтена при выборе следующего узла сетки
и может быть учтена при выборе следующего узла сетки 
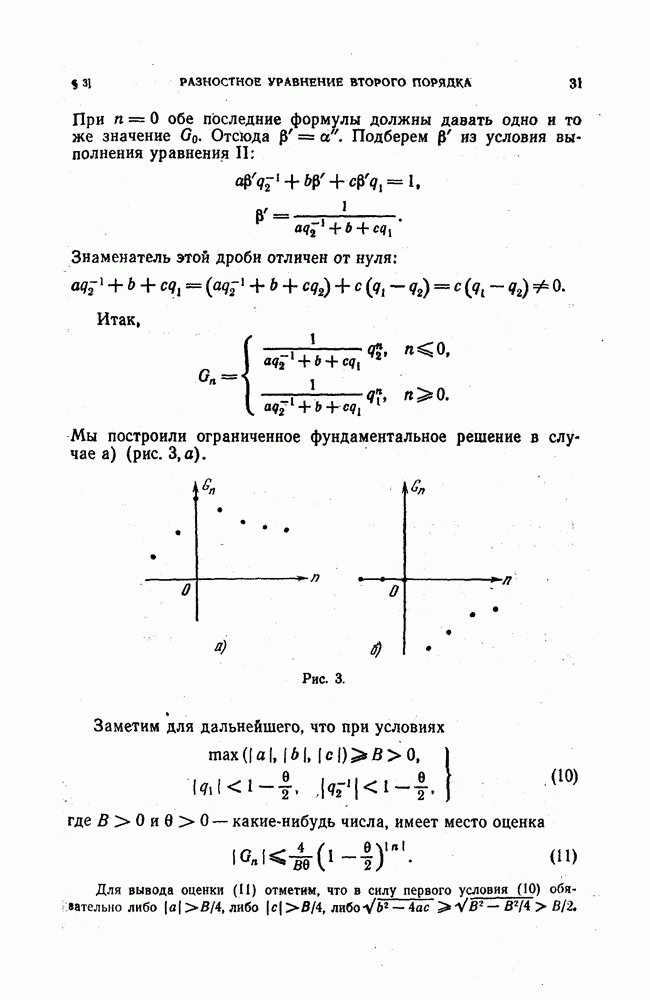
Мы ограничимся приведенными примерами для иллюстрации понятия сетки и искомой сеточной функции (или вектор-функции) — таблицы значений решения  Заметим только, что в качестве искомой таблицы
Заметим только, что в качестве искомой таблицы  значений решения не обязательно рассматривать сеточную функцию, совпадающую с решением и в точках сетки. Возможны и другие способы установления соответствия между функцией и ее таблицей. Например, таблицей
значений решения не обязательно рассматривать сеточную функцию, совпадающую с решением и в точках сетки. Возможны и другие способы установления соответствия между функцией и ее таблицей. Например, таблицей  можно считать сеточную функцию
можно считать сеточную функцию  , определенную в точках
, определенную в точках  равенством
равенством

Такой способ установления соответствия удобен в случае, когда  не является непрерывной функцией, но известно, что интеграл от нее по любому отрезку существует. Это может быть, например, при рассмотрении обобщенных — разрывных — решений, если существует
не является непрерывной функцией, но известно, что интеграл от нее по любому отрезку существует. Это может быть, например, при рассмотрении обобщенных — разрывных — решений, если существует

Всюду в дальнейшем, если не оговорено противное, мы будем считать, что и— непрерывная функция, а под  понимать сеточную функцию, совпадающую
понимать сеточную функцию, совпадающую  точках сетки.
точках сетки.
Мы ставим вопрос о вычислении сеточной функции  потому, что при измельчении сетки, т. е. при
потому, что при измельчении сетки, т. е. при  она является все более подробной таблицей искомого решения и и дает о нем все более полное представление. Пользуясь интерполяцией, можно было бы с возрастающей при
она является все более подробной таблицей искомого решения и и дает о нем все более полное представление. Пользуясь интерполяцией, можно было бы с возрастающей при  точностью восстановить решение и всюду в области D. Ясно, что точность, с которой это можно сделать при заданном фиксированном числе и расположении узлов сетки
точностью восстановить решение и всюду в области D. Ясно, что точность, с которой это можно сделать при заданном фиксированном числе и расположении узлов сетки  зависит от дополнительно известных сведений о решении типа оценок для его производных, а также от расположения узлов сетки
зависит от дополнительно известных сведений о решении типа оценок для его производных, а также от расположения узлов сетки 
Ограничимся этими беглыми замечаниями о восстановлении функции и по ее таблице  Подробное рассмотрение вопросов восстановления функции по ее таблице составляет предмет теории интерполяции. Мы будем заниматься только задачей вычисления таблицы
Подробное рассмотрение вопросов восстановления функции по ее таблице составляет предмет теории интерполяции. Мы будем заниматься только задачей вычисления таблицы  Поэтому условимся считать, что задача (1) решена точно, если найдена сеточная функция
Поэтому условимся считать, что задача (1) решена точно, если найдена сеточная функция  Однако нам не удастся вычислять ее точно. Вместо сеточной функции
Однако нам не удастся вычислять ее точно. Вместо сеточной функции  будем искать другую сеточную функцию
будем искать другую сеточную функцию  которая «сходится» к
которая «сходится» к  при измельчении сетки. Для этой цели можно использовать разностные уравнения.
при измельчении сетки. Для этой цели можно использовать разностные уравнения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
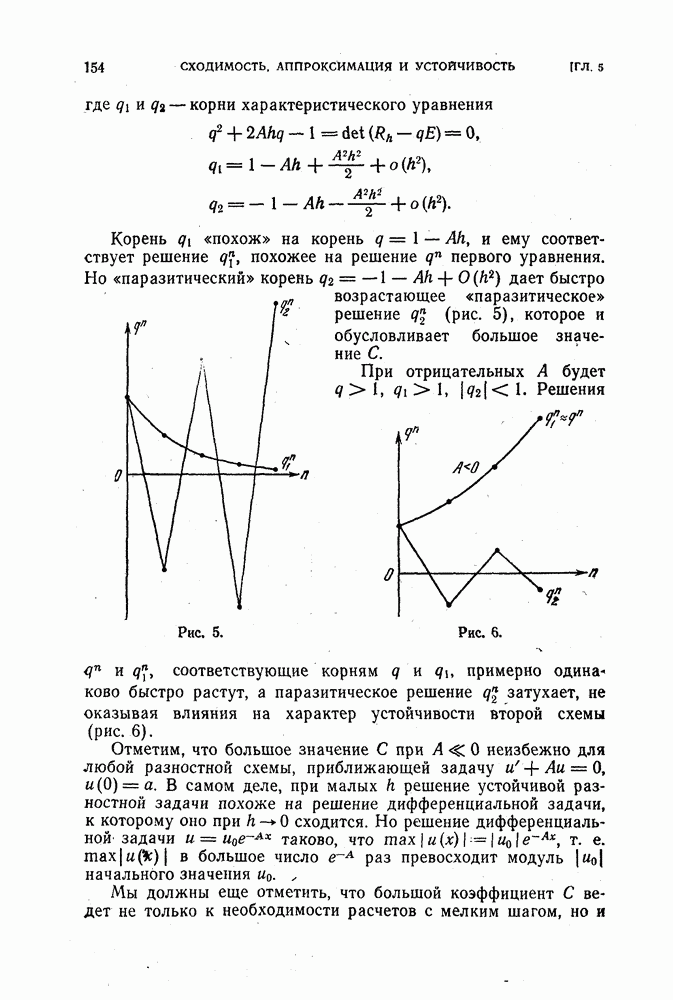
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
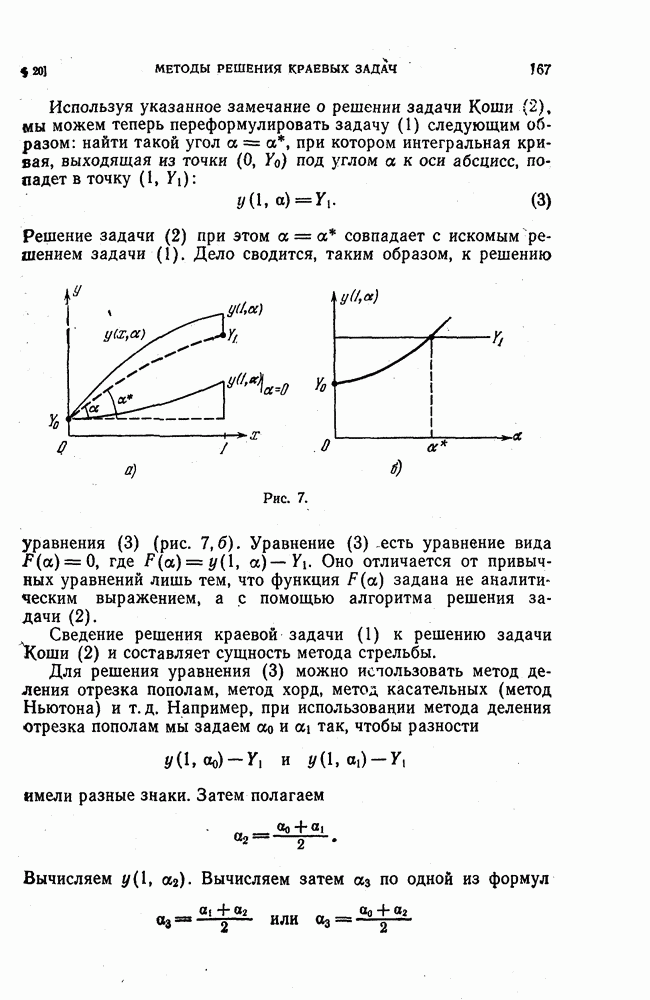
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
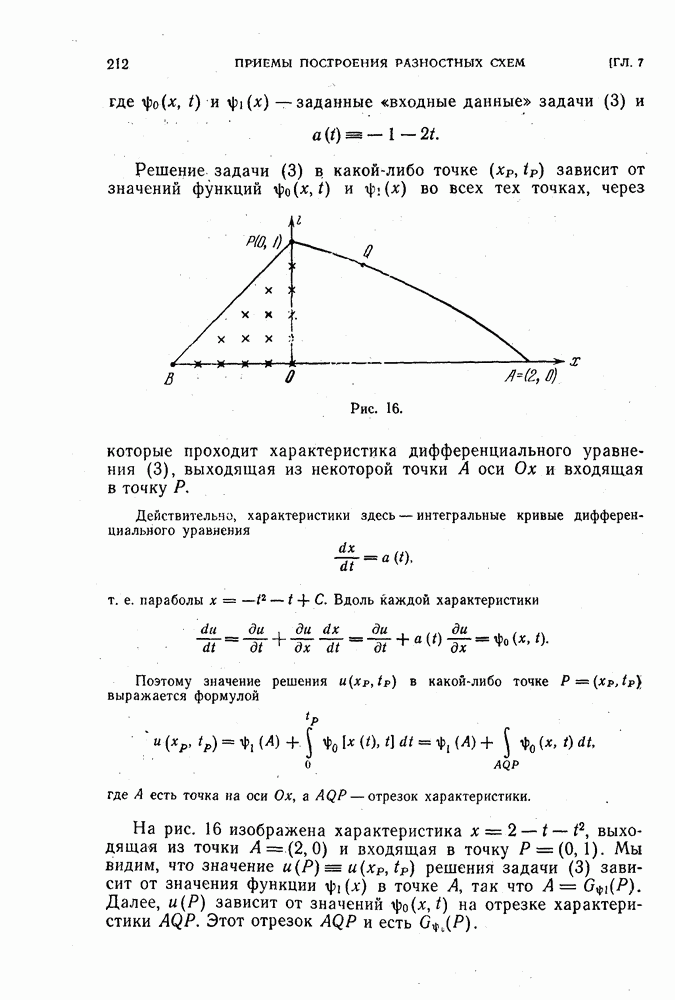
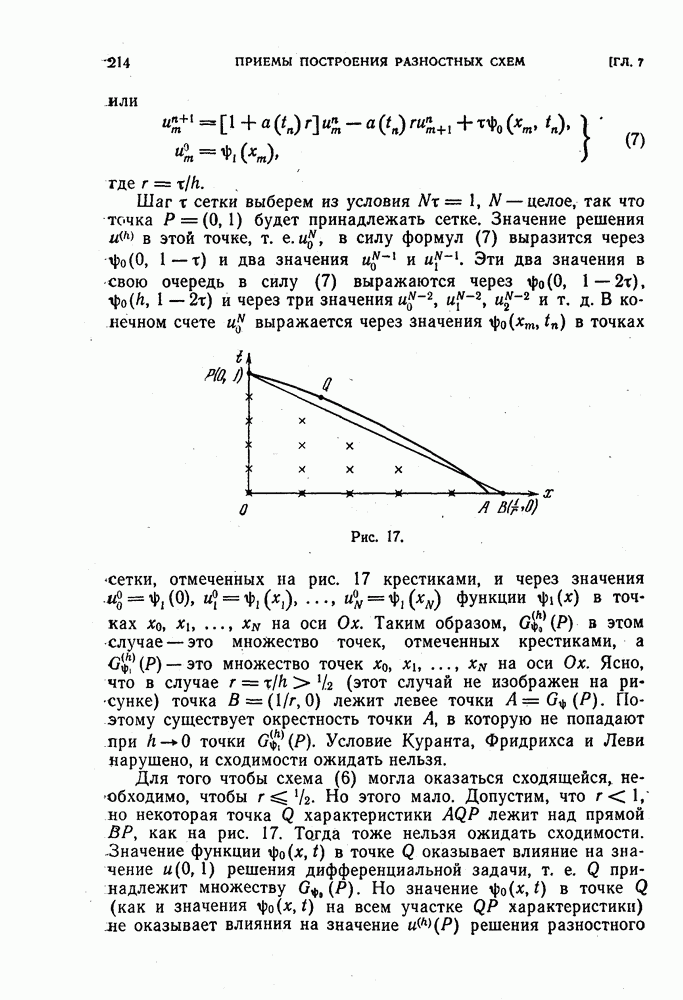
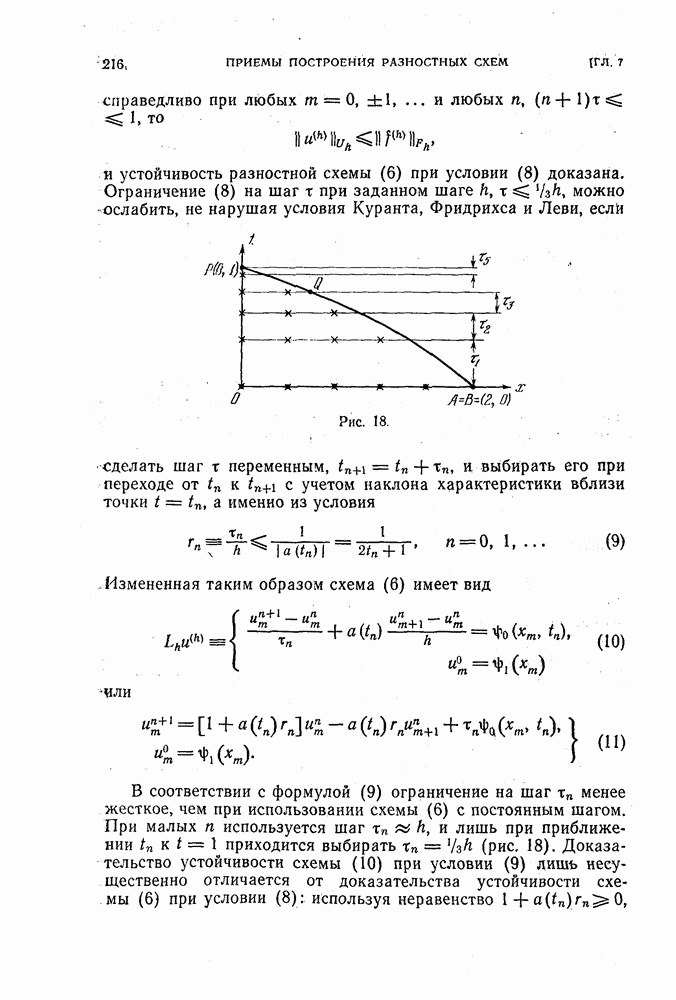
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
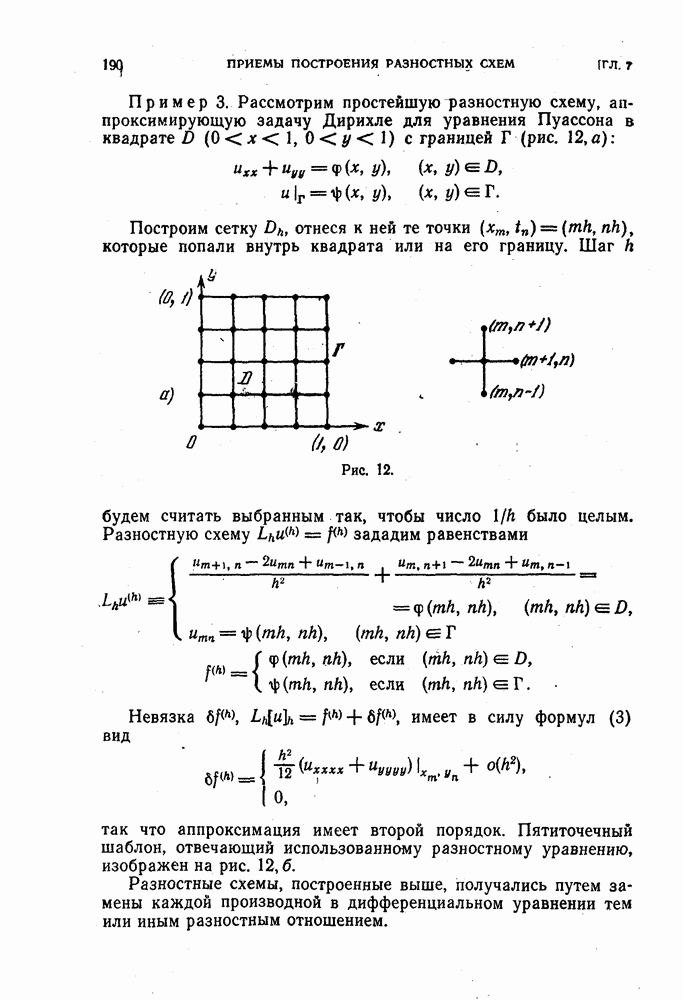
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА