| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Признак Бабенко и Гельфанда.
При рассмотрении задачи (1) мы полагали, что возмущения, сообщенные решению задачи (1) в окрестности произвольной внутренней точки  , при мелкой сетке развиваются примерно так же, как такие же возмущения, сообщенные решению задачи Коши (2) с замороженными в точке
, при мелкой сетке развиваются примерно так же, как такие же возмущения, сообщенные решению задачи Коши (2) с замороженными в точке  коэффициентами. В обоснование этого принципа мы принимали во внимание, что расстояния от внутренней точки
коэффициентами. В обоснование этого принципа мы принимали во внимание, что расстояния от внутренней точки  до границ, измеренные числом шагов сетки,
до границ, измеренные числом шагов сетки,  измельчении сетки неограниченно возрастают. Но если точка
измельчении сетки неограниченно возрастают. Но если точка  лежит на боковой границе
лежит на боковой границе  или
или  то это эвристическое рассуждение теряет убедительность. Пусть, например,
то это эвристическое рассуждение теряет убедительность. Пусть, например,  Тогда расстояние от точки
Тогда расстояние от точки  до любой фиксированной точки
до любой фиксированной точки  (в частности, до правого конца отрезка х=1),
(в частности, до правого конца отрезка х=1),
измеренное числом шагов сетки, при  по-прежнему неограниченно возрастает, но число шагов до левого конца
по-прежнему неограниченно возрастает, но число шагов до левого конца  не меняется и остается равным нулю.
не меняется и остается равным нулю.
Поэтому возмущение решения задачи (1) вблизи левой границы  за малое время должно развиваться подобно возмущению решения задачи
за малое время должно развиваться подобно возмущению решения задачи

Эта задача получилась из исходной задачи (1) при замораживании коэффициента  в левом конце отрезка
в левом конце отрезка  и одновременном удалении правой границы в
и одновременном удалении правой границы в  Задачу (4) естественно рассматривать только на тех функциях
Задачу (4) естественно рассматривать только на тех функциях  которых
которых

Только в этом случае возмущение сосредоточено вблизи границы  и только относительно возмущений такого вида задача (1) и задача (4) вблизи левой границы
и только относительно возмущений такого вида задача (1) и задача (4) вблизи левой границы  сходны между собой.
сходны между собой.
Точно так же развитие возмущений решения задачи (1) вблизи правой границы  должно быть похоже на развитие таких же возмущений для задачи
должно быть похоже на развитие таких же возмущений для задачи

с одной только правой границей. Эта задача возникла из исходной задачи (1) при замораживании коэффициента  и правом конце
и правом конце  и при удалении левой границы в
и при удалении левой границы в  За дачу (5) надо рассматривать на сеточных функциях
За дачу (5) надо рассматривать на сеточных функциях  удовлетворяющих условию
удовлетворяющих условию 
Задачи (2), (4) и (5) проще исходной задачи (1) в том от ношении, что при фиксированном  они не зависят от h и являются задачами с постоянными коэффициентами.
они не зависят от h и являются задачами с постоянными коэффициентами.
Таким образом, процедура исследования устойчивости, учитывающая влияние границ, применительно к задаче (1) состоит в следующем. Надо составить три вспомогательные задачи (2), (4) и (5). Для каждой из этих трех задач, не зависящих от h, надо найти все те числа  (собственные числа
(собственные числа
оператора перехода от  , при которых существуют решения вида
, при которых существуют решения вида

При этом в случае задачи  должно быть ограничено. В случае задачи
должно быть ограничено. В случае задачи  при
при  , а в случае задачи (5)
, а в случае задачи (5)

Для устойчивости задачи (1) совокупность собственных чисел каждой из трех задач (2), (4) и (5) должна лежать в единичном круге  . (Задача (2) рассматривается при каждом фиксированном
. (Задача (2) рассматривается при каждом фиксированном  )
)
Продолжим рассмотрение задачи (1). Будем считать в дальнейшем, что  и вычислим спектры для всех, трех задач (2), (4) и (5) при различных краевых условиях
и вычислим спектры для всех, трех задач (2), (4) и (5) при различных краевых условиях 
Подставляя решение  Хрит в разностное уравнение (2), получаем
Хрит в разностное уравнение (2), получаем

или

Это — уравнение второго порядка. Подобными уравнениями мы занимались в гл. 1. Чтобы написать общее решение уравнения (6), составим характеристическое уравнение

Если q — корень этого уравнения, то сеточная функция

есть одно из решений уравнения

Если  ограниченная при
ограниченная при  и при
и при  сеточная функция
сеточная функция

как мы видели в § 25, является решением при

Эти  заполняют отрезок
заполняют отрезок  на вещественной оси. Этот отрезок и есть спектр задачи (2). Собственных значений
на вещественной оси. Этот отрезок и есть спектр задачи (2). Собственных значений  , не лежащих на этом отрезке, задача (2) не имеет, так как в случае отсутствия у характеристического уравнения (7) корня q, по модулю равного единице, задача (6) не имеет ограниченного при
, не лежащих на этом отрезке, задача (2) не имеет, так как в случае отсутствия у характеристического уравнения (7) корня q, по модулю равного единице, задача (6) не имеет ограниченного при  решения.
решения.
Если X не лежит на отрезке  , то оба корня характеристического уравнения (7) отличны по модулю от единицы, но их произведение равно свободному члену квадратного уравнения (7), т. е. единице. Поэтому среди корней уравнения (7) один по модулю больше, а другой меньше единицы. Пусть для определенности
, то оба корня характеристического уравнения (7) отличны по модулю от единицы, но их произведение равно свободному члену квадратного уравнения (7), т. е. единице. Поэтому среди корней уравнения (7) один по модулю больше, а другой меньше единицы. Пусть для определенности  Тогда общее решение уравнения (6), убывающее по модулю при
Тогда общее решение уравнения (6), убывающее по модулю при  имеет вид
имеет вид

а общее решение уравнения (6), стремящееся к нулю при  , имеет вид
, имеет вид

Для определения собственных значений задачи (4) надо подставить  в левое граничное условие
в левое граничное условие  и найти все те
и найти все те  , при которых оно выполняется. Это и будут все собственные значения задачи (4). Если, например,
, при которых оно выполняется. Это и будут все собственные значения задачи (4). Если, например,

то условие  выполняется ни при каком с
выполняется ни при каком с  , так что собственных значений нет.
, так что собственных значений нет.
Если  то условие
то условие  ввиду
ввиду  приводит к
приводит к  так что собственных значений опять нет.
так что собственных значений опять нет.
Если  то условие
то условие  выполняется при
выполняется при  , если
, если 
Из уравнения (7) находим, что в случае  число
число  - есть
- есть

Это и есть единственное собственное значение задачи (4). Оно лежит вне единичного круга, так как,  Аналогично вычисляются собственные значения задачи (5). Они получаются из уравнения
Аналогично вычисляются собственные значения задачи (5). Они получаются из уравнения

при

Рассмотрим в качестве еще одного примера разностную схему

аппроксимирующую задачу

Применим для исследования ее устойчивости признак Бабенко — Гельфанда. Сопоставим схеме (8) три задачи: задачу без боковых границ

задачу с одной только левой боковой границей

и задачу с одной только правой боковой границей

В случае задачи (10) с одной только левой боковой границей граничного условия нет, так как его не было в исходной задаче (8).
Надо найти совокупность собственных чисел всех трех операторов перехода от  соответствующих каждой из трех вспомогательных задач (9), (10), (11), и выяснить, при каких, условиях все они лежат в круге
соответствующих каждой из трех вспомогательных задач (9), (10), (11), и выяснить, при каких, условиях все они лежат в круге 
Решение вида

при подстановке в разностное уравнение

приводит к следующему обыкновенному разностному уравнению первого порядка для собственной функции:

Соответствующее характеристическое уравнение

дает связь между  и q. Общее решение уравнения (12) есть
и q. Общее решение уравнения (12) есть 

При 

Точка  пробегает окружность с центром в точке
пробегает окружность с центром в точке  и радиусом
и радиусом  . Это и есть собственные значения задачи (9) (рис. 26, а).
. Это и есть собственные значения задачи (9) (рис. 26, а).

Рис. 26.
Убывающее при  нетривиальное решение
нетривиальное решение

задачи (10) существует при любом 
Соответствующие  заполняют, очевидно, всю внутренность круга, ограниченного окружностью
заполняют, очевидно, всю внутренность круга, ограниченного окружностью  .
.
Наконец, решения задачи  крит, убывающие при
крит, убывающие при  должны иметь вид
должны иметь вид

где  и q связаны равенством (13).
и q связаны равенством (13).
Из граничного условия  следует, что нетривиальное решение
следует, что нетривиальное решение  существует только при
существует только при  , т. е.
, т. е.
при  . Эта величина q по модулю больше единицы в случае выполнения одного из неравенств
. Эта величина q по модулю больше единицы в случае выполнения одного из неравенств  или
или  Первое неравенство решений не имеет. Решение второго:
Первое неравенство решений не имеет. Решение второго: 
Итак, при  задача (10) имеет собственное значение
задача (10) имеет собственное значение  (рис. 26, б). На рис. 27, а,б,в изображены объединения собственных значений всех трех задач соответственно для случаев
(рис. 26, б). На рис. 27, а,б,в изображены объединения собственных значений всех трех задач соответственно для случаев  .
.

Рис. 27.
Ясно, что объединение собственных значений всех трех задач лежит в круге  , где с не зависит от h, в том и только том случае, если
, где с не зависит от h, в том и только том случае, если  .
.
Изложенный здесь признак устойчивости нестационарных разностных задач на отрезке, учитывающий влияние граничных условий, применим и в случае краевых задач на отрезке для систем разностных уравнений. В этом случае естественные на первый взгляд схемы, удовлетворяющие признаку Неймана, часто оказываются неустойчивыми из-за неудачной аппроксимации граничных условий, и важно уметь подбирать схемы, свободные от этого недостатка.
В гл. 14 мы еще вернемся к обсуждению спектрального признака Бабенко — Гельфанда с некоторой более общей точки зрения. В частности, будет строго доказано, что его выполнение необходимо для устойчивости и что при его выполнении устойчивость не может «грубо» нарушаться.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
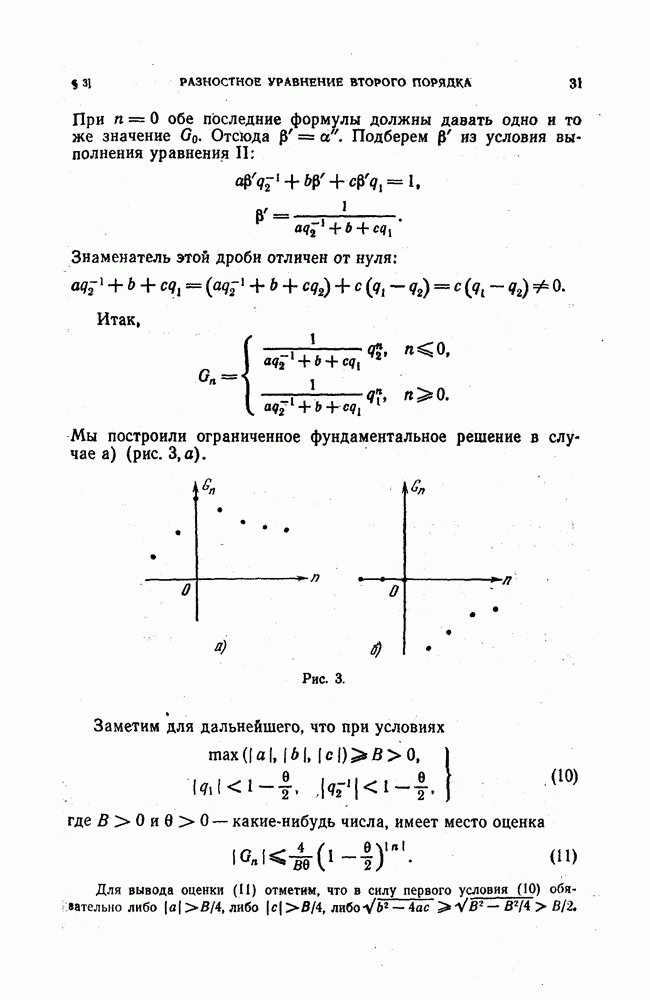
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
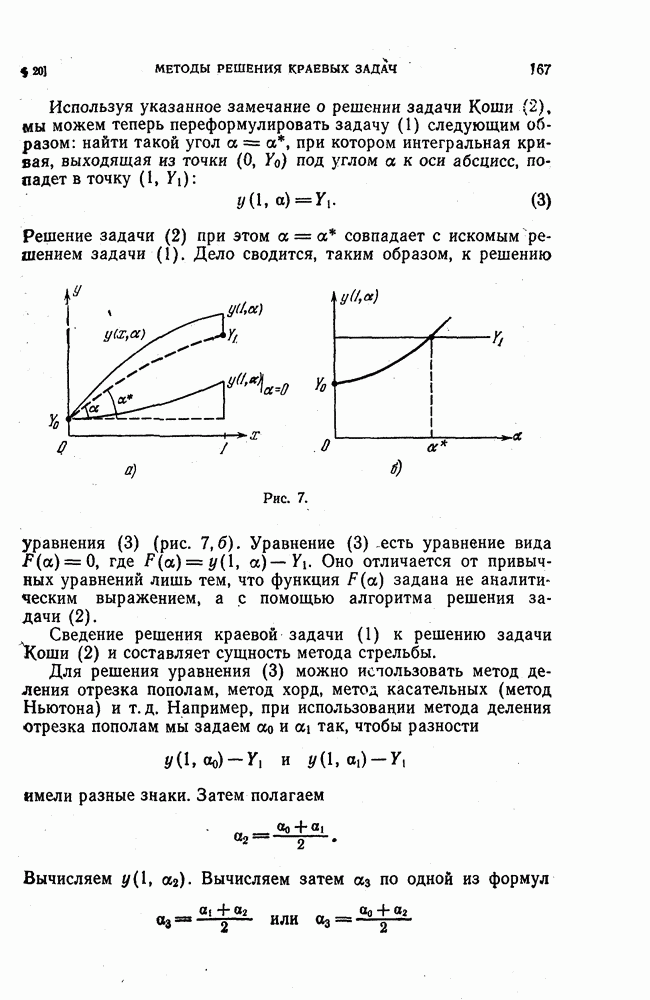
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА