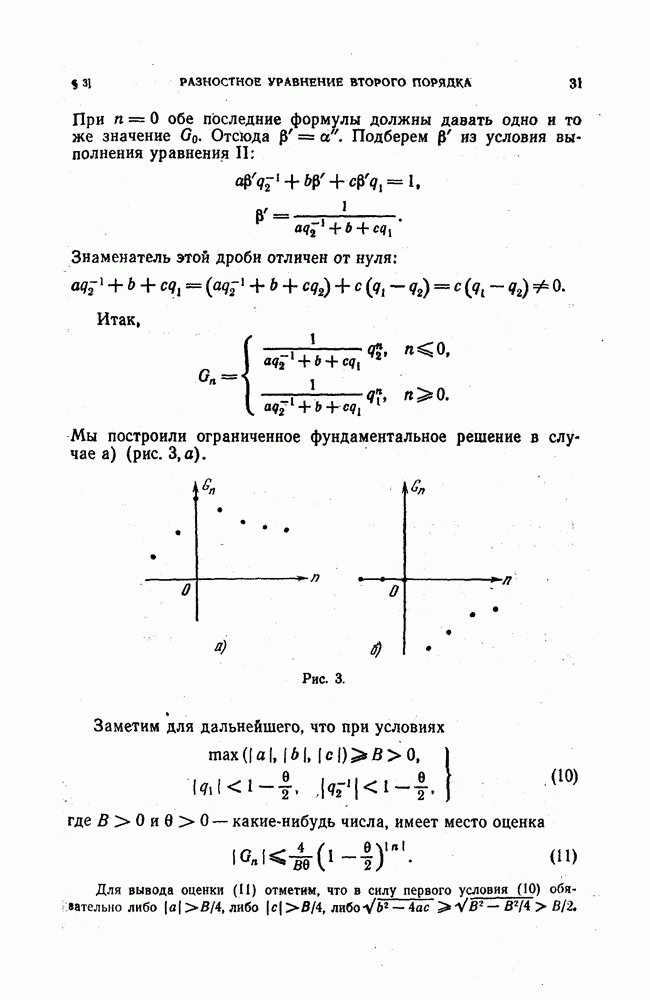
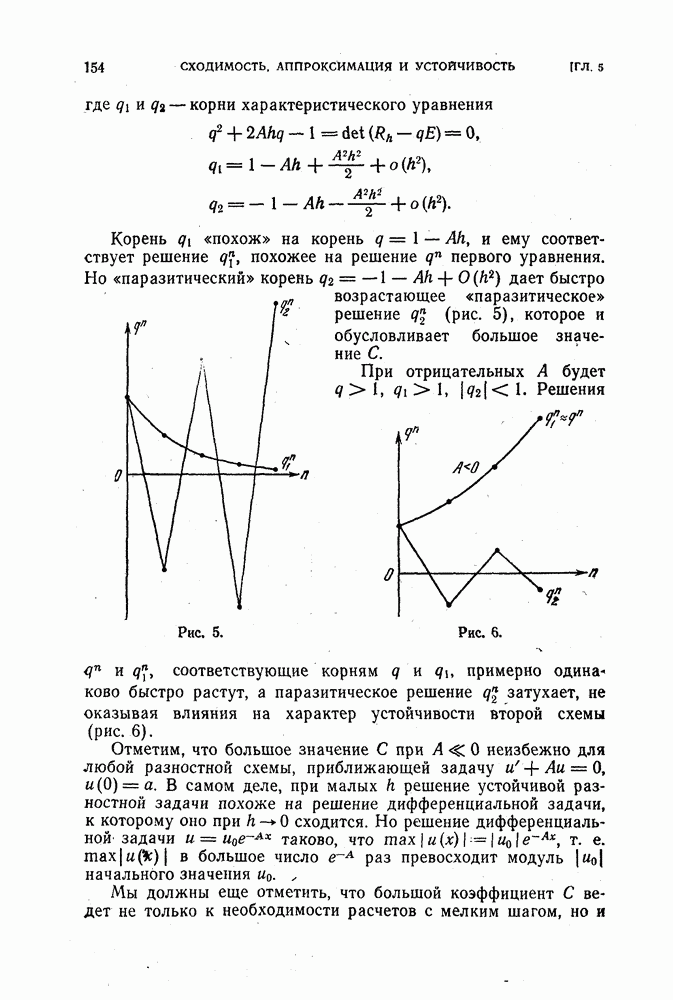
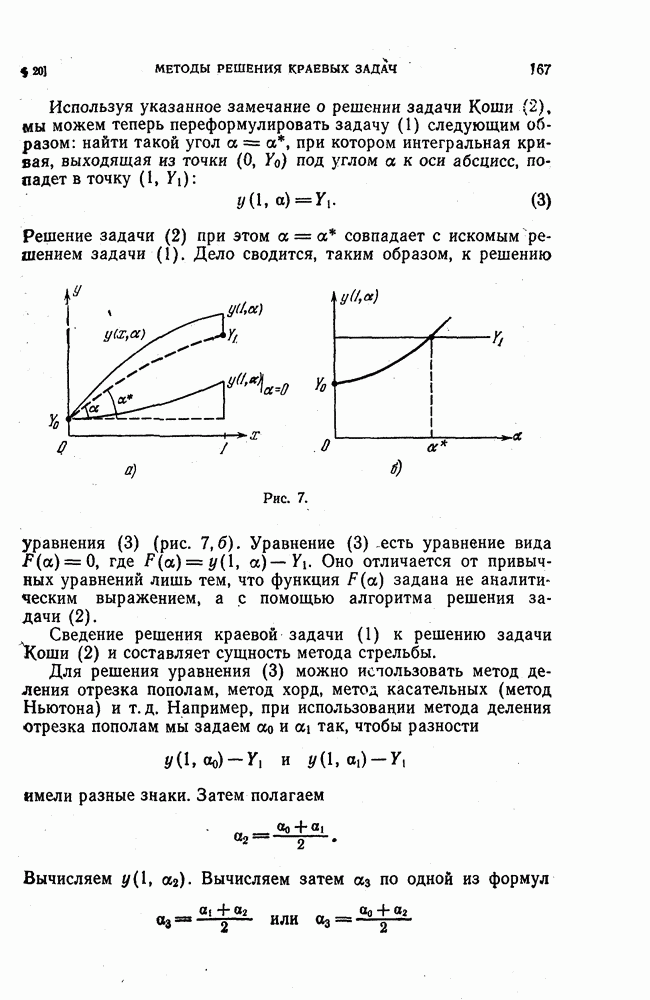
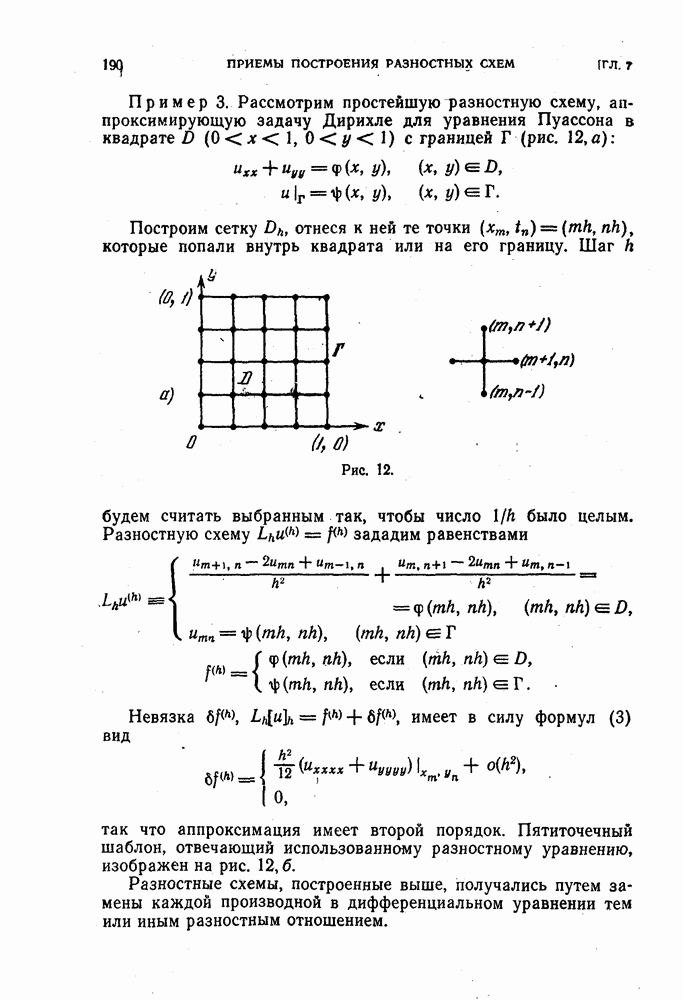
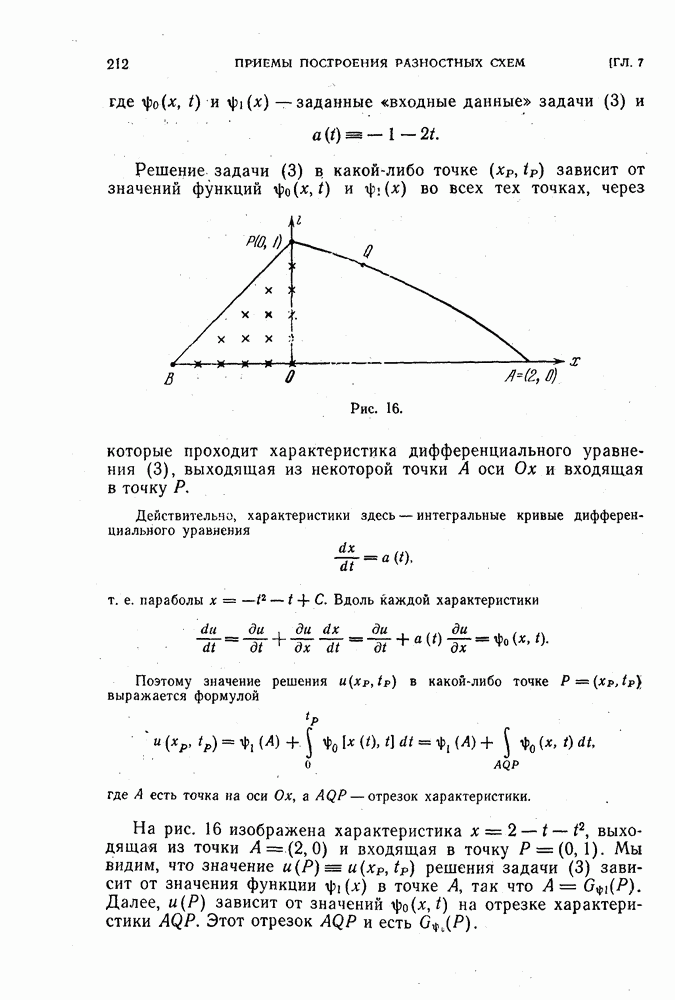
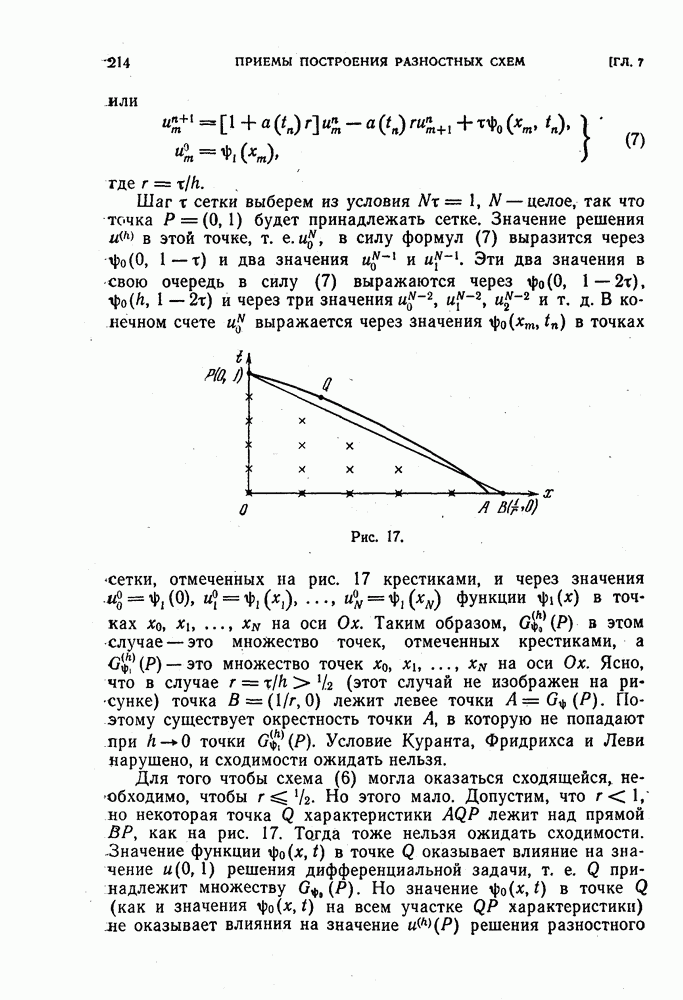
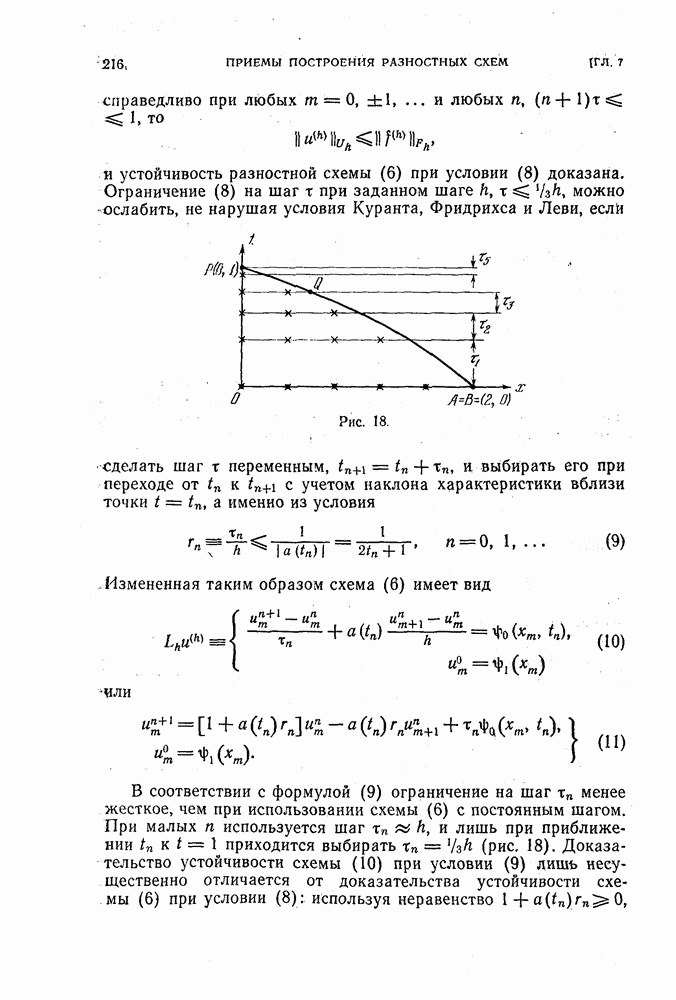
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
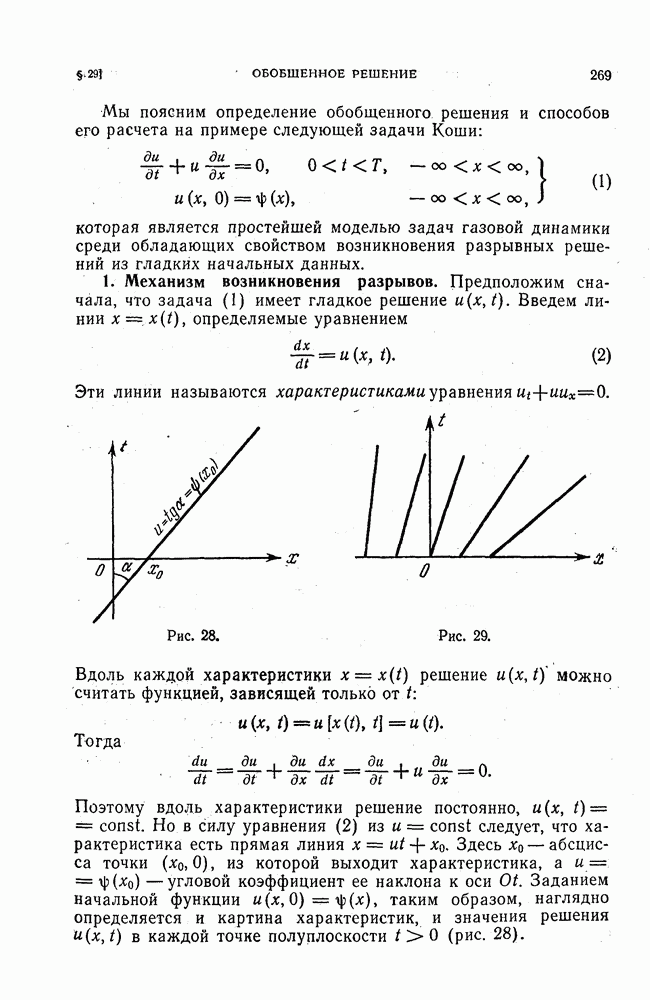
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Определение устойчивости.
Напомним и проиллюстрируем теперь определение устойчивости. Разностная краевая задача (2), по определению, устойчива, если существуют числа  такие, что при любом
такие, что при любом  и любом
и любом  из
из  удовлетворяющем неравенству
удовлетворяющем неравенству  разностная краевая задача
разностная краевая задача

имеет одно и только одно решение, причем выполняется условие

где С — некоторая постоянная, не зависящая от Н.
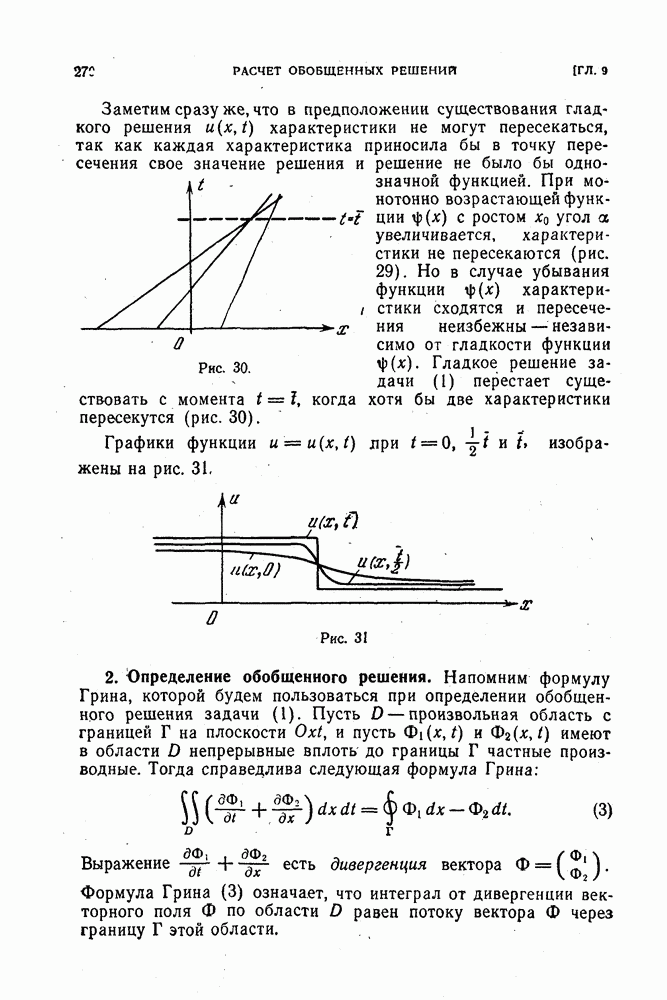
В § 12, где введено понятие устойчивости, показано, что в случае линейного оператора  сформулированное определение равносильно следующему.
сформулированное определение равносильно следующему.
Определение. Разностная краевая задача (2) устойчива, если существует  такое, что при
такое, что при  и любом
и любом  она однозначно разрешима, причем
она однозначно разрешима, причем

где С — некоторая постоянная, не зависящая от h и от 
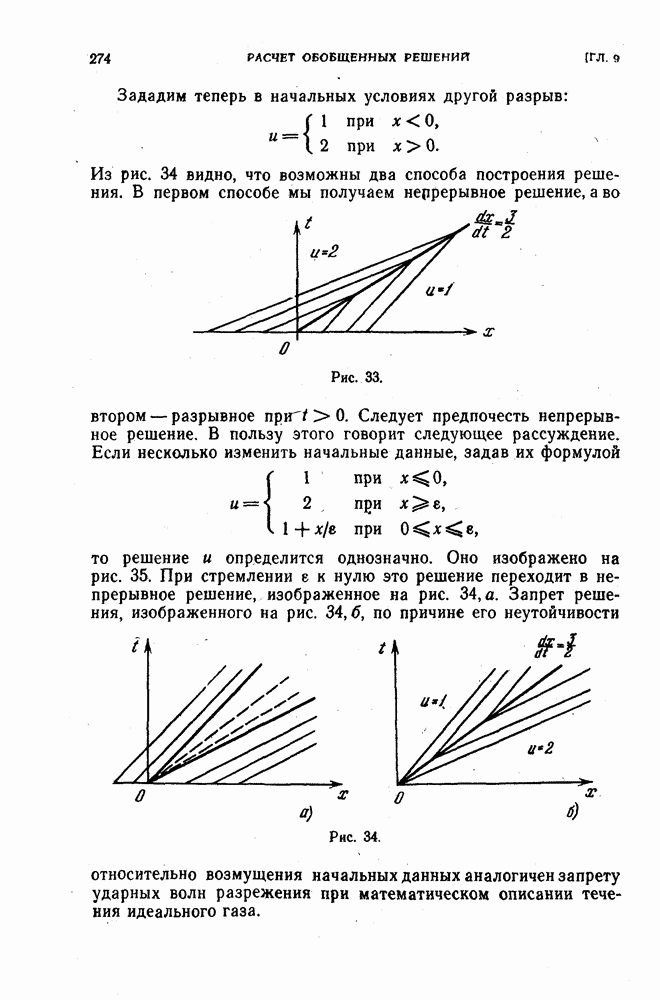
Свойство устойчивости можно трактовать как равномерную относительно h чувствительность решения разностной краевой задачи (2) к возмущениям  правой части.
правой части.
Подчеркнем, что в силу приведенного определения устойчивость есть некоторое внутреннее свойство разностной краевой задачи. Оно формулируется независимо от какой-либо связи с дифференциальной краевой задачей, в частности независимо от аппроксимации или сходимости. 
Однако если разностная краевая задача аппроксимирует на решении и дифференциальную и устойчива, то имеет место сходимость (3). При этом порядок относительно h скорости сходимости совпадает с порядком аппроксимации.
Доказательство этой важной теоремы проведено в § 12. Покажем, что разностная схема (5) при  устойчива. При этом норму
устойчива. При этом норму  определим равенством
определим равенством

Норму  будем понимать, как выше: если
будем понимать, как выше: если 

то

Разностную задачу

которая отличается от задачи (5) только тем, что,  произвольные правые части, вообще говоря, не совпадающие с
произвольные правые части, вообще говоря, не совпадающие с  перепишем в форме
перепишем в форме

Поскольку  то
то  . В этом случае справедлива оценка
. В этом случае справедлива оценка

Используя эту оценку, выводим из (6) неравенство

Отметим, что в случае  из неравенства
из неравенства  следует, что
следует, что  не возрастает с ростом
не возрастает с ростом  . Отмеченное свойство разностной схемы принято называть принципом максимума. Для краткости будем иногда пользоваться этим названием для всего неравенства
. Отмеченное свойство разностной схемы принято называть принципом максимума. Для краткости будем иногда пользоваться этим названием для всего неравенства

Правая часть этого неравенства не зависит от  , так что в левой части вместо
, так что в левой части вместо  можно написать
можно написать  получив неравенство
получив неравенство

Аналогично получаем неравенства

После почленного сложения этих неравенств и приведения подобных членов получим

Отсюда непосредственно следует

Доказанное неравенство

имеет место для всех  , так что оно останется справедливым, если вместо
, так что оно останется справедливым, если вместо  написать
написать 

Неравенство (9) означает устойчивость линейной задачи (5), поскольку существование и единственность решения задачи (6) при произвольных ограниченных  и очевидно, имеют место. Роль постоянной С в неравенстве (8) играет здесь число
и очевидно, имеют место. Роль постоянной С в неравенстве (8) играет здесь число 
Не следует думать, что одна только аппроксимация дифференциальной краевой задачи (1) разностной краевой задачей (2) обеспечивает устойчивость и, следовательно, сходимость (3). Мы убедились в этом в § 9 с помощью специально сконструированного примера аппроксимирующей, но расходящейся разностной схемы.
В случае уравнений с частными производными непригодность наудачу взятой аппроксимирующей разностной схемы является правилом, а выбор устойчивой  следовательно, сходящейся) разностной схемы — постоянной заботой вычислителя.
следовательно, сходящейся) разностной схемы — постоянной заботой вычислителя.
Напомним, например, что доказательство устойчивости разностной схемы (5) мы провели в предположении, что  . В случае
. В случае  разностная задача (5) по-прежнему аппроксимирует задачу (4), но наше доказательство устойчивости не проходит. Покажем, что в этом случае нет сходимости решения разностной задачи (5) к решению
разностная задача (5) по-прежнему аппроксимирует задачу (4), но наше доказательство устойчивости не проходит. Покажем, что в этом случае нет сходимости решения разностной задачи (5) к решению  дифференциальной задачи (4), а значит, не может быть и устойчивости, так как устойчивость влечет за собою сходимость.
дифференциальной задачи (4), а значит, не может быть и устойчивости, так как устойчивость влечет за собою сходимость.
Пусть, для определенности,  так что также
так что также  пусть, далее,
пусть, далее,  . Шаг h будем выбирать так чтобы точка (0, 1) на плоскости
. Шаг h будем выбирать так чтобы точка (0, 1) на плоскости  принадлежала сетке, т. е. чтобы число
принадлежала сетке, т. е. чтобы число

было целым (рис. 9). В силу разностного уравнения имеем

Значение  решения
решения  в точке (0, 1) сетки выражается, через значения и
в точке (0, 1) сетки выражается, через значения и  решения в точках
решения в точках  сетки. Два значения
сетки. Два значения  выражаются через значения
выражаются через значения  решения в трех точках сетки
решения в трех точках сетки  Значения решения
Значения решения  свою очередь выражаются через значения решения в четырех точках
свою очередь выражаются через значения решения в четырех точках  и т. д.
и т. д.
В конечном счете значение  выражается через значения
выражается через значения  решения в точках сетки
решения в точках сетки  . Все эти точки лежат на отрезке
. Все эти точки лежат на отрезке

прямой t = 0 (см. рис. 9), где задано начальное условие

для дифференциального уравнения. Таким образом, решение разностного уравнения в точке (0,1) сетки не зависит от значений функции  в точках
в точках  лежащих вне отрезка
лежащих вне отрезка

Далее, решением задачи

как легко проверить, является функция

Она постоянна на каждой характеристике  , в частности, на прямой
, в частности, на прямой  которая проходит через точки (0, 1) и (1,0) (см. рис. 9), и в точке (0, 1) принимает значение
которая проходит через точки (0, 1) и (1,0) (см. рис. 9), и в точке (0, 1) принимает значение  Отсюда видно, что в случае
Отсюда видно, что в случае  сходимости, вообще говоря, быть не может. Действительно, в этом случае отрезок оси абсцисс
сходимости, вообще говоря, быть не может. Действительно, в этом случае отрезок оси абсцисс


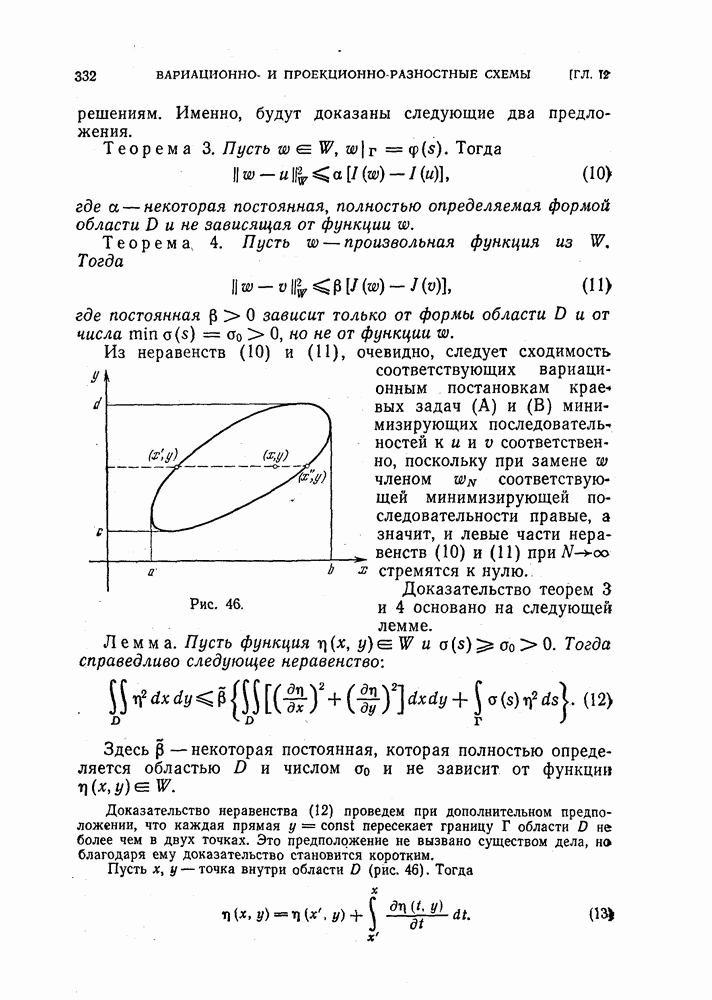
Рис. 9.
не содержит точку (1, 0). Если бы при какой-нибудь функции  сходимость, случайно, имела место, то, не меняя значения
сходимость, случайно, имела место, то, не меняя значения  на отрезке
на отрезке

и не меняя, таким образом, значения решения разностного уравнения в точке (0, 1), мы могли бы нарушить сходимость, изменив  в точке
в точке  и ее окрестности, что отразилось бы на значений
и ее окрестности, что отразилось бы на значений  решения дифференциального уравнения. Изменение
решения дифференциального уравнения. Изменение  в точке
в точке  и ее окрестности можно внести так, чтобы не нарушить существования вторых производных функции и решения
и ее окрестности можно внести так, чтобы не нарушить существования вторых производных функции и решения  так что аппроксимация на решении и
так что аппроксимация на решении и  будет иметь место. В этих условиях из устойчивости схемы (5) вытекала бы сходимость. Но поскольку при
будет иметь место. В этих условиях из устойчивости схемы (5) вытекала бы сходимость. Но поскольку при  нет сходимости, то нет и устойчивости.
нет сходимости, то нет и устойчивости.
Проведенное доказательство неустойчивости разностной схемы (5) носит косвенный характер. Интересно проследить непосредственно, как сказывается неустойчивость при  разностной схемы (5) на чувствительности решения
разностной схемы (5) на чувствительности решения  ошибкам при задании
ошибкам при задании  Ведь именно равномерная относительно h чувствительность решения к ошибкам при задании
Ведь именно равномерная относительно h чувствительность решения к ошибкам при задании  и определена выше как устойчивость.
и определена выше как устойчивость.
Допустим, что при всех h выполняются тождества  так что
так что

и решение  задачи (5) есть тождественный нуль,
задачи (5) есть тождественный нуль,  Допустим, далее, что при задании начальных данных допущена ошибка и вместо
Допустим, далее, что при задании начальных данных допущена ошибка и вместо  задано
задано  так что вместо
так что вместо

задано

Будем обозначать получающееся при этом решение через В силу уравнений

для  получим
получим

Мы видим, что допущенная при  ошибка умножилась на число
ошибка умножилась на число  . При переходе к
. При переходе к  получим
получим

Вообще

При  будет
будет  так что ошибка
так что ошибка

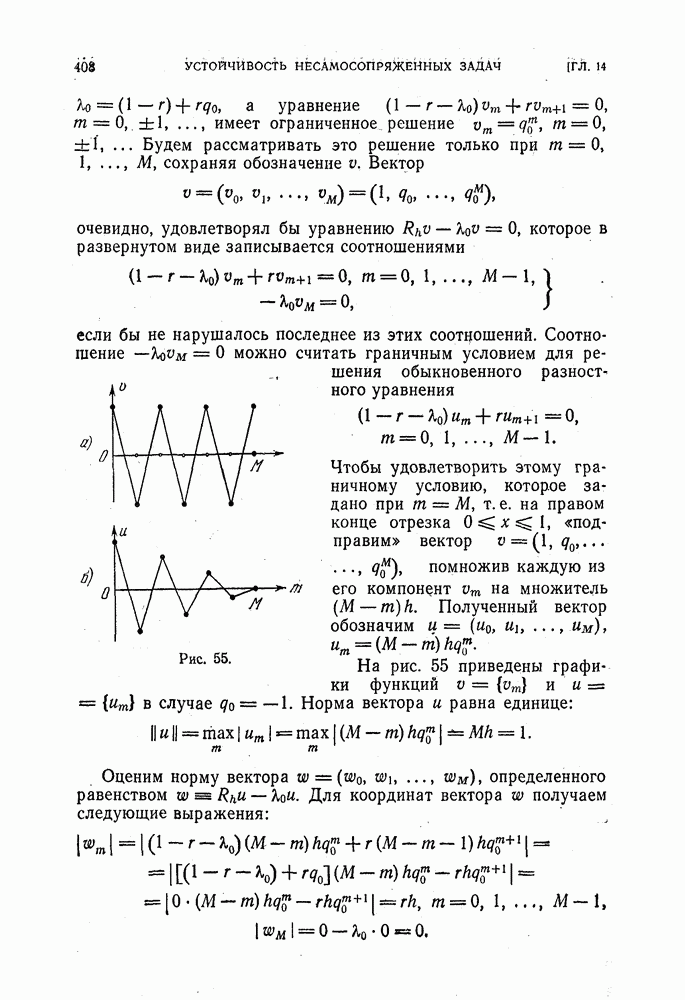
при переходе от одного слоя  сетки к следующему умножается на отрицательное число, превосходящее единицу по модулю. При
сетки к следующему умножается на отрицательное число, превосходящее единицу по модулю. При  будет
будет

Отсюда

При фиксированном  первоначально допущенная в начальных данных ошибка
первоначально допущенная в начальных данных ошибка  увеличивается в очень быстро возрастающее при
увеличивается в очень быстро возрастающее при  число раз, равное
число раз, равное 
Остановимся теперь кратко на критике принятого нами способа оценки качества аппроксимации сравнением величины нормы невязки  с той или иной степенью h. Как мы внаем, для устойчивых схем порядок аппроксимации совпадает С порядком погрешности
с той или иной степенью h. Как мы внаем, для устойчивых схем порядок аппроксимации совпадает С порядком погрешности  в решении. Качество схемы Естественно оценивать по количеству вычислительной работы. Необходимой для получения заданной точности. Количество же работы, вообще говоря, пропорционально числу точек N использованной разностной сетки. Для обыкновенных дифференциальных уравнений N пропорционально шагу h. Поэтому, когда мы говорим, что погрешность
в решении. Качество схемы Естественно оценивать по количеству вычислительной работы. Необходимой для получения заданной точности. Количество же работы, вообще говоря, пропорционально числу точек N использованной разностной сетки. Для обыкновенных дифференциальных уравнений N пропорционально шагу h. Поэтому, когда мы говорим, что погрешность  мы тем самым утверждаем, что в
мы тем самым утверждаем, что в  т. е. что уменьшение погрешности вдвое требует увеличения работы в у 2 раз. Таким образом, в случае обыкновенных разностных уравнений порядок аппроксимации относительно h характеризует объем работы.
т. е. что уменьшение погрешности вдвое требует увеличения работы в у 2 раз. Таким образом, в случае обыкновенных разностных уравнений порядок аппроксимации относительно h характеризует объем работы.
Для уравнений с частными производными дело обстоит уже не так. В рассмотренном нами примере задачи с двумя
переменными  и t сетка задается двумя шагами
и t сетка задается двумя шагами  . Число N точек сетки, помещающихся в ограниченной области на плоскости
. Число N точек сетки, помещающихся в ограниченной области на плоскости  имеет порядок
имеет порядок  . Это число также может применяться для оценки количества работы, затрачиваемой при решении разностных уравнений. Пусть
. Это число также может применяться для оценки количества работы, затрачиваемой при решении разностных уравнений. Пусть  . В этом случае
. В этом случае  утверждение, что
утверждение, что  эквивалентно утверждению
эквивалентно утверждению  . Если
. Если  , то
, то  и утверждение
и утверждение  эквивалентно тому, что
эквивалентно тому, что 
Мы видим, что в случае уравнений с частными производными «порядок погрешности естественнее было бы измерять не в степенях  а в степенях
а в степенях  Мы все же остановимся на описанном выше способе оценки аппроксимации степенями h, так как это удобнее при проведении выкладок. Читатель, однако, должен при оценке качества разностных схем иметь в виду отмеченное обстоятельство.
Мы все же остановимся на описанном выше способе оценки аппроксимации степенями h, так как это удобнее при проведении выкладок. Читатель, однако, должен при оценке качества разностных схем иметь в виду отмеченное обстоятельство.
Надо еще заметить, что утверждение о пропорциональности вычислительной работы числу N точек сетки тоже не всегда является верным. Можно привести примеры разностных схем, для вычисления решения по которым требуется произвести  арифметических операций, где
арифметических операций, где  или даже 2. С этим приходится встречаться при решении разностных краевых задач, аппроксимирующих эллиптические уравнения, или при решении задач в случае трех и более независимых переменных (например,
или даже 2. С этим приходится встречаться при решении разностных краевых задач, аппроксимирующих эллиптические уравнения, или при решении задач в случае трех и более независимых переменных (например,  ). В многомерном случае построение разностных схем, для вычисления решения по которым
). В многомерном случае построение разностных схем, для вычисления решения по которым  арифметических операций, является непростой задачей, о которой будет идти речь в §§ 31, 32.
арифметических операций, является непростой задачей, о которой будет идти речь в §§ 31, 32.
При реальных расчетах на вычислительной машине для сравнительной оценки используемых алгоритмов за меру качества схемы обычно естественно принять машинное время. Машинное время не обязательно пропорционально числу арифметических действий.
Играют роль, иногда превалирующую, затраты времени на пересылку информации из одного блока машинной памяти в другой. Может играть роль время, расходуемое на логические операции.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА