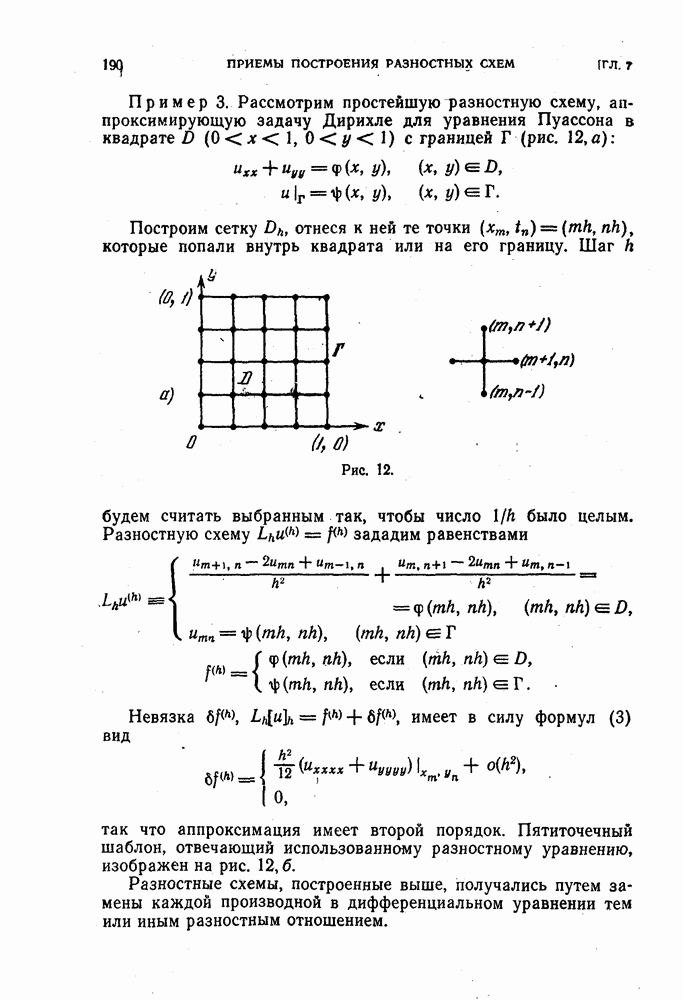
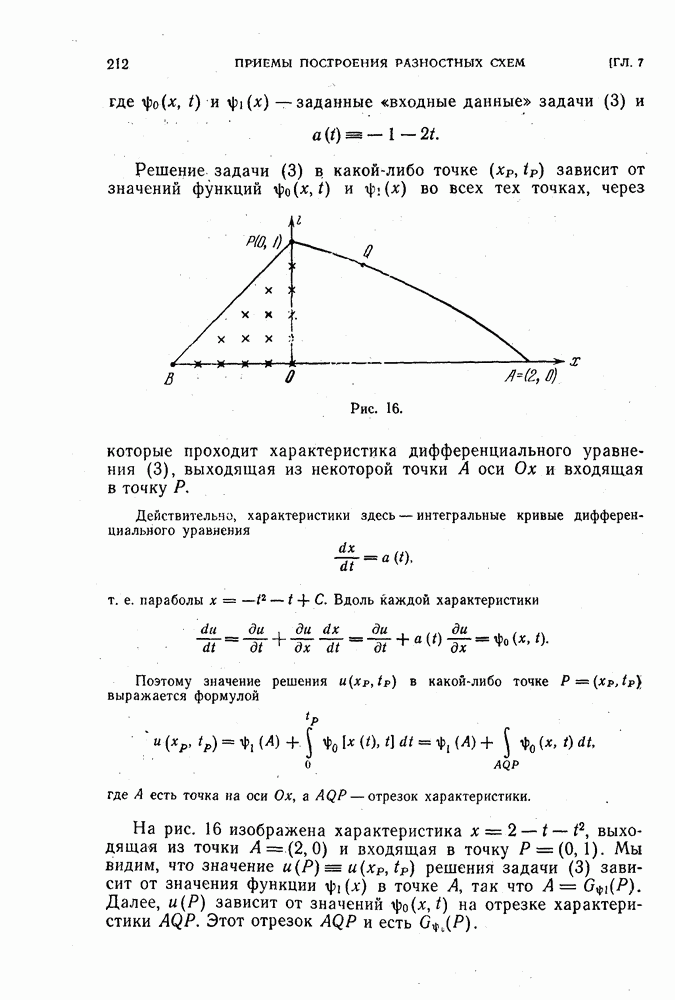
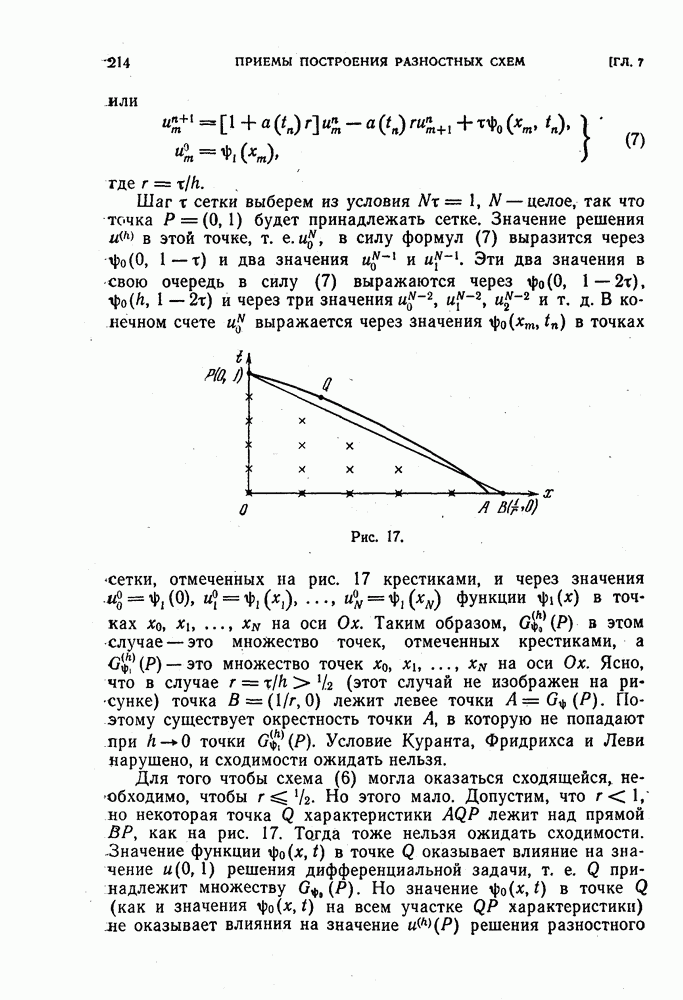
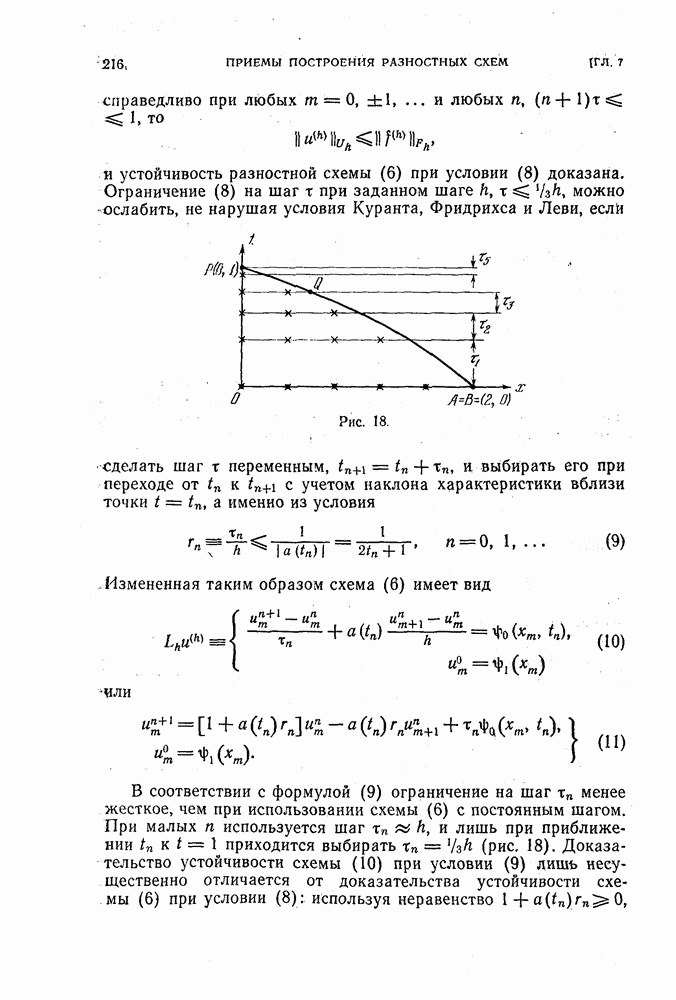
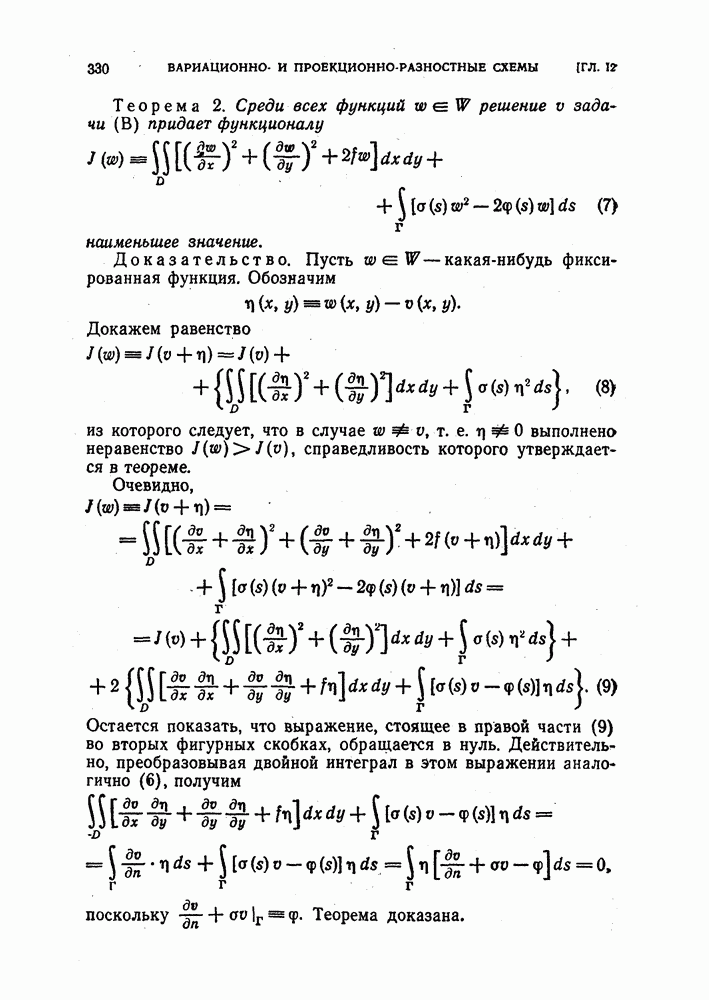| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 46. Ядра спектров семейств операторов
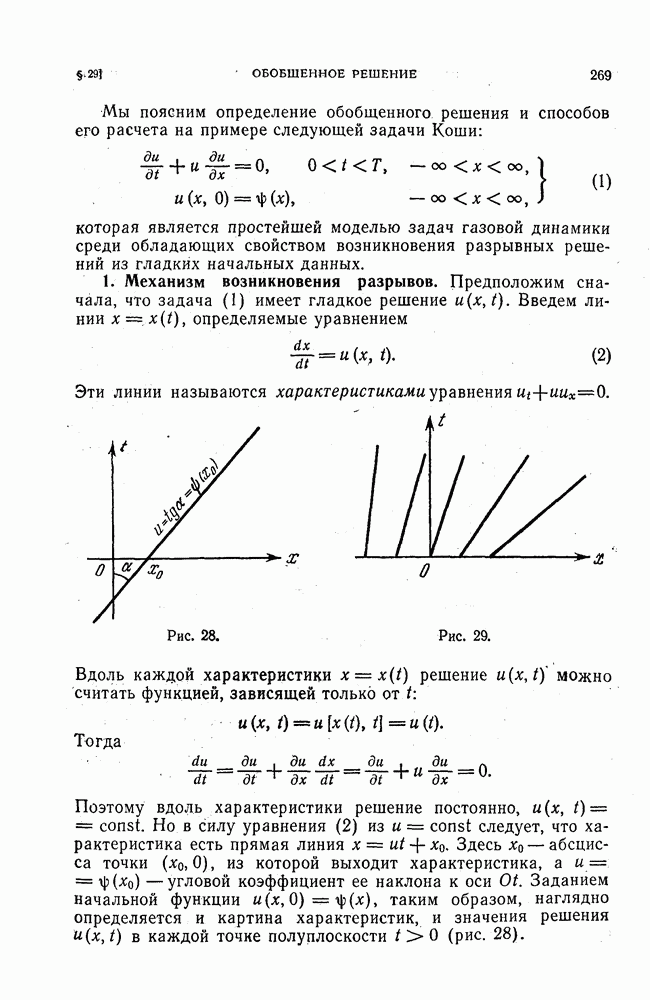
Пусть  отображает линейное нормированное пространство
отображает линейное нормированное пространство  некоторой размерности
некоторой размерности  в себя. Будем писать вместо
в себя. Будем писать вместо  и U соответственно
и U соответственно  чтобы в Обозначениях была ябно указана размерность. Предполагается, что
чтобы в Обозначениях была ябно указана размерность. Предполагается, что  при
при 
Здесь мы обсудим вопрос о том, насколько спектр семейства операторов  зависит от выбора последовательности норм
зависит от выбора последовательности норм  в пространствах
в пространствах  и, тем самым, насколько инвариантен спектральный признак ограниченности норм степеней оператора
и, тем самым, насколько инвариантен спектральный признак ограниченности норм степеней оператора  (теорема 1 из § 44) относительно выбора норм.
(теорема 1 из § 44) относительно выбора норм.
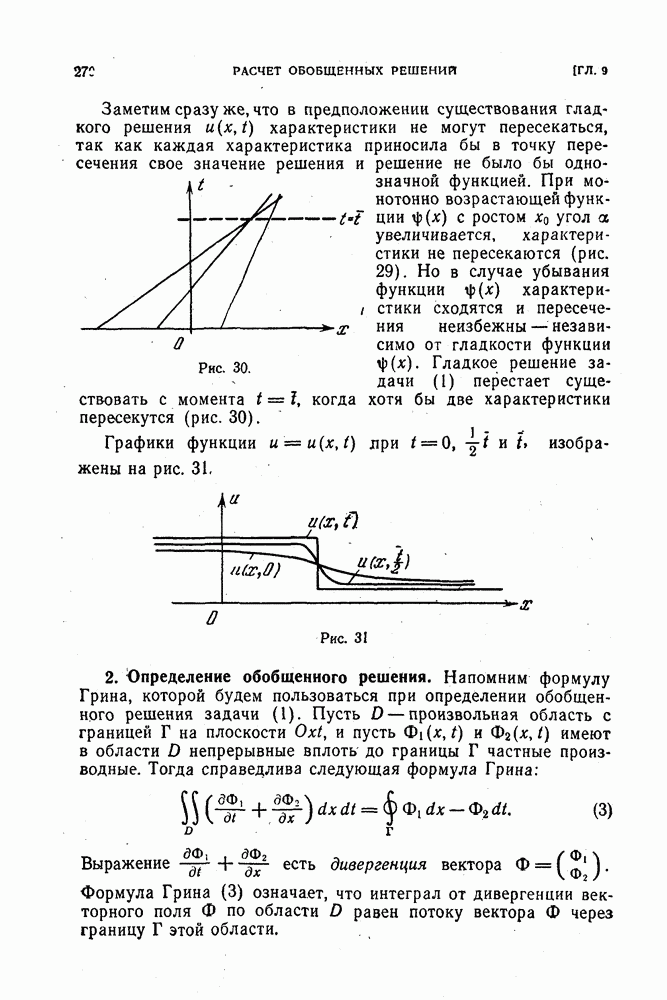
Относительно семейства операторов  будем предполагать, что собственные числа всех операторов
будем предполагать, что собственные числа всех операторов  ограничены в совокупности, т. е. лежат в некотором круге
ограничены в совокупности, т. е. лежат в некотором круге

Очевидно, что для выполнения условия (1) достаточно, чтобы существовала хотя бы одна последовательность норм  такая, чтобы выполнялись неравенства
такая, чтобы выполнялись неравенства  Отсюда видно, что ограничение (1) естественно: оно выполняется для семейств операторов
Отсюда видно, что ограничение (1) естественно: оно выполняется для семейств операторов  перехода со слоя на слой, возникающих при рассмотрении эволюционных разностных краевых задач. Переходим к определению понятия ядра спектра, с помощью которого и будут сформулированы результаты этого параграфа.
перехода со слоя на слой, возникающих при рассмотрении эволюционных разностных краевых задач. Переходим к определению понятия ядра спектра, с помощью которого и будут сформулированы результаты этого параграфа.
Пусть заданы: какая-либо последовательность норм  , число
, число  и целое
и целое  . Обозначим чере
. Обозначим чере  множество точек
множество точек  , для которых неравенство
, для которых неравенство  и
и  имеет решение
имеет решение  Значок N при написании норм мы опускаем.
Значок N при написании норм мы опускаем.
Определение. Ядром показателя а  семейства операторов
семейства операторов  назовем следующее множество
назовем следующее множество  на комплексной плоскости:
на комплексной плоскости:

Здесь

есть теоретико-множественное замыкание объединения множеств  при всех
при всех  пересечение всех множеств
пересечение всех множеств  пересечение всех множеств
пересечение всех множеств 
Теорема 1. Ядро  целиком содержится в. спектре семейства операторов
целиком содержится в. спектре семейства операторов  и замкнуто.
и замкнуто.
Доказательство. Покажем, что если точка  не принадлежит спектру семейства операторов
не принадлежит спектру семейства операторов  то она не принадлежит и ядру. Действительно, найдутся
то она не принадлежит и ядру. Действительно, найдутся  такие, что при всех
такие, что при всех  для любого и
для любого и  выполнено неравенство
выполнено неравенство  Но тогда для всех
Но тогда для всех  из круга
из круга  выполненотакже неравенство
выполненотакже неравенство  Ввиду этого при
Ввиду этого при  ни одно множество
ни одно множество  не содержит точек в круге
не содержит точек в круге  Отсюда следует справедливость первого утверждения теоремы. Для доказательства замкнутости ядра
Отсюда следует справедливость первого утверждения теоремы. Для доказательства замкнутости ядра  заметим, что
заметим, что  замкнуты по построению, а множества
замкнуты по построению, а множества  как пересечения замкнутых множеств.
как пересечения замкнутых множеств.
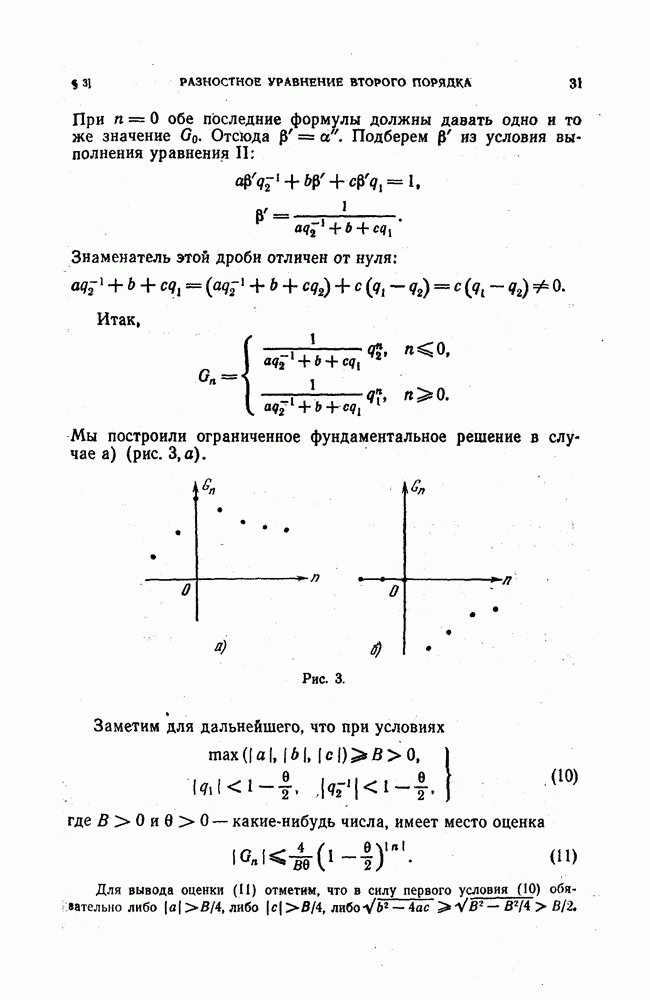
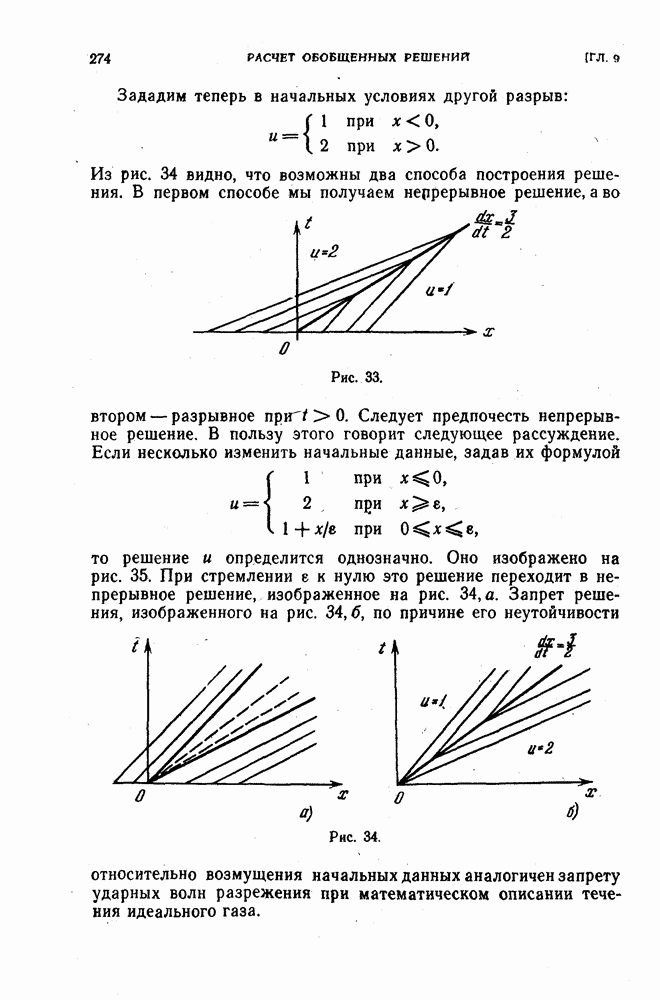
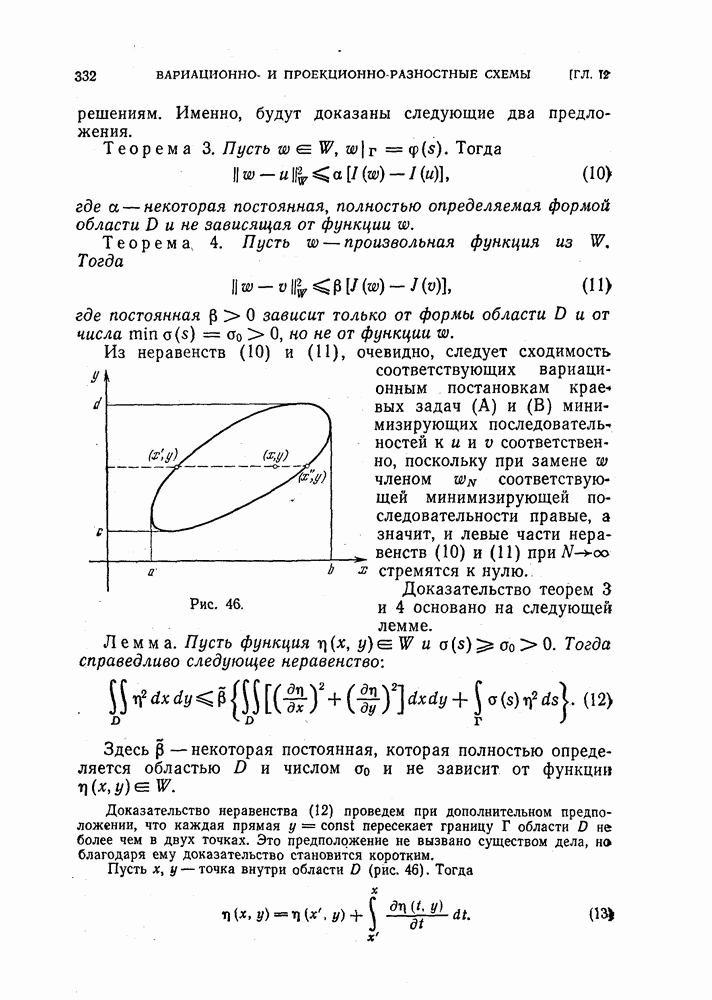
Пример. Вычислим ядро  для семейства операторов
для семейства операторов  если оператор
если оператор  задан равенствами
задан равенствами

а норма — равенством 
Покажем, что  состоит из точки
состоит из точки  и из замкнутого круга радиуса
и из замкнутого круга радиуса  с центром в точке
с центром в точке  :
:

Действительно,  как мы видели в п. 1 § 42, является собственным числом для всёх операторов
как мы видели в п. 1 § 42, является собственным числом для всёх операторов  , а потому принадлежит всем множествам
, а потому принадлежит всем множествам  и, следовательно, ядру. Далее, для любого
и, следовательно, ядру. Далее, для любого  лежащего строго внутри круга (3), при некоторых вещественном а О и
лежащего строго внутри круга (3), при некоторых вещественном а О и  имеет место представление
имеет место представление

Неравенство  при любом фиксированном k и всех достаточно больших N имеет решение
при любом фиксированном k и всех достаточно больших N имеет решение

Следовательно, при всех достаточно больших N множества  содержат точку
содержат точку  а значит, ее содержит и
а значит, ее содержит и  . Итак, внутренние точки круга (3) принадлежат ядру
. Итак, внутренние точки круга (3) принадлежат ядру  а ввиду замкнутости ядра ему принадлежит и граница круга (3).
а ввиду замкнутости ядра ему принадлежит и граница круга (3).
Если точка  не принадлежит кругу (3), т. е.
не принадлежит кругу (3), т. е.

то, выписав функцию Грина разностного уравнения первого порядка (§ 2), можно установить, что при любом  из круга
из круга  при всех достаточно больших N и всех и
при всех достаточно больших N и всех и  выполнено неравенство
выполнено неравенство  Отсюда следует, что точки этого круга не принадлежат
Отсюда следует, что точки этого круга не принадлежат  если N достаточно велико, а следовательно, и не принадлежат ни замыканию их объединений
если N достаточно велико, а следовательно, и не принадлежат ни замыканию их объединений  ни ядру
ни ядру 
Заметим, что ядро  показателя
показателя  в рассмотренном примере состоит из двух точек
в рассмотренном примере состоит из двух точек  , а ядро
, а ядро  совпадает со всем спектром семейства операторов
совпадает со всем спектром семейства операторов  который был вычислен в § 45.
который был вычислен в § 45.
На этом закончим рассмотрение примера и вернемся к общим  построениям.
построениям.
Определение. Ядро  назовем абсолютным ядром.
назовем абсолютным ядром.
Теорема 2. Абсолютное ядро семейства операторов  не зависит от выбора последовательности норм
не зависит от выбора последовательности норм 
Доказательство следует из того факта, что при  множество
множество  совпадает при каждом N с множеством собственных значений оператора
совпадает при каждом N с множеством собственных значений оператора  которое не зависит от нормы в пространстве
которое не зависит от нормы в пространстве 
Теорема 3. При условии (1) последовательность норм  всегда можно выбрать так, чтобы спектр семейства операторов
всегда можно выбрать так, чтобы спектр семейства операторов  совпадал со своим абсолютным ядром.
совпадал со своим абсолютным ядром.
Доказательство. Укажем конструкцию норм, существование которых утверждается в теореме. Выберем базис в пространстве  так, чтобы матрица преобразования
так, чтобы матрица преобразования  в этом базисе была жордановой и модули всех внедиагональных членов были меньше чем
в этом базисе была жордановой и модули всех внедиагональных членов были меньше чем  Введем скалярное умножение и порожденную им норму, объявив этот базис ортонормальным. Если
Введем скалярное умножение и порожденную им норму, объявив этот базис ортонормальным. Если  произвольная точка, не принадлежащая
произвольная точка, не принадлежащая  расстояние от этой
расстояние от этой
точки до замкнутого в силу теоремы 1 множества  то можно проверить, что
то можно проверить, что  при всех
при всех  всех
всех  так что U не принадлежит спектру семейства операторов
так что U не принадлежит спектру семейства операторов
Итак, если спектр семейства операторов  не совпадает со своим ядром
не совпадает со своим ядром  показателя
показателя  при заданном выборе норм, как это имеет место в рассмотренном выше примере
при заданном выборе норм, как это имеет место в рассмотренном выше примере  при норме
при норме  то за счет выбора другой последовательности норм можно получить в качестве спектра более узкое множество
то за счет выбора другой последовательности норм можно получить в качестве спектра более узкое множество 
Однако в теории разностных схем используются не вполне произвольные нормы.
Обозначим через  норму, равную максимуму абсолютных величии всех компонент, образующих сеточную функцию (или вектор-функцию) из
норму, равную максимуму абсолютных величии всех компонент, образующих сеточную функцию (или вектор-функцию) из  . Выделим класс последовательностей норм
. Выделим класс последовательностей норм  для которых существует натуральное s, зависящее от последовательности, и такое, что при всех достаточно больших N справедливо неравенство
для которых существует натуральное s, зависящее от последовательности, и такое, что при всех достаточно больших N справедливо неравенство

Очевидно, что сама норма  и все встречавшиеся нам в связи с разностными уравнениями нормы при возрастающем N образуют последовательности из указанного класса (4).
и все встречавшиеся нам в связи с разностными уравнениями нормы при возрастающем N образуют последовательности из указанного класса (4).
Теорема 4. Ядро  показателя а
показателя а  не зависит от выбора последовательности норм из числа удовлетворяющих требованию (4).
не зависит от выбора последовательности норм из числа удовлетворяющих требованию (4).
Доказательство непосредственно следует из определений.
Рассмотрим теперь семейство операторов  определенных равенствами (18) и (19) из § 45, предположив дополнительно, что матричные коэффициенты
определенных равенствами (18) и (19) из § 45, предположив дополнительно, что матричные коэффициенты  постоянны:
постоянны:  Для этого семейства операторов справедлива следующая важная
Для этого семейства операторов справедлива следующая важная
Теорема 5 (А. В. Соколов). Если в пространствах  где действуют операторы
где действуют операторы  введены нормы
введены нормы  то ядро
то ядро  показателя
показателя  спектра семейства операторов
спектра семейства операторов  совпадает со всем спектром этого семейства операторов.
совпадает со всем спектром этого семейства операторов.
Из этой теоремы и теоремы 4 следует, что при любом выборе последовательности норм из класса норм, удовлетворяющих условию (4), спектр семейства операторов  содержит спектр семейства операторов
содержит спектр семейства операторов  полученного при использовании
полученного при использовании  способ вычисления которого описан в п. 2 § 45. Поэтому если не выполнено спектральное условие ограниченности норм степеней операторов
способ вычисления которого описан в п. 2 § 45. Поэтому если не выполнено спектральное условие ограниченности норм степеней операторов  (теорема 1 из § 44) при выборе норм
(теорема 1 из § 44) при выборе норм  то оно не выполнено и при любом другом выборе последовательности норм из числа удовлетворяющих условию (4).
то оно не выполнено и при любом другом выборе последовательности норм из числа удовлетворяющих условию (4).
Доказательство теоремы А. В. Соколова требует сложного исследования, и мы его не излагаем.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА