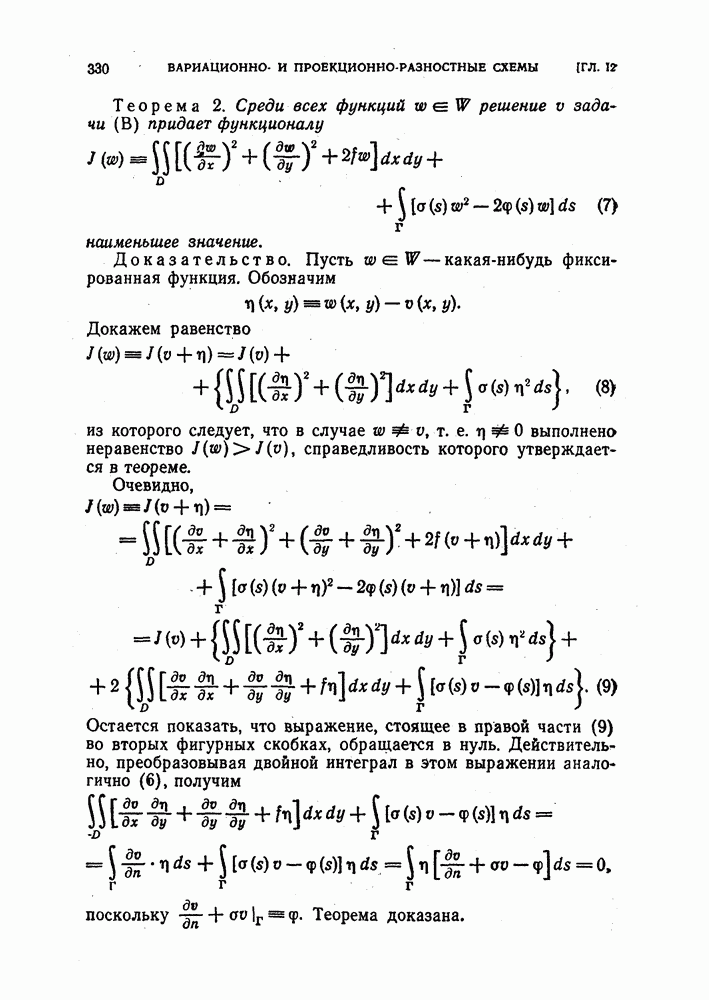| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
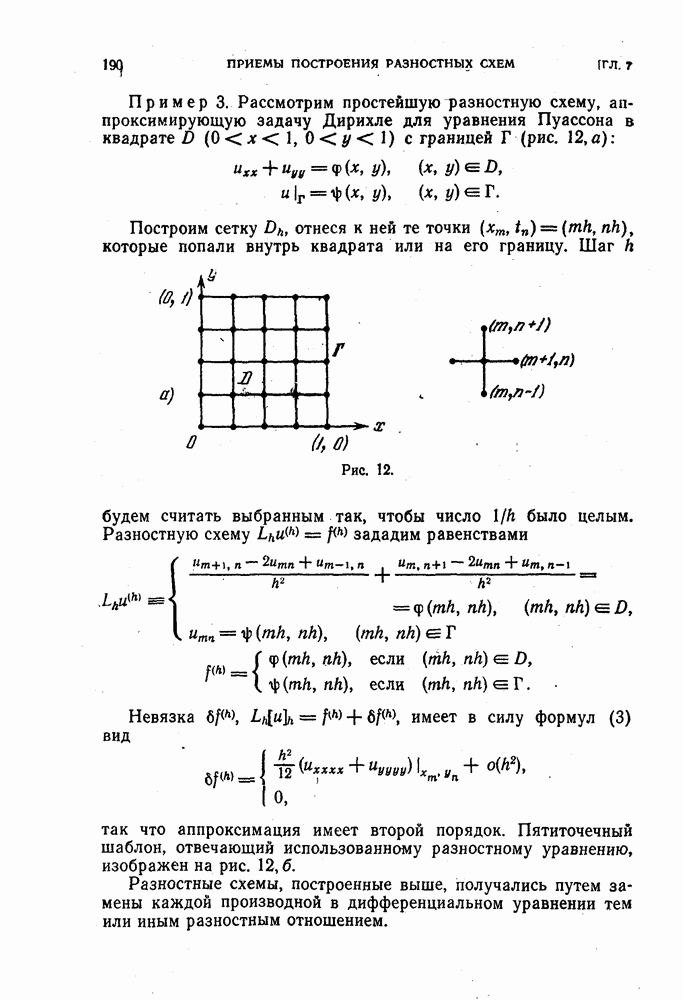
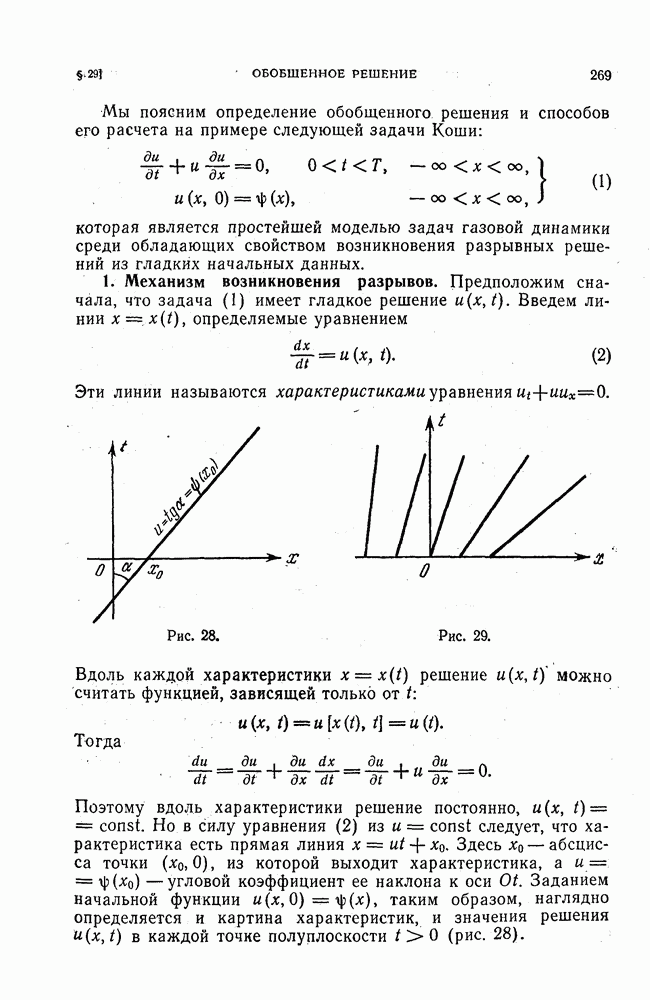
3. Дивергентные разностные схемы.
Разностные схемы, не использующие искусственно введенную вязкость и не использующие
условия на разрыве, как было выяснено, должны опираться на интегральные законы сохранения.
Проведем на плоскости  сетку прямых
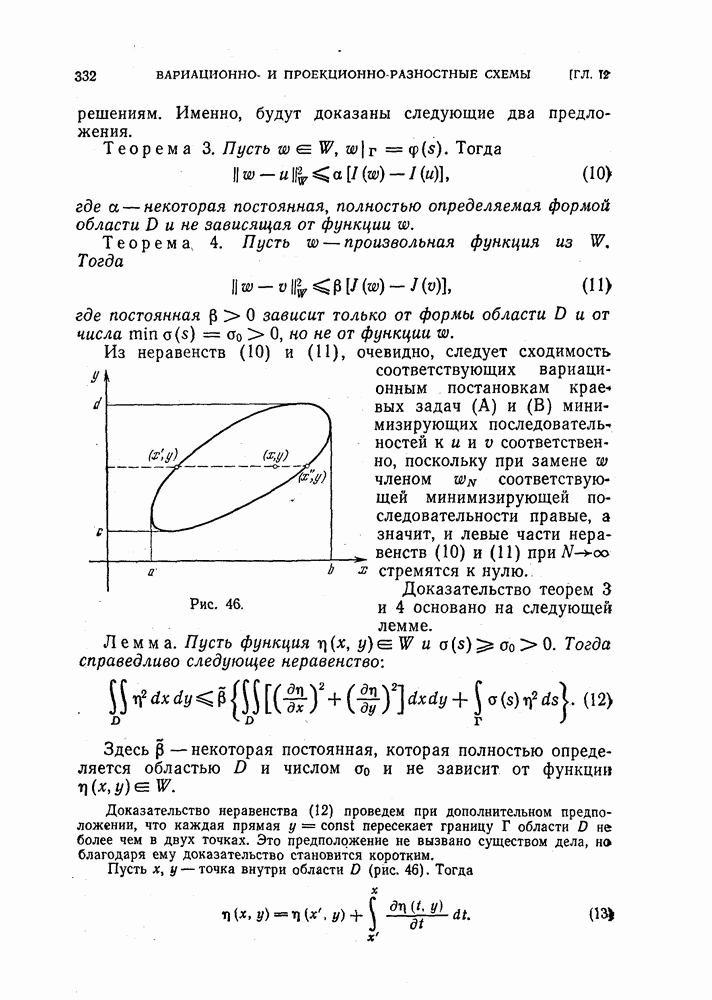
сетку прямых  . Отметим на сторонах возникающих прямоугольников их середины (рис. 37) и отнесем их к сетке
. Отметим на сторонах возникающих прямоугольников их середины (рис. 37) и отнесем их к сетке  (оси координат на рисунке не показаны).
(оси координат на рисунке не показаны).
Искомой функцией  будем считать сеточную функцию, определенную в точках сетки
будем считать сеточную функцию, определенную в точках сетки  путем усреднения решения
путем усреднения решения  по той стороне сеточного прямоугольничка, которому принадлежит рассматриваемая точка сетки:
по той стороне сеточного прямоугольничка, которому принадлежит рассматриваемая точка сетки:

Приближенное решение задачи определено на той же сетке  . Значения в точках
. Значения в точках  лежащих на горизонтальных сторонах прямоугольничков, будем обозначать
лежащих на горизонтальных сторонах прямоугольничков, будем обозначать  , а в точках
, а в точках  вертикальных сторон — через
вертикальных сторон — через 
Величину  можно считать продолженной на всю сторону
можно считать продолженной на всю сторону  прямоугольничка, которому принадлежит точка
прямоугольничка, которому принадлежит точка  Аналогично будем считать, что
Аналогично будем считать, что  определена на всем вертикальном промежутке
определена на всем вертикальном промежутке

Таким образом, и будет функцией, определенной на прямых  . Связь между величиной,
. Связь между величиной,  , установим, исходя из интегрального закона сохранения
, установим, исходя из интегрального закона сохранения

Рассмотрим в качестве контура Г элементарный прямоугольник сетки и положим

или в развернутом виде

Если будет указано правило вычисления величин  по уже известным величинам
по уже известным величинам  , то формула (7) позволяет вычислить величины
, то формула (7) позволяет вычислить величины  , т. е. продвинуться на один шаг по времени. Однако независимо от конкретного способа, который мы изберем для вычисления величины
, т. е. продвинуться на один шаг по времени. Однако независимо от конкретного способа, который мы изберем для вычисления величины  разностная схема вида (7) обладает свойством дивергентности, которое состоит в следующем. Проведем в полуплоскости
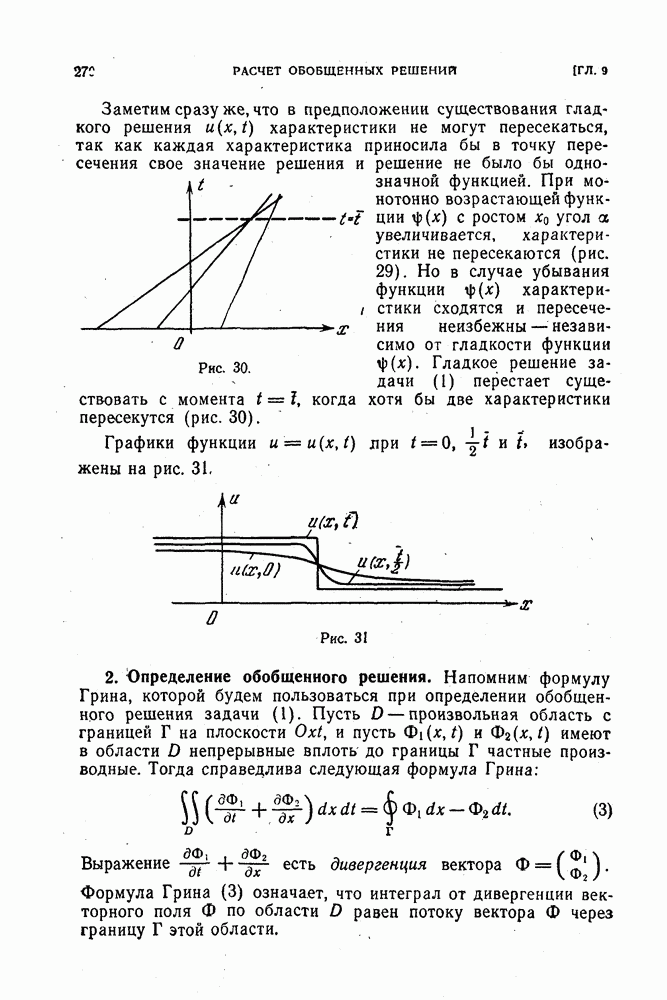
разностная схема вида (7) обладает свойством дивергентности, которое состоит в следующем. Проведем в полуплоскости  какой-либо замкнутый несамопересекающийся контур, целиком состоящий из сторон сеточных прямоугольников (рис. 38).
какой-либо замкнутый несамопересекающийся контур, целиком состоящий из сторон сеточных прямоугольников (рис. 38).

Рис. 38.
Этот контур  ограничит некоторую область
ограничит некоторую область  составленную из сеточных прямоугольников.
составленную из сеточных прямоугольников.
Просуммируем почленно все уравнения (7), относящиеся к прямоугольничкам, составляющим область  . Уравнения (7) и (6) отличаются только формой записи. Поэтому можно считать, что мы суммируем уравнения (6). Получим
. Уравнения (7) и (6) отличаются только формой записи. Поэтому можно считать, что мы суммируем уравнения (6). Получим 

Интегралы по тем сторонам прямоугольничков, которые не лежат на границе  области
области  но входят в выражение (6), после суммирования уравнений (6) взаимно уничтожатся.
но входят в выражение (6), после суммирования уравнений (6) взаимно уничтожатся.
Действительно, каждая из этих сторон принадлежит двум соседним прямоугольничкам, так что интегрирование функции по ней встречается дважды и ведется в противоположных направлениях (рис. 39).
Разностные схемы, при суммировании которых по точкам сеточной области  остаются только алгебраические суммы значений неизвестных или функций от них вдоль границы области, называют дивергентными, или консервативными. Такие схемы аналогичны дифференциальным уравнениям дивергентного вида
остаются только алгебраические суммы значений неизвестных или функций от них вдоль границы области, называют дивергентными, или консервативными. Такие схемы аналогичны дифференциальным уравнениям дивергентного вида

при почленном интегрировании которых по двумерной области D в левой части возникает контурный интеграл (3) § 29. Разностная схема (2) недивергентна, схема (7) дивергентна.
Заметим следующее. Пусть сеточная функция  удовлетворяющая уравнению (7), при
удовлетворяющая уравнению (7), при  равномерно сходится к некоторой кусочно-непрерывной функции
равномерно сходится к некоторой кусочно-непрерывной функции  во всякой замкнутой области, не содержащей линий разрыва, и пусть
во всякой замкнутой области, не содержащей линий разрыва, и пусть  равномерно по h ограничена. Тогда
равномерно по h ограничена. Тогда  удовлетворяет интегральному закону сохранения
удовлетворяет интегральному закону сохранения

где g — произвольный кусочно-гладкий контур.

Рис. 39.
Это непосредственно следует из возможности приблизить контур g контуром  из равенства (8) и предположенной сходимости
из равенства (8) и предположенной сходимости 
Чтобы схема (7) приобрела смысл, надо указать способ вычисления величин по величинам  . В схеме С. К. Годунова, которую мы используем для иллюстрации понятия дивергентных схем, для этого используется решение следующей задачи о «распаде разрыва». Пусть в начальный момент решение
. В схеме С. К. Годунова, которую мы используем для иллюстрации понятия дивергентных схем, для этого используется решение следующей задачи о «распаде разрыва». Пусть в начальный момент решение  задано условиями
задано условиями

где  и
и  . Тогда можно найти соответствующее обобщенное решение. Как это делается, мы видел» в § 29 при разборе примера
. Тогда можно найти соответствующее обобщенное решение. Как это делается, мы видел» в § 29 при разборе примера  и примера
и примера  . Нам важно знать значение
. Нам важно знать значение  решения
решения  при
при 
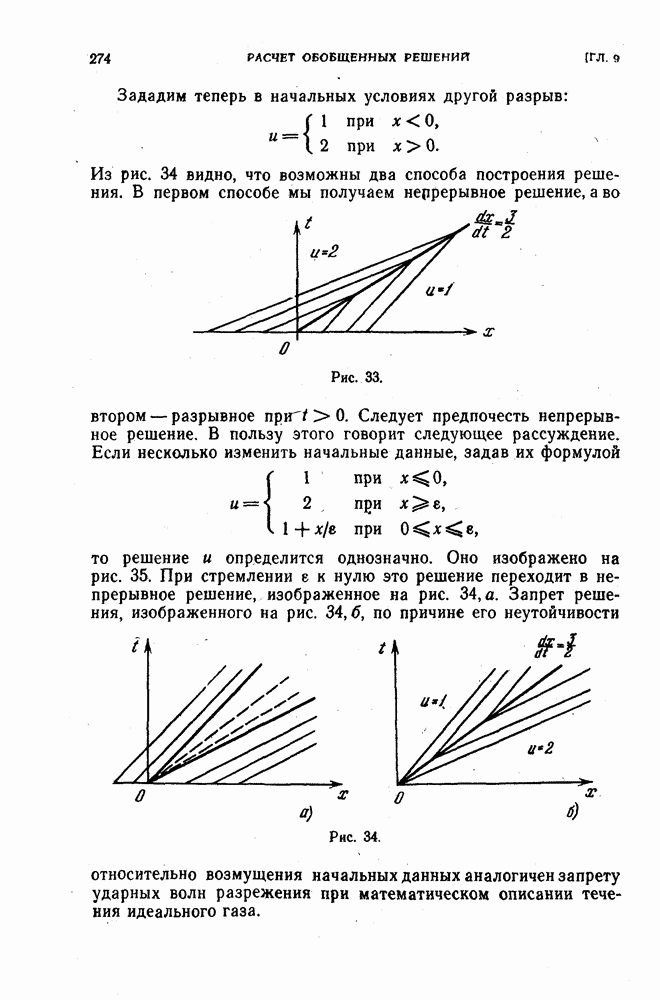
Читатель, построив картинки типа рис. 33, 34, изображающие решение  легко проверит, что на прямой
легко проверит, что на прямой  решение принимает значения «лев, «прав или 0 в зависимости от заданных начальных данных, и выяснит для каждой конкретной пары чисел илев и иправ какое именно. Например, при
решение принимает значения «лев, «прав или 0 в зависимости от заданных начальных данных, и выяснит для каждой конкретной пары чисел илев и иправ какое именно. Например, при  будет
будет  , а при
, а при  будет
будет  .
.
Величину  в схеме (7) будем определять из задачи о распаде разрыва, возникающего на границе
в схеме (7) будем определять из задачи о распаде разрыва, возникающего на границе  каждых двух участков, где заданы постоянные значения
каждых двух участков, где заданы постоянные значения
Если, например,  , то
, то

и схема (7) примет вид

ИЛИ

Легко видеть, что при

имеет место принцип максимума

Отсюда видно, что при  можно надеяться, что полученная разностная схема устойчива при некотором разумном выборе норм. Мы не будем фактически указывать эти нормы: экспериментальные расчеты подтверждают, что при измельчении сетки решение и задачи (7) с кусочно-монотонными и кусочно-гладкими начальными данными
можно надеяться, что полученная разностная схема устойчива при некотором разумном выборе норм. Мы не будем фактически указывать эти нормы: экспериментальные расчеты подтверждают, что при измельчении сетки решение и задачи (7) с кусочно-монотонными и кусочно-гладкими начальными данными  сходится к некоторой функции
сходится к некоторой функции  имеющей конечное число разрывов, причем вне любой окрестности разрывов сходимость равномерная.
имеющей конечное число разрывов, причем вне любой окрестности разрывов сходимость равномерная.
Схема (7) с вычислением  путем использования распада разрыва не является, конечно, единственной дивергентной схемой для задачи (1). Укажем, например, еще простейшую схему, основанную на идее пересчета. Эту идею мы изложили в п. 3 § 22. Для простоты ограничимся случаем
путем использования распада разрыва не является, конечно, единственной дивергентной схемой для задачи (1). Укажем, например, еще простейшую схему, основанную на идее пересчета. Эту идею мы изложили в п. 3 § 22. Для простоты ограничимся случаем 
Сначала ищем вспомогательные величины и по недивергенной неявной разностной схеме

Значение коэффициента при их в уравнении  заменяем через
заменяем через  , а не через
, а не через  , чтобы возникающая схема была линейна относительно подлежащих вычислению величин.
, чтобы возникающая схема была линейна относительно подлежащих вычислению величин.
Далее полагаем

и пользуемся схемой (7), (9).
Получаемая так дивергентная схема на гладком решении имеет второй порядок аппроксимаций:
Эвристическое исследование с помощью спектрального признака Неймана при линеаризации и замораживании коэффициента указывает на устойчивость при произвольном  . Проведем это исследование.
. Проведем это исследование.
В результате линеаризации и замораживания коэффициента придем к схеме вида

Для решения с начальными данными

получим

где

Далее,

где

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
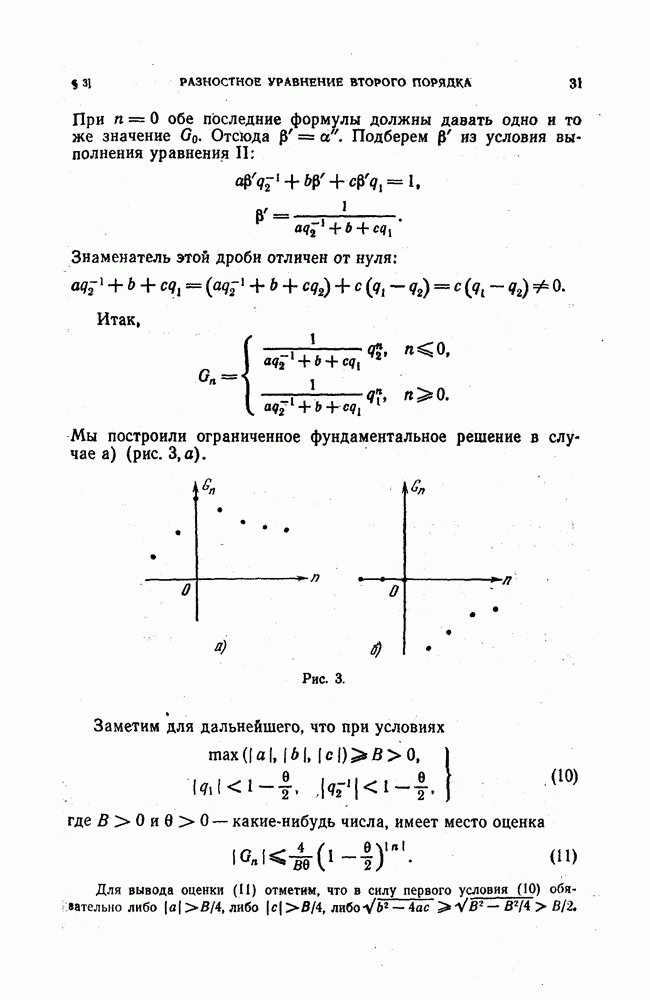
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
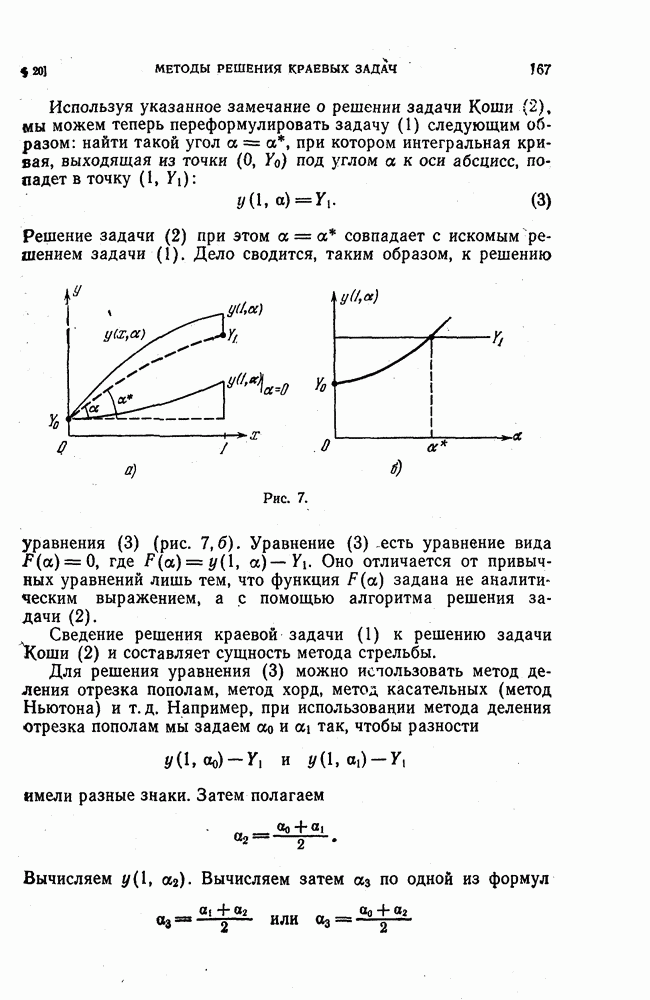
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА