| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Схемы Адамса.
В схемах Адамса, одну из разновидностей которых мы сейчас опишем, для вычисления каждого следующего значения  достаточно дополнительно вычислить значение
достаточно дополнительно вычислить значение  лишь в одной точке независимо от порядка аппроксимации. Кроме того, приходится проделать небольшое число вычитаний и сложений, которые требуют во много раз меньше времени, чем каждое вычисление сколько-нибудь сложной функции
лишь в одной точке независимо от порядка аппроксимации. Кроме того, приходится проделать небольшое число вычитаний и сложений, которые требуют во много раз меньше времени, чем каждое вычисление сколько-нибудь сложной функции  .
.
Обозначим

и положим  Выпишем несколько разностных уравнений, используемых в схемах Адамса для вычисления
Выпишем несколько разностных уравнений, используемых в схемах Адамса для вычисления  если
если  уже вычислены:
уже вычислены:

Первое из этих уравнений — разностное уравнение Эйлера. При подстановке в левые части уравнений  вместо
вместо  значений
значений  точного решения
точного решения  в равенствах (7) — (10) возникают невязки порядка
в равенствах (7) — (10) возникают невязки порядка  соответственно.
соответственно.
Формулы Адамса получаются следующим образом. Пусть  -решение уравнения
-решение уравнения

Обозначим

Тогда

Из тгеории интерполяции функций известно, что существует один и только один многочлен  степени не выше k, принимающий в
степени не выше k, принимающий в  точке
точке  заданные значения
заданные значения  соответственно. Этот многочлен
соответственно. Этот многочлен  в случае достаточно гладкой функции
в случае достаточно гладкой функции  уклоняется от
уклоняется от  на отрезке
на отрезке  на величину порядка
на величину порядка  так что
так что

Разностная формула Адамса имеет вид 4

При подстановке в левую часть вместо

соответственно значений

получим невязку порядка 

При  интерполяционный многочлен
интерполяционный многочлен

и формула (12) превращается в (7).

Далее,

Следовательно, формула (12) превращается в (8). Аналогично при  из (12) получаются формулы (9) и (10) соответственно.
из (12) получаются формулы (9) и (10) соответственно.
Для вычисления по схеме (7) достаточно знать  . Для того чтобы начать вычисления по схеме (8), надо заранее знать, кроме
. Для того чтобы начать вычисления по схеме (8), надо заранее знать, кроме  также еще и
также еще и  Схема (9) требует использования
Схема (9) требует использования  , а схема (10) — четырех значений:
, а схема (10) — четырех значений:  . Эти значения могут быть найдены по схеме Рунге — Кутта; с помощью схемы Эйлера с мелким шагом; с помощью разложения решения в окрестности точки
. Эти значения могут быть найдены по схеме Рунге — Кутта; с помощью схемы Эйлера с мелким шагом; с помощью разложения решения в окрестности точки  в степенной ряд. Нестандартное начало счета является одним из недостатков схем Адамса по сравнению со схемами Рунге — Кутта. Отмечавшимся ранее достоинством схем Адамса является то, что для вычисления
в степенной ряд. Нестандартное начало счета является одним из недостатков схем Адамса по сравнению со схемами Рунге — Кутта. Отмечавшимся ранее достоинством схем Адамса является то, что для вычисления  нужно, в дополнение к уже вычисленным в процессе отыскания
нужно, в дополнение к уже вычисленным в процессе отыскания  значениям
значениям  вычислить только одно значение функций
вычислить только одно значение функций  и произвести некоторое число вычитаний для вычисления
и произвести некоторое число вычитаний для вычисления  .
.
Итак, преимущества методов Адамса перед методами Рунге—Кутта заключаются в меньшей трудоемкости вычислений на один шаг. Основные недостатки — нестандартное начало счета, невозможность (без усложнения формул) в процессе счета изменить, начиная с какой-то точки  , шаг
, шаг  с которым ведутся вычисления. Последнее обстоятельство существенно в тех случаях, когда решение и его производные на некоторых участках меняются быстро, а на других изменяются медленно.
с которым ведутся вычисления. Последнее обстоятельство существенно в тех случаях, когда решение и его производные на некоторых участках меняются быстро, а на других изменяются медленно.
Схема Рунге — Кутта, если такого рода обстоятельства выясняются в процессе счета, может, например, но заданной подпрограмме автоматически уменьшить шаг или увеличить шаг на гладких участках, чтобы не производить лишней работы.
По-видимому, наиболее рационально использование обоих методов — Рунге—Кутта и Адамса с автоматическим переходом с одного из них на другой в процессе счета. При этом начинать счет надо по схеме Рунге — Кутта. В программе должен быть предусмотрен автоматический выбор шага, при котором  расчет ведется с нужной точностью. При этом программа выбора шага должна предусматривать некоторый «консерватизм при выборе шага: диктовать изменение шага только в случае.
расчет ведется с нужной точностью. При этом программа выбора шага должна предусматривать некоторый «консерватизм при выборе шага: диктовать изменение шага только в случае.
если требуется «довольно сильно» его изменить. Если оказывается, что при вычислении нескольких последовательных значений  по схеме Рунге — Кутта не происходит изменения шага, целесообразен автоматический переход на счет по более экономной схеме Адамса. Как только вновь появляется необходимость изменить шаг, программа расчета должна переходить на вычисления по схеме Рунге — Кутта и т. д.
по схеме Рунге — Кутта не происходит изменения шага, целесообразен автоматический переход на счет по более экономной схеме Адамса. Как только вновь появляется необходимость изменить шаг, программа расчета должна переходить на вычисления по схеме Рунге — Кутта и т. д.
Для контроля правильности выбора шага обычно параллельно ведут вычисления с некоторым заданным и вдвое меньшим шагом. В пределах требуемой точности решения должны совпадать. В противном случае надо вести вычисления с более мелким шагом. Нужно также предусмотреть пробу на возможность увеличить шаг.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
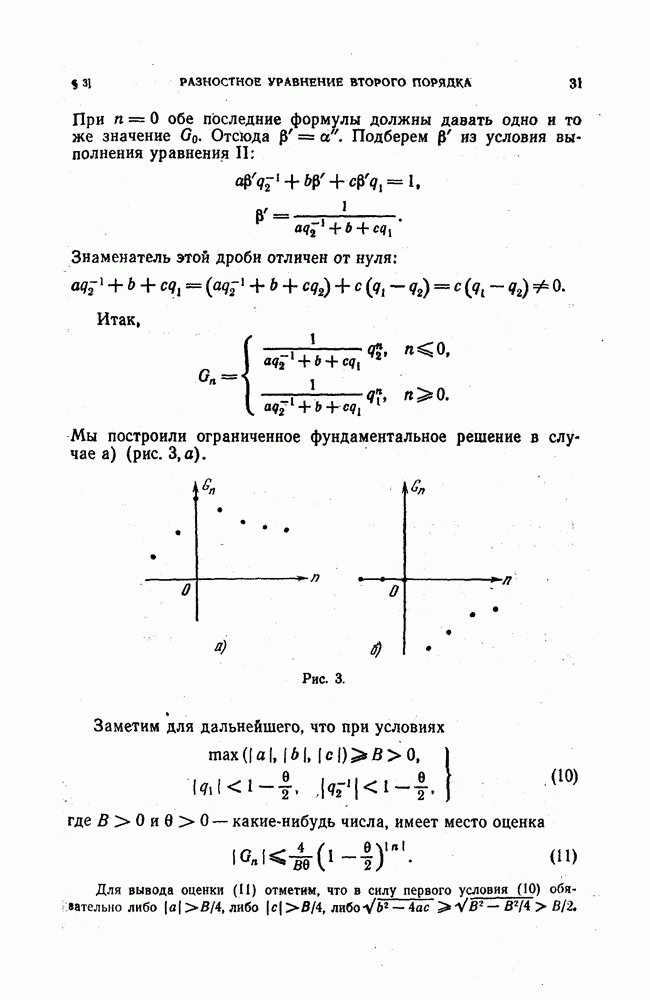
- § 3. Разностное уравнение второго порядка
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
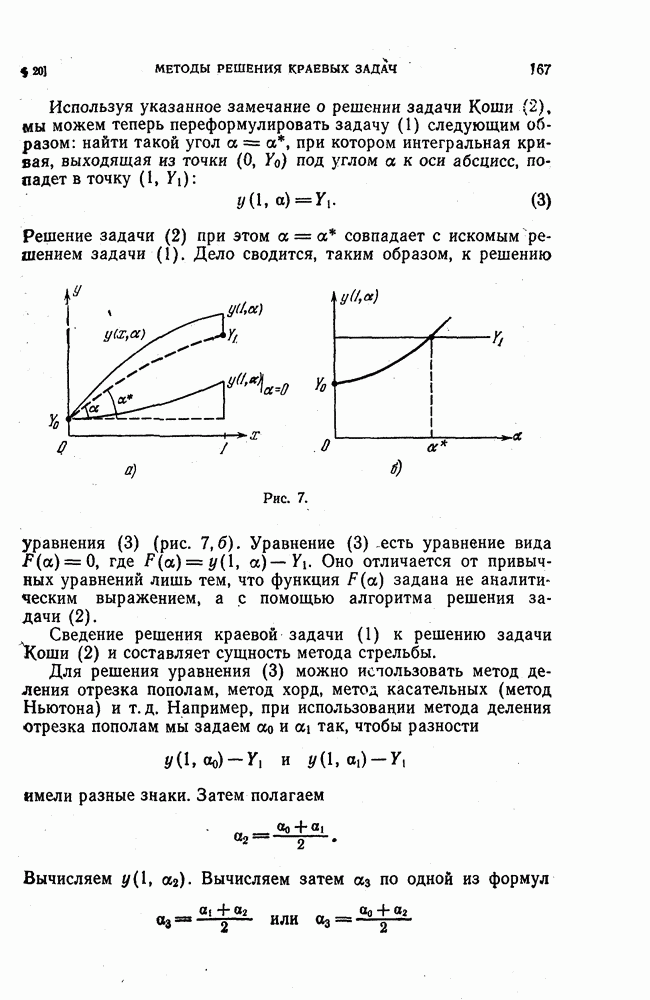
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА