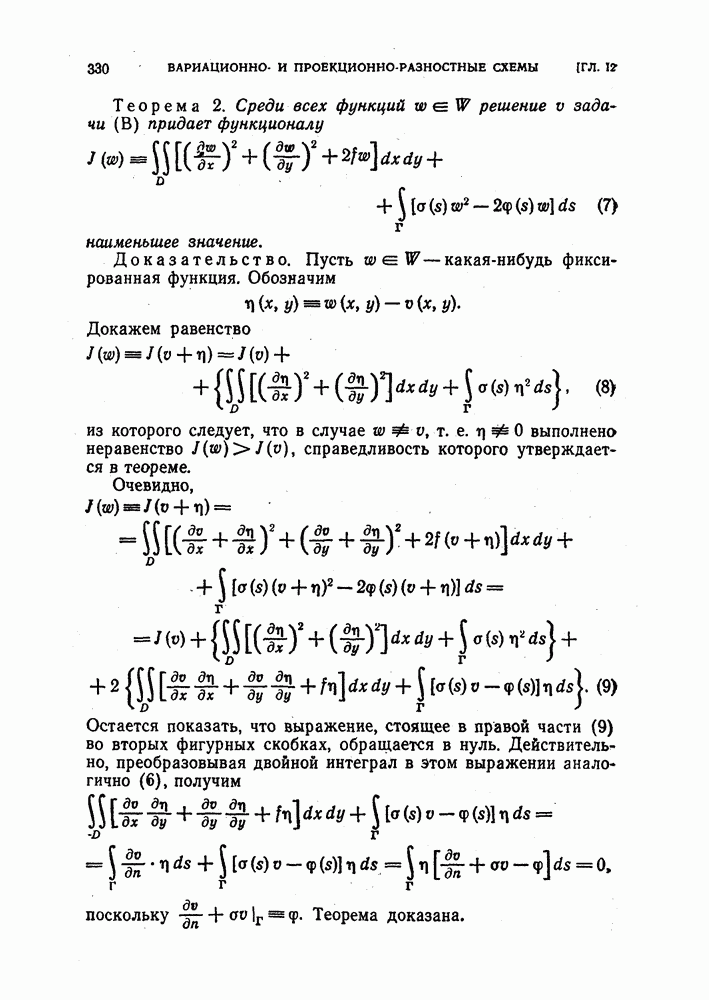| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 22. Простейшие приемы построения аппроксимирующих разностных схем
1. Замена производных разностными отношениями.
Простейший прием построения разностных краевых задач, аппроксимирующих дифференциальные, состоит в замене производных соответствующими разностными отношениями. Приведем, несколько примеров разностных схем, полученных таким способом. В этих примерах будут использованы приближенные формулы

Предполагая функцию  имеющей достаточное числоограниченных производных, можно выписать выражения для
имеющей достаточное числоограниченных производных, можно выписать выражения для
остаточных членов этих формул. По формуле Тейлора

Используя разложения (2), можно получить выражения для остаточных членов приближенных формул (1). Именно, справедливы равенства

Остаточные члены приближенных формул (1) входят в соответствующие равенства (3) в виде выражений в квадратных скобках.
Очевидно, что формулы (1) и выражения остаточных членов, выписанные в формулах (3), можно использовать и при замене частных производных разностными отношениями. Например,

причем

Точно так же справедливы формулы

и при этом

и т. д.
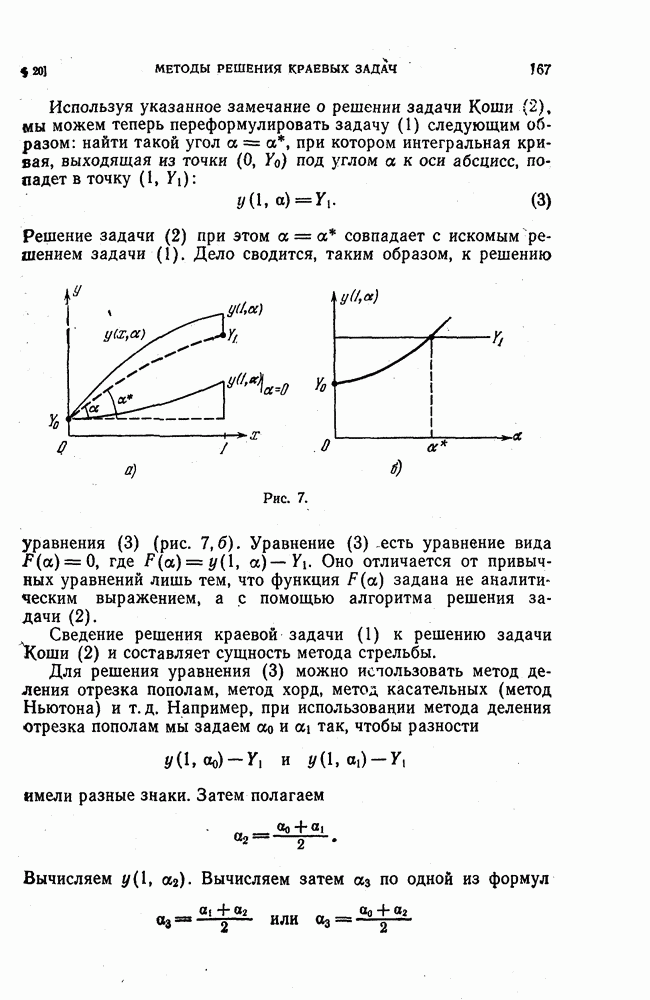
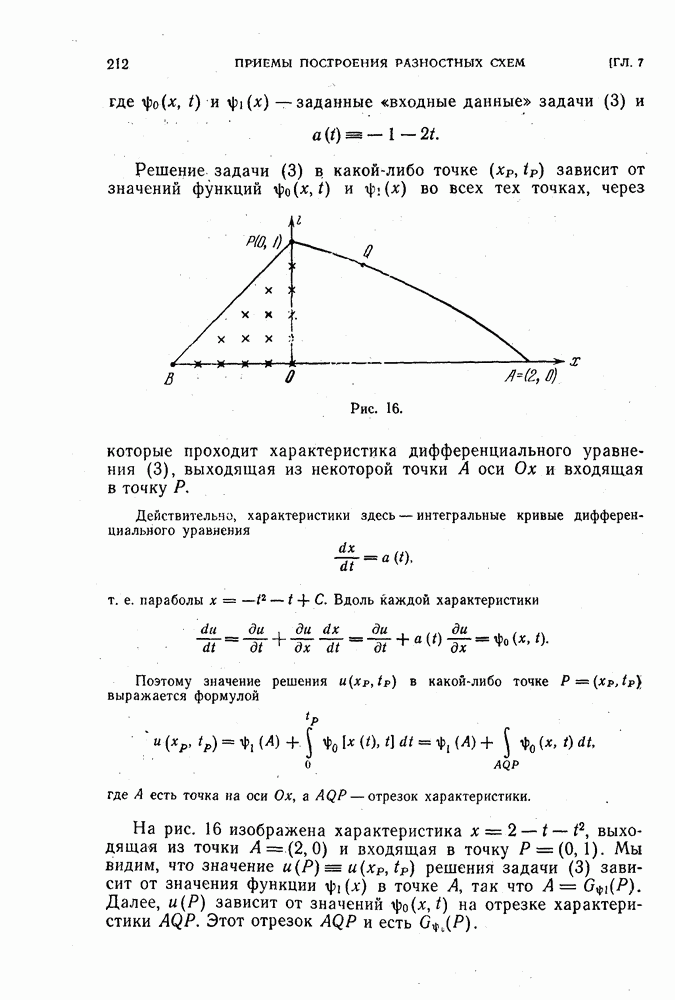
Пример 1. Вернемся к задаче Коши (4) из § 21:

Для аппроксимации этой задачи Коши построим три схемы. Во всех этих схемах используем сетку  , образованную точками пересечения прямых
, образованную точками пересечения прямых  , попавшими в полосу
, попавшими в полосу  . Значения
. Значения  будем считать связанными соотношением
будем считать связанными соотношением  , где
, где  — некоторая положительная постоянная. Простейшая из этих схем имеет вид (5) из § 21:
— некоторая положительная постоянная. Простейшая из этих схем имеет вид (5) из § 21:

и получается при замене производных  и
и  во приближенным формулам
во приближенным формулам

Мы подробно исследовали эту схему в § 21. Для нее невязка  , возникающая при подстановке решения
, возникающая при подстановке решения  дифференциальной задачи в левую часть разностной задачи
дифференциальной задачи в левую часть разностной задачи

выражается формулой

За норму элемента пространства  примем в этом параграфе максимум всех компонент элемента
примем в этом параграфе максимум всех компонент элемента  . Тогда, очевидно,
. Тогда, очевидно,

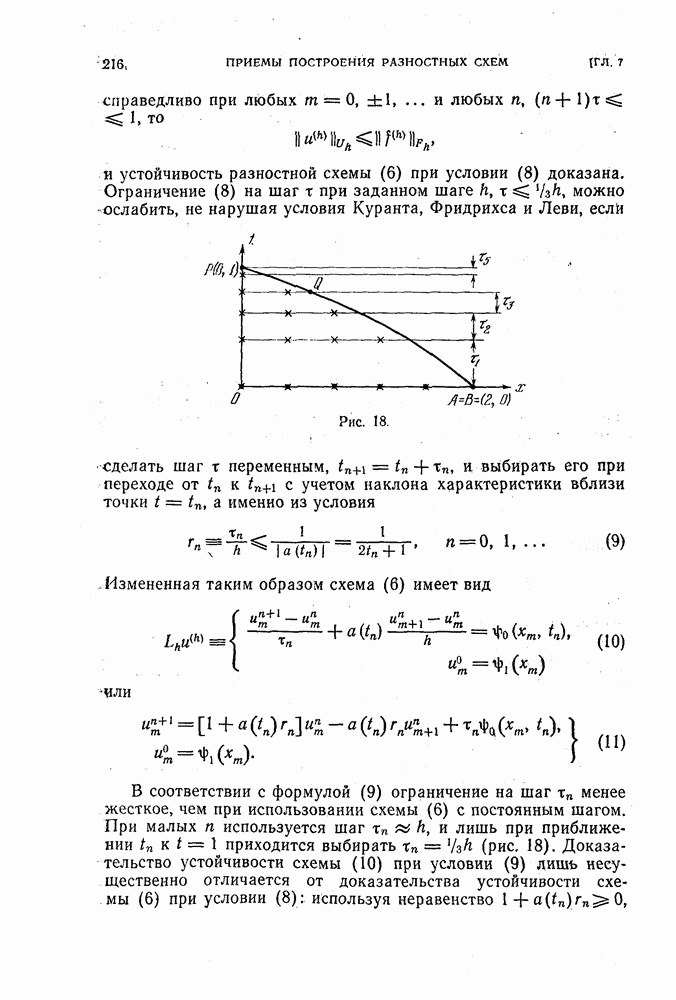
В порядок аппроксимации получается первый, t Вторая схема получается при использовании другой формулы для замены 

она имеет вид

Здесь

и порядок аппроксимации снова получается первый.
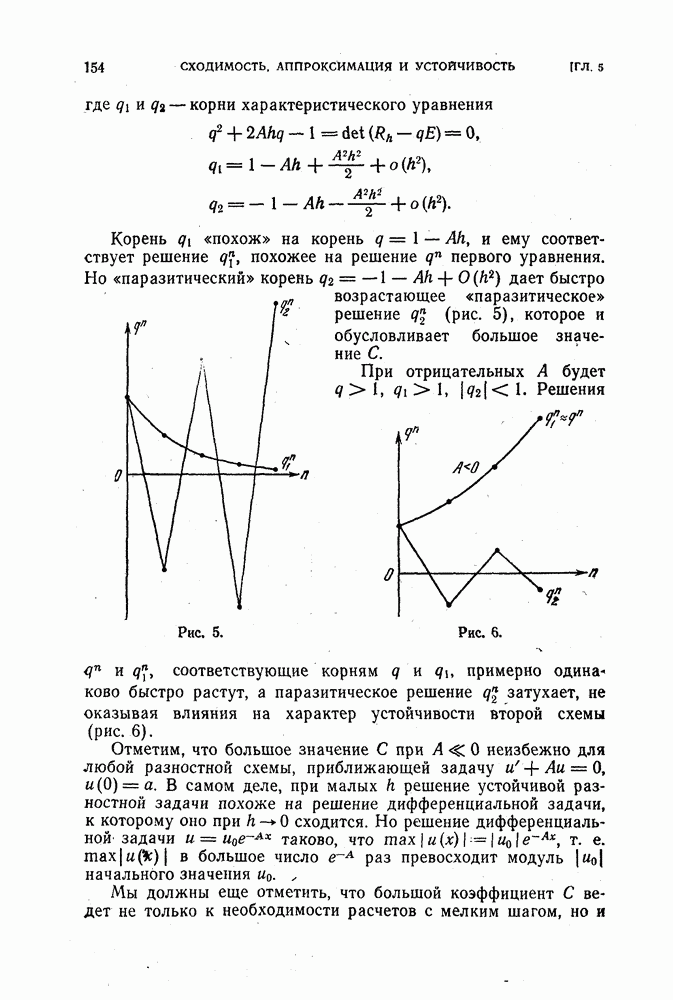
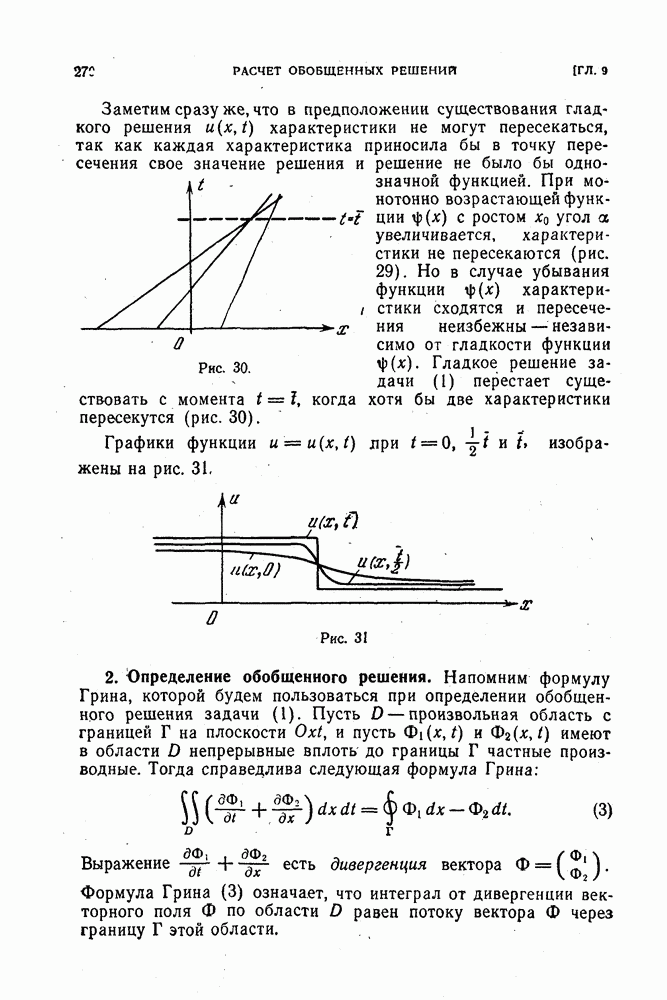
Вторая схема, казалось бы, совсем несущественно отличается от первой. В дальнейшем мы увидим, однако, что вторая схема непригодна для счета: она неустойчива при любом 
Третья схема,

получается при замене производных разностными отношениями «о приближенным формулам

С помощью тейлоровских разложений (2) для достаточно гладкого решения  задачи (1) получаем
задачи (1) получаем

Поэтому

так что  из формулы
из формулы

имеет вид

Следовательно,  и имеет место аппроксимация первого порядка, как и в двух первых примерах.
и имеет место аппроксимация первого порядка, как и в двух первых примерах.

Рис. 10.
Рассмотрим теперь случай, когда связь между шагами сетки задается не формулой  как выше, а формулой
как выше, а формулой

предписывающей ускоренное измельчение шага  по сравнению с шагом
по сравнению с шагом  . В этом случае
. В этом случае

Отсюда видно, что рассматриваемая разностная схема аппроксимирует задачу

а вовсе не задачу Коши (4), которую мы хотели аппроксимировать.
Мы столкнулись с тем фактом, что одна и та же разностная схема может в случае различной связи  аппроксимировать при
аппроксимировать при  различные дифференциальные задачи. Такого рода разностные схемы называют негибкими.
различные дифференциальные задачи. Такого рода разностные схемы называют негибкими.
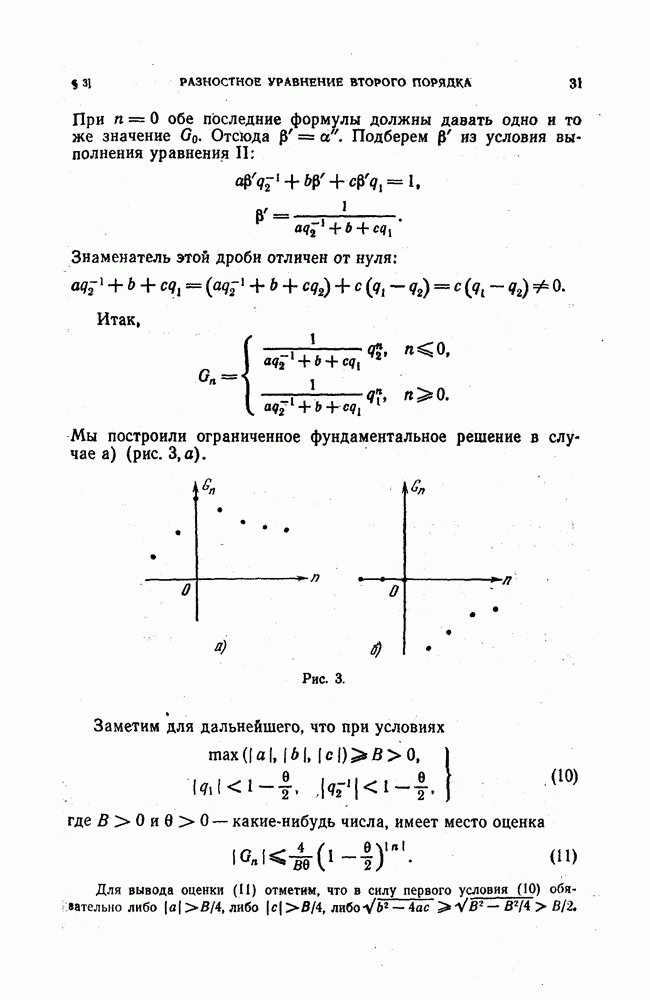
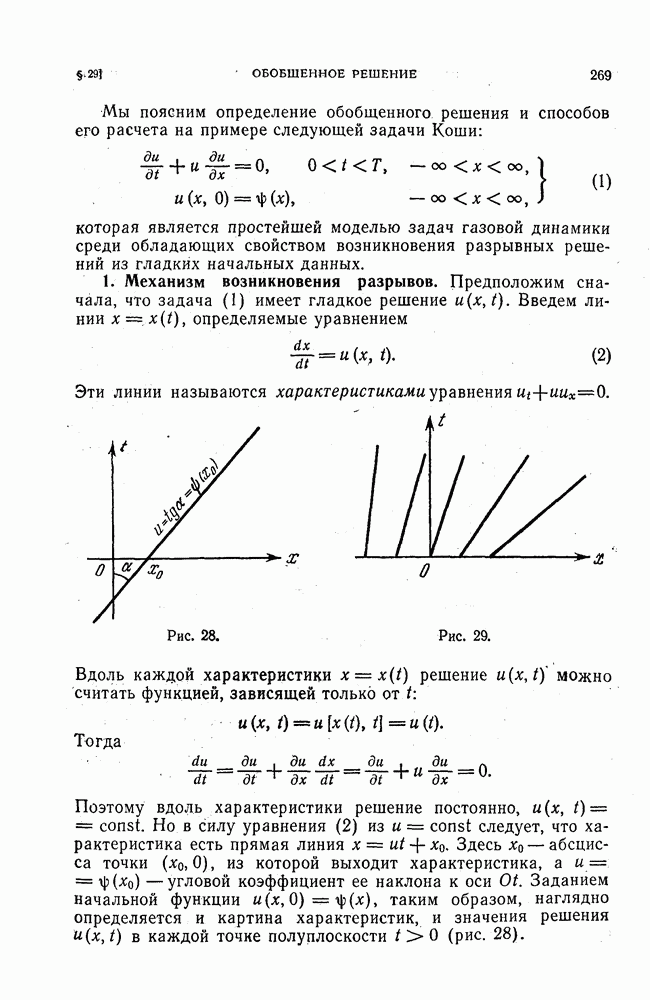
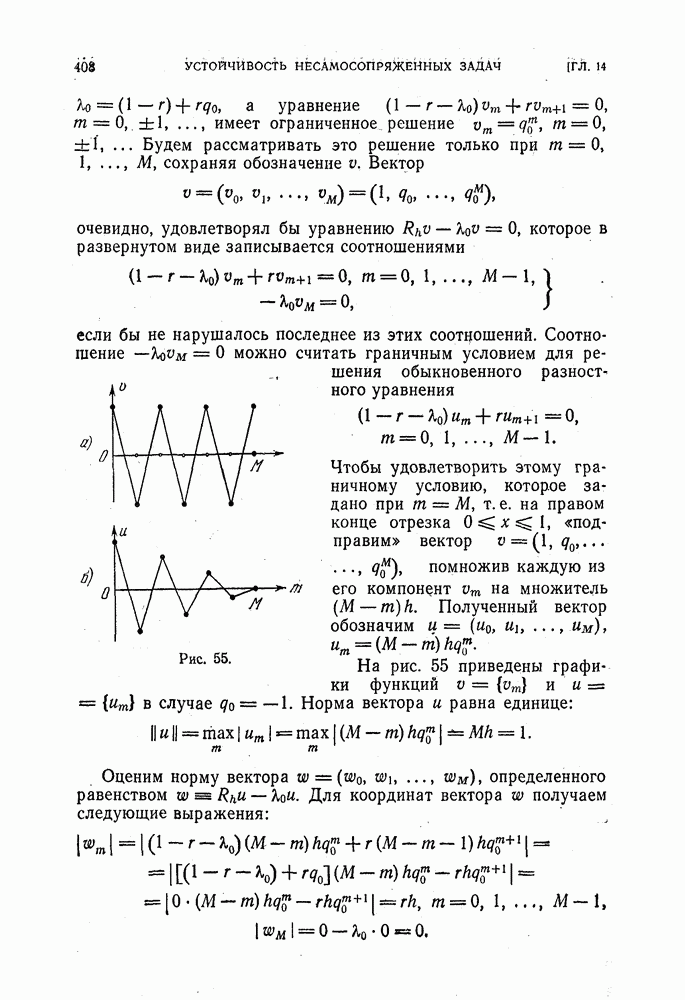
Для облегчения запоминания разностной схемы ее обычно принято сопоставлять с картинкой, на которой изображено взаимное расположение точек сетки («шаблон»), значения решения в которых связывает разностное уравнение при некоторых фиксированных значениях тип.
Для трех рассмотренных схем эти картинки изображены  рис. 10.
рис. 10.
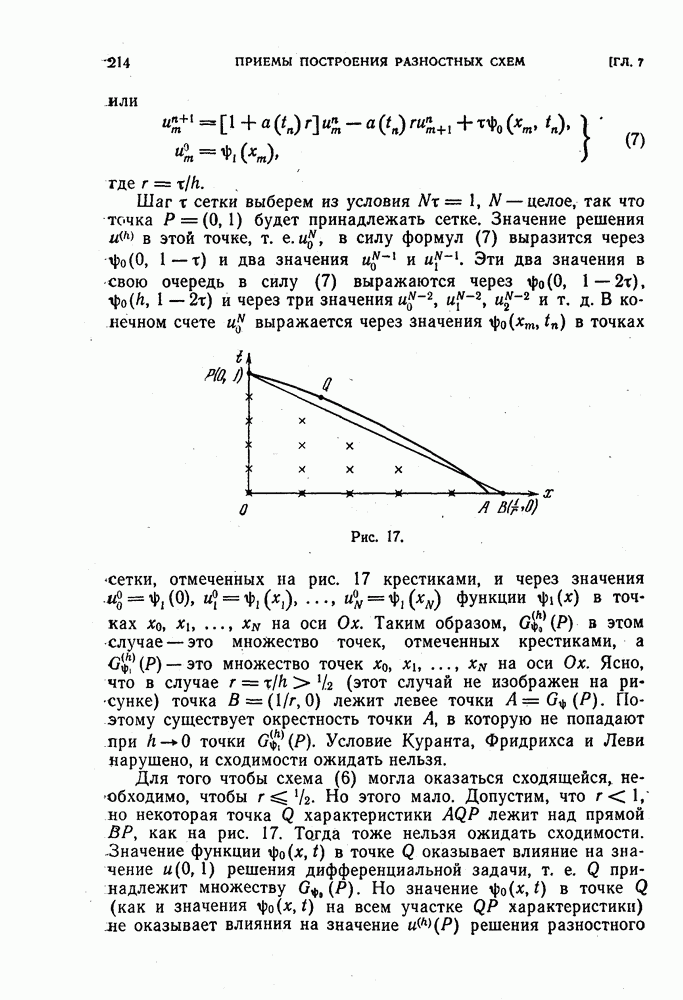
Пример 2. Приведем две разностные схемы, аппроксимирующие задачу Коши для уравнения теплопроводности

Простейшая из них,

получается при замене производных  разностными отношениями по формулам
разностными отношениями по формулам

Если для замены  использовать другую формулу:
использовать другую формулу:

мы придем к другой схеме для того же уравнения:

Чтобы различать операторы  этих двух схем, мы снабдили их номерами <и написали
этих двух схем, мы снабдили их номерами <и написали  Шаблоны, соответствующие этим разностным схемам, изображены на рис. 11.
Шаблоны, соответствующие этим разностным схемам, изображены на рис. 11.

Рис. 11.
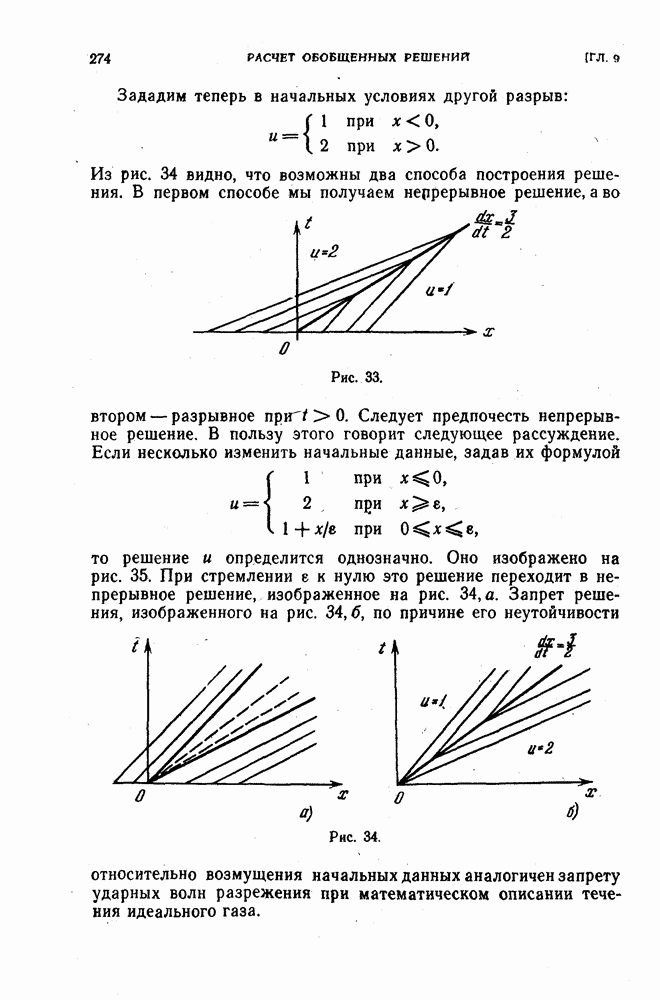
Эти схемы существенно отличаются. Вычисление решения  по первой из них не представляет труда и проводится по явной формуле
по первой из них не представляет труда и проводится по явной формуле

где  . Эта формула получена из разностного уравнения в результате решения его относительно
. Эта формула получена из разностного уравнения в результате решения его относительно  . Зная значения решения
. Зная значения решения  на слое
на слое  сетки, мы можем вычислить его значения
сетки, мы можем вычислить его значения  на следующем слое
на следующем слое 
Вторая схема  лишена этого удобного свойства. Поэтому ее называют неявной. В этом случае разностное уравнение, выписанное при фиксированных тип, нельзя разрешить относительно
лишена этого удобного свойства. Поэтому ее называют неявной. В этом случае разностное уравнение, выписанное при фиксированных тип, нельзя разрешить относительно  выразив это значение через известные значения
выразив это значение через известные значения  с предыдущего слоя. Дело в том, что в это уравнение входит не только неизвестное значение
с предыдущего слоя. Дело в том, что в это уравнение входит не только неизвестное значение  но также И неизвестные
но также И неизвестные  Поэтому для определения
Поэтому для определения  придется решать разностное уравнение относительно сеточной функции
придется решать разностное уравнение относительно сеточной функции  аргумента
аргумента  . Тем не менее, в дальнейшем будет показано, что схема
. Тем не менее, в дальнейшем будет показано, что схема  как правило, удобнее схемы
как правило, удобнее схемы  .
.
При  , обе схемы имеют второй порядок аппроксимации относительно, h. Вычислим невязку
, обе схемы имеют второй порядок аппроксимации относительно, h. Вычислим невязку  оценим порядок аппроксимации для второй из этих схем. Пользуясь формулами (3), можно написать
оценим порядок аппроксимации для второй из этих схем. Пользуясь формулами (3), можно написать

Отсюда, с учетом  можно написать
можно написать

Но

Поэтому

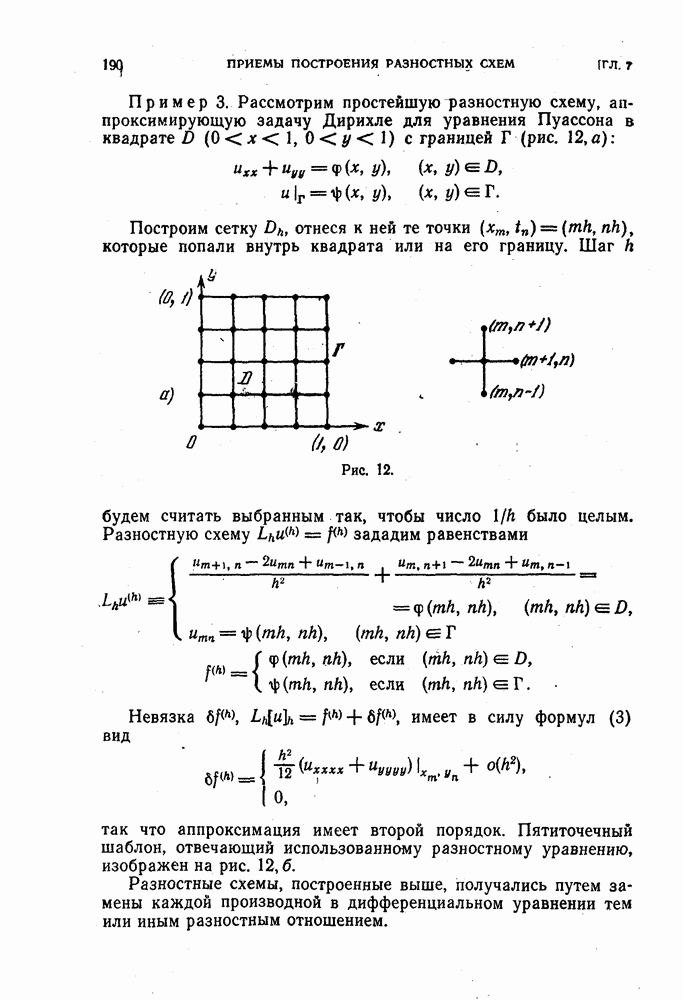
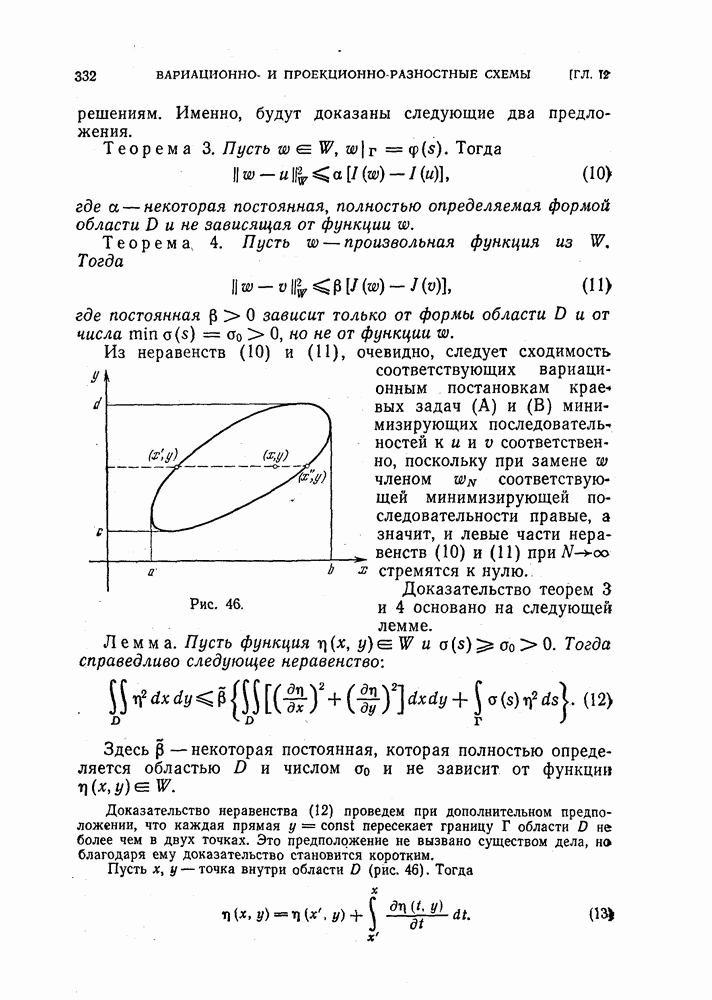
Пример 3. Рассмотрим простейшую разностную схему, аппроксимирующую задачу Дирихле для уравнения Пуассона в квадрате  с границей Г (рис. 12, а):
с границей Г (рис. 12, а):

Построим сетку  , отнеся к ней те точки
, отнеся к ней те точки  которые попали внутрь квадрата или на его границу.
которые попали внутрь квадрата или на его границу.

Рис. 12.
Шаг  будем считать выбранным так, чтобы число
будем считать выбранным так, чтобы число  было целым. Разностную схему
было целым. Разностную схему  зададим равенствами
зададим равенствами

Невязка  имеет в силу формул (3)
имеет в силу формул (3)

так что аппроксимация имеет второй порядок. Пятиточечный шаблон, отвечающий использованному разностному уравнению, изображен на рис. 12, б.
Разностные схемы, построенные выше, получались путем замены каждой производной в дифференциальном уравнении тем или иным разностным отношением.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА