| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Метод неопределенных коэффициентов.
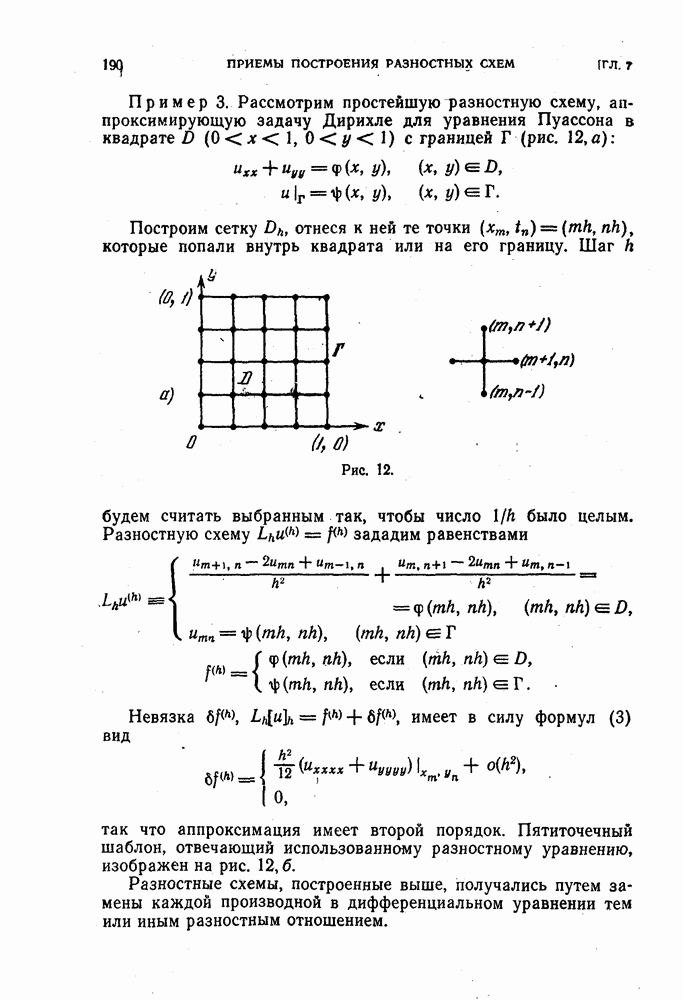
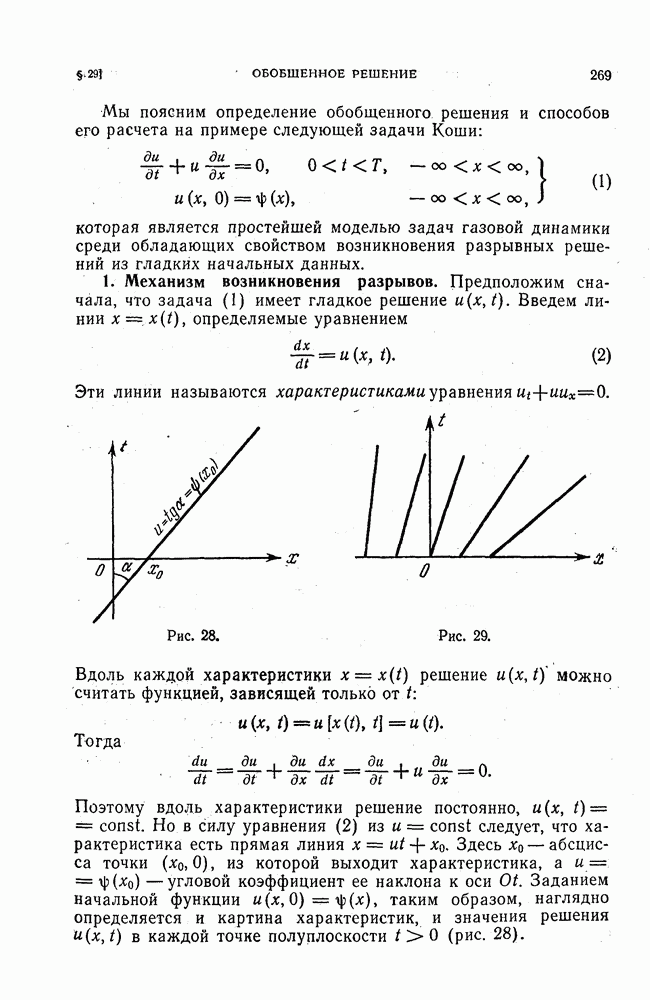
Более общий способ построения разностных схем состоит в том, что приближается не каждая производная в отдельности, а сразу весь дифференциальный оператор. Разъясним этот способ на примерах, разностных схем для задачи Коши (4), Сначала рассмотрим схему первого порядка аппроксимации (5). Она связывает значения искомой функции в трех точках, изображенных на рис. 10 слева. Разностное уравнение

используемое в этой схеме, имеет вид

Забудем на время, что нам уже известна разностная схема (5), для которой

и, считая эти коэффициенты неопределенными, постараемся подобрать их так, чтобы имело место равенство

или

где

Воспользуемся формулой Тейлора:

Подставив эти выражения в правую часть равенства

получим

Поскольку нашей целью является такой подбор коэффициентов  чтобы выполнялось условие аппроксимации (6), то естественно предварительно так сгруппировать слагаемые в правой части равенства (8), чтобы выделился член (7). Тогда остальные слагаемые образуют остаточный член аппроксимации, который должен быть мал. Чтобы выделить член
чтобы выполнялось условие аппроксимации (6), то естественно предварительно так сгруппировать слагаемые в правой части равенства (8), чтобы выделился член (7). Тогда остальные слагаемые образуют остаточный член аппроксимации, который должен быть мал. Чтобы выделить член  можно заменить в правой части равенства (8) производные
можно заменить в правой части равенства (8) производные  или
или  соответственно по одной из формул:
соответственно по одной из формул:

Для определенности воспользуемся первой из них.
Кроме того, подчиним шаги  связи
связи  , где
, где  — какая-нибудь постоянная. После этого равенство (8) примет следующий вид:
— какая-нибудь постоянная. После этого равенство (8) примет следующий вид:

Среди всех гладких функций и  можно указать такие, для которых и,
можно указать такие, для которых и,  в любой заранее заданной фиксированной точке принимают любые независимые друг от друга значения. Следовательно, и значения
в любой заранее заданной фиксированной точке принимают любые независимые друг от друга значения. Следовательно, и значения

также можно считать независимыми друг от друга. Ввиду этого из равенства (9) следует, что для выполнения при любой правой части  задачи (4) условия аппроксимации
задачи (4) условия аппроксимации

необходимо, чтобы выполнялись равенства

где  — какие-нибудь произвольные величины порядка А. Положим
— какие-нибудь произвольные величины порядка А. Положим  . Получающаяся при этом система
. Получающаяся при этом система

имеет единственное решение

которое приводит к уже известной схеме (5).
Теперь мы, однако, дополнительно узнали, что среди разностных схем вида

она является единственной, аппроксимирующей рассматриваемую задачу Коши. Говоря о единственности, мы пренебрегаем тем произволом, который вносит, свобода выбора функций 
Всюду в дальнейших примерах мы также будем пренебрегать подобного рода очевидным произволом и даже не всегда будем вводить произвольные величины, аналогичные величинам  с самого начала полагая их равными нулю.
с самого начала полагая их равными нулю.
Читатель без труда убедится, что в рассмотренном сейчас примере учет этих величин привел бы к следующему несущественному изменению результата:

Аналогично будет обстоять дело и в других примерах, которые нам встретятся.
Посмотрим теперь, как можно строить для задачи (4) разностные схемы

более общего вида, связывающие значения искомой функции в четырех точках, изображенных на рис. 13.

Рис. 13.
Шаги сетки снова свяжем равенством  и введем обозначение
и введем обозначение  положив
положив

Для всякой достаточно гладкой функции и  с помощью формулы Тейлора можно написать
с помощью формулы Тейлора можно написать

Выделим в правой части этого равенства член  воспользовавшись для этого тождеством
воспользовавшись для этого тождеством  . Имеем
. Имеем

Если предполагать, что величина  достаточно мала, — это предположение подтвердится в дальнейшем, — то для выполнения условия аппроксимации
достаточно мала, — это предположение подтвердится в дальнейшем, — то для выполнения условия аппроксимации

необходимо, чтобы четыре числа  удовлетворяли следующим трем равенствам:
удовлетворяли следующим трем равенствам:

Положим, как условились, произвольные величины  порядка А равными нулю. Получим систему уравнений
порядка А равными нулю. Получим систему уравнений

Если условия 13 выполнены, то

Система (13) имеет много решений — семейство решений, зависящее от одного параметра. Одно из этих решений:

дает уже рассмотренную схему (5). Решению

соответствует схема

Выбрав какое-либо решение системы (13), надо его подставить в остаточный член и убедиться, что он мал. Для двух сейчас приведенных решений подстановка чисел  дает остаточные члены
дает остаточные члены

порядка  .
.
Среди гладких функций и  есть многочлены второй степени, для которых
есть многочлены второй степени, для которых  принимают в любой фиксированной точке любые независимые наперед заданные значения. При этом член
принимают в любой фиксированной точке любые независимые наперед заданные значения. При этом член  в который входят третьи производные многочлена
в который входят третьи производные многочлена  обращается в нуль. Поэтому для того, чтобы остаточный член был порядка h, необходимо, чтобы коэффициенты при
обращается в нуль. Поэтому для того, чтобы остаточный член был порядка h, необходимо, чтобы коэффициенты при  каждый в отдельности были порядка h. Поскольку из первого уравнения (13) имеем
каждый в отдельности были порядка h. Поскольку из первого уравнения (13) имеем  , то коэффициент при
, то коэффициент при  есть
есть  и порядок остаточного члена всегда не выше первого.
и порядок остаточного члена всегда не выше первого.
Мы установили, что нельзя построить разностную схему вида (10), которая аппроксимирует задачу

с порядком  . Для увеличения порядка аппроксимации пришлось бы увеличить число точек разностной сетки, используемых в конструируемой схеме.
. Для увеличения порядка аппроксимации пришлось бы увеличить число точек разностной сетки, используемых в конструируемой схеме.
Укажем некоторый способ, позволяющий все же построить разностную схему с аппроксимацией порядка  использующую только четыре указанные точки разностной сетки. Способ повышения порядка аппроксимации, который мы сейчас изложим с помощью примера, норит общий характер. Оказывается, что можно подобрать коэффициенты
использующую только четыре указанные точки разностной сетки. Способ повышения порядка аппроксимации, который мы сейчас изложим с помощью примера, норит общий характер. Оказывается, что можно подобрать коэффициенты  так, чтобы выполнялось равенство
так, чтобы выполнялось равенство

где

Е — оператор умножения на единицу. Тогда ввиду  разностная схема
разностная схема

где

будет аппроксимировать рассматриваемую дифференциальную задачу на решении  со вторым порядком относительно
со вторым порядком относительно 
Коэффициенты  снова могут быть подобраны методом неопределенных коэффициентов. Они оказываются следующими:
снова могут быть подобраны методом неопределенных коэффициентов. Они оказываются следующими:

Оператор  при этом получается таким:
при этом получается таким:

Методом неопределенных коэффициентов можно не только подобрать коэффициенты  , при которых
, при которых

при выписанном выше операторе Р, но и построить все такие операторы.
Покажем, как это делается.
Считая, что

и пользуясь формулой Тейлора, получим

Это выражение мы сейчас преобразуем. Начнем с вывода тождества

которое вытекает из определения  :
:

Доказательство содержится в цепочке очевидных тождеств:

Используя эти тождества, можно выражение (14) переписать в следующем эквивалентном виде:

Построим оператор  удовлетворяющий условию
удовлетворяющий условию  Члены, содержащие
Члены, содержащие  , включим в выражение
, включим в выражение  поскольку
поскольку
выбор оператора  в наших руках. Все остальные члены
в наших руках. Все остальные члены

обязательно войдут слагаемыми в остаточный член равенства

как бы мы ни выбрали оператор  . Справедливость последнего утверждения доказывается тем, что среди функций
. Справедливость последнего утверждения доказывается тем, что среди функций  существуют такие, для которых и,
существуют такие, для которых и,  принимают в любой фиксированной точке
принимают в любой фиксированной точке  любые, независимые друг от друга, наперед заданные значения
любые, независимые друг от друга, наперед заданные значения  . Такой функцией является, например, многочлен
. Такой функцией является, например, многочлен

Ввиду независимости значений  при любом выборе оператора
при любом выборе оператора  для аппроксимации второго порядка необходимо, чтобы каждое в отдельности слагаемое, входящее в остаточный член, было порядка
для аппроксимации второго порядка необходимо, чтобы каждое в отдельности слагаемое, входящее в остаточный член, было порядка  . Это требование можно записать такими равенствами:
. Это требование можно записать такими равенствами:

Решение системы (16) определено с точностью до множителя. Дополним эту систему уравнением

которое выражает естественное, хотя и не необходимое ограничение на вы бор оператора  коэффициент при
коэффициент при  в выражении
в выражении  равен единице.
равен единице.
В правые части равенств (6), (7) можно было бы добавить произвольные слагаемые  но мы считаем их равными нулю, как условились.
но мы считаем их равными нулю, как условились.
Решая систему уравнений (16), (17), получаем коэффициенты  , которые были уже нами приведены:
, которые были уже нами приведены:

При этих значениях коэффициентов остаточный член равенства (15)

удовлетворяет оценке

где  — некоторая постоянная, зависящая только от максимума абсолютных величин производных третьего порядка функции
— некоторая постоянная, зависящая только от максимума абсолютных величин производных третьего порядка функции  Это можно записать также в форме
Это можно записать также в форме

Итак, мы установили, что с точностью до несущественных изменений только одна разностная схема

среди всех разностных схем вида

аппроксимирует дифференциальную краевую задачу (4) на решении  последней со вторым порядком относительно А.
последней со вторым порядком относительно А.
Во всех рассмотренных до сих пор в этой главе примерах разностных схем  оператор
оператор  , который отображает пространство
, который отображает пространство  в пространство
в пространство  , задается явными формулами. Но часто оказываются полезными разностные схемы, в которых оператор
, задается явными формулами. Но часто оказываются полезными разностные схемы, в которых оператор  описывается тем или иным
описывается тем или иным  сложным образом. В дальнейшем мы еще встретимся с задачами, где такие схемы возникают естественным образом.
сложным образом. В дальнейшем мы еще встретимся с задачами, где такие схемы возникают естественным образом.
Изложенные приемы построения разностных схем остаются применимыми и в случае задач с переменными коэффициентами, в случае нелинейных задач, в случае сеток с переменным шагом. Например, в случае неравномерной сетки, изображенной на рис. 14, для замены производных, входящих в дифференциальное уравнение  разностными отношениями с целью построения разностной схемы можно воспользоваться
разностными отношениями с целью построения разностной схемы можно воспользоваться

Рис. 14.
формулами

отбросив в них остаточные члены.
Указанные формулы проверяются с помощью разложений Тейлора (2). Методом неопределенных коэффициентов можно убедиться в единственности этих формул: с точностью до несущественного произвола есть только один набор коэффициентов  при котором для любой достаточно гладкой функции
при котором для любой достаточно гладкой функции  имеет место формула
имеет место формула

с остаточным членом первого порядка малости относительно  .
.
Формулы вида

с остаточным членом второго порядка малости при  не существует.
не существует.
Для более точной замены производной разностным отношением здесь необходимо привлечь более трех точек сетки.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
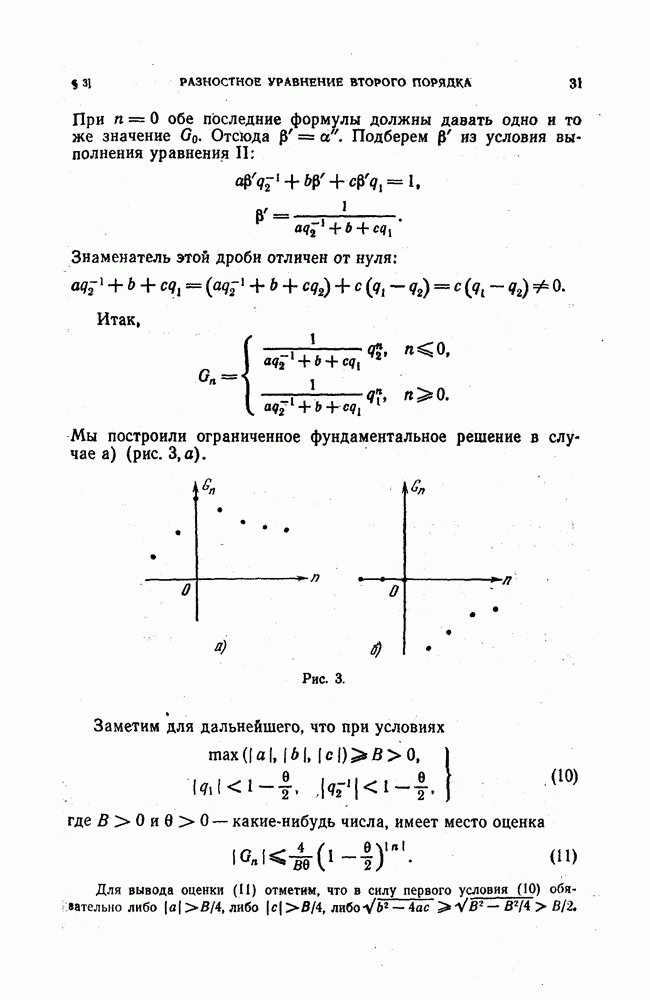
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
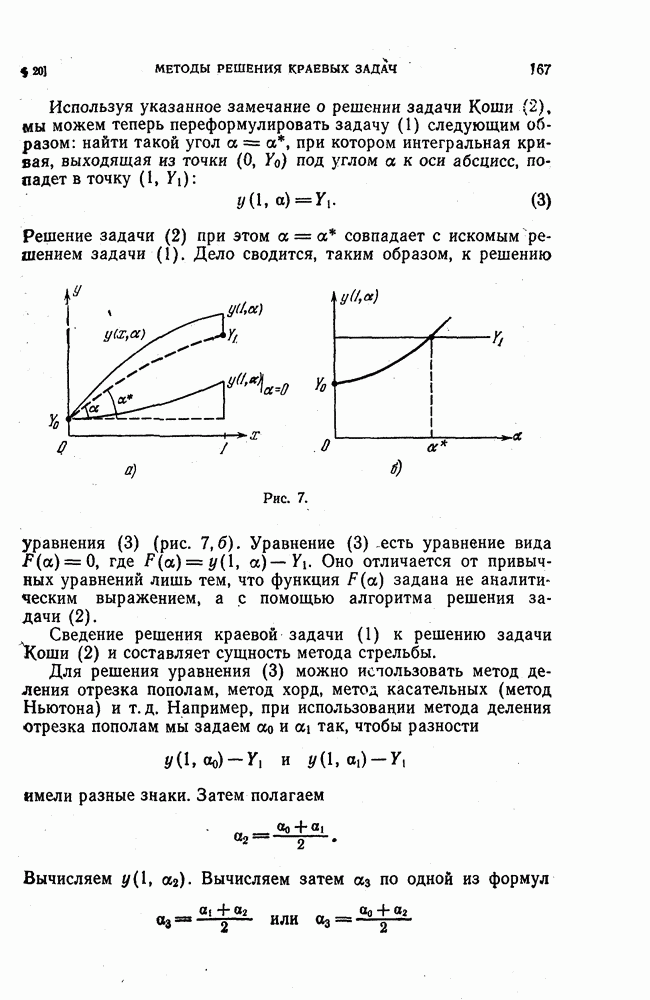
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА