| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6. Замена производных разностными отношениями.
В рассмотренных примерах для получения разностных схеммы заменяли производные в дифференциальном уравнении разностными отношениями. Этот прием весьма универсален и позволяет построить для любой дифференциальной краевой задачи, имеющей достаточно гладкое решение  разностную схему с любым наперед заданным порядком аппроксимации.
разностную схему с любым наперед заданным порядком аппроксимации.
Действительно, покажем, что производную  произвольного порядка к можно заменить разностным отношением так, чтобы погрешность от такой замены для достаточно гладкой функции
произвольного порядка к можно заменить разностным отношением так, чтобы погрешность от такой замены для достаточно гладкой функции  была любого наперед для заданного порядка
была любого наперед для заданного порядка  относительно шага h разностной сетки. Воспользуемся для этого методом неопределенных коэффициентов.
относительно шага h разностной сетки. Воспользуемся для этого методом неопределенных коэффициентов.
Напишем равенство вида

и постараемся подобрать не зависящие от h неопределенные коэффициенты  так, чтобы оно оказалось справедливым. Пределы суммирования
так, чтобы оно оказалось справедливым. Пределы суммирования  можно взять произвольными, но так, чтобы порядок
можно взять произвольными, но так, чтобы порядок  разностного отношения
разностного отношения  удовлетворял неравенству
удовлетворял неравенству  . По формуле Тейлора
. По формуле Тейлора

Подставим это выражение вместо  в (24) и приведем подобные члены. Получим
в (24) и приведем подобные члены. Получим

Приравнивая коэффициенты при одинаковых степенях  в левой и правой частях этого равенства, получим
в левой и правой частях этого равенства, получим
следующую систему уравнений для определения  :
:

Если  , то выписанные
, то выписанные  равенств образуют линейную систему относительно того же числа неизвестных а. Определитель этой системы
равенств образуют линейную систему относительно того же числа неизвестных а. Определитель этой системы

есть известный определитель Вандермонда и отличен от нуля. Таким образом, существует единственный набор коэффициентов  удовлетворяющий системе (25). Если
удовлетворяющий системе (25). Если  , то, очевидно, таких систем коэффициентов а, много.
, то, очевидно, таких систем коэффициентов а, много.
Так, например, существует единственное разностное отношение первого порядка вида

приближающее  с первым относительно h порядком. Оно получается при
с первым относительно h порядком. Оно получается при

Точно так же существует единственное разностное отношение первого порядка вида

приближающее  с первым относительно
с первым относительно  порядком:
порядком:

Среди разностных отношений второго порядка вида

существует бесконечно много приближающих  с первым порядком относительно
с первым порядком относительно  , но только одно со вторым порядком. Решая систему (25) для этого случая увидим, что при
, но только одно со вторым порядком. Решая систему (25) для этого случая увидим, что при 

Если мы хотим приблизить  с порядком
с порядком  то
то  надо, чтобы
надо, чтобы  . Поэтому среди разностных отношений вида
. Поэтому среди разностных отношений вида

только одно является искомым. Решая систему (26) для определения коэффициентов  , получим
, получим

т. е. уже неоднократно использованное нами равенство

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
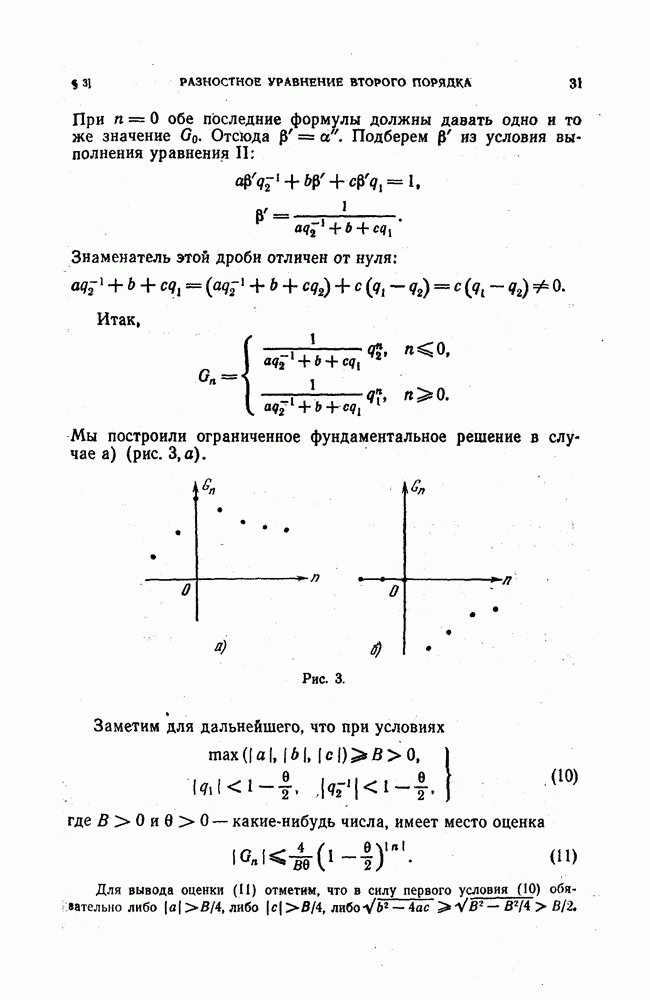
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
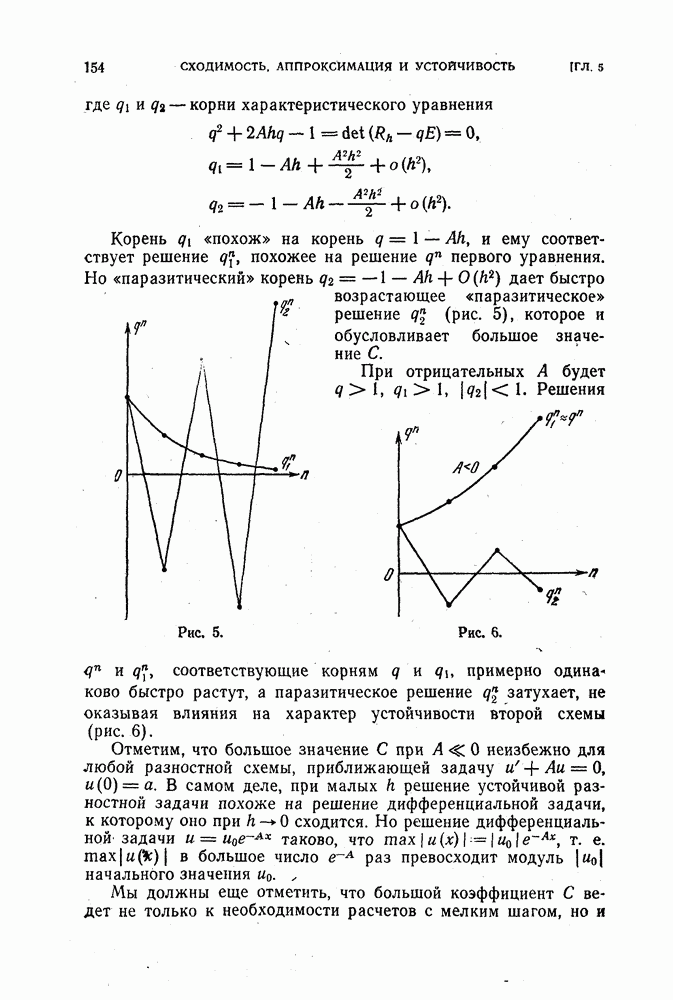
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
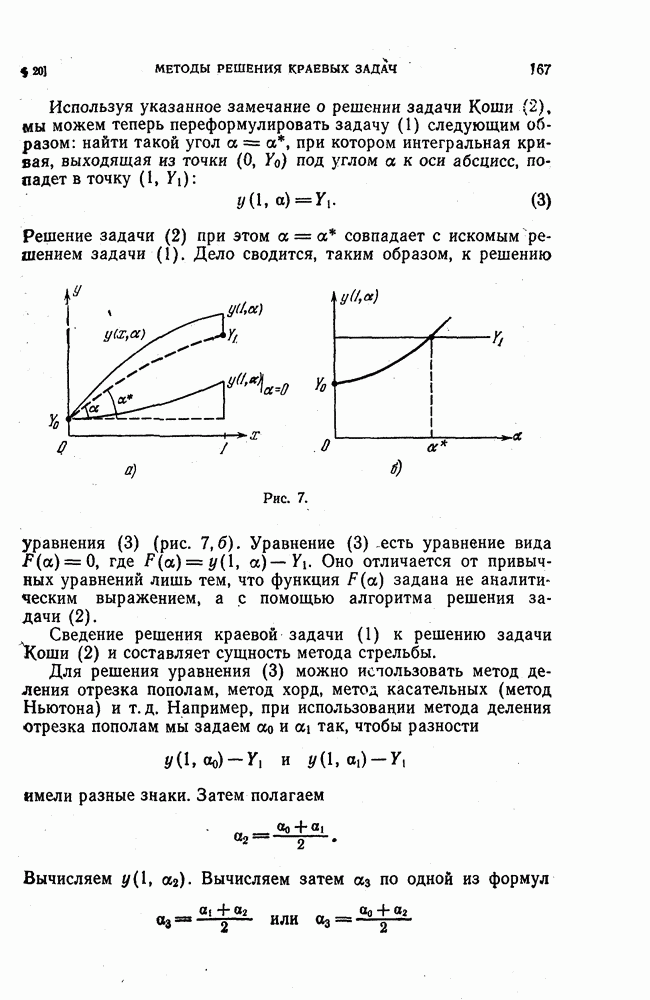
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
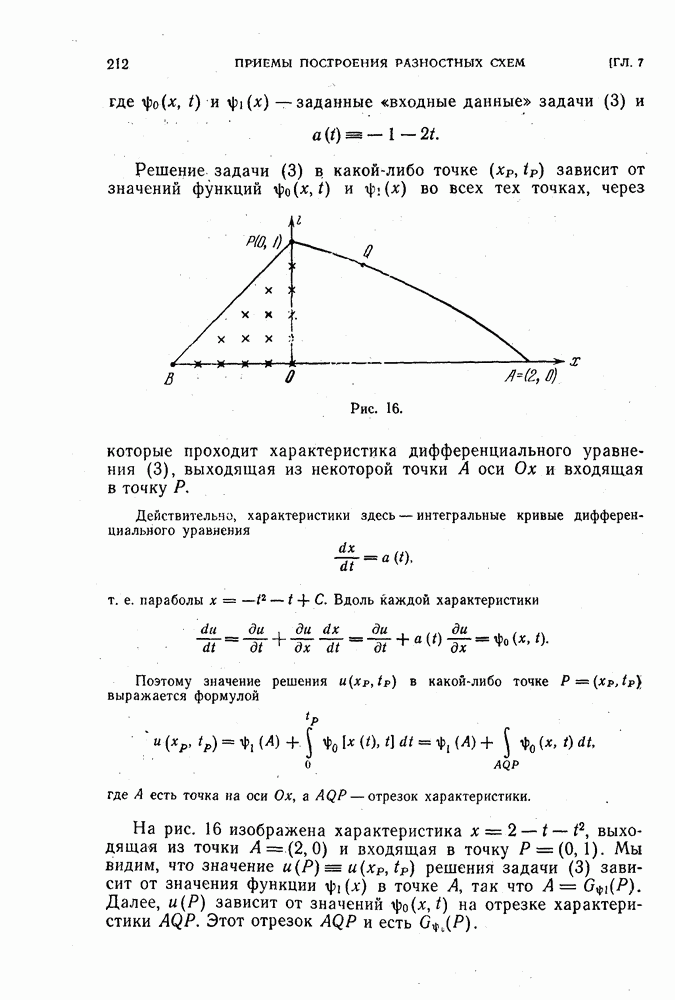
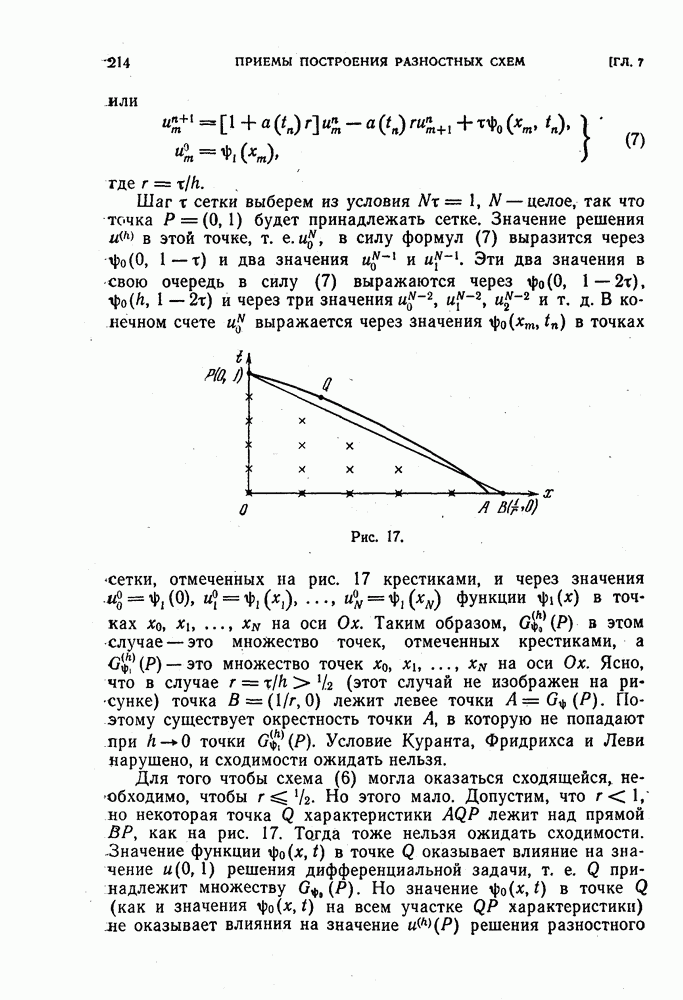
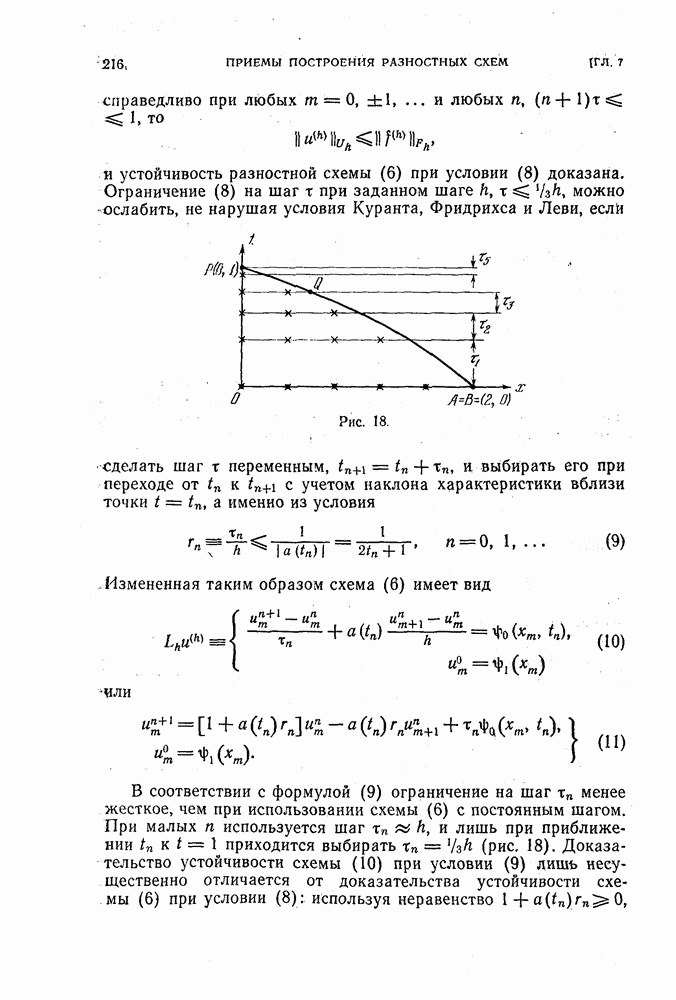
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
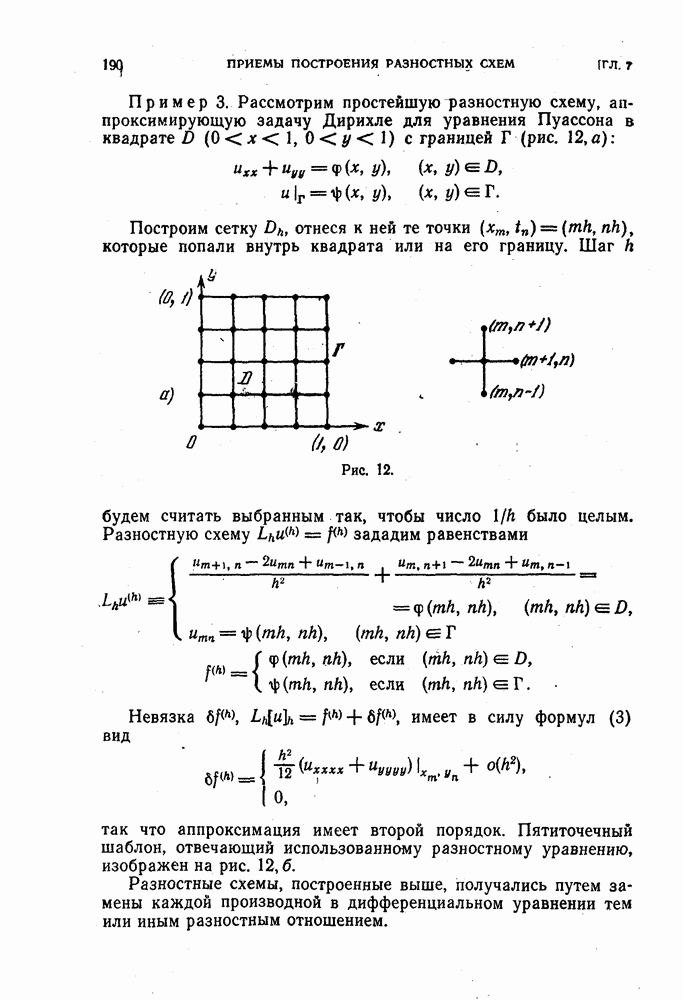
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА