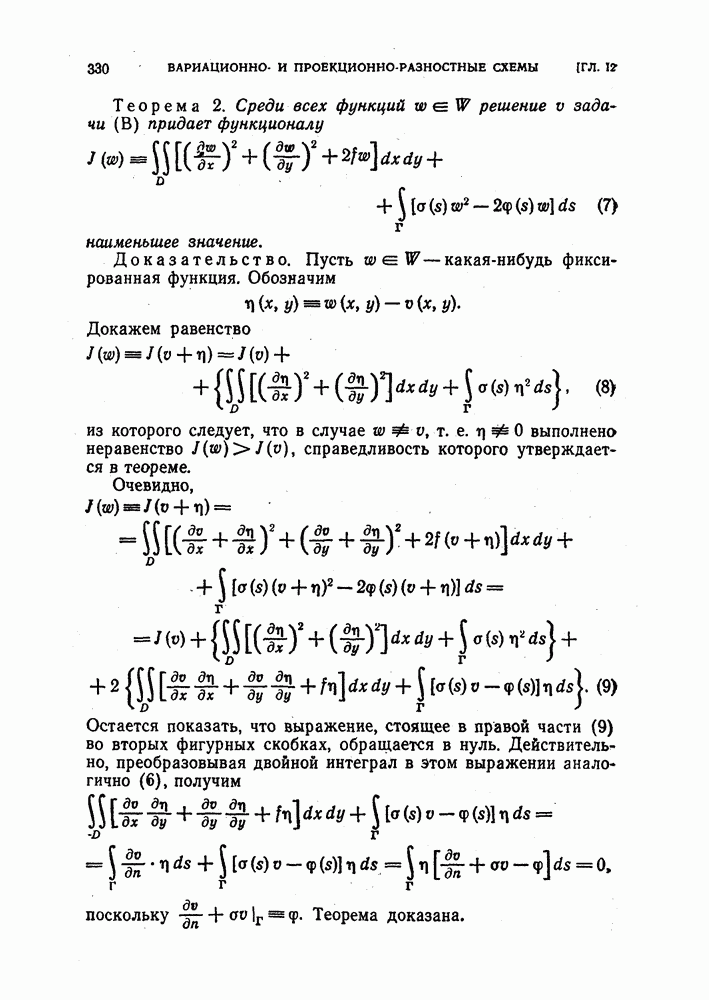| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 42. Использование частных решений при конструировании оператора перехода
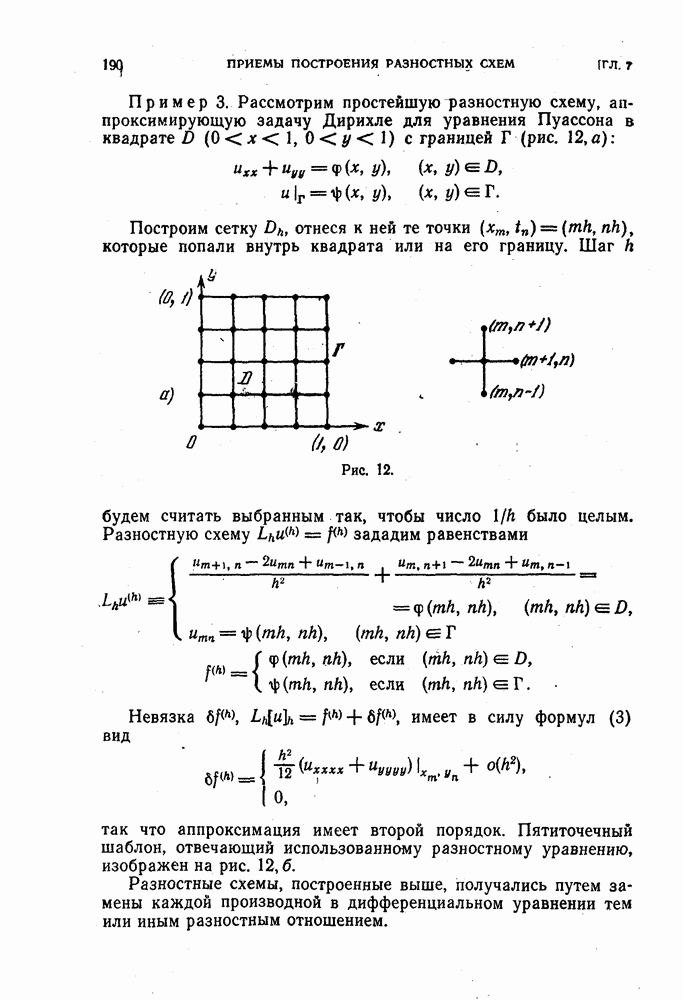
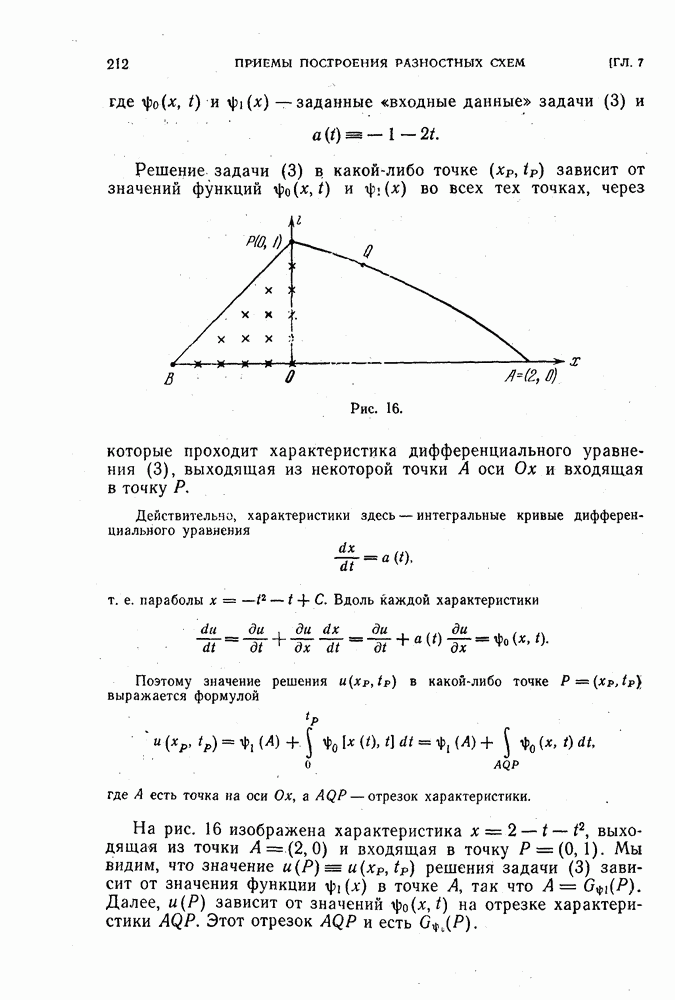
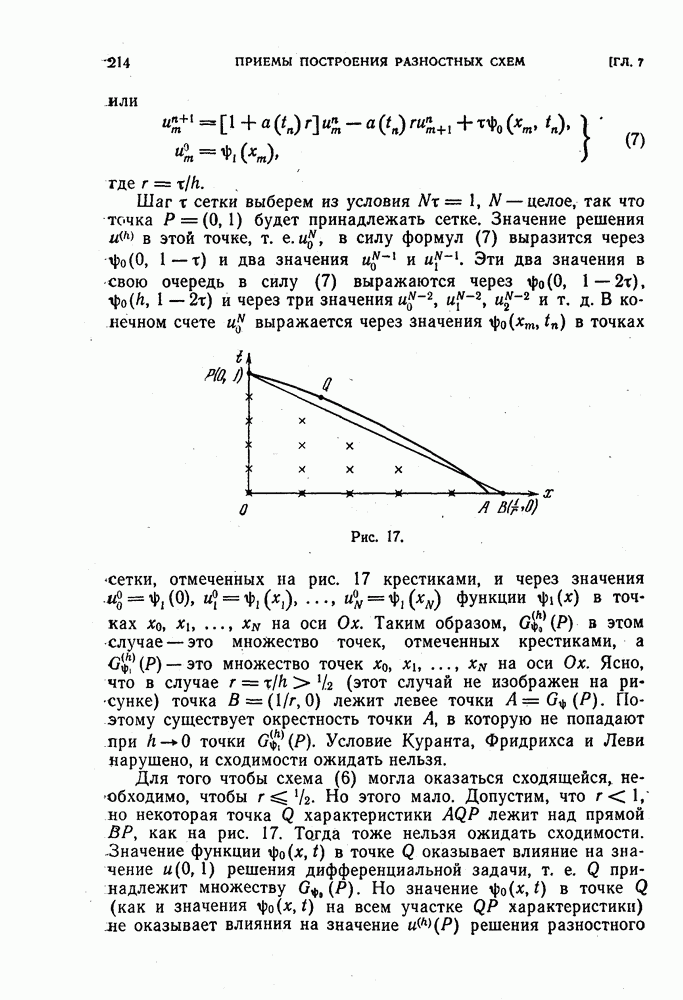
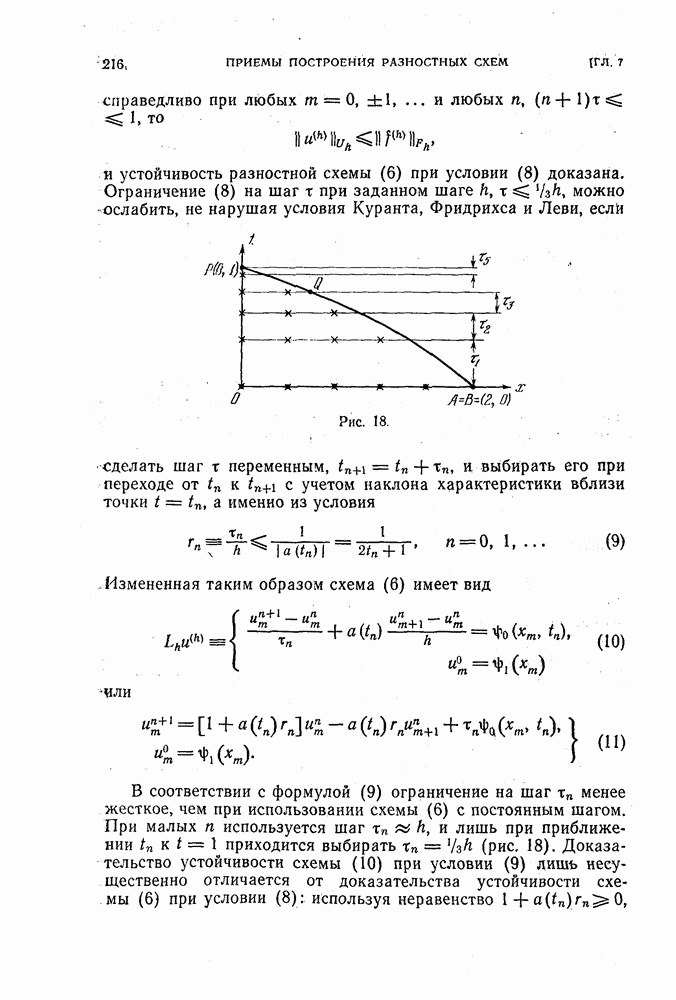
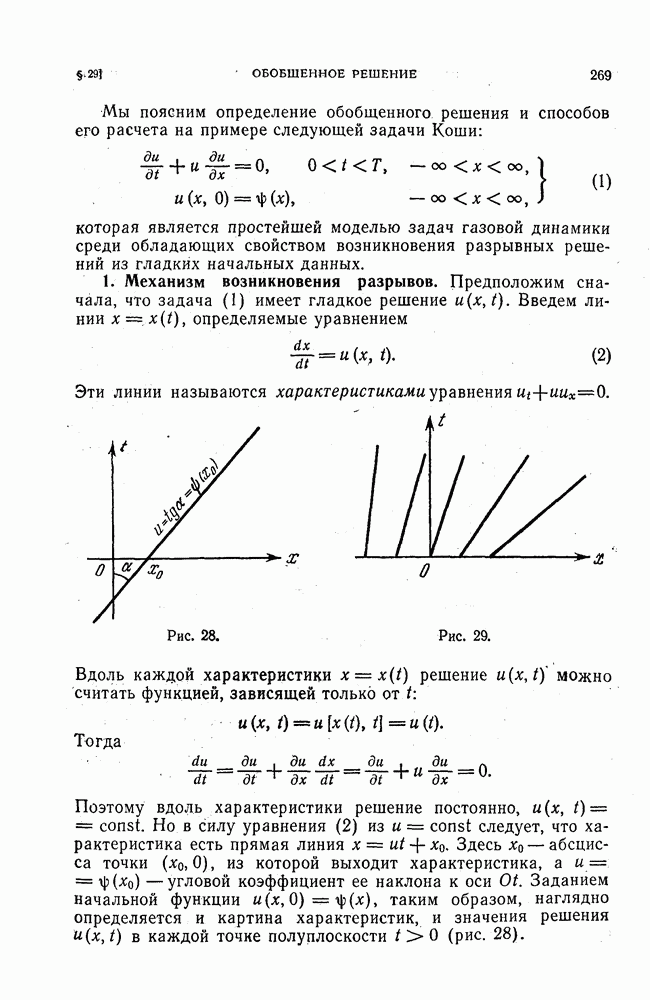
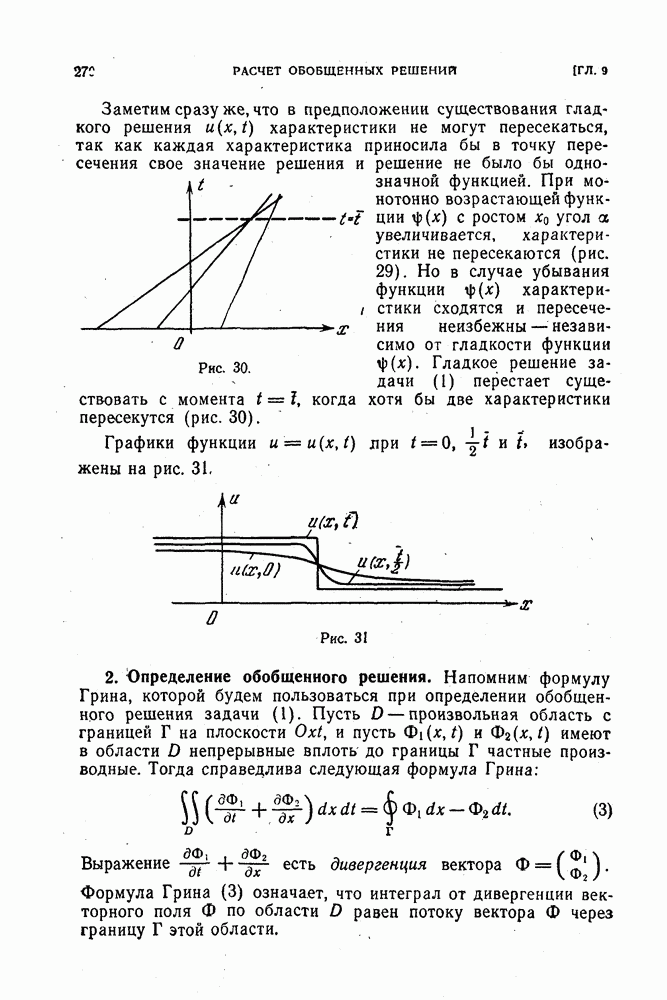
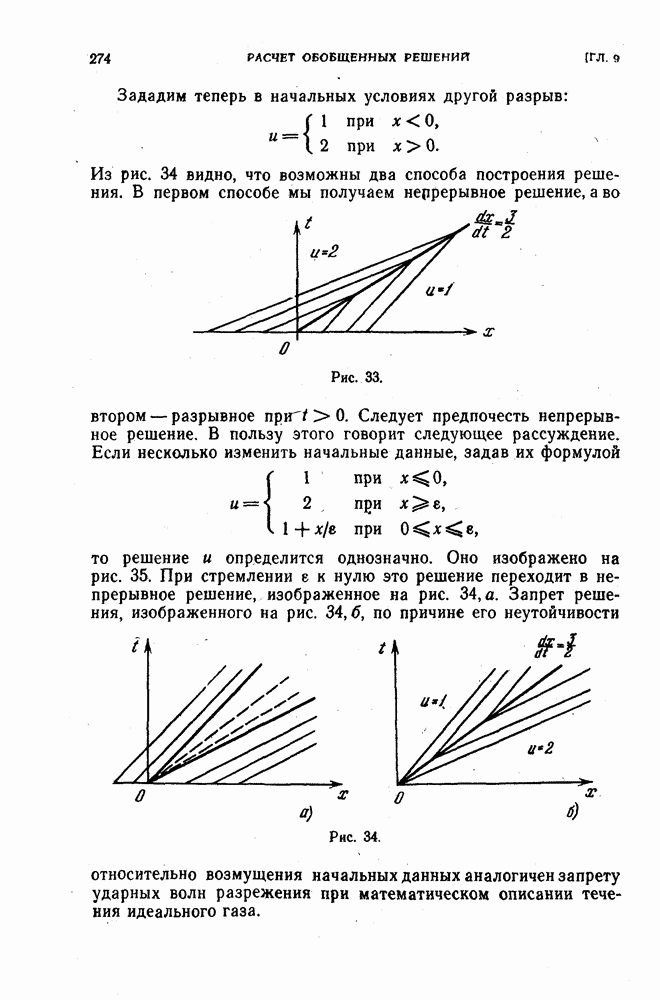
В § 41 рассказывалось о приведении разностной краевой задачи

к виду

При этом оператор  можно выбирать по-разному. Цель приведения к виду (2) состоит в том, чтобы по оценкам величин можно было судить об устойчивости. Было показано, что оценка
можно выбирать по-разному. Цель приведения к виду (2) состоит в том, чтобы по оценкам величин можно было судить об устойчивости. Было показано, что оценка

обеспечивает устойчивость, если только оператор  и нормы, выбраны так, что выполняются условия:
и нормы, выбраны так, что выполняются условия:

где  пробегает всё значения, при которых
пробегает всё значения, при которых  определено;
определено;

В примерах, рассмотренных в § 41, оператор  удавалось выбрать достаточно простым и в то же время обеспечить выполнение условий 1° и 2°. Однако могут встретиться и такие примеры — один из них мы рассмотрим в этом параграфе, — когда условие Г является слишком жестким, так что оператор
удавалось выбрать достаточно простым и в то же время обеспечить выполнение условий 1° и 2°. Однако могут встретиться и такие примеры — один из них мы рассмотрим в этом параграфе, — когда условие Г является слишком жестким, так что оператор  с учетом этого условия нельзя взять достаточно простым.
с учетом этого условия нельзя взять достаточно простым.
В этом параграфе будет показано, что оценка (3) остается достаточной для устойчивости, если условие 1° заменить менее ограничительным условием 1. Благодаря замене условия 1° условием 1 оператор  при приведении разностной схемы к виду (2) можно выбрать тем проще, чем больше сведений имеется о решениях рассматриваемой разностной задачи (1). В частности, структура оператора
при приведении разностной схемы к виду (2) можно выбрать тем проще, чем больше сведений имеется о решениях рассматриваемой разностной задачи (1). В частности, структура оператора  пригодного при приведении разностной схемы к виду (2), упрощается, если известны некоторые частные решения разностного уравнения, входящего в состав разностной краевой задачи (1). Соответственно упрощается доказательство неравенства (3), из которого вытекает устойчивость.
пригодного при приведении разностной схемы к виду (2), упрощается, если известны некоторые частные решения разностного уравнения, входящего в состав разностной краевой задачи (1). Соответственно упрощается доказательство неравенства (3), из которого вытекает устойчивость.
Все это мы поясним позже примерами. Перейдем к формулированию условия 1.
Пусть  какая-нибудь сеточная функция на
какая-нибудь сеточная функция на  зависящая, вообще говоря, от
зависящая, вообще говоря, от  При приведении разностной схемы (1) к каноническому виду (2) мы расслаиваем сеточную функцию на функции
При приведении разностной схемы (1) к каноническому виду (2) мы расслаиваем сеточную функцию на функции  Проведем такое же расслоение функции
Проведем такое же расслоение функции  на функции
на функции  и предположим, что
и предположим, что  удовлетворяют неравенствам вида
удовлетворяют неравенствам вида

где К — некоторая постоянная, а  пробегает те значения
пробегает те значения  при которых
при которых  определено.
определено.
Условие 1. Существует функция  удовлетворяющая неравенствам (4) и такая, что справедливы оценки
удовлетворяющая неравенствам (4) и такая, что справедливы оценки

Если в качестве  можно взять
можно взять  то выполняется не только условие 1, но и более жесткое условие 1°.
то выполняется не только условие 1, но и более жесткое условие 1°.
Теорема. Если разностная задача (1) записывается в каноническом виде (2) с соблюдением условий 1 и 2°, то из оценки (3) вытекает неравенство

означающее устойчивость. Постоянная с может быть выбрана по формуле

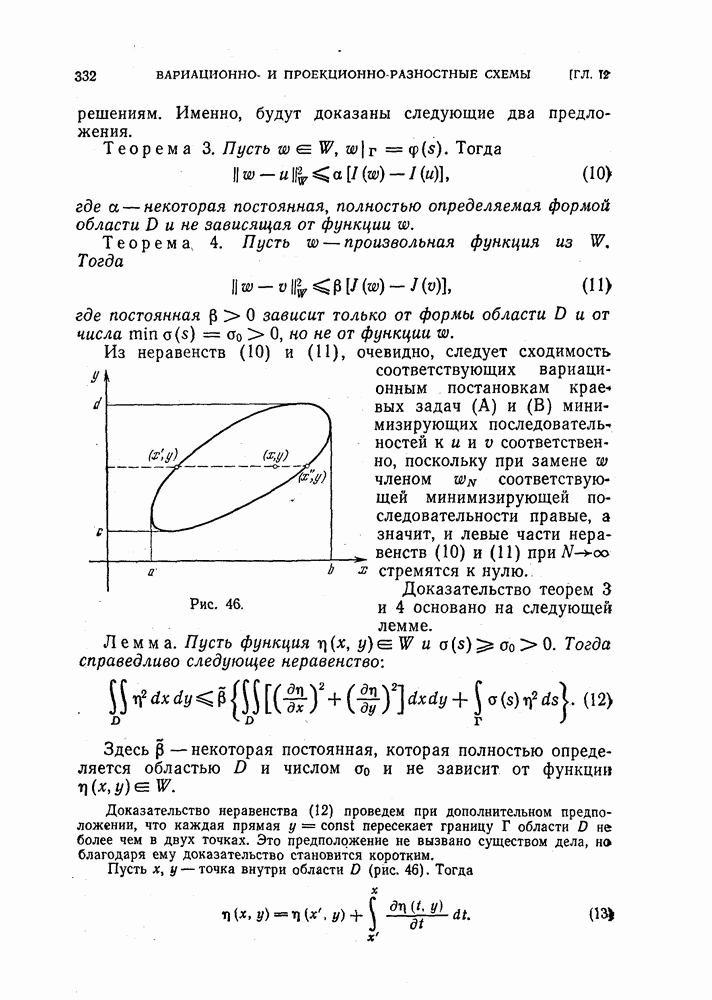
Доказательство. Введем функцию  для которой из уравнения
для которой из уравнения

вытекает равенство

где

В силу условия 1 имеем

Пользуясь равенством (6) и неравенством (3), без труда находим, как мы много раз делали,

Далее,

Это следует из неравенств

второе из которых совпадает с условием 2°, а третье — с нера венством (4) при 
Подставив оценку (8) для  в (7), находим
в (7), находим 

Остается только заметить, что

Благодаря замене условия Г условием 1 при исследовании устойчивости можно распределить трудности между построением такого оператора  нормы степеней которого не слишком трудно оценить, и доказательством существования функции
нормы степеней которого не слишком трудно оценить, и доказательством существования функции  . Потребовав с самого начала, чтобы условие 1 выполнялось при
. Потребовав с самого начала, чтобы условие 1 выполнялось при  , т. е. чтобы было выполнено условие 1°, мы накладываем тем самые жесткие ограничения на выбор оператора
, т. е. чтобы было выполнено условие 1°, мы накладываем тем самые жесткие ограничения на выбор оператора  может оказаться, что любой оператор
может оказаться, что любой оператор  который нам удается подобрать с выполнением условия 1°, имеет сложный вид,
который нам удается подобрать с выполнением условия 1°, имеет сложный вид,
так что оценка нормы его степеней слишком трудна. С другой стороны, выбрав оператор  предельно простым, скажем единичным, и не увязав его с разностной задачей, мы перенесем всю трудность на проверку выполнения условия 1, т. е. на получение оценок для функции которую в этом случае наиболее естественно выбрать совпадающей с
предельно простым, скажем единичным, и не увязав его с разностной задачей, мы перенесем всю трудность на проверку выполнения условия 1, т. е. на получение оценок для функции которую в этом случае наиболее естественно выбрать совпадающей с  Введение такого оператора
Введение такого оператора  и такой функции нисколько не продвинуло бы нас в исследовании устойчивости.
и такой функции нисколько не продвинуло бы нас в исследовании устойчивости.
В качестве оператора  надо стараться брать как можно более простой оператор. Однако
надо стараться брать как можно более простой оператор. Однако  должен настолько полно учитывать свойства разностной задачи
должен настолько полно учитывать свойства разностной задачи  чтобы выполнение условия 1, т. е. существование функции было достаточно очевидным. Часто удается воспользоваться свободой в выборе
чтобы выполнение условия 1, т. е. существование функции было достаточно очевидным. Часто удается воспользоваться свободой в выборе  , которая возникает благодаря тому, что вместо условия 1° должно выполняться лишь менее ограничительное условие 1, для облегчения доказательства устойчивости. В качестве функции
, которая возникает благодаря тому, что вместо условия 1° должно выполняться лишь менее ограничительное условие 1, для облегчения доказательства устойчивости. В качестве функции  при этом используются функции, которые строятся из решений разностных задач при правой части
при этом используются функции, которые строятся из решений разностных задач при правой части  того или иного - специального вида.
того или иного - специального вида.
Мы сейчас покажем на примерах, как пользоваться предлагаемым приемом.
Пример 1. Рассмотрим разностную краевую задачу (I) вида

Это разностная задача аппроксимирует задачу

при следующем выборе норм:

Для приведения задачи (9) к каноническому виду (2) положим

Оператор  переводящий элемент
переводящий элемент  пространства
пространства  в элемент
в элемент  того же пространства, определим равенствами
того же пространства, определим равенствами

Тогда, очевидно,

Ясно, что условие

не выполнено из-за того, что последняя компонента вектора  есть
есть  и растет при
и растет при  этой задаче легко было бы задать оператор
этой задаче легко было бы задать оператор  так, чтобы условие 1° выполнялось. Для этого достаточно в определении оператора
так, чтобы условие 1° выполнялось. Для этого достаточно в определении оператора  равенство
равенство  заменить равенством
заменить равенством  . Между тем нетрудно указать такое
. Между тем нетрудно указать такое  что условие 1
что условие 1

окажется выполненным. Левая часть этого неравенства записывается в виде

Поэтому для доказательства выполнения условия 1 достаточно построить функцию  удовлетворяющую уравнению
удовлетворяющую уравнению

которое можно записать в виде

или

B случае, если  не зависит от t, эта задача имеет стационарное (не зависящее от
не зависит от t, эта задача имеет стационарное (не зависящее от  ) решение
) решение

В общем случае  зависит от
зависит от  , но при ограниченной
, но при ограниченной  норме
норме  содержащей член
содержащей член  не может быстро меняться. Поэтому функция определенная равенством
не может быстро меняться. Поэтому функция определенная равенством

хоть и не будет стационарным решением (да и вообще решением) задачи (11), но «почти» удовлетворяет соотношениям (11). Именно

Поэтому

Условие 1 выполнено;  удовлетворяют неравенству
удовлетворяют неравенству

Условие 2°

также выполнено:

Для доказательства устойчивости, которая имеет место при, достаточно показать, что  . Справедливость этого вытекает из оценки
. Справедливость этого вытекает из оценки 

Пример 2. Рассмотрим в качестве более сложного примера другую разностную схему для той же дифференциальной крае вой задачи (10):

Порядок по  разностного уравнения, входящего в эту схему, — второй, а порядок соответствующего дифференциального уравнения (10) — первый. Поэтому на левой границе
разностного уравнения, входящего в эту схему, — второй, а порядок соответствующего дифференциального уравнения (10) — первый. Поэтому на левой границе  добавлено условие
добавлено условие

которое мы будем использовать в форме

Разностную схему (12) мы уже рассматривали в § 23, где обсуждались вопросы аппроксимации. Норма в пространстве  там была введена следующим образом: если
там была введена следующим образом: если

то

Как было показано в § 23, аппроксимация в этом случае имеет порядок  Покажем, что при выборе нормы
Покажем, что при выборе нормы  по формуле
по формуле

где  наряду с аппроксимацией имеет место и устойчивость.
наряду с аппроксимацией имеет место и устойчивость.
Мы проверим устойчивость, приведя разностную схему (12) к каноническому виду (2). Положим для этого

с нормой

Оператор  определим следующими формулами:
определим следующими формулами:
Если

В таком случае

Условие Г, очевидно, при нашем выборе норм не выполняется В самом деле, если, например,

то

так что ни при каком  не может выполняться для всех h неравенство
не может выполняться для всех h неравенство

При сделанном нами выборе пространства  состоящего из векторов
состоящего из векторов  и при нашем выборе норм,
и при нашем выборе норм,  по-видимому, нельзя указать оператор
по-видимому, нельзя указать оператор  так, чтобы условие 1° выполнялось, но условию 1 удовлетворить можно.
так, чтобы условие 1° выполнялось, но условию 1 удовлетворить можно.
Прежде чем доказать последнее утверждение, заметим, что если изменить норму  положив
положив

то оператор  определенный формулами (13), будет удовлетворять условию 1°, но порядок аппроксимации будет не
определенный формулами (13), будет удовлетворять условию 1°, но порядок аппроксимации будет не  а только
а только  . Мы умеем, не меняя норм, привести разностную краевую задачу (12) к каноническому виду (2) с соблюдением условий 1° и 2°, если за
. Мы умеем, не меняя норм, привести разностную краевую задачу (12) к каноническому виду (2) с соблюдением условий 1° и 2°, если за  принять совокупность сеточных вектор-функций
принять совокупность сеточных вектор-функций

При этом усложнится конструкция оператора  и оценка нормы его степеней. Поэтому мы не будем рассматривать такое приведение.
и оценка нормы его степеней. Поэтому мы не будем рассматривать такое приведение.
Покажем, что при сделанном  выборе (13) оператора
выборе (13) оператора  существуют
существуют  удовлетворяющие условию 1:
удовлетворяющие условию 1:

Для построения функции  поступим аналогично тому, как мы делали в примере 1, и выпишем стационарное (не зависящее от
поступим аналогично тому, как мы делали в примере 1, и выпишем стационарное (не зависящее от  ) решение задачи
) решение задачи

в предположении, что  и фиксированы и от
и фиксированы и от  не зависят,
не зависят,
Это решение имеет вид

Функция  удовлетворяет оценке
удовлетворяет оценке

Действительно,

Пусть

Поскольку — решение стационарной задачи, можно написать

где

Поэтому

так что

Следовательно, координаты вектора  имеют вид
имеют вид

Неравенство, означающее условие 1

выполнено:

Выполнение условия 2°

очевидно:

Для доказательства устойчивости, которая имеет место при  , остается показать, что при этом условии
, остается показать, что при этом условии

где  некоторая постоянная, не зависящая от h. Докажем сначала, что для любого вектора
некоторая постоянная, не зависящая от h. Докажем сначала, что для любого вектора  , компонента им которого равна нулю, справедливо неравенство
, компонента им которого равна нулю, справедливо неравенство

Далее, применяя оператор  к вектору
к вектору  получим вектор
получим вектор  норма которого не превосходит
норма которого не превосходит  . Поэтому для произвольного вектора
. Поэтому для произвольного вектора  , компонента которого им не обязательно равна нулю, имеем с учетом неравенства (16), справедливого для вектора и вида
, компонента которого им не обязательно равна нулю, имеем с учетом неравенства (16), справедливого для вектора и вида 

Теперь докажем неравенство (15). В силу определения оператора  вектор
вектор  имеет нулевую компоненту
имеет нулевую компоненту  Поэтому, используя (16) и (17), получаем
Поэтому, используя (16) и (17), получаем

Остается обосновать неравенство (16), на которое мы опирались, т. е. доказать следующее предложение.
Пусть  произвольный вектор, компонента им которого равна нулю, и пусть
произвольный вектор, компонента им которого равна нулю, и пусть  . Тогда
. Тогда

Напомним, что в силу определения (13) оператора 

Отметим неравенство

которое выполнено при  а также очевидное тождество
а также очевидное тождество

Теперь при  легко проследить справедливость следующей цепочки неравенств, не считая при этом, что
легко проследить справедливость следующей цепочки неравенств, не считая при этом, что 

Полученное энергетическое неравенство

сильнее неравенства (18), которое мы доказываем.
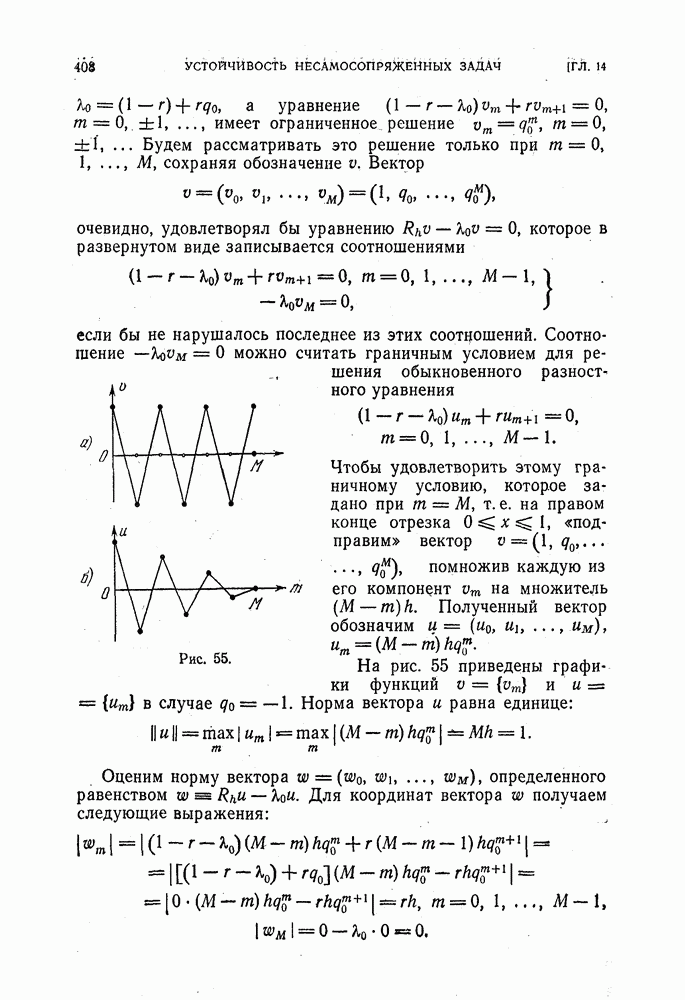
Итак, устойчивость схемы (12) при  установлена. При
установлена. При  устойчивости нет ни при каком разумном выборе норм, так как нарушено необходимое условие устойчивости Куранта, Фридрихса и Леви.
устойчивости нет ни при каком разумном выборе норм, так как нарушено необходимое условие устойчивости Куранта, Фридрихса и Леви.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА