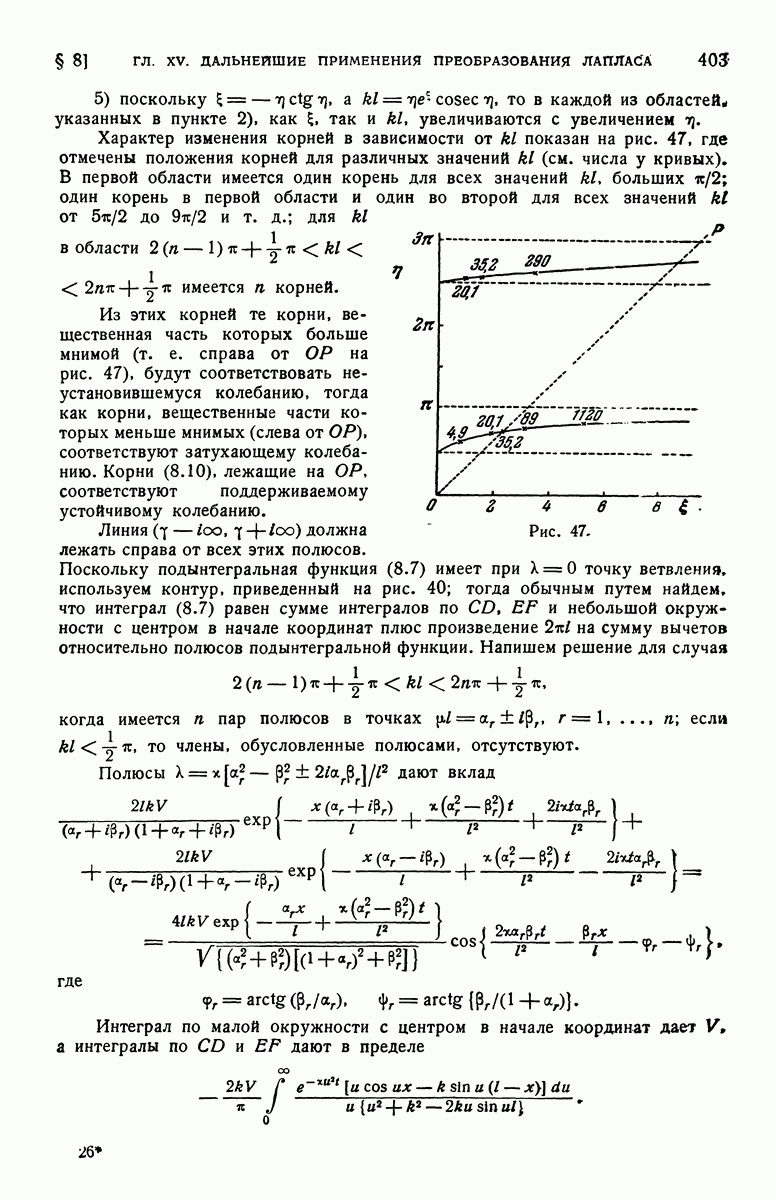
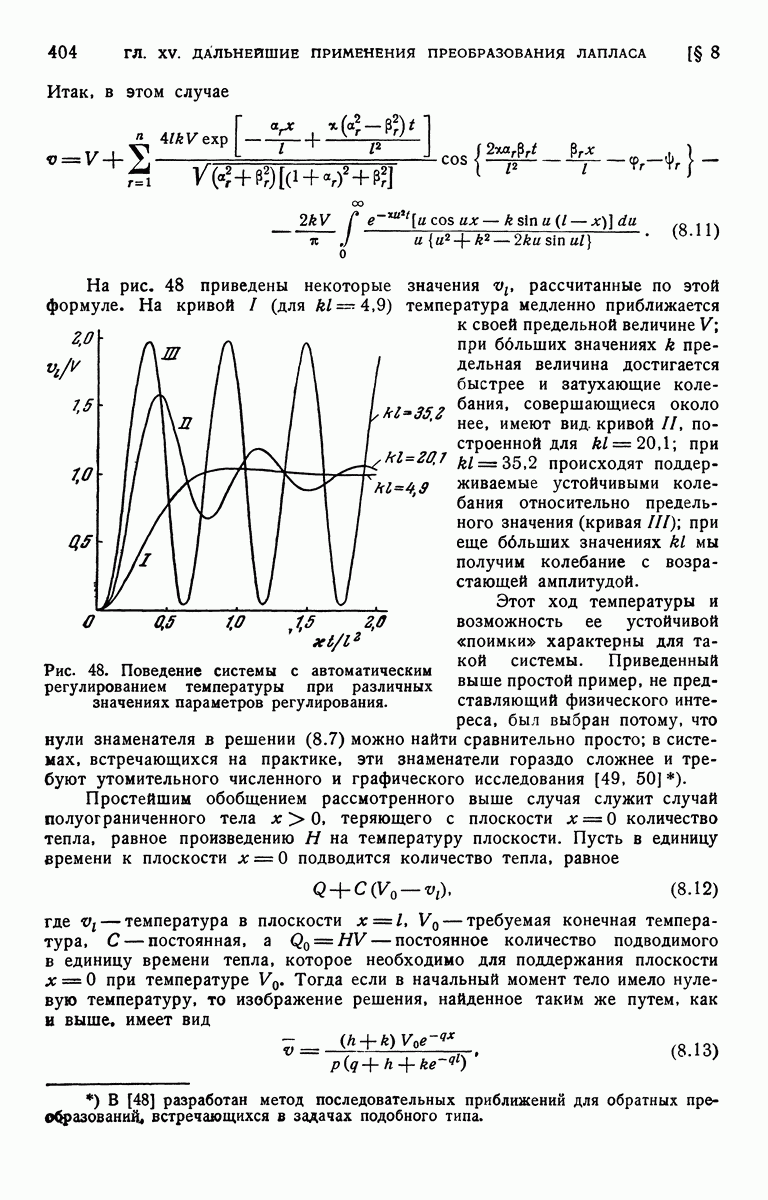
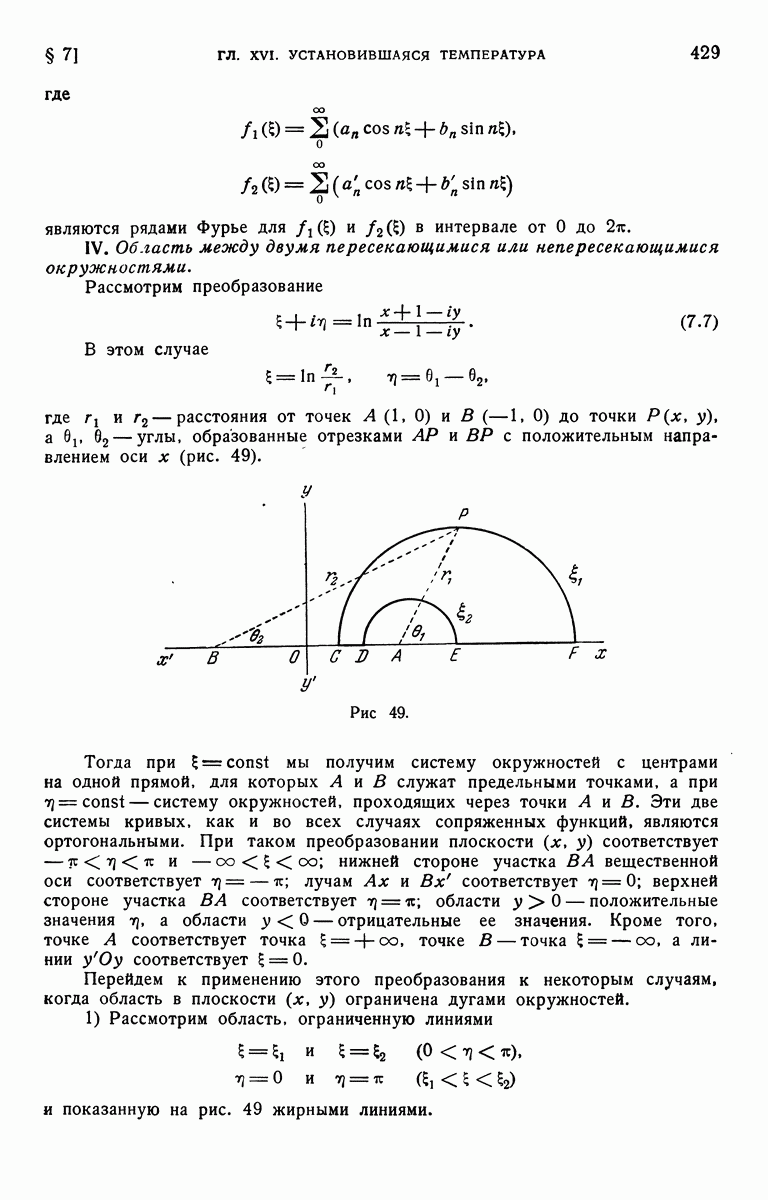
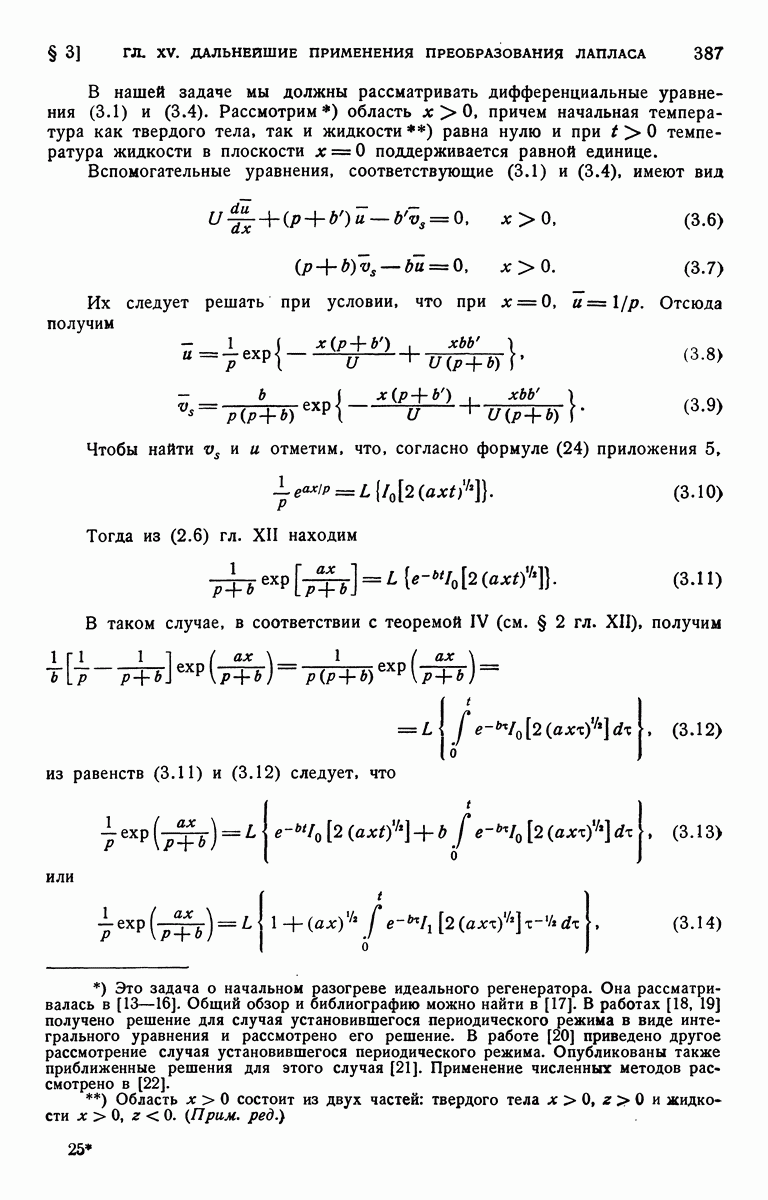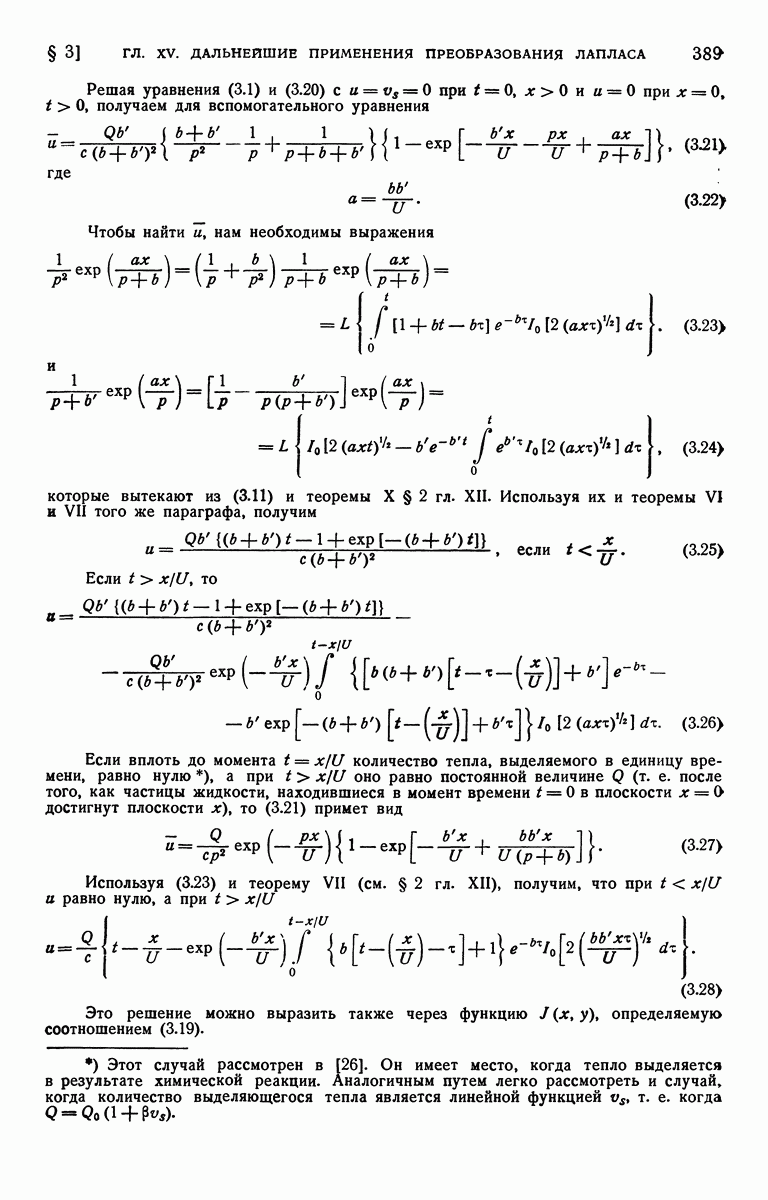| Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
Книга Карслоу выдержала много изданий. Первоначально — в 1906 г.— она составляла одно целое с другой книгой Карслоу по теории рядов и интегралов Фурье. Это в известной степени предопределило содержание книги — как первого, так и последующих ее изданий. Настоящая книга представляет собой как бы вторую часть первоначальной, в которой излагается применение математических методов, приведенных в первой части, к соответствующим задачам теплопроводности. В последующих изданиях (1946 и 1959 гг.) число разбираемых задач значительно возросло, но приемы разбора и глубина рассмотрения изменились незначительно. Как отмечают авторы в предисловии к изданию 1946 г., материал книги разобран методами Фурье. В этом и состоит ее главная особенность.
После опубликования первого издания книги наступил период интенсивного развития методов математической физики. Для характеристики их глубины достаточно упомянуть о ряде фундаментальных трудов, например о книгах Н. Poincare, Theorie de la propagation de la chaleur, Paris, 1895; В. А. Стеклова, Основные задачи математической физики, ч. 1 -1922 г., ч. 2-1923 г., Петербург; Ф. Франка и Р. Мизеса, Дифференциальные и интегральные уравнения математической физики, ч. II, ОНТИ, 1937; Р. Куранта и Д. Гильберта, Методы математической физики, т. I-1933 г., т. II- 1945 г.
В указанных трудах разобраны основные вопросы теории теплопроводности, а именно: 1) общие свойства решений задач теплопроводности, 2) обоснование метода разделения переменных, 3) развитие метода источников тепла, 4) теория плавления.
Работы редактора перевода по этим вопросам, задуманные как дополнения к настоящей книге, публикуются отдельно от нее.
Следует отметить, что в настоящем издании автор книги существенно изменил свое отношение к операционным методам решения задач теплопроводности. В первом издании книги Карслоу характеризует операционный метод Хевисайда следующим образом:
«Операционный метод Хевисайда можно назвать своего рода стенографией. Его фэрмулы можно получить с помощью контурных интегралов, которыми мы будем пользоваться на следующих далее страницах. Результаты, которые здесь получаются, сведены в этой главе. Но за выводами формул Хевисайда трудно следить, и можно смело сказать, что сам он мало заботится о строгости своих выводов. Действительно строгое обоснование его метода
можно провести, пользуясь контурными интегралами, как показано ниже».
В последнем издании Карслоу пересмотрел свое отношение к операционным методам. Он их принял в качестве рабочих методов решения задач теплопроводности и изложил — как сами методы, так и их применение — в главах XII, XIII и XV. В 1941 г. Карслоу выпустил специальную книгу по операционному исчислению.
В главе XI «Изменение физического состояния» дается обзор работ по теории плавления. Глава написана Егером недостаточно полно и глубоко. В основном автор изложил в ней работы, вышедшие до 1950 г. После 1950 г. появились работы принципиального характера, в которых а) исследовались общие свойства решений задачи плавления — существования и единственности и б) развивались эффективные методы решения задачи. При этом в общем случае задача плавления рассматривалась нелинейной — в неоднородном веществе, плотность и теплопроводность которого изменяются с температурой.
Укажем эти работы:
(см. скан)
Главы I и II и приложения настоящей книги переведены канд. техн. наук Ю. Н. Петровым, главы III - VIII - канд. техн. наук В. М. Ерошенко, главы IX - XVIII - канд. техн. наук М. Г. Морозовым.
Редактирование и проверку математического текста перевода книги выполнили Г. И. Басс и Г. А. Шадрин.
ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ
Смерть профессора Карслоу заставила меня самостоятельно готовить новое издание настоящей книги. При этом я старался — по возможности сохраняя форму и дух изложения Карслоу — наиболее полно изложить все точные решения и разрешимые задачи теории теплопроводности. Для этого пришлось ввести дополнительно очень много новых решений и значительно расширить изложение ряда вопросов, в частности вопросов генерирования тепла, поверхностного нагрева, плавления и затвердевания. Более подробно рассмотрены также применение теории теплопроводности к геофизике, анизотропные среды, движущиеся среды и вещества с переменными термическими коэффициентами.
Добавлены также новые таблицы и рисунки, где приведены численные данные по наиболее важным проблемам.
При этом оказалось, что число литературных ссылок превысило 700. Поскольку невозможно перечислить всю литературу, посвященную вопросам теплопроводности, мне пришлось ограничиться только теми статьями, с которыми я мог ознакомиться лично; однако при этом я пытался дать правильное представление о литературе по всем интересующим нас разделам.
В настоящую книгу введены еще две обзорные главы. В одной из них излагается как введение в метод интегральных преобразований, так и связь этого метода с классическим методом Фурье. В другой главе приведен обзор численных методов, получивших в последние годы широкое распространение, и указана связь полученных результатов с точными решениями, изложенными выше в тексте.
1959 г., Д. Егер.
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Книга Карслоу «Введение в теорию рядов Фурье и интегралов Фурье и математическая теория теплопроводности» (Carslaw, Introduction to the Theory of Fourier’s Series and Integrals and the Mathematical Theory of the Conduction of Heat) была опубликована в конце 1906 г. В 1920-1921 гг. она была полностью переработана и разделена на два тома. Второй том этого труда под названием «Введение в математическую теорию теплопроводности твердых тел» (Carslaw, Introduction to the Mathematical Theory of the Conduction of Heat in Solids) был издан в 1921 г. За последние 25 лет было выполнено столько работ как теоретического, так и прикладного характера, содержащих применение полученных результатов, что книгу, отражающую достижения и успехи в этой области, следует считать новой, а не переработанным изданием старой. В данной книге, призванной заменить
изданную ранее, весь материал трактуется в рамках современных математических методов. В частности, в нее включено полное изложение метода преобразования Лапласа и его применение к задачам теплопроводности. Этот метод заменил собой метод использования контурных интегралов, изложенный в гл. X и XI издания 1921 г. Хотя в принципе эти методы родственны друг другу, первый из них даже проще и глубже. При написании этой книги мы стремились сделать ее по возможности полезной инженерам и физикам, не изменяя ее математической сущности. Так, в ней приводятся подробные решения целого ряда задач практического характера и множество данных в виде таблиц и графиков. Значительно расширено изложение теории систем, применяемых в экспериментальных работах; другие вопросы, представляющие практический интерес, изложены довольно кратко (например, теория автоматической регулировки температуры; до сих пор в книгах математического характера такие вопросы не рассматривались).
Можно считать, что первое издание настоящей книги (кроме последних глав) посвящено в основном изложению методов Фурье, рассматриваемых классически. В первых десяти главах нового издания мы придерживались той же схемы. В них точно воспроизведена значительная часть материала, изложенного в главах I - IX старого издания, но обращено большое внимание на вопросы, интересующие инженеров и физиков.
В главах XII — XV метод преобразований Лапласа вводится и применяется к более сложным задачам. Прочитав главу XII, читатель увидит, что применение этого метода значительно упрощает решение задач, изложенных в предыдущих главах, и, вероятно, привыкнет пользоваться им.
Много интересных решений напечатано петитом; часто они приводятся без доказательств и их можно считать примерами. Все главы снабжены библиографическими ссылками на работы, посвященные как математической теории теплопроводности, так и физическим применениям теории. Мы надеемся, что они послужат полезным введением к литературе. Число таких статей выросло за последнее время настолько, что привести их все невозможно.
Г. Карслоу, Д. Егер
| Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ
- § 2. Теплопроводность
- § 3. Тепловой поток через произвольную поверхность
- § 4. Изотермические поверхности
- § 5. Теплопроводность изотропных тел
- § 6. Дифференциальное уравнение теплопроводности для изотропного твердого тела
- § 7. Дифференциальное уравнение теплопроводности для движущейся среды
- § 8. Преобразование координат
- § 9. Начальные и граничные условия
- § 10. Безразмерные параметры
- § 11. Экспериментальные методы определения теплопроводности
- § 12. Математическая интерпретация начальных и граничных условий
- § 13. Родственные дифференциальные уравнения
- § 14. Упрощение общей задачи теплопроводности
- § 15. Задачи, решения которых можно выразить в виде произведения решений более простых задач
- § 16. Единственность решения задачи теплопроводности
- § 17. Теплопроводность анизотропных твердых тел
- § 18. Дифференциальное уравнение теплопроводности для анизотропных твердых тел
- § 19. Теплопроводность тонкой кристаллической пластины
- § 20. Изменение теплопроводности и вектор теплового потока в анизотропных твердых телах
- ГЛАВА II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА. НЕОГРАНИЧЕННОЕ И ПОЛУОГРАНИЧЕННОЕ ТВЕРДОЕ ТЕЛО
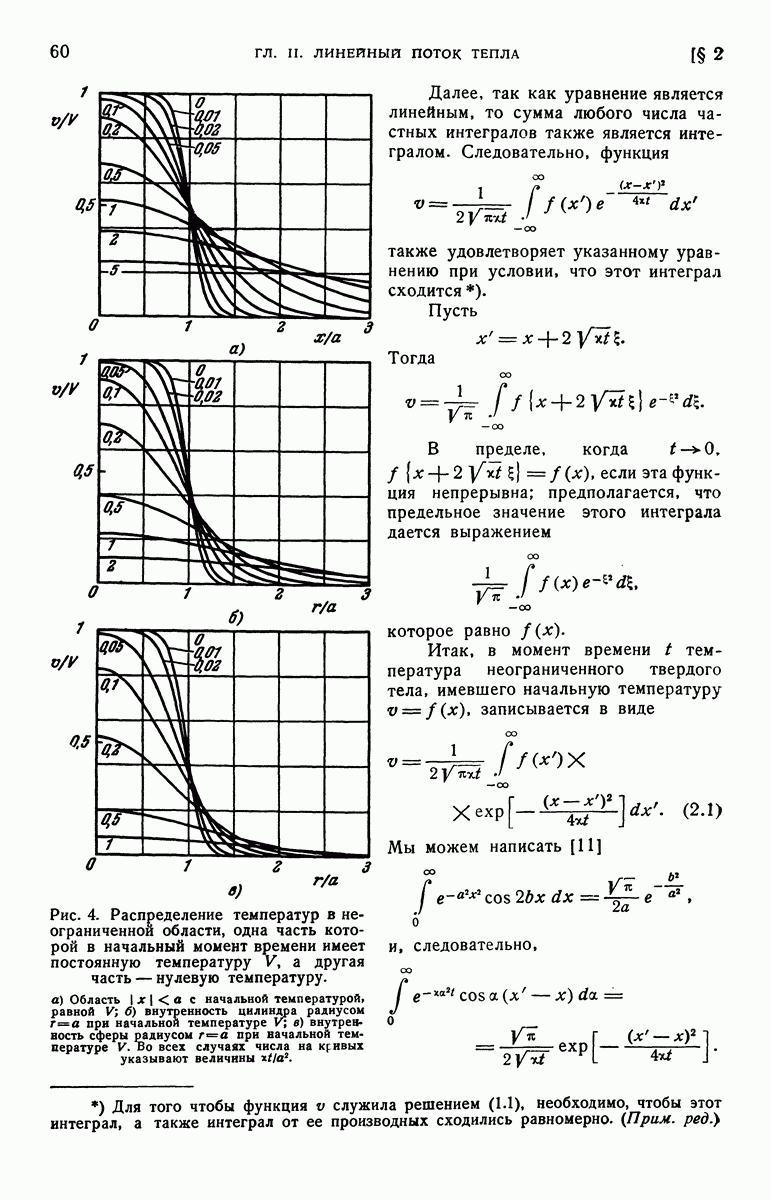
- § 2. Неограниченное твердое тело. Решение Лапласа
- § 3. Использование интегралов Фурье и преобразований Фурье
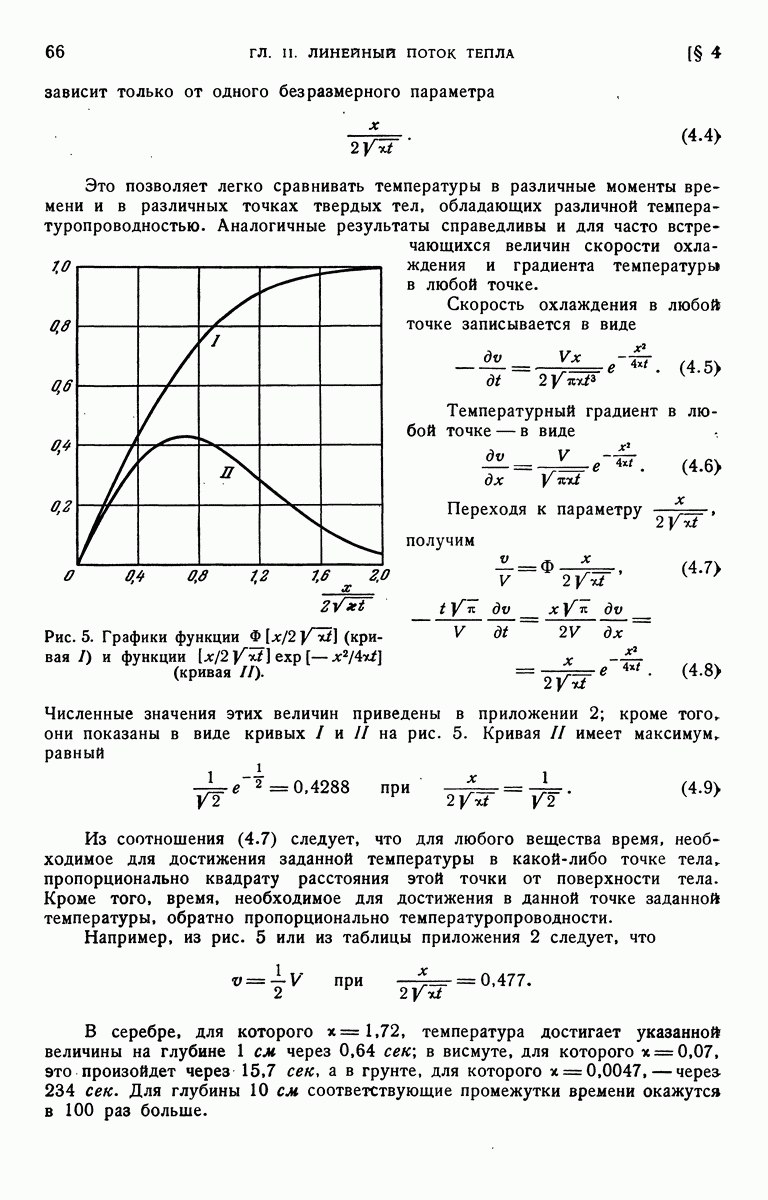
- § 4. Полуограниченное тело с начальной температурой f(x) и нулевой температурой поверхности
- § 5. Полуограниченное твердое тело. Начальная температура равна нулю. Поверхность находится при температуре …
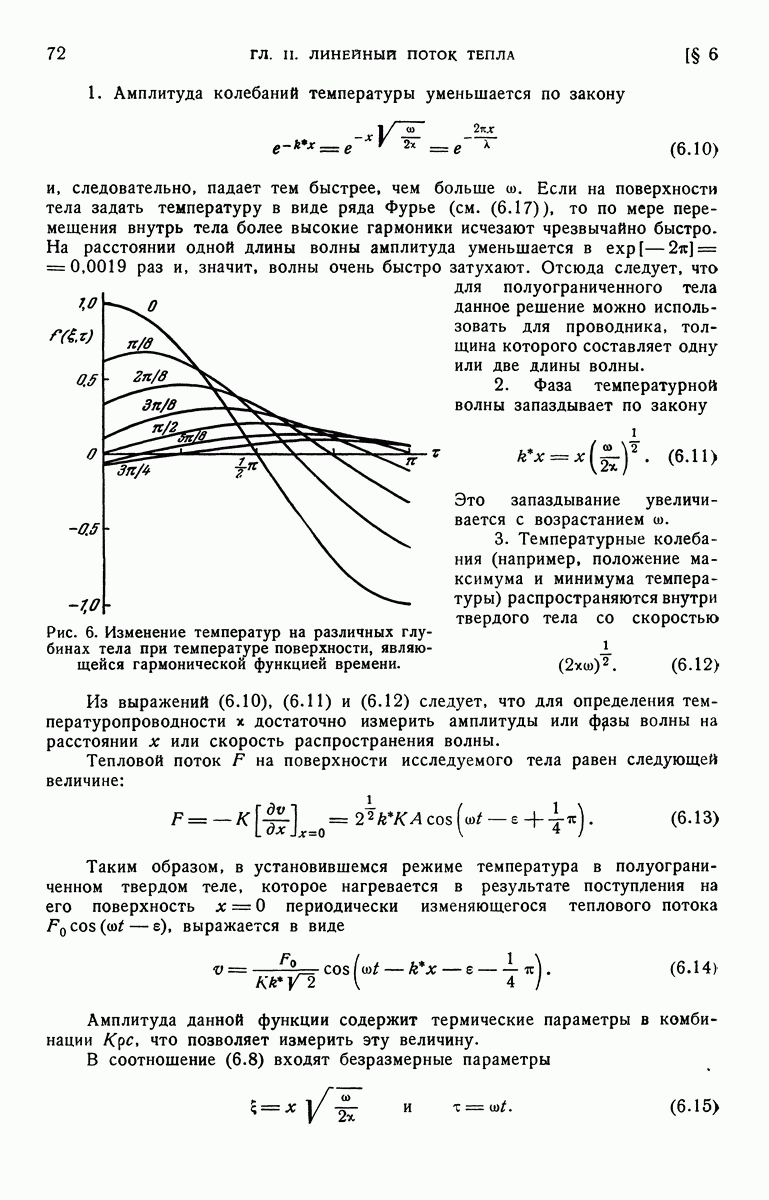
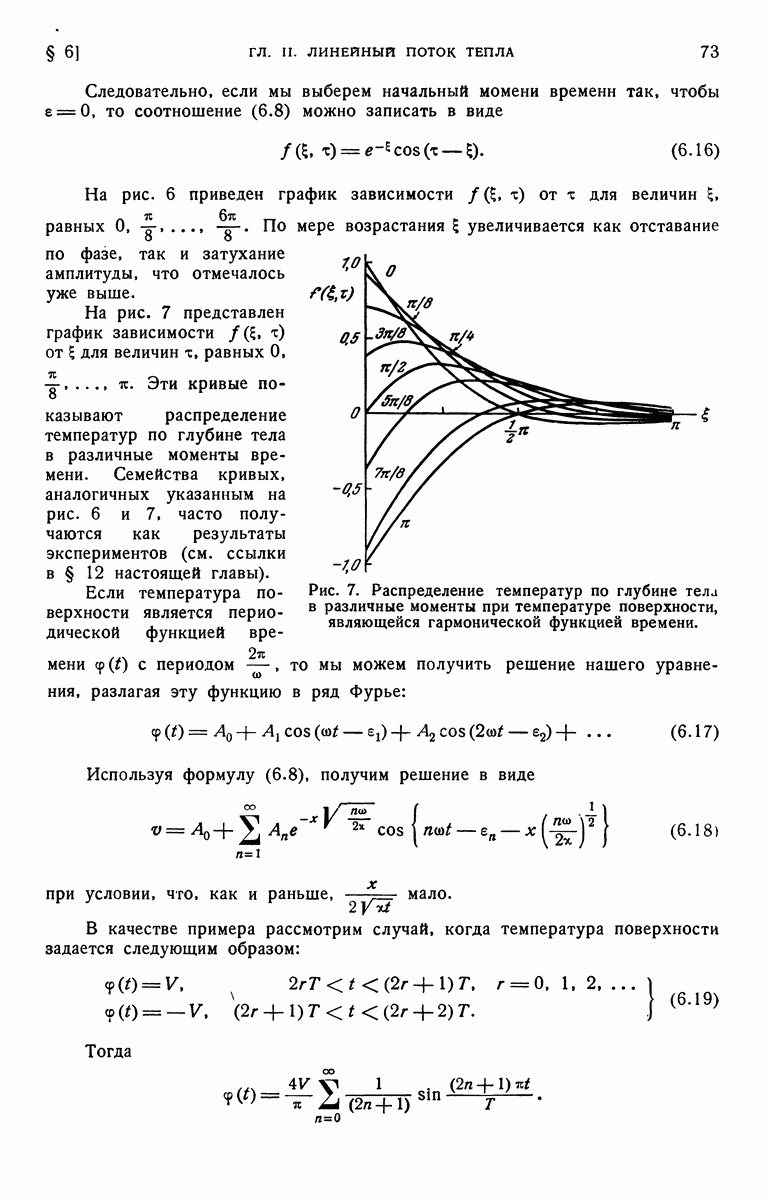
- § 6. Полуограниченное твердое тело. Температура поверхности является гармонической функцией времени
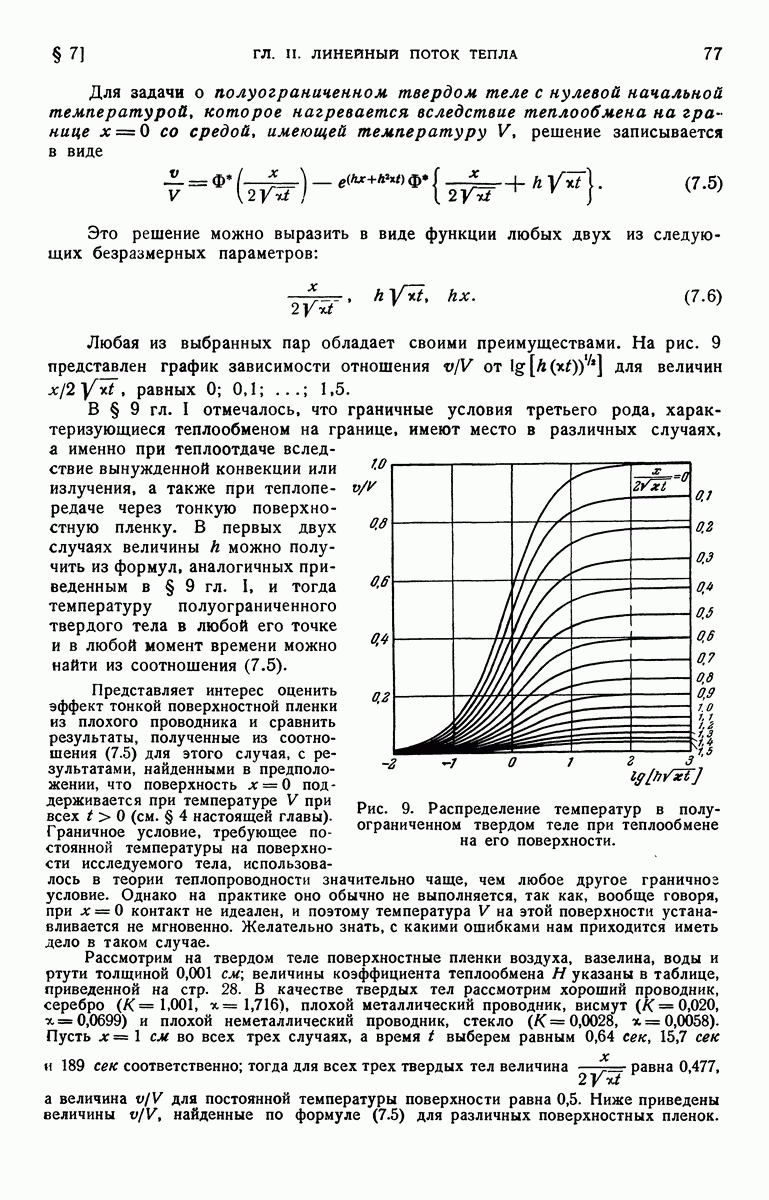
- § 7. Полуограниченное твердое тело. Теплообмен на поверхности в среду с нулевой температурой. Начальная температура постоянна
- § 8. Полуограниченное твердое тело. Теплообмен на поверхности в среду с температурой f(t). Начальная температура равна нулю
- § 9. Полуограниченное тело. Тепловой поток на границе х = 0 является заданной функцией времени. Начальная температура равна нулю
- § 10. Применение полученных результатов к определению теплопроводности
- § 11. Полуограниченное твердое тело, внутри которого находится источник тепла
- § 12. Температура Земли и колебания температуры на ее поверхности
- § 13. Геотермический градиент и поток тепла
- § 14. Возраст Земли. Анализ Кельвина
- § 15. Неограниченное составное твердое тело
- § 16. Случай зависимости термических характеристик вещества от температуры
- ГЛАВА III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ, ОГРАНИЧЕННОМ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
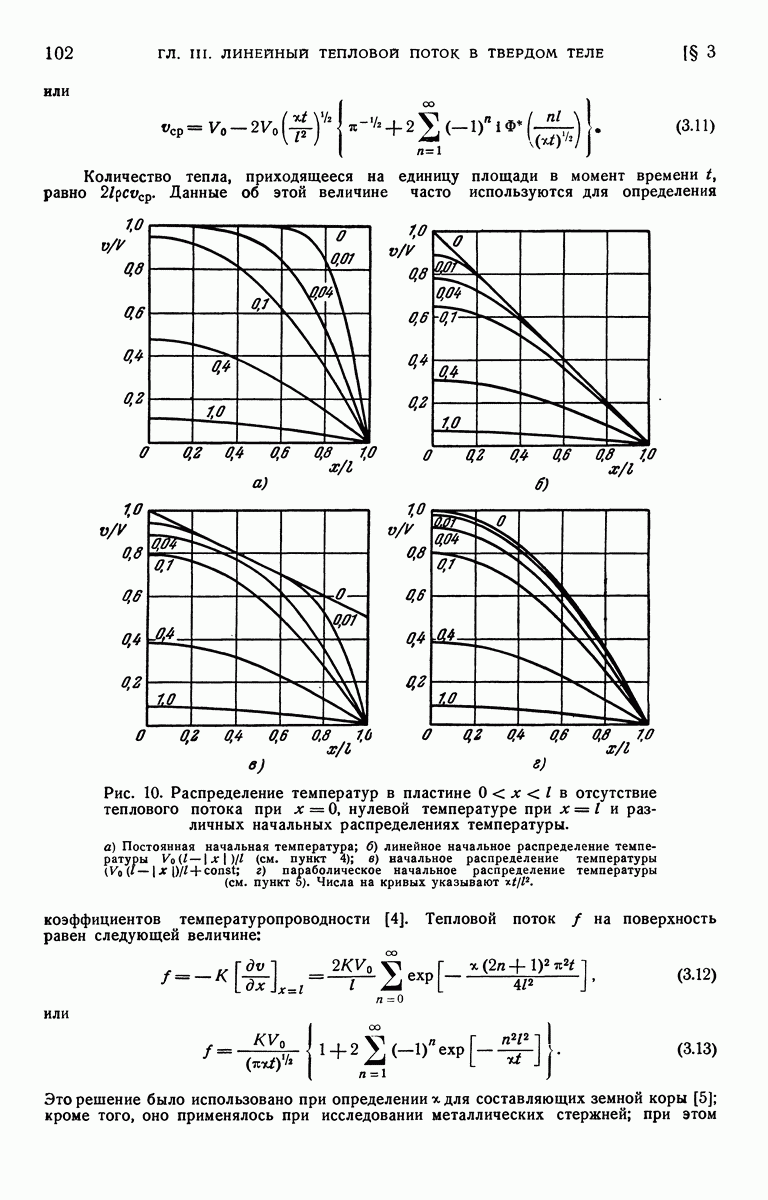
- § 3. Область [0, l]. Границы поддерживаются при нулевой температуре. Начальная температура f(x)
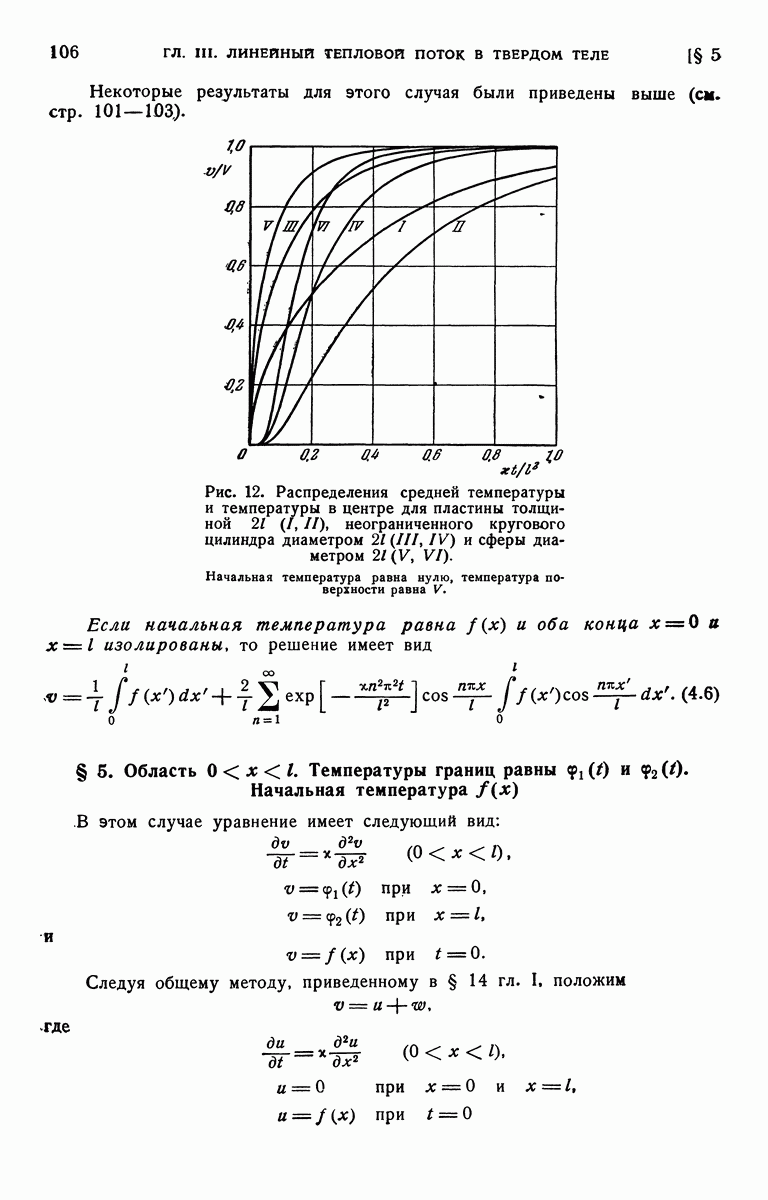
- § 4. Область [0, l] Начальная температура f(x). Границы поддерживаются при постоянной температуре или изолированы
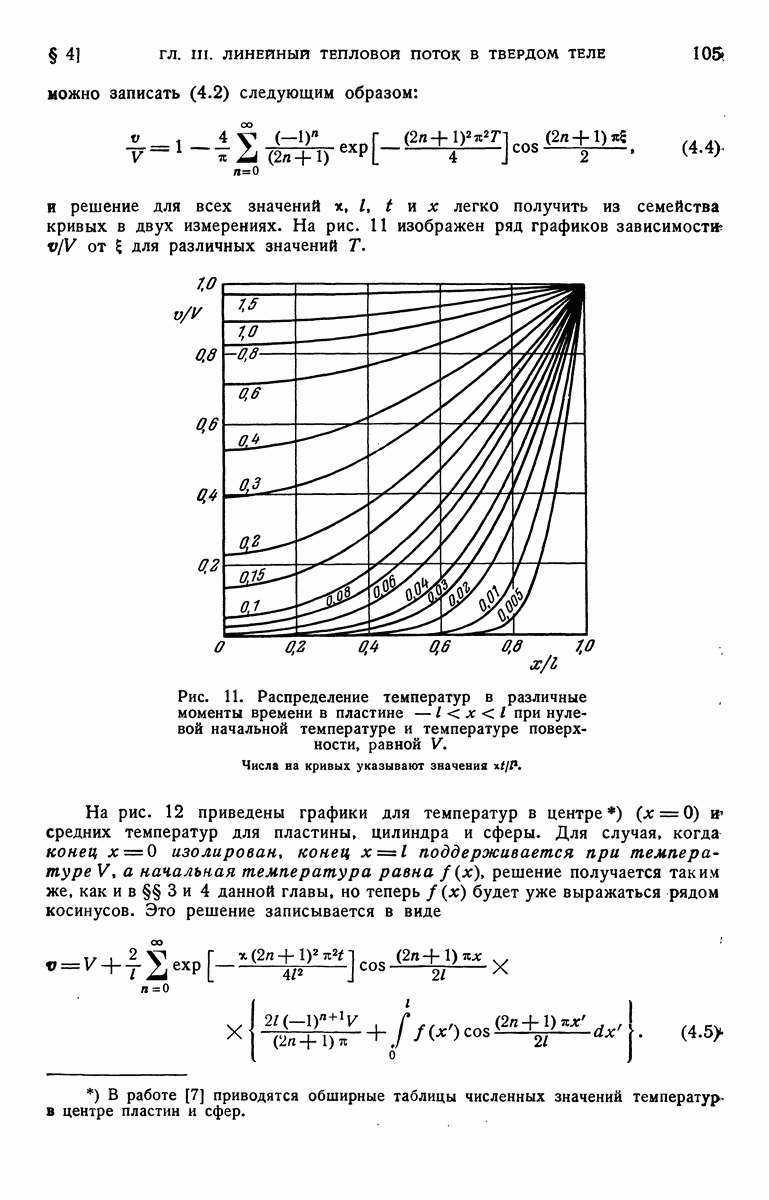
- § 5. Область [0, l]. Температуры границ равны … Начальная температура f(x)
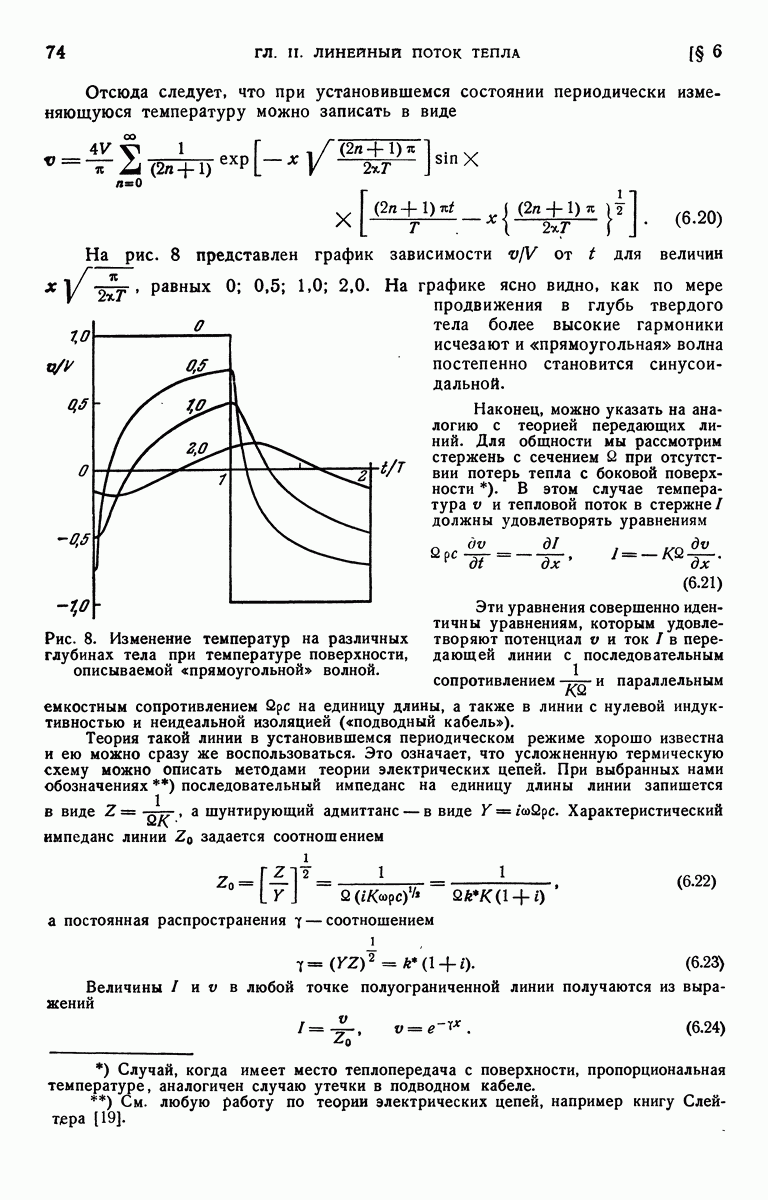
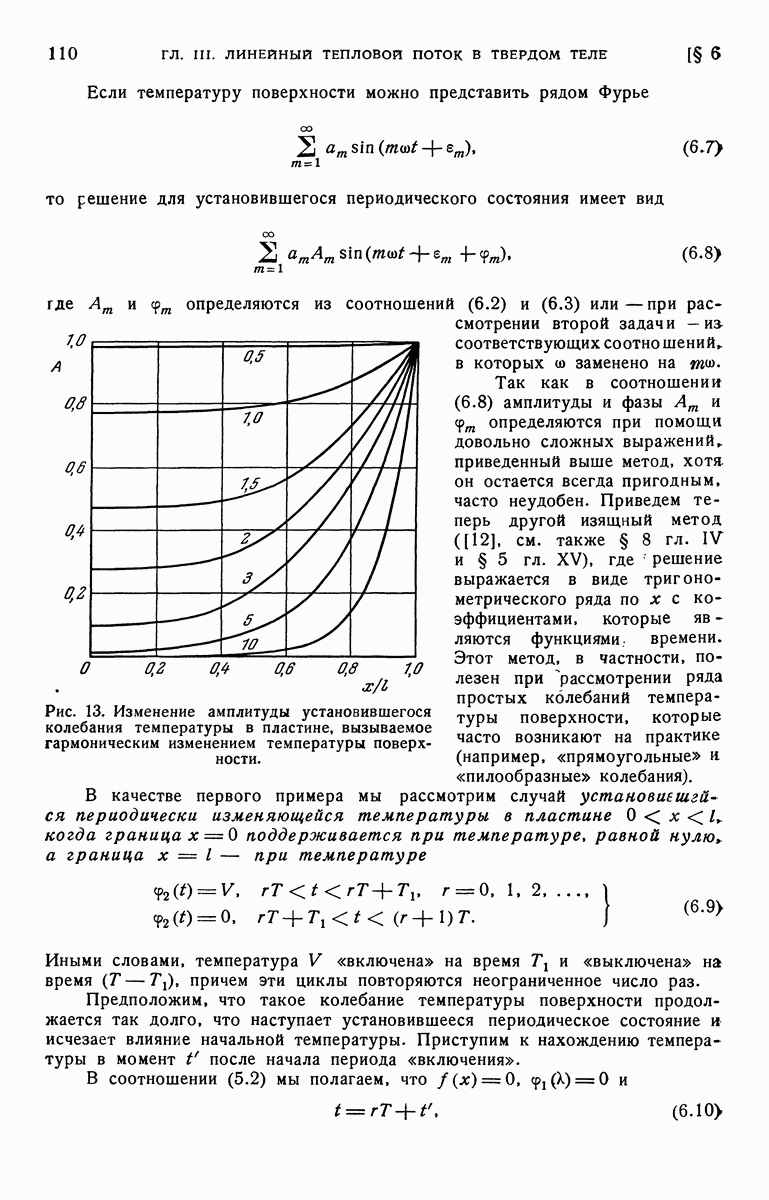
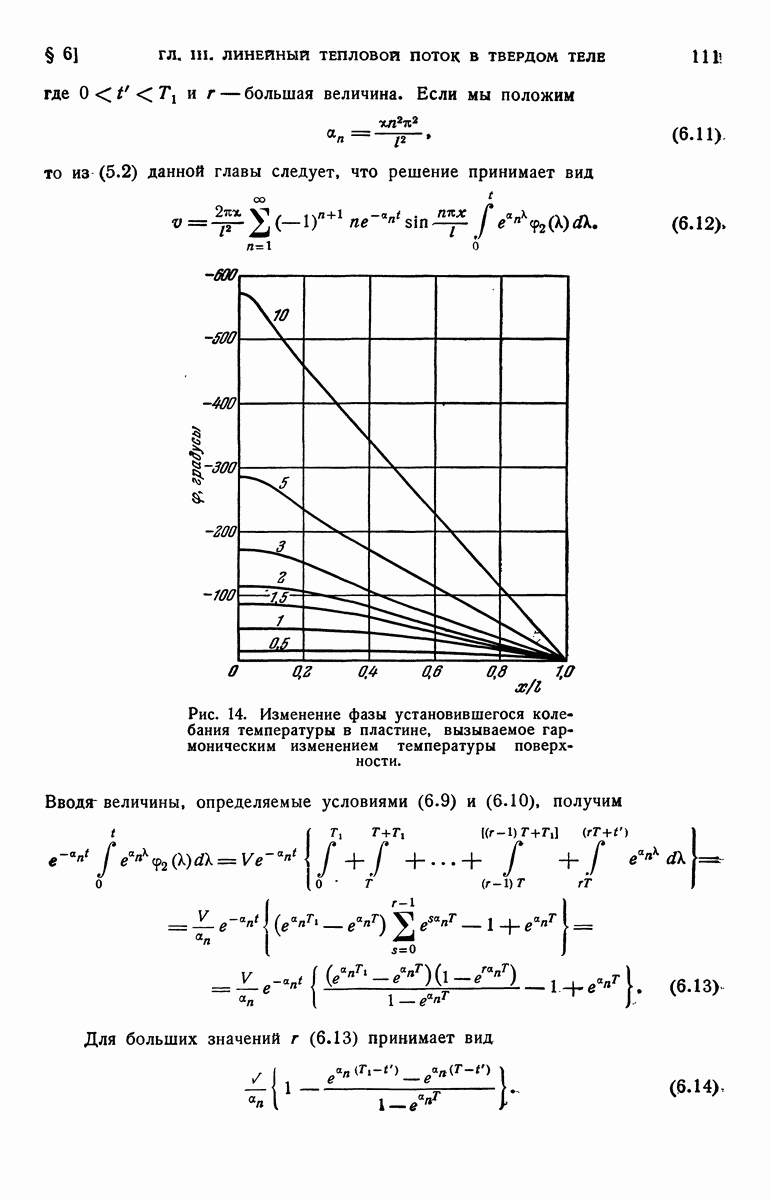
- § 6. Пластина с периодически изменяющейся температурой поверхности
- § 7. Установившаяся периодически изменяющаяся температура в составных пластинах
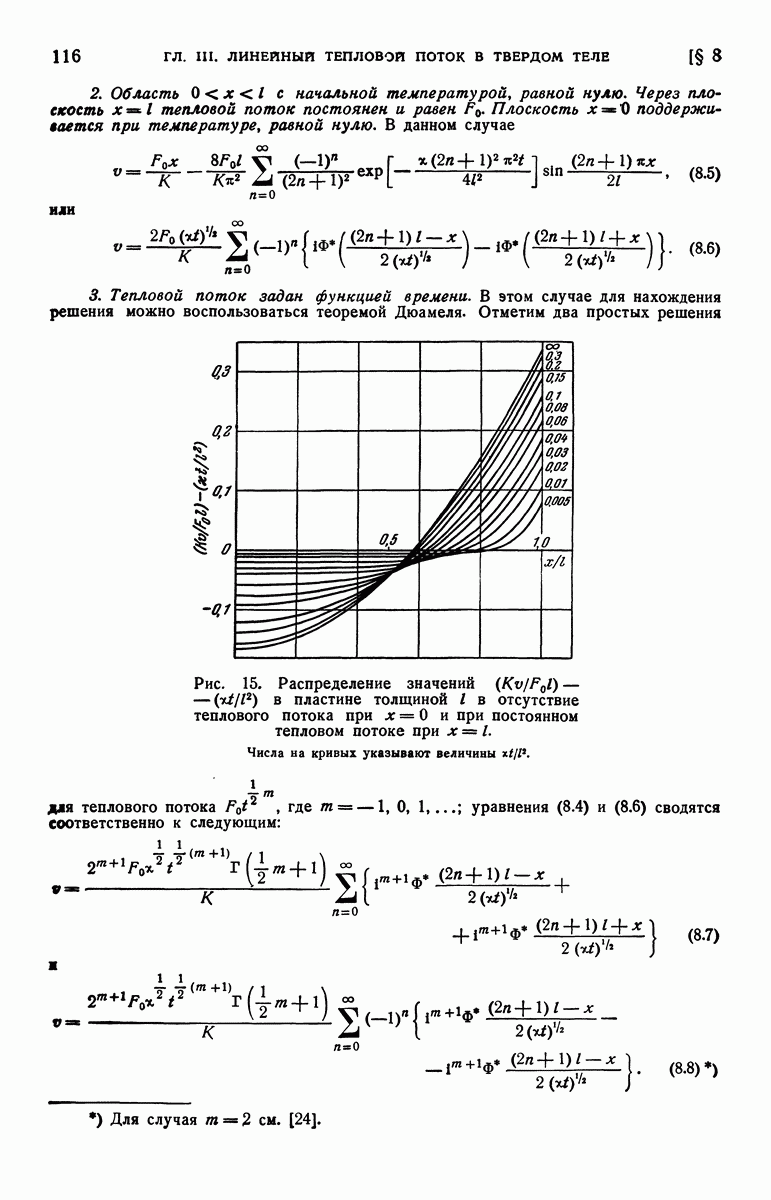
- § 8. Пластина с заданным тепловым потоком на ее границе
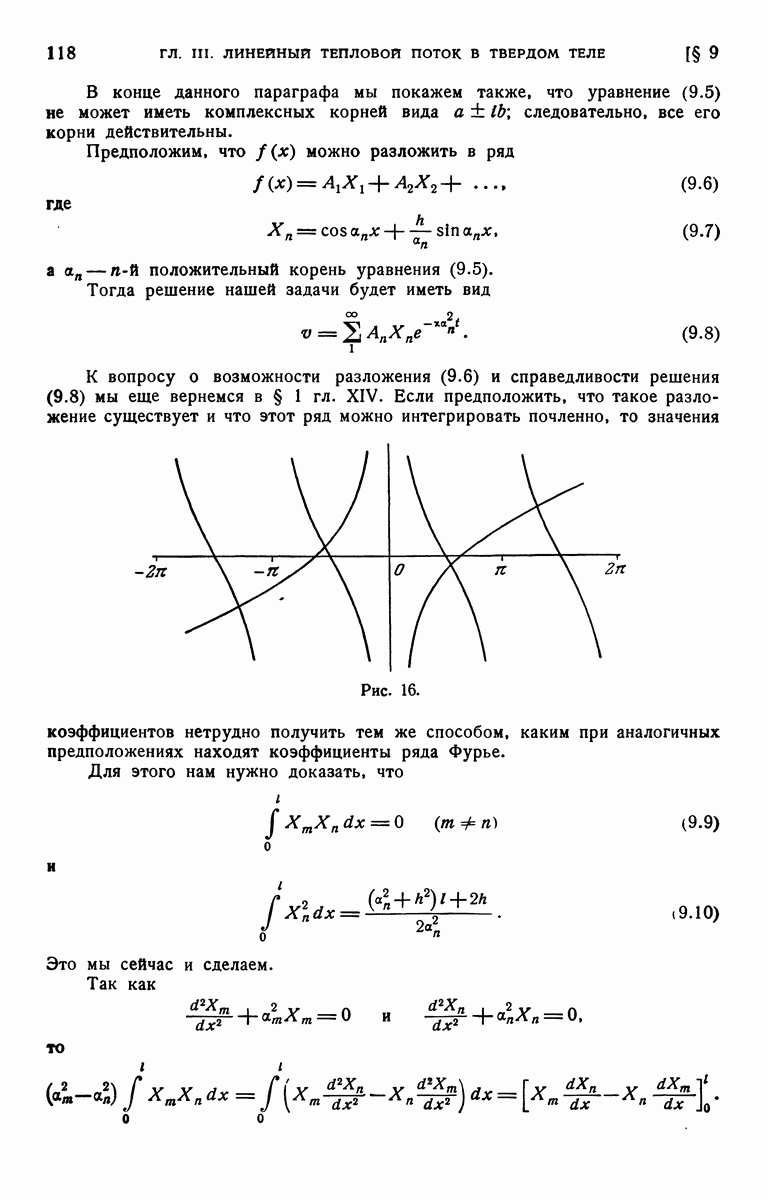
- § 9. Область [0, l]. Теплообмен на границах в среду с температурой, равной нулю. Начальная температура равна f(х)
- § 10. Область [-l, l]. На границах х=+l происходит теплообмен со средой нулевой температуры. Начальная температура f(x)
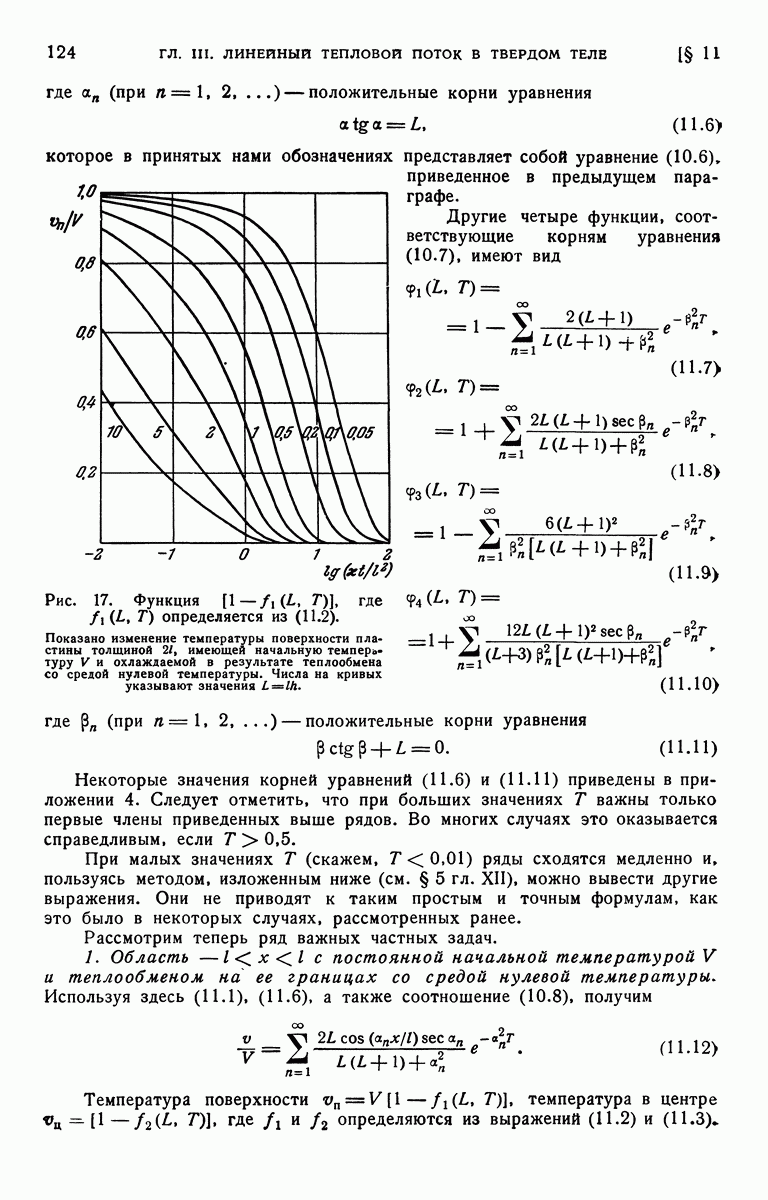
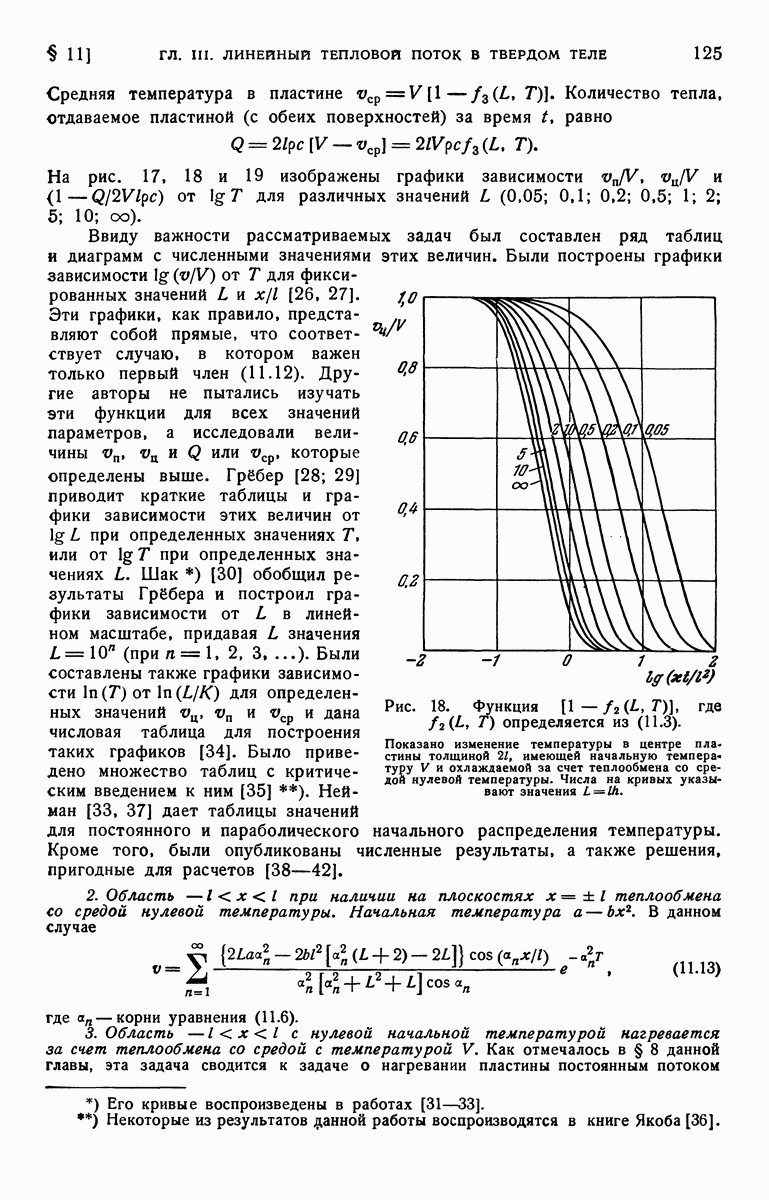
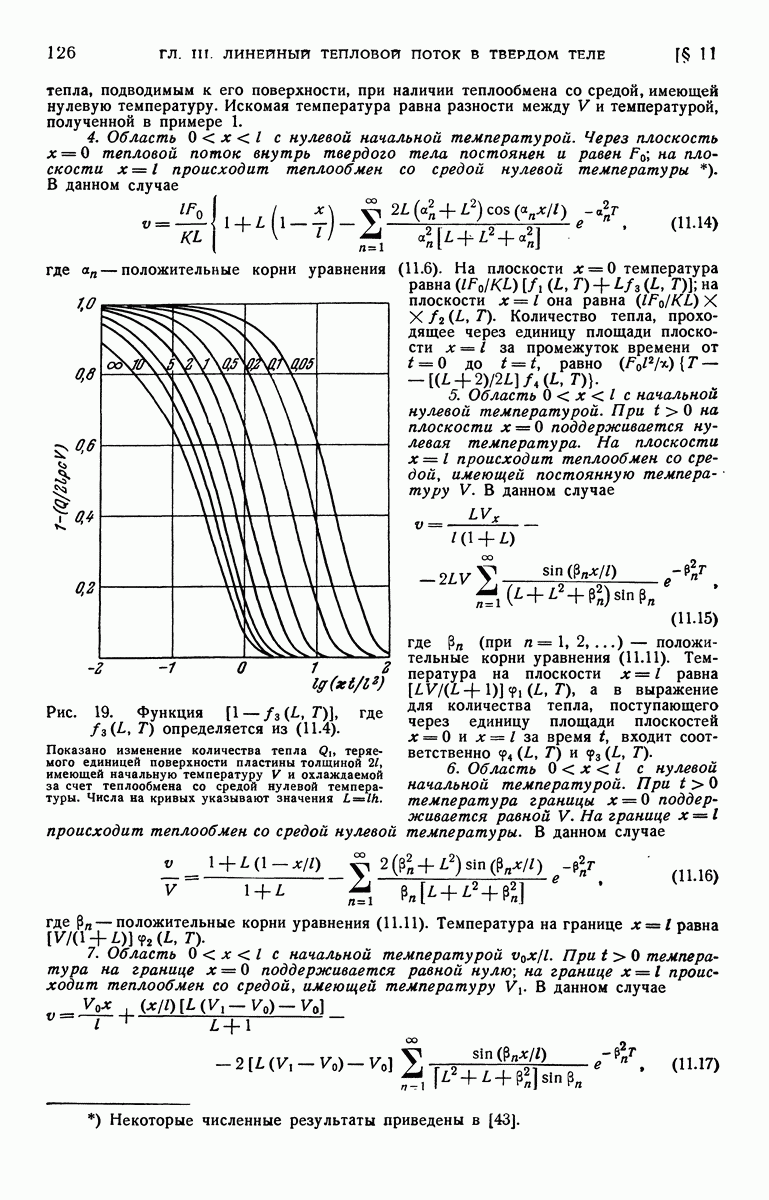
- § 11. Частные случаи и численные результаты для пластины с граничным условием третьего рода
- § 12. Область [-l, l] с нулевой начальной температурой и теплообменом на границах со средой, имеющей температуру …
- § 13. Пластина, одна из поверхностей которой соприкасается со слоем идеального проводника или хорошо перемешиваемой жидкости
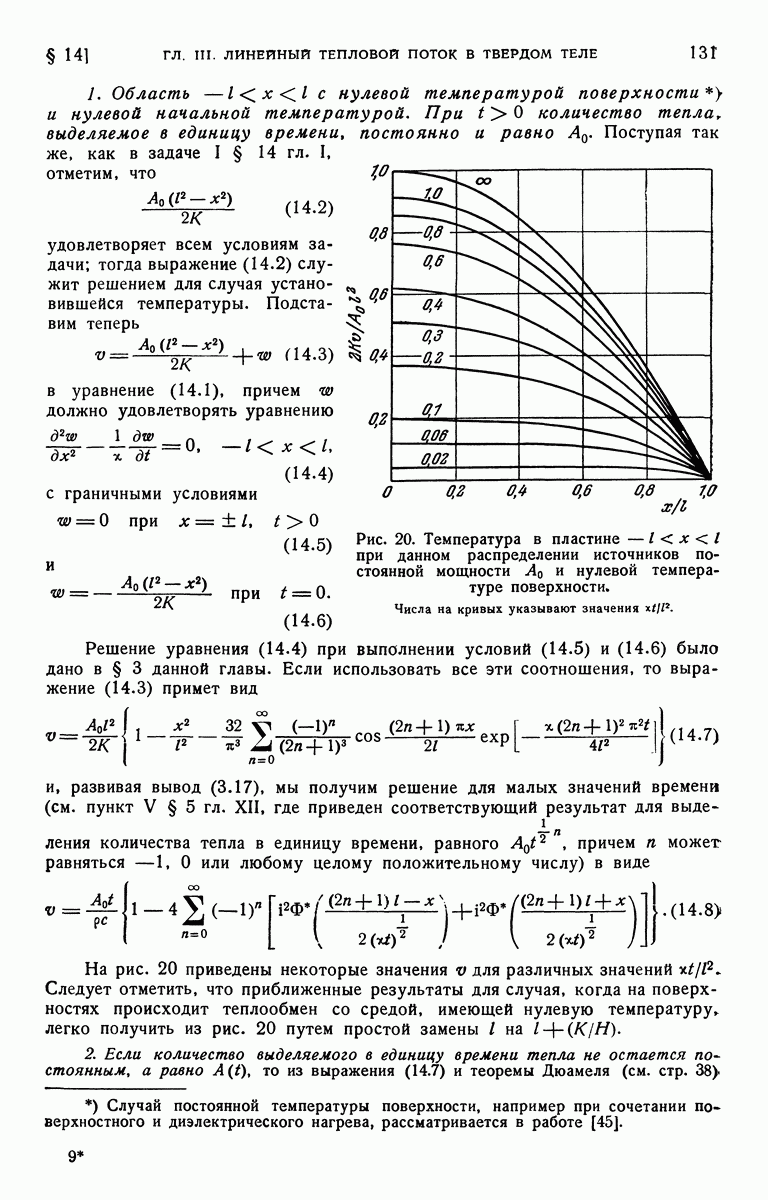
- § 14. Пластина с внутренним источником тепла
- ГЛАВА IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ
- § 3. Полуограниченный стержень. Случай установившейся температуры. Метод Форбса
- § 4. Полуограниченный стержень. Периодически изменяющаяся температура. Метод Ангстрема [5—10]
- § 5. Ограниченный стержень, концы которого находятся при фиксированных температурах. Случай установившейся температуры
- § 6. Стержень переменного сечения с охлаждающимися ребрами. Случай установившейся температуры
- § 7. Ограниченный стержень при наличии теплообмена на его поверхности. Случай неустановившейся температуры
- § 8. Ограниченный стержень с периодически изменяющейся температурой концов. Метод Неймана
- § 9. Задачи по теплопроводности в движущемся стержне
- § 10. Уравнение теплопроводности для тонкой проволоки, нагреваемой постоянным электрическим током
- § 11. Установившаяся температура. Определение коэффициента теплопроводности
- § 12. Сильно нагретая проволока, по которой протекает электрический ток
- § 13. Установившийся поток тепла в составной проволоке
- § 14. Неустановившаяся температура в проволоке, по которой течет электрический ток
- § 15. Кольцо Фурье
- ГЛАВА V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
- § 2. Неограниченное твердое тело прямоугольного сечения. Установившаяся температура
- § 3. Установившаяся температура в неограниченном теле прямоугольного сечения
- § 4. Тонкая пластина с прямоугольным сечением при наличии теплообмена на ее поверхности
- § 5. Установившаяся температура в теле прямоугольного сечения при наличии источника тепла
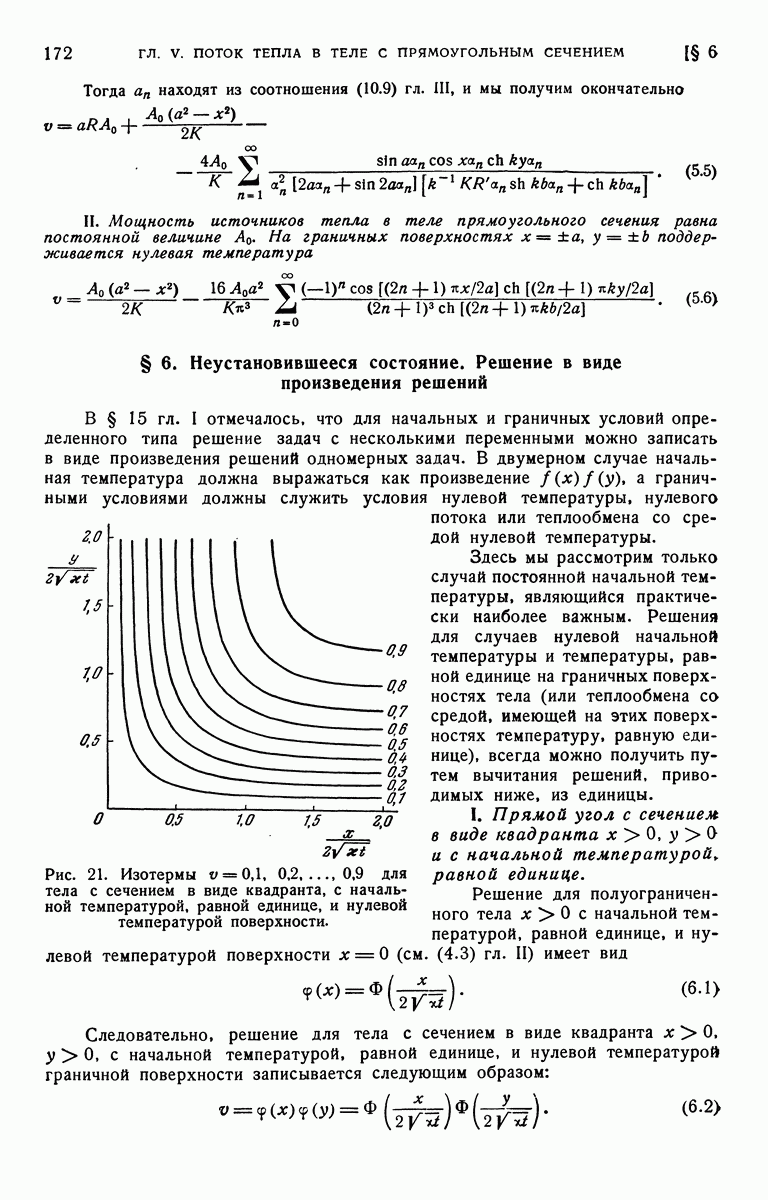
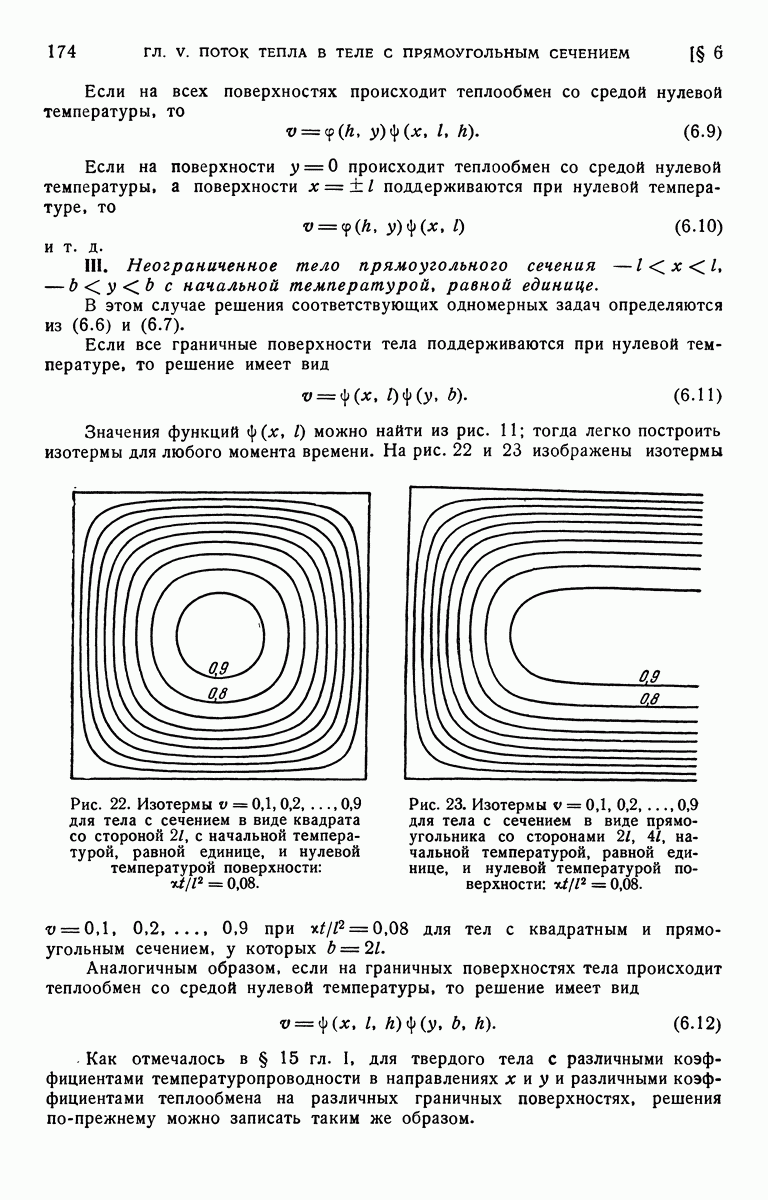
- § 6. Неустановившееся состояние. Решение в виде произведения решений
- § 7. Неустановившееся состояние. Произвольные начальные и граничные условия
- ГЛАВА VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ
- § 2. Установившаяся температура
- § 3. Двойные и кратные ряды Фурье
- § 4. Неустановившаяся температура. Решение в виде произведения решений
- § 5. Определение коэффициента теплопроводности и экстраполяция кривых охлаждения
- § 6. Неустановившаяся температура. Тройной ряд Фурье
- ГЛАВА VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ КРУГОВОГО СЕЧЕНИЯ
- § 2. Установившаяся температура. Радиальный поток
- § 3. Установившаяся, периодически изменяющаяся температура в круговых цилиндрах [19—22]
- § 4. Неограниченный цилиндр. Радиальный поток. Неустановившаяся температура
- § 5. Интегралы …
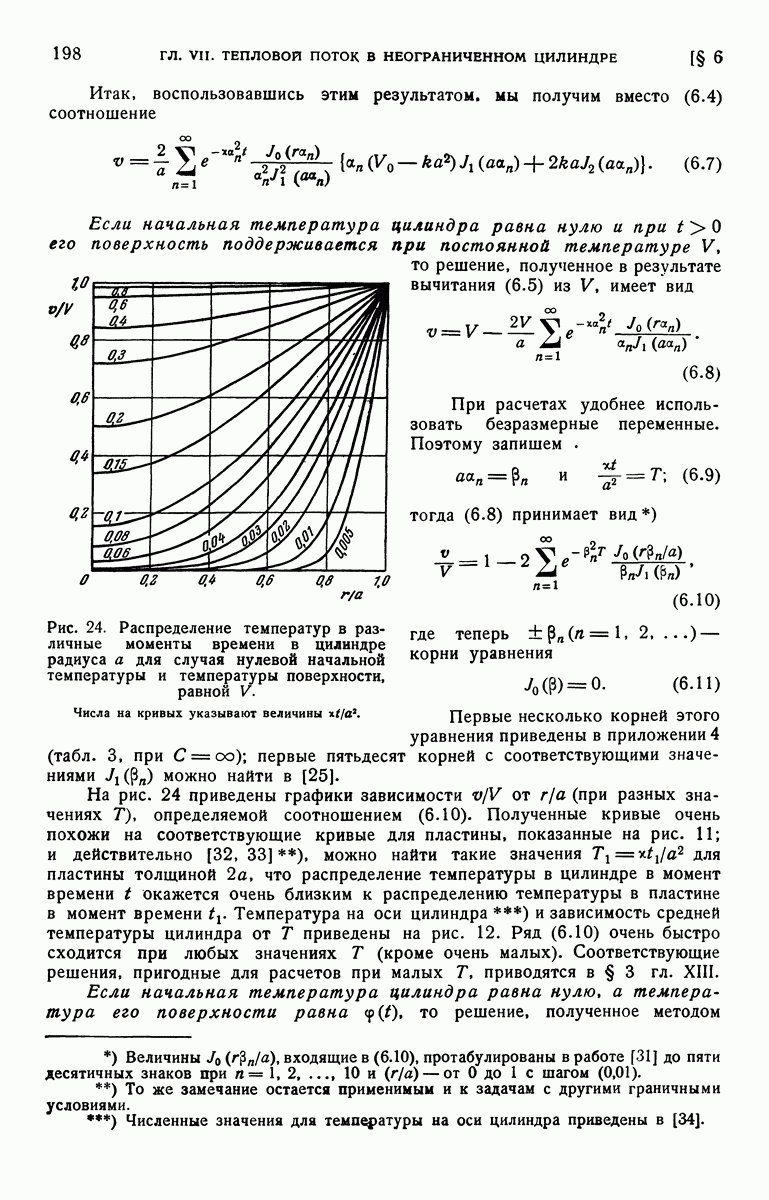
- § 6. Неограниченный цилиндр с температурой поверхности … и начальной температурой f(r)
- § 7. Неограниченный цилиндр с теплообменом на поверхности
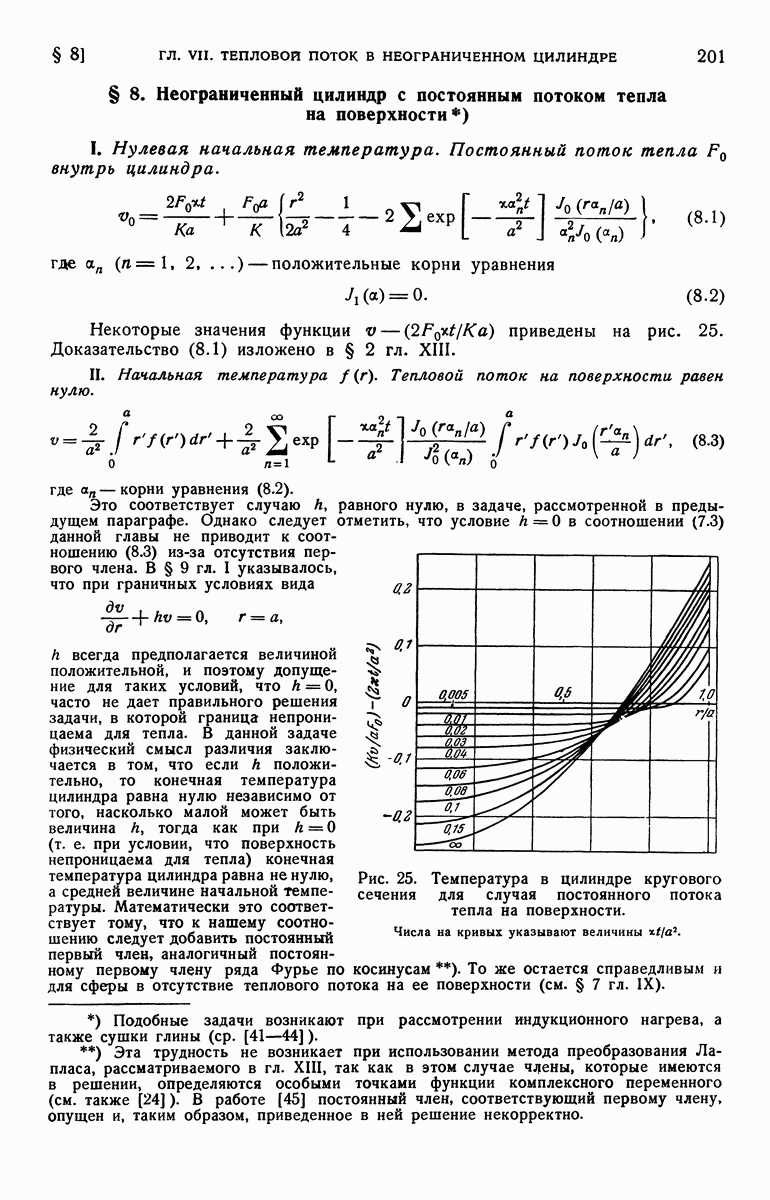
- § 8. Неограниченный цилиндр с постоянным потоком тепла на поверхности
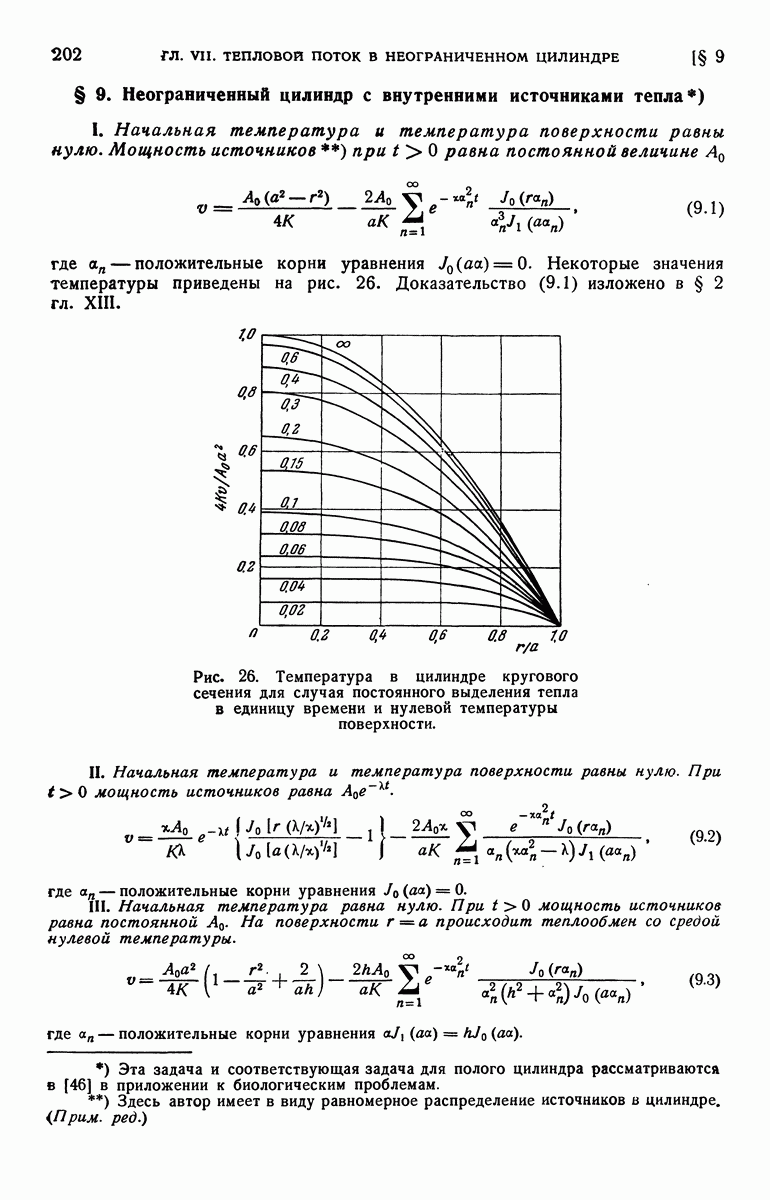
- § 9. Неограниченный цилиндр с внутренними источниками тепла
- § 10. Неограниченный полый цилиндр. Радиальный поток
- § 11. Неограниченный цилиндр. Установившаяся температура. Общий случай
- § 12. Неограниченный цилиндр. Неустановившаяся температура. Общий случай
- ГЛАВА VIII. ТЕПЛОВОЙ ПОТОК В ОБЛАСТЯХ, ОГРАНИЧЕННЫХ КООРДИНАТНЫМИ ПОВЕРХНОСТЯМИ ЦИЛИНДРИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ
- § 3. Установившаяся температура в ограниченном и полуограниченном цилиндрах
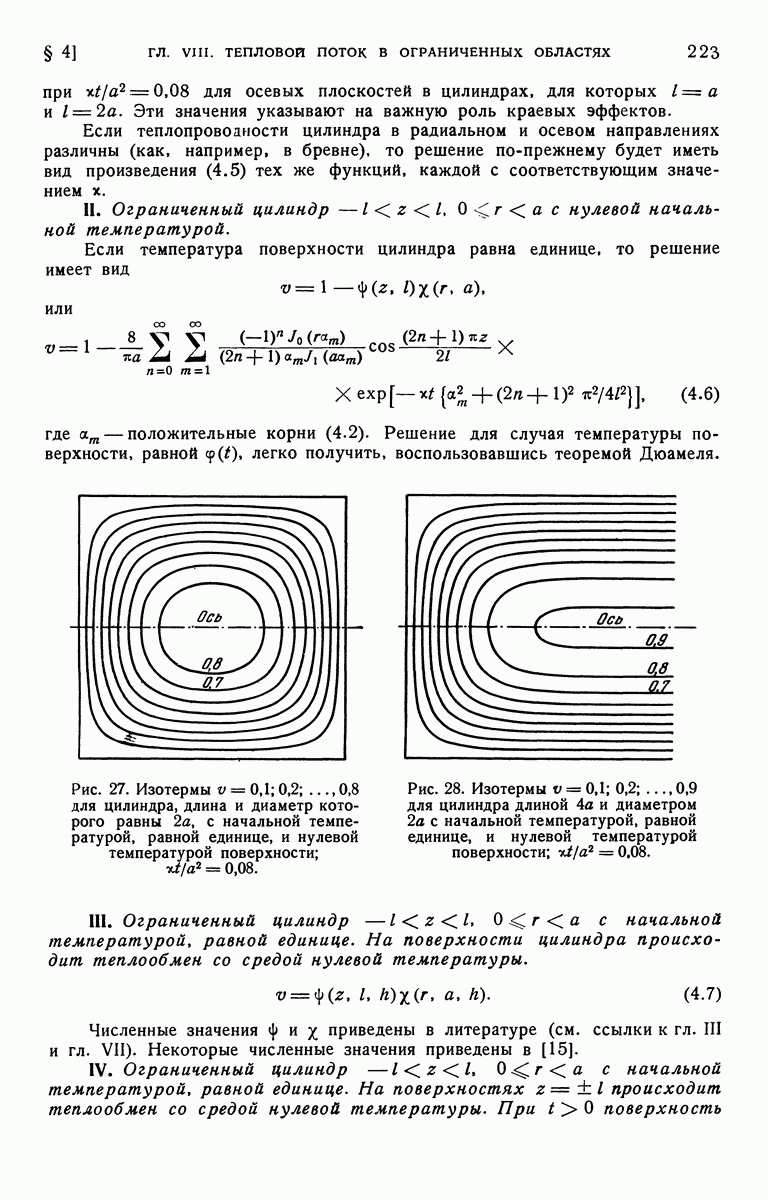
- § 4. Неустановившееся состояние. Решения в форме произведений
- § 5. Определение теплопроводности вещества в форме цилиндра
- § 6. Ограниченный цилиндр с начальной температурой …
- § 7. Полуограниченный цилиндр
- ГЛАВА IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ
- § 2. Установившаяся температура. Радиальный тепловой поток
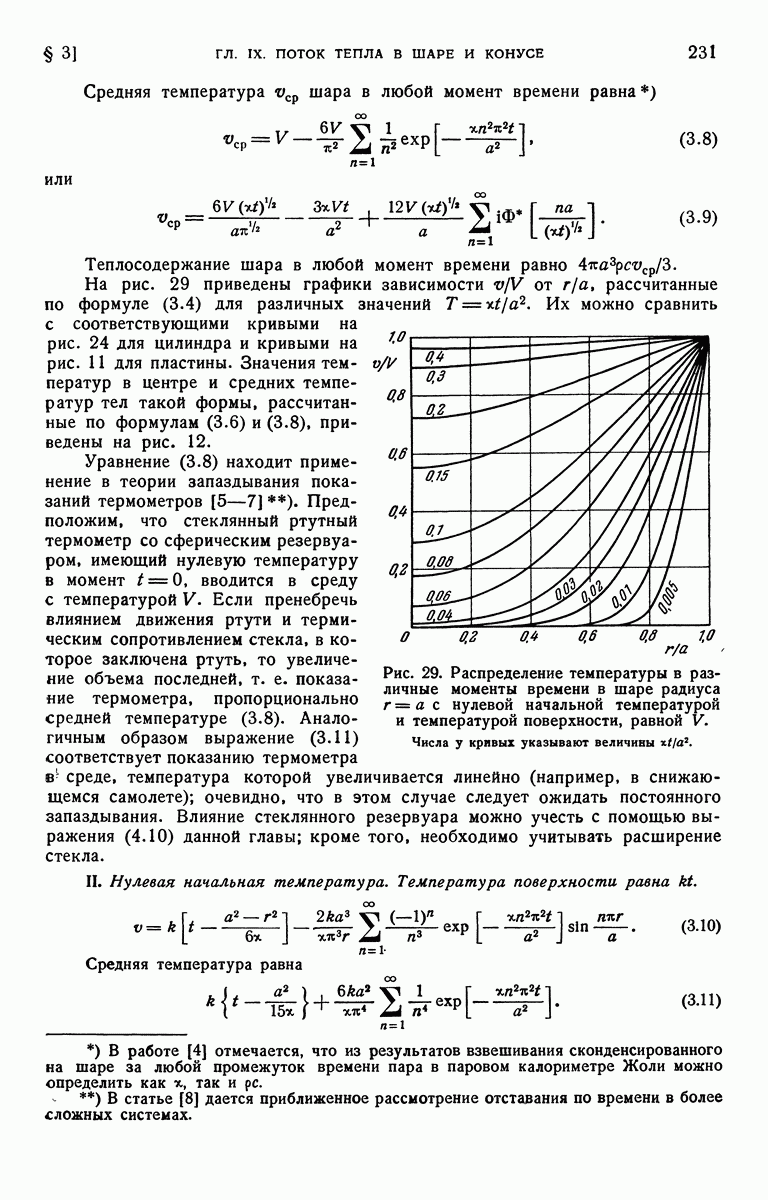
- § 3. Шар с начальной температурой f(r) и температурой поверхности …
- § 4. Шар. Начальная температура f(r). На поверхности сферы происходит теплообмен
- § 5. Определение коэффициентов теплопроводности плохих проводников
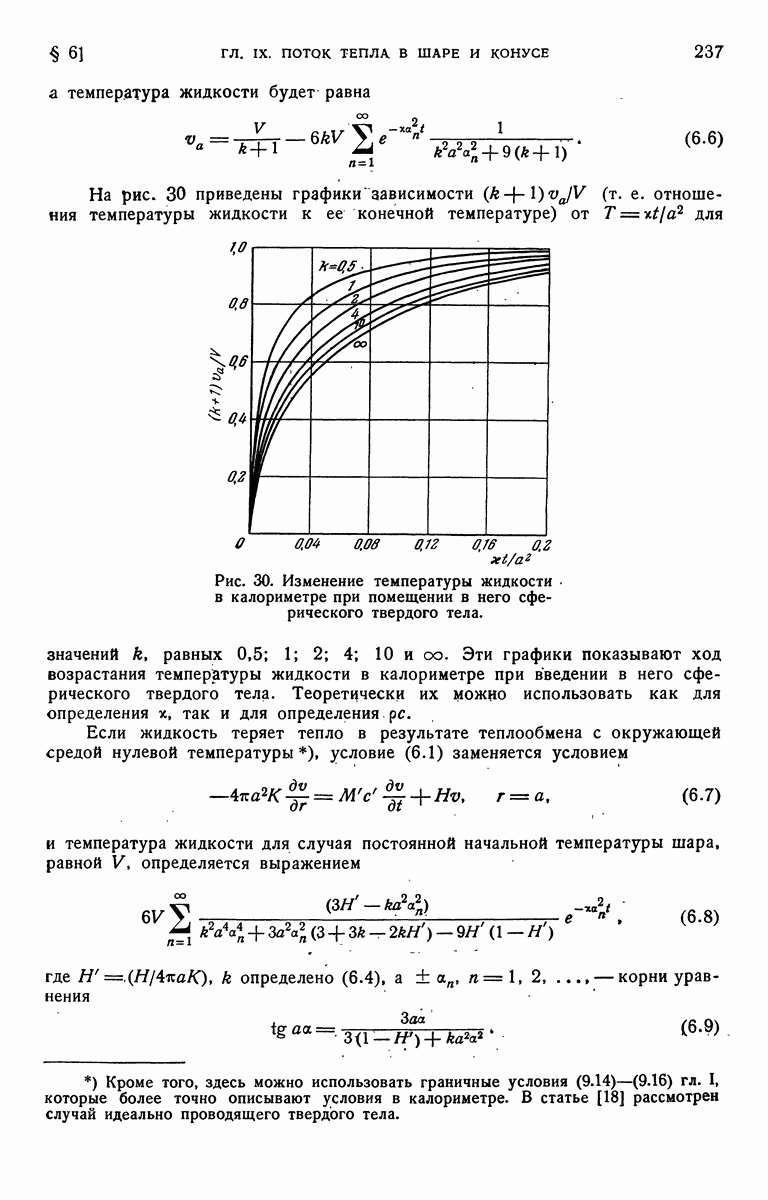
- § 6. Случай шара, находящегося в контакте с хорошо перемешиваемой жидкостью
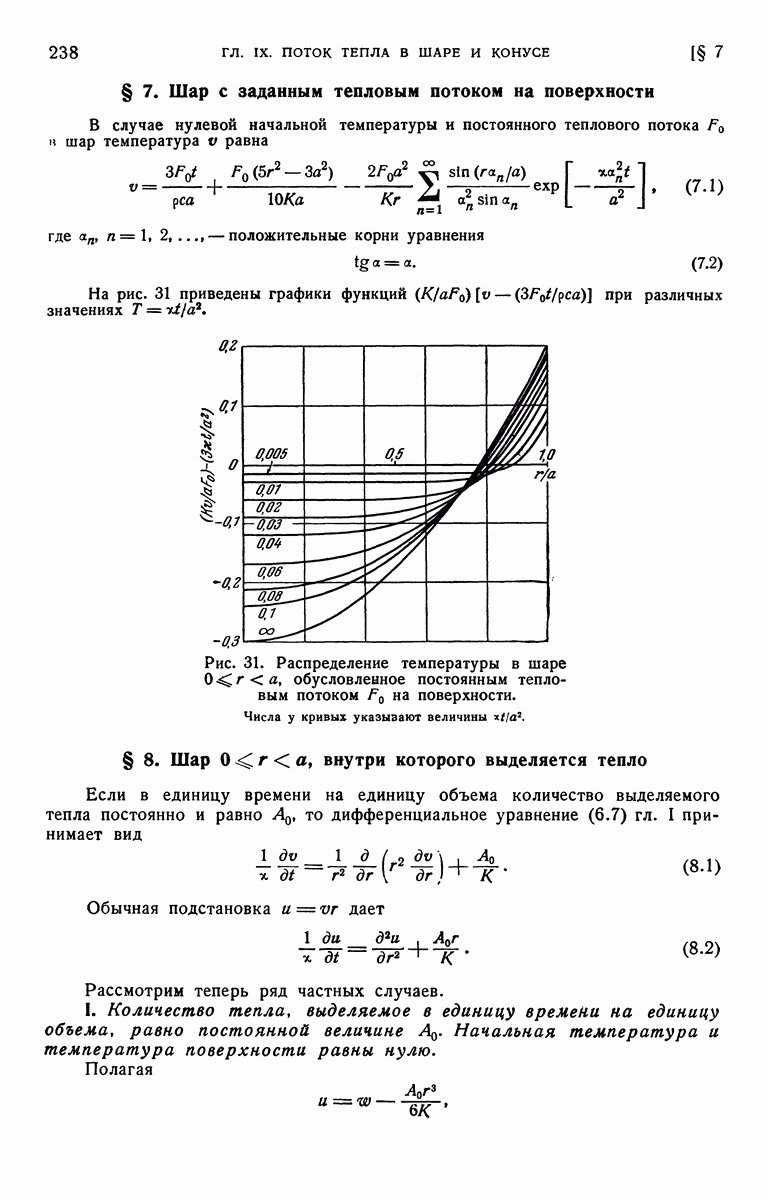
- § 7. Шар с заданным тепловым потоком на поверхности
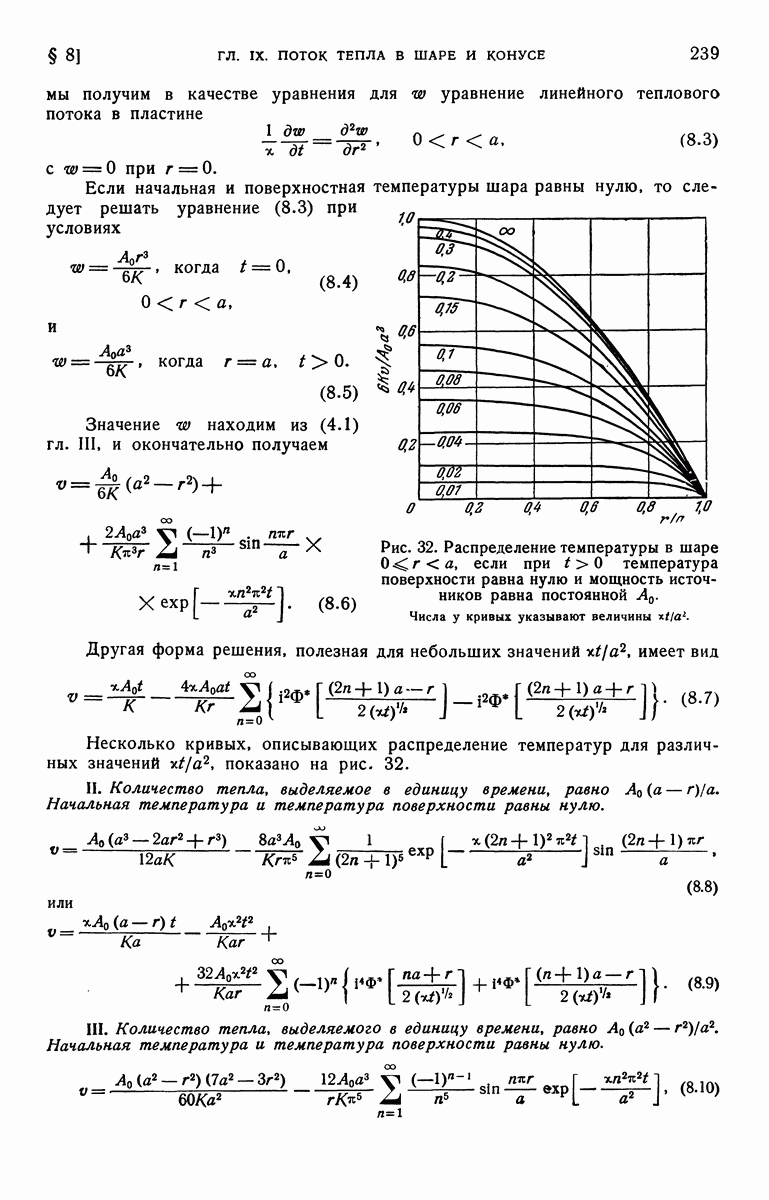
- § 8. Шар, внутри которого выделяется тепло
- § 9. Полый шар
- § 10. Область, ограниченная изнутри сферической поверхностью r=a
- § 11. Шар с начальной температурой … Температура поверхности r=a равна нулю
- § 12. Поверхность шара r=a поддерживается при температуре …
- § 13. Часть шара, вырезаемая конусом … Температура поверхности равна нулю, начальная температура равна …
- § 14. Температура внутри Земли
- ГЛАВА Х. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ К ЗАДАЧАМ С НЕУСТАНОВИВШЕЙСЯ ТЕМПЕРАТУРОЙ
- § 2. Мгновенный точечный источник
- § 3. Мгновенные источники; линейный, плоский и поверхностные цилиндрический и сферический источники
- § 4. Непрерывные и периодические источники
- § 5. Поверхностный нагрев полуограниченной области
- § 6. Выделение тепла в неограниченной среде
- § 7. Движущиеся источники тепла
- § 8. Дублеты
- § 9. Метод последовательных волн
- § 10. Метод изображений. Линейный тепловой поток
- § 11. Применение метода изображений к двумерным и трехмерным задачам
- § 12. Обобщение метода изображений Зоммерфельдом
- ГЛАВА XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ
- § 2. Одномерные случаи плавления и затвердевания. Решение Неймана и его обобщение
- § 3. Область … при других граничных условиях
- § 4. Методы интегрального уравнения. Рассмотрение задач затвердевания, предложенное Лайтфутом
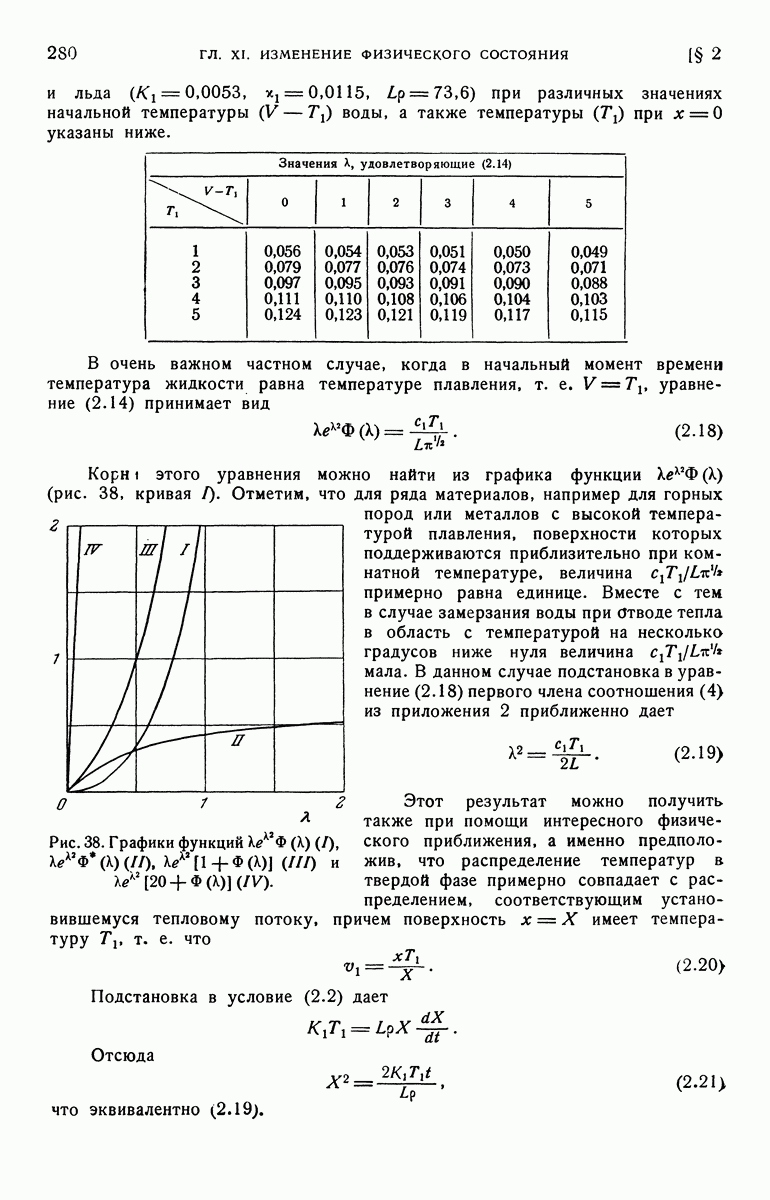
- § 5. Решения в цилиндрических и сферических координатах
- § 6. Осесимметричные задачи о замерзании и плавлении
- ГЛАВА XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЛИНЕЙНОГО ТЕПЛОВОГО ПОТОКА
- § 2. Преобразование Лапласа. Основные свойства
- § 3. Решение уравнения теплопроводности методом преобразования Лапласа
- § 4. Полуограниченная область. Решения, получаемые из таблицы изображений
- § 5. Ограниченная область (0, l). Решения, получаемые из таблицы изображений. Решения для небольших значений времени
- § 6. Ограниченная область (0, l). Применение теоремы обращения
- § 7. Полуограниченная область. Применение теоремы обращения
- § 8. Составные твердые тела
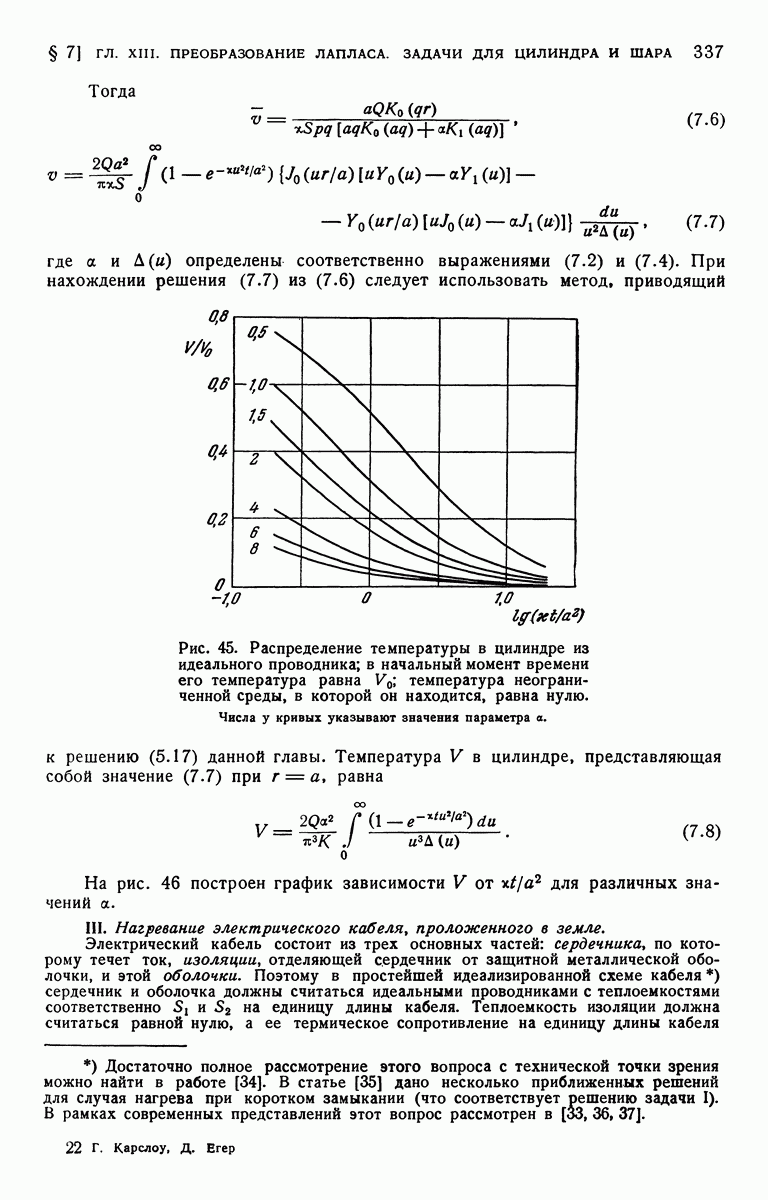
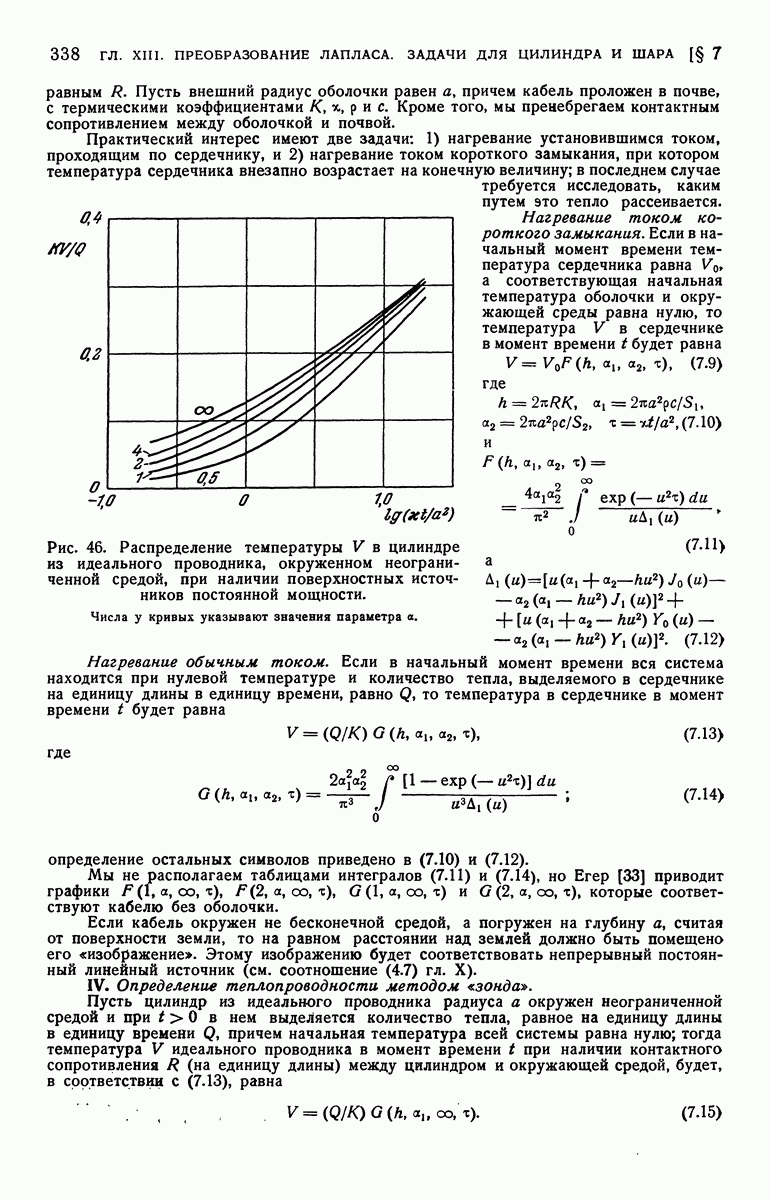
- ГЛАВА XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА
- § 3. Решения, применимые для малых интервалов времени
- § 4. Полый цилиндр
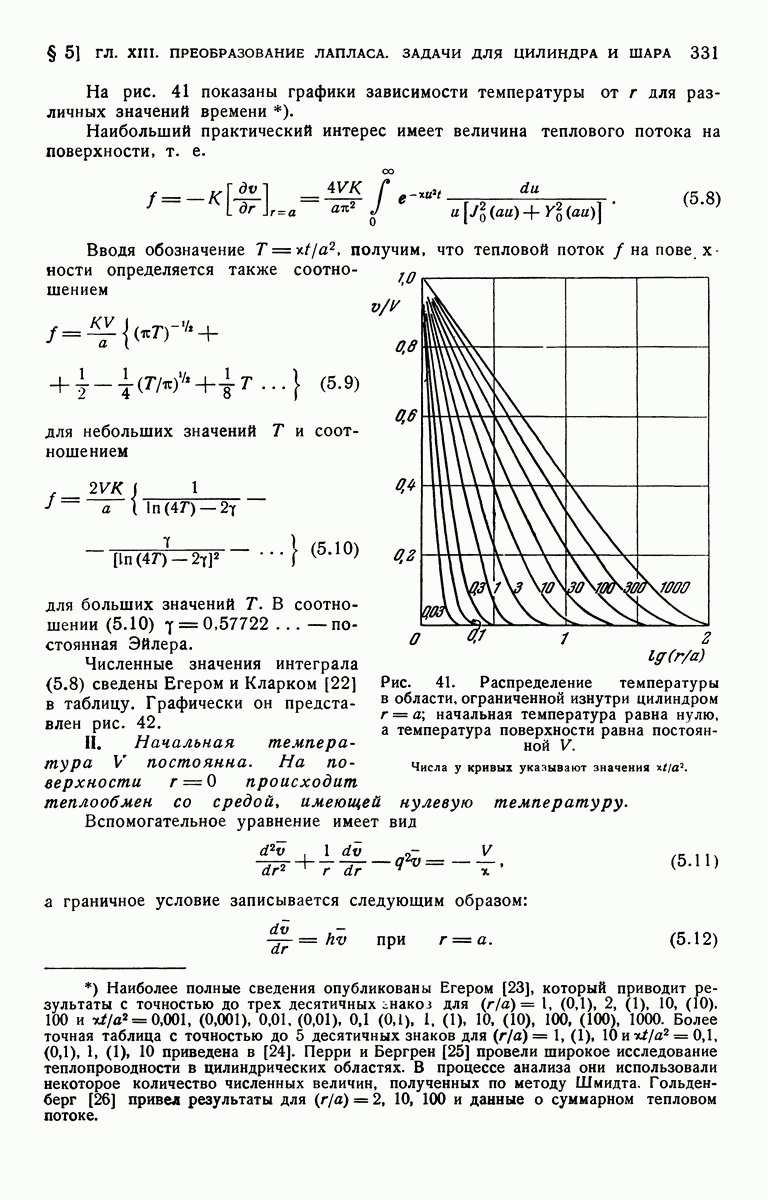
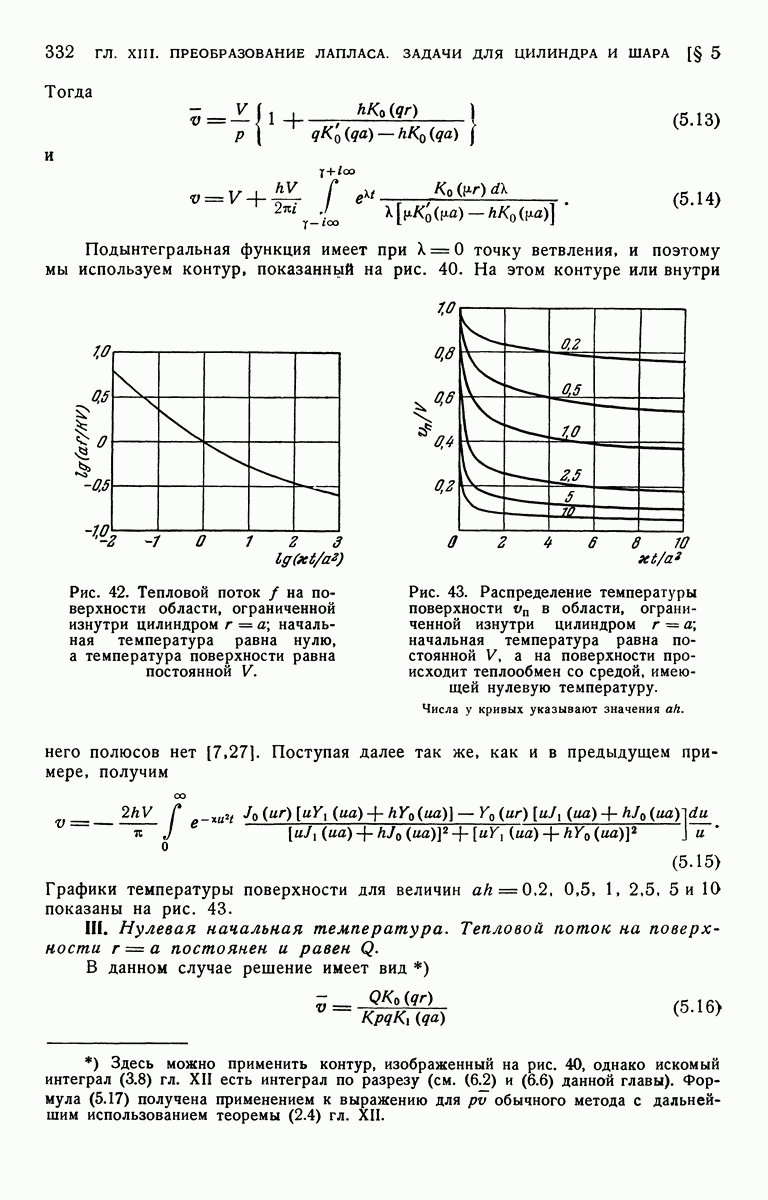
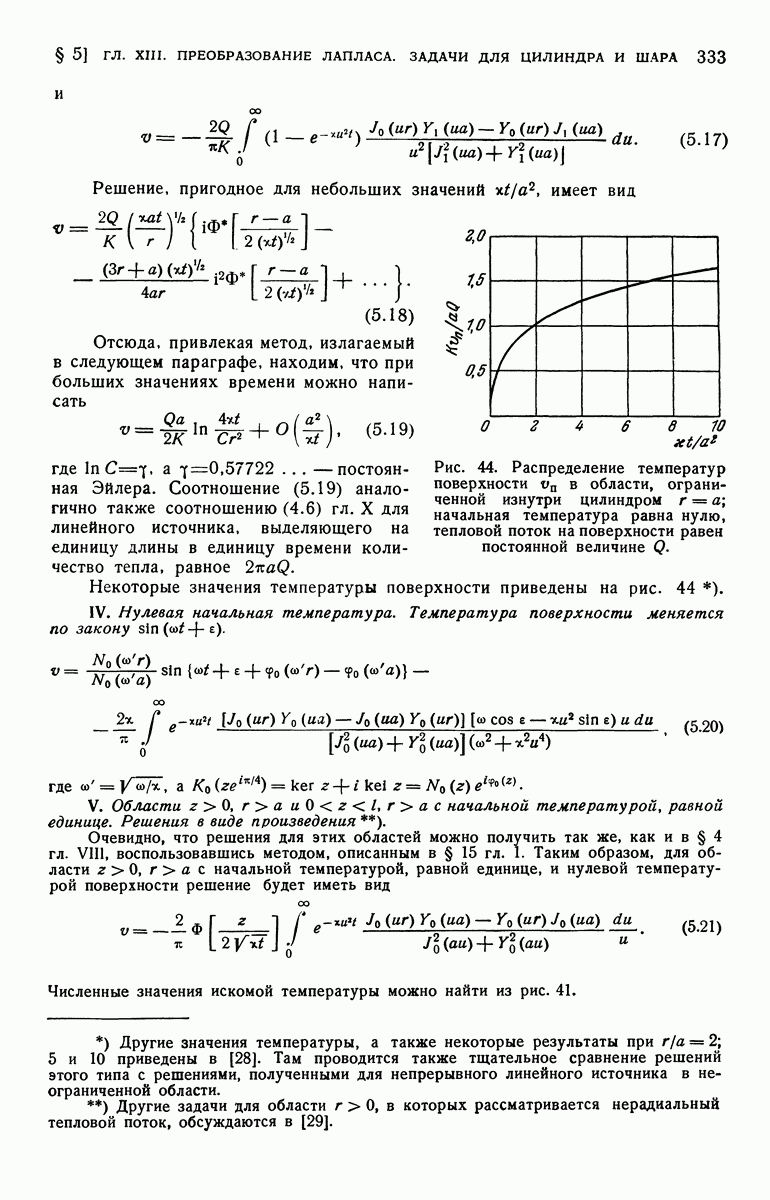
- § 5. Область ограничена изнутри цилиндром кругового сечения r=a
- § 6. Решения, применимые при больших значениях времени
- § 7. Область, ограниченная изнутри круговым цилиндром из идеального проводника
- § 8. Составная цилиндрическая область
- § 9. Шар. Радиальный тепловой поток
- ГЛАВА XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА К РЕШЕНИЮ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 2. Линейный тепловой поток. Полуограниченное твердое тело
- § 3. Линейный тепловой поток в области (0, a)
- § 4. Двумерные задачи. Тела с прямоугольным сечением
- § 5. Прямоугольный параллелепипед
- § 6. Линейный тепловой поток. Составные твердые тела
- § 7. Шар. Радиальный поток тепла
- § 8. Цилиндр. Радиальный тепловой поток
- § 9. Полуограниченное твердое тело. Трехмерные задачи
- § 10. Область, ограниченная двумя параллельными плоскостями
- § 11. Полуограниченное твердое тело с тонкой пленкой на плоскости z=0 из материала, имеющего значительно большую теплопроводность. В точке … расположен единичный мгновенный источник
- § 12. Неограниченное составное твердое тело. В точке действует мгновенный единичный источник
- § 13. Области, ограниченные цилиндрической поверхностью r=a
- § 14 Клин
- § 15. Цилиндрическая область
- § 16. Области, ограниченные сферической поверхностью r=a
- § 17. Конус
- § 18. Непрерывные источники
- ГЛАВА XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 3. Тепловые регенераторы и теплообменники
- § 4. Тепловой поток в слоистых системах
- § 5. Установившийся периодический режим
- § 6. Линейная асимптотика и запаздывание
- § 7. Выделение тепла
- § 8. Система автоматического регулирования температуры
- § 9. Неоднородные тела
- § 11. Прямое применение метода преобразования Лапласа к двумерным и трехмерным задачам
- ГЛАВА XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
- § 2. Источники и стоки при установившейся температуре
- § 3. Установившийся поток к почти плоской поверхности. Топографические поправки для геотермического потока
- § 4. Установившийся тепловой поток в составном теле
- § 5. Практические задачи
- § 6. Использование сопряженных гармонических функций в задачах с установившейся температурой
- § 7. Приложения этого метода [20, 21]
- § 8. Установившийся тепловой поток в многоугольнике
- § 9. Тепловой поток между изотермическими поверхностями
- ГЛАВА XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- § 2. Интегральные преобразования и формулы их обращения
- § 3. Неустановившийся тепловой поток
- § 4. Установившийся тепловой поток
- § 5. Конечные преобразования
- § 6. Последовательные преобразования
- ГЛАВА XVIII. ЧИСЛЕННЫЕ МЕТОДЫ
- § 3. Линейный тепловой поток в неограниченном пространстве
- § 4. Граничные условия
- § 5. Выделение тепла, переменная температуропроводность и скрытая теплота
- § 6. Релаксационные методы
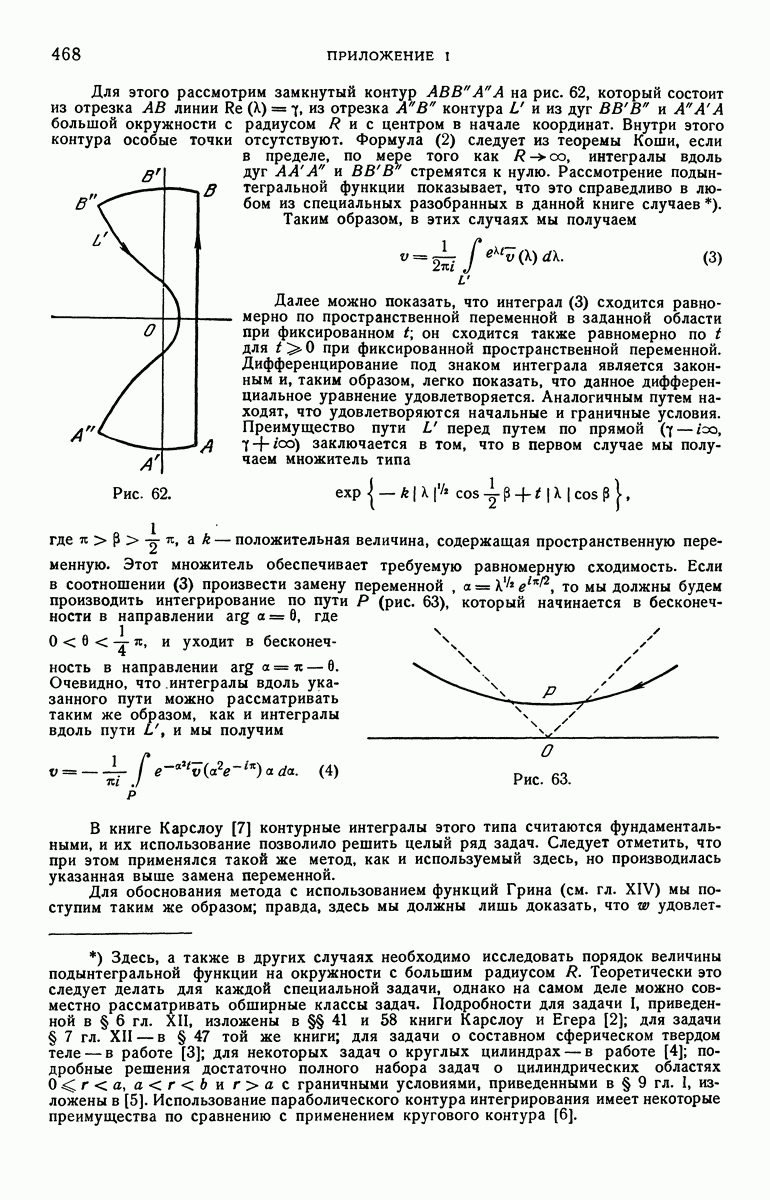
- ПРИЛОЖЕНИЕ 1. КОНТУРНЫЕ ИНТЕГРАЛЫ И ПРОВЕРКА РЕШЕНИЙ, ПОЛУЧЕННЫХ ПРИ ПОМОЩИ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
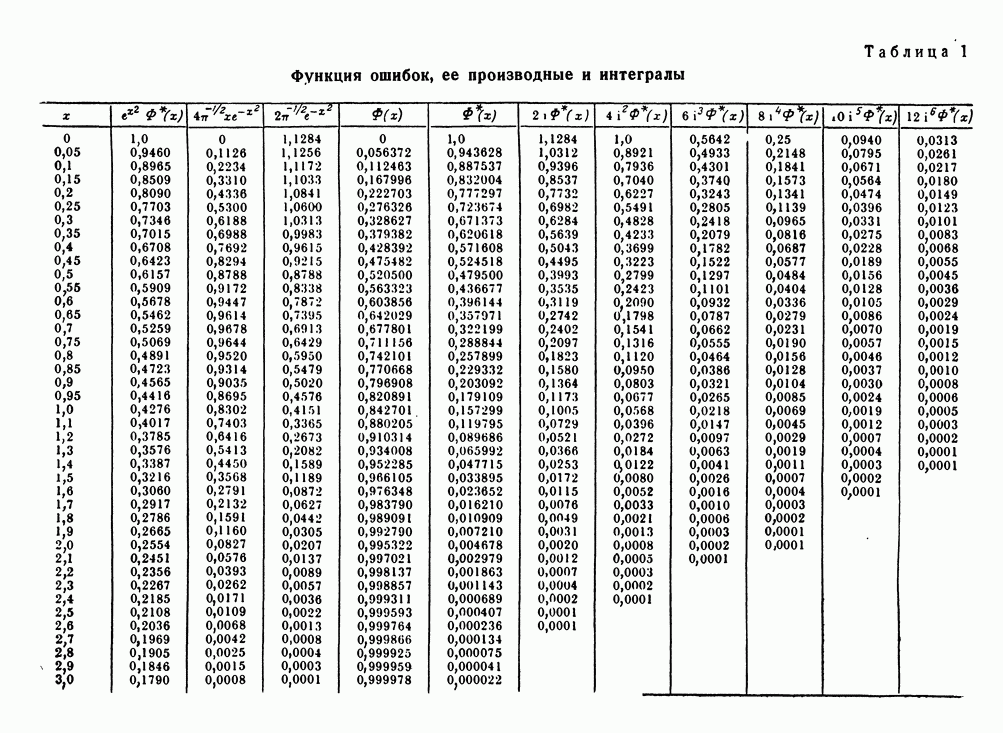
- ПРИЛОЖЕНИЕ 2. ФУНКЦИЯ ОШИБОК И РОДСТВЕННЫЕ ФУНКЦИИ
- ПРИЛОЖЕНИЕ 3. О ФУНКЦИЯХ БЕССЕЛЯ
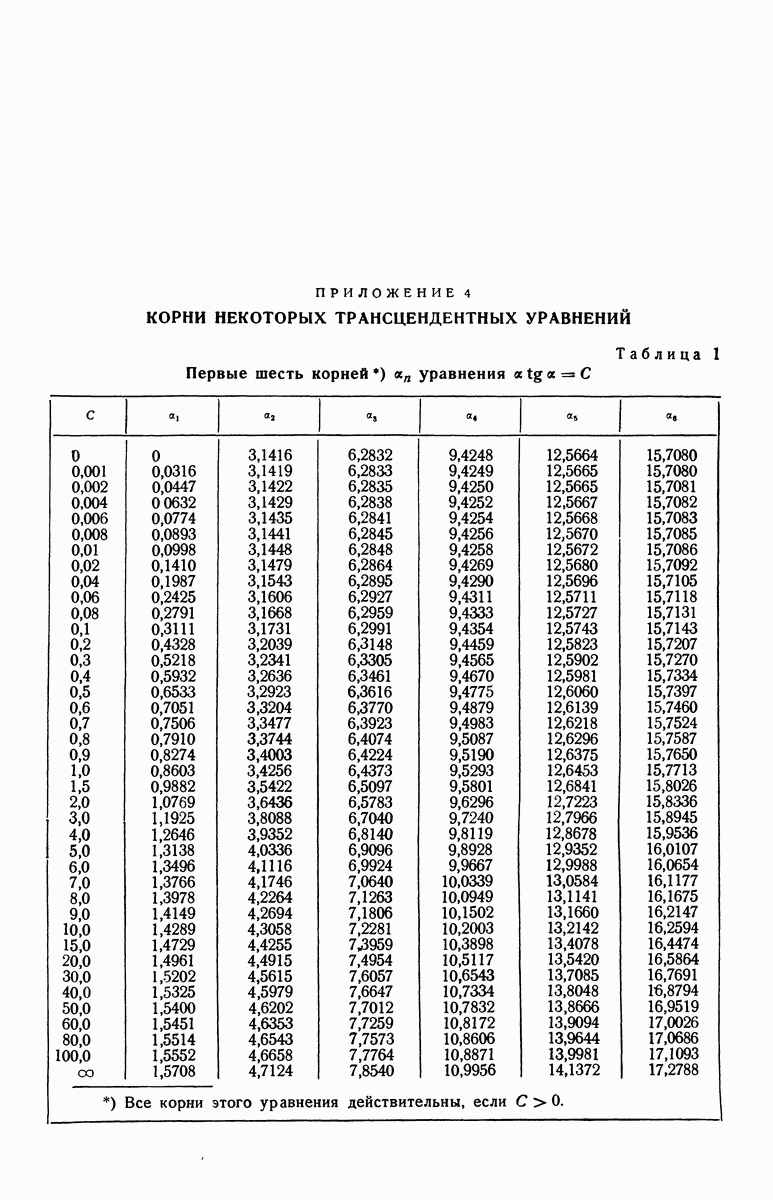
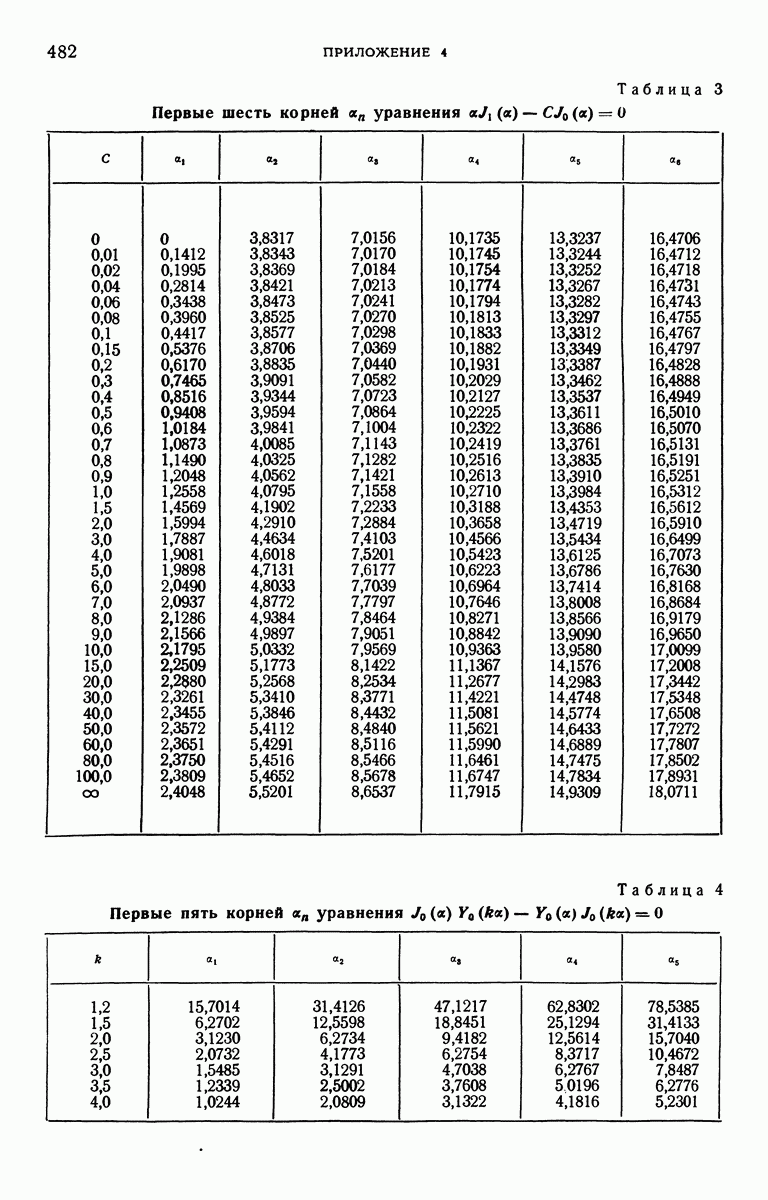
- ПРИЛОЖЕНИЕ 4. КОРНИ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- ПРИЛОЖЕНИЕ 5. ТАБЛИЦА ПРЕОБРАЗОВАНИЙ ЛАПЛАСА …
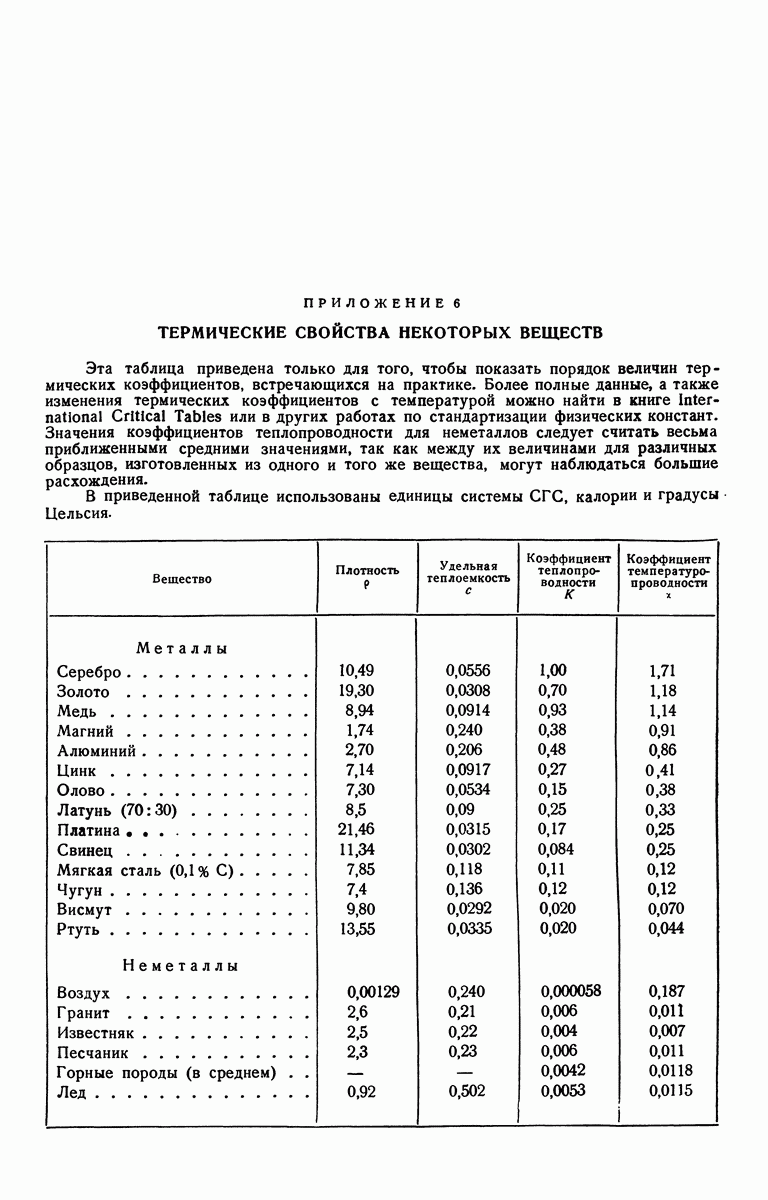
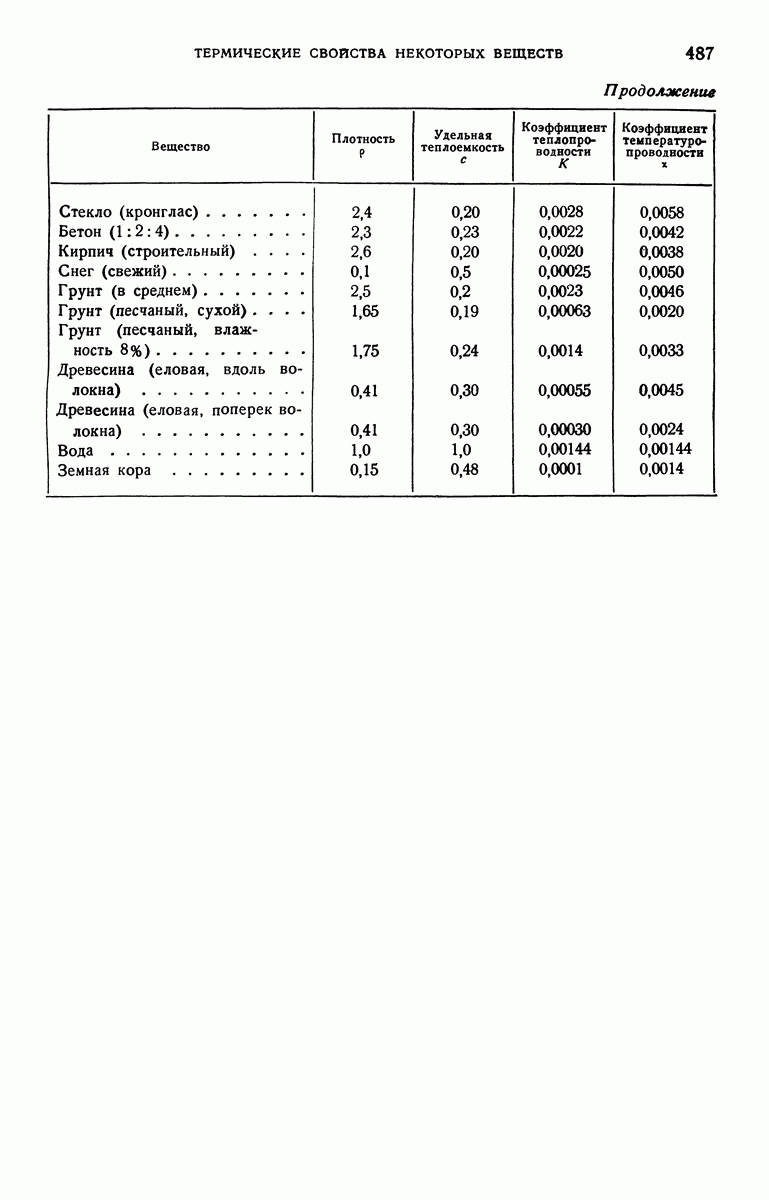
- ПРИЛОЖЕНИЕ 6. ТЕРМИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ВЕЩЕСТВ