| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6. Дифференциальное уравнение теплопроводности для изотропного твердого тела
Рассмотрим сначала случай, когда тепло течет через твердое тело, причем внутри тела источники тепла отсутствуют. Температура  в точке
в точке  является непрерывной функцией
является непрерывной функцией  как показано в § 3, то же утверждение справедливо и для теплового потока.
как показано в § 3, то же утверждение справедливо и для теплового потока.
Выделим в данном твердом теле элемент объема — прямоугольный параллелепипед с центром в точке  и ребрами длиной
и ребрами длиной  параллельными осям координат. Пусть
параллельными осям координат. Пусть  и
и  грани, перпендикулярные оси х и отстоящие от центра параллелепипеда соответственно на расстоянии
грани, перпендикулярные оси х и отстоящие от центра параллелепипеда соответственно на расстоянии  Тогда количество тепла, поступающее в параллелепипед через грань
Тогда количество тепла, поступающее в параллелепипед через грань  записывается в виде
записывается в виде

где  величина теплового потока в точке
величина теплового потока в точке  через плоскость, параллельную
через плоскость, параллельную  Аналогичным образом количество тепла, вытекающее через грань
Аналогичным образом количество тепла, вытекающее через грань  равно
равно

Тогда приращение количества тепла в параллелепипеде, обусловленное тепловым потоком через эти две грани, равно

Точно так же находят аналогичные выражения для приращения количества тепла, обусловленного потоком тепла через остальные пары граней. Суммируя эти выражения, мы получим общее приращение количества тепла в параллелепипеде в виде

где  -вектор, определенный соотношением (3.4). Вместе с тем это же увеличение количества тепла в параллелепипеде можно представить в виде
-вектор, определенный соотношением (3.4). Вместе с тем это же увеличение количества тепла в параллелепипеде можно представить в виде

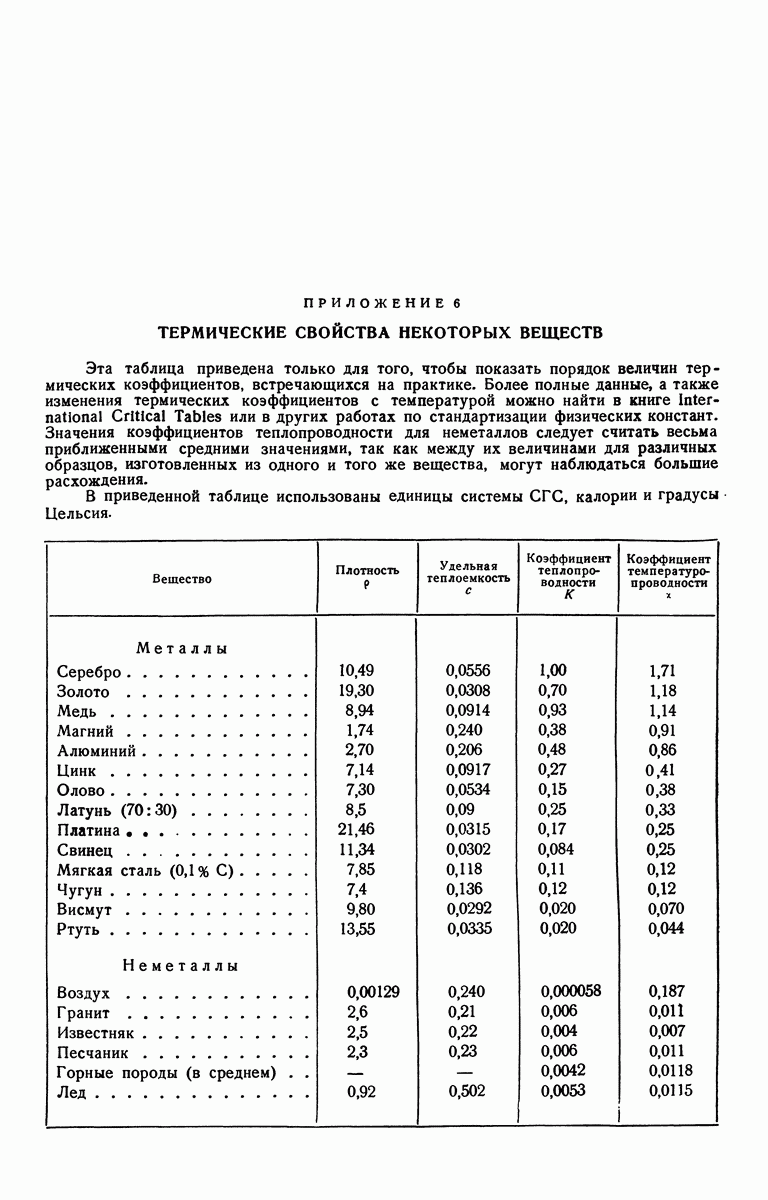
где  плотность, а с — удельная теплоемкость (при температуре V) твердого тела.
плотность, а с — удельная теплоемкость (при температуре V) твердого тела.
Приравнивая выражения (6.1) и (6.2), получаем

Полученное уравнение справедливо для любой точки твердого тела при условии, что в этой точке отсутствует источник тепла. При использовании этого уравнения не требуется, чтобы твердое тело было однородным или изотропным. Уравнение (6.3) соответствует уравнению неразрывности в гидродинамике.
Для однородного изотропного тела, у которого коэффициент теплопроводности не зависит от температуры,  даются соотношениями (5.3) и уравнение (6.3) приобретает следующий вид:
даются соотношениями (5.3) и уравнение (6.3) приобретает следующий вид:

где

Константу  Кельвин назвал коэффициентом тепловой диффузии, а Максвелл — коэффициентом температуропроводности
Кельвин назвал коэффициентом тепловой диффузии, а Максвелл — коэффициентом температуропроводности  так как х характеризует то изменение температуры, происходящее в единице объема вещества, которое обусловлено количеством тепла, протекающим в единицу времени через единичную площадку в слое единичной толщины и при единичной разности температур на его поверхностях.
так как х характеризует то изменение температуры, происходящее в единице объема вещества, которое обусловлено количеством тепла, протекающим в единицу времени через единичную площадку в слое единичной толщины и при единичной разности температур на его поверхностях.
Уравнение (6.4) известно как уравнение теплопроводности. В случае установившейся температуры, когда  не изменяется со временем, это уравнение превращается в уравнение Лапласа
не изменяется со временем, это уравнение превращается в уравнение Лапласа

Если в точке  твердого тела существует источник тепла, выделяющий в единице объема за единицу времени количество тепла
твердого тела существует источник тепла, выделяющий в единице объема за единицу времени количество тепла  то в соотношение (6.1) следует ввести дополнительный член
то в соотношение (6.1) следует ввести дополнительный член  в случае постоянного К соотношение (6.4) принимает вид
в случае постоянного К соотношение (6.4) принимает вид

Для установившегося режима,  при
при  уравнение (6.7) превращается в уравнение Пуассона.
уравнение (6.7) превращается в уравнение Пуассона.
Почти во всех задачах, имеющих точное решение, а также в задачах, рассматриваемых в настоящей книге (если нет специальных указаний), термические характеристики вещества  с считаются постоянными, т. е. не зависящими от положения выбранной точки и от температуры тела. Если это не так, то соотношение (6. 3) все же остается справедливым, причем при
с считаются постоянными, т. е. не зависящими от положения выбранной точки и от температуры тела. Если это не так, то соотношение (6. 3) все же остается справедливым, причем при
наличии источника тепла к правой его части добавляют член  а соотношение (6.7) принимает следующий вид:
а соотношение (6.7) принимает следующий вид:

Если  являются функциями только положения, то при решении уравнения (6.8), в принципе, не приходится сталкиваться с большими трудностями, и для тел, в которых термические характеристики имеют разрыв (составные тела), и тел, в которых изменение К с положением подчиняется простому закону, пригоден целый ряд решений. Если же термические свойства зависят от температуры, то ситуация значительно усложняется, так как уравнение становится нелинейным. Таких случаев, связанных с теплопроводностью, исследовано очень мало, что объясняется относительно слабым изменением термических свойств с температурой, а имеющиеся данные по этому вопросу весьма скудны и неточны. Между тем подобные задачи приобретают все большее значение в тех случаях, когда приходится рассматривать значительные изменения температуры, как, например, при застывании отливок. Кроме того, те же уравнения играют важную роль в теории диффузии, когда имеет место резкое изменение коэффициентов диффузии в зависимости от концентрации (см. [71], гл. IX—XI). Для решений в большинстве случаев были использованы численные методы; несколько общих результатов и случаи, для которых возможно точное решение, будут изложены ниже.
являются функциями только положения, то при решении уравнения (6.8), в принципе, не приходится сталкиваться с большими трудностями, и для тел, в которых термические характеристики имеют разрыв (составные тела), и тел, в которых изменение К с положением подчиняется простому закону, пригоден целый ряд решений. Если же термические свойства зависят от температуры, то ситуация значительно усложняется, так как уравнение становится нелинейным. Таких случаев, связанных с теплопроводностью, исследовано очень мало, что объясняется относительно слабым изменением термических свойств с температурой, а имеющиеся данные по этому вопросу весьма скудны и неточны. Между тем подобные задачи приобретают все большее значение в тех случаях, когда приходится рассматривать значительные изменения температуры, как, например, при застывании отливок. Кроме того, те же уравнения играют важную роль в теории диффузии, когда имеет место резкое изменение коэффициентов диффузии в зависимости от концентрации (см. [71], гл. IX—XI). Для решений в большинстве случаев были использованы численные методы; несколько общих результатов и случаи, для которых возможно точное решение, будут изложены ниже.
I. Термические характеристики изменяются с температурой и не зависят от положения.
В данном случае соотнэшение (6.8) принимает следующий вид:

Как мы видим, это уравнение нелинейно. Соотношению (6.8) можно придать более простую форму  вводя новую переменную
вводя новую переменную

где  — значение К при
— значение К при  и нижний предел интегрирования вводят только для того, чтобы придать величине
и нижний предел интегрирования вводят только для того, чтобы придать величине  размерность температуры и определенное значение. Из соотношения (6.10) следует, что
размерность температуры и определенное значение. Из соотношения (6.10) следует, что

и соотношение (6.8) принимает вид

где  выражены через новую переменную
выражены через новую переменную  Таким образом, при использовании этой новой переменной сохраняется форма уравнения теплопроводности (6.7), но коэффициент температуропроводности
Таким образом, при использовании этой новой переменной сохраняется форма уравнения теплопроводности (6.7), но коэффициент температуропроводности  становится зависимым от
становится зависимым от  . В большинстве случаев изменение
. В большинстве случаев изменение  с температурой значительно менее важно, чем аналогичное изменение К и, таким образом, с достаточным приближением можно считать
с температурой значительно менее важно, чем аналогичное изменение К и, таким образом, с достаточным приближением можно считать  постоянным. Например, для металлов, находящихся при температурах, близких к абсолютному нулю, как К, так и с приблизительно пропорциональны абсолютной температуре. В таких случаях, если А не зависит от
постоянным. Например, для металлов, находящихся при температурах, близких к абсолютному нулю, как К, так и с приблизительно пропорциональны абсолютной температуре. В таких случаях, если А не зависит от  то уравнение (6.11) принимает тот же вид, что и (6.7). Для случая постоянной теплопроводности можно сразу же
то уравнение (6.11) принимает тот же вид, что и (6.7). Для случая постоянной теплопроводности можно сразу же
получить решение, заменив  на
на  но при этом граничные условия должны определяться только
но при этом граничные условия должны определяться только  или
или  если они записываются в виде
если они записываются в виде 

где  постоянная, то это замечание не имеет силы.
постоянная, то это замечание не имеет силы.
Случай установившегося теплового потока представляет особый интерес, так как при  уравнение (6.11) превращается в уравнение Пуассона, а при
уравнение (6.11) превращается в уравнение Пуассона, а при  в уравнение Лапласа. Таким образом, решения задач об установившемся тепловом потоке при теплопроводности, являющейся произвольной функцией температуры, и с граничными условиями для температуры или теплового потока, можно непосредственно получить из соответствующих решений для случаев постоянной теплопроводности.
в уравнение Лапласа. Таким образом, решения задач об установившемся тепловом потоке при теплопроводности, являющейся произвольной функцией температуры, и с граничными условиями для температуры или теплового потока, можно непосредственно получить из соответствующих решений для случаев постоянной теплопроводности.
Другую удобную форму уравнения легко получить, вводя переменную  теплосодержание единицы массы вещества, измеренное относительно некоторого произвольного нулевого значения температуры. Подставляя
теплосодержание единицы массы вещества, измеренное относительно некоторого произвольного нулевого значения температуры. Подставляя  в уравнение (6.8), получим
в уравнение (6.8), получим

или, воспользовавшись соотношением (6.10),

где  связано с
связано с  каким-то определенным образом.
каким-то определенным образом.
Введение величины  имеет ряд преимуществ при решении задач, в которых учитывается скрытая теплота.
имеет ряд преимуществ при решении задач, в которых учитывается скрытая теплота.
II. Источник тепла внутри твердого тела.
Случаи, когда внутри твердого тела имеется источник тепла, приобретают все большее и большее значение в технике. Внутри твердого тела тепло может образовываться в результате следующих процессов: а) пропускание электрического тока, б) диэлектрический или индукционный нагрев [9—12]; в) радиоактивный распад ([13, 14]; см. также библиографию к гл. II и IX); г) поглощение излучения, д) переход механической энергии в тепловую при вязких или пластических деформациях; е) химические реакции ([71], гл. VIII; см. также библиографию к гл. XV настоящей книги), в том числе ряд самых различных процессов, начиная от гидратации цемента [15—19] и кончая созреванием яблок [20].
Во всех случаях, кроме последнего, количество выделяемого тепла в первом приближении не зависит от  ; в более точном приближении оно обычно соответствует формуле
; в более точном приближении оно обычно соответствует формуле

где  постоянные, которые могут иметь любой знак.
постоянные, которые могут иметь любой знак.
Следует отметить, что уравнение (6.7) с величиной А, соответствующей выражению (6.14), можно точно решить многими способами (см. § 14 гл. I и § 7 гл. XV).
Количество тепла, выделяющегося в результате химической реакции нулевого порядка, обычно рассчитывают по формуле Аррениуса

где  постоянные,
постоянные,  абсолютная температура [22—24]. Для реакций более высокого порядка следует использовать аналогичное, но более сложное выражение. В некоторых случаях его находят экспериментально, и оно имеет вид
абсолютная температура [22—24]. Для реакций более высокого порядка следует использовать аналогичное, но более сложное выражение. В некоторых случаях его находят экспериментально, и оно имеет вид

Для всех описанных выше случаев не существует аналитических решений, и поэтому следует применять численные методы. Выражением (6.14) можно пользоваться как самым грубым приближением, но, по-видимому, точные решения очень сильно отличаются от перечисленных приближений.
III. Эффекты термического расширения.
Уравнение (6.3) выведено в предположении, что в результате деформации твердого тела работа не совершается, и поэтому с является удельной теплоемкостью только при постоянной деформации. Если напряжения в твердом теле вызывают деформацию, т. е. совершается работа, то это надо учесть, соответственно изменив уравнение (6.3). Если возможно неограниченное расширение при постоянном давлении, то уравнение (6.3) все еще имеет силу при условии, что с считают равным  т. е. удельной теплоемкости при постоянном давлении. Если же это расширение ограничено, то в уравнении появляются дополнительные члены. Так, в случае напряжений, обусловленных, например, гидростатическим давлением
т. е. удельной теплоемкости при постоянном давлении. Если же это расширение ограничено, то в уравнении появляются дополнительные члены. Так, в случае напряжений, обусловленных, например, гидростатическим давлением  в правую часть уравнения (6.3) следует добавить член
в правую часть уравнения (6.3) следует добавить член

где  абсолютная температура, а— термический коэффициент линейного расширения, а под с в уравнении (6.3) следует понимать
абсолютная температура, а— термический коэффициент линейного расширения, а под с в уравнении (6.3) следует понимать  т. е. теплоемкость при постоянном давлении. Общий случай напряжений разобран в работах [28, 29].
т. е. теплоемкость при постоянном давлении. Общий случай напряжений разобран в работах [28, 29].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ
- § 2. Теплопроводность
- § 3. Тепловой поток через произвольную поверхность
- § 4. Изотермические поверхности
- § 5. Теплопроводность изотропных тел
- § 6. Дифференциальное уравнение теплопроводности для изотропного твердого тела
- § 7. Дифференциальное уравнение теплопроводности для движущейся среды
- § 8. Преобразование координат
- § 9. Начальные и граничные условия
- § 10. Безразмерные параметры
- § 11. Экспериментальные методы определения теплопроводности
- § 12. Математическая интерпретация начальных и граничных условий
- § 13. Родственные дифференциальные уравнения
- § 14. Упрощение общей задачи теплопроводности
- § 15. Задачи, решения которых можно выразить в виде произведения решений более простых задач
- § 16. Единственность решения задачи теплопроводности
- § 17. Теплопроводность анизотропных твердых тел
- § 18. Дифференциальное уравнение теплопроводности для анизотропных твердых тел
- § 19. Теплопроводность тонкой кристаллической пластины
- § 20. Изменение теплопроводности и вектор теплового потока в анизотропных твердых телах
- ГЛАВА II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА. НЕОГРАНИЧЕННОЕ И ПОЛУОГРАНИЧЕННОЕ ТВЕРДОЕ ТЕЛО
- § 2. Неограниченное твердое тело. Решение Лапласа
- § 3. Использование интегралов Фурье и преобразований Фурье
- § 4. Полуограниченное тело с начальной температурой f(x) и нулевой температурой поверхности
- § 5. Полуограниченное твердое тело. Начальная температура равна нулю. Поверхность находится при температуре …
- § 6. Полуограниченное твердое тело. Температура поверхности является гармонической функцией времени
- § 7. Полуограниченное твердое тело. Теплообмен на поверхности в среду с нулевой температурой. Начальная температура постоянна
- § 8. Полуограниченное твердое тело. Теплообмен на поверхности в среду с температурой f(t). Начальная температура равна нулю
- § 9. Полуограниченное тело. Тепловой поток на границе х = 0 является заданной функцией времени. Начальная температура равна нулю
- § 10. Применение полученных результатов к определению теплопроводности
- § 11. Полуограниченное твердое тело, внутри которого находится источник тепла
- § 12. Температура Земли и колебания температуры на ее поверхности
- § 13. Геотермический градиент и поток тепла
- § 14. Возраст Земли. Анализ Кельвина
- § 15. Неограниченное составное твердое тело
- § 16. Случай зависимости термических характеристик вещества от температуры
- ГЛАВА III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ, ОГРАНИЧЕННОМ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
- § 3. Область [0, l]. Границы поддерживаются при нулевой температуре. Начальная температура f(x)
- § 4. Область [0, l] Начальная температура f(x). Границы поддерживаются при постоянной температуре или изолированы
- § 5. Область [0, l]. Температуры границ равны … Начальная температура f(x)
- § 6. Пластина с периодически изменяющейся температурой поверхности
- § 7. Установившаяся периодически изменяющаяся температура в составных пластинах
- § 8. Пластина с заданным тепловым потоком на ее границе
- § 9. Область [0, l]. Теплообмен на границах в среду с температурой, равной нулю. Начальная температура равна f(х)
- § 10. Область [-l, l]. На границах х=+l происходит теплообмен со средой нулевой температуры. Начальная температура f(x)
- § 11. Частные случаи и численные результаты для пластины с граничным условием третьего рода
- § 12. Область [-l, l] с нулевой начальной температурой и теплообменом на границах со средой, имеющей температуру …
- § 13. Пластина, одна из поверхностей которой соприкасается со слоем идеального проводника или хорошо перемешиваемой жидкости
- § 14. Пластина с внутренним источником тепла
- ГЛАВА IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ
- § 3. Полуограниченный стержень. Случай установившейся температуры. Метод Форбса
- § 4. Полуограниченный стержень. Периодически изменяющаяся температура. Метод Ангстрема [5—10]
- § 5. Ограниченный стержень, концы которого находятся при фиксированных температурах. Случай установившейся температуры
- § 6. Стержень переменного сечения с охлаждающимися ребрами. Случай установившейся температуры
- § 7. Ограниченный стержень при наличии теплообмена на его поверхности. Случай неустановившейся температуры
- § 8. Ограниченный стержень с периодически изменяющейся температурой концов. Метод Неймана
- § 9. Задачи по теплопроводности в движущемся стержне
- § 10. Уравнение теплопроводности для тонкой проволоки, нагреваемой постоянным электрическим током
- § 11. Установившаяся температура. Определение коэффициента теплопроводности
- § 12. Сильно нагретая проволока, по которой протекает электрический ток
- § 13. Установившийся поток тепла в составной проволоке
- § 14. Неустановившаяся температура в проволоке, по которой течет электрический ток
- § 15. Кольцо Фурье
- ГЛАВА V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
- § 2. Неограниченное твердое тело прямоугольного сечения. Установившаяся температура
- § 3. Установившаяся температура в неограниченном теле прямоугольного сечения
- § 4. Тонкая пластина с прямоугольным сечением при наличии теплообмена на ее поверхности
- § 5. Установившаяся температура в теле прямоугольного сечения при наличии источника тепла
- § 6. Неустановившееся состояние. Решение в виде произведения решений
- § 7. Неустановившееся состояние. Произвольные начальные и граничные условия
- ГЛАВА VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ
- § 2. Установившаяся температура
- § 3. Двойные и кратные ряды Фурье
- § 4. Неустановившаяся температура. Решение в виде произведения решений
- § 5. Определение коэффициента теплопроводности и экстраполяция кривых охлаждения
- § 6. Неустановившаяся температура. Тройной ряд Фурье
- ГЛАВА VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ КРУГОВОГО СЕЧЕНИЯ
- § 2. Установившаяся температура. Радиальный поток
- § 3. Установившаяся, периодически изменяющаяся температура в круговых цилиндрах [19—22]
- § 4. Неограниченный цилиндр. Радиальный поток. Неустановившаяся температура
- § 5. Интегралы …
- § 6. Неограниченный цилиндр с температурой поверхности … и начальной температурой f(r)
- § 7. Неограниченный цилиндр с теплообменом на поверхности
- § 8. Неограниченный цилиндр с постоянным потоком тепла на поверхности
- § 9. Неограниченный цилиндр с внутренними источниками тепла
- § 10. Неограниченный полый цилиндр. Радиальный поток
- § 11. Неограниченный цилиндр. Установившаяся температура. Общий случай
- § 12. Неограниченный цилиндр. Неустановившаяся температура. Общий случай
- ГЛАВА VIII. ТЕПЛОВОЙ ПОТОК В ОБЛАСТЯХ, ОГРАНИЧЕННЫХ КООРДИНАТНЫМИ ПОВЕРХНОСТЯМИ ЦИЛИНДРИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ
- § 3. Установившаяся температура в ограниченном и полуограниченном цилиндрах
- § 4. Неустановившееся состояние. Решения в форме произведений
- § 5. Определение теплопроводности вещества в форме цилиндра
- § 6. Ограниченный цилиндр с начальной температурой …
- § 7. Полуограниченный цилиндр
- ГЛАВА IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ
- § 2. Установившаяся температура. Радиальный тепловой поток
- § 3. Шар с начальной температурой f(r) и температурой поверхности …
- § 4. Шар. Начальная температура f(r). На поверхности сферы происходит теплообмен
- § 5. Определение коэффициентов теплопроводности плохих проводников
- § 6. Случай шара, находящегося в контакте с хорошо перемешиваемой жидкостью
- § 7. Шар с заданным тепловым потоком на поверхности
- § 8. Шар, внутри которого выделяется тепло
- § 9. Полый шар
- § 10. Область, ограниченная изнутри сферической поверхностью r=a
- § 11. Шар с начальной температурой … Температура поверхности r=a равна нулю
- § 12. Поверхность шара r=a поддерживается при температуре …
- § 13. Часть шара, вырезаемая конусом … Температура поверхности равна нулю, начальная температура равна …
- § 14. Температура внутри Земли
- ГЛАВА Х. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ К ЗАДАЧАМ С НЕУСТАНОВИВШЕЙСЯ ТЕМПЕРАТУРОЙ
- § 2. Мгновенный точечный источник
- § 3. Мгновенные источники; линейный, плоский и поверхностные цилиндрический и сферический источники
- § 4. Непрерывные и периодические источники
- § 5. Поверхностный нагрев полуограниченной области
- § 6. Выделение тепла в неограниченной среде
- § 7. Движущиеся источники тепла
- § 8. Дублеты
- § 9. Метод последовательных волн
- § 10. Метод изображений. Линейный тепловой поток
- § 11. Применение метода изображений к двумерным и трехмерным задачам
- § 12. Обобщение метода изображений Зоммерфельдом
- ГЛАВА XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ
- § 2. Одномерные случаи плавления и затвердевания. Решение Неймана и его обобщение
- § 3. Область … при других граничных условиях
- § 4. Методы интегрального уравнения. Рассмотрение задач затвердевания, предложенное Лайтфутом
- § 5. Решения в цилиндрических и сферических координатах
- § 6. Осесимметричные задачи о замерзании и плавлении
- ГЛАВА XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЛИНЕЙНОГО ТЕПЛОВОГО ПОТОКА
- § 2. Преобразование Лапласа. Основные свойства
- § 3. Решение уравнения теплопроводности методом преобразования Лапласа
- § 4. Полуограниченная область. Решения, получаемые из таблицы изображений
- § 5. Ограниченная область (0, l). Решения, получаемые из таблицы изображений. Решения для небольших значений времени
- § 6. Ограниченная область (0, l). Применение теоремы обращения
- § 7. Полуограниченная область. Применение теоремы обращения
- § 8. Составные твердые тела
- ГЛАВА XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА
- § 3. Решения, применимые для малых интервалов времени
- § 4. Полый цилиндр
- § 5. Область ограничена изнутри цилиндром кругового сечения r=a
- § 6. Решения, применимые при больших значениях времени
- § 7. Область, ограниченная изнутри круговым цилиндром из идеального проводника
- § 8. Составная цилиндрическая область
- § 9. Шар. Радиальный тепловой поток
- ГЛАВА XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА К РЕШЕНИЮ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 2. Линейный тепловой поток. Полуограниченное твердое тело
- § 3. Линейный тепловой поток в области (0, a)
- § 4. Двумерные задачи. Тела с прямоугольным сечением
- § 5. Прямоугольный параллелепипед
- § 6. Линейный тепловой поток. Составные твердые тела
- § 7. Шар. Радиальный поток тепла
- § 8. Цилиндр. Радиальный тепловой поток
- § 9. Полуограниченное твердое тело. Трехмерные задачи
- § 10. Область, ограниченная двумя параллельными плоскостями
- § 11. Полуограниченное твердое тело с тонкой пленкой на плоскости z=0 из материала, имеющего значительно большую теплопроводность. В точке … расположен единичный мгновенный источник
- § 12. Неограниченное составное твердое тело. В точке действует мгновенный единичный источник
- § 13. Области, ограниченные цилиндрической поверхностью r=a
- § 14 Клин
- § 15. Цилиндрическая область
- § 16. Области, ограниченные сферической поверхностью r=a
- § 17. Конус
- § 18. Непрерывные источники
- ГЛАВА XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 3. Тепловые регенераторы и теплообменники
- § 4. Тепловой поток в слоистых системах
- § 5. Установившийся периодический режим
- § 6. Линейная асимптотика и запаздывание
- § 7. Выделение тепла
- § 8. Система автоматического регулирования температуры
- § 9. Неоднородные тела
- § 11. Прямое применение метода преобразования Лапласа к двумерным и трехмерным задачам
- ГЛАВА XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
- § 2. Источники и стоки при установившейся температуре
- § 3. Установившийся поток к почти плоской поверхности. Топографические поправки для геотермического потока
- § 4. Установившийся тепловой поток в составном теле
- § 5. Практические задачи
- § 6. Использование сопряженных гармонических функций в задачах с установившейся температурой
- § 7. Приложения этого метода [20, 21]
- § 8. Установившийся тепловой поток в многоугольнике
- § 9. Тепловой поток между изотермическими поверхностями
- ГЛАВА XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- § 2. Интегральные преобразования и формулы их обращения
- § 3. Неустановившийся тепловой поток
- § 4. Установившийся тепловой поток
- § 5. Конечные преобразования
- § 6. Последовательные преобразования
- ГЛАВА XVIII. ЧИСЛЕННЫЕ МЕТОДЫ
- § 3. Линейный тепловой поток в неограниченном пространстве
- § 4. Граничные условия
- § 5. Выделение тепла, переменная температуропроводность и скрытая теплота
- § 6. Релаксационные методы
- ПРИЛОЖЕНИЕ 1. КОНТУРНЫЕ ИНТЕГРАЛЫ И ПРОВЕРКА РЕШЕНИЙ, ПОЛУЧЕННЫХ ПРИ ПОМОЩИ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- ПРИЛОЖЕНИЕ 2. ФУНКЦИЯ ОШИБОК И РОДСТВЕННЫЕ ФУНКЦИИ
- ПРИЛОЖЕНИЕ 3. О ФУНКЦИЯХ БЕССЕЛЯ
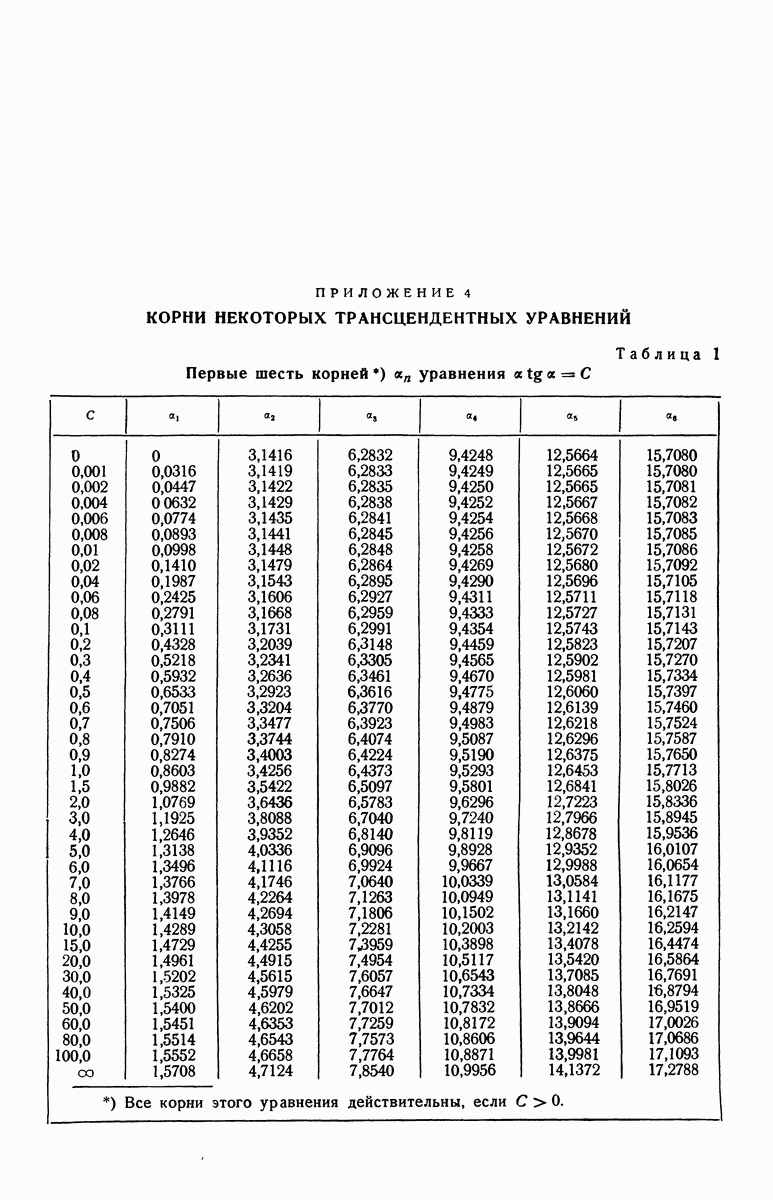
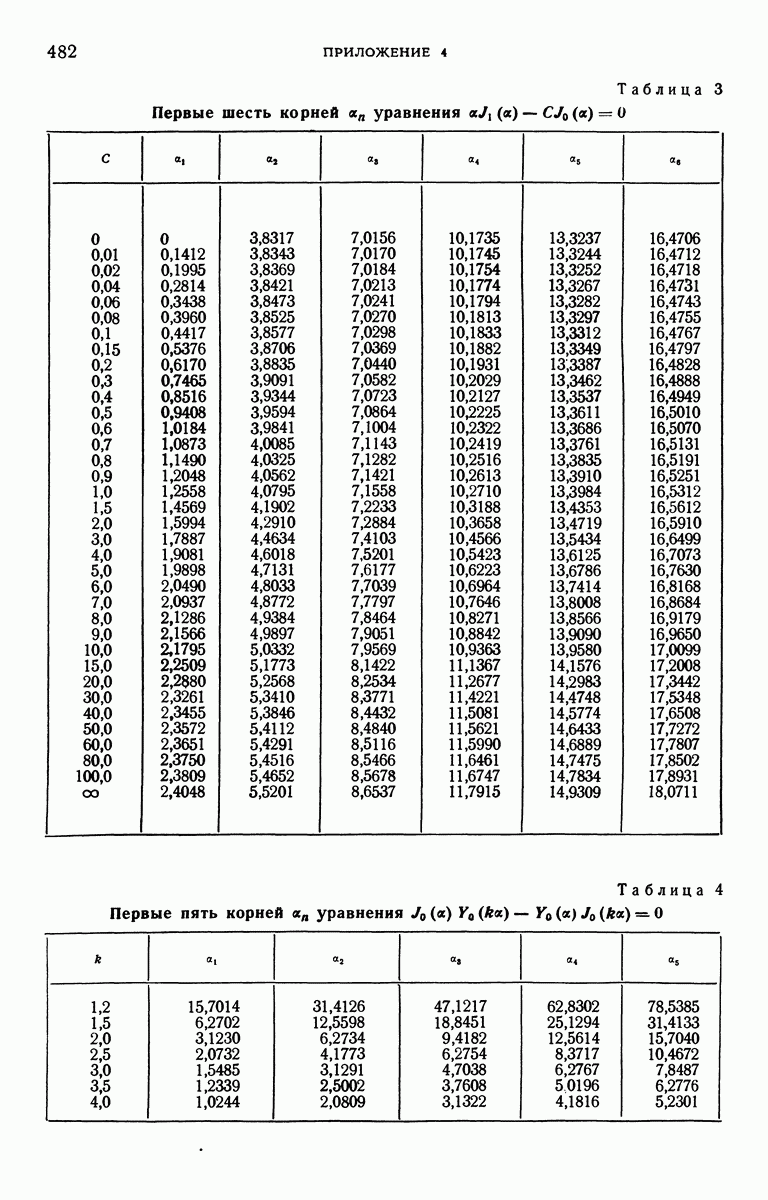
- ПРИЛОЖЕНИЕ 4. КОРНИ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- ПРИЛОЖЕНИЕ 5. ТАБЛИЦА ПРЕОБРАЗОВАНИЙ ЛАПЛАСА …
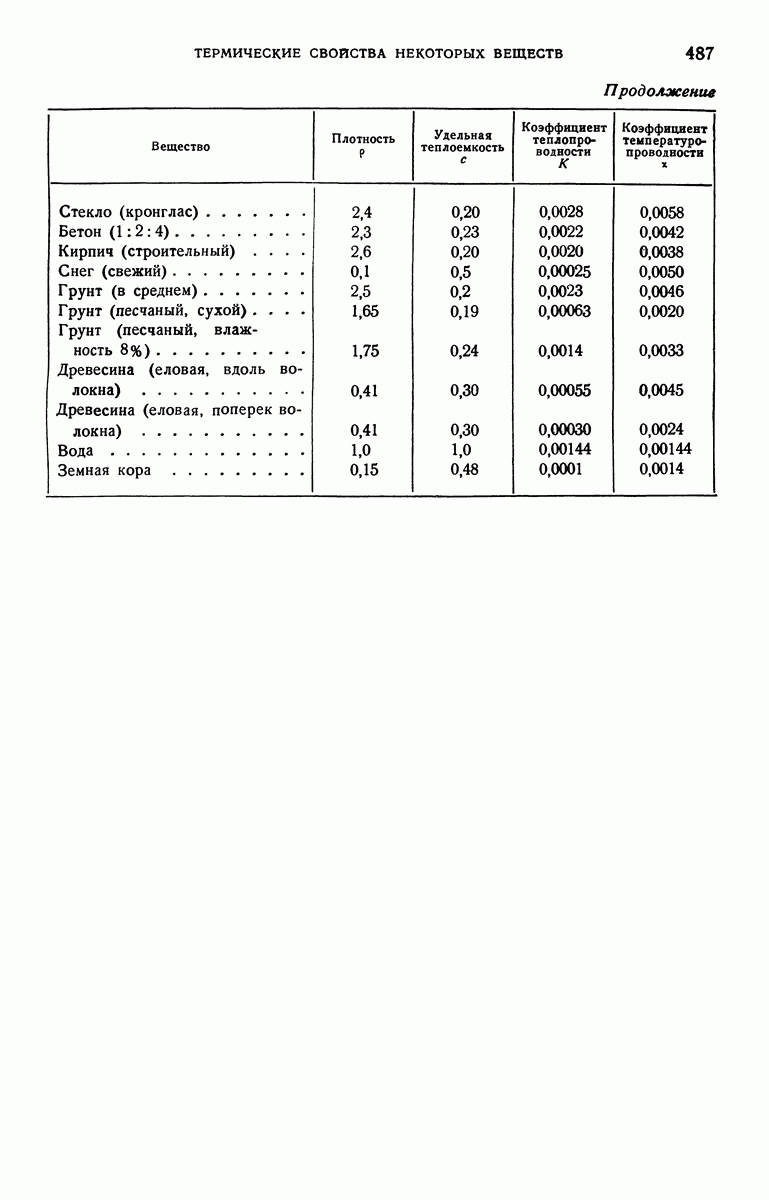
- ПРИЛОЖЕНИЕ 6. ТЕРМИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ВЕЩЕСТВ