| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА Х. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ К ЗАДАЧАМ С НЕУСТАНОВИВШЕЙСЯ ТЕМПЕРАТУРОЙ
§ 1. Введение
Представление о мгновенном точечном источнике тепла, т. е. о конечном количестве тепла, мгновенно выделяемом в определенный момент времени в заданной точке неограниченного тела, оказалось в теории теплопроводности чрезвычайно плодотворным [1]. Одно из больших преимуществ этого метода заключается в том, что он основан на очень простом физическом представлении, что дает возможность получить решение большого числа важных задач, исходя непосредственно из ряда фундаментальных положений. С теоретической точки зрения всегда признавалось, что в случае точечного источника получается фундаментальное решение  встречающееся в теории потенциала, и что полная разработка теории теплопроводности для ограниченных областей может быть достигнута путем построения функций Грина, аналогичных этим функциям в теории потенциала.
встречающееся в теории потенциала, и что полная разработка теории теплопроводности для ограниченных областей может быть достигнута путем построения функций Грина, аналогичных этим функциям в теории потенциала.
Будем называть решение для случая мгновенного точечного источника фундаментальным. Интегрируя по времени, мы получим решение для непрерывного точечного источника, что соответствует случаю выделения заданного количества тепла в данной точке в единицу времени, равного  Если
Если  равно постоянной величине
равно постоянной величине  и выделение тепла продолжается достаточно долго, то в пределе решение совпадает с решением для стационарного точечного источника и соответствует хорошо известным фундаментальным решениям гидродинамики. Задачи со стационарными источниками рассматриваются в гл. XVI.
и выделение тепла продолжается достаточно долго, то в пределе решение совпадает с решением для стационарного точечного источника и соответствует хорошо известным фундаментальным решениям гидродинамики. Задачи со стационарными источниками рассматриваются в гл. XVI.
Интегрируя решения для точечных источников по соответствующим координатам, мы получим решения для мгновенных и непрерывных линейных, плоских, сферических и цилиндрических поверхностных источников, причем каждое имеет свою собственную простую физическую интерпретацию.
Применяя для конечных областей эти решения или соответствующие решения гл. XIX, можно сразу же получить решения многих задач в виде определенных интегралов.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ
- § 2. Теплопроводность
- § 3. Тепловой поток через произвольную поверхность
- § 4. Изотермические поверхности
- § 5. Теплопроводность изотропных тел
- § 6. Дифференциальное уравнение теплопроводности для изотропного твердого тела
- § 7. Дифференциальное уравнение теплопроводности для движущейся среды
- § 8. Преобразование координат
- § 9. Начальные и граничные условия
- § 10. Безразмерные параметры
- § 11. Экспериментальные методы определения теплопроводности
- § 12. Математическая интерпретация начальных и граничных условий
- § 13. Родственные дифференциальные уравнения
- § 14. Упрощение общей задачи теплопроводности
- § 15. Задачи, решения которых можно выразить в виде произведения решений более простых задач
- § 16. Единственность решения задачи теплопроводности
- § 17. Теплопроводность анизотропных твердых тел
- § 18. Дифференциальное уравнение теплопроводности для анизотропных твердых тел
- § 19. Теплопроводность тонкой кристаллической пластины
- § 20. Изменение теплопроводности и вектор теплового потока в анизотропных твердых телах
- ГЛАВА II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА. НЕОГРАНИЧЕННОЕ И ПОЛУОГРАНИЧЕННОЕ ТВЕРДОЕ ТЕЛО
- § 2. Неограниченное твердое тело. Решение Лапласа
- § 3. Использование интегралов Фурье и преобразований Фурье
- § 4. Полуограниченное тело с начальной температурой f(x) и нулевой температурой поверхности
- § 5. Полуограниченное твердое тело. Начальная температура равна нулю. Поверхность находится при температуре …
- § 6. Полуограниченное твердое тело. Температура поверхности является гармонической функцией времени
- § 7. Полуограниченное твердое тело. Теплообмен на поверхности в среду с нулевой температурой. Начальная температура постоянна
- § 8. Полуограниченное твердое тело. Теплообмен на поверхности в среду с температурой f(t). Начальная температура равна нулю
- § 9. Полуограниченное тело. Тепловой поток на границе х = 0 является заданной функцией времени. Начальная температура равна нулю
- § 10. Применение полученных результатов к определению теплопроводности
- § 11. Полуограниченное твердое тело, внутри которого находится источник тепла
- § 12. Температура Земли и колебания температуры на ее поверхности
- § 13. Геотермический градиент и поток тепла
- § 14. Возраст Земли. Анализ Кельвина
- § 15. Неограниченное составное твердое тело
- § 16. Случай зависимости термических характеристик вещества от температуры
- ГЛАВА III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ, ОГРАНИЧЕННОМ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
- § 3. Область [0, l]. Границы поддерживаются при нулевой температуре. Начальная температура f(x)
- § 4. Область [0, l] Начальная температура f(x). Границы поддерживаются при постоянной температуре или изолированы
- § 5. Область [0, l]. Температуры границ равны … Начальная температура f(x)
- § 6. Пластина с периодически изменяющейся температурой поверхности
- § 7. Установившаяся периодически изменяющаяся температура в составных пластинах
- § 8. Пластина с заданным тепловым потоком на ее границе
- § 9. Область [0, l]. Теплообмен на границах в среду с температурой, равной нулю. Начальная температура равна f(х)
- § 10. Область [-l, l]. На границах х=+l происходит теплообмен со средой нулевой температуры. Начальная температура f(x)
- § 11. Частные случаи и численные результаты для пластины с граничным условием третьего рода
- § 12. Область [-l, l] с нулевой начальной температурой и теплообменом на границах со средой, имеющей температуру …
- § 13. Пластина, одна из поверхностей которой соприкасается со слоем идеального проводника или хорошо перемешиваемой жидкости
- § 14. Пластина с внутренним источником тепла
- ГЛАВА IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ
- § 3. Полуограниченный стержень. Случай установившейся температуры. Метод Форбса
- § 4. Полуограниченный стержень. Периодически изменяющаяся температура. Метод Ангстрема [5—10]
- § 5. Ограниченный стержень, концы которого находятся при фиксированных температурах. Случай установившейся температуры
- § 6. Стержень переменного сечения с охлаждающимися ребрами. Случай установившейся температуры
- § 7. Ограниченный стержень при наличии теплообмена на его поверхности. Случай неустановившейся температуры
- § 8. Ограниченный стержень с периодически изменяющейся температурой концов. Метод Неймана
- § 9. Задачи по теплопроводности в движущемся стержне
- § 10. Уравнение теплопроводности для тонкой проволоки, нагреваемой постоянным электрическим током
- § 11. Установившаяся температура. Определение коэффициента теплопроводности
- § 12. Сильно нагретая проволока, по которой протекает электрический ток
- § 13. Установившийся поток тепла в составной проволоке
- § 14. Неустановившаяся температура в проволоке, по которой течет электрический ток
- § 15. Кольцо Фурье
- ГЛАВА V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
- § 2. Неограниченное твердое тело прямоугольного сечения. Установившаяся температура
- § 3. Установившаяся температура в неограниченном теле прямоугольного сечения
- § 4. Тонкая пластина с прямоугольным сечением при наличии теплообмена на ее поверхности
- § 5. Установившаяся температура в теле прямоугольного сечения при наличии источника тепла
- § 6. Неустановившееся состояние. Решение в виде произведения решений
- § 7. Неустановившееся состояние. Произвольные начальные и граничные условия
- ГЛАВА VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ
- § 2. Установившаяся температура
- § 3. Двойные и кратные ряды Фурье
- § 4. Неустановившаяся температура. Решение в виде произведения решений
- § 5. Определение коэффициента теплопроводности и экстраполяция кривых охлаждения
- § 6. Неустановившаяся температура. Тройной ряд Фурье
- ГЛАВА VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ КРУГОВОГО СЕЧЕНИЯ
- § 2. Установившаяся температура. Радиальный поток
- § 3. Установившаяся, периодически изменяющаяся температура в круговых цилиндрах [19—22]
- § 4. Неограниченный цилиндр. Радиальный поток. Неустановившаяся температура
- § 5. Интегралы …
- § 6. Неограниченный цилиндр с температурой поверхности … и начальной температурой f(r)
- § 7. Неограниченный цилиндр с теплообменом на поверхности
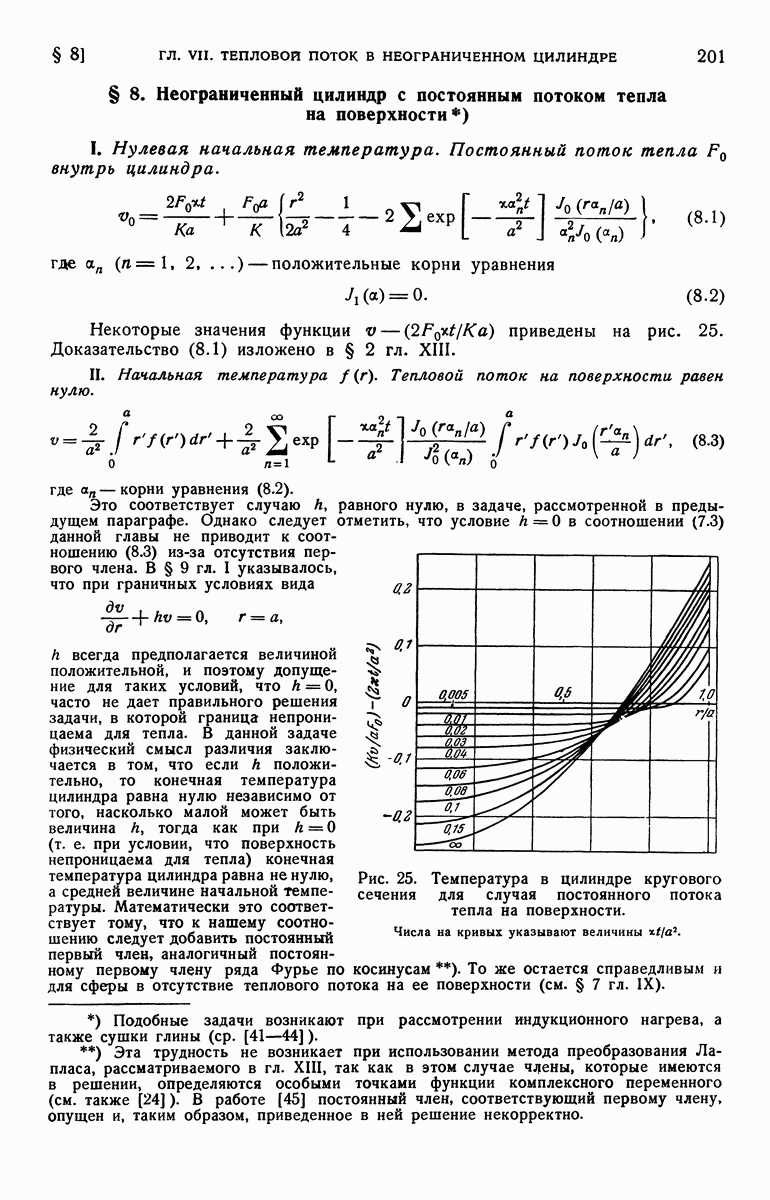
- § 8. Неограниченный цилиндр с постоянным потоком тепла на поверхности
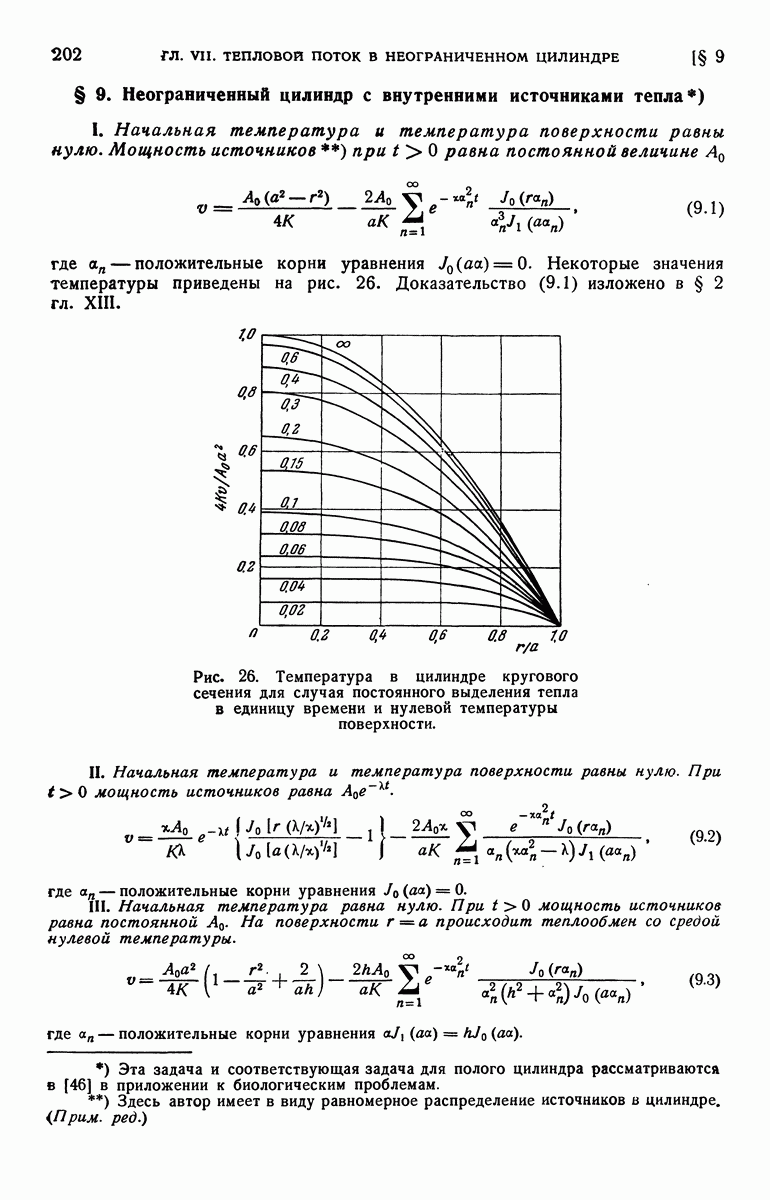
- § 9. Неограниченный цилиндр с внутренними источниками тепла
- § 10. Неограниченный полый цилиндр. Радиальный поток
- § 11. Неограниченный цилиндр. Установившаяся температура. Общий случай
- § 12. Неограниченный цилиндр. Неустановившаяся температура. Общий случай
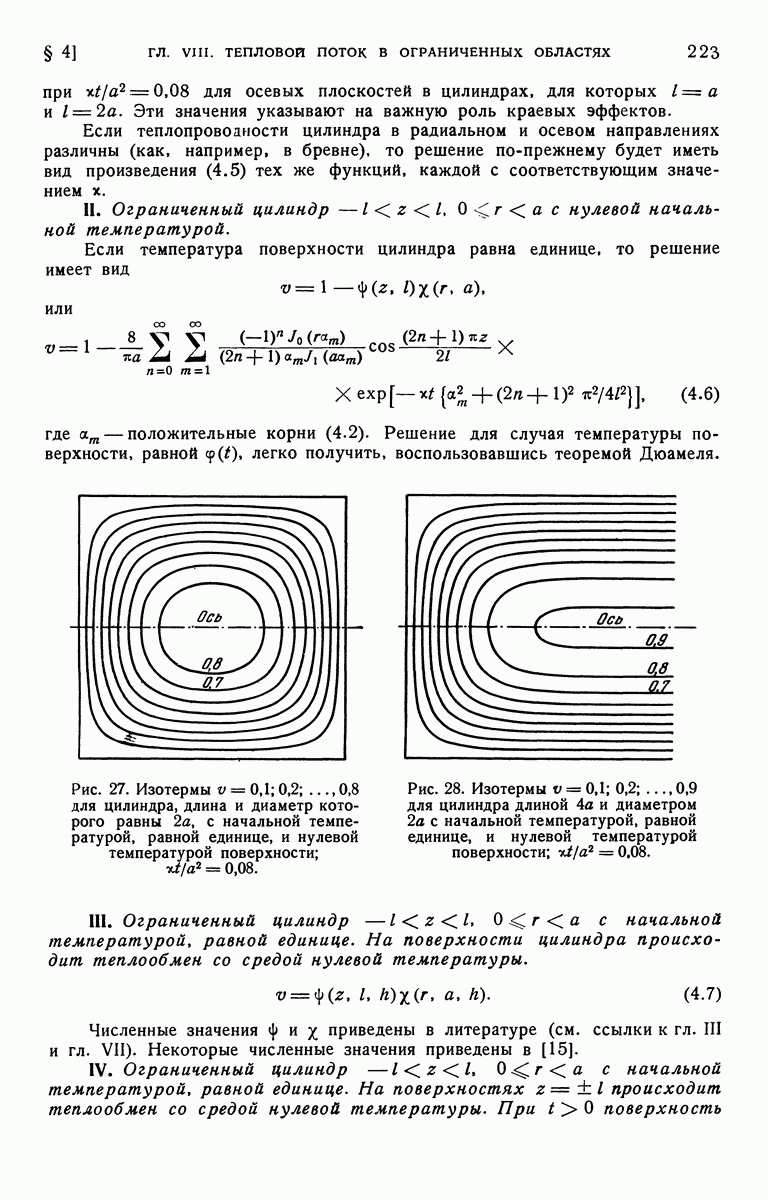
- ГЛАВА VIII. ТЕПЛОВОЙ ПОТОК В ОБЛАСТЯХ, ОГРАНИЧЕННЫХ КООРДИНАТНЫМИ ПОВЕРХНОСТЯМИ ЦИЛИНДРИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ
- § 3. Установившаяся температура в ограниченном и полуограниченном цилиндрах
- § 4. Неустановившееся состояние. Решения в форме произведений
- § 5. Определение теплопроводности вещества в форме цилиндра
- § 6. Ограниченный цилиндр с начальной температурой …
- § 7. Полуограниченный цилиндр
- ГЛАВА IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ
- § 2. Установившаяся температура. Радиальный тепловой поток
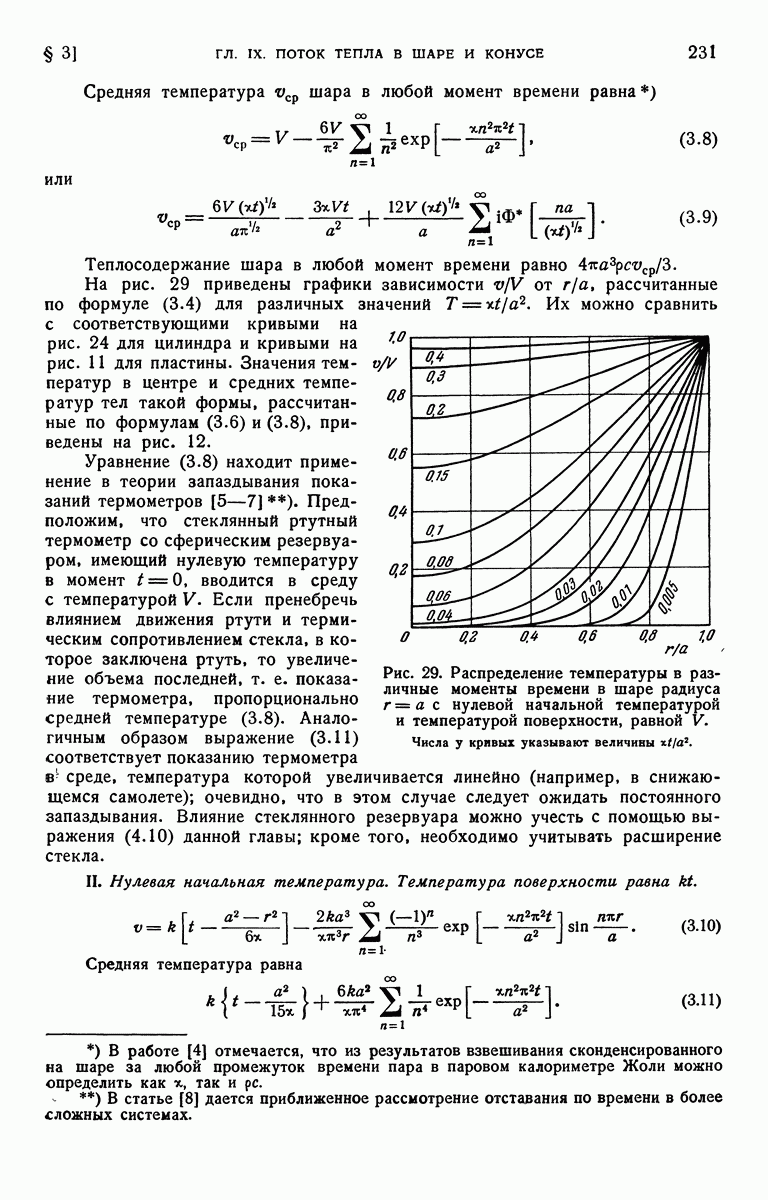
- § 3. Шар с начальной температурой f(r) и температурой поверхности …
- § 4. Шар. Начальная температура f(r). На поверхности сферы происходит теплообмен
- § 5. Определение коэффициентов теплопроводности плохих проводников
- § 6. Случай шара, находящегося в контакте с хорошо перемешиваемой жидкостью
- § 7. Шар с заданным тепловым потоком на поверхности
- § 8. Шар, внутри которого выделяется тепло
- § 9. Полый шар
- § 10. Область, ограниченная изнутри сферической поверхностью r=a
- § 11. Шар с начальной температурой … Температура поверхности r=a равна нулю
- § 12. Поверхность шара r=a поддерживается при температуре …
- § 13. Часть шара, вырезаемая конусом … Температура поверхности равна нулю, начальная температура равна …
- § 14. Температура внутри Земли
- ГЛАВА Х. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ К ЗАДАЧАМ С НЕУСТАНОВИВШЕЙСЯ ТЕМПЕРАТУРОЙ
- § 2. Мгновенный точечный источник
- § 3. Мгновенные источники; линейный, плоский и поверхностные цилиндрический и сферический источники
- § 4. Непрерывные и периодические источники
- § 5. Поверхностный нагрев полуограниченной области
- § 6. Выделение тепла в неограниченной среде
- § 7. Движущиеся источники тепла
- § 8. Дублеты
- § 9. Метод последовательных волн
- § 10. Метод изображений. Линейный тепловой поток
- § 11. Применение метода изображений к двумерным и трехмерным задачам
- § 12. Обобщение метода изображений Зоммерфельдом
- ГЛАВА XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ
- § 2. Одномерные случаи плавления и затвердевания. Решение Неймана и его обобщение
- § 3. Область … при других граничных условиях
- § 4. Методы интегрального уравнения. Рассмотрение задач затвердевания, предложенное Лайтфутом
- § 5. Решения в цилиндрических и сферических координатах
- § 6. Осесимметричные задачи о замерзании и плавлении
- ГЛАВА XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЛИНЕЙНОГО ТЕПЛОВОГО ПОТОКА
- § 2. Преобразование Лапласа. Основные свойства
- § 3. Решение уравнения теплопроводности методом преобразования Лапласа
- § 4. Полуограниченная область. Решения, получаемые из таблицы изображений
- § 5. Ограниченная область (0, l). Решения, получаемые из таблицы изображений. Решения для небольших значений времени
- § 6. Ограниченная область (0, l). Применение теоремы обращения
- § 7. Полуограниченная область. Применение теоремы обращения
- § 8. Составные твердые тела
- ГЛАВА XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА
- § 3. Решения, применимые для малых интервалов времени
- § 4. Полый цилиндр
- § 5. Область ограничена изнутри цилиндром кругового сечения r=a
- § 6. Решения, применимые при больших значениях времени
- § 7. Область, ограниченная изнутри круговым цилиндром из идеального проводника
- § 8. Составная цилиндрическая область
- § 9. Шар. Радиальный тепловой поток
- ГЛАВА XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА К РЕШЕНИЮ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 2. Линейный тепловой поток. Полуограниченное твердое тело
- § 3. Линейный тепловой поток в области (0, a)
- § 4. Двумерные задачи. Тела с прямоугольным сечением
- § 5. Прямоугольный параллелепипед
- § 6. Линейный тепловой поток. Составные твердые тела
- § 7. Шар. Радиальный поток тепла
- § 8. Цилиндр. Радиальный тепловой поток
- § 9. Полуограниченное твердое тело. Трехмерные задачи
- § 10. Область, ограниченная двумя параллельными плоскостями
- § 11. Полуограниченное твердое тело с тонкой пленкой на плоскости z=0 из материала, имеющего значительно большую теплопроводность. В точке … расположен единичный мгновенный источник
- § 12. Неограниченное составное твердое тело. В точке действует мгновенный единичный источник
- § 13. Области, ограниченные цилиндрической поверхностью r=a
- § 14 Клин
- § 15. Цилиндрическая область
- § 16. Области, ограниченные сферической поверхностью r=a
- § 17. Конус
- § 18. Непрерывные источники
- ГЛАВА XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 3. Тепловые регенераторы и теплообменники
- § 4. Тепловой поток в слоистых системах
- § 5. Установившийся периодический режим
- § 6. Линейная асимптотика и запаздывание
- § 7. Выделение тепла
- § 8. Система автоматического регулирования температуры
- § 9. Неоднородные тела
- § 11. Прямое применение метода преобразования Лапласа к двумерным и трехмерным задачам
- ГЛАВА XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
- § 2. Источники и стоки при установившейся температуре
- § 3. Установившийся поток к почти плоской поверхности. Топографические поправки для геотермического потока
- § 4. Установившийся тепловой поток в составном теле
- § 5. Практические задачи
- § 6. Использование сопряженных гармонических функций в задачах с установившейся температурой
- § 7. Приложения этого метода [20, 21]
- § 8. Установившийся тепловой поток в многоугольнике
- § 9. Тепловой поток между изотермическими поверхностями
- ГЛАВА XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- § 2. Интегральные преобразования и формулы их обращения
- § 3. Неустановившийся тепловой поток
- § 4. Установившийся тепловой поток
- § 5. Конечные преобразования
- § 6. Последовательные преобразования
- ГЛАВА XVIII. ЧИСЛЕННЫЕ МЕТОДЫ
- § 3. Линейный тепловой поток в неограниченном пространстве
- § 4. Граничные условия
- § 5. Выделение тепла, переменная температуропроводность и скрытая теплота
- § 6. Релаксационные методы
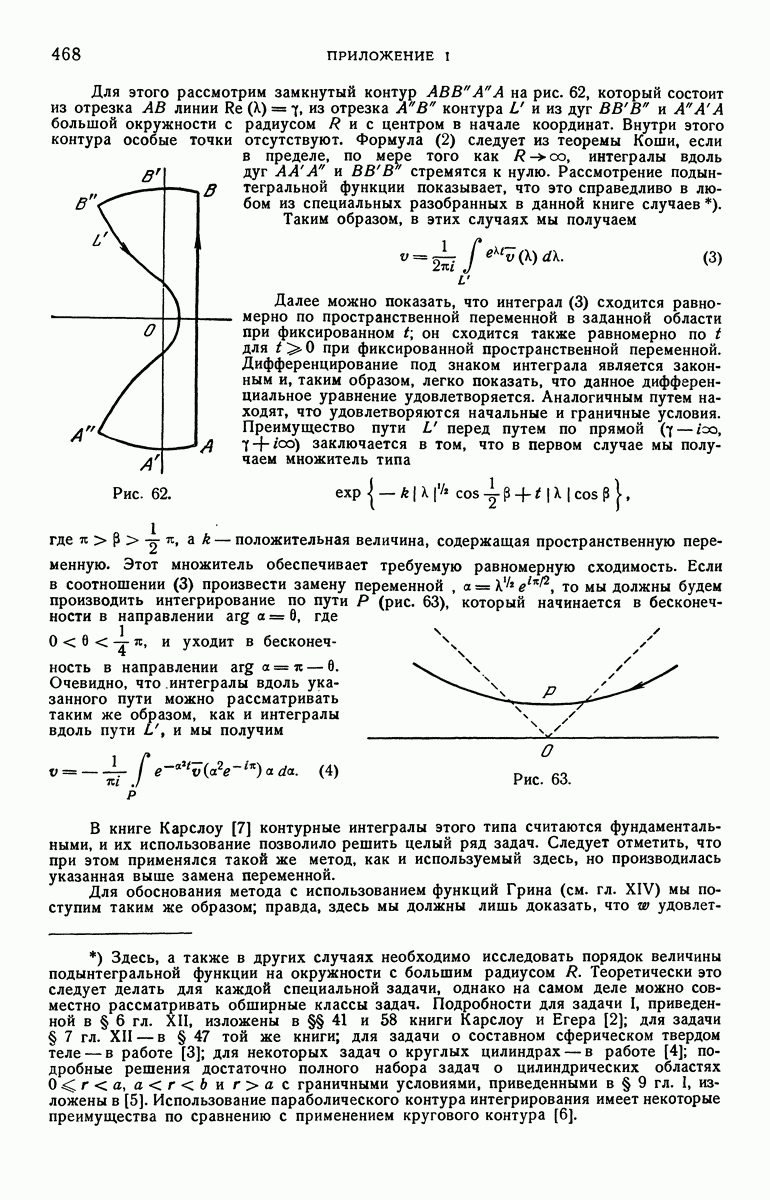
- ПРИЛОЖЕНИЕ 1. КОНТУРНЫЕ ИНТЕГРАЛЫ И ПРОВЕРКА РЕШЕНИЙ, ПОЛУЧЕННЫХ ПРИ ПОМОЩИ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
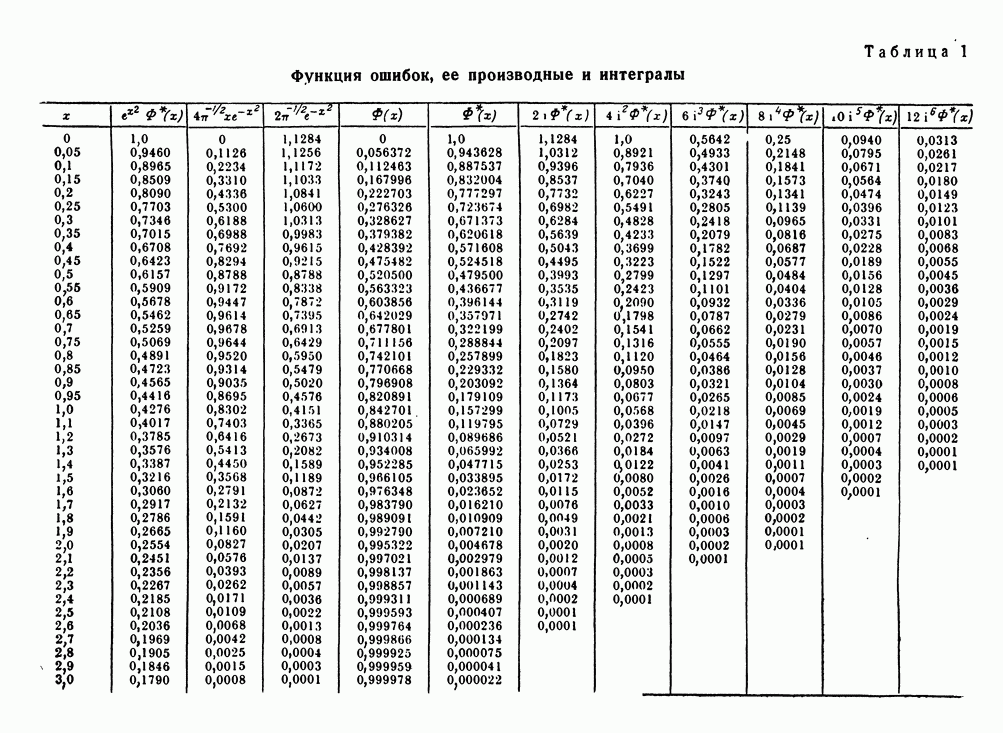
- ПРИЛОЖЕНИЕ 2. ФУНКЦИЯ ОШИБОК И РОДСТВЕННЫЕ ФУНКЦИИ
- ПРИЛОЖЕНИЕ 3. О ФУНКЦИЯХ БЕССЕЛЯ
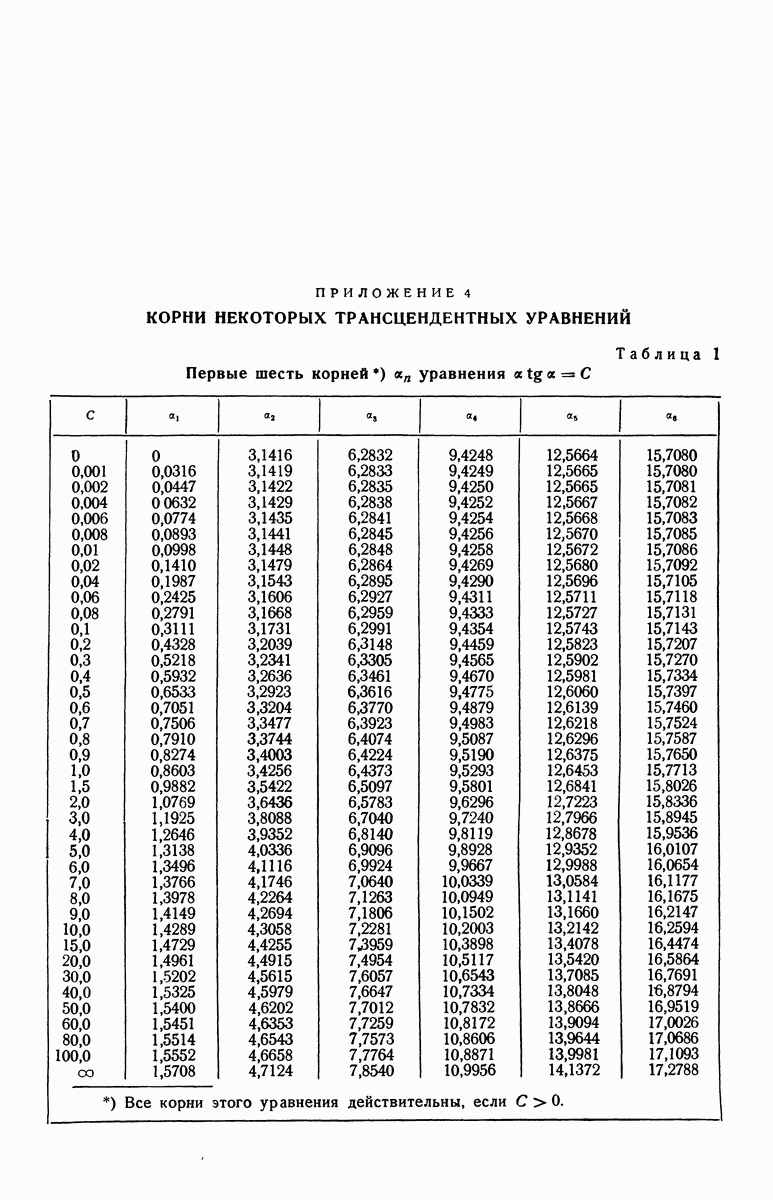
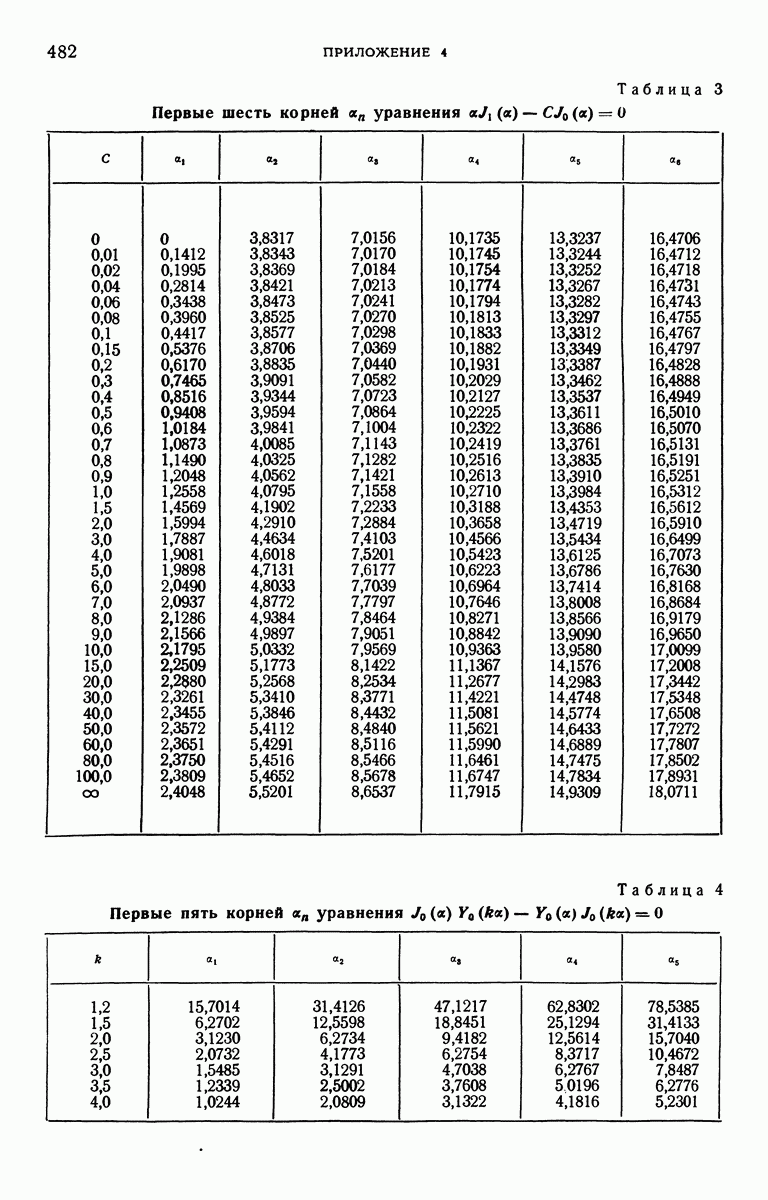
- ПРИЛОЖЕНИЕ 4. КОРНИ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- ПРИЛОЖЕНИЕ 5. ТАБЛИЦА ПРЕОБРАЗОВАНИЙ ЛАПЛАСА …
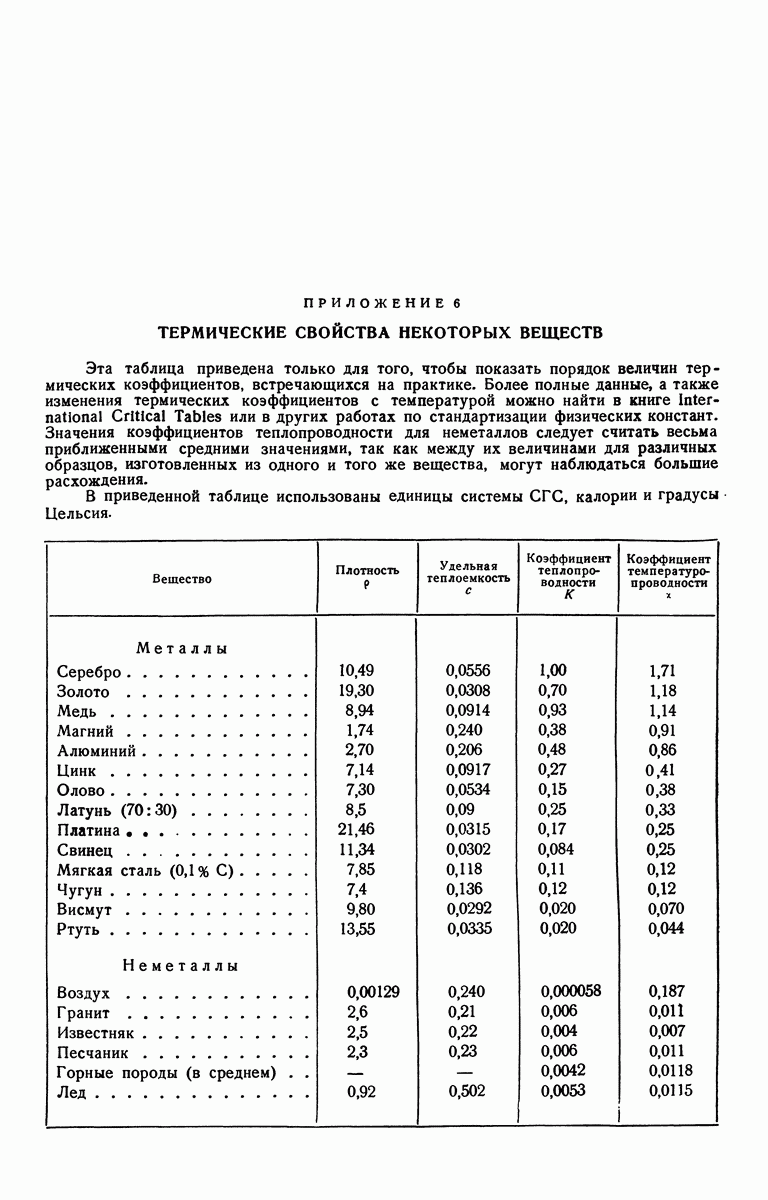
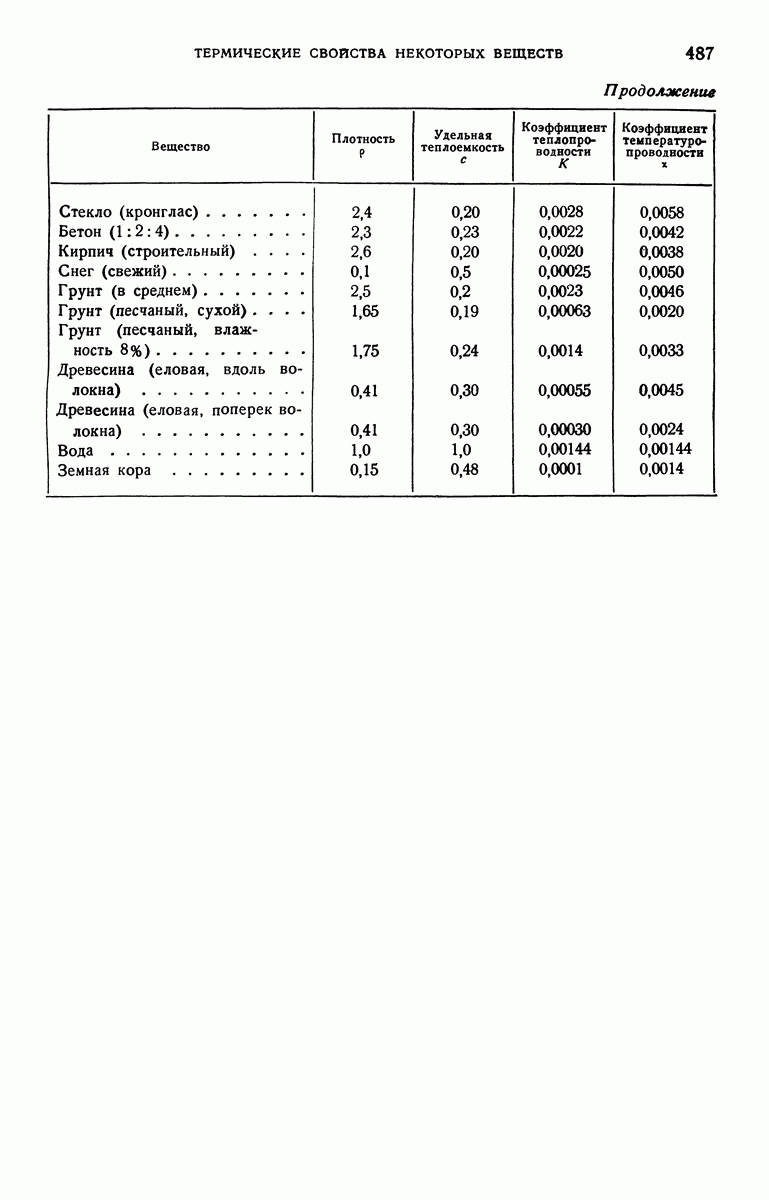
- ПРИЛОЖЕНИЕ 6. ТЕРМИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ВЕЩЕСТВ