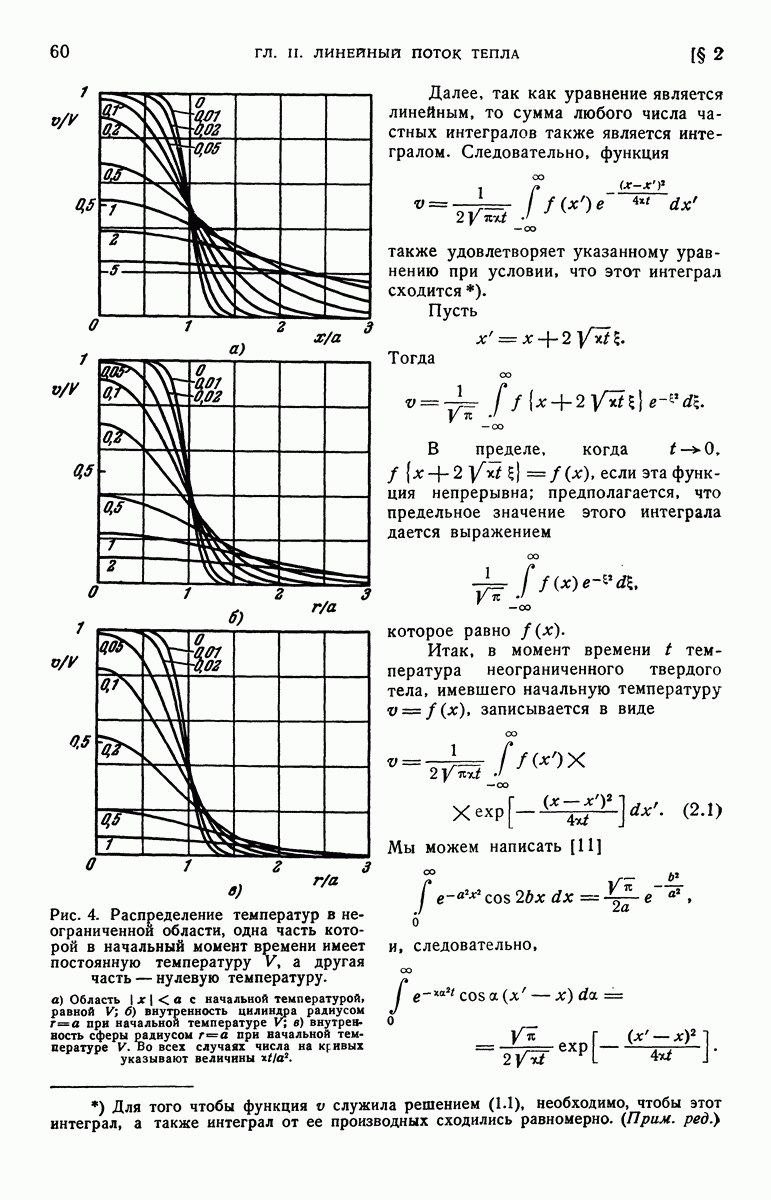
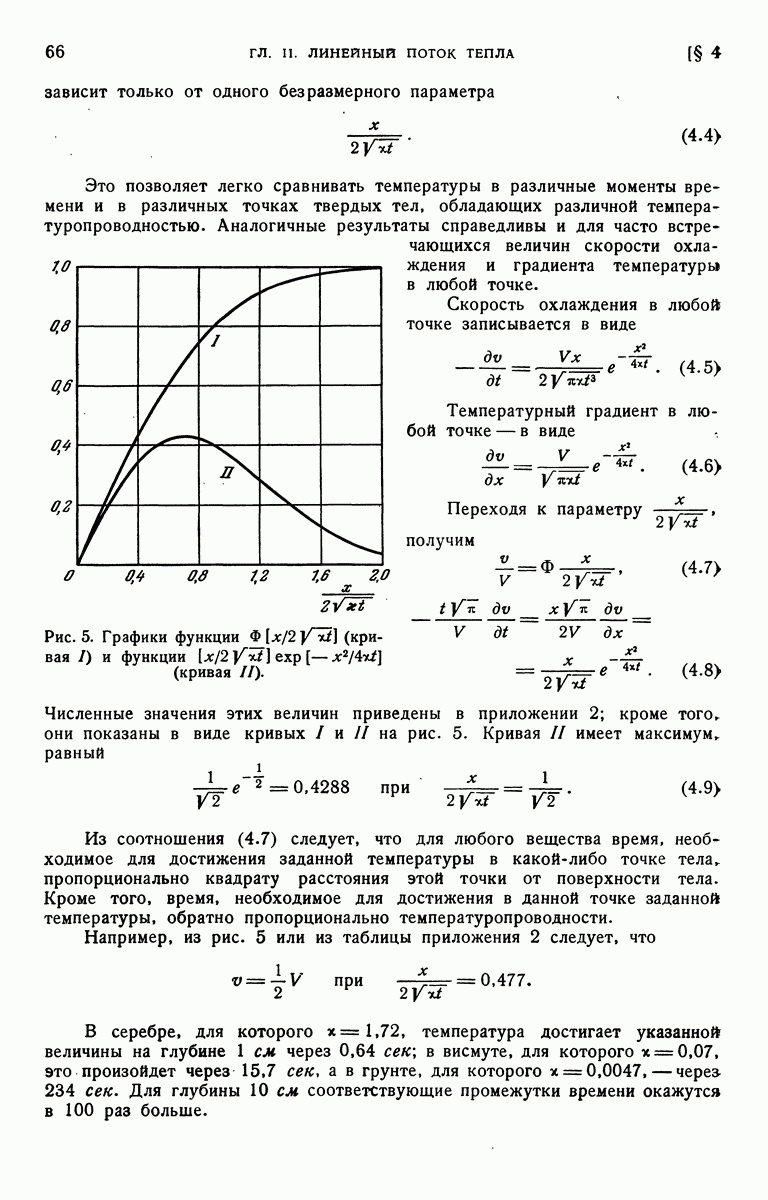
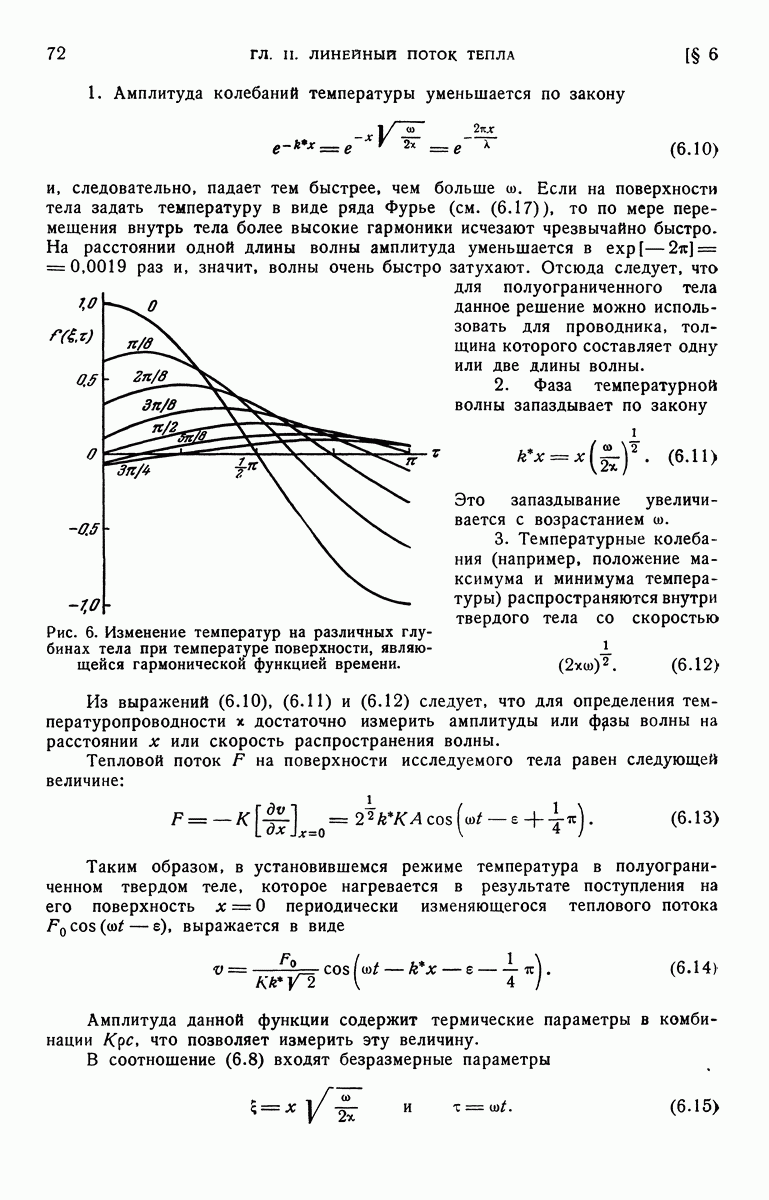
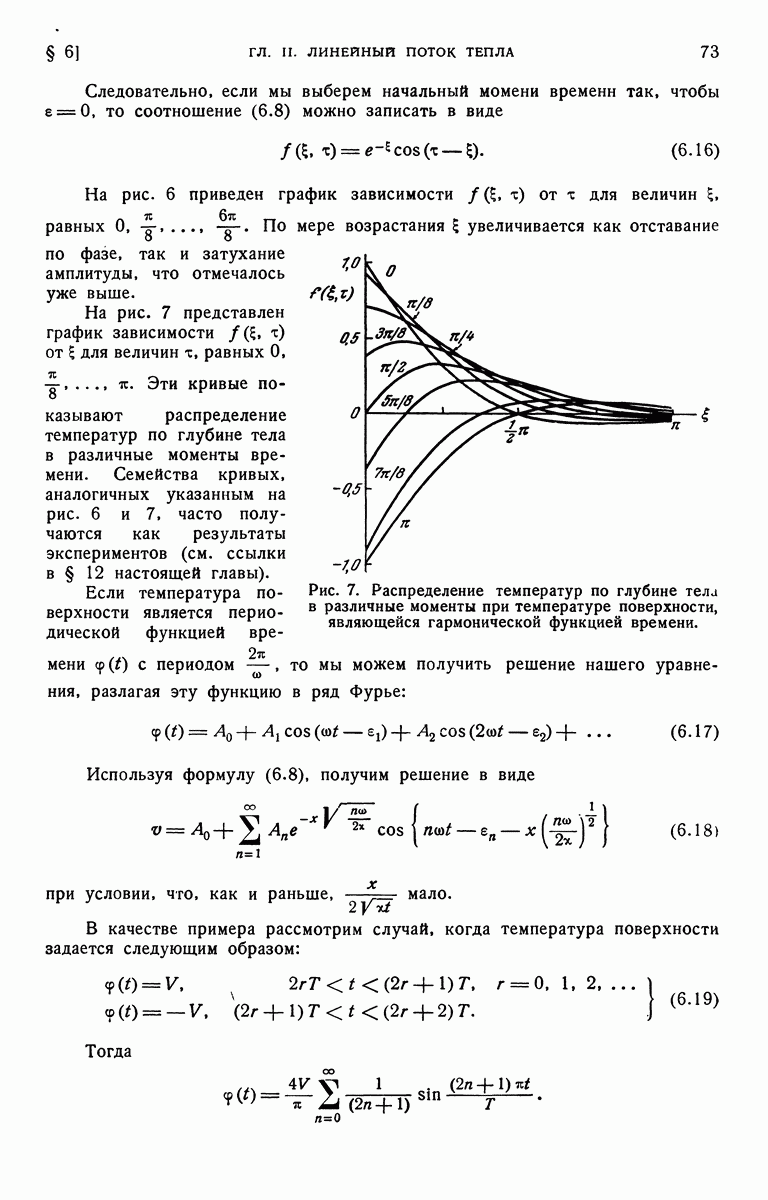
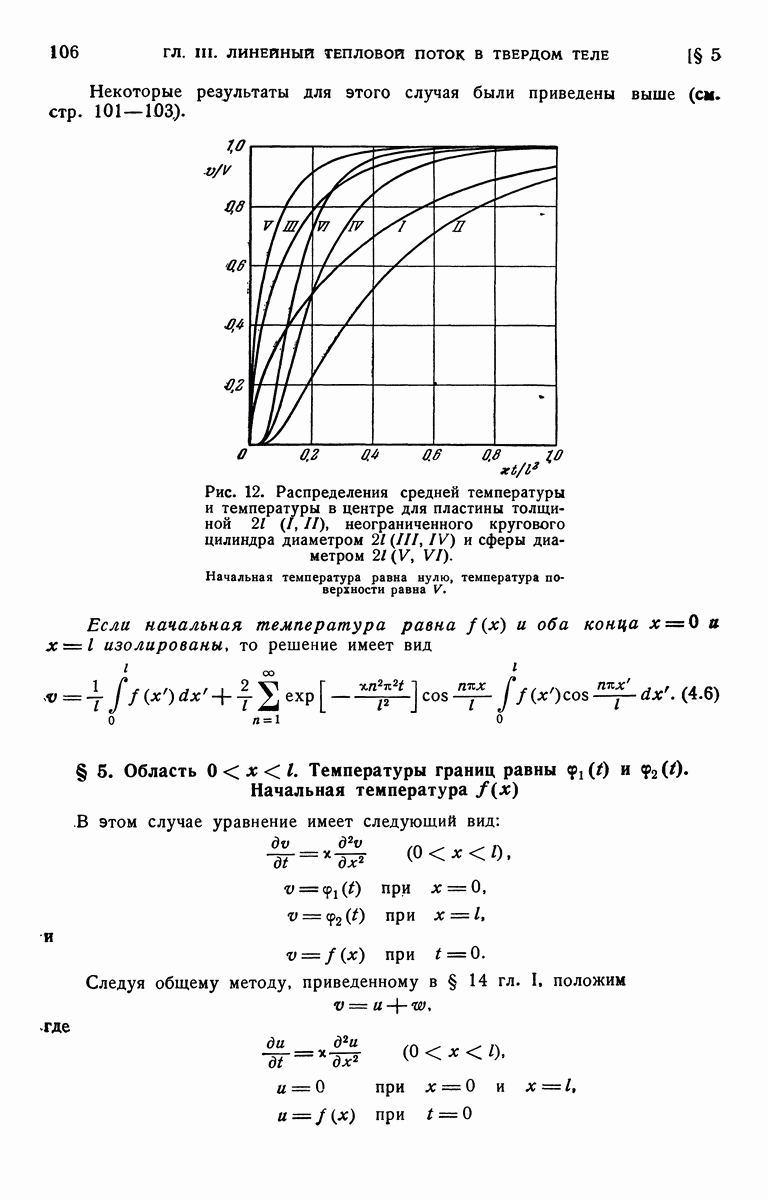
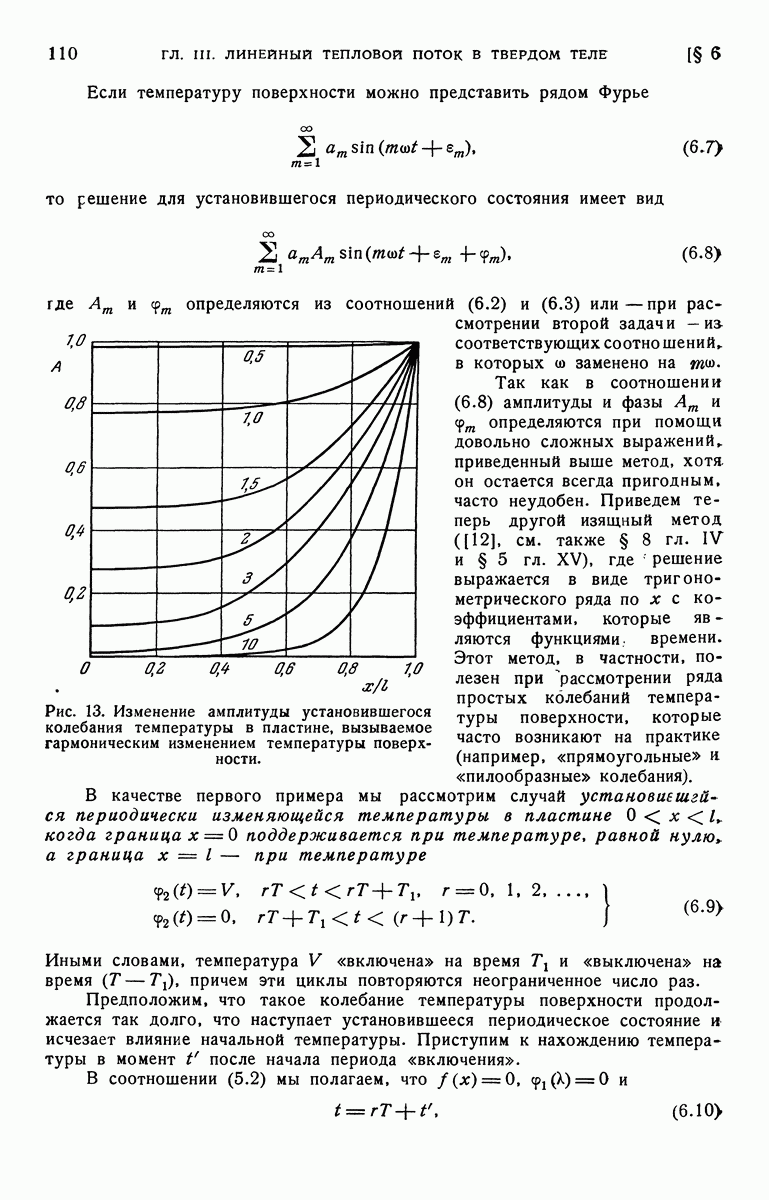
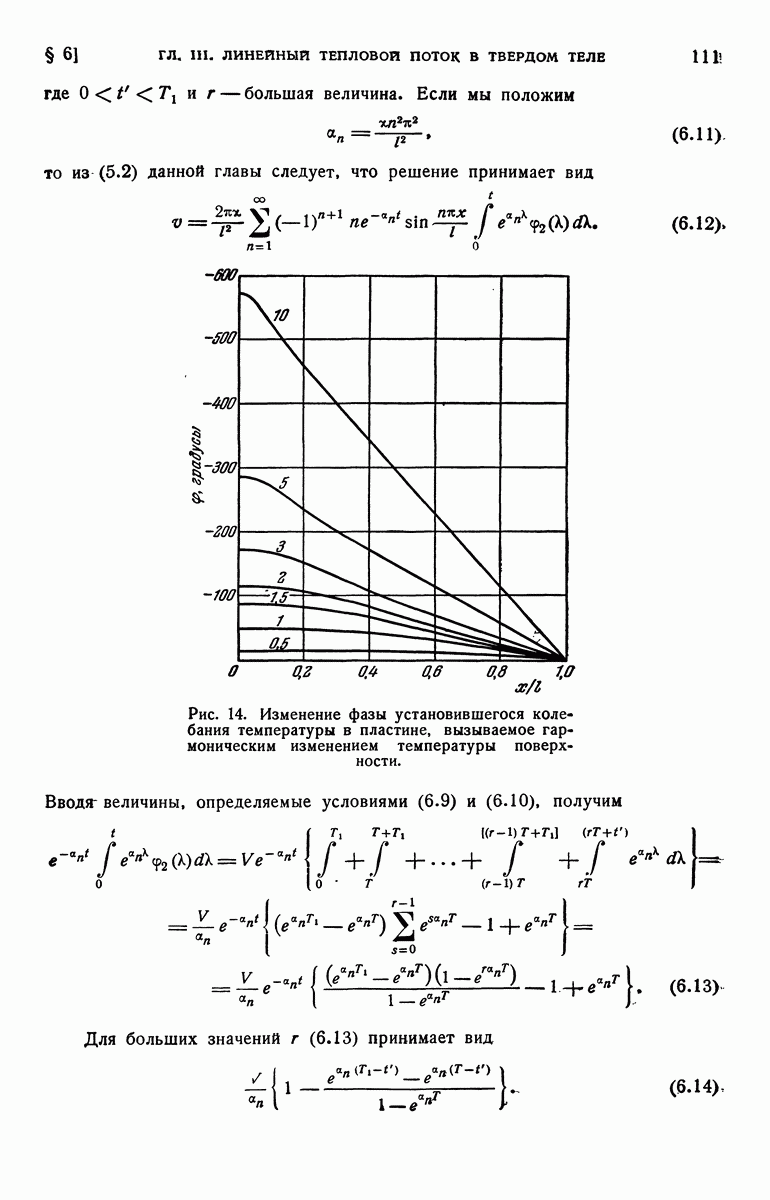
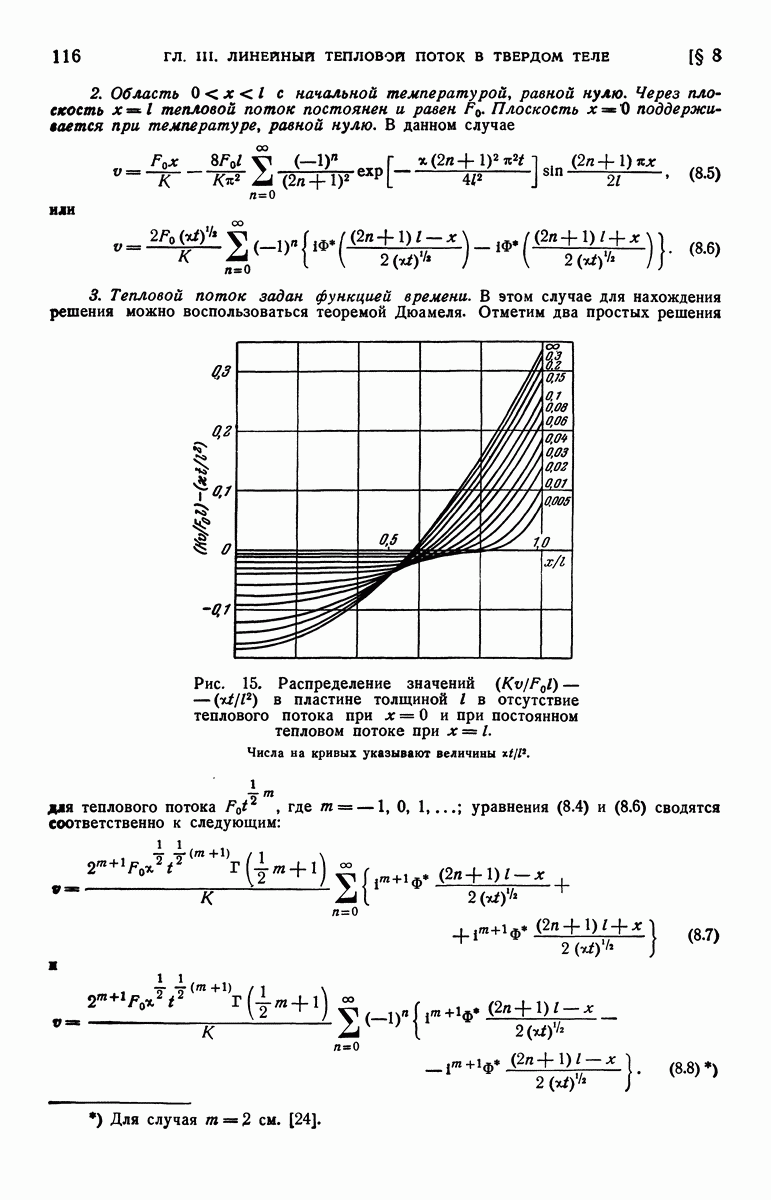
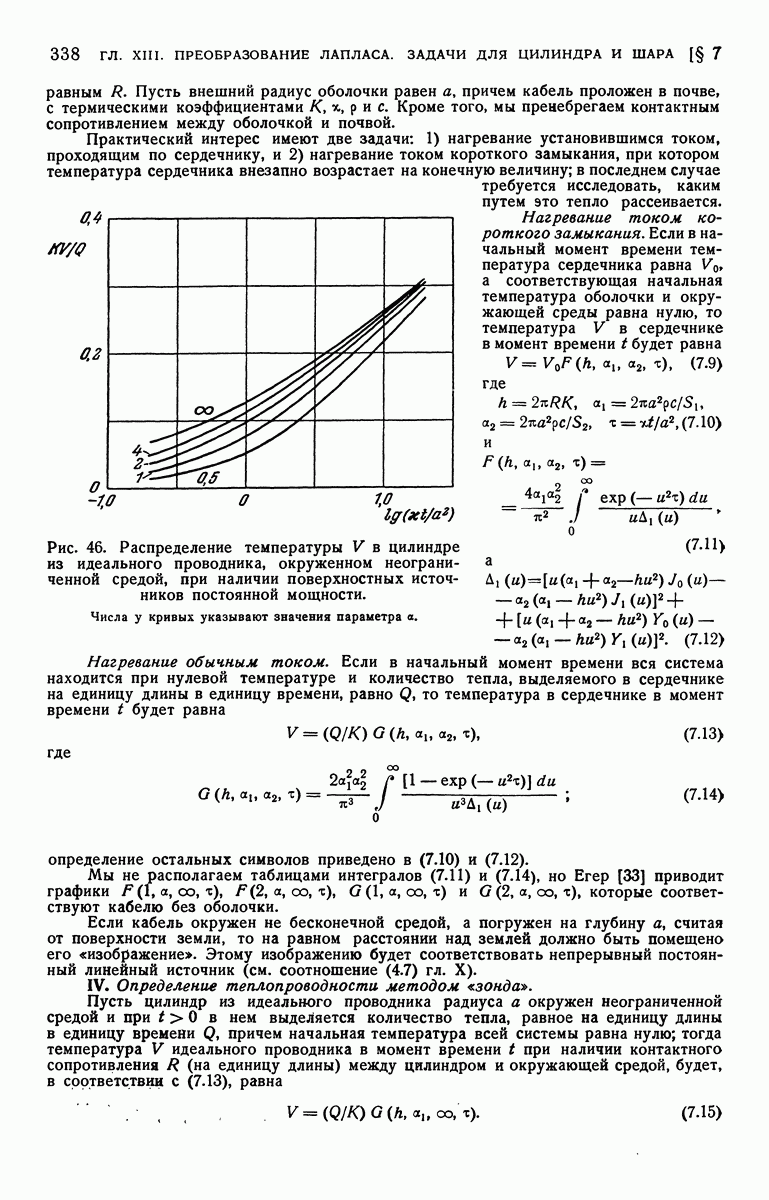
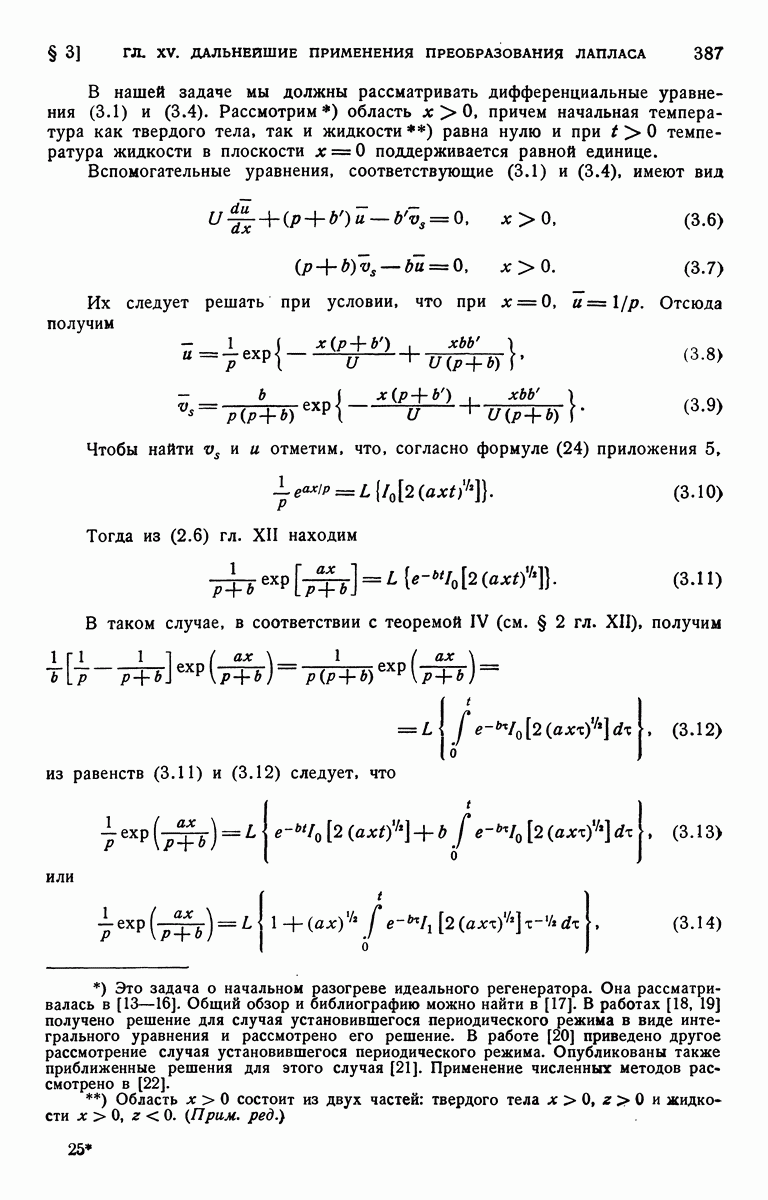| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
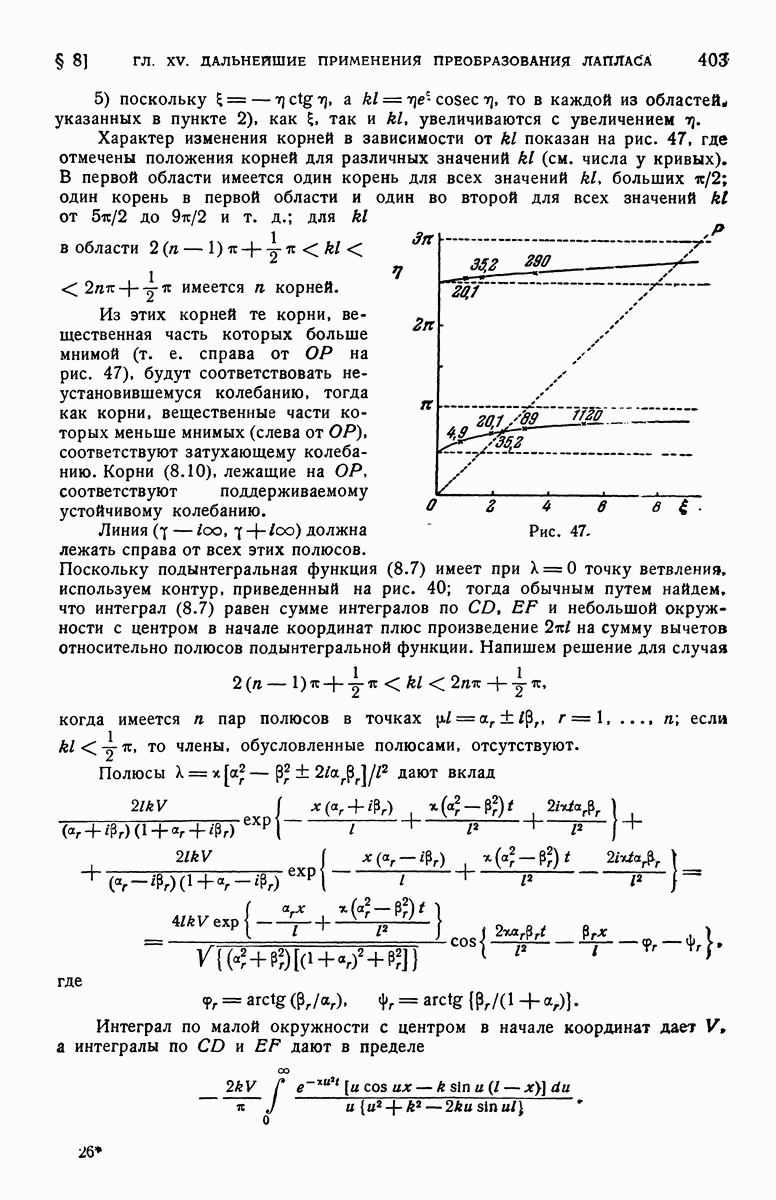
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. Решение уравнения теплопроводности методом преобразования Лапласа
Предположим, что нам надо решить следующее уравнение для линейного потока тепла:

при условиях

Применим к уравнению (3.1) преобразование Лапласа, т. е. умножим обе его части на  и проинтегрируем по
и проинтегрируем по  в пределах от
в пределах от  до
до  Это дает
Это дает

Используя соотношения (2.2) и (2.3) предыдущего параграфа, получим

Таким образом, преобразование Лапласа свело дифференциальное уравнение с частными производными к обыкновенному дифференциальному уравнению (3.5). Полученное этим путем уравнение для  мы всегда будем называть вспомогательным уравнением. Преобразуя аналогичным образом граничные условия (3.3) и (3.4), получим
мы всегда будем называть вспомогательным уравнением. Преобразуя аналогичным образом граничные условия (3.3) и (3.4), получим

Изображение  (т. е. преобразование Лапласа
(т. е. преобразование Лапласа  решения задачи известно, если решено вспомогательное уравнение (3.5) при граничных
решения задачи известно, если решено вспомогательное уравнение (3.5) при граничных
условиях (3.6) и (3.7). Перед тем как перейти к методам нахождения  из
из  следует отметить, что более общие дифференциальные уравнения (например, уравнение (10.5) гл. IV) и более общие граничные условия (например (9.14) гл. I) приводят точно таким же путем к обыкновенному дифференциальному уравнению с граничными условиями при
следует отметить, что более общие дифференциальные уравнения (например, уравнение (10.5) гл. IV) и более общие граничные условия (например (9.14) гл. I) приводят точно таким же путем к обыкновенному дифференциальному уравнению с граничными условиями при  следовательно, к величине
следовательно, к величине 
Если мы имеем более одной пространственной переменной, например если дифференциальное уравнение

нужно решать в некоторой области с начальным условием  и заданными граничными условиями, то найденное описанным выше путем вспомогательное уравнение имеет вид
и заданными граничными условиями, то найденное описанным выше путем вспомогательное уравнение имеет вид

т. е. остается дифференциальным уравнением в частных производных, но с тремя переменными вместо четырех.
Предположим теперь, что вспомогательное уравнение решено при соответствующих граничных условиях и, следовательно, известна зависимость  от
от  (и пространственных переменных). Тогда требуется по
(и пространственных переменных). Тогда требуется по  найти
найти  как функцию времени, что и будет служить решением исходной задачи.
как функцию времени, что и будет служить решением исходной задачи.
Проще всего найти  по таблице изображений и подобрать соответствующую функцию от
по таблице изображений и подобрать соответствующую функцию от  Таким путем очень просто можно решить целый ряд задач с линейным потоком. Соответствующие примеры приведены в двух следующих параграфах.
Таким путем очень просто можно решить целый ряд задач с линейным потоком. Соответствующие примеры приведены в двух следующих параграфах.
Если изображения  в таблице нет, то
в таблице нет, то  определяется из
определяется из  при помощи теоремы обращения преобразования Лапласа. Согласно этой теореме
при помощи теоремы обращения преобразования Лапласа. Согласно этой теореме

где у должна быть настолько большой величиной, чтобы все особые точки  лежали слева от линии
лежали слева от линии  В соотношении (3.8) мы заменили
В соотношении (3.8) мы заменили  на
на  для того, чтобы подчеркнуть, что в этом соотношении мы рассматриваем поведение функции
для того, чтобы подчеркнуть, что в этом соотношении мы рассматриваем поведение функции  считая ее функцией комплексного переменного, тогда как ранее
считая ее функцией комплексного переменного, тогда как ранее  вообще не должно было быть комплексной величиной.
вообще не должно было быть комплексной величиной.
Соотношение (3.8) будет справедливым только в том случае, если функции  или
или  удовлетворяют определенным условиям; однако здесь нет необходимости рассматривать ни эти условия, ни доказательство самой теоремы, поскольку в ходе изложения были сделаны другие предположения, например, что
удовлетворяют определенным условиям; однако здесь нет необходимости рассматривать ни эти условия, ни доказательство самой теоремы, поскольку в ходе изложения были сделаны другие предположения, например, что  имеет изображение, что последовательность операций дифференцирования и интегрирования в соотношении (2.3) предыдущего параграфа можно изменить и т. д. Таким образом, с точки зрения чистой математики необходимо проверить, удовлетворяет ли полученное решение дифференциальному уравнению и начальному и граничному условиям данной задачи. Эту проверку
имеет изображение, что последовательность операций дифференцирования и интегрирования в соотношении (2.3) предыдущего параграфа можно изменить и т. д. Таким образом, с точки зрения чистой математики необходимо проверить, удовлетворяет ли полученное решение дифференциальному уравнению и начальному и граничному условиям данной задачи. Эту проверку
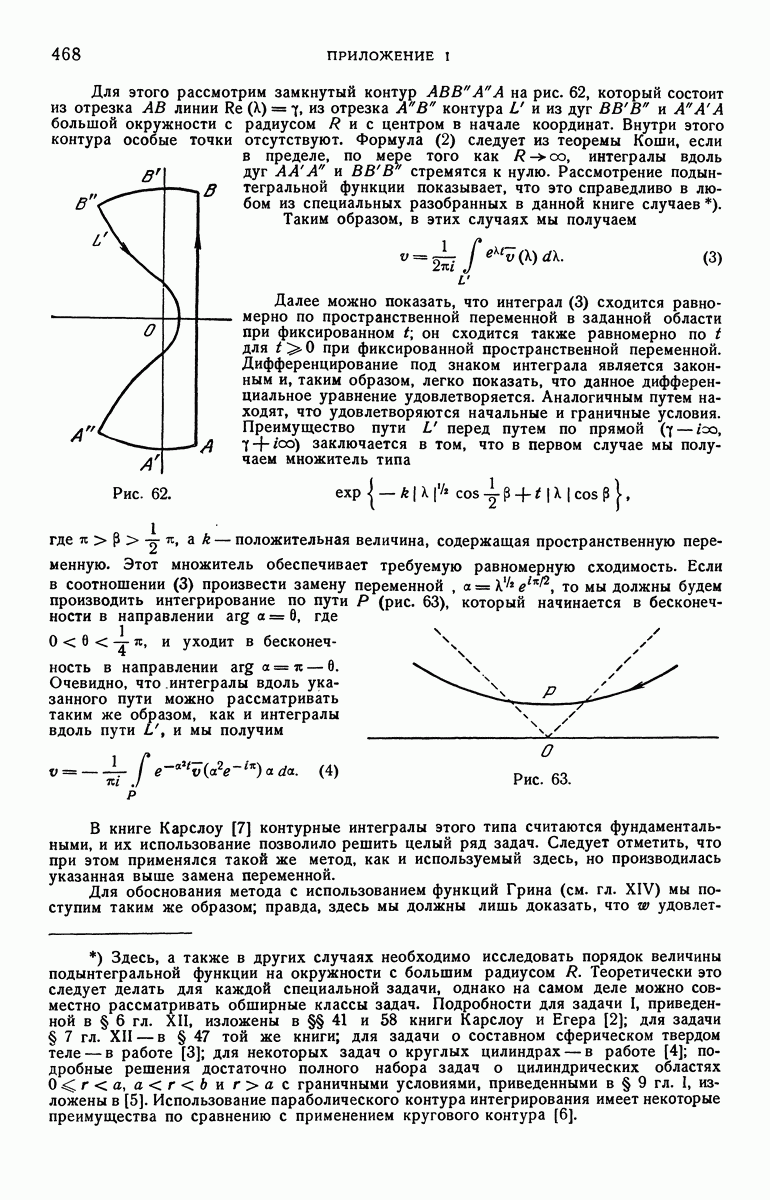
проще всего выполнить при помощи контурного интеграла (3.8). Метод проверки рассматривается в приложении 1. Все полученные здесь решения можно проверить приведенным там способом.
После нахождения решения в виде контурного интеграла (3.8), его обычно можно привести к вещественному виду одним из двух стандартных методов.
1). Если  является однозначной функцией
является однозначной функцией  с рядом полюсов, лежащих вдоль отрицательной вещественной оси (возможны и другие полюсы), мы замыкаем контур большой окружностью
с рядом полюсов, лежащих вдоль отрицательной вещественной оси (возможны и другие полюсы), мы замыкаем контур большой окружностью  с радиусом
с радиусом  не проходящей ни через один полюс подынтегральной функции (рис. 39).
не проходящей ни через один полюс подынтегральной функции (рис. 39).
Во всех рассматриваемых здесь задачах можно показать, что интеграл по большой окружности  при
при  в пределе равен нулю (дальнейшее изложение этого вопроса дано в приложении 1). Таким образом, согласно теореме Коши, интеграл (3.8) равен в пределе произведению
в пределе равен нулю (дальнейшее изложение этого вопроса дано в приложении 1). Таким образом, согласно теореме Коши, интеграл (3.8) равен в пределе произведению  на сумму вычетов относительно полюсов его подынтегральной функции. Этот случай обычно встречается в задачах теплопроводности в ограниченных областях.
на сумму вычетов относительно полюсов его подынтегральной функции. Этот случай обычно встречается в задачах теплопроводности в ограниченных областях.

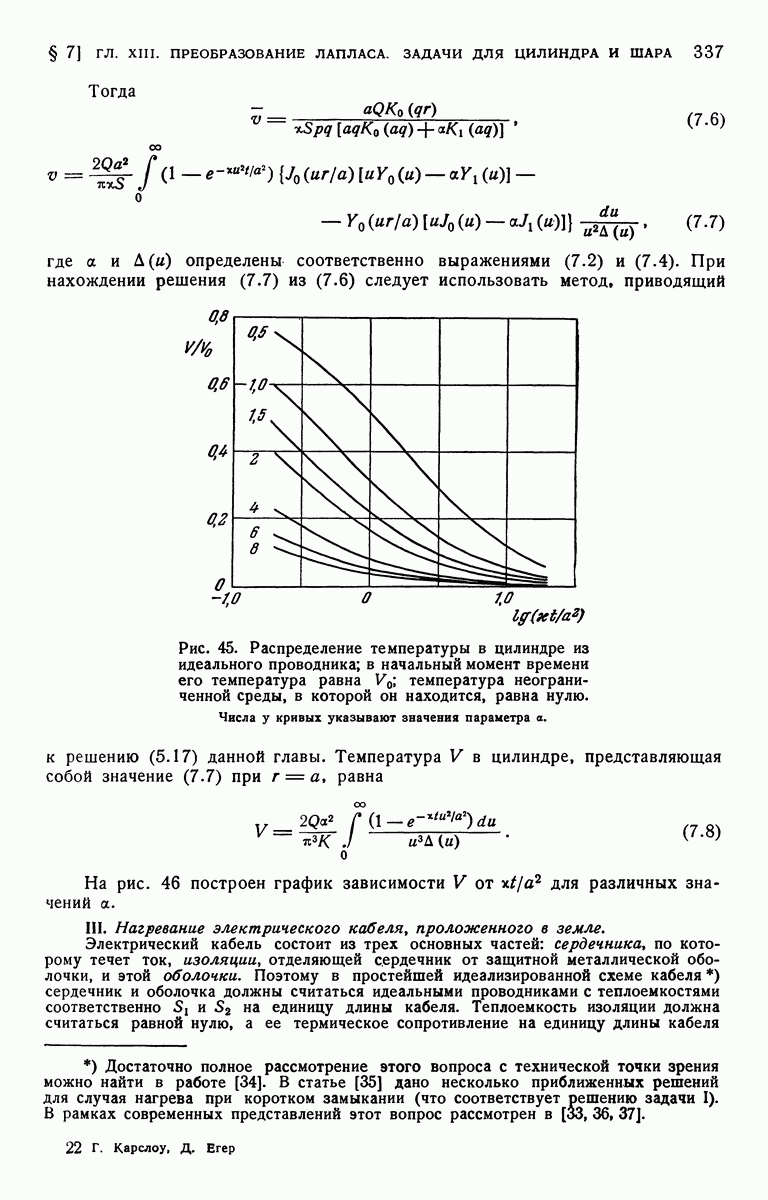
Рис. 39.

Рис. 40.
2) В задачах теплопроводности для полуограниченных областей  обычно имеет точку ветвления при
обычно имеет точку ветвления при  . В таких случаях используется контур, показанный на рис.
. В таких случаях используется контур, показанный на рис.  с «разрезом» вдоль отрицательной вещественной оси, так что
с «разрезом» вдоль отрицательной вещественной оси, так что  является однозначной функцией
является однозначной функцией  на контуре и внутри него. Можно показать, что в пределе, по мере стремления радиуса большой окружности к бесконечности, интеграл по контуру стремится к нулю, и интеграл (3.8) заменяется двумя несобственными интегралами по отрицательной вещественной полуоси, полученными из интегралов вдоль
на контуре и внутри него. Можно показать, что в пределе, по мере стремления радиуса большой окружности к бесконечности, интеграл по контуру стремится к нулю, и интеграл (3.8) заменяется двумя несобственными интегралами по отрицательной вещественной полуоси, полученными из интегралов вдоль  и
и  возможно, что к ним добавляется вклад от интеграла по малой окружности с центром в начале координат, а также вклады от любых полюсов подынтегральной функции.
возможно, что к ним добавляется вклад от интеграла по малой окружности с центром в начале координат, а также вклады от любых полюсов подынтегральной функции.
Если функция  не принадлежит ни к одному из указанных выше типов, то для ее рассмотрения должны быть разработаны специальные методы.
не принадлежит ни к одному из указанных выше типов, то для ее рассмотрения должны быть разработаны специальные методы.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ
- § 2. Теплопроводность
- § 3. Тепловой поток через произвольную поверхность
- § 4. Изотермические поверхности
- § 5. Теплопроводность изотропных тел
- § 6. Дифференциальное уравнение теплопроводности для изотропного твердого тела
- § 7. Дифференциальное уравнение теплопроводности для движущейся среды
- § 8. Преобразование координат
- § 9. Начальные и граничные условия
- § 10. Безразмерные параметры
- § 11. Экспериментальные методы определения теплопроводности
- § 12. Математическая интерпретация начальных и граничных условий
- § 13. Родственные дифференциальные уравнения
- § 14. Упрощение общей задачи теплопроводности
- § 15. Задачи, решения которых можно выразить в виде произведения решений более простых задач
- § 16. Единственность решения задачи теплопроводности
- § 17. Теплопроводность анизотропных твердых тел
- § 18. Дифференциальное уравнение теплопроводности для анизотропных твердых тел
- § 19. Теплопроводность тонкой кристаллической пластины
- § 20. Изменение теплопроводности и вектор теплового потока в анизотропных твердых телах
- ГЛАВА II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА. НЕОГРАНИЧЕННОЕ И ПОЛУОГРАНИЧЕННОЕ ТВЕРДОЕ ТЕЛО
- § 2. Неограниченное твердое тело. Решение Лапласа
- § 3. Использование интегралов Фурье и преобразований Фурье
- § 4. Полуограниченное тело с начальной температурой f(x) и нулевой температурой поверхности
- § 5. Полуограниченное твердое тело. Начальная температура равна нулю. Поверхность находится при температуре …
- § 6. Полуограниченное твердое тело. Температура поверхности является гармонической функцией времени
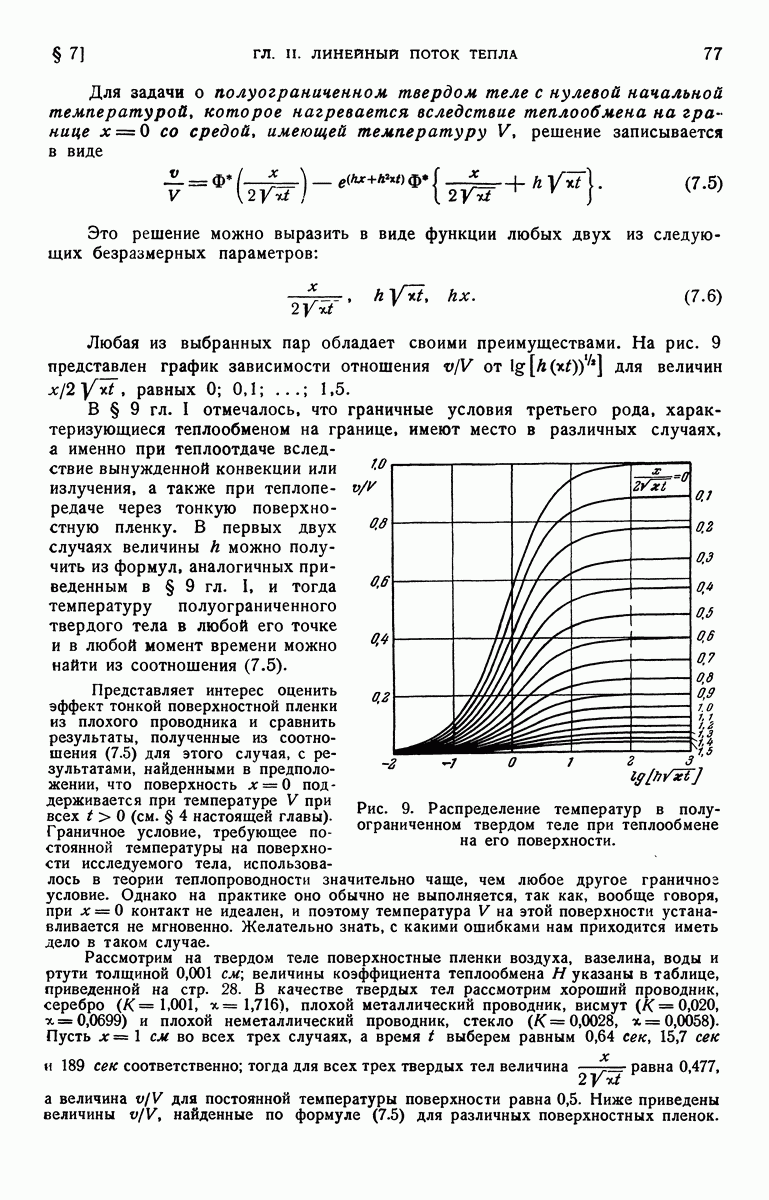
- § 7. Полуограниченное твердое тело. Теплообмен на поверхности в среду с нулевой температурой. Начальная температура постоянна
- § 8. Полуограниченное твердое тело. Теплообмен на поверхности в среду с температурой f(t). Начальная температура равна нулю
- § 9. Полуограниченное тело. Тепловой поток на границе х = 0 является заданной функцией времени. Начальная температура равна нулю
- § 10. Применение полученных результатов к определению теплопроводности
- § 11. Полуограниченное твердое тело, внутри которого находится источник тепла
- § 12. Температура Земли и колебания температуры на ее поверхности
- § 13. Геотермический градиент и поток тепла
- § 14. Возраст Земли. Анализ Кельвина
- § 15. Неограниченное составное твердое тело
- § 16. Случай зависимости термических характеристик вещества от температуры
- ГЛАВА III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ, ОГРАНИЧЕННОМ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
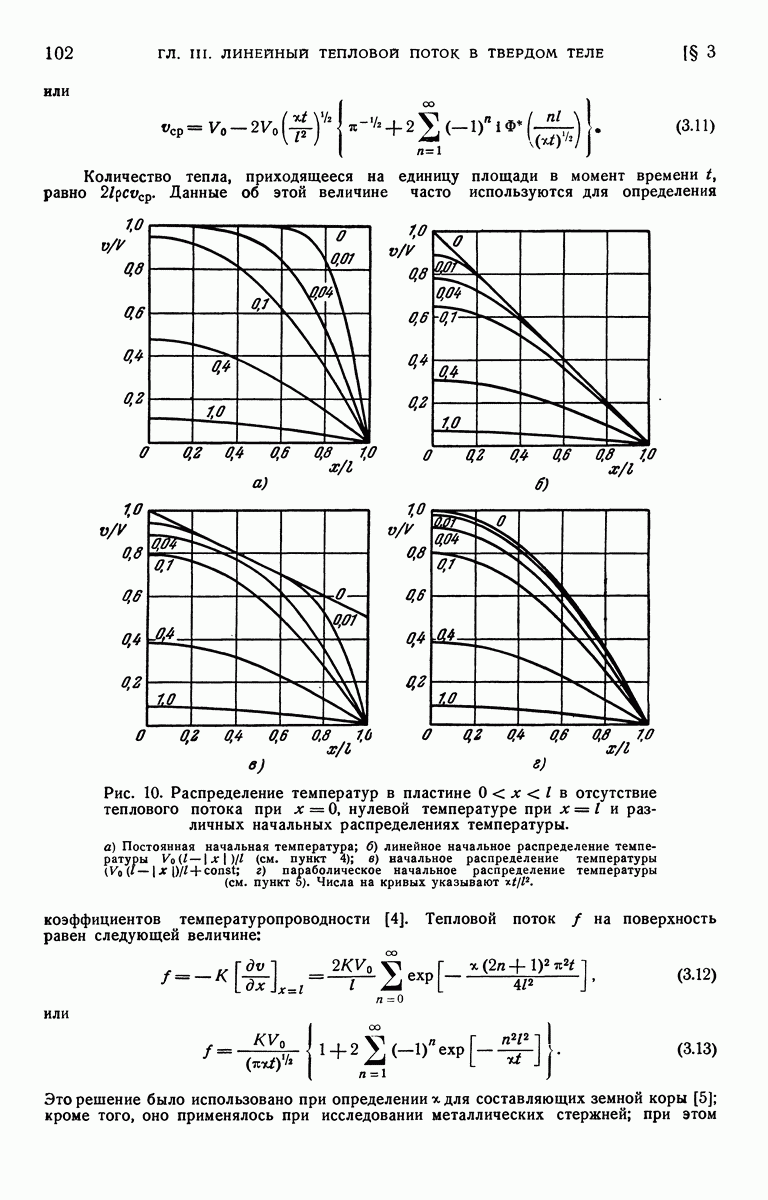
- § 3. Область [0, l]. Границы поддерживаются при нулевой температуре. Начальная температура f(x)
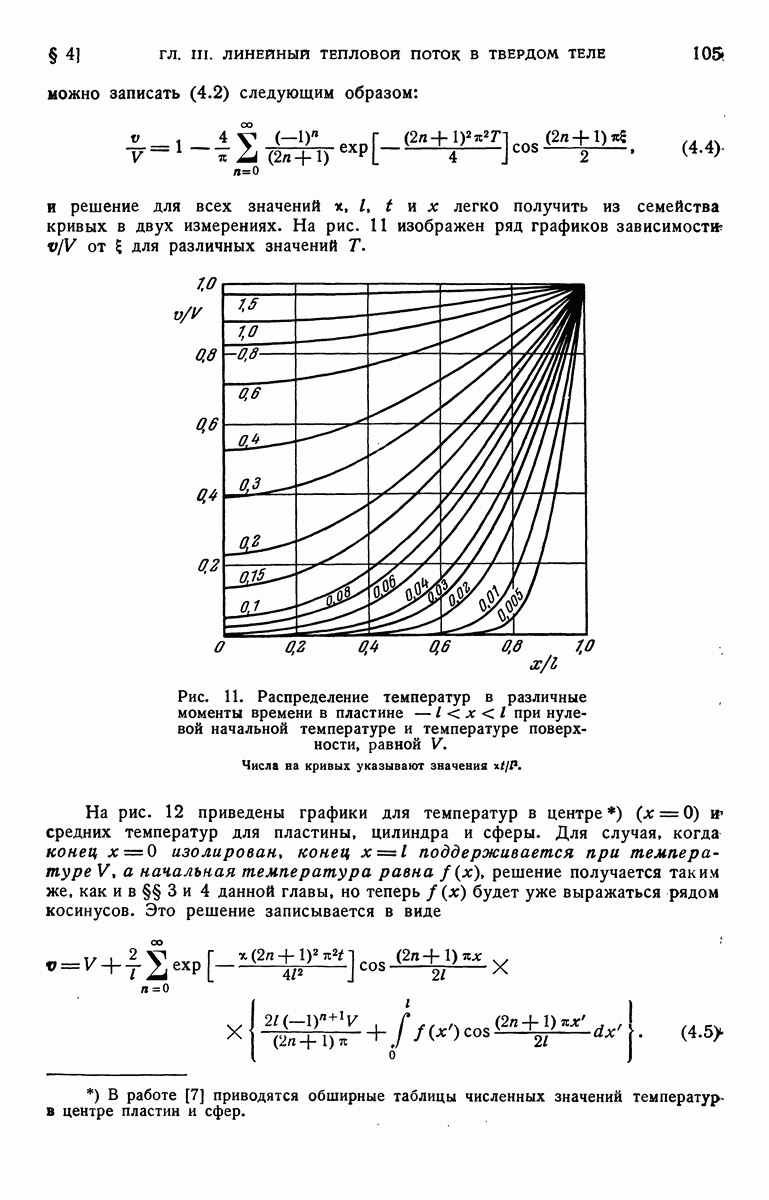
- § 4. Область [0, l] Начальная температура f(x). Границы поддерживаются при постоянной температуре или изолированы
- § 5. Область [0, l]. Температуры границ равны … Начальная температура f(x)
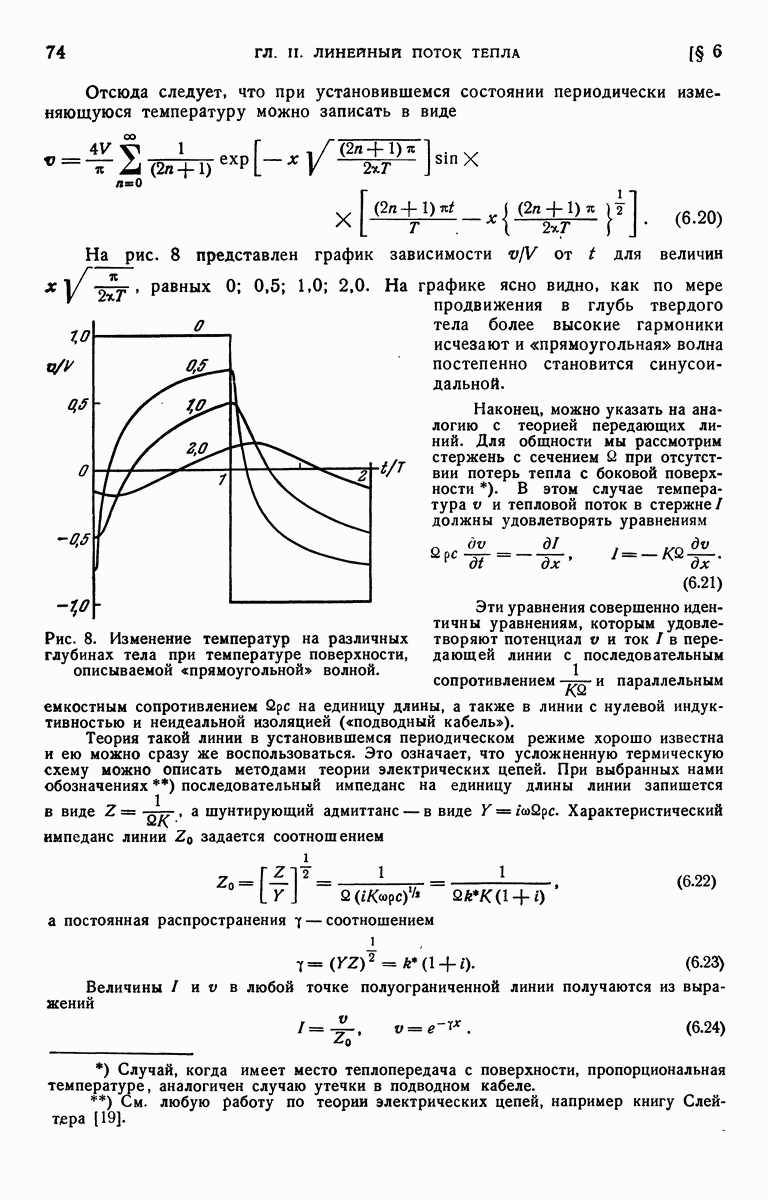
- § 6. Пластина с периодически изменяющейся температурой поверхности
- § 7. Установившаяся периодически изменяющаяся температура в составных пластинах
- § 8. Пластина с заданным тепловым потоком на ее границе
- § 9. Область [0, l]. Теплообмен на границах в среду с температурой, равной нулю. Начальная температура равна f(х)
- § 10. Область [-l, l]. На границах х=+l происходит теплообмен со средой нулевой температуры. Начальная температура f(x)
- § 11. Частные случаи и численные результаты для пластины с граничным условием третьего рода
- § 12. Область [-l, l] с нулевой начальной температурой и теплообменом на границах со средой, имеющей температуру …
- § 13. Пластина, одна из поверхностей которой соприкасается со слоем идеального проводника или хорошо перемешиваемой жидкости
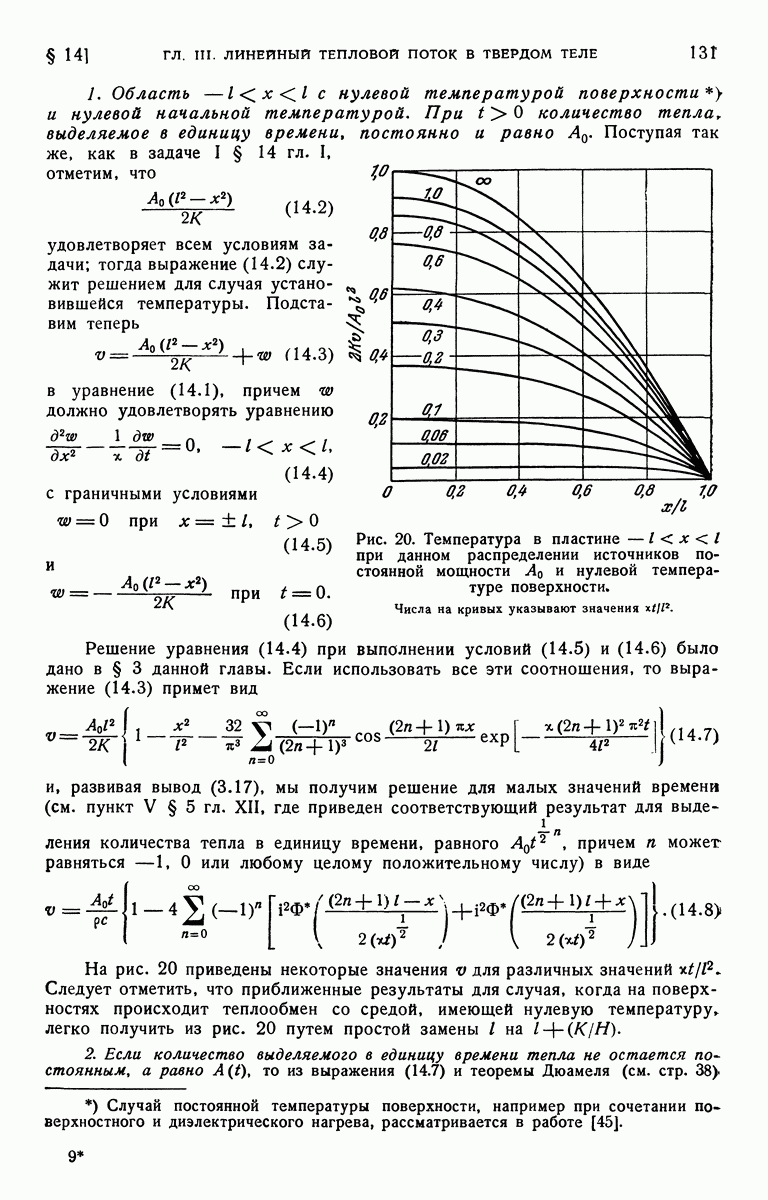
- § 14. Пластина с внутренним источником тепла
- ГЛАВА IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ
- § 3. Полуограниченный стержень. Случай установившейся температуры. Метод Форбса
- § 4. Полуограниченный стержень. Периодически изменяющаяся температура. Метод Ангстрема [5—10]
- § 5. Ограниченный стержень, концы которого находятся при фиксированных температурах. Случай установившейся температуры
- § 6. Стержень переменного сечения с охлаждающимися ребрами. Случай установившейся температуры
- § 7. Ограниченный стержень при наличии теплообмена на его поверхности. Случай неустановившейся температуры
- § 8. Ограниченный стержень с периодически изменяющейся температурой концов. Метод Неймана
- § 9. Задачи по теплопроводности в движущемся стержне
- § 10. Уравнение теплопроводности для тонкой проволоки, нагреваемой постоянным электрическим током
- § 11. Установившаяся температура. Определение коэффициента теплопроводности
- § 12. Сильно нагретая проволока, по которой протекает электрический ток
- § 13. Установившийся поток тепла в составной проволоке
- § 14. Неустановившаяся температура в проволоке, по которой течет электрический ток
- § 15. Кольцо Фурье
- ГЛАВА V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
- § 2. Неограниченное твердое тело прямоугольного сечения. Установившаяся температура
- § 3. Установившаяся температура в неограниченном теле прямоугольного сечения
- § 4. Тонкая пластина с прямоугольным сечением при наличии теплообмена на ее поверхности
- § 5. Установившаяся температура в теле прямоугольного сечения при наличии источника тепла
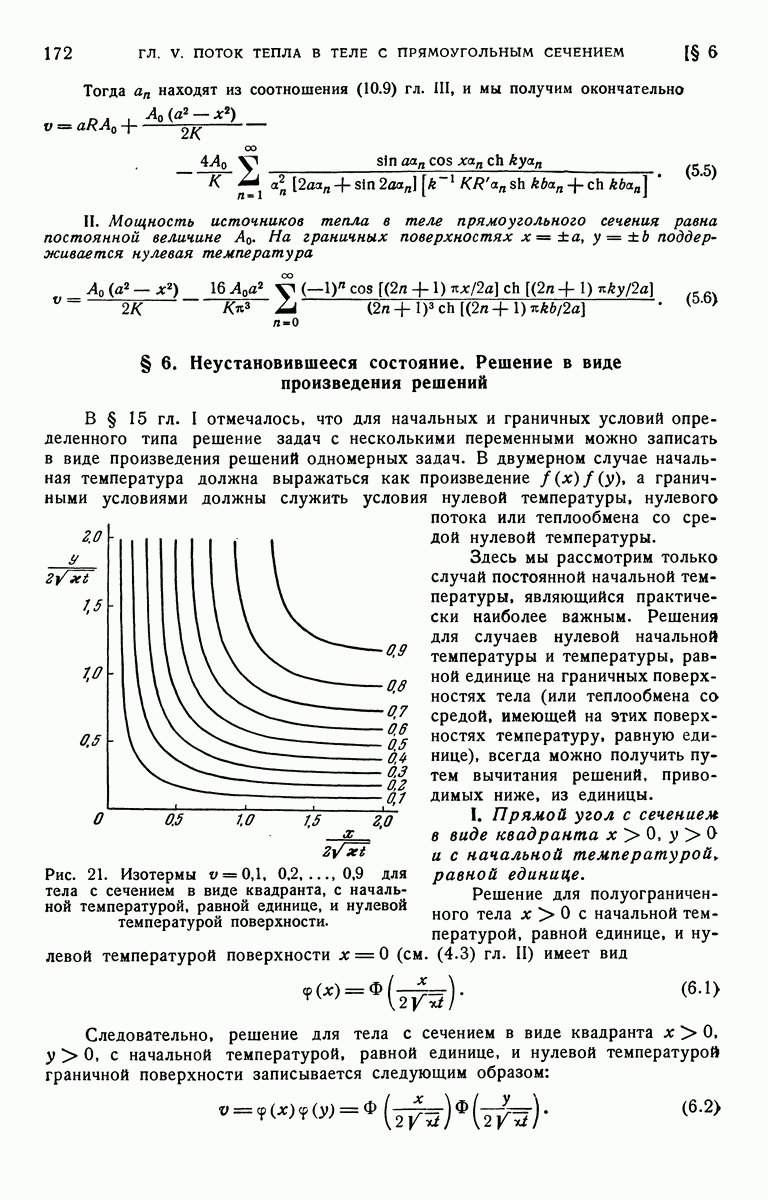
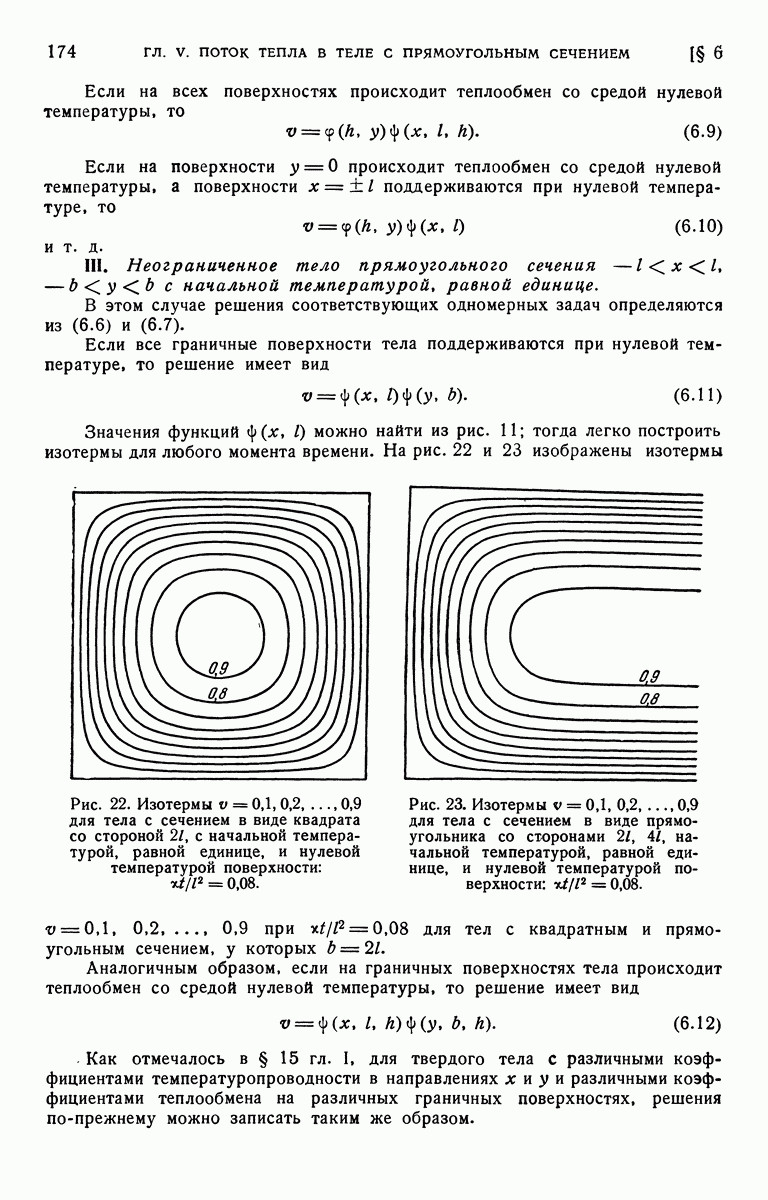
- § 6. Неустановившееся состояние. Решение в виде произведения решений
- § 7. Неустановившееся состояние. Произвольные начальные и граничные условия
- ГЛАВА VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ
- § 2. Установившаяся температура
- § 3. Двойные и кратные ряды Фурье
- § 4. Неустановившаяся температура. Решение в виде произведения решений
- § 5. Определение коэффициента теплопроводности и экстраполяция кривых охлаждения
- § 6. Неустановившаяся температура. Тройной ряд Фурье
- ГЛАВА VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ КРУГОВОГО СЕЧЕНИЯ
- § 2. Установившаяся температура. Радиальный поток
- § 3. Установившаяся, периодически изменяющаяся температура в круговых цилиндрах [19—22]
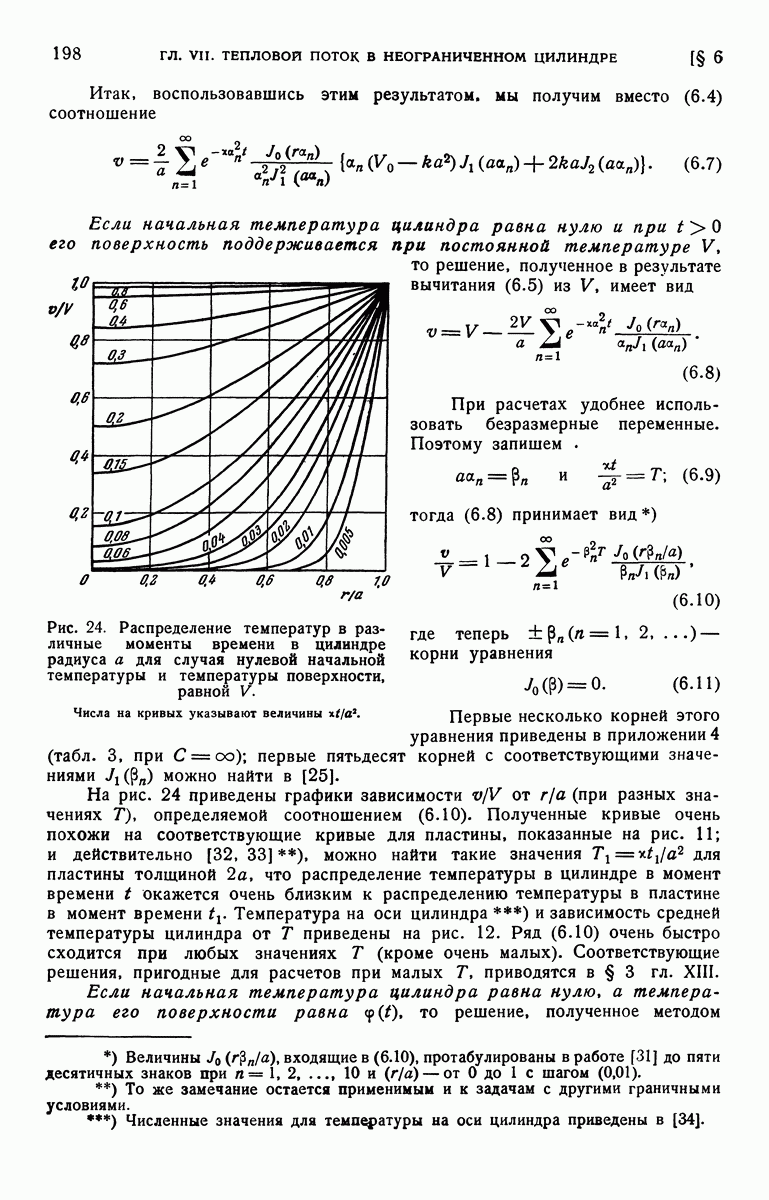
- § 4. Неограниченный цилиндр. Радиальный поток. Неустановившаяся температура
- § 5. Интегралы …
- § 6. Неограниченный цилиндр с температурой поверхности … и начальной температурой f(r)
- § 7. Неограниченный цилиндр с теплообменом на поверхности
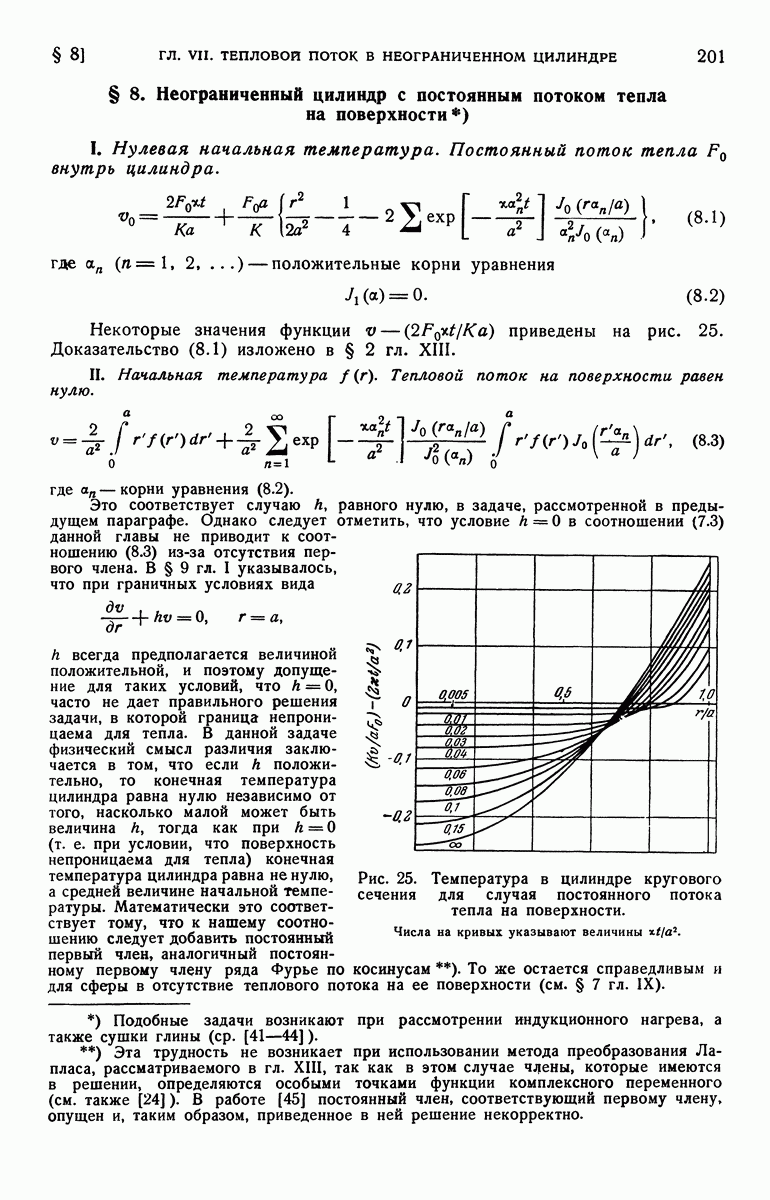
- § 8. Неограниченный цилиндр с постоянным потоком тепла на поверхности
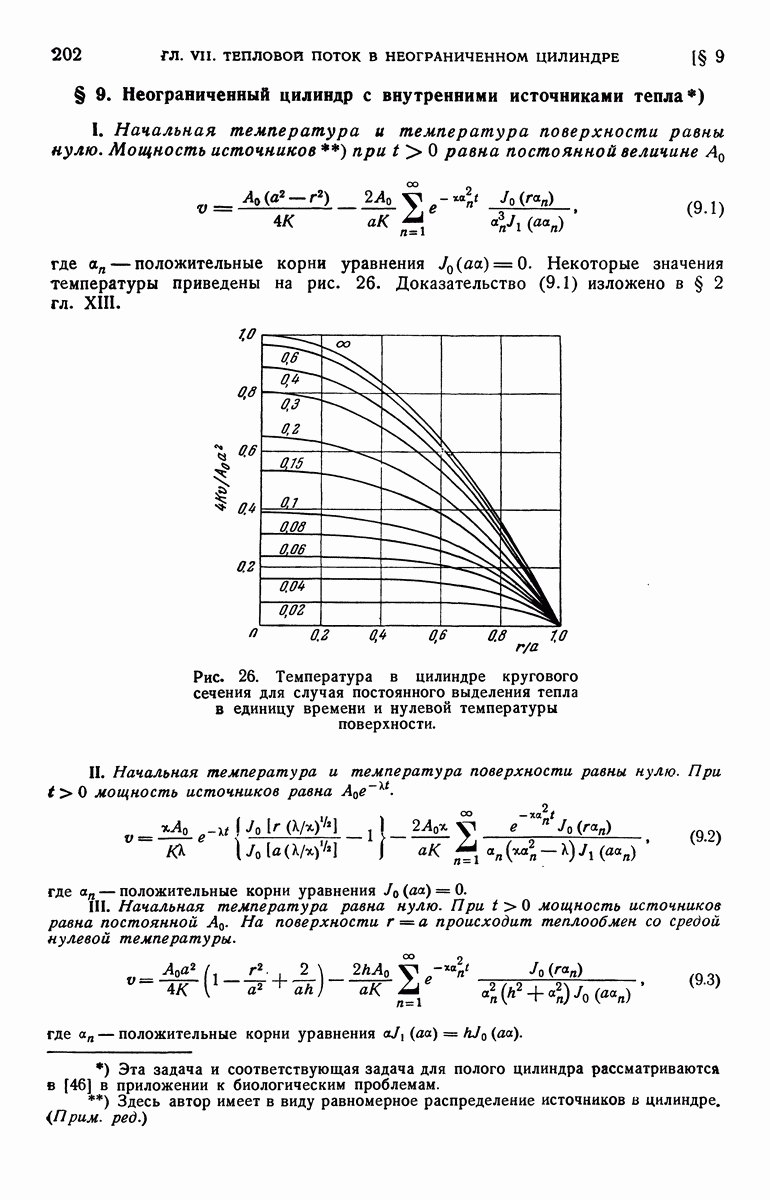
- § 9. Неограниченный цилиндр с внутренними источниками тепла
- § 10. Неограниченный полый цилиндр. Радиальный поток
- § 11. Неограниченный цилиндр. Установившаяся температура. Общий случай
- § 12. Неограниченный цилиндр. Неустановившаяся температура. Общий случай
- ГЛАВА VIII. ТЕПЛОВОЙ ПОТОК В ОБЛАСТЯХ, ОГРАНИЧЕННЫХ КООРДИНАТНЫМИ ПОВЕРХНОСТЯМИ ЦИЛИНДРИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ
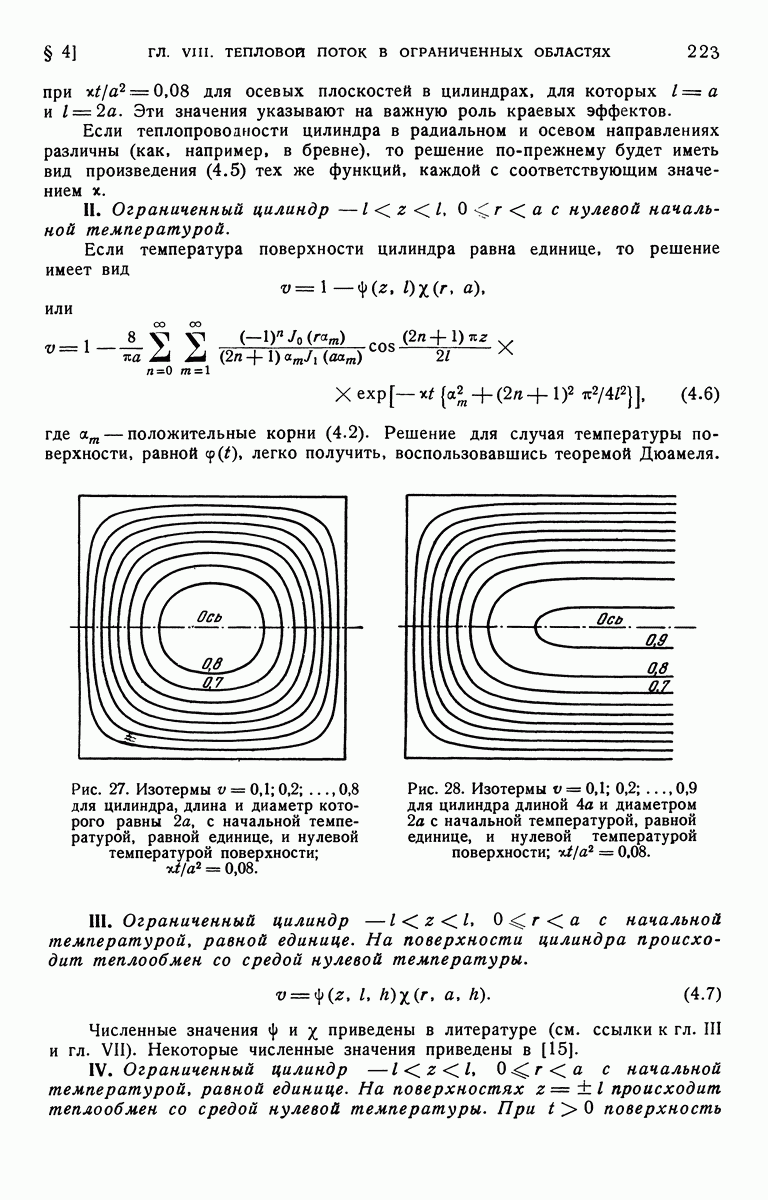
- § 3. Установившаяся температура в ограниченном и полуограниченном цилиндрах
- § 4. Неустановившееся состояние. Решения в форме произведений
- § 5. Определение теплопроводности вещества в форме цилиндра
- § 6. Ограниченный цилиндр с начальной температурой …
- § 7. Полуограниченный цилиндр
- ГЛАВА IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ
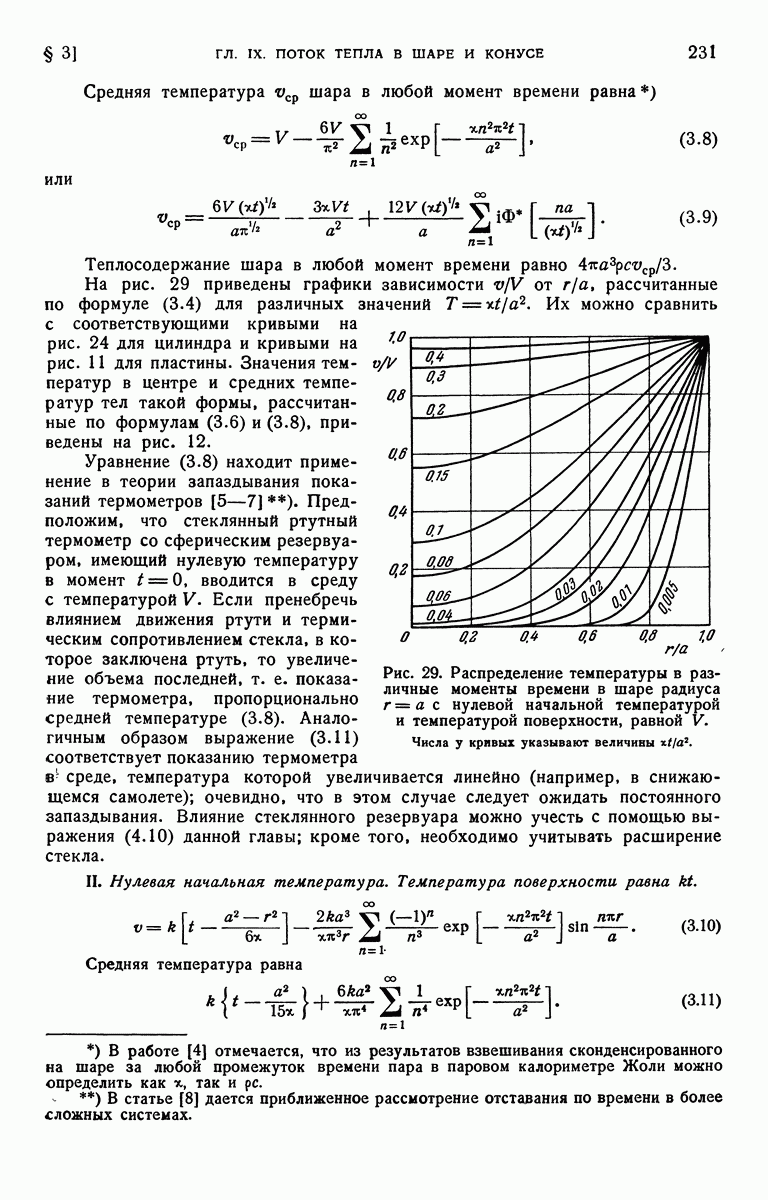
- § 2. Установившаяся температура. Радиальный тепловой поток
- § 3. Шар с начальной температурой f(r) и температурой поверхности …
- § 4. Шар. Начальная температура f(r). На поверхности сферы происходит теплообмен
- § 5. Определение коэффициентов теплопроводности плохих проводников
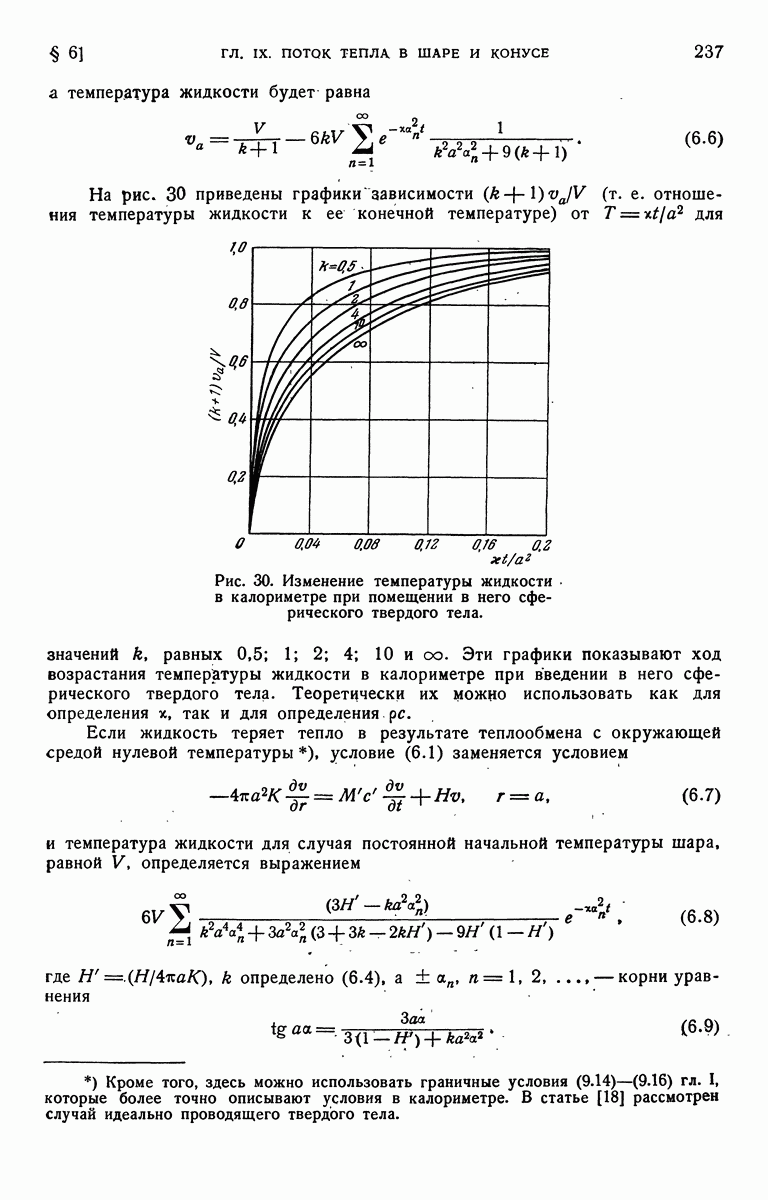
- § 6. Случай шара, находящегося в контакте с хорошо перемешиваемой жидкостью
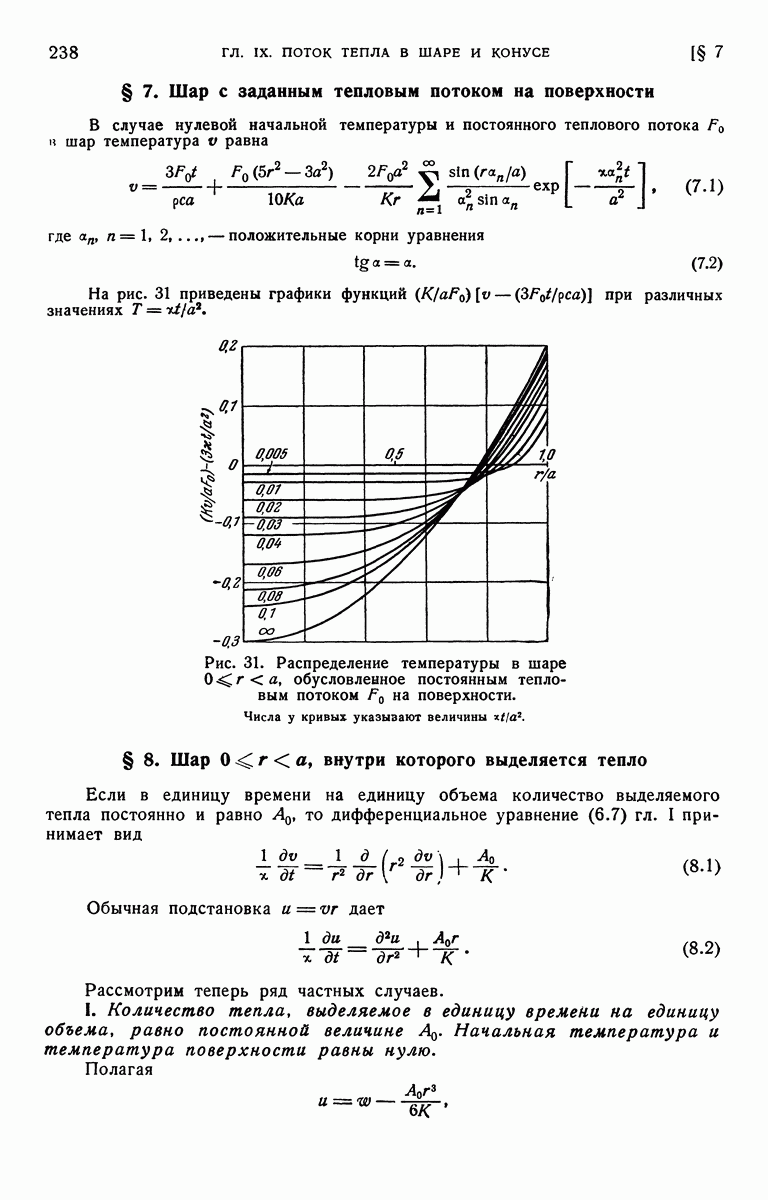
- § 7. Шар с заданным тепловым потоком на поверхности
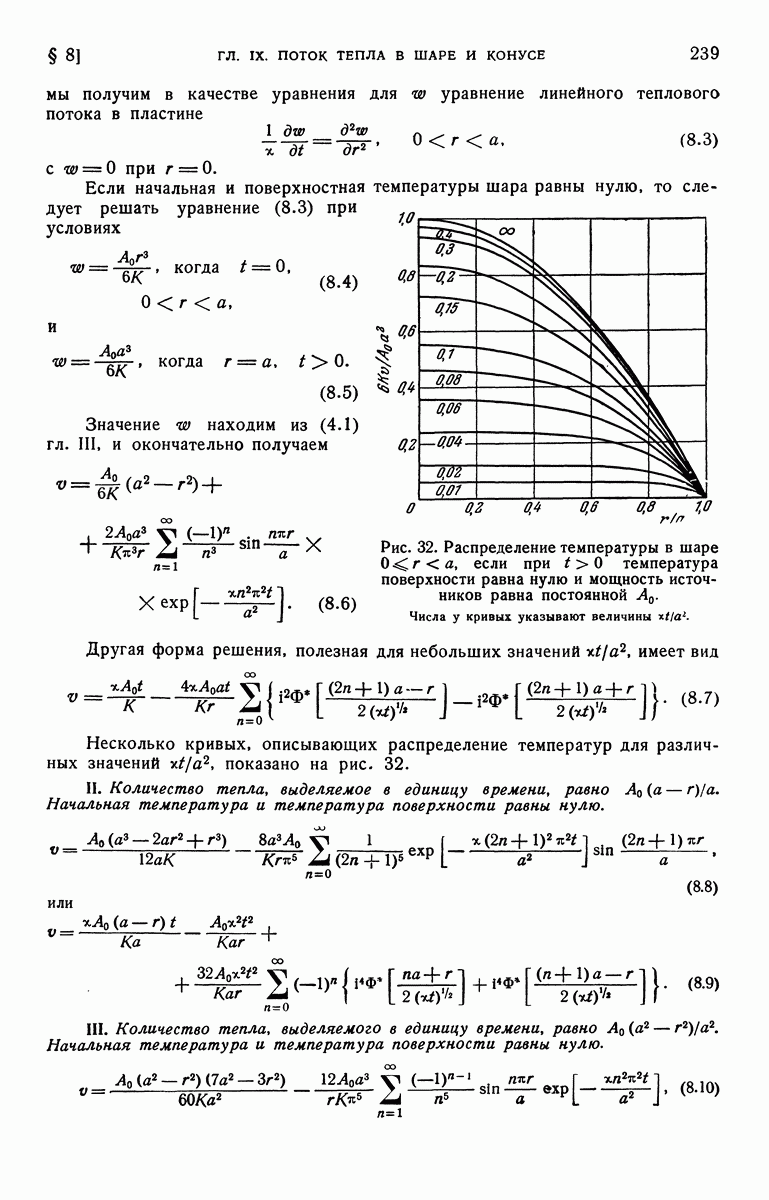
- § 8. Шар, внутри которого выделяется тепло
- § 9. Полый шар
- § 10. Область, ограниченная изнутри сферической поверхностью r=a
- § 11. Шар с начальной температурой … Температура поверхности r=a равна нулю
- § 12. Поверхность шара r=a поддерживается при температуре …
- § 13. Часть шара, вырезаемая конусом … Температура поверхности равна нулю, начальная температура равна …
- § 14. Температура внутри Земли
- ГЛАВА Х. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ К ЗАДАЧАМ С НЕУСТАНОВИВШЕЙСЯ ТЕМПЕРАТУРОЙ
- § 2. Мгновенный точечный источник
- § 3. Мгновенные источники; линейный, плоский и поверхностные цилиндрический и сферический источники
- § 4. Непрерывные и периодические источники
- § 5. Поверхностный нагрев полуограниченной области
- § 6. Выделение тепла в неограниченной среде
- § 7. Движущиеся источники тепла
- § 8. Дублеты
- § 9. Метод последовательных волн
- § 10. Метод изображений. Линейный тепловой поток
- § 11. Применение метода изображений к двумерным и трехмерным задачам
- § 12. Обобщение метода изображений Зоммерфельдом
- ГЛАВА XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ
- § 2. Одномерные случаи плавления и затвердевания. Решение Неймана и его обобщение
- § 3. Область … при других граничных условиях
- § 4. Методы интегрального уравнения. Рассмотрение задач затвердевания, предложенное Лайтфутом
- § 5. Решения в цилиндрических и сферических координатах
- § 6. Осесимметричные задачи о замерзании и плавлении
- ГЛАВА XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЛИНЕЙНОГО ТЕПЛОВОГО ПОТОКА
- § 2. Преобразование Лапласа. Основные свойства
- § 3. Решение уравнения теплопроводности методом преобразования Лапласа
- § 4. Полуограниченная область. Решения, получаемые из таблицы изображений
- § 5. Ограниченная область (0, l). Решения, получаемые из таблицы изображений. Решения для небольших значений времени
- § 6. Ограниченная область (0, l). Применение теоремы обращения
- § 7. Полуограниченная область. Применение теоремы обращения
- § 8. Составные твердые тела
- ГЛАВА XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА
- § 3. Решения, применимые для малых интервалов времени
- § 4. Полый цилиндр
- § 5. Область ограничена изнутри цилиндром кругового сечения r=a
- § 6. Решения, применимые при больших значениях времени
- § 7. Область, ограниченная изнутри круговым цилиндром из идеального проводника
- § 8. Составная цилиндрическая область
- § 9. Шар. Радиальный тепловой поток
- ГЛАВА XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА К РЕШЕНИЮ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 2. Линейный тепловой поток. Полуограниченное твердое тело
- § 3. Линейный тепловой поток в области (0, a)
- § 4. Двумерные задачи. Тела с прямоугольным сечением
- § 5. Прямоугольный параллелепипед
- § 6. Линейный тепловой поток. Составные твердые тела
- § 7. Шар. Радиальный поток тепла
- § 8. Цилиндр. Радиальный тепловой поток
- § 9. Полуограниченное твердое тело. Трехмерные задачи
- § 10. Область, ограниченная двумя параллельными плоскостями
- § 11. Полуограниченное твердое тело с тонкой пленкой на плоскости z=0 из материала, имеющего значительно большую теплопроводность. В точке … расположен единичный мгновенный источник
- § 12. Неограниченное составное твердое тело. В точке действует мгновенный единичный источник
- § 13. Области, ограниченные цилиндрической поверхностью r=a
- § 14 Клин
- § 15. Цилиндрическая область
- § 16. Области, ограниченные сферической поверхностью r=a
- § 17. Конус
- § 18. Непрерывные источники
- ГЛАВА XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 3. Тепловые регенераторы и теплообменники
- § 4. Тепловой поток в слоистых системах
- § 5. Установившийся периодический режим
- § 6. Линейная асимптотика и запаздывание
- § 7. Выделение тепла
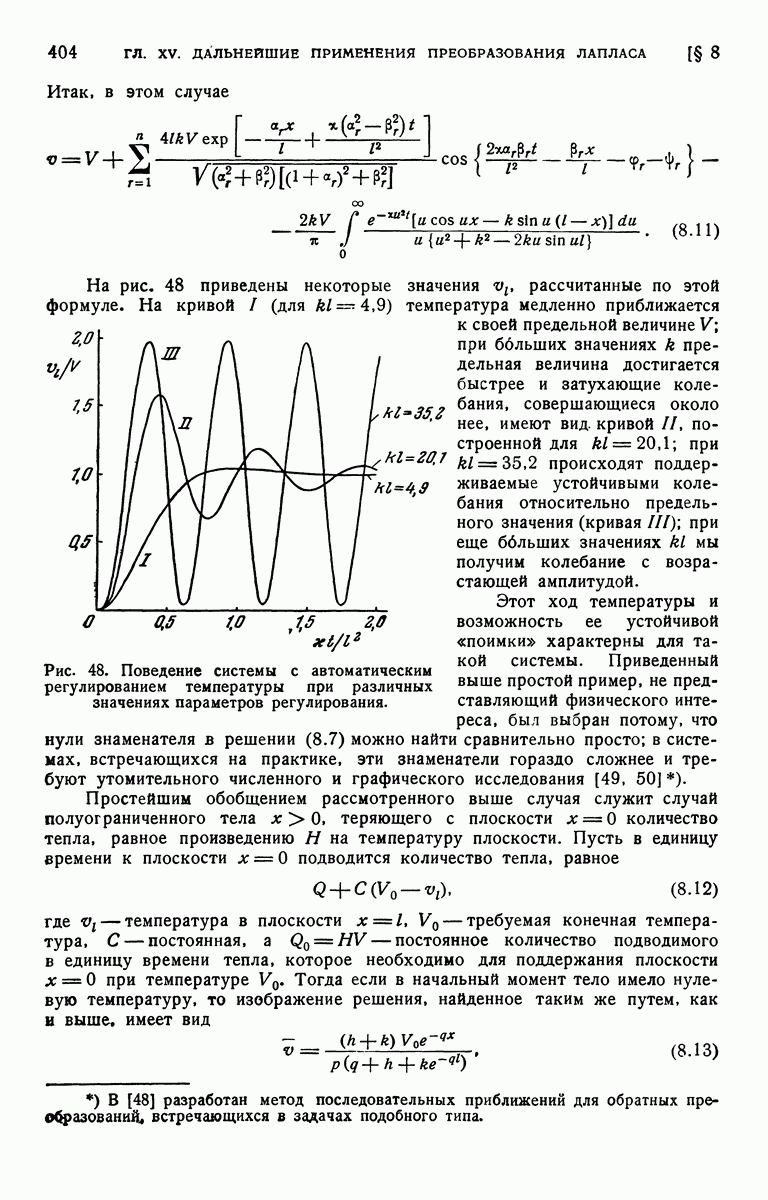
- § 8. Система автоматического регулирования температуры
- § 9. Неоднородные тела
- § 11. Прямое применение метода преобразования Лапласа к двумерным и трехмерным задачам
- ГЛАВА XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
- § 2. Источники и стоки при установившейся температуре
- § 3. Установившийся поток к почти плоской поверхности. Топографические поправки для геотермического потока
- § 4. Установившийся тепловой поток в составном теле
- § 5. Практические задачи
- § 6. Использование сопряженных гармонических функций в задачах с установившейся температурой
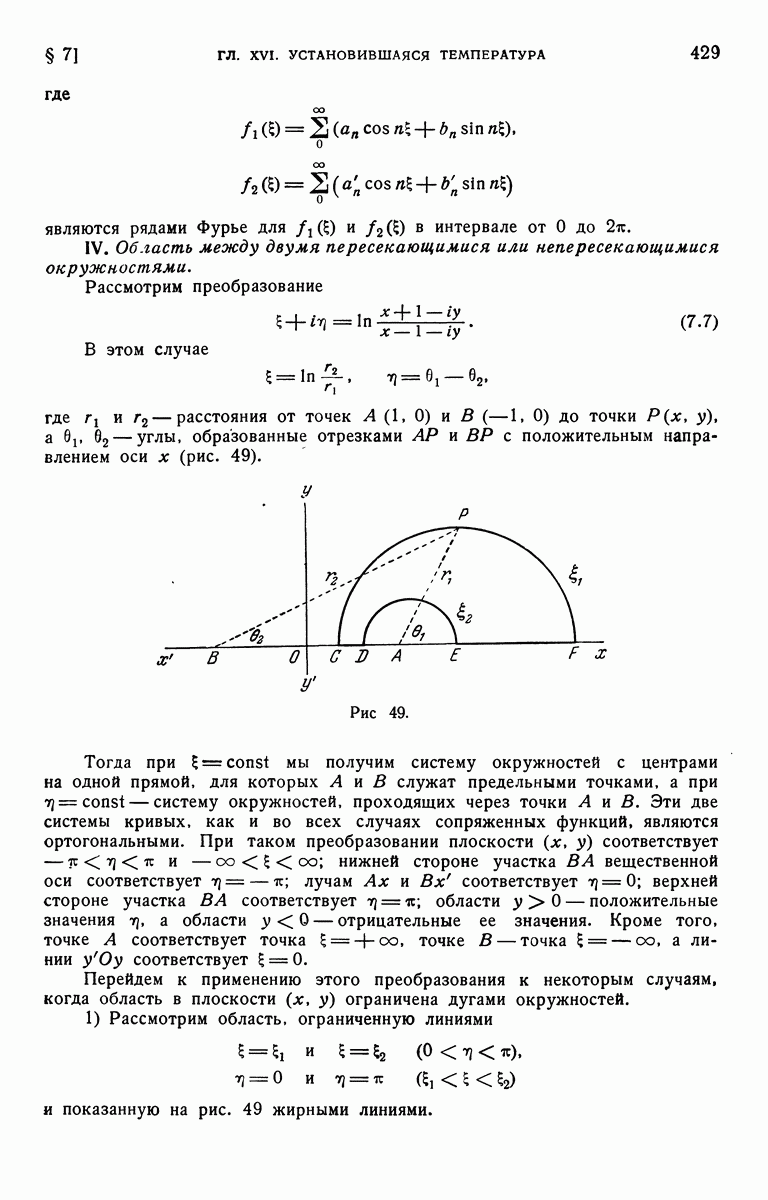
- § 7. Приложения этого метода [20, 21]
- § 8. Установившийся тепловой поток в многоугольнике
- § 9. Тепловой поток между изотермическими поверхностями
- ГЛАВА XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- § 2. Интегральные преобразования и формулы их обращения
- § 3. Неустановившийся тепловой поток
- § 4. Установившийся тепловой поток
- § 5. Конечные преобразования
- § 6. Последовательные преобразования
- ГЛАВА XVIII. ЧИСЛЕННЫЕ МЕТОДЫ
- § 3. Линейный тепловой поток в неограниченном пространстве
- § 4. Граничные условия
- § 5. Выделение тепла, переменная температуропроводность и скрытая теплота
- § 6. Релаксационные методы
- ПРИЛОЖЕНИЕ 1. КОНТУРНЫЕ ИНТЕГРАЛЫ И ПРОВЕРКА РЕШЕНИЙ, ПОЛУЧЕННЫХ ПРИ ПОМОЩИ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
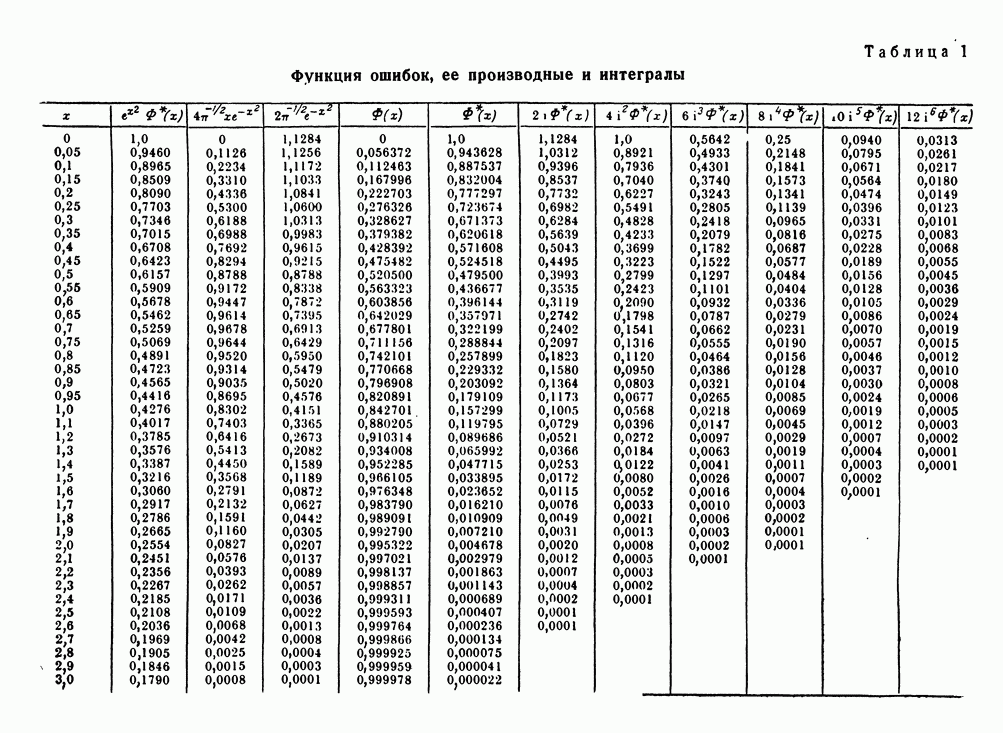
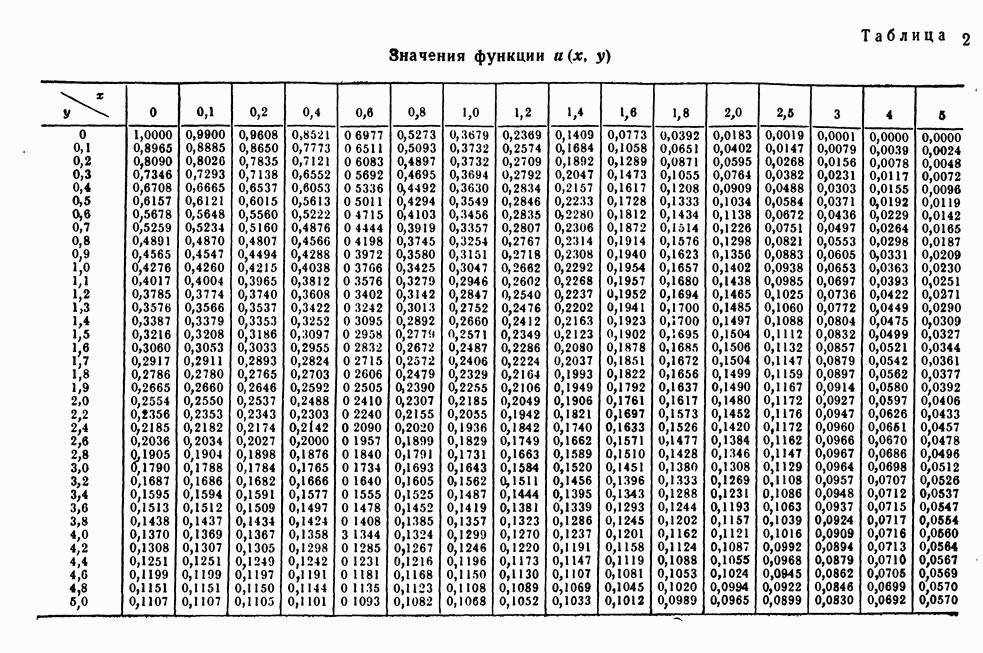
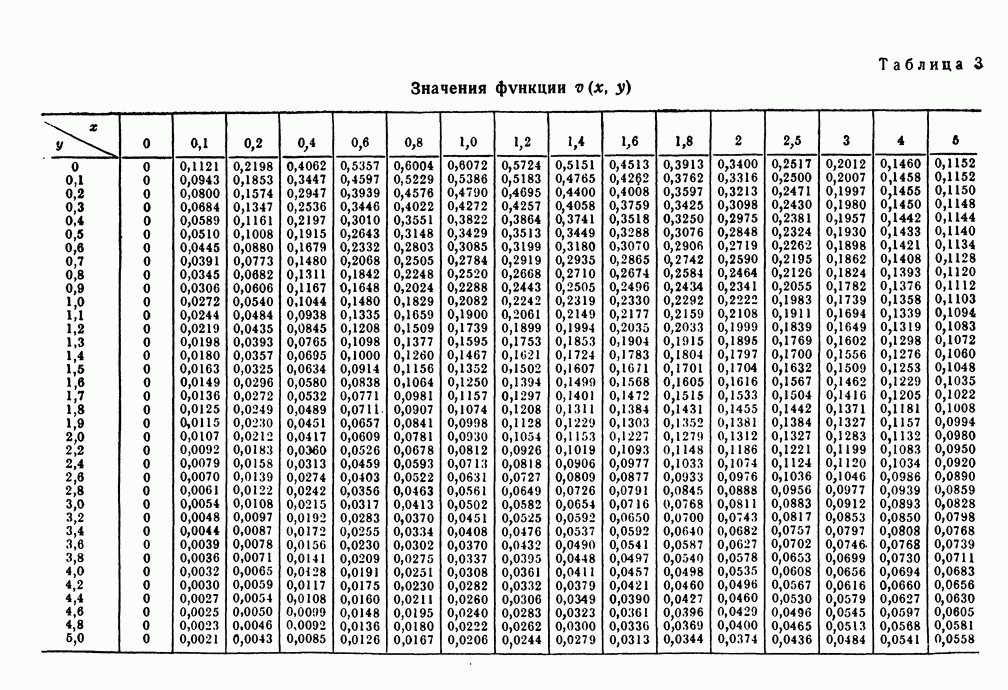
- ПРИЛОЖЕНИЕ 2. ФУНКЦИЯ ОШИБОК И РОДСТВЕННЫЕ ФУНКЦИИ
- ПРИЛОЖЕНИЕ 3. О ФУНКЦИЯХ БЕССЕЛЯ
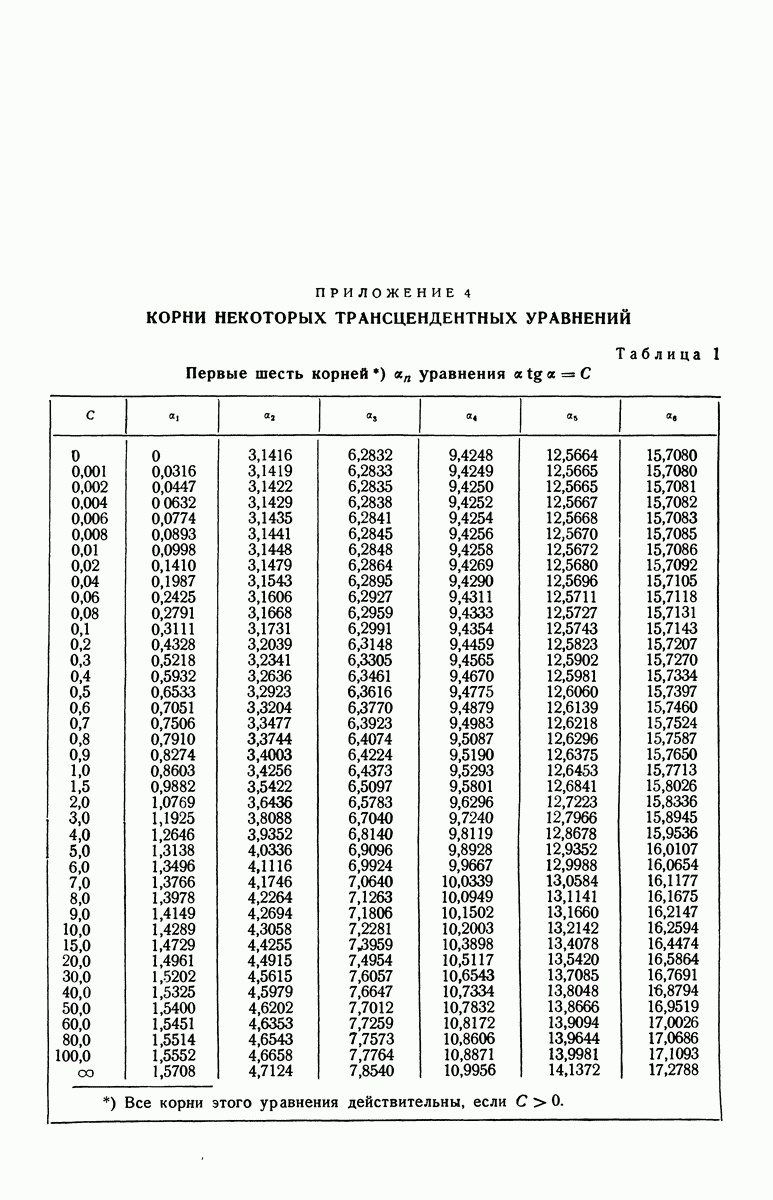
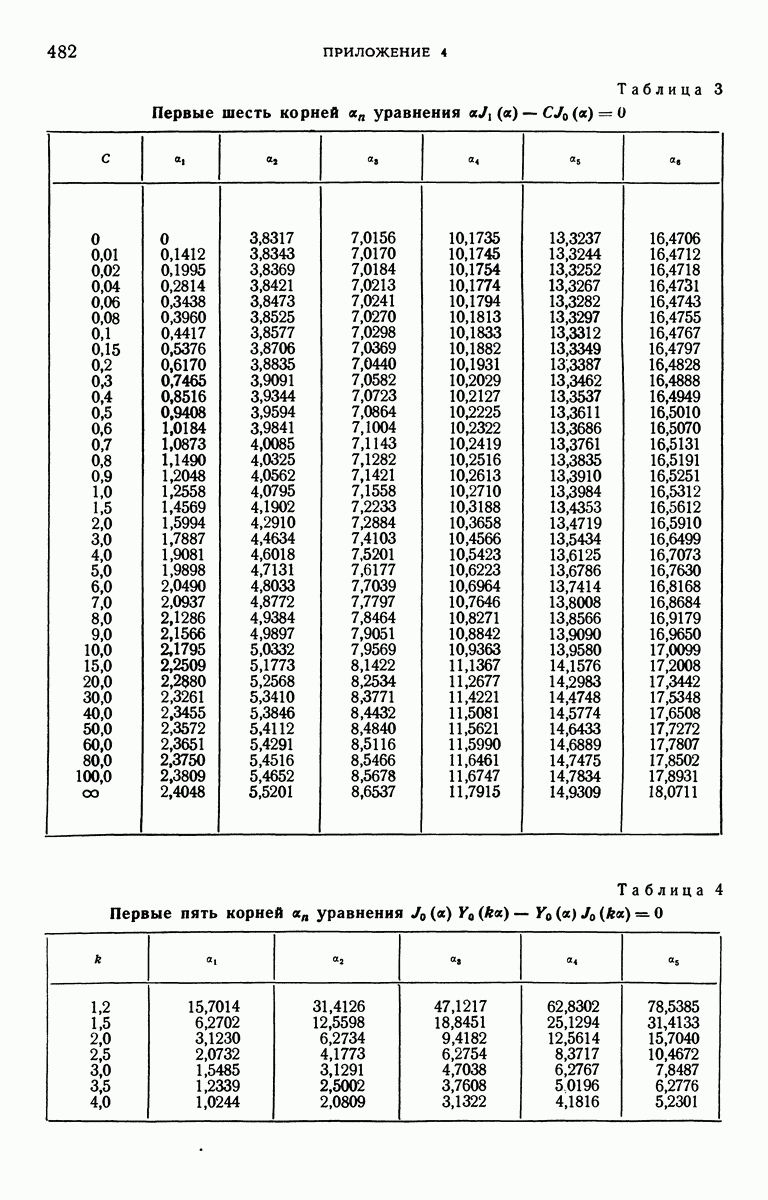
- ПРИЛОЖЕНИЕ 4. КОРНИ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- ПРИЛОЖЕНИЕ 5. ТАБЛИЦА ПРЕОБРАЗОВАНИЙ ЛАПЛАСА …
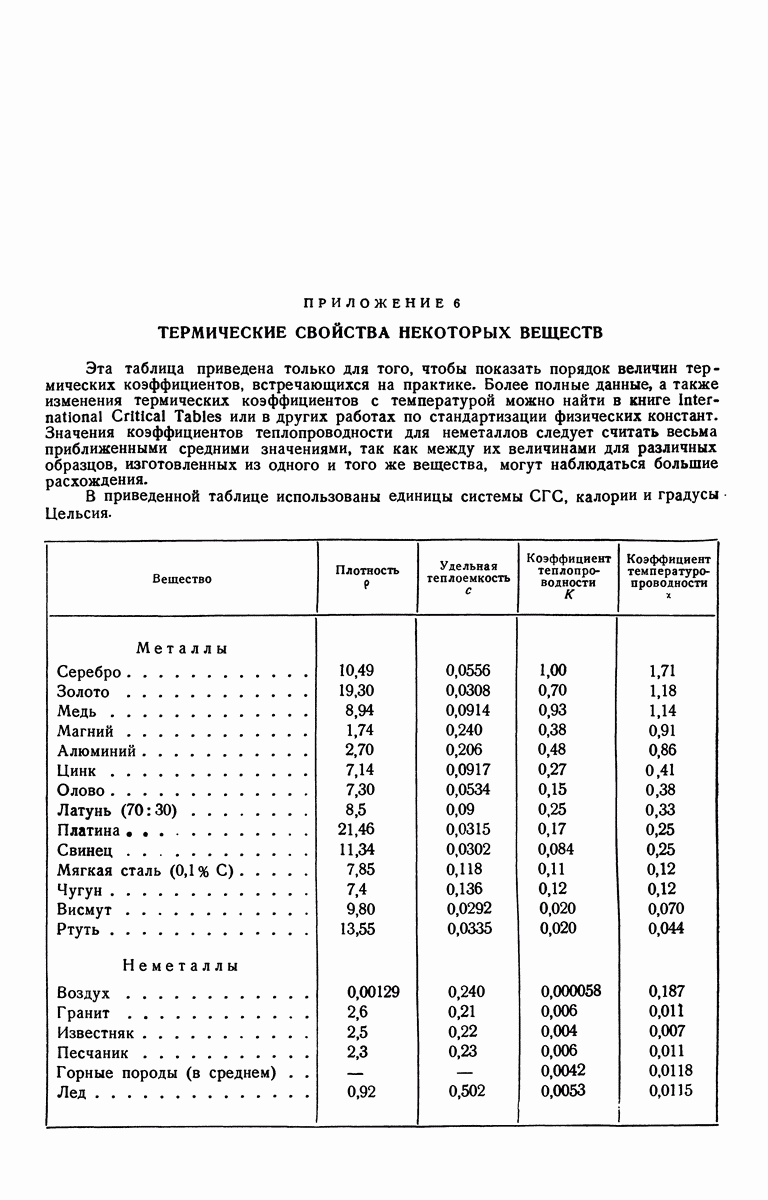
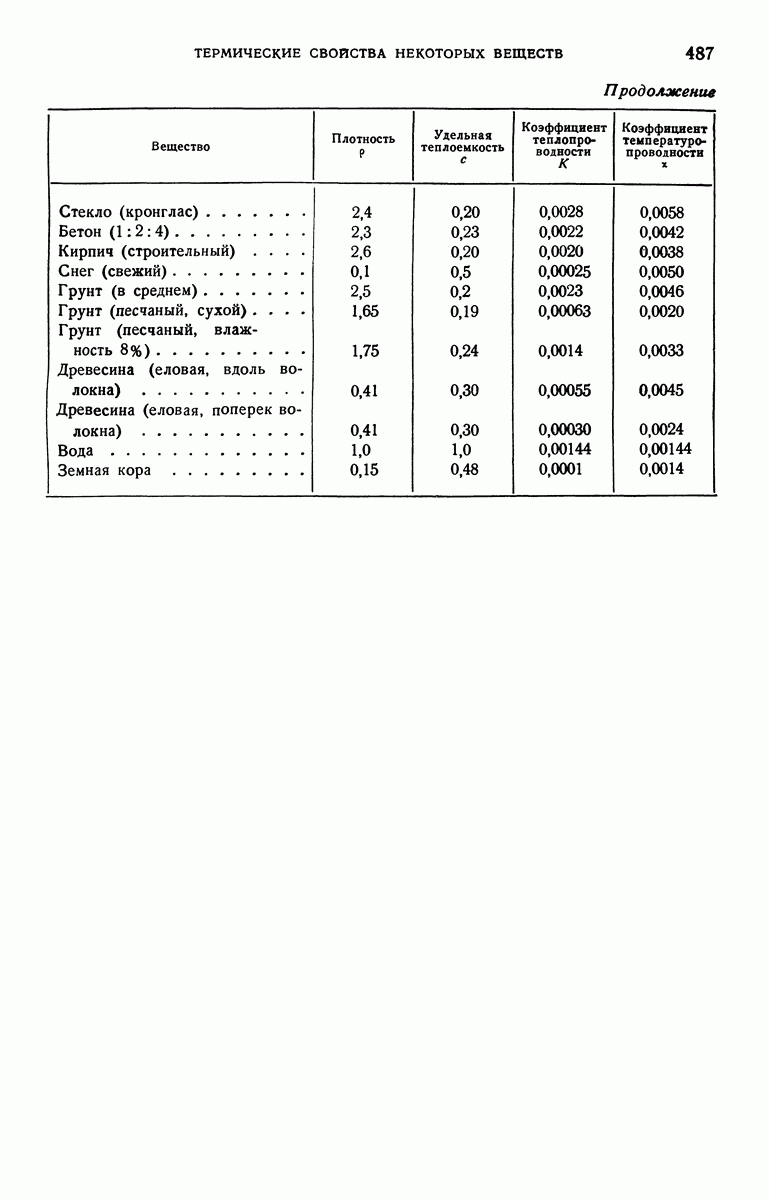
- ПРИЛОЖЕНИЕ 6. ТЕРМИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ВЕЩЕСТВ