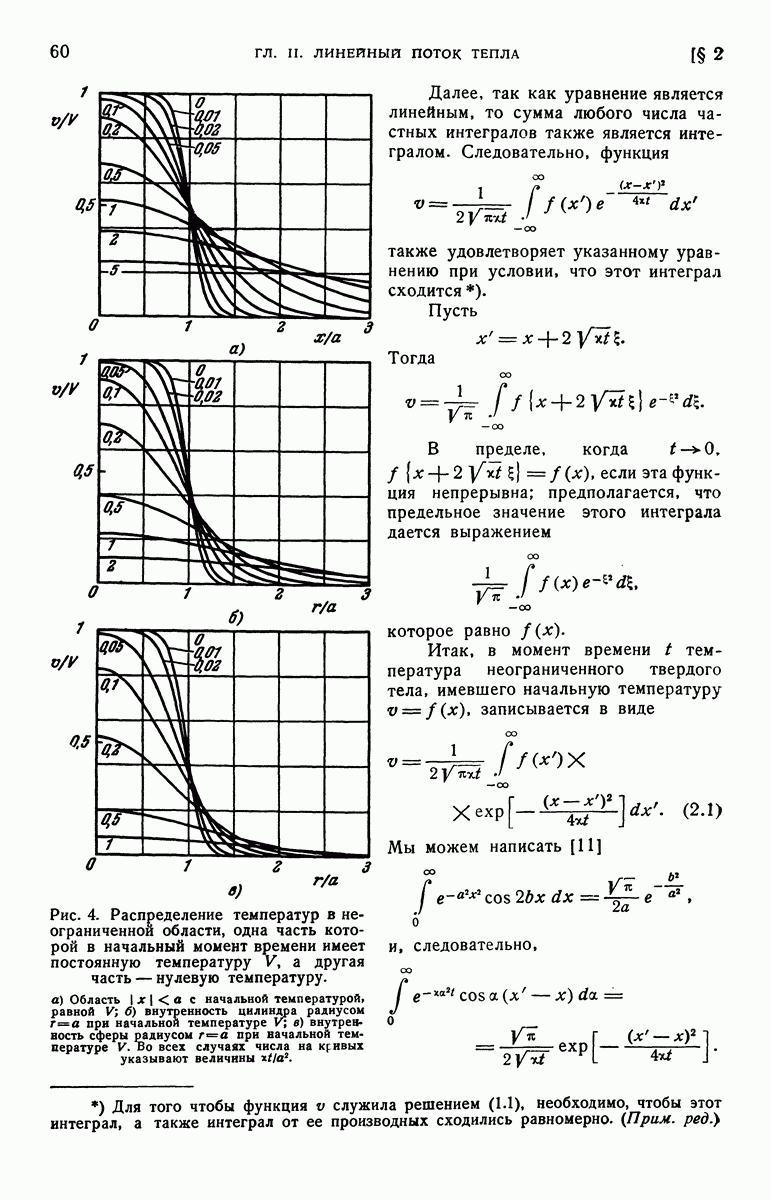
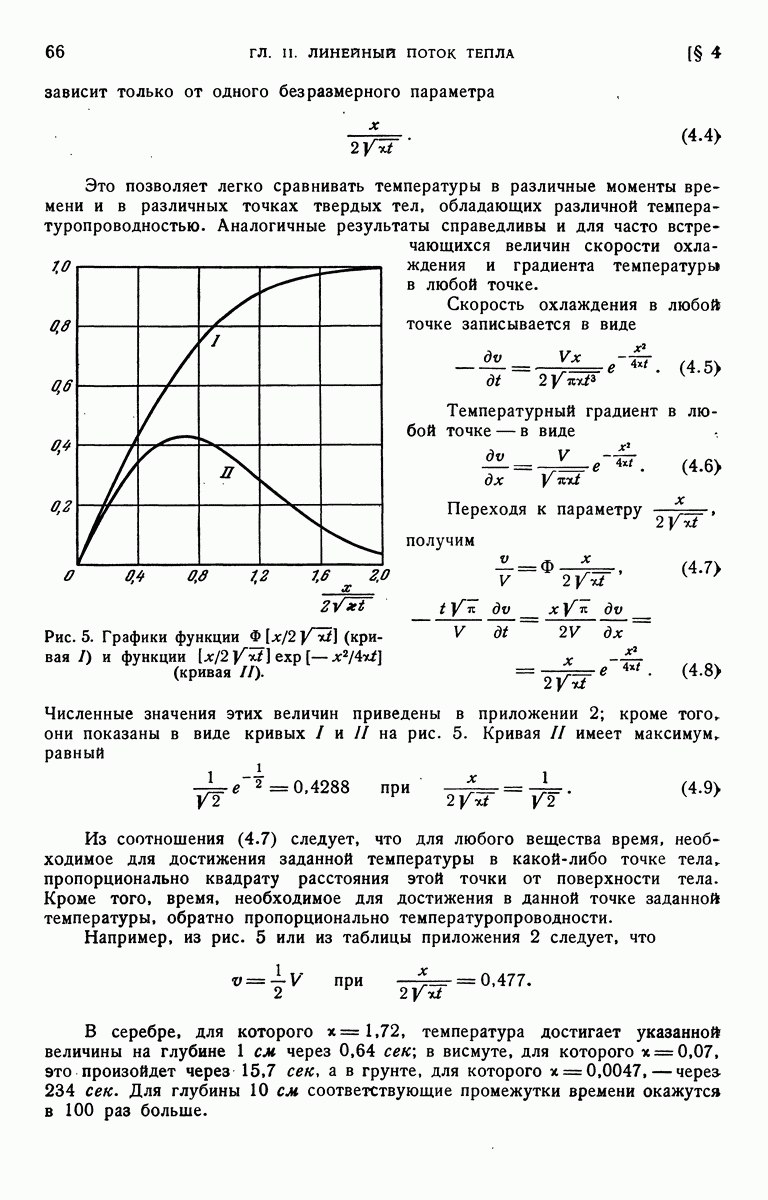
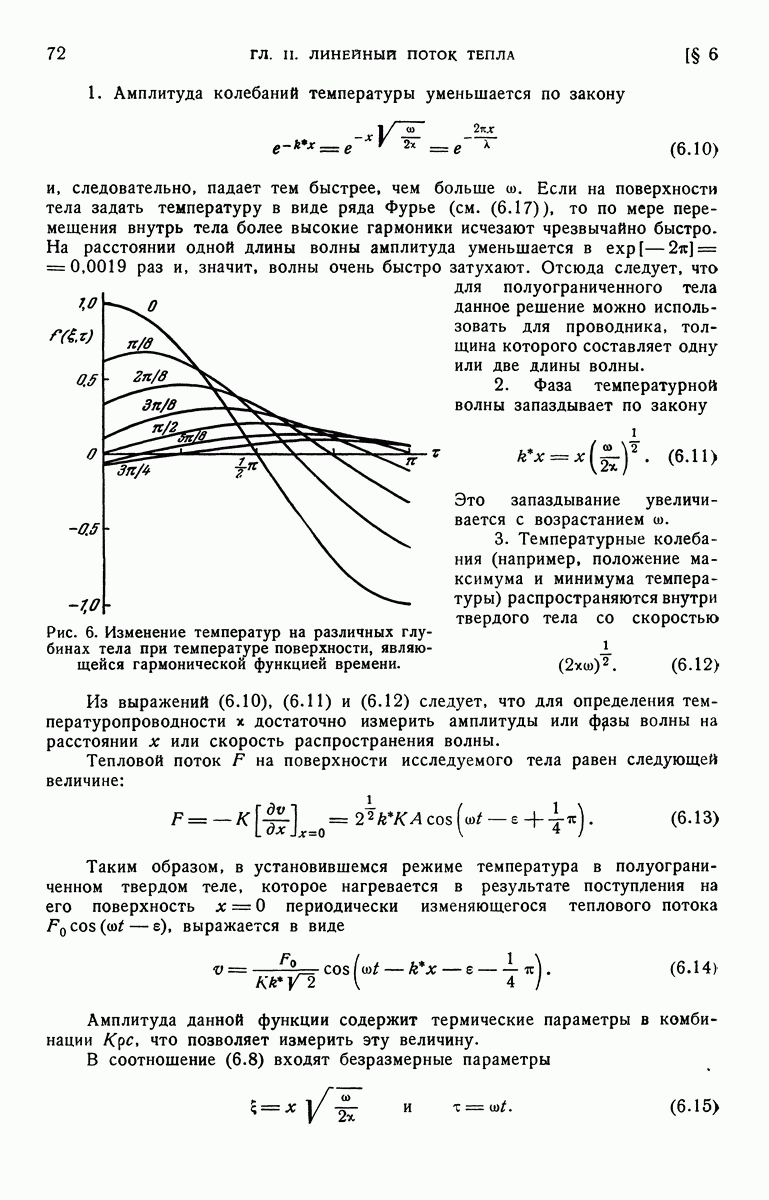
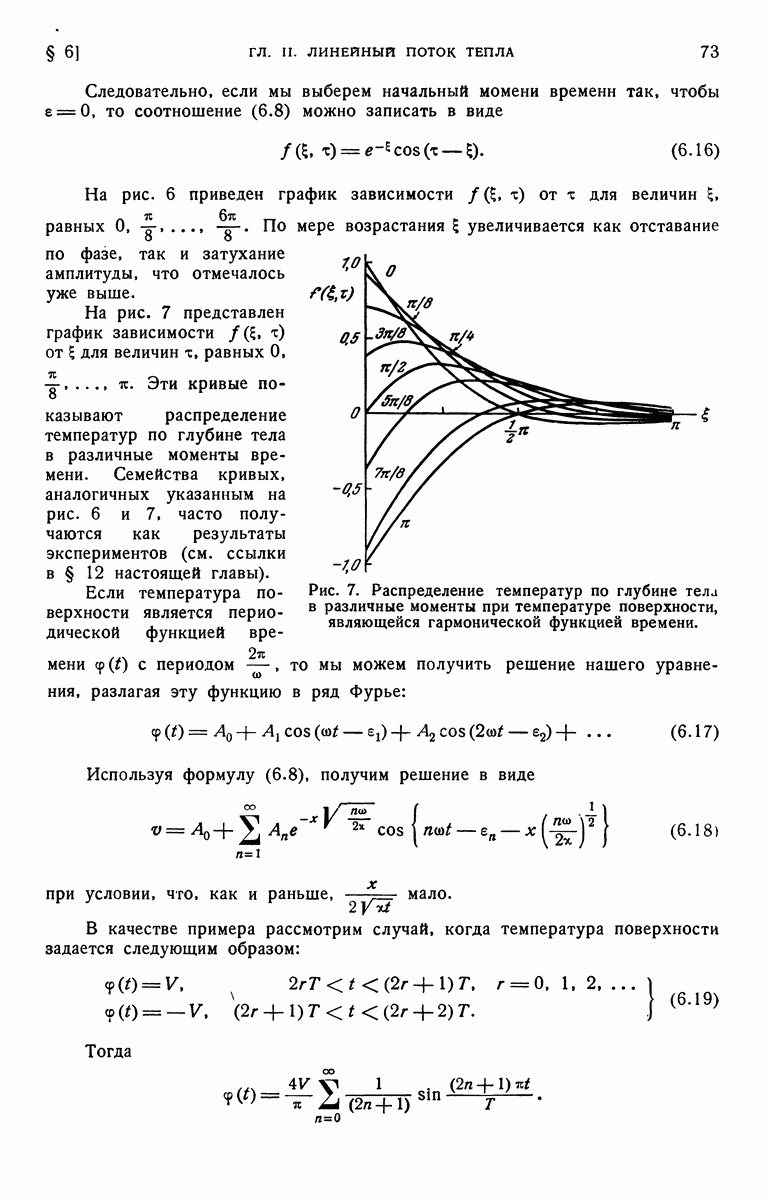
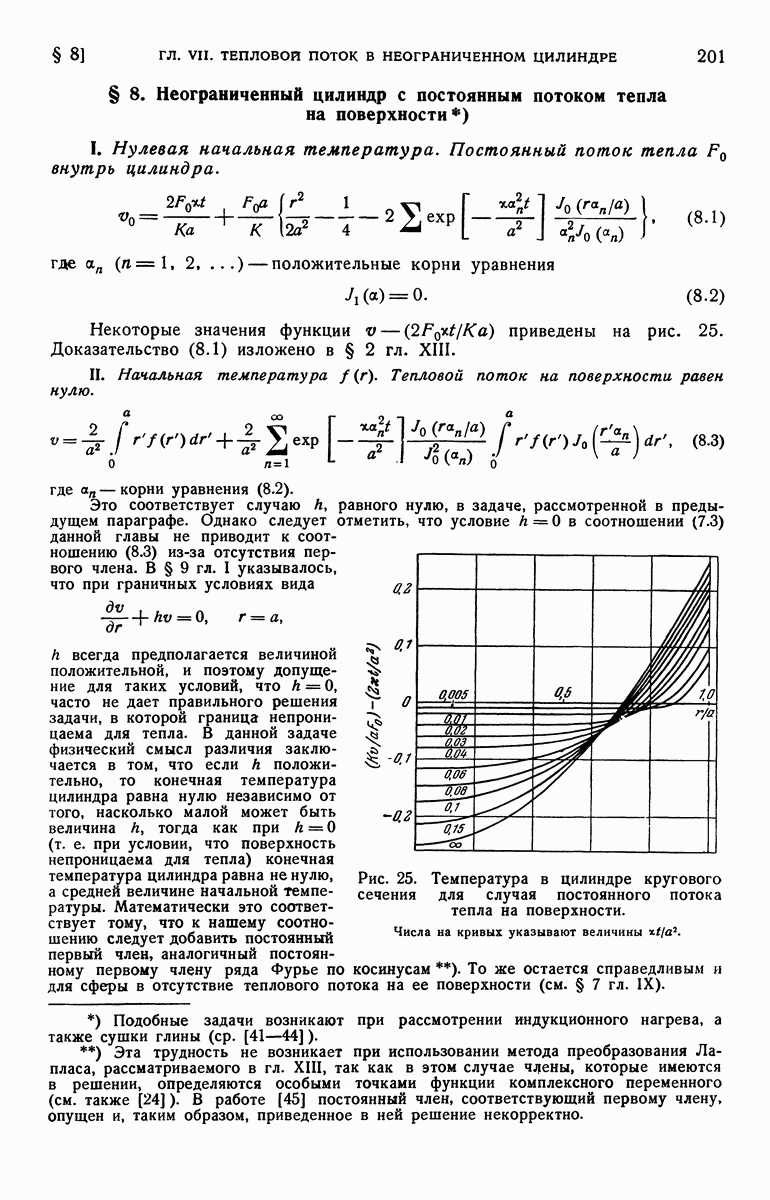
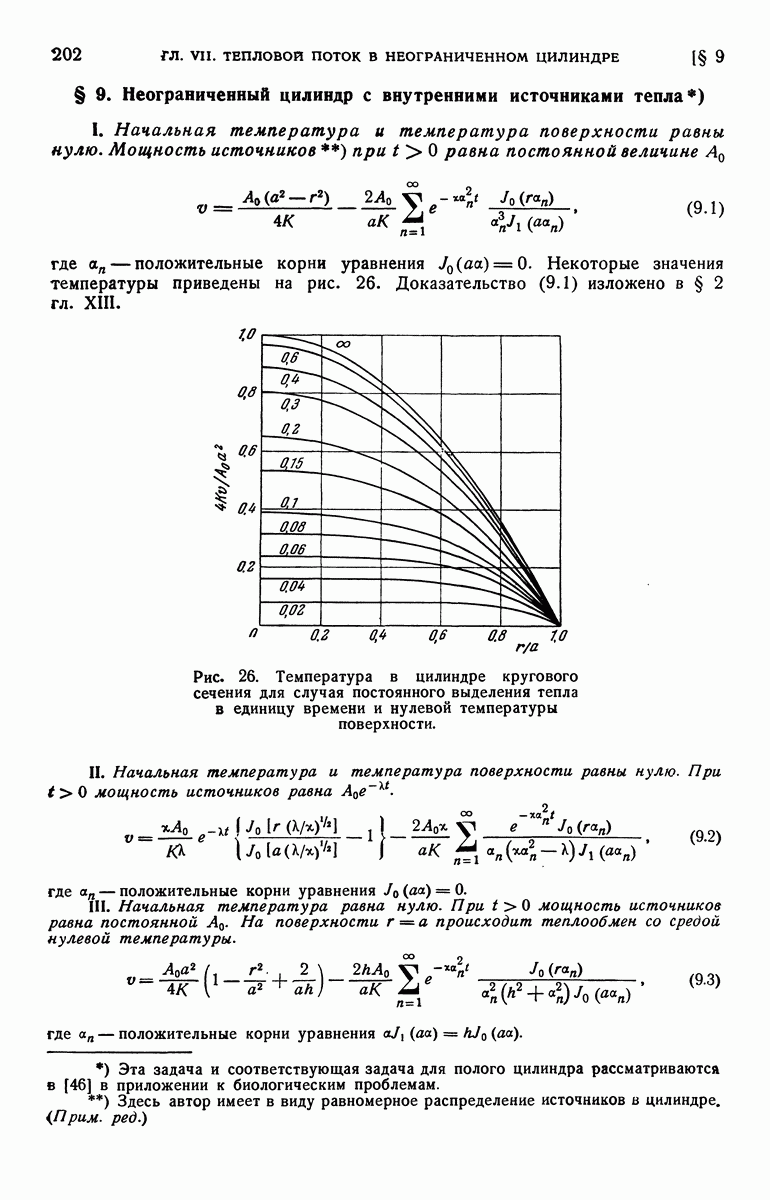
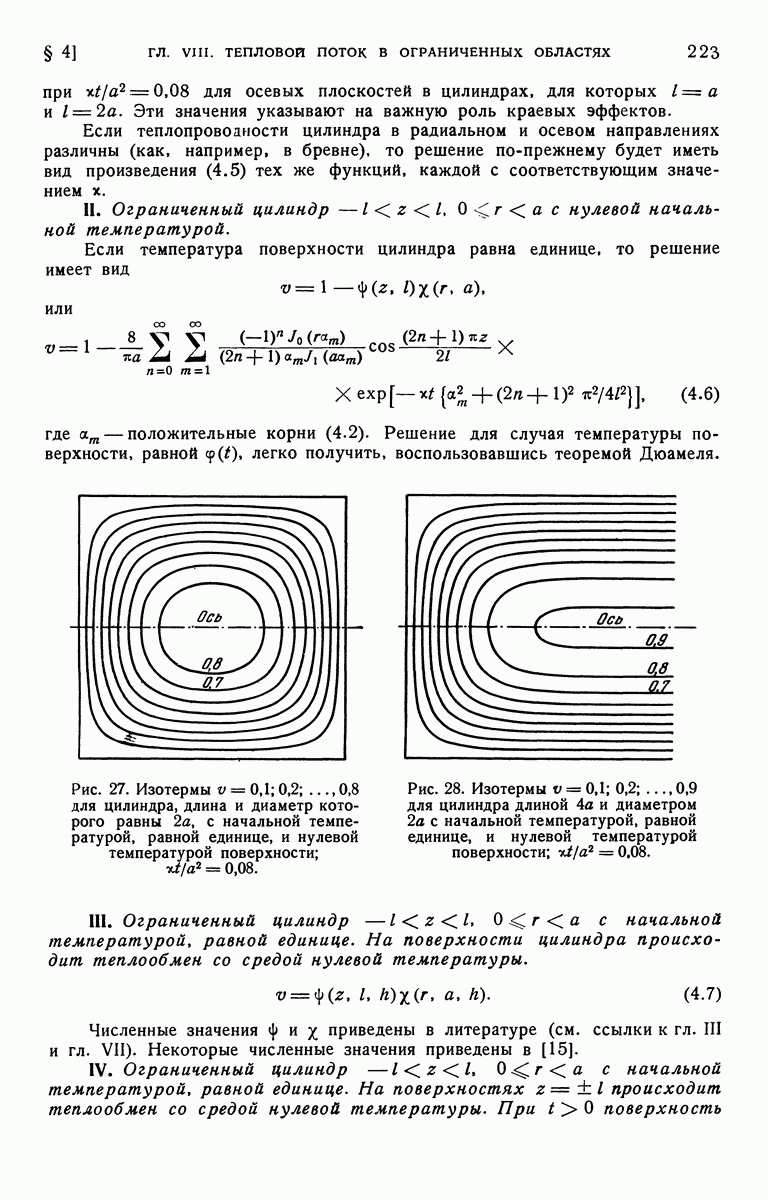
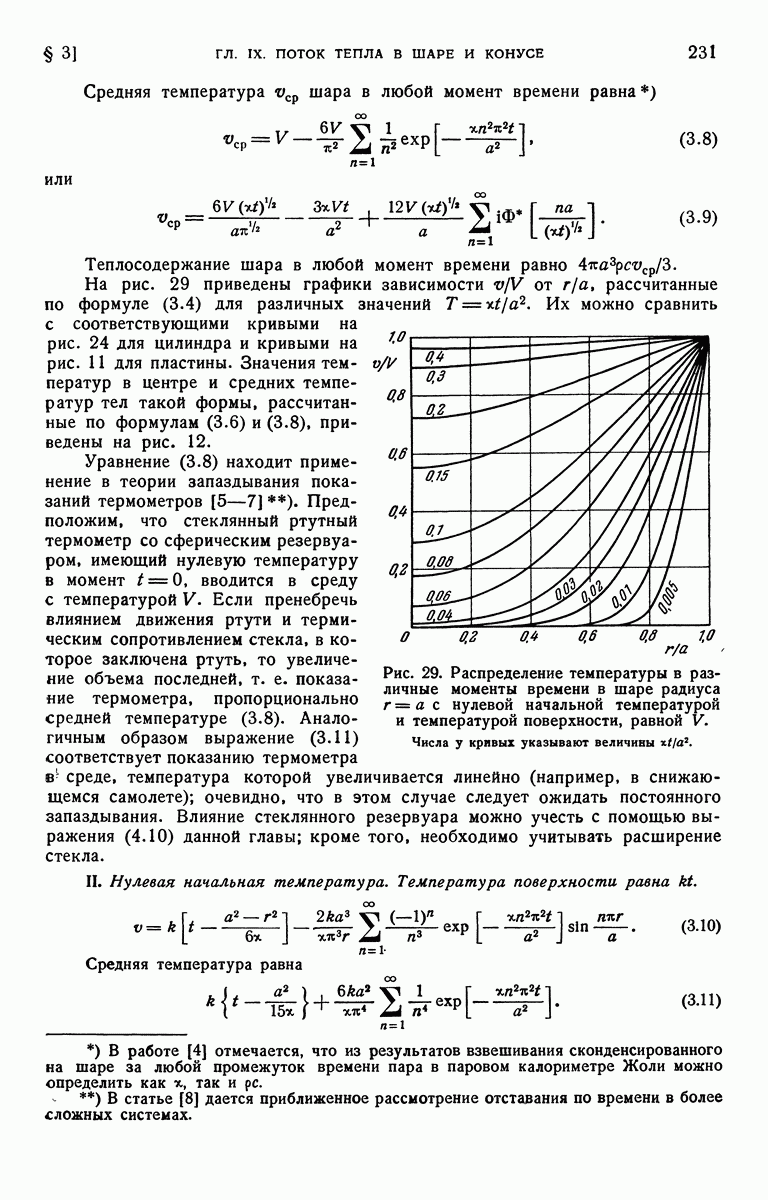
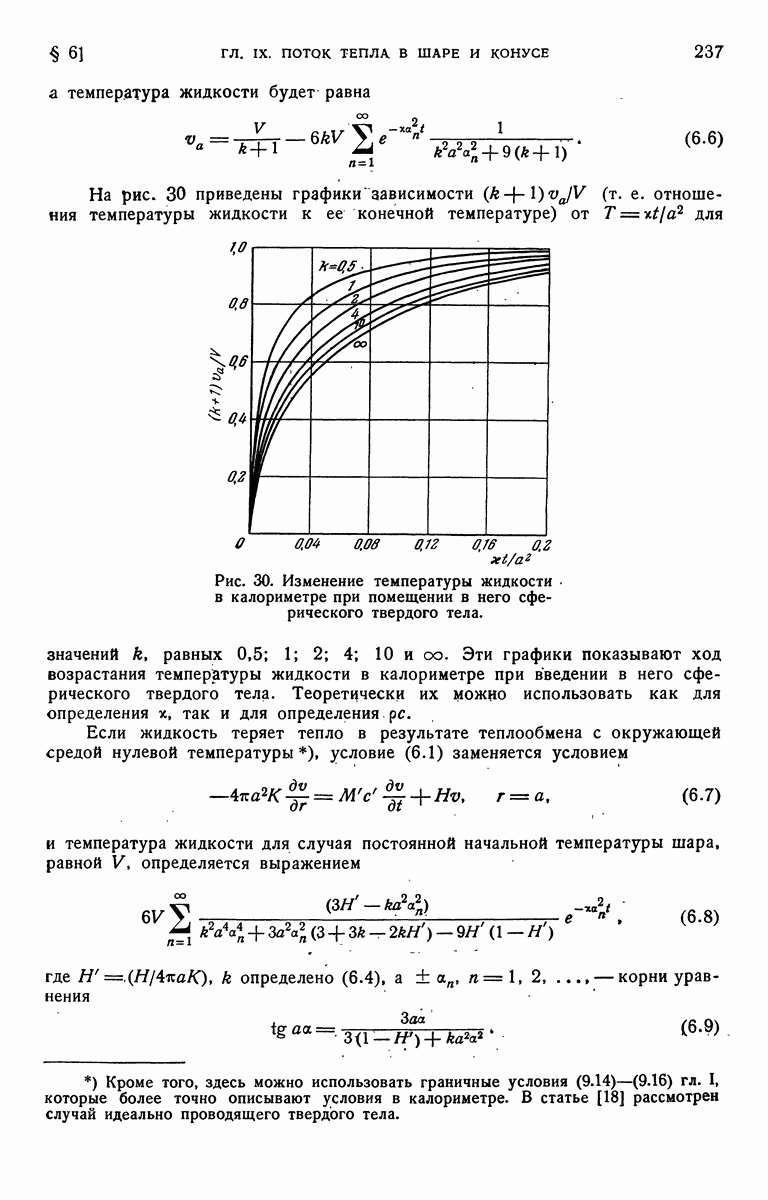
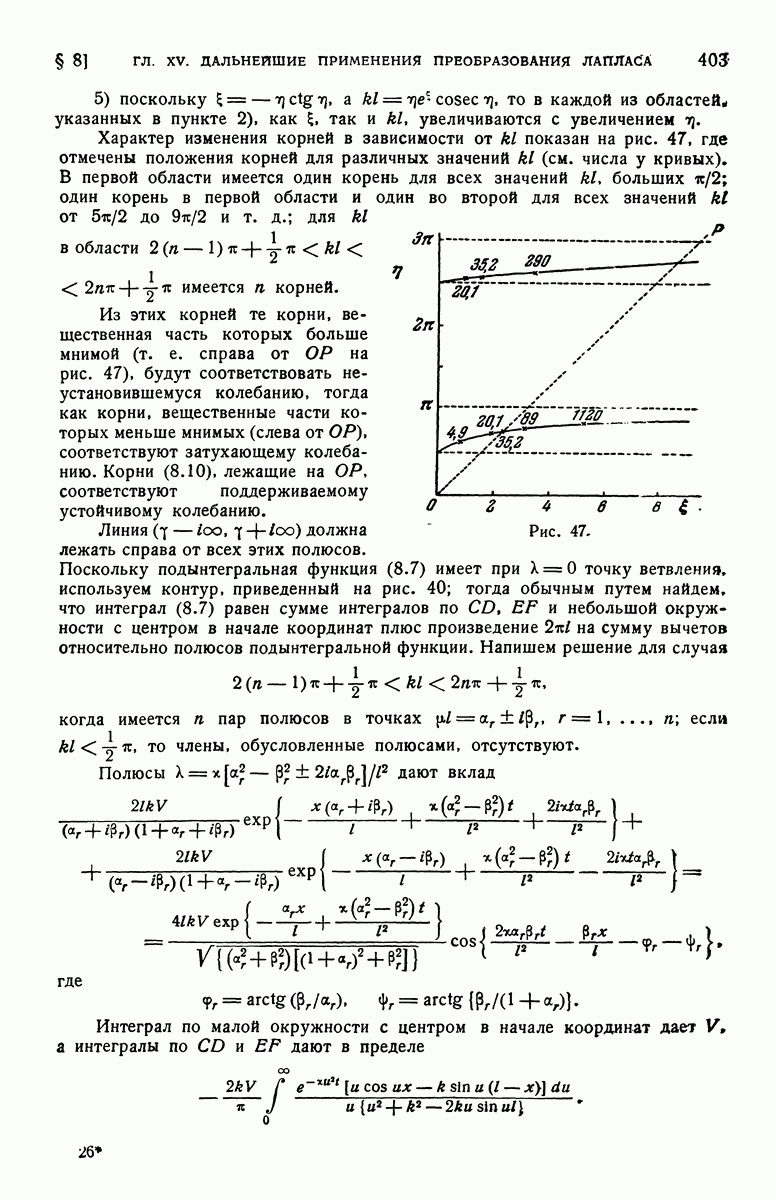
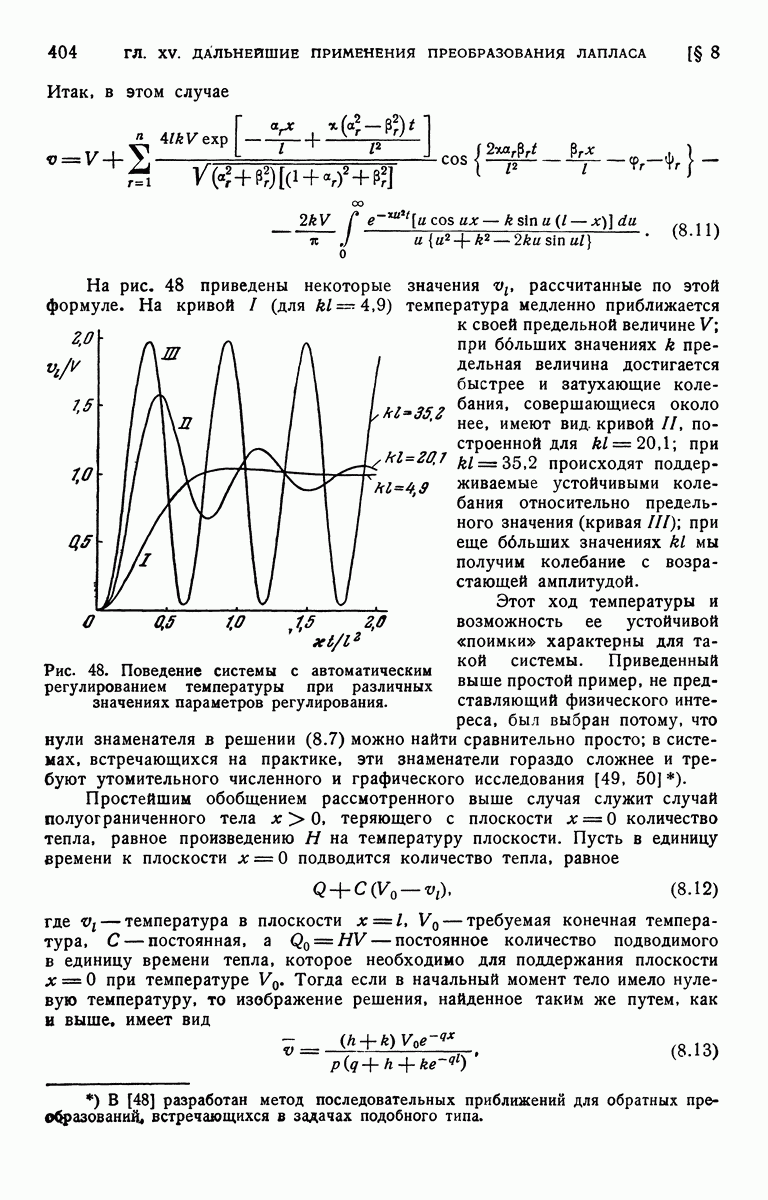
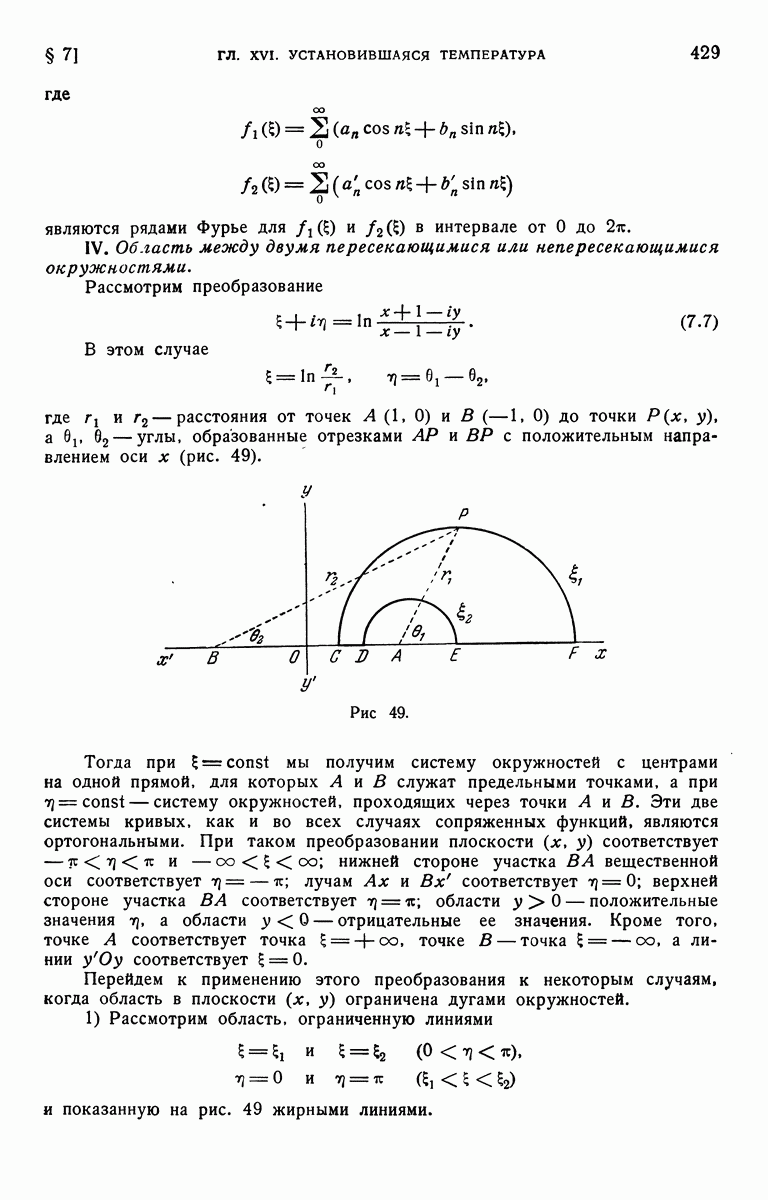
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
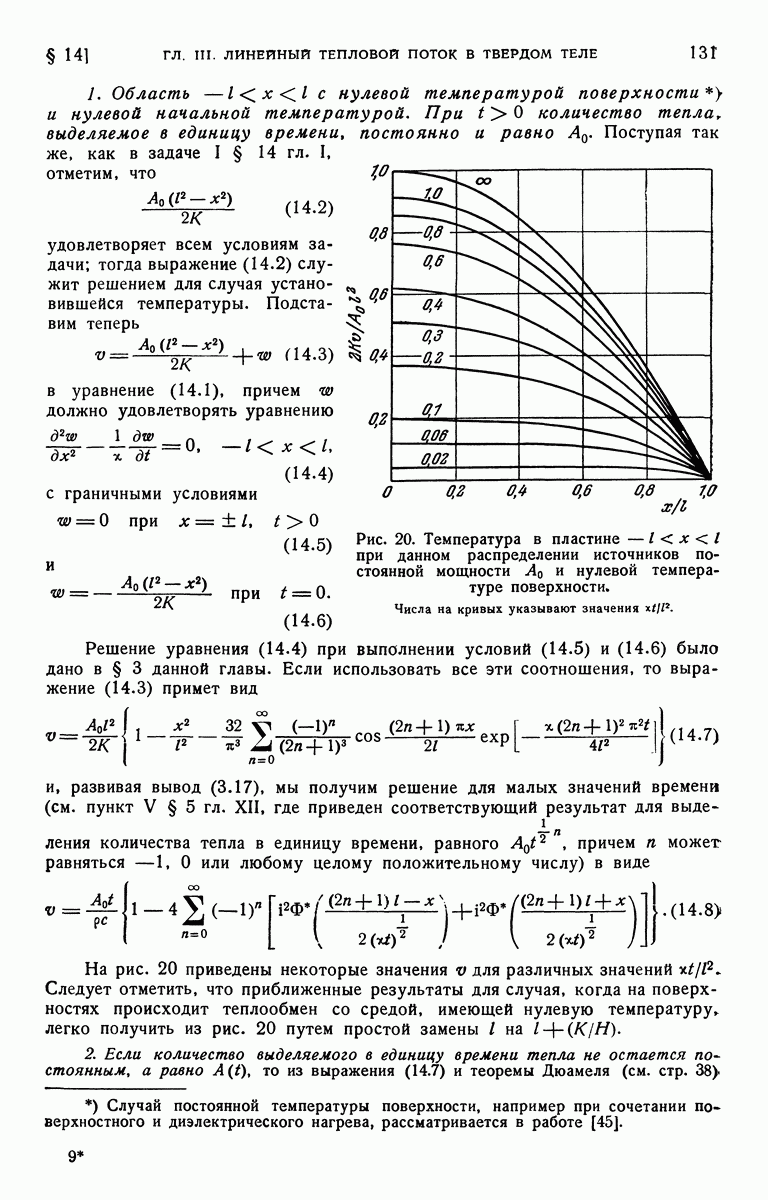
ZADANIA.TO
§ 8. Составные твердые тела
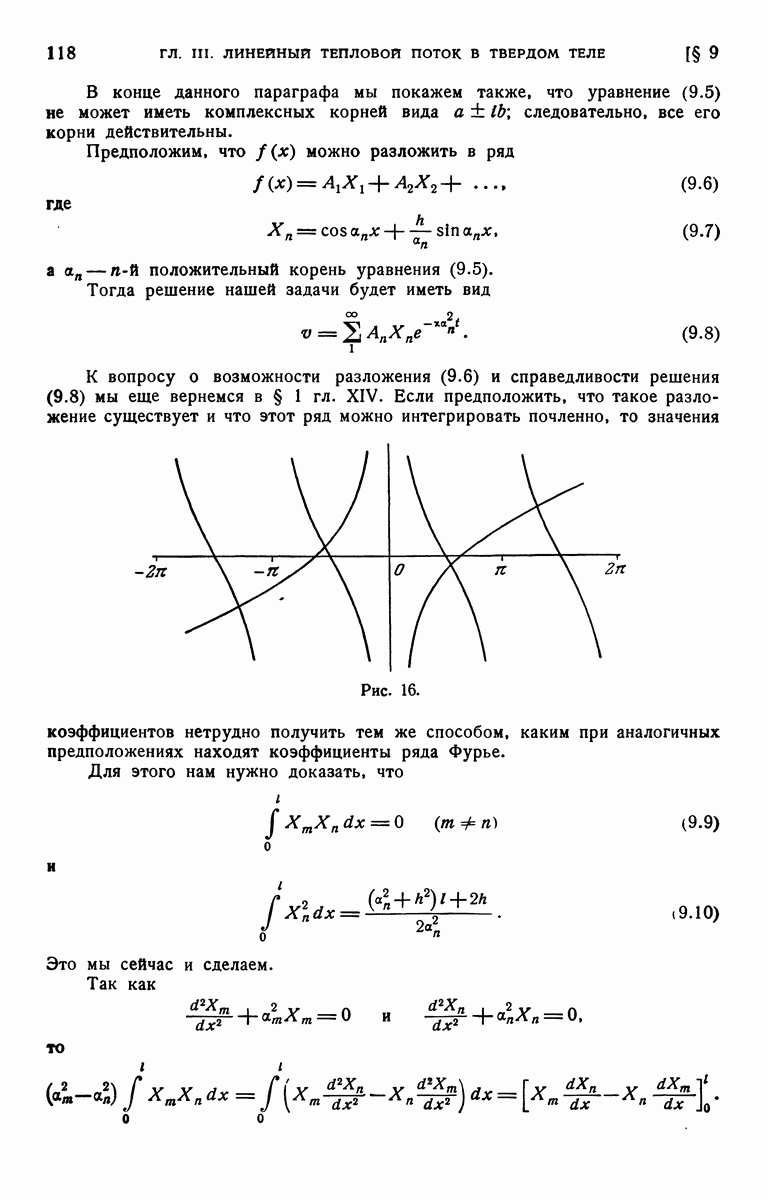
Задачи теплопроводности в составных твердых телах обычно лучше всего решаются методом преобразования Лапласа. Как изображения, так и решения могут оказаться достаточно сложными, однако при этом не появляется никаких новых правил. В § 15 гл. II изучалось несколько задач, в которых рассматривается составное твердое тело. Их можно также решать данным методом. Здесь будут рассмотрены полуограниченные и конечные составные области.
Рассмотрим сначала полуограниченную область —  в которой при
в которой при  находится одно вещество, а при
находится одно вещество, а при  другое. Обозначим теплопроводность, плотность, удельную теплоемкость, коэффициент температуропроводности и температуру в области
другое. Обозначим теплопроводность, плотность, удельную теплоемкость, коэффициент температуропроводности и температуру в области  через
через  а соответствующие величины в области
а соответствующие величины в области  через
через 
Требуется найти решения следующих дифференциальных уравнений:

Если допустить, что на поверхности раздела  контактное тепловое сопротивление отсутствует (ср. пример Ж § 9 гл. I), то граничные условия запишутся в виде
контактное тепловое сопротивление отсутствует (ср. пример Ж § 9 гл. I), то граничные условия запишутся в виде

I. Для описанного выше твердого тела с нулевой начальной температурой и плоскостью  поддерживаемой при
поддерживаемой при  при постоянной температуре, вспомогательные уравнения имеют вид
при постоянной температуре, вспомогательные уравнения имеют вид

где

Эти уравнения должны быть решены при условиях

Решение уравнения (8.3), удовлетворяющее условию (8.7), имеет вид

решение уравнения (8.4), удовлетворяющее условию (8.8), имеет вид

Неизвестные  находят из (8.6), и окончательно мы получим
находят из (8.6), и окончательно мы получим

здесь используются следующие обозначения:

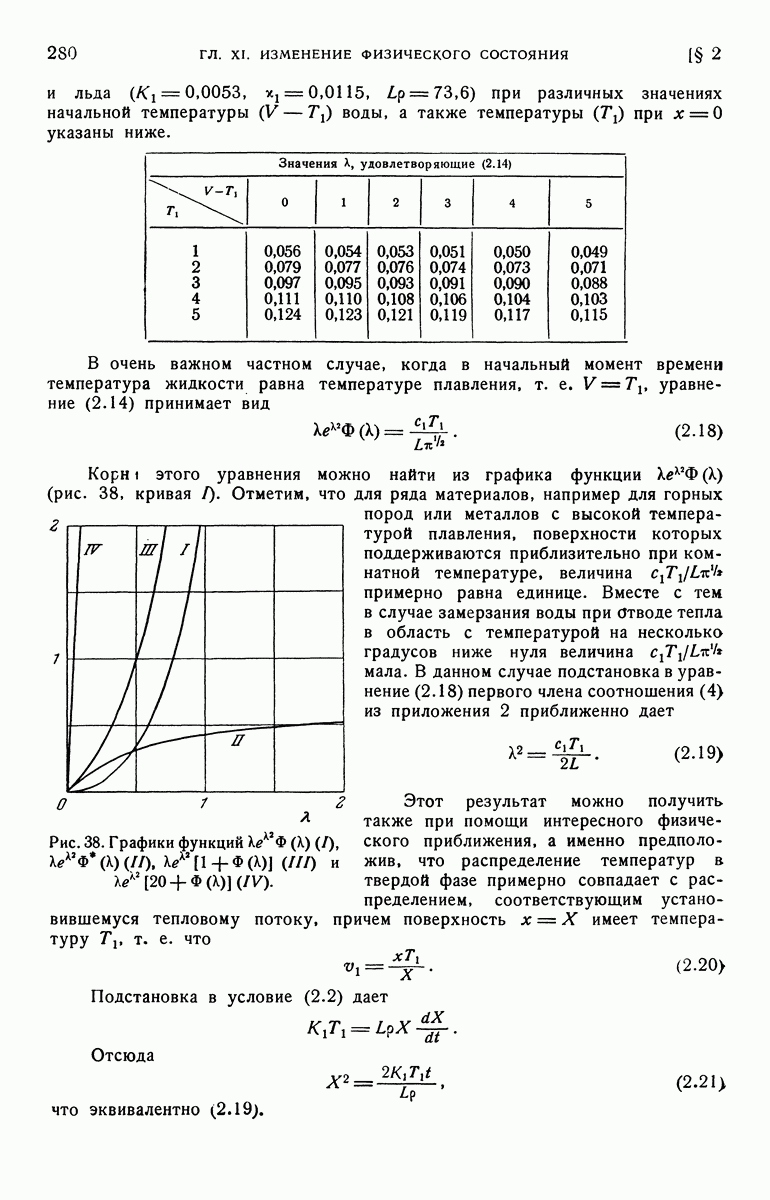
Для оценки  можно использовать либо теорему обращения, либо метод разложения в ряд, описанный в § 5 данной главы. Согласно теореме обращения можно написать
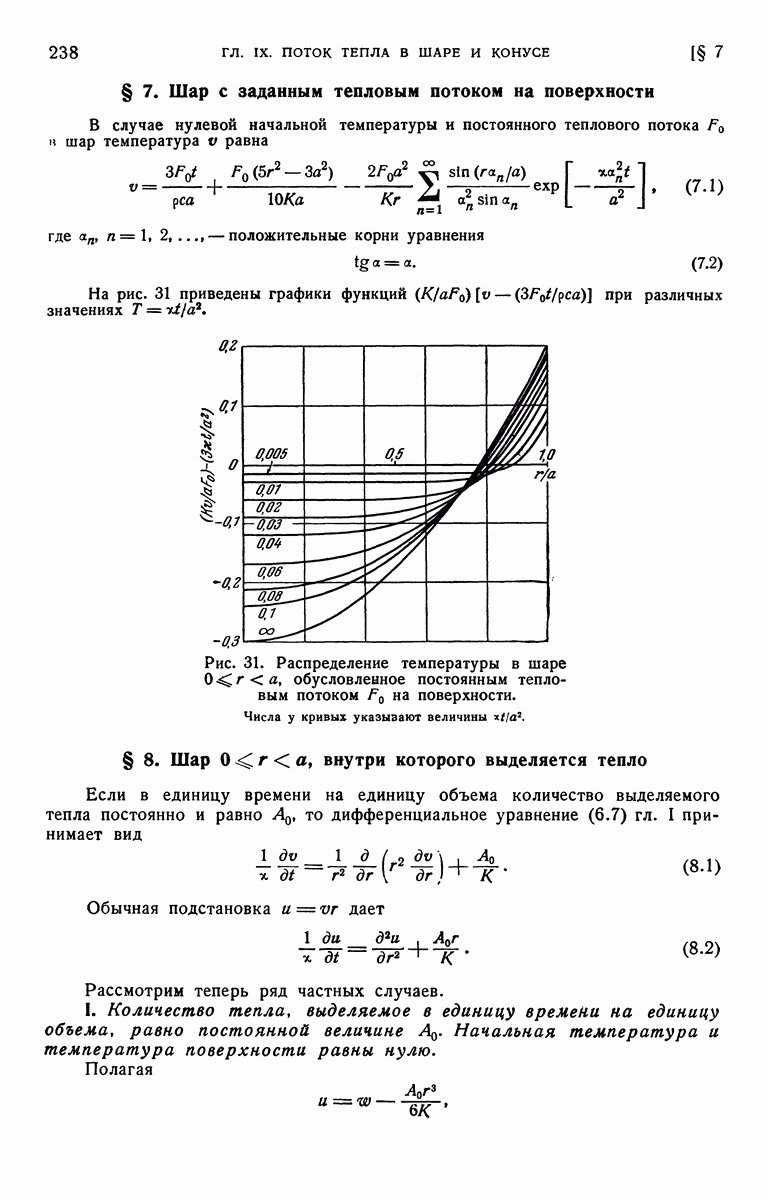
можно использовать либо теорему обращения, либо метод разложения в ряд, описанный в § 5 данной главы. Согласно теореме обращения можно написать

где  Подынтегральная функция в соотношении (8.12) имеет при
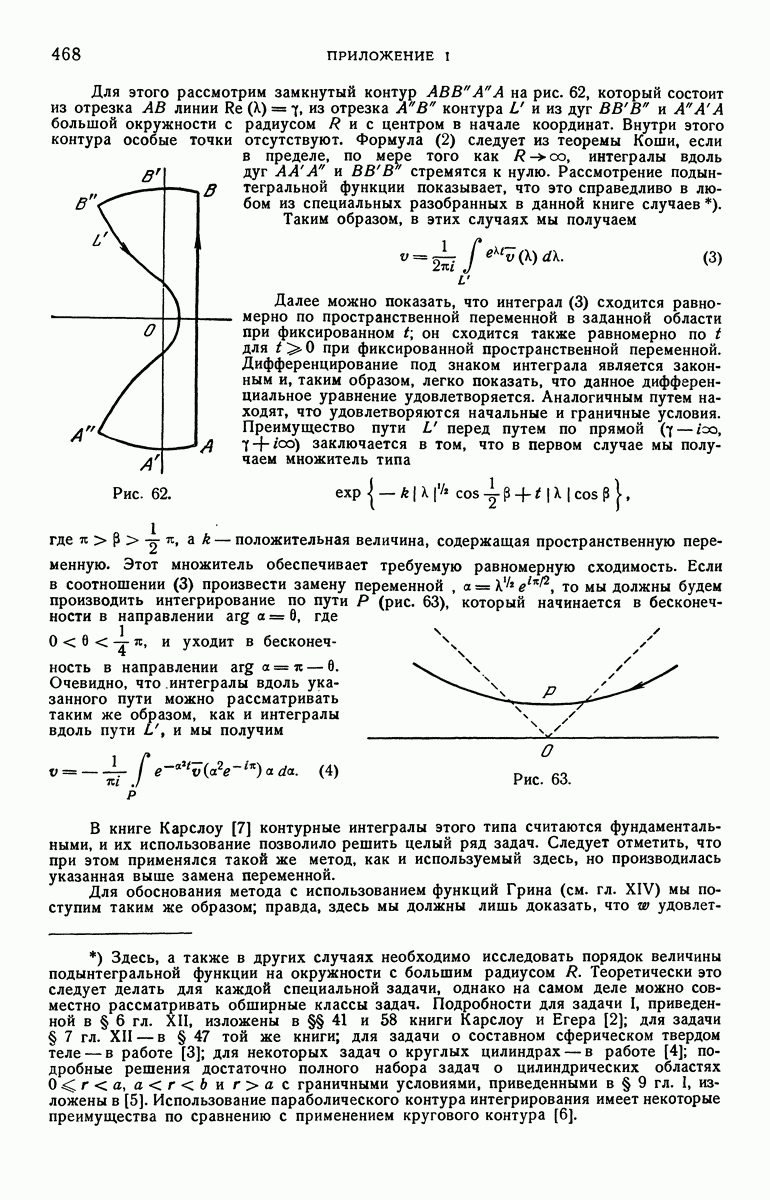
Подынтегральная функция в соотношении (8.12) имеет при  точку ветвления; поэтому, как и в предыдущем параграфе, мы используем контур, изображенный на рис. 40; тогда интеграл в (8.12) окажется равным сумме интегралов по малой окружности с центром в начале координат и по прямым
точку ветвления; поэтому, как и в предыдущем параграфе, мы используем контур, изображенный на рис. 40; тогда интеграл в (8.12) окажется равным сумме интегралов по малой окружности с центром в начале координат и по прямым  и
и 
Интегрируя по малой окружности, получаем 
Полагая, что на  а на
а на  получим, что вклад со стороны
получим, что вклад со стороны  и
и  равен
равен

Таким образом,

Аналогичным образом получим

Изложенный в § 5 данной главы метод дает решение в форме, которая зачастую оказывается более удобной. Используя обозначения (8.11), можно из (8.10)
получить

Из (8) приложения  следует, что
следует, что

Подобным же образом

Используя (7) приложения 5, таким же путем находим градиент температуры на поверхности в виде

Для очень больших значений времени все показательные функции в (8.18) можно заменить единицей, и мы приближенно получим

Если поверхность поддерживается при нулевой температуре, а начальная температура всего твердого тела равна V, то, очевидно, что градиент температуры при  будет равен написанному выше выражению с обратным знаком. Этот результат был использован Перри и Хевисайдом при определении возраста Земли. Кельвин в своей классической работе (см. § 14 гл. II) установил, что градиент температуры равен
будет равен написанному выше выражению с обратным знаком. Этот результат был использован Перри и Хевисайдом при определении возраста Земли. Кельвин в своей классической работе (см. § 14 гл. II) установил, что градиент температуры равен  Теперь известно, что плотность и физические свойства ядра Земли значительно отличаются от соответствующих величин для наружной оболочки. Приняв это, мы увидим, что время, необходимое для уменьшения температурного градиента до существующего в настоящее время уровня, в
Теперь известно, что плотность и физические свойства ядра Земли значительно отличаются от соответствующих величин для наружной оболочки. Приняв это, мы увидим, что время, необходимое для уменьшения температурного градиента до существующего в настоящее время уровня, в  Раз больше времени, получающегося из теории Кельвина. По данным, принятым Перри и Хевисайдом, это отношение примерно равно 450, и оценку Кельвина, равную 108 лет, следует увеличить до
Раз больше времени, получающегося из теории Кельвина. По данным, принятым Перри и Хевисайдом, это отношение примерно равно 450, и оценку Кельвина, равную 108 лет, следует увеличить до  лет.
лет.
Представляет некоторый интерес случай малого  т. е. случай тонкой пленки иного материала, находящейся на поверхности полуограниченного твердого тела. Разлагая гиперболические функции в знаменателе решения (8.10) по возрастающим степеням
т. е. случай тонкой пленки иного материала, находящейся на поверхности полуограниченного твердого тела. Разлагая гиперболические функции в знаменателе решения (8.10) по возрастающим степеням  найдем
найдем

Учитывая только первую степень I, получим

где  Это равно значению
Это равно значению  полученному с учетом приближенного граничного условия (9.7) гл. I, в котором мы полностью пренебрегали теплоемкостью пленки. Во втором приближении, учитывающем также член с
полученному с учетом приближенного граничного условия (9.7) гл. I, в котором мы полностью пренебрегали теплоемкостью пленки. Во втором приближении, учитывающем также член с 
получим

где  Изображения такого типа появлялись в примере III § 4 данной главы. Выражение (8.21) является изображением решения задачи о полуограниченном твердом теле с нулевой начальной температурой и граничным условием в виде
Изображения такого типа появлялись в примере III § 4 данной главы. Выражение (8.21) является изображением решения задачи о полуограниченном твердом теле с нулевой начальной температурой и граничным условием в виде

Таким образом, это условие можно считать приближенным граничным условием, учитывающим теплоемкость пленки.
II. Описанное выше составное твердое тело с нулевой начальной температурой" При  в области
в области  в единицу времени на единицу объема выделяется постоянное количество тепла
в единицу времени на единицу объема выделяется постоянное количество тепла  В области
В области  тепло не выделяется. Плоскость
тепло не выделяется. Плоскость  поддерживается при нулевой температуре.
поддерживается при нулевой температуре.
В данном случае, используя обозначения (8.11), получим следующие решения:

или

или

III. Пластина конечных размеров. Область пластины —  содержит материал с параметрами
содержит материал с параметрами  а область
а область  другой материал, с параметрами
другой материал, с параметрами  Начальная температура равна нулю. При
Начальная температура равна нулю. При  плоскость
плоскость  поддерживается при постоянной температуре V, а плоскость
поддерживается при постоянной температуре V, а плоскость  нулевой температуре.
нулевой температуре.
Вспомогательными уравнениями здесь служат уравнения (8.3) — (8.7), но условие (8.8) заменяется на условие

Решая эти уравнения, находим

Разложение этих выражений в ряды типа (8.15) довольно сложно, и поэтому мы рассмотрим только решения, получаемые при помощи теоремы обращения. В данном случае подынтегральные функции являются однозначными функциями  с простыми полюсами при
с простыми полюсами при  где
где  корни уравнения
корни уравнения

Применяя обычным образом теорему обращения, найдем

Ряды в решениях (8.30) и (8.31) можно немного упростить, используя снова (8.29), Следует отметить, что корни уравнения (8.29) служат корнями уравнения

и общими корнями (если вообще они имеются) уравнений

Последние уравнения имеют общие корни тогда и только тогда, когда отношение  есть рациональная величина. Таким образом, если
есть рациональная величина. Таким образом, если

есть несократимая рациональная дробь, то общие положительные корни (8.33) равны  и эти корни уравнения (8.29) дадут для
и эти корни уравнения (8.29) дадут для  соответственно ряды
соответственно ряды

и

Если дробь  иррациональна, эти ряды не появятся.
иррациональна, эти ряды не появятся.
Во всех случаях существует ряд членов, соответствующих положительным корням  уравнения (8.32).
уравнения (8.32).
Воспользовавшись уравнением (8.32), можно представить члены рядов (8.30) и (8.31), соответствующие этим корням, в виде

и

соответственно для  .
.
IV. Характер корней уравнения (8.32) и уравнений, появляющихся в аналогичных задачах.
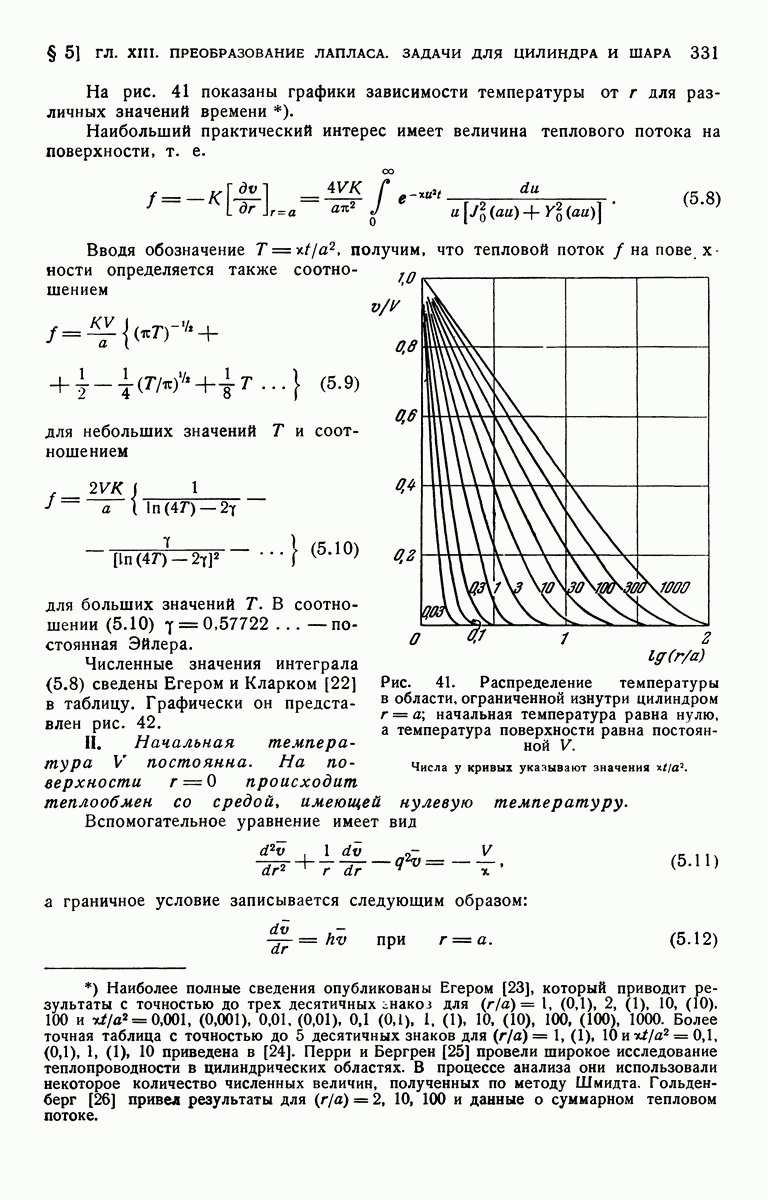
При получении решений в виде бесконечных рядов с помощью теоремы обращения мы обычно еще должны доказать, что все корни определенного трансцендентного уравнения действительны и просты. В примере III таким уравнением было уравнение (8.32); в задаче о твердом теле в виде составного шара им является уравнение (9.35) гл. XIII; в случае более общих граничных условий появляются другие типы уравнений, например уравнение (9.25) гл. XIII и т. п.
В § 9 гл. III было исследовано очень простое уравнение. Обобщение примененного там метода [27, 38] можно использовать во всех случаях. Здесь же в качестве примера мы рассмотрим уравнение (8.32).
Очевидно, что оно не может иметь чисто мнимого корня  так как
так как

Покажем теперь, что оно не может иметь комплексного корня вида  Рассмотрим функцию
Рассмотрим функцию  определяемую следующим образом:
определяемую следующим образом:

где  корень уравнения (8.32).
корень уравнения (8.32).
В таком случае получим

Кроме того,

и

так как  корень уравнения (8.32).
корень уравнения (8.32).
Пусть теперь  — два различных корня уравнения (8.32), и пусть
— два различных корня уравнения (8.32), и пусть  и
и  величины, соответствующие величинам
величины, соответствующие величинам  при замене
при замене  на а.
на а.
Тогда из соотношений (8.41) и соответствующих уравнений для  и
и  получим
получим

Отсюда, используя соотношения (8.42) и (8.43), находим

Из последнего соотношения следует, что  не могут иметь вид
не могут иметь вид  поскольку
поскольку  были бы тогда сопряженными комплексными величинами и величина
были бы тогда сопряженными комплексными величинами и величина

была бы положительной.
Таким образом, мы доказали, что все корни уравнения (8.32) являются вещественными. Их симметричное расположение относительно начала координат и то обстоятельство, что они не повторяются, следует в данном случае из рассмотрения кривых  Другие случаи можно рассмотреть путем обобщения описанного выше метода (см. [38]).
Другие случаи можно рассмотреть путем обобщения описанного выше метода (см. [38]).
V. Составная пластина из произвольного числа слоев.
При написании изображения любой требуемой функции для общего случая  слоев трудностей не встречается. Легче всего это сделать при помощи описываемого ниже метода матриц. Вследствие сложности получаемых решений рассмотрение корней знаменателя в изображении решения и численная оценка температур требуют проведения очень сложных вычислений. Следует отметить, что, когда изображение найдено, оно непосредственно дает стационарное периодическое решение; кроме того, в тех случаях, когда рассматриваемая величина имеет прямолинейную асимптоту в виде
слоев трудностей не встречается. Легче всего это сделать при помощи описываемого ниже метода матриц. Вследствие сложности получаемых решений рассмотрение корней знаменателя в изображении решения и численная оценка температур требуют проведения очень сложных вычислений. Следует отметить, что, когда изображение найдено, оно непосредственно дает стационарное периодическое решение; кроме того, в тех случаях, когда рассматриваемая величина имеет прямолинейную асимптоту в виде  ее легко найти простым хорошо известным численным методом (ср. § 6 гл. XV).
ее легко найти простым хорошо известным численным методом (ср. § 6 гл. XV).
Для определения изображения рассмотрим сначала пластину  Тогда, если
Тогда, если  изображения температуры и теплового потока в точке х, то из вспомогательных уравнений сразу же получим
изображения температуры и теплового потока в точке х, то из вспомогательных уравнений сразу же получим

или в матричном обозначении, определенном в § 7 гл. III,

Рассмотрим теперь пластину, состоящую из  слоев,
слоев,  Пусть
Пусть  теплопроводность и температуропроводность
теплопроводность и температуропроводность  слоя,
слоя,  изображения температуры и теплового потока на границе этого слоя
изображения температуры и теплового потока на границе этого слоя  их значения на границе слоя
их значения на границе слоя  Тогда из (8.47) получим
Тогда из (8.47) получим

где

и

Если между пластинами имеется идеальный тепловой контакт, то повторное применение (8.49) дает

Если теплопередача происходит по линейному закону, контактные сопротивления равны  при
при  область
область  имеет температуру
имеет температуру  а область
а область  — температуру
— температуру  то
то

Таким способом определяются изображения для температуры или тепловых потоков при любом из  а значения для промежуточных точек можно найти затем из уравнений (8.45) и (8.46). Этим способом можно, например, вывести соотношения (8.27) и (8.28).
а значения для промежуточных точек можно найти затем из уравнений (8.45) и (8.46). Этим способом можно, например, вывести соотношения (8.27) и (8.28).
VI. Область  состоит из одного материала, а область
состоит из одного материала, а область  из другого. Тепловой поток при
из другого. Тепловой поток при  отсутствует. Начальная температура в области
отсутствует. Начальная температура в области  постоянна, а в области
постоянна, а в области  равна нулю.
равна нулю.
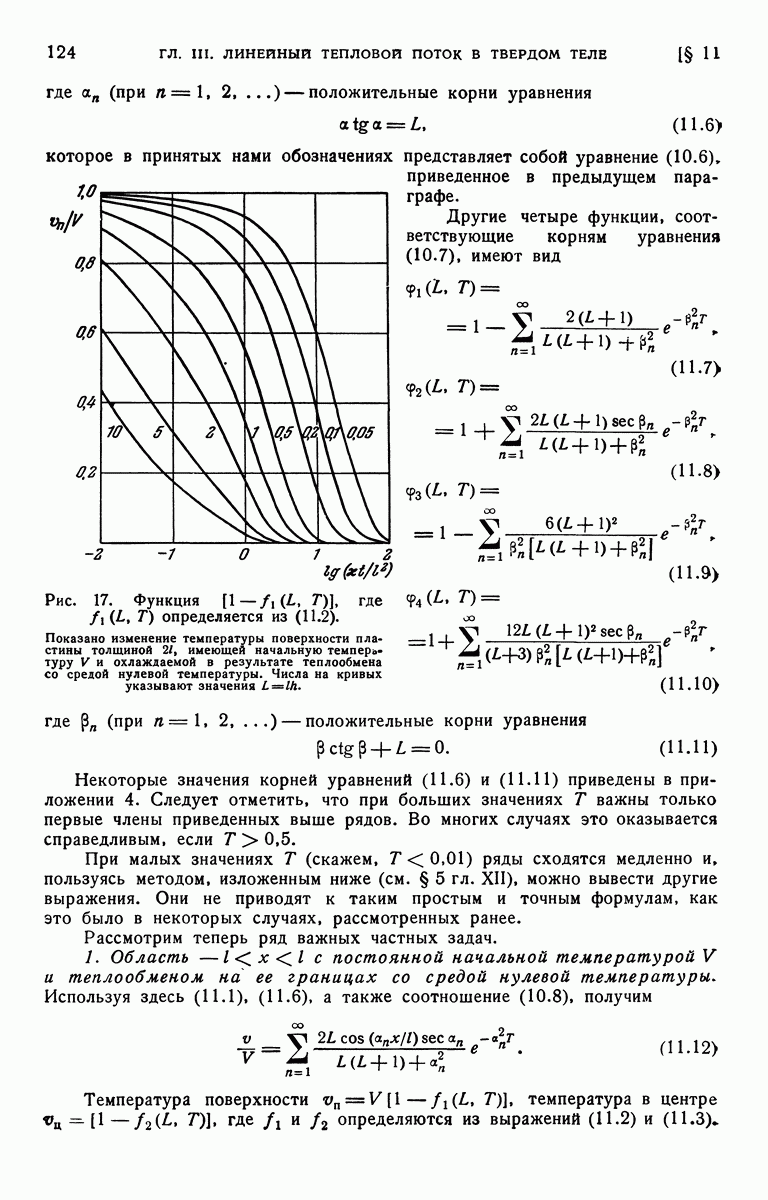
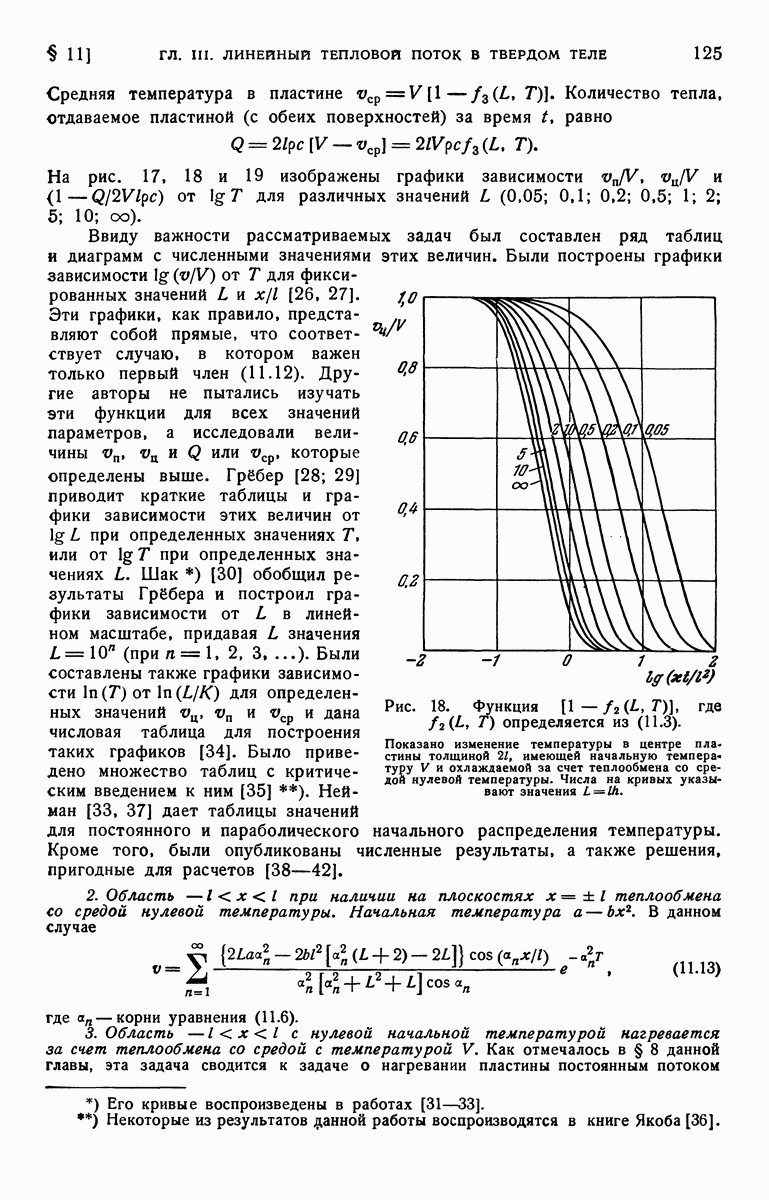
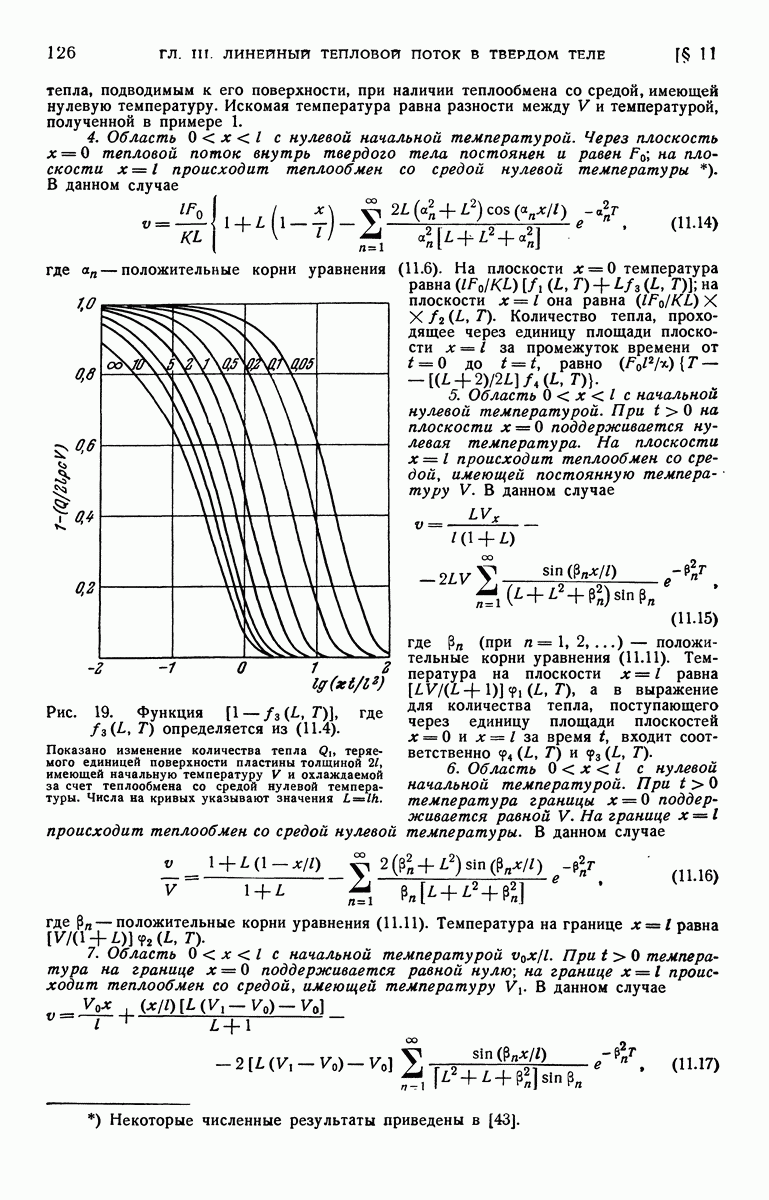
Решение этой задачи и численные значения температур при  приведены в статье [39].
приведены в статье [39].
ЛИТЕРАТУРА
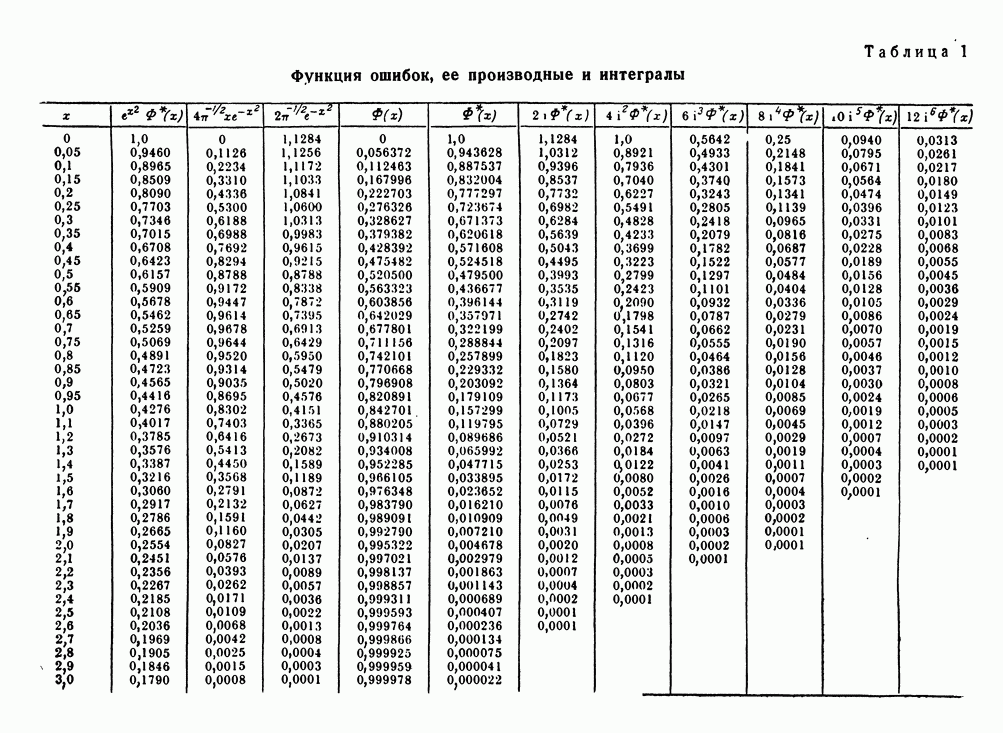
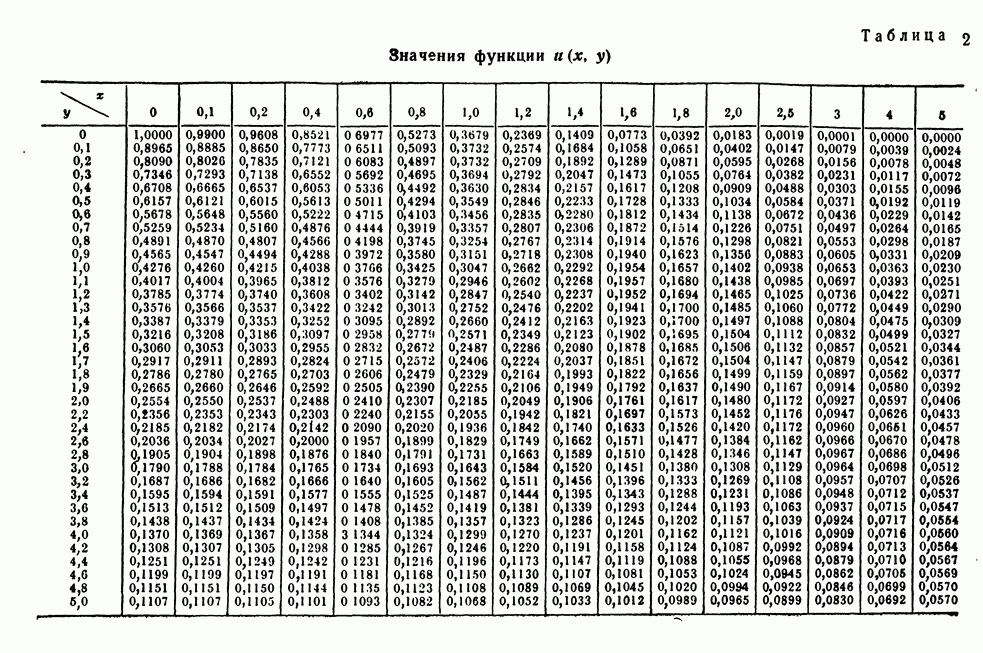
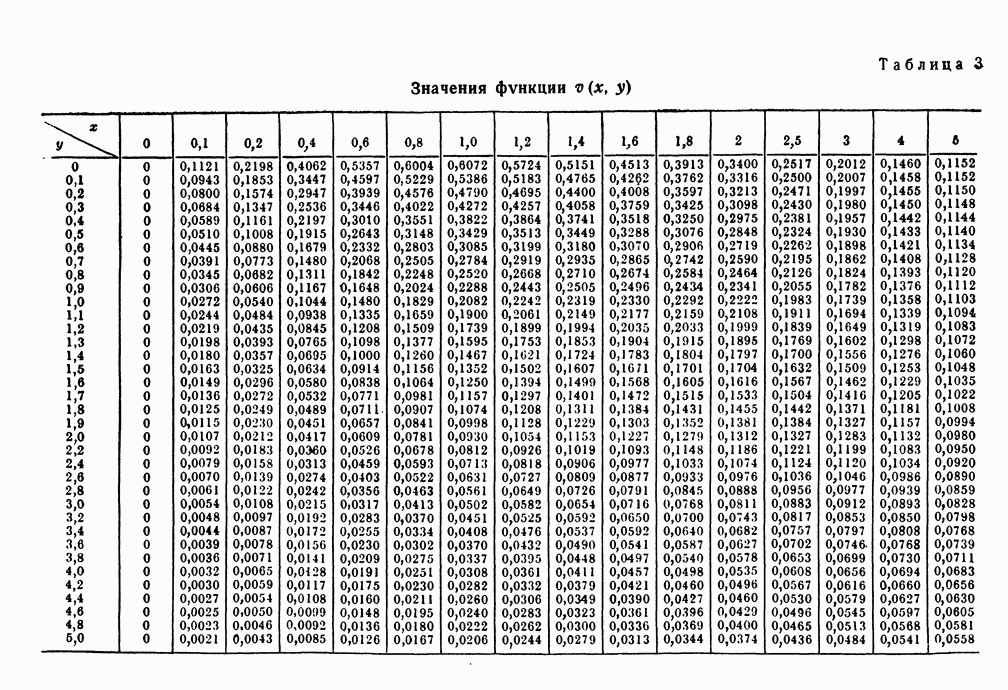
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ
- § 2. Теплопроводность
- § 3. Тепловой поток через произвольную поверхность
- § 4. Изотермические поверхности
- § 5. Теплопроводность изотропных тел
- § 6. Дифференциальное уравнение теплопроводности для изотропного твердого тела
- § 7. Дифференциальное уравнение теплопроводности для движущейся среды
- § 8. Преобразование координат
- § 9. Начальные и граничные условия
- § 10. Безразмерные параметры
- § 11. Экспериментальные методы определения теплопроводности
- § 12. Математическая интерпретация начальных и граничных условий
- § 13. Родственные дифференциальные уравнения
- § 14. Упрощение общей задачи теплопроводности
- § 15. Задачи, решения которых можно выразить в виде произведения решений более простых задач
- § 16. Единственность решения задачи теплопроводности
- § 17. Теплопроводность анизотропных твердых тел
- § 18. Дифференциальное уравнение теплопроводности для анизотропных твердых тел
- § 19. Теплопроводность тонкой кристаллической пластины
- § 20. Изменение теплопроводности и вектор теплового потока в анизотропных твердых телах
- ГЛАВА II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА. НЕОГРАНИЧЕННОЕ И ПОЛУОГРАНИЧЕННОЕ ТВЕРДОЕ ТЕЛО
- § 2. Неограниченное твердое тело. Решение Лапласа
- § 3. Использование интегралов Фурье и преобразований Фурье
- § 4. Полуограниченное тело с начальной температурой f(x) и нулевой температурой поверхности
- § 5. Полуограниченное твердое тело. Начальная температура равна нулю. Поверхность находится при температуре …
- § 6. Полуограниченное твердое тело. Температура поверхности является гармонической функцией времени
- § 7. Полуограниченное твердое тело. Теплообмен на поверхности в среду с нулевой температурой. Начальная температура постоянна
- § 8. Полуограниченное твердое тело. Теплообмен на поверхности в среду с температурой f(t). Начальная температура равна нулю
- § 9. Полуограниченное тело. Тепловой поток на границе х = 0 является заданной функцией времени. Начальная температура равна нулю
- § 10. Применение полученных результатов к определению теплопроводности
- § 11. Полуограниченное твердое тело, внутри которого находится источник тепла
- § 12. Температура Земли и колебания температуры на ее поверхности
- § 13. Геотермический градиент и поток тепла
- § 14. Возраст Земли. Анализ Кельвина
- § 15. Неограниченное составное твердое тело
- § 16. Случай зависимости термических характеристик вещества от температуры
- ГЛАВА III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ, ОГРАНИЧЕННОМ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
- § 3. Область [0, l]. Границы поддерживаются при нулевой температуре. Начальная температура f(x)
- § 4. Область [0, l] Начальная температура f(x). Границы поддерживаются при постоянной температуре или изолированы
- § 5. Область [0, l]. Температуры границ равны … Начальная температура f(x)
- § 6. Пластина с периодически изменяющейся температурой поверхности
- § 7. Установившаяся периодически изменяющаяся температура в составных пластинах
- § 8. Пластина с заданным тепловым потоком на ее границе
- § 9. Область [0, l]. Теплообмен на границах в среду с температурой, равной нулю. Начальная температура равна f(х)
- § 10. Область [-l, l]. На границах х=+l происходит теплообмен со средой нулевой температуры. Начальная температура f(x)
- § 11. Частные случаи и численные результаты для пластины с граничным условием третьего рода
- § 12. Область [-l, l] с нулевой начальной температурой и теплообменом на границах со средой, имеющей температуру …
- § 13. Пластина, одна из поверхностей которой соприкасается со слоем идеального проводника или хорошо перемешиваемой жидкости
- § 14. Пластина с внутренним источником тепла
- ГЛАВА IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ
- § 3. Полуограниченный стержень. Случай установившейся температуры. Метод Форбса
- § 4. Полуограниченный стержень. Периодически изменяющаяся температура. Метод Ангстрема [5—10]
- § 5. Ограниченный стержень, концы которого находятся при фиксированных температурах. Случай установившейся температуры
- § 6. Стержень переменного сечения с охлаждающимися ребрами. Случай установившейся температуры
- § 7. Ограниченный стержень при наличии теплообмена на его поверхности. Случай неустановившейся температуры
- § 8. Ограниченный стержень с периодически изменяющейся температурой концов. Метод Неймана
- § 9. Задачи по теплопроводности в движущемся стержне
- § 10. Уравнение теплопроводности для тонкой проволоки, нагреваемой постоянным электрическим током
- § 11. Установившаяся температура. Определение коэффициента теплопроводности
- § 12. Сильно нагретая проволока, по которой протекает электрический ток
- § 13. Установившийся поток тепла в составной проволоке
- § 14. Неустановившаяся температура в проволоке, по которой течет электрический ток
- § 15. Кольцо Фурье
- ГЛАВА V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
- § 2. Неограниченное твердое тело прямоугольного сечения. Установившаяся температура
- § 3. Установившаяся температура в неограниченном теле прямоугольного сечения
- § 4. Тонкая пластина с прямоугольным сечением при наличии теплообмена на ее поверхности
- § 5. Установившаяся температура в теле прямоугольного сечения при наличии источника тепла
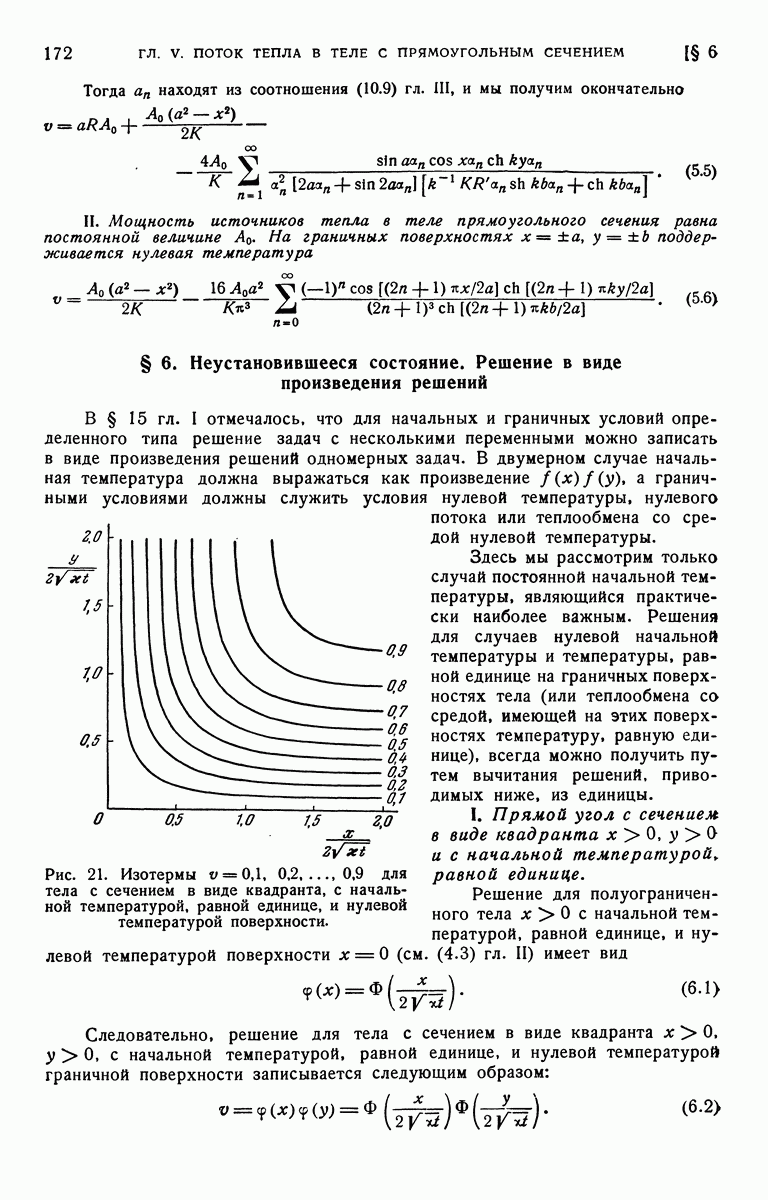
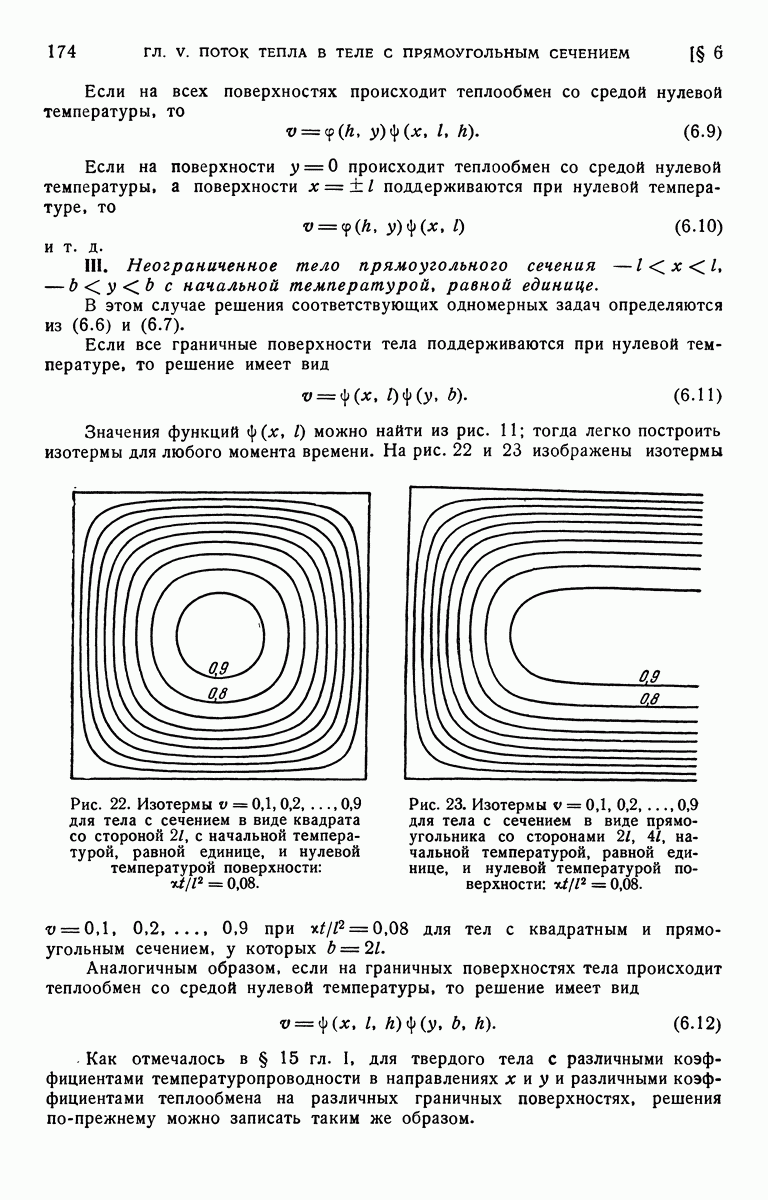
- § 6. Неустановившееся состояние. Решение в виде произведения решений
- § 7. Неустановившееся состояние. Произвольные начальные и граничные условия
- ГЛАВА VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ
- § 2. Установившаяся температура
- § 3. Двойные и кратные ряды Фурье
- § 4. Неустановившаяся температура. Решение в виде произведения решений
- § 5. Определение коэффициента теплопроводности и экстраполяция кривых охлаждения
- § 6. Неустановившаяся температура. Тройной ряд Фурье
- ГЛАВА VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ КРУГОВОГО СЕЧЕНИЯ
- § 2. Установившаяся температура. Радиальный поток
- § 3. Установившаяся, периодически изменяющаяся температура в круговых цилиндрах [19—22]
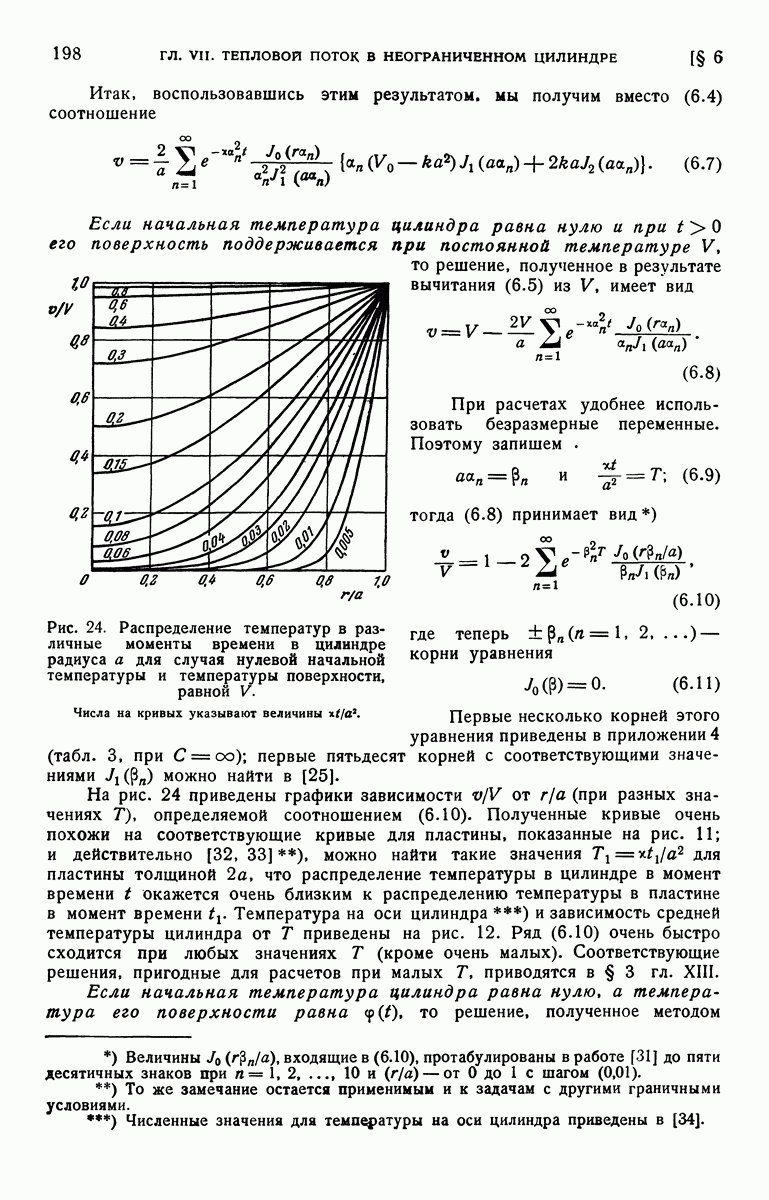
- § 4. Неограниченный цилиндр. Радиальный поток. Неустановившаяся температура
- § 5. Интегралы …
- § 6. Неограниченный цилиндр с температурой поверхности … и начальной температурой f(r)
- § 7. Неограниченный цилиндр с теплообменом на поверхности
- § 8. Неограниченный цилиндр с постоянным потоком тепла на поверхности
- § 9. Неограниченный цилиндр с внутренними источниками тепла
- § 10. Неограниченный полый цилиндр. Радиальный поток
- § 11. Неограниченный цилиндр. Установившаяся температура. Общий случай
- § 12. Неограниченный цилиндр. Неустановившаяся температура. Общий случай
- ГЛАВА VIII. ТЕПЛОВОЙ ПОТОК В ОБЛАСТЯХ, ОГРАНИЧЕННЫХ КООРДИНАТНЫМИ ПОВЕРХНОСТЯМИ ЦИЛИНДРИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ
- § 3. Установившаяся температура в ограниченном и полуограниченном цилиндрах
- § 4. Неустановившееся состояние. Решения в форме произведений
- § 5. Определение теплопроводности вещества в форме цилиндра
- § 6. Ограниченный цилиндр с начальной температурой …
- § 7. Полуограниченный цилиндр
- ГЛАВА IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ
- § 2. Установившаяся температура. Радиальный тепловой поток
- § 3. Шар с начальной температурой f(r) и температурой поверхности …
- § 4. Шар. Начальная температура f(r). На поверхности сферы происходит теплообмен
- § 5. Определение коэффициентов теплопроводности плохих проводников
- § 6. Случай шара, находящегося в контакте с хорошо перемешиваемой жидкостью
- § 7. Шар с заданным тепловым потоком на поверхности
- § 8. Шар, внутри которого выделяется тепло
- § 9. Полый шар
- § 10. Область, ограниченная изнутри сферической поверхностью r=a
- § 11. Шар с начальной температурой … Температура поверхности r=a равна нулю
- § 12. Поверхность шара r=a поддерживается при температуре …
- § 13. Часть шара, вырезаемая конусом … Температура поверхности равна нулю, начальная температура равна …
- § 14. Температура внутри Земли
- ГЛАВА Х. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ К ЗАДАЧАМ С НЕУСТАНОВИВШЕЙСЯ ТЕМПЕРАТУРОЙ
- § 2. Мгновенный точечный источник
- § 3. Мгновенные источники; линейный, плоский и поверхностные цилиндрический и сферический источники
- § 4. Непрерывные и периодические источники
- § 5. Поверхностный нагрев полуограниченной области
- § 6. Выделение тепла в неограниченной среде
- § 7. Движущиеся источники тепла
- § 8. Дублеты
- § 9. Метод последовательных волн
- § 10. Метод изображений. Линейный тепловой поток
- § 11. Применение метода изображений к двумерным и трехмерным задачам
- § 12. Обобщение метода изображений Зоммерфельдом
- ГЛАВА XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ
- § 2. Одномерные случаи плавления и затвердевания. Решение Неймана и его обобщение
- § 3. Область … при других граничных условиях
- § 4. Методы интегрального уравнения. Рассмотрение задач затвердевания, предложенное Лайтфутом
- § 5. Решения в цилиндрических и сферических координатах
- § 6. Осесимметричные задачи о замерзании и плавлении
- ГЛАВА XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЛИНЕЙНОГО ТЕПЛОВОГО ПОТОКА
- § 2. Преобразование Лапласа. Основные свойства
- § 3. Решение уравнения теплопроводности методом преобразования Лапласа
- § 4. Полуограниченная область. Решения, получаемые из таблицы изображений
- § 5. Ограниченная область (0, l). Решения, получаемые из таблицы изображений. Решения для небольших значений времени
- § 6. Ограниченная область (0, l). Применение теоремы обращения
- § 7. Полуограниченная область. Применение теоремы обращения
- § 8. Составные твердые тела
- ГЛАВА XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА
- § 3. Решения, применимые для малых интервалов времени
- § 4. Полый цилиндр
- § 5. Область ограничена изнутри цилиндром кругового сечения r=a
- § 6. Решения, применимые при больших значениях времени
- § 7. Область, ограниченная изнутри круговым цилиндром из идеального проводника
- § 8. Составная цилиндрическая область
- § 9. Шар. Радиальный тепловой поток
- ГЛАВА XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА К РЕШЕНИЮ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 2. Линейный тепловой поток. Полуограниченное твердое тело
- § 3. Линейный тепловой поток в области (0, a)
- § 4. Двумерные задачи. Тела с прямоугольным сечением
- § 5. Прямоугольный параллелепипед
- § 6. Линейный тепловой поток. Составные твердые тела
- § 7. Шар. Радиальный поток тепла
- § 8. Цилиндр. Радиальный тепловой поток
- § 9. Полуограниченное твердое тело. Трехмерные задачи
- § 10. Область, ограниченная двумя параллельными плоскостями
- § 11. Полуограниченное твердое тело с тонкой пленкой на плоскости z=0 из материала, имеющего значительно большую теплопроводность. В точке … расположен единичный мгновенный источник
- § 12. Неограниченное составное твердое тело. В точке действует мгновенный единичный источник
- § 13. Области, ограниченные цилиндрической поверхностью r=a
- § 14 Клин
- § 15. Цилиндрическая область
- § 16. Области, ограниченные сферической поверхностью r=a
- § 17. Конус
- § 18. Непрерывные источники
- ГЛАВА XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 3. Тепловые регенераторы и теплообменники
- § 4. Тепловой поток в слоистых системах
- § 5. Установившийся периодический режим
- § 6. Линейная асимптотика и запаздывание
- § 7. Выделение тепла
- § 8. Система автоматического регулирования температуры
- § 9. Неоднородные тела
- § 11. Прямое применение метода преобразования Лапласа к двумерным и трехмерным задачам
- ГЛАВА XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
- § 2. Источники и стоки при установившейся температуре
- § 3. Установившийся поток к почти плоской поверхности. Топографические поправки для геотермического потока
- § 4. Установившийся тепловой поток в составном теле
- § 5. Практические задачи
- § 6. Использование сопряженных гармонических функций в задачах с установившейся температурой
- § 7. Приложения этого метода [20, 21]
- § 8. Установившийся тепловой поток в многоугольнике
- § 9. Тепловой поток между изотермическими поверхностями
- ГЛАВА XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- § 2. Интегральные преобразования и формулы их обращения
- § 3. Неустановившийся тепловой поток
- § 4. Установившийся тепловой поток
- § 5. Конечные преобразования
- § 6. Последовательные преобразования
- ГЛАВА XVIII. ЧИСЛЕННЫЕ МЕТОДЫ
- § 3. Линейный тепловой поток в неограниченном пространстве
- § 4. Граничные условия
- § 5. Выделение тепла, переменная температуропроводность и скрытая теплота
- § 6. Релаксационные методы
- ПРИЛОЖЕНИЕ 1. КОНТУРНЫЕ ИНТЕГРАЛЫ И ПРОВЕРКА РЕШЕНИЙ, ПОЛУЧЕННЫХ ПРИ ПОМОЩИ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- ПРИЛОЖЕНИЕ 2. ФУНКЦИЯ ОШИБОК И РОДСТВЕННЫЕ ФУНКЦИИ
- ПРИЛОЖЕНИЕ 3. О ФУНКЦИЯХ БЕССЕЛЯ
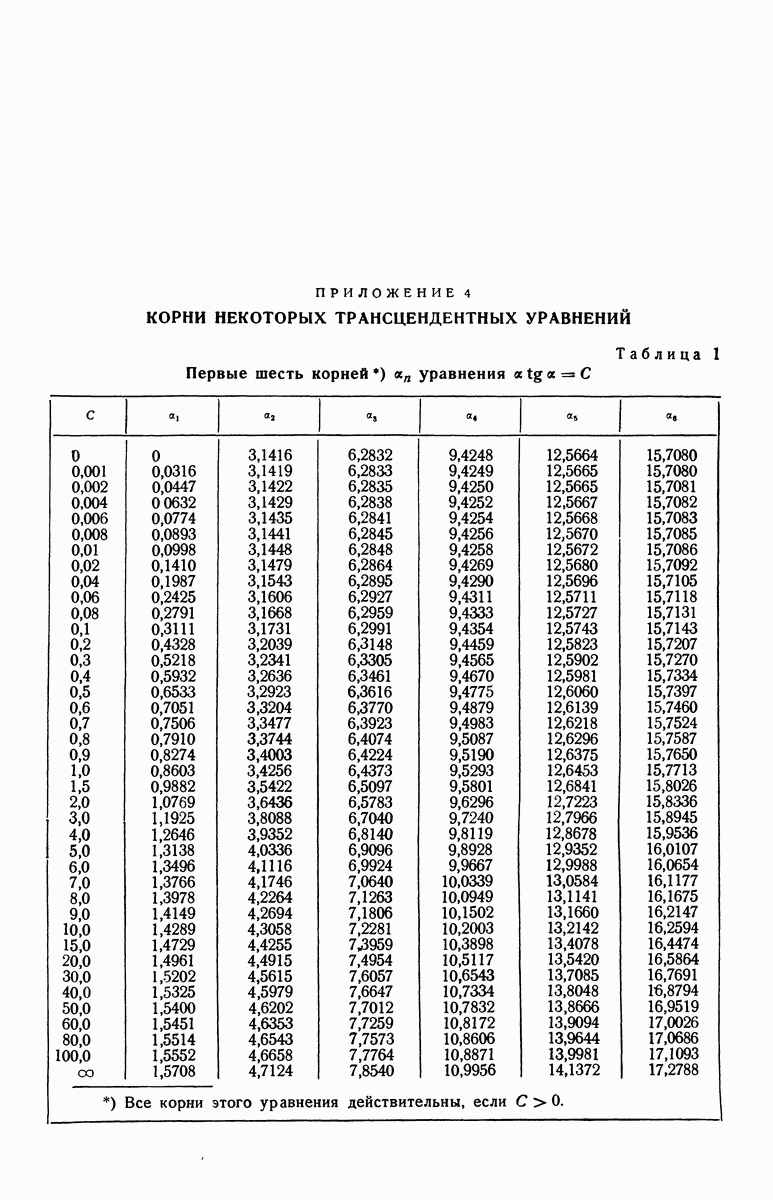
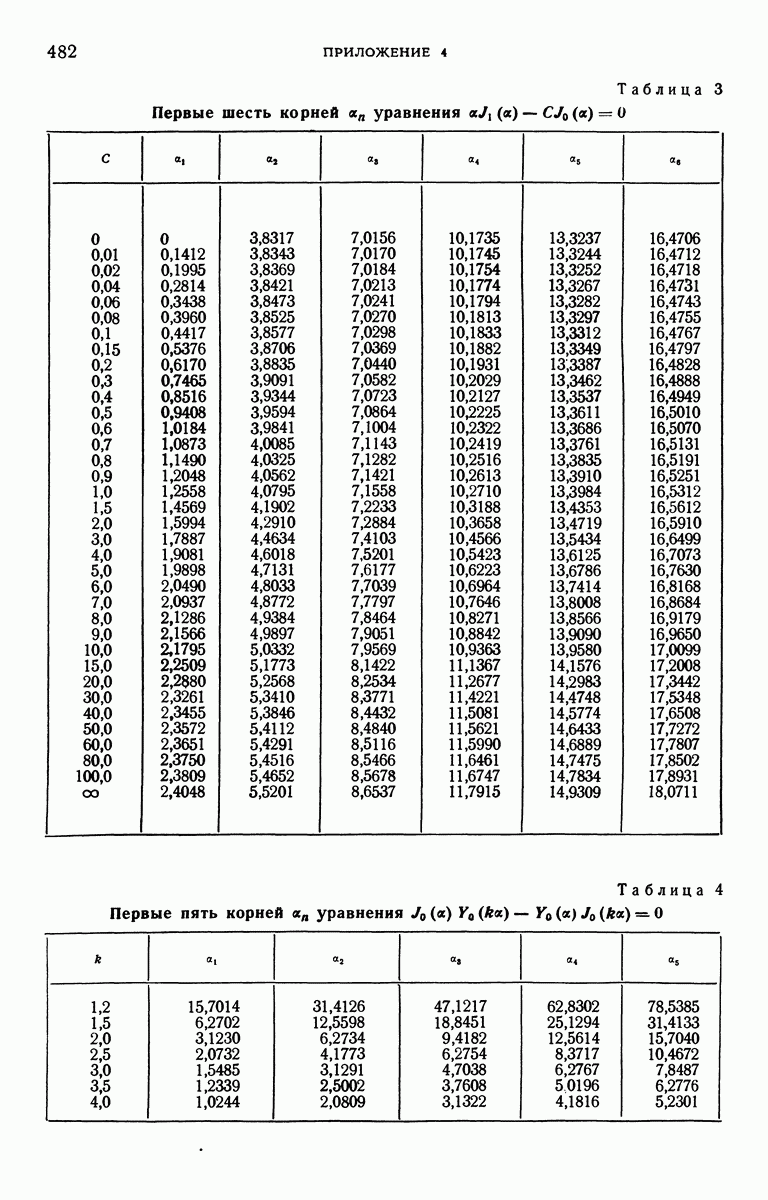
- ПРИЛОЖЕНИЕ 4. КОРНИ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- ПРИЛОЖЕНИЕ 5. ТАБЛИЦА ПРЕОБРАЗОВАНИЙ ЛАПЛАСА …
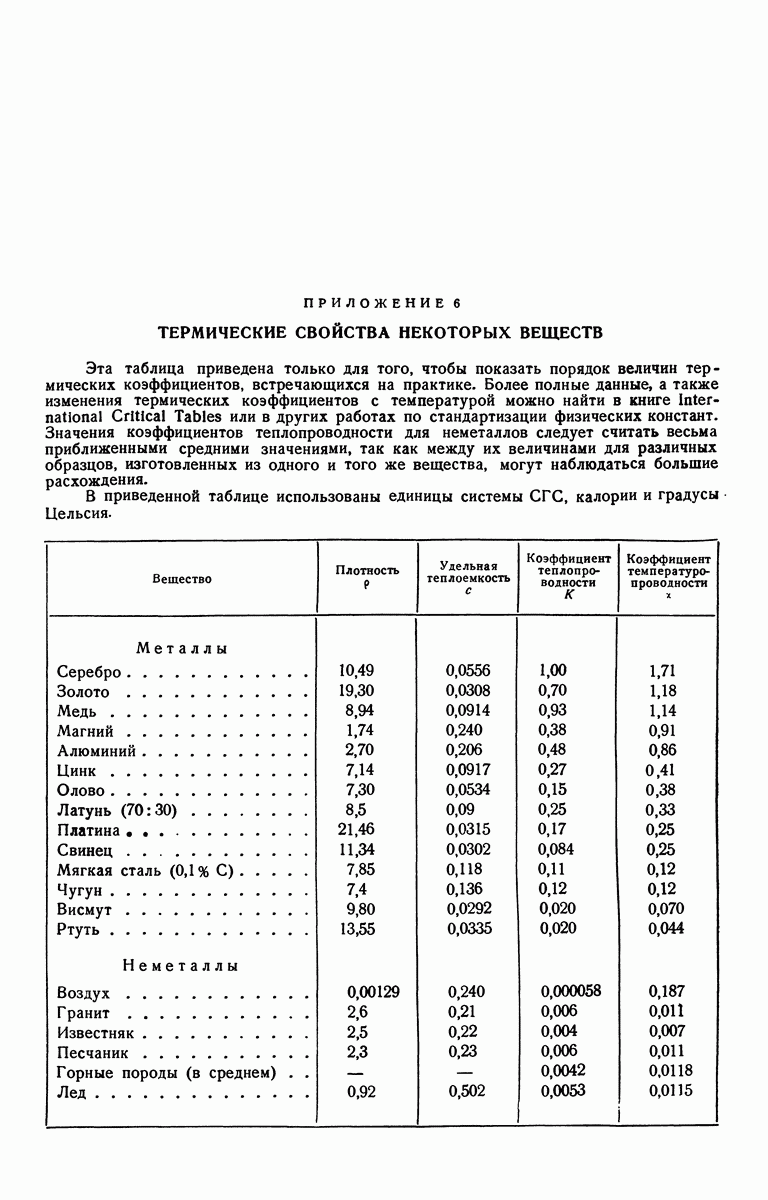
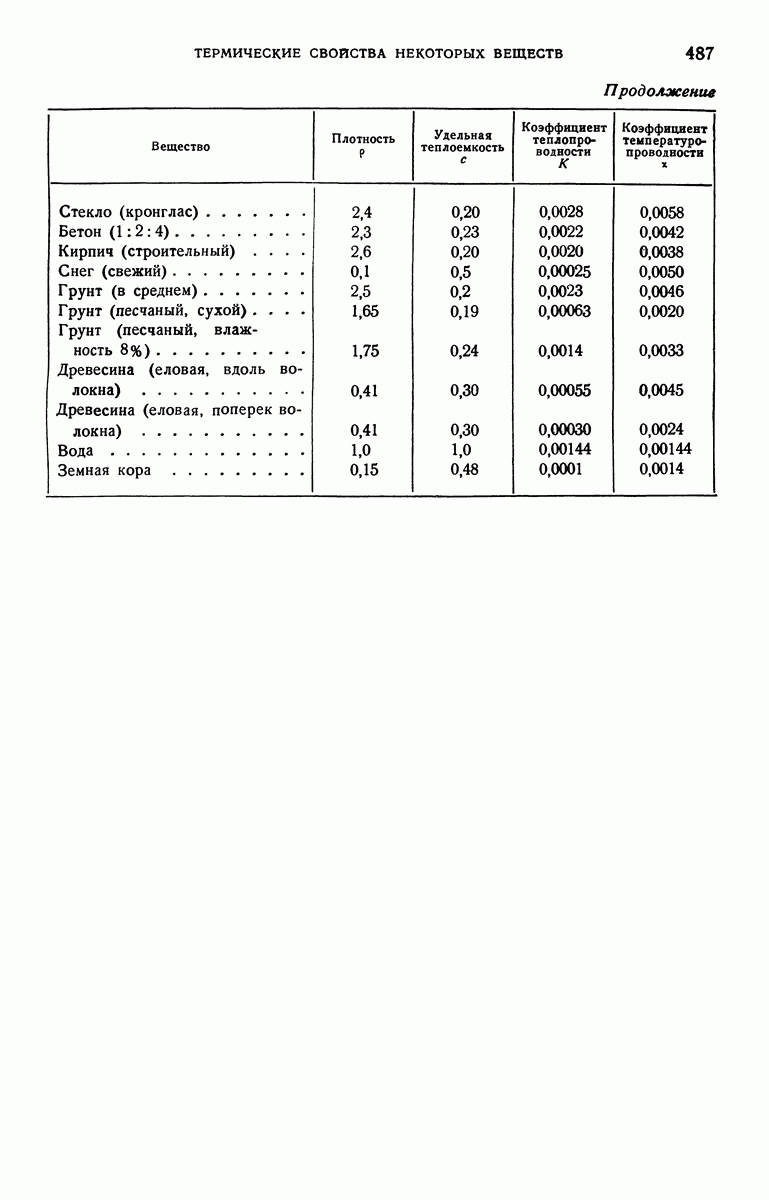
- ПРИЛОЖЕНИЕ 6. ТЕРМИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ВЕЩЕСТВ