| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9. Начальные и граничные условия
Прежде чем приступить к математическому рассмотрению задач теории теплопроводности, необходимо сформулировать начальные и граничные условия, которым должна удовлетворять температура. Эти условия определяются? частично непосредственными результатами экспериментов, а частично математической трактовкой гипотез, основанных на этих результатах.
Пусть внутри твердого тела температура  является непрерывной функцией
является непрерывной функцией  пусть ее первая производная по
пусть ее первая производная по  и первые и вторые производные по
и первые и вторые производные по  также непрерывны. Указанные предположения не распространяются на границу твердого тела, а также на некоторый момент времени, с которого, как предполагается, начинается поступление тепла.
также непрерывны. Указанные предположения не распространяются на границу твердого тела, а также на некоторый момент времени, с которого, как предполагается, начинается поступление тепла.
I. Начальные условия.
Предполагается, что в некоторый момент времени, принятый нами за начало отсчета координаты  температура по всему телу задана произвольно. Если эта произвольная функция непрерывна, то мы должны найти такое решение задачи, которое по мере приближения
температура по всему телу задана произвольно. Если эта произвольная функция непрерывна, то мы должны найти такое решение задачи, которое по мере приближения  к нулю стремилось бы к заданной величине. Другими словами, если начальная температура задана в виде
к нулю стремилось бы к заданной величине. Другими словами, если начальная температура задана в виде

то наше решение уравнения

должно быть таким, чтобы для всех точек твердого тела выполнялось условие

Если начальное распределение температуры разрывно в некоторых точках или на поверхностях, то эти разрывы должны исчезнуть через очень короткое время, и тогда наше решение должно стремиться к заданной величине начальной температуры во всех точках, где распределение непрерывно.
II. Граничные условия, или условия на поверхности.
Перечислим условия на поверхности, обычно встречающиеся в теории теплопроводности.
А. Задана температура на поверхности. В этом случае температура может быть либо постоянной, либо зависеть от времени, либо от положения, либо, наконец, зависеть и от времени и от положения. Подобный случай граничных условий наиболее прост и уже достаточно хорошо изучен. Следует, однако, отметить, что на практике часто очень трудно задать температуру на поверхности, и поэтому существующие в действительности
условия лучше всего описываются граничными условиями, рассматриваемыми  пункте
пункте  (см. ниже).
(см. ниже).
Б. Отсутствует тепловой поток через поверхность исследуемого тела, т. е. во всех точках поверхности имеет место соотношение

где  обозначает дифференцирование вдоль внешней нормали к поверхности.
обозначает дифференцирование вдоль внешней нормали к поверхности.
В. Задан тепловой поток через поверхность.
Г. Теплопередача на поверхности линейна или происходит теплообмен «излучением» по закону Ньютона.
Если тепловой поток через поверхность пропорционален разности температур между поверхностью и окружающей ее средой, то он равен

где  температура среды,
температура среды,  константа; тогда граничные условия записываются в виде
константа; тогда граничные условия записываются в виде

где

Если  то указанные условия обращаются в граничные условия типа
то указанные условия обращаются в граничные условия типа  если же
если же  то они обращаются в условия типа А.
то они обращаются в условия типа А.
Величина  была названа внешней, или поверхностной, теплопроводностью, но теперь ее обычно называют коэффициентом поверхностной теплопередачи или теплоотдачи. Очень часто удобно пользоваться величиной поверхностного термического сопротивления, отнесенного к единице площади, т. е. величиной, обратной
была названа внешней, или поверхностной, теплопроводностью, но теперь ее обычно называют коэффициентом поверхностной теплопередачи или теплоотдачи. Очень часто удобно пользоваться величиной поверхностного термического сопротивления, отнесенного к единице площади, т. е. величиной, обратной 
Если к тому же задан тепловой поток  на поверхности, то выражение (9.2) примет следующий вид:
на поверхности, то выражение (9.2) примет следующий вид:

Соотношение (9.4) совпадает с соотношением (9.2), в котором  заменено
заменено 
Это граничное условие называется в классических работах граничным условием при теплообмене излучением (см. соотношение (9.12)). Однако в действительности такое название приводит к некоторому заблуждению, так как, когда речь идет о передаче тепла излучением, тепловой поток пропорционален четвертой степени абсолютной температуры; все же, ради краткости, в настоящей книге мы обычно будем определять граничное условие  как «теплообмен излучением в среду с температурой
как «теплообмен излучением в среду с температурой  вместо
вместо
громоздкого, но более точного «линейная теплопередача в среду с температурой  Иногда это условие называют законом Ньютона, так как закон Ньютона говорит, что при охлаждении тела обдувом (т. е. в условиях вынужденной конвекции, см. ниже) количество теряемого тепла выражается соотношением (9.1).
Иногда это условие называют законом Ньютона, так как закон Ньютона говорит, что при охлаждении тела обдувом (т. е. в условиях вынужденной конвекции, см. ниже) количество теряемого тепла выражается соотношением (9.1).
Ниже будет кратко изложено несколько различных физических явлений, при которых тепловой поток через граничную поверхность выражается соотношением (9.1). В каждом случае дается несколько численных значений, что позволяет грубо оценить порядок величины  для практических задач; точные значения
для практических задач; точные значения  можно найти в работах по теплопередаче [35, 36, 46, 47].
можно найти в работах по теплопередаче [35, 36, 46, 47].
1. Вынужденная конвекция. Экспериментально установлено, что если жидкость (или газ) с температурой  быстро движется по поверхности твердого тела, то количество тепла, теряемого с его поверхности, выражается формулой (9,1), причем коэффициент теплообмена
быстро движется по поверхности твердого тела, то количество тепла, теряемого с его поверхности, выражается формулой (9,1), причем коэффициент теплообмена  зависит от скорости движения и природы жидкости, а также от формы поверхности. Большинство экспериментов было проведено с жидкостью, движущейся внутри трубок с круговым сечением, и с жидкостью, обтекающей цилиндры с круговым сечением в направлении, перпендикулярном оси цилиндра. На основании полученных результатов были найдены соотношения, приближенно определяемые степенными законами следующих типов:
зависит от скорости движения и природы жидкости, а также от формы поверхности. Большинство экспериментов было проведено с жидкостью, движущейся внутри трубок с круговым сечением, и с жидкостью, обтекающей цилиндры с круговым сечением в направлении, перпендикулярном оси цилиндра. На основании полученных результатов были найдены соотношения, приближенно определяемые степенными законами следующих типов:
Для случая турбулентного течения воздуха со скоростью и см/сек внутри трубки диаметром  см находим
см находим

для воды в аналогичном случае было получено такое же выражение, но большее в 500—1000 раз.
Для случая турбулентного течения воздуха со скоростью а, направленной перпендикулярно оси цилиндра с диаметром сечения  находим
находим

для воды эта величина оказывается примерно в 100 раз больше.
Очевидно, что во всех случаях потеря тепла с единицы поверхности в единицу времени значительно увеличивается с уменьшением диаметра цилиндра. Для плоской поверхности величина  имеет тот же порядок, что и для цилиндра очень большого диаметра.
имеет тот же порядок, что и для цилиндра очень большого диаметра.
Зависимость типа (9.1) приближенно справедлива для случая теплопередачи в результате комбинации вынужденной конвекции и испарения.
2. Случай тонкой оболочки из плохо проводящего материала. Очень часто оказывается, что на поверхности тела имеется тонкая пленка плохо проводящих материалов, например окалины (накипи), смазочных масел, окислов. Кроме того, при охлаждении тела газом или жидкостью, текущей по его поверхности, к последней обычно прилипает тонкий слой невозмущенной жидкости, а так как этот слой не движется, то отдаваемое им количество тепла относительно мало.
Если теплопроводность указанной пленки толщиной  равна К и если в качестве первого приближения мы пренебрежем ее теплоемкостью, то количество тепла, протекающего через эту пленку, отнесенное к единице площади в единицу времени, равно
равна К и если в качестве первого приближения мы пренебрежем ее теплоемкостью, то количество тепла, протекающего через эту пленку, отнесенное к единице площади в единицу времени, равно

где  температуры на внутренней и наружной стороне пленки соответственно.
температуры на внутренней и наружной стороне пленки соответственно.
Это соотношение равносильно граничному условию

для среды с внутренней стороны пленки.
Ниже приводятся значения  в единицах
в единицах  и градусах Цельсия для слоев различных веществ разной толщины.
и градусах Цельсия для слоев различных веществ разной толщины.
Типичная толщина пленки накипи равна 0,1 см.
Если с внешней стороны пленки не поддерживается температура  и происходит потеря тепла, величина которой равна произведению
и происходит потеря тепла, величина которой равна произведению  на разность между
на разность между  и температурой окружающей среды
и температурой окружающей среды  то граничное условие примет вид
то граничное условие примет вид

Д. Теплопередача нелинейна. В большинстве практических задач тепловой поток с поверхности не является линейной функцией разности температур между этой поверхностью и окружающей ее средой. Однако для малых диапазонов температур он может быть аппроксимирован зависимостью типа (9.1). Ниже приведены типичные примеры.
1. Излучение черного тела. Твердое тело с абсолютной температурой  окруженное черным телом с абсолютной температурой
окруженное черным телом с абсолютной температурой  будет терять количество тепла, отнесенное к единице поверхности и в единицу времени, равное
будет терять количество тепла, отнесенное к единице поверхности и в единицу времени, равное

где  постоянная Стефана — Больцмана,
постоянная Стефана — Больцмана,  относительная излучательная способность поверхности (степень черноты), т. е. отношение количества тепла, излучаемого указанной поверхностью, к количеству тепла, излучаемого черным телом при той же температуре.
относительная излучательная способность поверхности (степень черноты), т. е. отношение количества тепла, излучаемого указанной поверхностью, к количеству тепла, излучаемого черным телом при той же температуре.
Для полированных металлов величина  меняется от 0,02 до 0,05; для оксидированных металлов она примерно равна
меняется от 0,02 до 0,05; для оксидированных металлов она примерно равна  для других веществ, например для красок, стекла, бумаги, древесины, она равна 0,7 — 0,9, для копоти, ламповой сажи и т. п. она может достигать 0,98.
для других веществ, например для красок, стекла, бумаги, древесины, она равна 0,7 — 0,9, для копоти, ламповой сажи и т. п. она может достигать 0,98.
Подставляя численное значение величины  в (9.10), получим
в (9.10), получим

Если разность  не очень велика, то в первом приближении находим
не очень велика, то в первом приближении находим

а если  то указанная величина становится равной
то указанная величина становится равной 
Таким образом, применительно к этому случаю выражение (9.1) с константой Н является весьма приближенным, а если  велико, то оно может даже привести к серьезным ошибкам. Известно лишь несколько точных решений задач теплопроводности с точным граничным условием типа (9.10).
велико, то оно может даже привести к серьезным ошибкам. Известно лишь несколько точных решений задач теплопроводности с точным граничным условием типа (9.10).
В обычных условиях потеря тепла твердым телом обусловлена как конвекцией, так и излучением, и поэтому в коэффициенте  в выражении (9.1) должны быть учтены оба эти фактора.
в выражении (9.1) должны быть учтены оба эти фактора.
2. Естественная конвекция. Когда нагретое твердое тело окружено жидкостью, то более нагретые части жидкости, находящиеся поблизости от тела, стремятся подняться вверх и таким образом устанавливаются сети конвекционных токов. Такой процесс называется естественной конвекцией. Экспериментально установлено, что в данном случае количество тепла, теряемое твердым телом (с единицы площади в единицу времени), пропорционально разности температур  между телом и окружающей жидкостью в степени, приблизительно равной
между телом и окружающей жидкостью в степени, приблизительно равной  Например, для поверхностей толщиной несколько сантиметров потеря тепла в воздух, отнесенная к единице площади в единицу времени, приближенно равна
Например, для поверхностей толщиной несколько сантиметров потеря тепла в воздух, отнесенная к единице площади в единицу времени, приближенно равна

Для очень тонких проволок, находящихся в воздухе, эта величина в 20 раз больше. В воде те же величины оказываются примерно в 100 раз больше.
Для этого случая, так же как и для случая теплопередачи излучением, нельзя, пользуясь выражением (9.13), найти точные решения, и поэтому в выражении (9.1) используется приближенная величина  Следует отметить, что для тела, находящегося в воздухе при нормальной температуре, соотношения (9.12) и (9.13) дают величины одинакового порядка и поэтому оба они могут быть использованы в расчетах.
Следует отметить, что для тела, находящегося в воздухе при нормальной температуре, соотношения (9.12) и (9.13) дают величины одинакового порядка и поэтому оба они могут быть использованы в расчетах.
Е. Контакт с хорошо перемешиваемой жидкостью или с идеальным проводником. В калориметрии и в других методах измерения, связанных с теплопередачей, часто оказывается, что поверхность твердого тела соприкасается с жидкостью, перемешиваемой настолько хорошо, что температура жидкости всюду одинакова. Пусть твердое тело имеет теплопроводность К, площадь поверхности  и температуру поверхности
и температуру поверхности  причем
причем  сохраняет постоянное значение на всей поверхности. Пусть, далее, хорошо перемешиваемая жидкость, соприкасающаяся с твердым телом, имеет массу
сохраняет постоянное значение на всей поверхности. Пусть, далее, хорошо перемешиваемая жидкость, соприкасающаяся с твердым телом, имеет массу  и удельную теплоемкость
и удельную теплоемкость  и пусть ее температура равна
и пусть ее температура равна  Для общности предположим, что в жидкость с массой
Для общности предположим, что в жидкость с массой  поступает в единицу времени от внешнего источника количество тепла
поступает в единицу времени от внешнего источника количество тепла  и что потеря тепла вследствие излучения в среду с температурой
и что потеря тепла вследствие излучения в среду с температурой  (отнесенная к единице площади в единицу времени) составляет
(отнесенная к единице площади в единицу времени) составляет  Если
Если  увеличение температуры жидкости с массой
увеличение температуры жидкости с массой  за время
за время  то мы можем написать
то мы можем написать

т. е.

Если предположить, что с некоторого момента времени  температура поверхности твердого тела равна температуре жидкости (при
температура поверхности твердого тела равна температуре жидкости (при  они, разумеется, могут быть не равны), то в дополнение к соотношению (9.14) получим
они, разумеется, могут быть не равны), то в дополнение к соотношению (9.14) получим

Если же вместо этого между твердым телом и жидкостью имеет место теплопередача по закону типа  то условие (9.15) заменяется другим, а именно
то условие (9.15) заменяется другим, а именно

Другие физические условия приводят к граничным условиям типа (9.14); например, для случая, когда поверхность твердого тела соприкасается с хорошо перемешиваемой жидкостью массы  из которой в единицу времени
из которой в единицу времени
удаляется масса  и замещается той же массой жидкости с температурой
и замещается той же массой жидкости с температурой  находим
находим

Такие же граничные условия (9.14), (9.15) и (9.16) имеют место для идеально проводящего твердого тела с массой М. Если неметалл соприкасается с металлическим проводником со значительно большей теплопроводностью, то последний с достаточно хорошим приближением можно считать идеальным проводником. Такая задача решается значительно проще, чем задача для составной области.
Существенная разница между этими граничными условиями и условиями, определенными в пунктах  заключается в появлении члена
заключается в появлении члена  а в некоторых случаях — члена
а в некоторых случаях — члена  . При использовании классических методов не всегда можно обойтись без их видоизменения, но преобразование Лапласа, изложенное в гл. XII, одинаково пригодно для обоих случаев. В этой главе будут приведены некоторые примеры.
. При использовании классических методов не всегда можно обойтись без их видоизменения, но преобразование Лапласа, изложенное в гл. XII, одинаково пригодно для обоих случаев. В этой главе будут приведены некоторые примеры.
Ж. Поверхность раздела двух сред с различными коэффициентами теплопроводности  Пусть
Пусть  температуры двух сред. В § 3 данной главы было показано, что тепловой поток непрерывен на поверхности раздела двух сред, т. е. что
температуры двух сред. В § 3 данной главы было показано, что тепловой поток непрерывен на поверхности раздела двух сред, т. е. что

где  означает дифференцирование вдоль нормали к поверхности раздела.
означает дифференцирование вдоль нормали к поверхности раздела.
Если предположить, что на поверхности раздела температуры обеих сред одинаковы, то в добавление к соотношению (9.18) имеем

Это предположение справедливо только для очень тесного контакта, как, например, в спаях; во всех других случаях, даже в двух оптически плоских поверхностях, слегка прижатых друг к другу, теплопередача между двумя средами осуществляется главным образом согласно механизму, изложенному в пунктах  и
и  т. е. тепловой поток между этими двумя поверхностями пропорционален разности их температур и, следовательно,
т. е. тепловой поток между этими двумя поверхностями пропорционален разности их температур и, следовательно,

Для этого случая граничными условиями служат соотношения (9.18) и 
3. Контакт вещества с тонкой оболочкой из значительно лучшего проводника. Подобная задача встречается при изучении, например, тонкого металлического листа или проволоки, соприкасающихся с относительно плохим проводником, таким, как грунт, пищевые продукты или изолирующие материалы. Этот случай
рассматривается также в задачах о поверхностной диффузии или о диффузии по границам зере» (65, 66]. Предполагается, что оболочка настолько тонка, что по всей ее толщине, равной  температура в любой точке одинакова. Если V — температура в произвольной точке оболочки, а
температура в любой точке одинакова. Если V — температура в произвольной точке оболочки, а  соответственно коэффициенты теплопроводности и температуропроводности вещества оболочки, то уравнение теплопроводности для оболочки, выведенное из рассмотрения баланса тепла в элементе ее площади, записывается в виде
соответственно коэффициенты теплопроводности и температуропроводности вещества оболочки, то уравнение теплопроводности для оболочки, выведенное из рассмотрения баланса тепла в элементе ее площади, записывается в виде

 обозначает дифференцирование по направлению внешней нормали к твердому телу,
обозначает дифференцирование по направлению внешней нормали к твердому телу,  соответственно по двум перпендикулярным ей направлениям.
соответственно по двум перпендикулярным ей направлениям.
При идеальном тепловом контакте между оболочкой и твердым телом граничные условия имеют вид (9.21) и  Если же между оболочкой и внутренней (ил» внешней) средой происходит теплопередача по линейному закону, эти условия несколько усложняются.
Если же между оболочкой и внутренней (ил» внешней) средой происходит теплопередача по линейному закону, эти условия несколько усложняются.
Для случая проволоки с радиусом а, расположенной вдоль оси  в твердом теле
в твердом теле  , соотношение (9.21) принимает вид
, соотношение (9.21) принимает вид

Если оболочка настолько тонка, что ее теплоемкостью можно пренебречь, то соотношение (9.21) записывается следующим образом:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ
- § 2. Теплопроводность
- § 3. Тепловой поток через произвольную поверхность
- § 4. Изотермические поверхности
- § 5. Теплопроводность изотропных тел
- § 6. Дифференциальное уравнение теплопроводности для изотропного твердого тела
- § 7. Дифференциальное уравнение теплопроводности для движущейся среды
- § 8. Преобразование координат
- § 9. Начальные и граничные условия
- § 10. Безразмерные параметры
- § 11. Экспериментальные методы определения теплопроводности
- § 12. Математическая интерпретация начальных и граничных условий
- § 13. Родственные дифференциальные уравнения
- § 14. Упрощение общей задачи теплопроводности
- § 15. Задачи, решения которых можно выразить в виде произведения решений более простых задач
- § 16. Единственность решения задачи теплопроводности
- § 17. Теплопроводность анизотропных твердых тел
- § 18. Дифференциальное уравнение теплопроводности для анизотропных твердых тел
- § 19. Теплопроводность тонкой кристаллической пластины
- § 20. Изменение теплопроводности и вектор теплового потока в анизотропных твердых телах
- ГЛАВА II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА. НЕОГРАНИЧЕННОЕ И ПОЛУОГРАНИЧЕННОЕ ТВЕРДОЕ ТЕЛО
- § 2. Неограниченное твердое тело. Решение Лапласа
- § 3. Использование интегралов Фурье и преобразований Фурье
- § 4. Полуограниченное тело с начальной температурой f(x) и нулевой температурой поверхности
- § 5. Полуограниченное твердое тело. Начальная температура равна нулю. Поверхность находится при температуре …
- § 6. Полуограниченное твердое тело. Температура поверхности является гармонической функцией времени
- § 7. Полуограниченное твердое тело. Теплообмен на поверхности в среду с нулевой температурой. Начальная температура постоянна
- § 8. Полуограниченное твердое тело. Теплообмен на поверхности в среду с температурой f(t). Начальная температура равна нулю
- § 9. Полуограниченное тело. Тепловой поток на границе х = 0 является заданной функцией времени. Начальная температура равна нулю
- § 10. Применение полученных результатов к определению теплопроводности
- § 11. Полуограниченное твердое тело, внутри которого находится источник тепла
- § 12. Температура Земли и колебания температуры на ее поверхности
- § 13. Геотермический градиент и поток тепла
- § 14. Возраст Земли. Анализ Кельвина
- § 15. Неограниченное составное твердое тело
- § 16. Случай зависимости термических характеристик вещества от температуры
- ГЛАВА III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ, ОГРАНИЧЕННОМ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
- § 3. Область [0, l]. Границы поддерживаются при нулевой температуре. Начальная температура f(x)
- § 4. Область [0, l] Начальная температура f(x). Границы поддерживаются при постоянной температуре или изолированы
- § 5. Область [0, l]. Температуры границ равны … Начальная температура f(x)
- § 6. Пластина с периодически изменяющейся температурой поверхности
- § 7. Установившаяся периодически изменяющаяся температура в составных пластинах
- § 8. Пластина с заданным тепловым потоком на ее границе
- § 9. Область [0, l]. Теплообмен на границах в среду с температурой, равной нулю. Начальная температура равна f(х)
- § 10. Область [-l, l]. На границах х=+l происходит теплообмен со средой нулевой температуры. Начальная температура f(x)
- § 11. Частные случаи и численные результаты для пластины с граничным условием третьего рода
- § 12. Область [-l, l] с нулевой начальной температурой и теплообменом на границах со средой, имеющей температуру …
- § 13. Пластина, одна из поверхностей которой соприкасается со слоем идеального проводника или хорошо перемешиваемой жидкости
- § 14. Пластина с внутренним источником тепла
- ГЛАВА IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ
- § 3. Полуограниченный стержень. Случай установившейся температуры. Метод Форбса
- § 4. Полуограниченный стержень. Периодически изменяющаяся температура. Метод Ангстрема [5—10]
- § 5. Ограниченный стержень, концы которого находятся при фиксированных температурах. Случай установившейся температуры
- § 6. Стержень переменного сечения с охлаждающимися ребрами. Случай установившейся температуры
- § 7. Ограниченный стержень при наличии теплообмена на его поверхности. Случай неустановившейся температуры
- § 8. Ограниченный стержень с периодически изменяющейся температурой концов. Метод Неймана
- § 9. Задачи по теплопроводности в движущемся стержне
- § 10. Уравнение теплопроводности для тонкой проволоки, нагреваемой постоянным электрическим током
- § 11. Установившаяся температура. Определение коэффициента теплопроводности
- § 12. Сильно нагретая проволока, по которой протекает электрический ток
- § 13. Установившийся поток тепла в составной проволоке
- § 14. Неустановившаяся температура в проволоке, по которой течет электрический ток
- § 15. Кольцо Фурье
- ГЛАВА V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
- § 2. Неограниченное твердое тело прямоугольного сечения. Установившаяся температура
- § 3. Установившаяся температура в неограниченном теле прямоугольного сечения
- § 4. Тонкая пластина с прямоугольным сечением при наличии теплообмена на ее поверхности
- § 5. Установившаяся температура в теле прямоугольного сечения при наличии источника тепла
- § 6. Неустановившееся состояние. Решение в виде произведения решений
- § 7. Неустановившееся состояние. Произвольные начальные и граничные условия
- ГЛАВА VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ
- § 2. Установившаяся температура
- § 3. Двойные и кратные ряды Фурье
- § 4. Неустановившаяся температура. Решение в виде произведения решений
- § 5. Определение коэффициента теплопроводности и экстраполяция кривых охлаждения
- § 6. Неустановившаяся температура. Тройной ряд Фурье
- ГЛАВА VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ КРУГОВОГО СЕЧЕНИЯ
- § 2. Установившаяся температура. Радиальный поток
- § 3. Установившаяся, периодически изменяющаяся температура в круговых цилиндрах [19—22]
- § 4. Неограниченный цилиндр. Радиальный поток. Неустановившаяся температура
- § 5. Интегралы …
- § 6. Неограниченный цилиндр с температурой поверхности … и начальной температурой f(r)
- § 7. Неограниченный цилиндр с теплообменом на поверхности
- § 8. Неограниченный цилиндр с постоянным потоком тепла на поверхности
- § 9. Неограниченный цилиндр с внутренними источниками тепла
- § 10. Неограниченный полый цилиндр. Радиальный поток
- § 11. Неограниченный цилиндр. Установившаяся температура. Общий случай
- § 12. Неограниченный цилиндр. Неустановившаяся температура. Общий случай
- ГЛАВА VIII. ТЕПЛОВОЙ ПОТОК В ОБЛАСТЯХ, ОГРАНИЧЕННЫХ КООРДИНАТНЫМИ ПОВЕРХНОСТЯМИ ЦИЛИНДРИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ
- § 3. Установившаяся температура в ограниченном и полуограниченном цилиндрах
- § 4. Неустановившееся состояние. Решения в форме произведений
- § 5. Определение теплопроводности вещества в форме цилиндра
- § 6. Ограниченный цилиндр с начальной температурой …
- § 7. Полуограниченный цилиндр
- ГЛАВА IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ
- § 2. Установившаяся температура. Радиальный тепловой поток
- § 3. Шар с начальной температурой f(r) и температурой поверхности …
- § 4. Шар. Начальная температура f(r). На поверхности сферы происходит теплообмен
- § 5. Определение коэффициентов теплопроводности плохих проводников
- § 6. Случай шара, находящегося в контакте с хорошо перемешиваемой жидкостью
- § 7. Шар с заданным тепловым потоком на поверхности
- § 8. Шар, внутри которого выделяется тепло
- § 9. Полый шар
- § 10. Область, ограниченная изнутри сферической поверхностью r=a
- § 11. Шар с начальной температурой … Температура поверхности r=a равна нулю
- § 12. Поверхность шара r=a поддерживается при температуре …
- § 13. Часть шара, вырезаемая конусом … Температура поверхности равна нулю, начальная температура равна …
- § 14. Температура внутри Земли
- ГЛАВА Х. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ К ЗАДАЧАМ С НЕУСТАНОВИВШЕЙСЯ ТЕМПЕРАТУРОЙ
- § 2. Мгновенный точечный источник
- § 3. Мгновенные источники; линейный, плоский и поверхностные цилиндрический и сферический источники
- § 4. Непрерывные и периодические источники
- § 5. Поверхностный нагрев полуограниченной области
- § 6. Выделение тепла в неограниченной среде
- § 7. Движущиеся источники тепла
- § 8. Дублеты
- § 9. Метод последовательных волн
- § 10. Метод изображений. Линейный тепловой поток
- § 11. Применение метода изображений к двумерным и трехмерным задачам
- § 12. Обобщение метода изображений Зоммерфельдом
- ГЛАВА XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ
- § 2. Одномерные случаи плавления и затвердевания. Решение Неймана и его обобщение
- § 3. Область … при других граничных условиях
- § 4. Методы интегрального уравнения. Рассмотрение задач затвердевания, предложенное Лайтфутом
- § 5. Решения в цилиндрических и сферических координатах
- § 6. Осесимметричные задачи о замерзании и плавлении
- ГЛАВА XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЛИНЕЙНОГО ТЕПЛОВОГО ПОТОКА
- § 2. Преобразование Лапласа. Основные свойства
- § 3. Решение уравнения теплопроводности методом преобразования Лапласа
- § 4. Полуограниченная область. Решения, получаемые из таблицы изображений
- § 5. Ограниченная область (0, l). Решения, получаемые из таблицы изображений. Решения для небольших значений времени
- § 6. Ограниченная область (0, l). Применение теоремы обращения
- § 7. Полуограниченная область. Применение теоремы обращения
- § 8. Составные твердые тела
- ГЛАВА XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА
- § 3. Решения, применимые для малых интервалов времени
- § 4. Полый цилиндр
- § 5. Область ограничена изнутри цилиндром кругового сечения r=a
- § 6. Решения, применимые при больших значениях времени
- § 7. Область, ограниченная изнутри круговым цилиндром из идеального проводника
- § 8. Составная цилиндрическая область
- § 9. Шар. Радиальный тепловой поток
- ГЛАВА XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА К РЕШЕНИЮ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 2. Линейный тепловой поток. Полуограниченное твердое тело
- § 3. Линейный тепловой поток в области (0, a)
- § 4. Двумерные задачи. Тела с прямоугольным сечением
- § 5. Прямоугольный параллелепипед
- § 6. Линейный тепловой поток. Составные твердые тела
- § 7. Шар. Радиальный поток тепла
- § 8. Цилиндр. Радиальный тепловой поток
- § 9. Полуограниченное твердое тело. Трехмерные задачи
- § 10. Область, ограниченная двумя параллельными плоскостями
- § 11. Полуограниченное твердое тело с тонкой пленкой на плоскости z=0 из материала, имеющего значительно большую теплопроводность. В точке … расположен единичный мгновенный источник
- § 12. Неограниченное составное твердое тело. В точке действует мгновенный единичный источник
- § 13. Области, ограниченные цилиндрической поверхностью r=a
- § 14 Клин
- § 15. Цилиндрическая область
- § 16. Области, ограниченные сферической поверхностью r=a
- § 17. Конус
- § 18. Непрерывные источники
- ГЛАВА XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 3. Тепловые регенераторы и теплообменники
- § 4. Тепловой поток в слоистых системах
- § 5. Установившийся периодический режим
- § 6. Линейная асимптотика и запаздывание
- § 7. Выделение тепла
- § 8. Система автоматического регулирования температуры
- § 9. Неоднородные тела
- § 11. Прямое применение метода преобразования Лапласа к двумерным и трехмерным задачам
- ГЛАВА XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
- § 2. Источники и стоки при установившейся температуре
- § 3. Установившийся поток к почти плоской поверхности. Топографические поправки для геотермического потока
- § 4. Установившийся тепловой поток в составном теле
- § 5. Практические задачи
- § 6. Использование сопряженных гармонических функций в задачах с установившейся температурой
- § 7. Приложения этого метода [20, 21]
- § 8. Установившийся тепловой поток в многоугольнике
- § 9. Тепловой поток между изотермическими поверхностями
- ГЛАВА XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- § 2. Интегральные преобразования и формулы их обращения
- § 3. Неустановившийся тепловой поток
- § 4. Установившийся тепловой поток
- § 5. Конечные преобразования
- § 6. Последовательные преобразования
- ГЛАВА XVIII. ЧИСЛЕННЫЕ МЕТОДЫ
- § 3. Линейный тепловой поток в неограниченном пространстве
- § 4. Граничные условия
- § 5. Выделение тепла, переменная температуропроводность и скрытая теплота
- § 6. Релаксационные методы
- ПРИЛОЖЕНИЕ 1. КОНТУРНЫЕ ИНТЕГРАЛЫ И ПРОВЕРКА РЕШЕНИЙ, ПОЛУЧЕННЫХ ПРИ ПОМОЩИ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- ПРИЛОЖЕНИЕ 2. ФУНКЦИЯ ОШИБОК И РОДСТВЕННЫЕ ФУНКЦИИ
- ПРИЛОЖЕНИЕ 3. О ФУНКЦИЯХ БЕССЕЛЯ
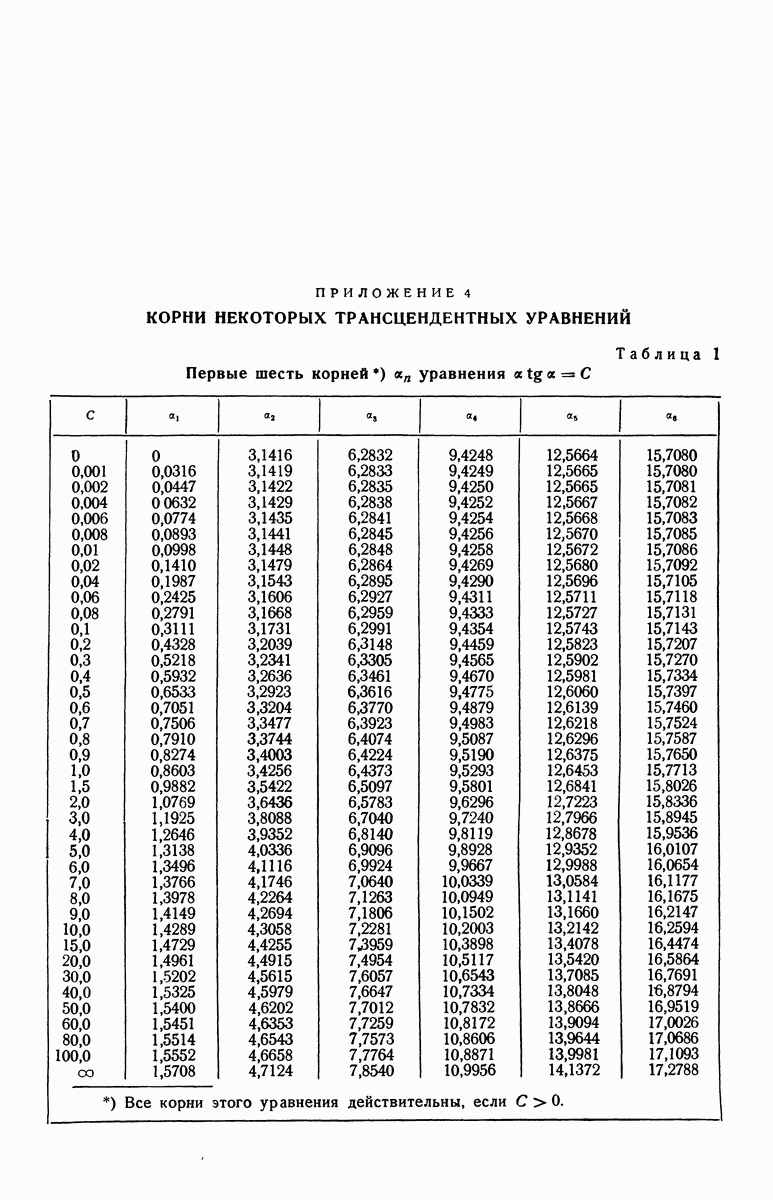
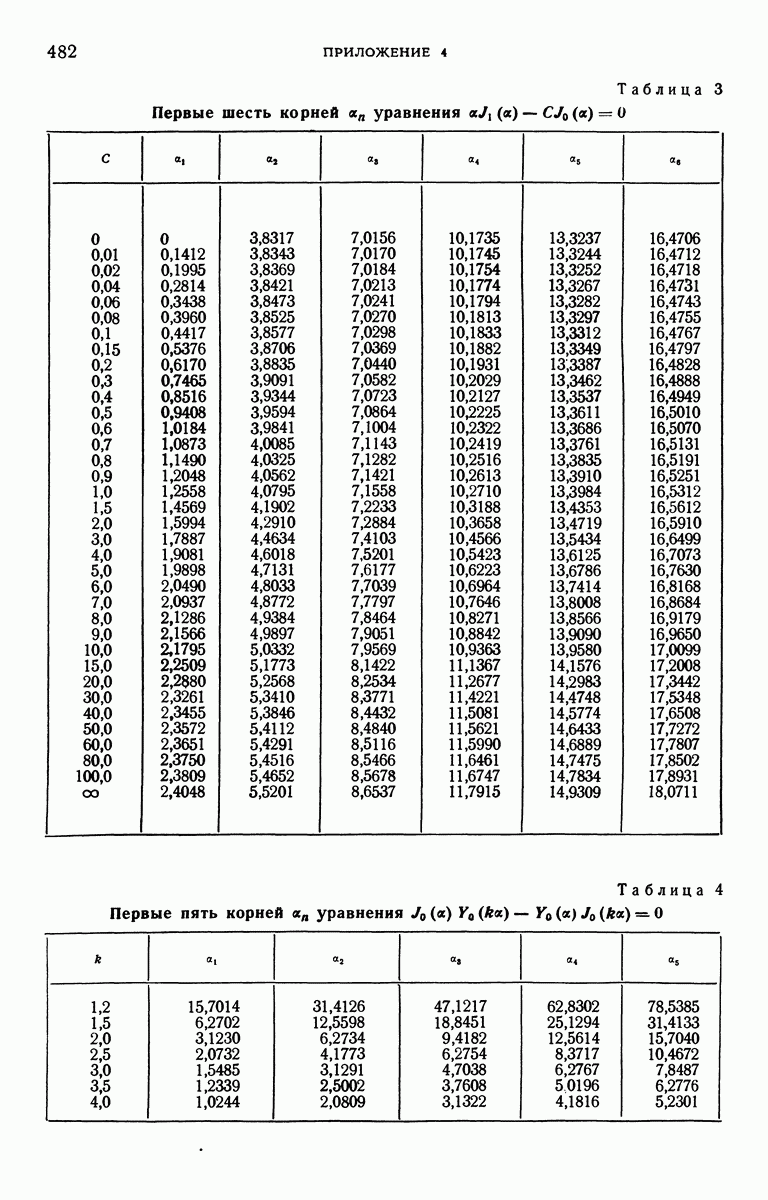
- ПРИЛОЖЕНИЕ 4. КОРНИ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- ПРИЛОЖЕНИЕ 5. ТАБЛИЦА ПРЕОБРАЗОВАНИЙ ЛАПЛАСА …
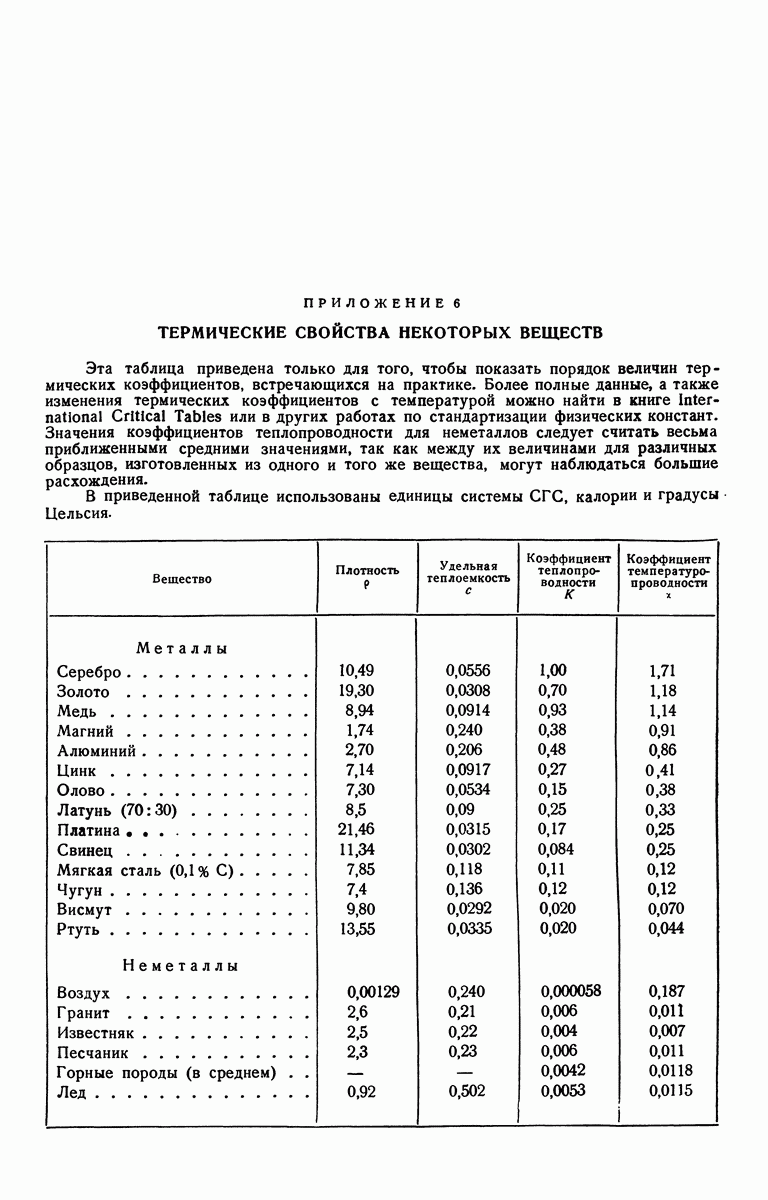
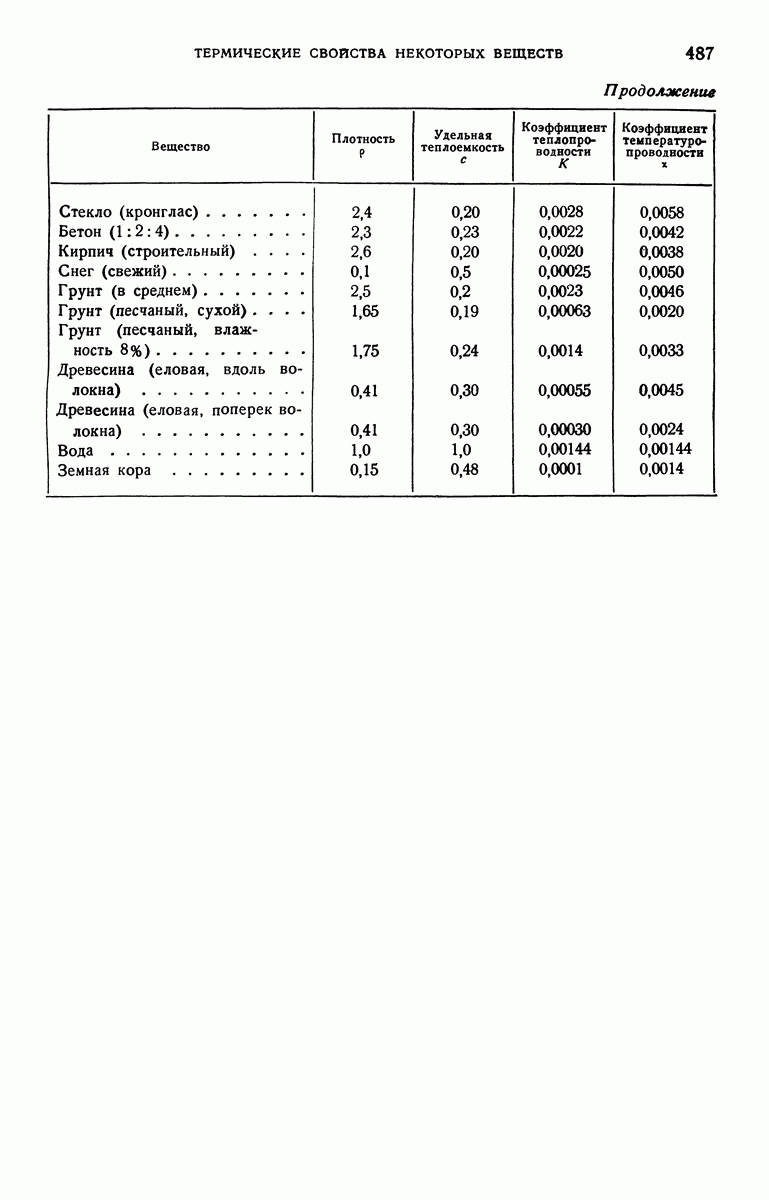
- ПРИЛОЖЕНИЕ 6. ТЕРМИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ВЕЩЕСТВ