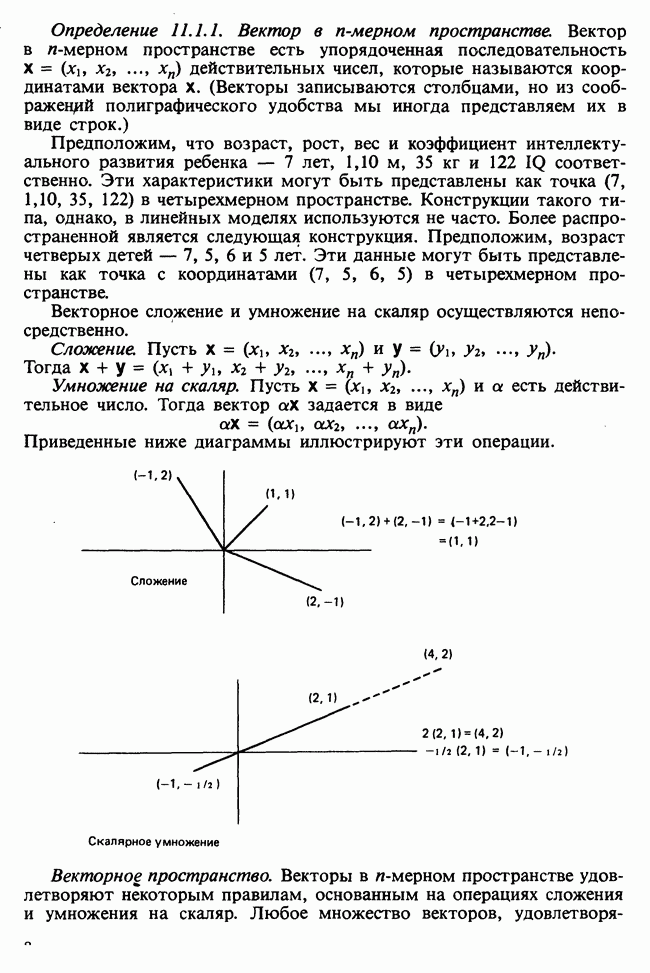
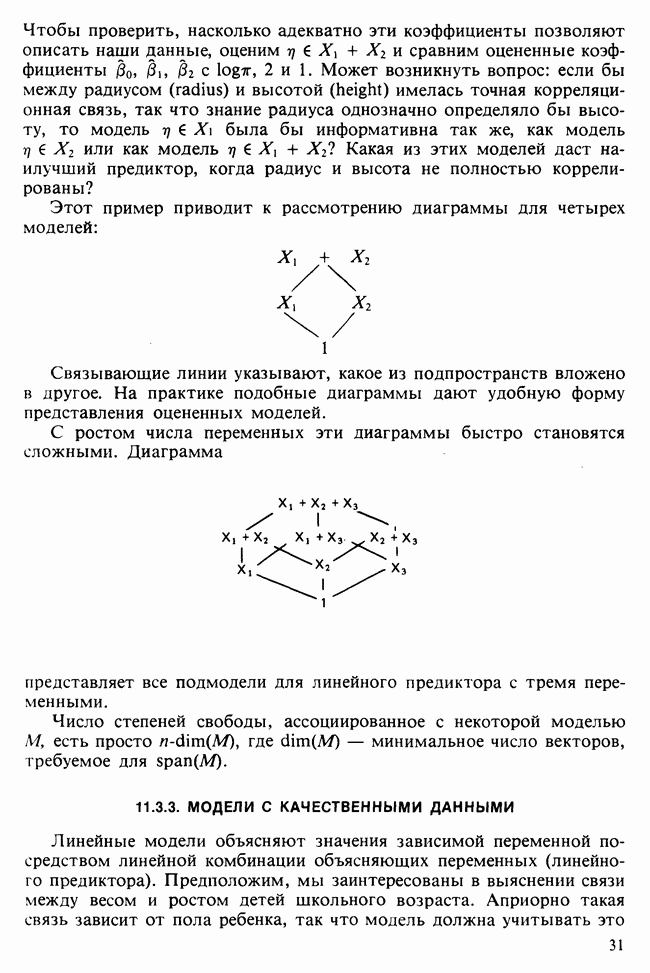
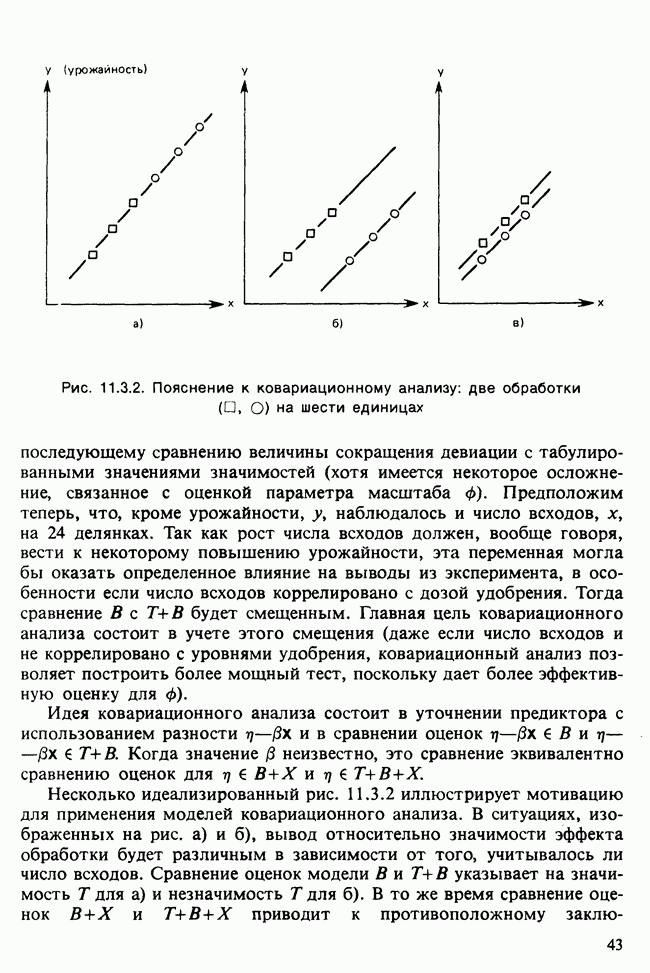
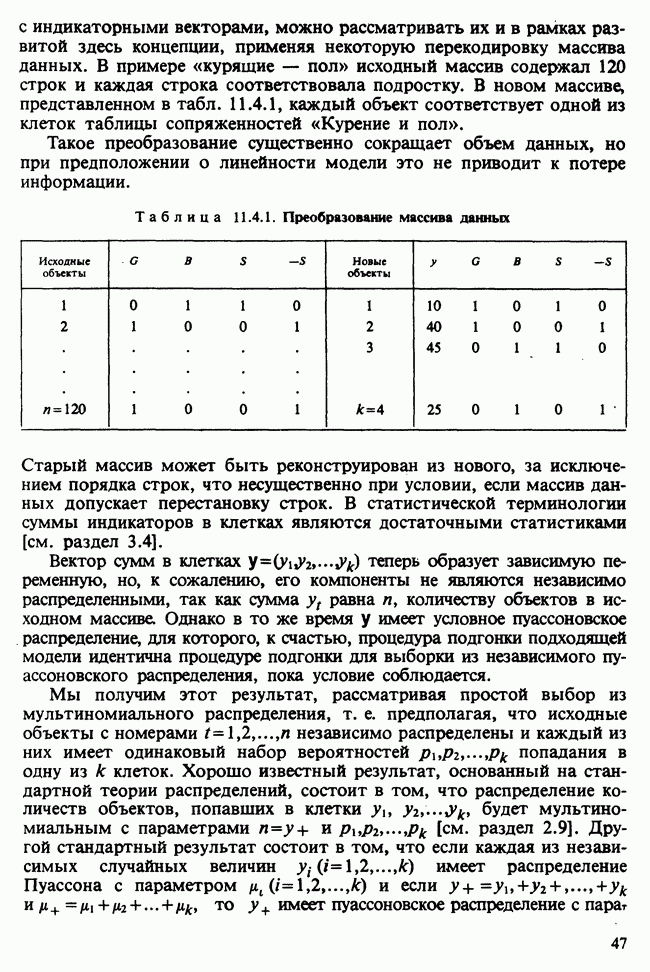
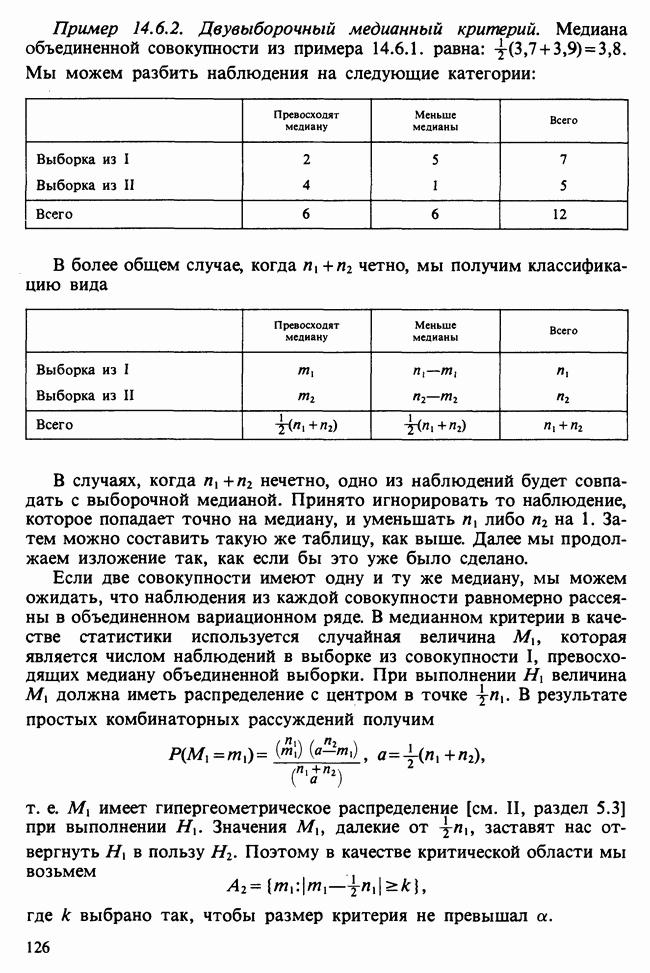
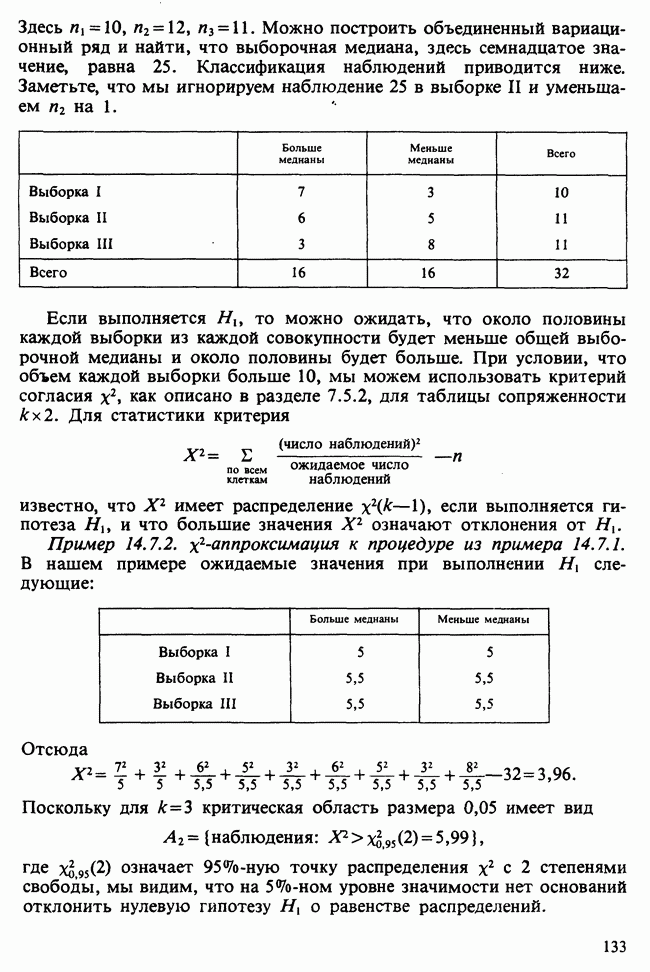
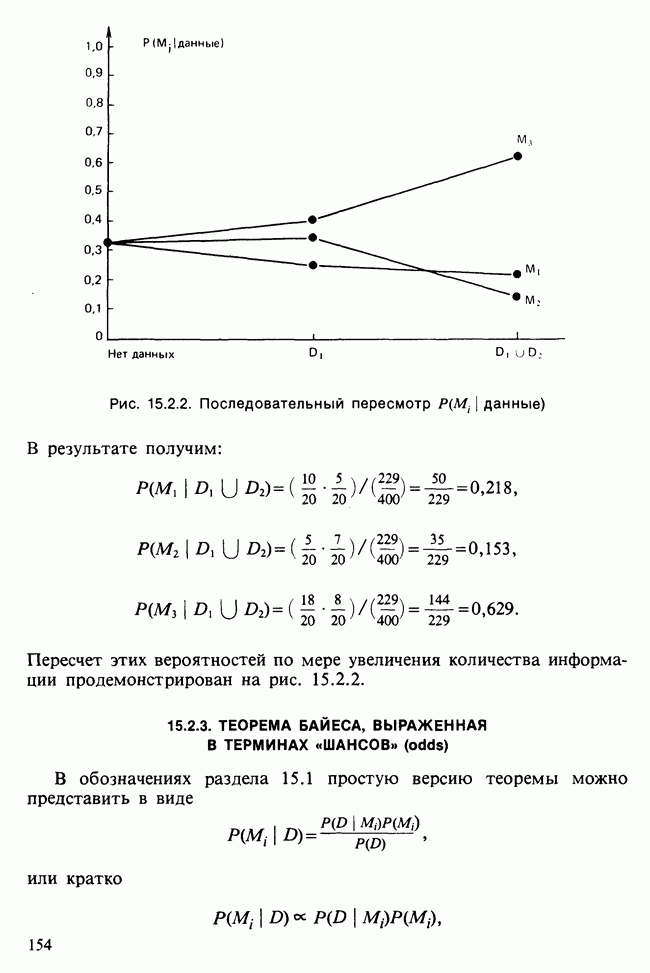
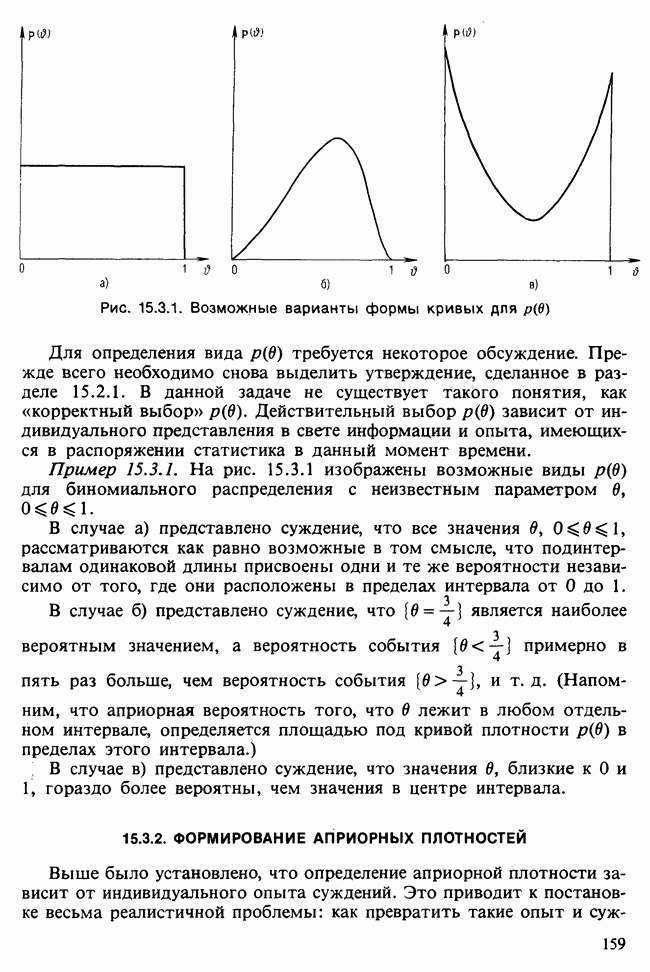
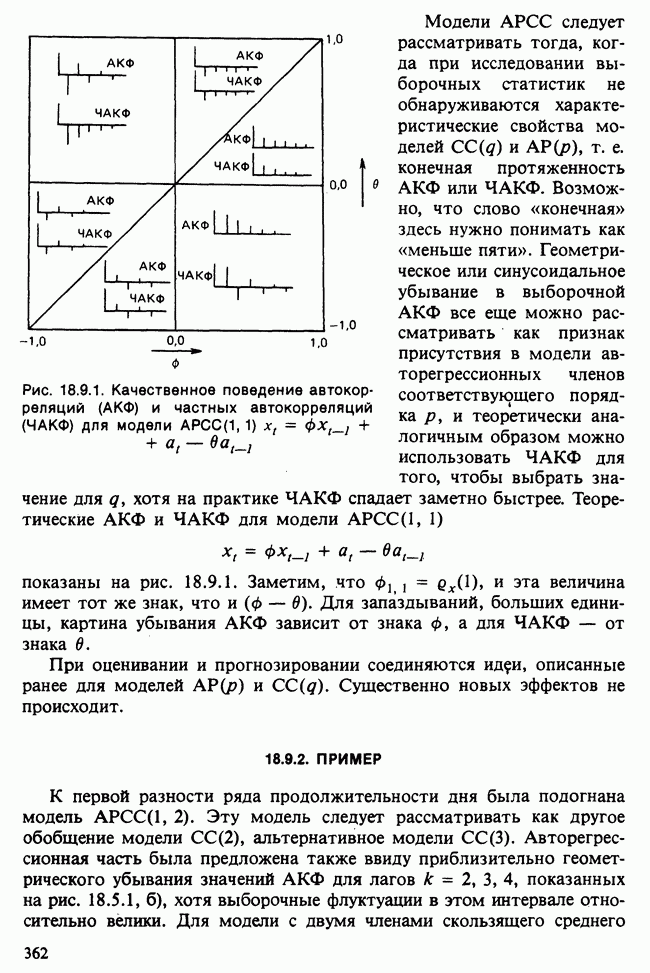
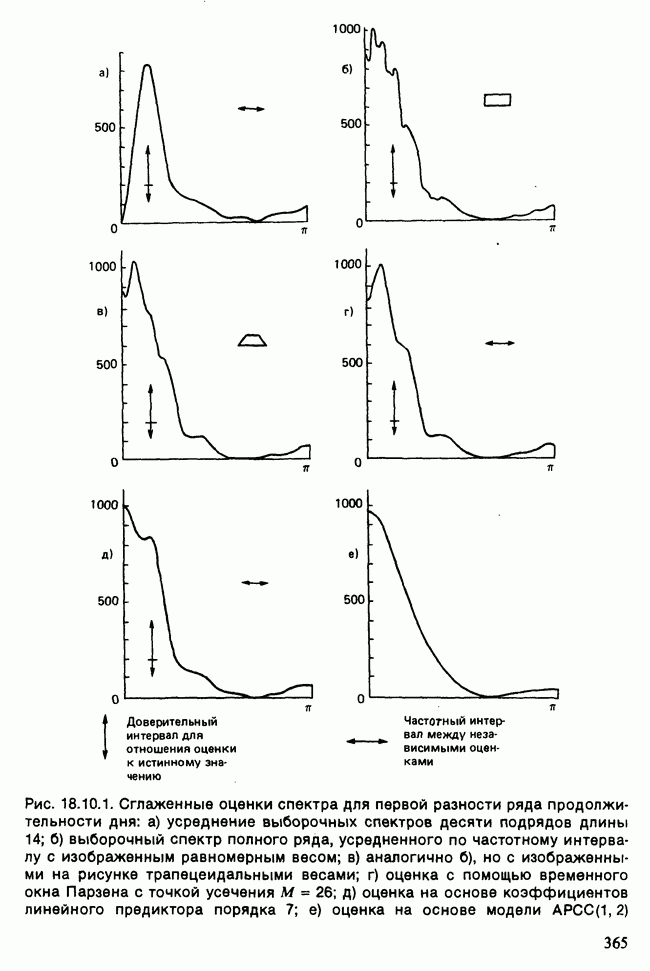
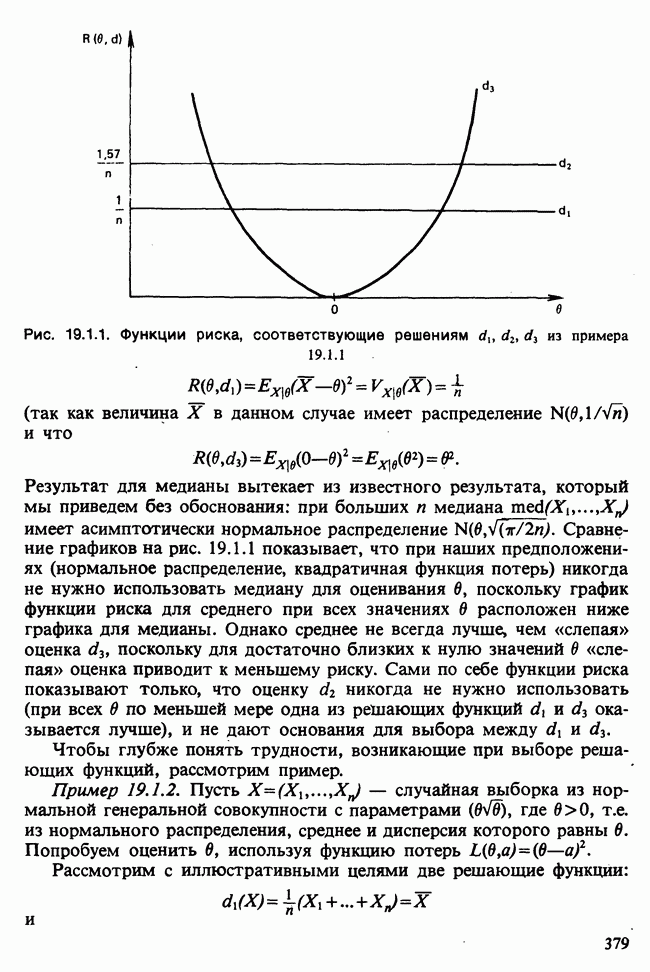
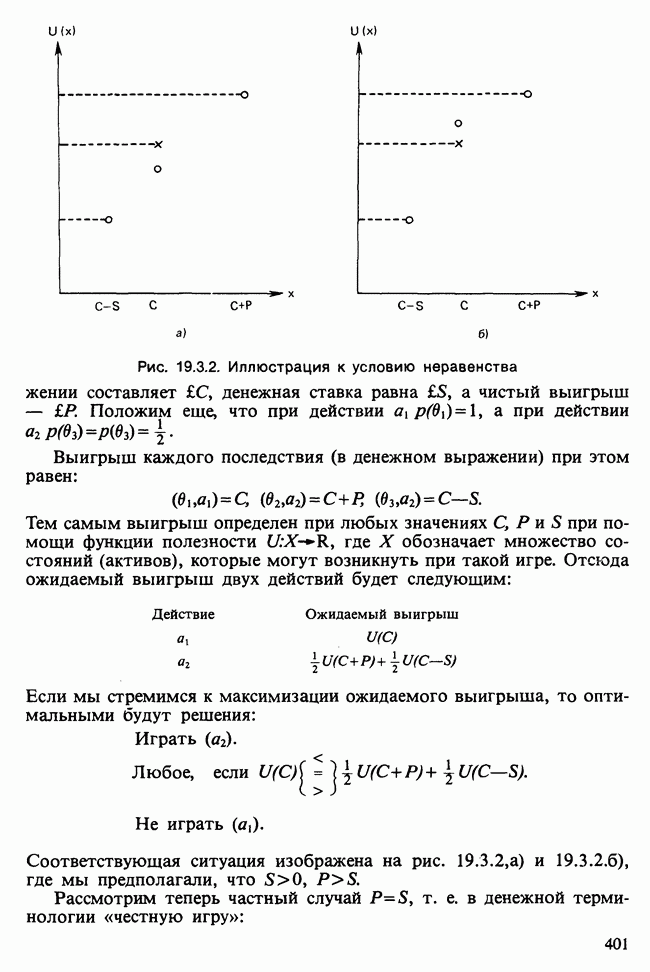
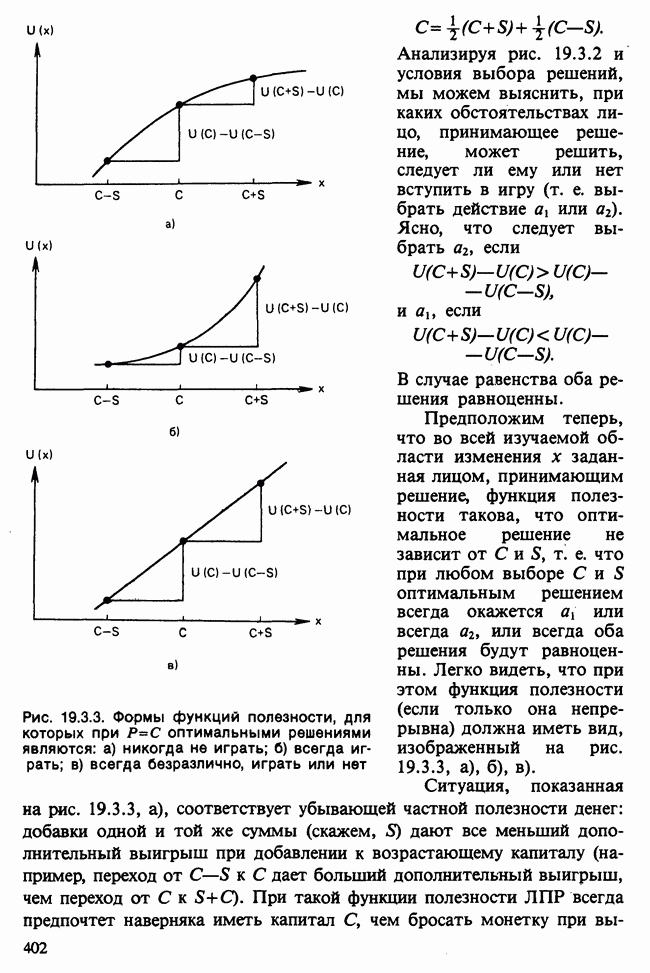
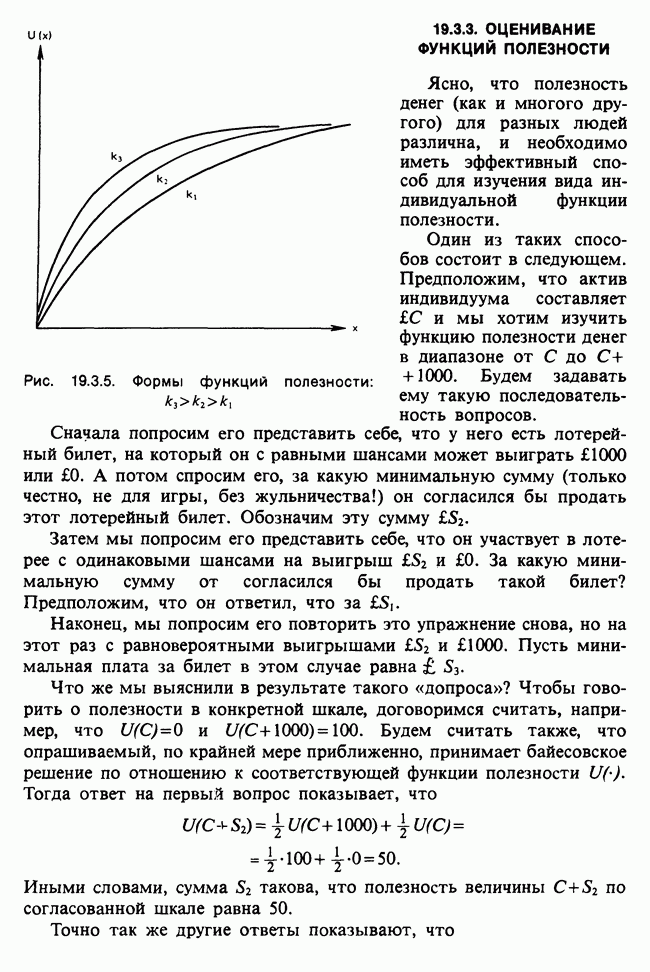
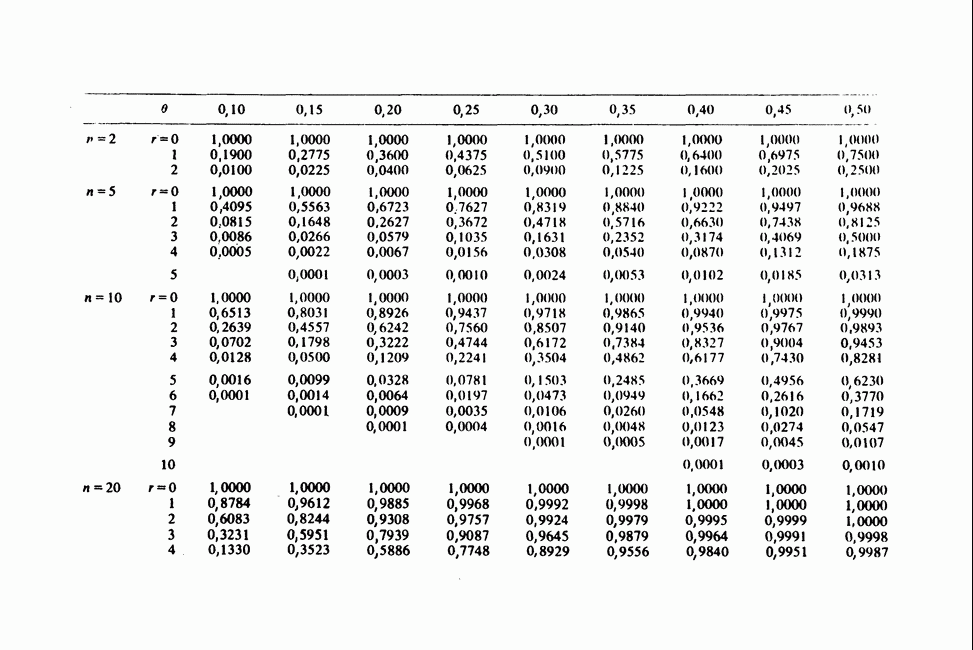
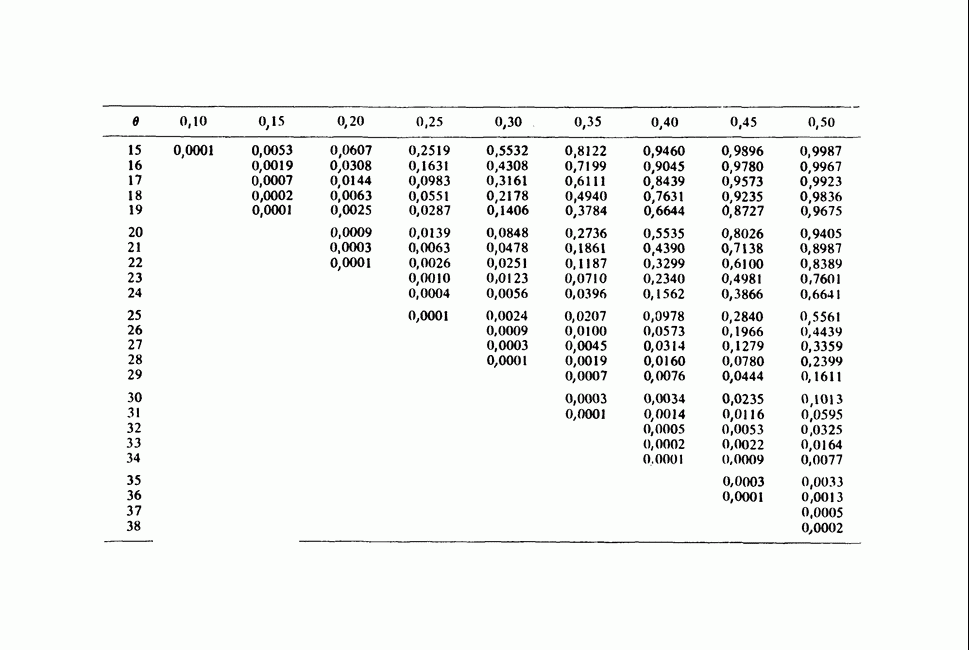
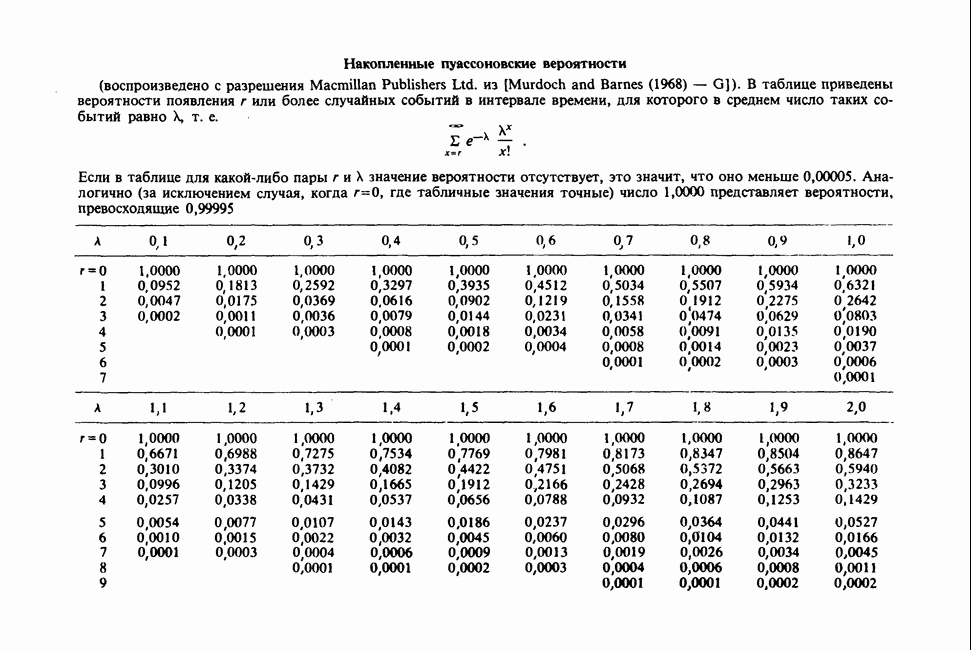
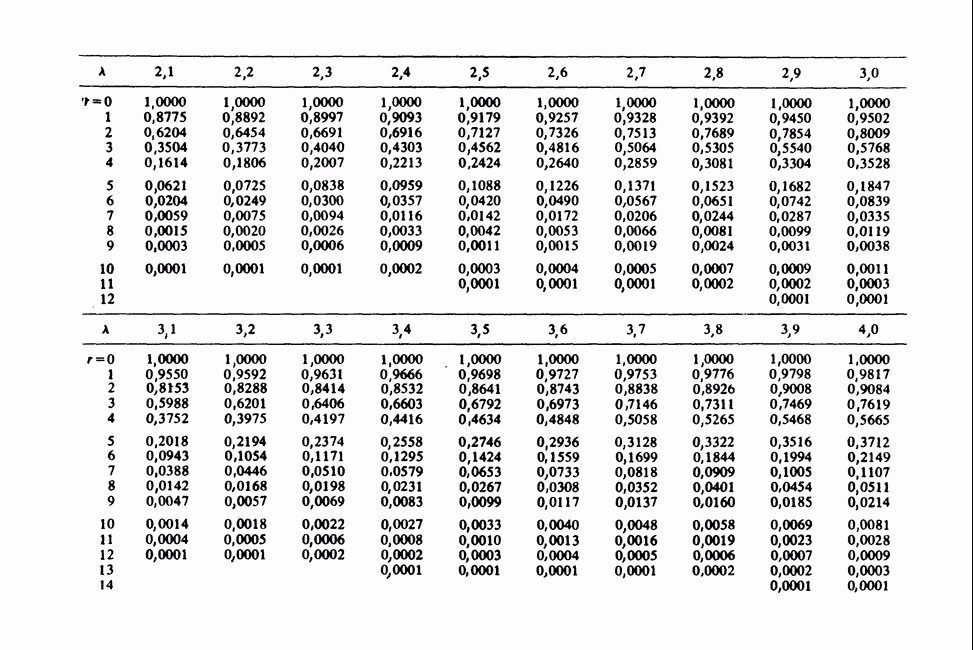
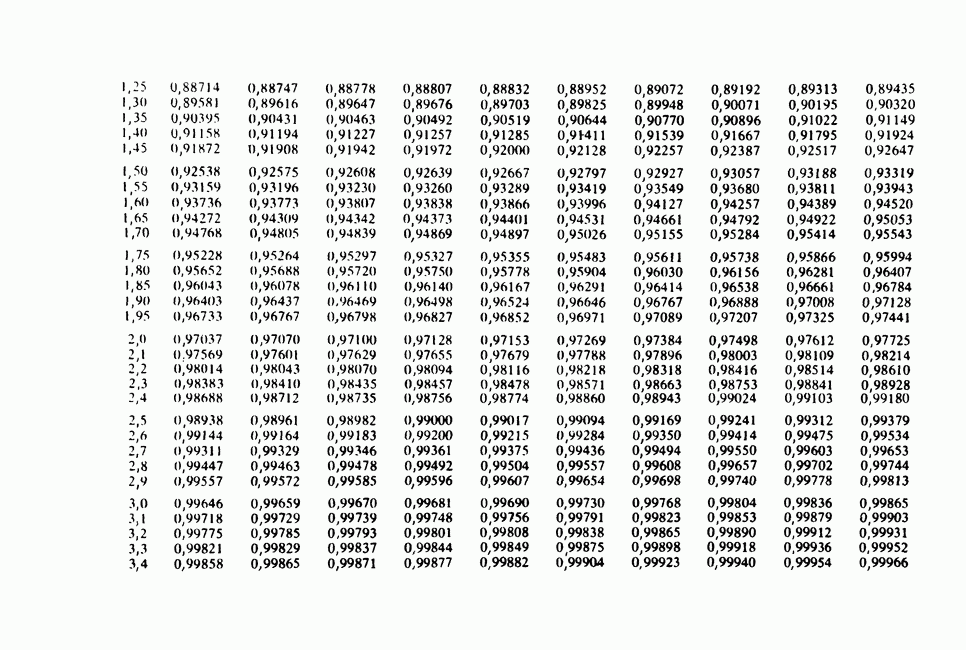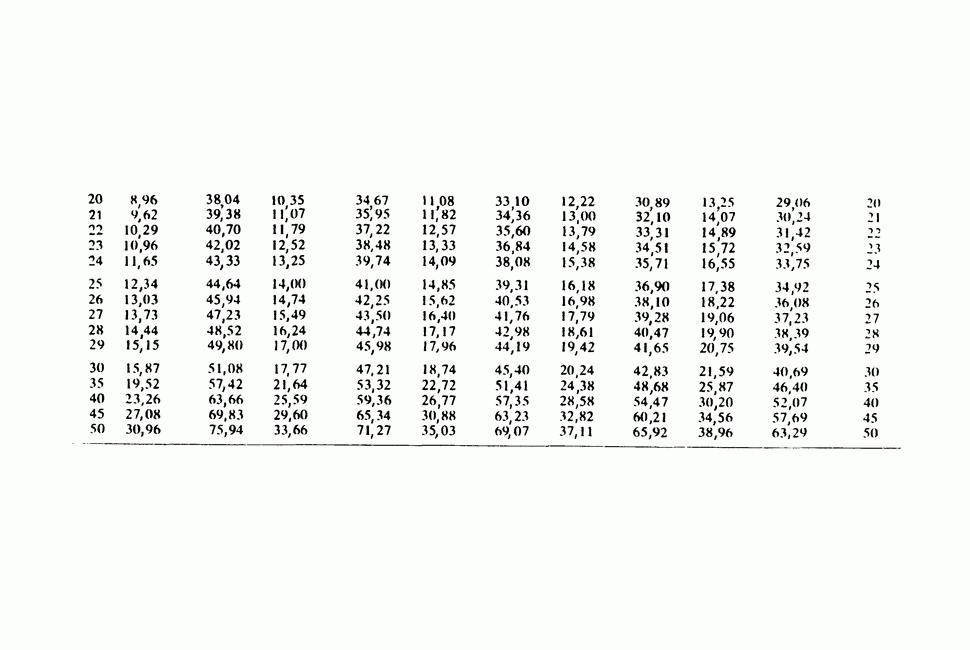| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
19.1.5. НЕКОТОРЫЕ ОСНОВНЫЕ ТЕОРЕМЫ
Приводимые далее результаты показывают, на каком пути пытаются искать общие связи между понятиями допустимого, байесовского и минимаксного решающих правил, и каковы эти связи.
Прежде чем сформулировать первую теорему, заметим, что может существовать два различных решающих правила и  для которых
для которых  при всех
при всех  . Так бывает, например, когда для непрерывной случайной величины X правила
. Так бывает, например, когда для непрерывной случайной величины X правила  различаются лишь в конечном числе точек. Поскольку функции риска
различаются лишь в конечном числе точек. Поскольку функции риска  выражаются интегралами, их значения совпадут. В этом случае мы будем говорить, что правила
выражаются интегралами, их значения совпадут. В этом случае мы будем говорить, что правила  равны с точностью до эквивалентности (т. е. их нельзя различить по значениям
равны с точностью до эквивалентности (т. е. их нельзя различить по значениям  Это понятие использует следующая теорема.
Это понятие использует следующая теорема.
Теорема 19.1.1 Пусть  произвольны,
произвольны,  — выборочное пространство непрерывной случайной величины X и
— выборочное пространство непрерывной случайной величины X и  — заданное априорное распределение Если байесовская решающая функция
— заданное априорное распределение Если байесовская решающая функция  единственна с точностью до эквивалентности, то она допустима.
единственна с точностью до эквивалентности, то она допустима.
Доказательство. (Мы считаем, что  есть плотность; случай дискретного множества
есть плотность; случай дискретного множества  рассматривается точно так же.) Предположим, что функция
рассматривается точно так же.) Предположим, что функция  недопустима. Тогда существует такое правило
недопустима. Тогда существует такое правило  что
что

и

поэтому

Но неравенство  не может быть строгим, потому что это противоречило бы предположению, что 8 — байесовское решающее правило. Оно не может быть и равенством, ибо это противоречило бы тому, что байесовское правило 8 единственно с точностью до эквивалентности.
не может быть строгим, потому что это противоречило бы предположению, что 8 — байесовское решающее правило. Оно не может быть и равенством, ибо это противоречило бы тому, что байесовское правило 8 единственно с точностью до эквивалентности.

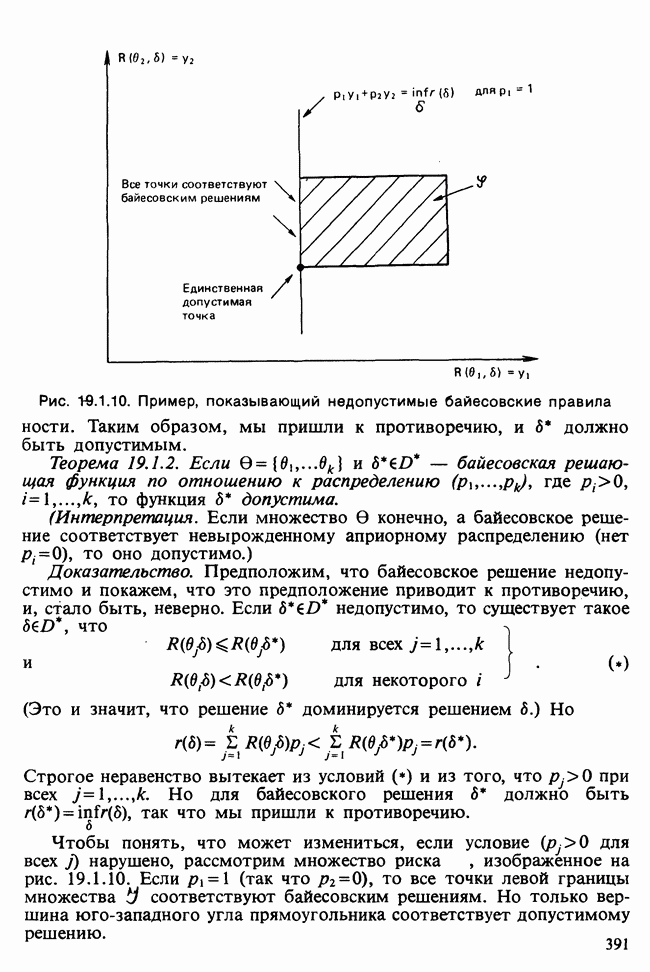
Рис. 19.1.10. Пример, показывающий недопустимые байесовские правила
Таким образом, мы пришли к противоречию, и 8 должно быть допустимым.
Теорема 19.1.2. Если  — байесовская решающая функция по отношению к распределению
— байесовская решающая функция по отношению к распределению  где
где  то функция 8 допустима.
то функция 8 допустима.
(Интерпретация. Если множество  конечно, а байесовское решение соответствует невырожденному априорному распределению (нет
конечно, а байесовское решение соответствует невырожденному априорному распределению (нет  то оно допустимо.)
то оно допустимо.)
Доказательство. Предположим, что байесовское решение недопустимо и покажем, что это предположение приводит к противоречию, и, стало быть, неверно. Если недопустимо, то существует такое

(Это и значит, что решение  доминируется решением
доминируется решением  ) Но
) Но

Строгое неравенство вытекает из условий  и из того, что
и из того, что  при всех
при всех  Но для байесовского решения
Но для байесовского решения  должно быть
должно быть  так что мы пришли к противоречию.
так что мы пришли к противоречию.
Чтобы понять, что может измениться, если условие  для всех
для всех  нарушено, рассмотрим множество риска
нарушено, рассмотрим множество риска  изображенное на рис. 19.1.10. Если
изображенное на рис. 19.1.10. Если  (так что
(так что  ), то все точки левой границы множества
), то все точки левой границы множества  соответствуют байесовским решениям. Но только вершина юго-западного угла прямоугольника соответствует допустимому решению.
соответствуют байесовским решениям. Но только вершина юго-западного угла прямоугольника соответствует допустимому решению.

Рис. 19.1.11. Набросок доказательства, что допустимое правило — байесовское
Теорема 19.1.3. Если множество  конечно,
конечно,  допустимое решение, то существует такое распределение
допустимое решение, то существует такое распределение  для всех
для всех  что решение
что решение  является байесовским по отношению к
является байесовским по отношению к 
(Интерпретация. Для задач с конечным множеством состояний  класс допустимых решений является подмножеством класса байесовских решений.)
класс допустимых решений является подмножеством класса байесовских решений.)
Набросок доказательства  Обозначим через х точку риска, соответствующую допустимому решению 6, а через
Обозначим через х точку риска, соответствующую допустимому решению 6, а через  — множество всех точек плоскости, расположенных к юго-западу (включая направления строго на юг и на запад) от точки х. И наконец, через
— множество всех точек плоскости, расположенных к юго-западу (включая направления строго на юг и на запад) от точки х. И наконец, через  обозначим множество
обозначим множество  из которого удалена точка х.
из которого удалена точка х.
Так как  — допустимое решение, то в множестве О нет точек, отличных от х и расположенных к юго-западу от х. Поэтому множества
— допустимое решение, то в множестве О нет точек, отличных от х и расположенных к юго-западу от х. Поэтому множества  не пересекаются [см. I, раздел 1.2.1]; кроме того, оба они выпуклы [см. раздел 19.1.4].
не пересекаются [см. I, раздел 1.2.1]; кроме того, оба они выпуклы [см. раздел 19.1.4].
Знаменитая теорема (теорема о разделяющей гиперплоскости) утверждает, что (когда  существует прямая
существует прямая  вроде изображенной на рис. 19.1.11. Для этой прямой
вроде изображенной на рис. 19.1.11. Для этой прямой  и без потери общности можно считать (поделив при необходимости на сумму
и без потери общности можно считать (поделив при необходимости на сумму  что
что  Но эта прямая является касательной к множеству
Но эта прямая является касательной к множеству  в точке
в точке  , стало быть, 8 есть байесовское решение по отношению к
, стало быть, 8 есть байесовское решение по отношению к 
Эти три теоремы показывают существо связей между допустимыми и байесовскими решениями. Следующие две теоремы характеризуют аналогичные связи между допустимыми и минимаксными решениями. Более детальное рассмотрение можно найти в книге [Ferguson (1967)].
Теорема 19.1.4. Если в некоторой задаче принятия решения минимаксное решение  единственно, то оно допустимо.
единственно, то оно допустимо.
Доказательство. Предположим обратное. Тогда найдется решение  для которого
для которого

Но отсюда следует, что

Строгое неравенство противоречит тому, что  — минимаксное решение, а равенство — тому, что минимаксное решение
— минимаксное решение, а равенство — тому, что минимаксное решение  единственно. Следовательно, наше исходное допущение о недопустимости
единственно. Следовательно, наше исходное допущение о недопустимости  ошибочно.
ошибочно.
Теорема 19.1.5. Если решение  допустимо и функция риска
допустимо и функция риска  постоянна при всех
постоянна при всех  то решение 8 является минимаксным. [Эта теорема описывает стратегию поиска минимаксных решений: сначала найти допустимое правило, а потом проверить, что для него функция риска постоянна.]
то решение 8 является минимаксным. [Эта теорема описывает стратегию поиска минимаксных решений: сначала найти допустимое правило, а потом проверить, что для него функция риска постоянна.]
Доказательство. Предположим противное. Тогда существует такое решение  что
что

Но если 

что противоречит допустимости решения  .
.
Основная классификационная теорема теории принятия решений утверждает, что, вообще говоря, чтобы быть допустимым, решение должно быть байесовским. (Конечно, при выполнении некоторых условий регулярности.) Это служит основанием для построения более простого метода поиска байесовских решающих правил, чем прямой поиск  Следующая теорема раскрывает существо этого простого метода.
Следующая теорема раскрывает существо этого простого метода.
Теорема 19.1.6. (нестрогая формулировка). Байесовская решающая функция 8 по отношению к априорному распределению  задается равенством
задается равенством  в котором действие а ищется из условия минимизации интеграла
в котором действие а ищется из условия минимизации интеграла

где

[.Интерпретация. Для любого  выбирается действие о, которое минимизирует апостериорные ожидаемые потери
выбирается действие о, которое минимизирует апостериорные ожидаемые потери  Доказательство (нестрогое).
Доказательство (нестрогое).

Предположим, что мы можем поменять порядок интегрирования (это и есть то место, где следует проявить наибольшую аккуратность при строгом доказательстве). Тогда

поскольку по определению условной плотности распределения вероятностей

Нахождение правила  , минимизирующего выражение
, минимизирующего выражение  эквивалентно минимизации внутреннего интеграла в последнем равенстве при каждом
эквивалентно минимизации внутреннего интеграла в последнем равенстве при каждом  Это и доказывает теорему.
Это и доказывает теорему.
Таким образом, поиск байесовских решающих функций может быть проведен в два этапа. На первом, используя теорему Байеса [см. гл. 15], находится  а на втором минимизируются апостериорные ожидаемые потери.
а на втором минимизируются апостериорные ожидаемые потери.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Глава 11. ЛИНЕЙНЫЕ МОДЕЛИ I
- 11.1.1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
- 11.1.2. БИНОМИАЛЬНАЯ ЛОГИСТИЧЕСКАЯ МОДЕЛЬ
- 11.1.3. ОБЩАЯ ЛИНЕЙНАЯ МОДЕЛЬ
- 11.1.4. МОДЕЛЬ С НОРМАЛЬНОЙ ФУНКЦИЕЙ ПЛОТНОСТИ И ТОЖДЕСТВЕННОЙ ФУНКЦИЕЙ СВЯЗИ (Normal-ldentity Model)
- 11.1.5. ЛИНЕЙНЫЙ ПРЕДИКТОР И ФУНКЦИЯ СВЯЗИ
- 11.1.6. ФУНКЦИЯ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ
- 11.1.7. ФУНКЦИЯ ПРАВДОПОДОБИЯ ДЛЯ ЭКСПОНЕНЦИАЛЬНОГО СЕМЕЙСТВА
- 11.1.8. ПРИМЕР С БИНОМИАЛЬНО-ЛОГИСТИЧЕСКОЙ МОДЕЛЬЮ
- 11.2. ПОДГОНКА МОДЕЛЕЙ ПО ДАННЫМ
- 11.2.2. ФУНКЦИЯ ПРАВДОПОДОБИЯ И ЕЕ МАКСИМУМ
- 11.2.3. ДЕВИАЦИЯ
- 11.2.4. РЕГРЕССИЯ, ПРОХОДЯЩАЯ ЧЕРЕЗ НАЧАЛО КООРДИНАТ
- 11.2.5. РАЗЛОЖЕНИЕ ДЕВИАЦИИ
- 11.3. СПЕЦИФИКАЦИЯ И ОТБОР МОДЕЛЕЙ
- 11.3.2. ФОРМУЛЫ МОДЕЛЕЙ ДЛЯ ЛИНЕЙНОГО ПРЕДИКТОРА
- 11.3.3. МОДЕЛИ С КАЧЕСТВЕННЫМИ ДАННЫМИ
- 11.3.4. ДВА ФАКТОРА: ГЛАВНЫЕ ЭФФЕКТЫ И ВЗАИМОДЕЙСТВИЕ
- 11.3.5. ДВУХФАКТОРНАЯ МОДЕЛЬ ДВУХВХОДОВОЙ МОДЕЛИ ДИСПЕРСИОННОГО АНАЛИЗА
- 11.3.6. ФАКТОРНАЯ МОДЕЛЬ ДЛЯ КРОСС-КЛАССИФИЦИРОВАННЫХ ДАННЫХ
- 11.3.7. СМЕШАННЫЕ МОДЕЛИ
- 11.3.8. ФАКТОРЫ С УПОРЯДОЧЕННЫМИ УРОВНЯМИ
- 11.4. ТАБЛИЦЫ СОПРЯЖЕННОСТЕЙ
- 11.4.2. МОДЕЛИ НЕЗАВИСИМОСТИ ДЛЯ ЛИНЕЙНОГО ПРЕДИКТОРА
- 11.4.3. МОДЕЛИ НЕЗАВИСИМОСТИ ДЛЯ ТРЕХВХОДОВЫХ ТАБЛИЦ
- 11.4.4. ФАКТОРЫ ОТКЛИКА И ОБРАБОТКИ
- Глава 12. ЛИНЕЙНЫЕ МОДЕЛИ II
- 12.1. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 12.1.2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ НА ПЛОСКОСТИ
- 12.1.3. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ДЛЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
- 12.1.4. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ В СЛУЧАЕ ДВУХ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ
- 12.1.5. НЕОРТОГОНАЛЬНЫЙ СЛУЧАЙ
- 12.1.6. ОБОБЩЕНИЯ НА СЛУЧАЙ НЕСКОЛЬКИХ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ
- 12.2. ВЫБОРОЧНЫЕ СВОЙСТВА
- 12.2.1. ТЕОРИЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
- 12.2.2. ПЕРВЫЕ И ВТОРЫЕ МОМЕНТЫ
- 12.2.3. ОДНА ОБЪЯСНЯЮЩАЯ ПЕРЕМЕННАЯ
- 12.2.4. ДВЕ ОРТОГОНАЛЬНЫЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ
- 12.2.5. НЕОРТОГОНАЛЬНЫЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ
- 12.3. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И ФУНКЦИЯ ПРАВДОПОДОБИЯ
- 12.3.2. АППРОКСИМАЦИЯ ФУНКЦИИ ПРАВДОПОДОБИЯ ОБОБЩЕННЫХ ЛИНЕЙНЫХ МОДЕЛЕЙ
- 12.3.3. ПРИМЕР: МОДЕЛЬ НЕЗАВИСИМОСТИ
- 12.3.4. ПРИМЕР С ЭКСПОНЕНЦИАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
- 12.3.5. ИТЕРАТИВНАЯ ПРОЦЕДУРА
- 12.3.6. АСИМПТОТИЧЕСКАЯ ТЕОРИЯ
- Глава 13. ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ
- 13.1. ПОСЛЕДОВАТЕЛЬНАЯ ПРОВЕРКА ГИПОТЕЗ
- 13.2. ПОСЛЕДОВАТЕЛЬНЫЙ КРИТЕРИЙ ОТНОШЕНИЯ ВЕРОЯТНОСТЕЙ (ПКОВ)
- 13.3. ОПЕРАТИВНАЯ ХАРАКТЕРИСТИКА ПКОВ
- 13.4. ОЖИДАЕМЫЙ ОБЪЕМ ВЫБОРКИ ДЛЯ ПКОВ
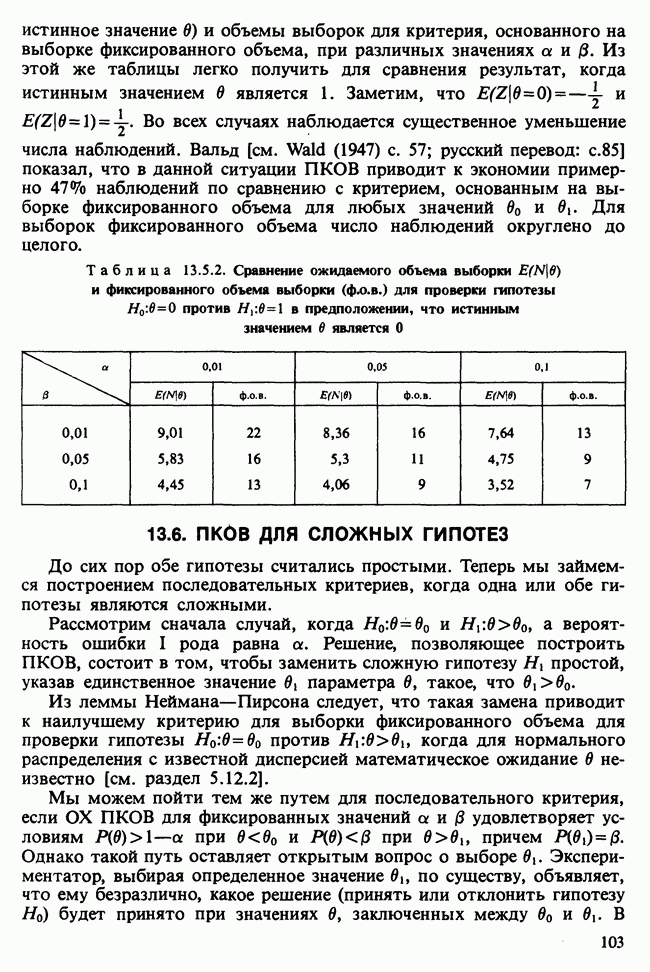
- 13.5. ПРИМЕРЫ
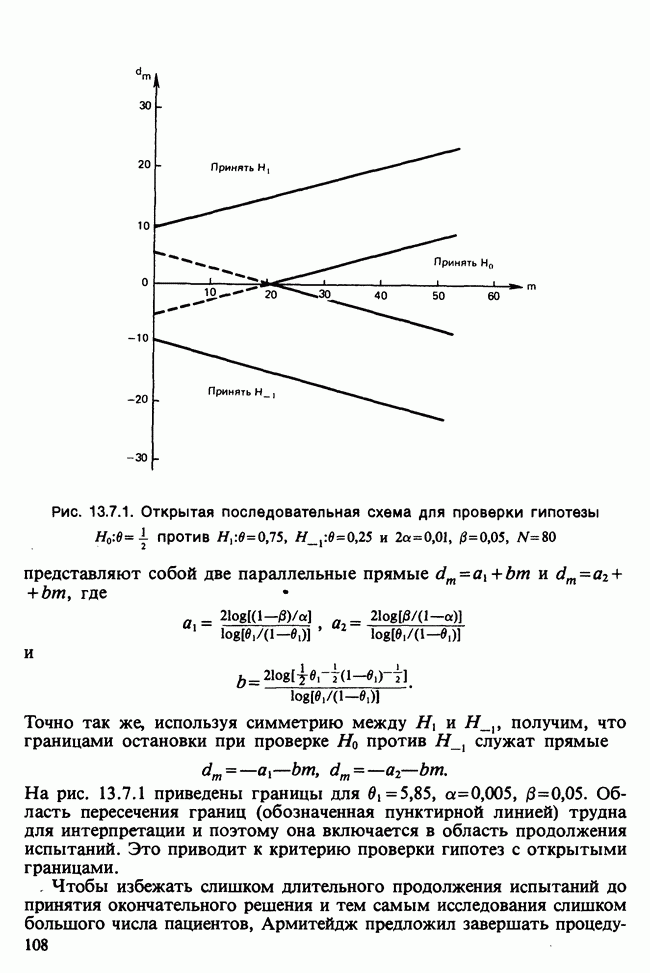
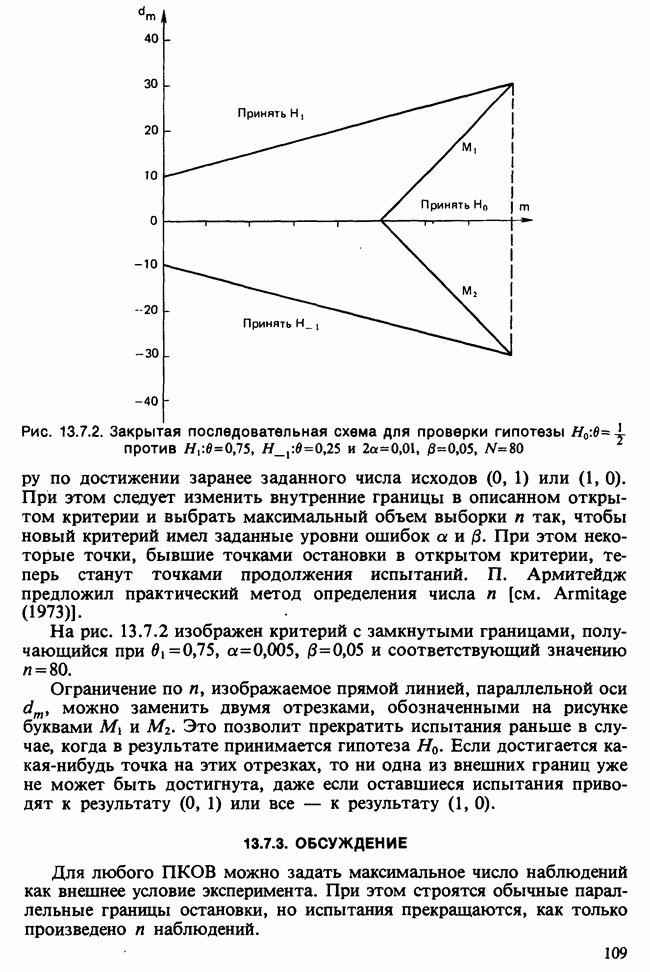
- 13.6. ПКОВ ДЛЯ СЛОЖНЫХ ГИПОТЕЗ
- 13.7. КРИТЕРИИ ОТНОСИТЕЛЬНО ДВУХ БИНОМИАЛЬНЫХ РАСПРЕДЕЛЕНИЙ
- 13.8. ДРУГИЕ ПОСЛЕДОВАТЕЛЬНЫЕ ПРОЦЕДУРЫ
- Глава 14. МЕТОДЫ, СВОБОДНЫЕ ОТ РАСПРЕДЕЛЕНИЯ
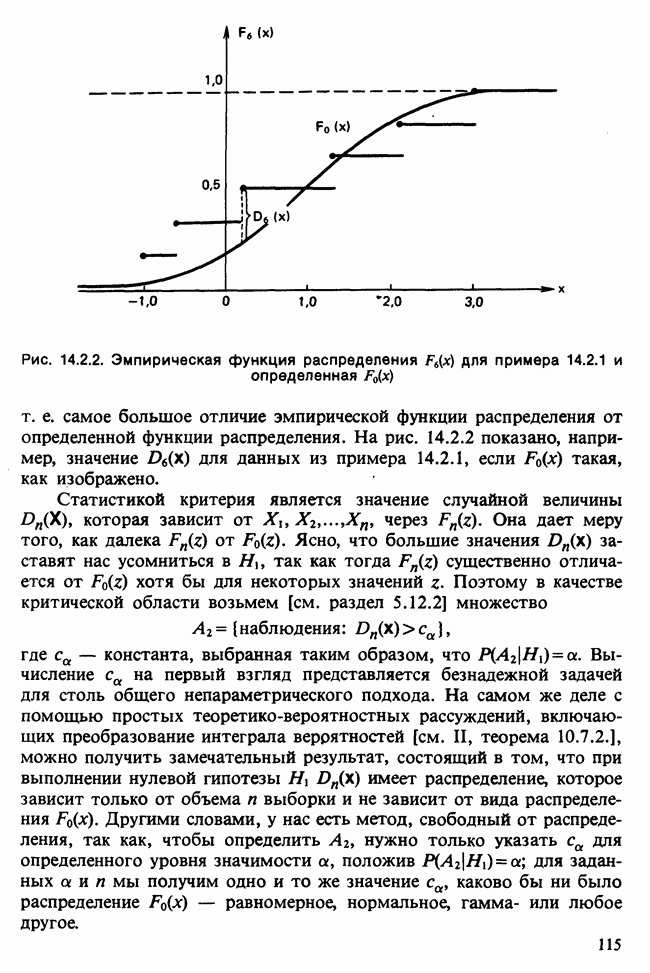
- 14.2. КРИТЕРИИ, ОСНОВАННЫЕ НА ЭМПИРИЧЕСКОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- 14.2.1. КРИТЕРИЙ КОЛМОГОРОВА. ОДНА ВЫБОРКА
- 14.2.2. КРИТЕРИЙ СМИРНОВА. ДВЕ ВЫБОРКИ
- 14.3. КРИТЕРИИ, ОСНОВАННЫЕ НА ПОРЯДКОВЫХ СТАТИСТИКАХ
- 14.4. ОДНОВЫБОРОЧНЫЕ КРИТЕРИИ
- 14.4.1. КРИТЕРИЙ ЗНАКОВ
- 14.4.2. КРИТЕРИЙ ЗНАКОВЫХ РАНГОВ УИЛКОКСОНА
- 14.5. СОПОСТАВЛЕННЫЕ ПАРЫ
- 14.6. ДВУВЫБОРОЧНЫЕ КРИТЕРИИ
- 14.6.1. ДВУВЫБОРОЧНЫЙ МЕДИАННЫЙ КРИТЕРИЙ
- 14.6.2. КРИТЕРИЙ УИЛКОКСОНА-МАННА-УИТНИ
- 14.6.3. КРИТЕРИЙ СЕРИЙ
- 14.7. НЕСКОЛЬКО ВЫБОРОК
- 14.7.1. МЕДИАННЫЙ КРИТЕРИЙ
- 14.7.2. КРИТЕРИЙ КРАСКЕЛА—УОЛЛИСА
- 14.8. РАНДОМИЗИРОВАННЫЕ КРИТЕРИИ
- 14.9. МЕРЫ РАНГОВОЙ КОРРЕЛЯЦИИ
- 14.9.2. КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ КЕНДЭЛА
- Глава 15. БАЙЕСОВСКИЙ ПОДХОД В СТАТИСТИКЕ
- 15.2. ТЕОРЕМА БАЙЕСА: ДИСКРЕТНЫЙ СЛУЧАЙ
- 15.2.2. ЗНАНИЯ, ИЗВЛЕКАЕМЫЕ ИЗ НЕСКОЛЬКИХ МНОЖЕСТВ ДАННЫХ
- 15.2.3. ТЕОРЕМА БАЙЕСА, ВЫРАЖЕННАЯ В ТЕРМИНАХ «ШАНСОВ» (odds)
- 15.2.4. ОБОБЩЕНИЕ НА СЛУЧАЙ БЕСКОНЕЧНОГО СПИСКА ВОЗМОЖНЫХ МОДЕЛЕЙ
- 15.3. ТЕОРЕМА БАЙЕСА: НЕПРЕРЫВНЫЙ СЛУЧАЙ
- 15.3.2. ФОРМИРОВАНИЕ АПРИОРНЫХ ПЛОТНОСТЕЙ
- 15.3.3. ТЕОРЕМА БАЙЕСА ДЛЯ ЕДИНСТВЕННОГО НЕИЗВЕСТНОГО ПАРАМЕТРА
- 15.3.4. ТЕОРЕМА БАЙЕСА ДЛЯ ДВУХ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ
- 15.3.5. ПРИБЛИЖЕННЫЙ АНАЛИЗ ПРИ БОЛЬШОЙ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ
- 15.4. БАЙЕСОВСКИЕ ПОДХОДЫ К ТИПИЧНЫМ СТАТИСТИЧЕСКИМ ЗАДАЧАМ
- 15.4.2. ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
- 15.4.3. ПРОВЕРКА ЗНАЧИМОСТИ
- 15.4.4. ПРОГНОЗИРОВАНИЕ
- 15.4.5. ПРИВЕДЕНИЕ ДАННЫХ: ДОСТАТОЧНЫЕ СТАТИСТИКИ
- 15.4.6. ПРИНЦИП ПРАВДОПОДОБИЯ
- 15.5. БАЙЕСОВСКИЙ ВЫВОД ДЛЯ НЕКОТОРЫХ ОДНОМЕРНЫХ ВЕРОЯТНОСТНЫХ МОДЕЛЕЙ
- 15.5.2. ВЫВОДЫ ДЛЯ РАСПРЕДЕЛЕНИЯ ПУАССОНА
- 15.5.3. ВЫВОДЫ В СЛУЧАЕ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
- 15.6. БАЙЕСОВСКИЕ МЕТОДЫ ДЛЯ МОДЕЛЕЙ, СОДЕРЖАЩИХ МНОГО ПАРАМЕТРОВ
- Глава 16. МНОГОМЕРНЫЙ АНАЛИЗ: КЛАССИЧЕСКИЕ МЕТОДЫ
- 16.2. ВЫБОРКИ ИЗ МНОГОМЕРНЫХ НОРМАЛЬНЫХ (MVN) РАСПРЕДЕЛЕНИЙ
- 16.2.1. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 16.2.2. НЕКОТОРЫЕ ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
- 16.2.3. ПРОВЕРКА ГИПОТЕЗ И ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ ВЕКТОРА МАТЕМАТИЧЕСКИХ ОЖИДАНИЙ
- 16.2.4. ЗАДАЧИ ДЛЯ ДВУХ ВЫБОРОК
- 16.2.5. ВЫВОДЫ ДЛЯ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
- 16.2.6. НЕЦЕНТРАЛЬНЫЕ РАСПРЕДЕЛЕНИЯ
- 16.3. ГЛАВНЫЕ КОМПОНЕНТЫ
- 16.4. ФАКТОРНЫЙ АНАЛИЗ
- 16.4.2. ФАКТОРНАЯ МОДЕЛЬ
- 16.4.3. НЕКОТОРЫЕ СВОЙСТВА
- 16.4.4. ОЦЕНИВАНИЕ
- 16.5. КАНОНИЧЕСКАЯ КОРРЕЛЯЦИЯ
- 16.5.2. КАНОНИЧЕСКИЕ КОРРЕЛЯЦИИ СОВОКУПНОСТИ
- 16.5.3. ВЫБОРОЧНЫЕ КАНОНИЧЕСКИЕ КОРРЕЛЯЦИИ
- 16.5.4. ЧИСЛЕННЫЙ ПРИМЕР
- 16.6. ДИСКРИМИНАНТНЫЙ АНАЛИЗ
- 16.6.3. ДИСКРИМИНАЦИЯ В ДВЕ МНОГОМЕРНЫЕ СОВОКУПНОСТИ
- 16.6.4. ДИСКРИМИНАЦИЯ В НЕСКОЛЬКО СОВОКУПНОСТЕЙ
- Глава 17. МНОГОМЕРНЫЙ АНАЛИЗ: ОРДИНАЦИЯ, МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ И СМЕЖНЫЕ ВОПРОСЫ
- 17.2. АНАЛИЗ ГЛАВНЫХ КОМПОНЕНТ
- 17.3. МУЛЬТИПЛИКАТИВНЫЕ МОДЕЛИ И ТЕОРЕМА ЭКАРТА—ЮНГА
- 17.4. ДВОЙСТВЕННЫЕ ГРАФИКИ (биплоты)
- 17.5. АНАЛИЗ СООТВЕТСТВИЙ
- 17.6. МЕТРИЧЕСКОЕ ШКАЛИРОВАНИЕ: АНАЛИЗ ГЛАВНЫХ КООРДИНАТ И КЛАССИЧЕСКОЕ ШКАЛИРОВАНИЕ
- 17.7. МЕТРИЧЕСКОЕ ШКАЛИРОВАНИЕ: ДРУГИЕ МЕТОДЫ
- 17.8. НЕМЕТРИЧЕСКОЕ МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
- 17.9. МНОГОМЕРНАЯ РАЗВЕРТКА
- 17.10. ОРТОГОНАЛЬНЫЙ ПРОКРУСТОВ АНАЛИЗ
- 17.11. ОБЩЕЕ СРАВНЕНИЕ МЕТОДОВ ШКАЛИРОВАНИЯ
- 17.12. ШКАЛИРОВАНИЕ МАТРИЦ С ТРЕМЯ ВХОДАМИ
- 17.13. АНАЛИЗ АСИММЕТРИИ
- Глава 18. ВРЕМЕННЫЕ РЯДЫ
- 18.2. КЛАССИЧЕСКИЕ РЕГРЕССИОННЫЕ МОДЕЛИ ДЛЯ ВРЕМЕННЫХ РЯДОВ
- 18.2.2. МОДЕЛЬ ЦИКЛИЧЕСКИХ КОМПОНЕНТ
- 18.3. ПЕРИОДОГРАММА ВРЕМЕННОГО РЯДА
- 18.3.2. ГАРМОНИЧЕСКИЙ РЕГРЕССИОННЫЙ АНАЛИЗ
- 18.3.3. ПЕРИОДОГРАММА
- 18.3.4. ВЛИЯНИЕ ИСКЛЮЧЕНИЯ СРЕДНЕГО ЗНАЧЕНИЯ НА ПЕРИОДОГРАММУ
- 18.3.5. ПЕРИОДОГРАММЫ ДЛЯ ПРОСТЫХ МОДЕЛЕЙ
- 18.3.6. ИНТЕРПРЕТАЦИЯ ПЕРИОДОГРАММЫ
- 18.4. РАЗНОСТНЫЕ ОПЕРАТОРЫ
- 18.5. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ
- 18.5.1. АВТОКОРРЕЛЯЦИОННАЯ ФУНКЦИЯ (АКФ)
- 18.5.2. СВЯЗЬ МЕЖДУ ПЕРИОДОГРАММОЙ И АКФ
- 18.5.3. СПЕКТР И ВЫБОРОЧНЫЙ СПЕКТР
- 18.5.4. СВОЙСТВА СПЕКТРА И АКФ
- 18.5.5. ЧАСТНАЯ АВТОКОРРЕЛЯЦИОННАЯ ФУНКЦИЯ (ЧАКФ)
- 18.5.6. ВЫБОРОЧНАЯ ЧАКФ
- 18.6. ОБЩАЯ ЛИНЕЙНАЯ МОДЕЛЬ
- 18.6.2. ЛИНЕЙНЫЕ ОПЕРАТОРЫ НАД ВРЕМЕННЫМИ РЯДАМИ
- 18.6.3. ЛИНЕЙНЫЕ ОПЕРАТОРЫ И СПЕКТР
- 18.6.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ НА КОНЕЧНЫХ ВЫБОРКАХ
- 18.6.5. ОГРАНИЧЕНИЯ НА ОЛМ
- 18.6.6. ПРОГНОЗИРОВАНИЕ С ПОМОЩЬЮ ОЛМ
- 18.7. МОДЕЛЬ СКОЛЬЗЯЩЕГО СРЕДНЕГО (СС)
- 18.7.2. ХАРАКТЕРИСТИЧЕСКИЕ СВОЙСТВА МОДЕЛИ СС(q)
- 18.7.3. ЭФФЕКТИВНЫЕ ОЦЕНКИ ДЛЯ МОДЕЛИ СС(q)
- 18.7.4. ПРОГНОЗИРОВАНИЕ С ПОМОЩЬЮ МОДЕЛЕЙ СС
- 18.7.5. ЭВСС-ПРЕДИКТОР
- 18.7.6. СЕЗОННАЯ МОДЕЛЬ БОКСА—ДЖЕНКИНСА ДЛЯ РЯДА АВИАПЕРЕВОЗОК
- 18.8. АВТОРЕГРЕССИОННЫЕ МОДЕЛИ
- 18.8.2. ПРИМЕРЫ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ
- 18.8.3. ХАРАКТЕРИСТИЧЕСКИЕ СВОЙСТВА МОДЕЛИ АР(р)
- 18.8.4. ЭФФЕКТИВНЫЕ ОЦЕНКИ ДЛЯ МОДЕЛИ АР(р)
- 18.8.5. ПРОГНОЗ С ПОМОЩЬЮ МОДЕЛИ АР(р)
- 18.9. СМЕШАННЫЕ МОДЕЛИ АВТОРЕГРЕССИИ И СКОЛЬЗЯЩЕГО СРЕДНЕГО (АРСС)
- 18.9.2. ПРИМЕР
- 18.10. ОЦЕНИВАНИЕ СПЕКТРА
- 18.10.2. ПРЯМЫЕ МЕТОДЫ ОЦЕНКИ
- 18.10.3. КОСВЕННЫЕ МЕТОДЫ ОЦЕНИВАНИЯ
- 18.10.4. ПРИМЕНЕНИЕ СПЕКТРАЛЬНОГО АНАЛИЗА
- 18.11. РЕГРЕССИОННЫЕ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ
- Глава 19. ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ
- 19.1.2. МИНИМАКСНЫЕ И БАЙЕСОВСКИЕ РЕШАЮЩИЕ ПРАВИЛА
- 19.1.3. ДОПУСТИМЫЕ РЕШАЮЩИЕ ФУНКЦИИ
- 19.1.4. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
- 19.1.5. НЕКОТОРЫЕ ОСНОВНЫЕ ТЕОРЕМЫ
- 19.2. СТАТИСТИКА И ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ
- 19.2.2. ПРОВЕРКА ПРОСТОЙ ГИПОТЕЗЫ ПРОТИВ ПРОСТОЙ АЛЬТЕРНАТИВЫ
- 19.2.3. ЛЕММА НЕЙМАНА-ПИРСОНА
- 19.3. ОТНОШЕНИЕ К РИСКУ И ТЕОРИИ ПОЛЕЗНОСТИ
- 19.3.2. ОДНОМЕРНЫЕ ФУНКЦИИ ПОЛЕЗНОСТИ
- 19.3.3. ОЦЕНИВАНИЕ ФУНКЦИЙ ПОЛЕЗНОСТИ
- 19.3.4. ФУНКЦИИ ПОЛЕЗНОСТИ ВЫСШИХ РАЗМЕРНОСТЕЙ
- 19.4. ПОСЛЕДОВАТЕЛЬНЫЕ ПРОЦЕДУРЫ ПРИНЯТИЯ РЕШЕНИЙ
- 19.4.2. ДЕРЕВЬЯ РЕШЕНИЙ
- 19.5. АКСИОМАТИЧЕСКИЕ ПОДХОДЫ
- 19.5.1. АКСИОМЫ СОГЛАСОВАННОСТИ В ПРИНЯТИИ РЕШЕНИЙ
- 19.5.2. СТЕПЕНЬ УВЕРЕННОСТИ КАК ВЕРОЯТНОСТЬ
- Глава 20. КАЛМАНОВСКАЯ ФИЛЬТРАЦИЯ
- 20.2. МОДЕЛИ В ФАЗОВОМ ПРОСТРАНСТВЕ
- 20.2.2. ПРОСТОЙ ПРИМЕР
- 20.3. ВЫВОД ФИЛЬТРА КАЛМАНА ДЛЯ ДИСКРЕТНОЙ ЛИНЕЙНОЙ ДИНАМИЧЕСКОМ СИСТЕМЫ
- 20.3.3. ОПТИМАЛЬНЫЙ ВЫБОР ФИЛЬТРА КАЛМАНА
- 20.3.4. ПРОГНОЗ СОСТОЯНИЯ
- 20.3.5. ИНТЕРПРЕТАЦИЯ УРАВНЕНИЙ ФИЛЬТРАЦИИ
- 20.3.6. РЕЗЮМЕ
- 20.4. ТЕСТЫ ПРОВЕРКИ КАЧЕСТВА ФИЛЬТРА
- 20.4.2. РАСХОДИМОСТЬ ФИЛЬТРА
- 20.5. КАЛМАНОВСКАЯ ФИЛЬТРАЦИЯ ДЛЯ НЕПРЕРЫВНОГО ВРЕМЕНИ И НЕЛИНЕЙНЫХ СИСТЕМ
- 20.5.2. НЕЛИНЕЙНЫЕ СИСТЕМЫ: ОБОБЩЕННЫЙ ФИЛЬТР КАЛМАНА
- 20.6 ИДЕНТИФИКАЦИЯ МОДЕЛИ И ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 20.6.2. ИДЕНТИФИКАЦИЯ МОДЕЛИ
- 20.6.3. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 20.7. ПРИМЕНЕНИЯ
- 20.7.1. ПРИМЕНЕНИЕ ДИСКРЕТНОГО ЛИНЕЙНОГО ФИЛЬТРА КАЛМАНА
- 20.7.2. ПРИЛОЖЕНИЯ ОБОБЩЕННОГО ФИЛЬТРА КАЛМАНА
- 20.8. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Литература
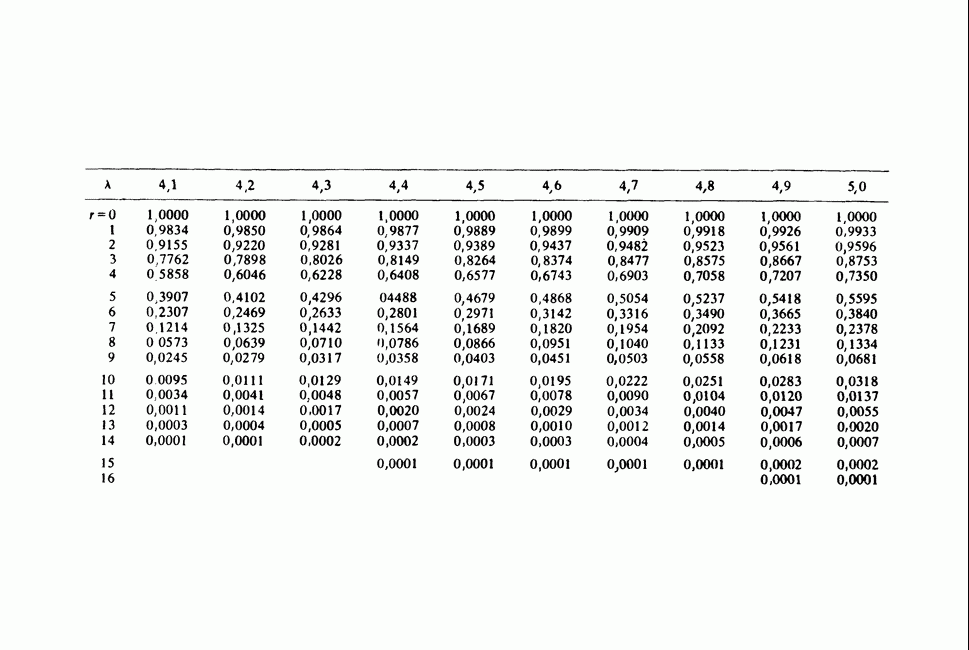
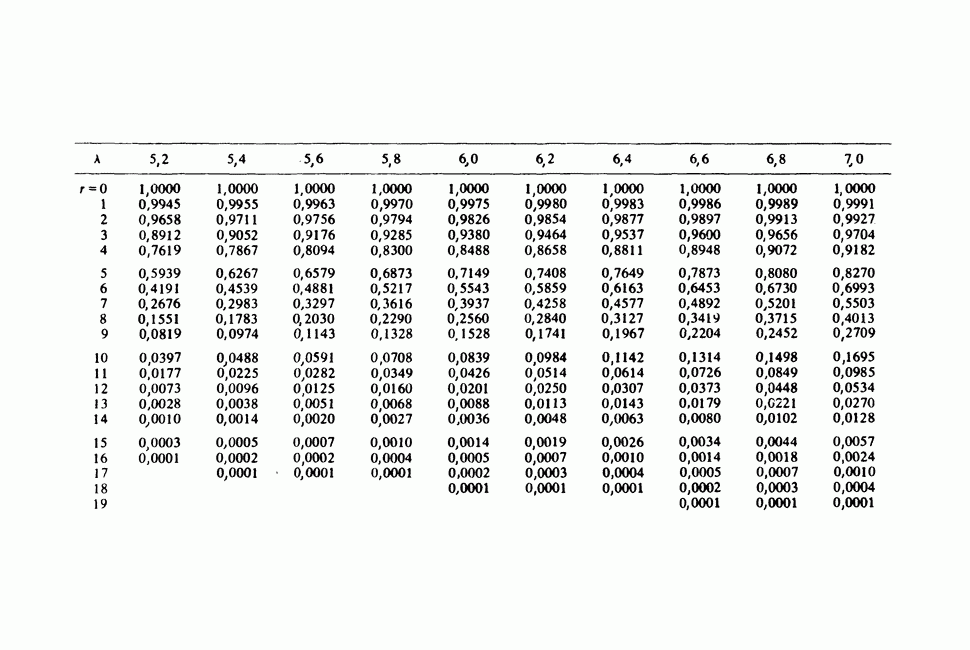
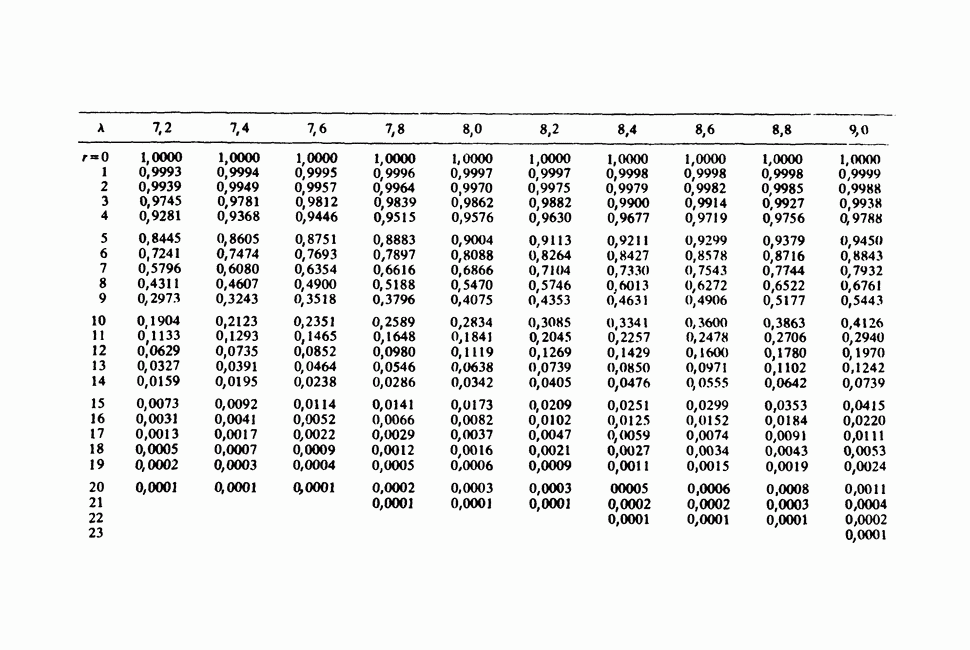
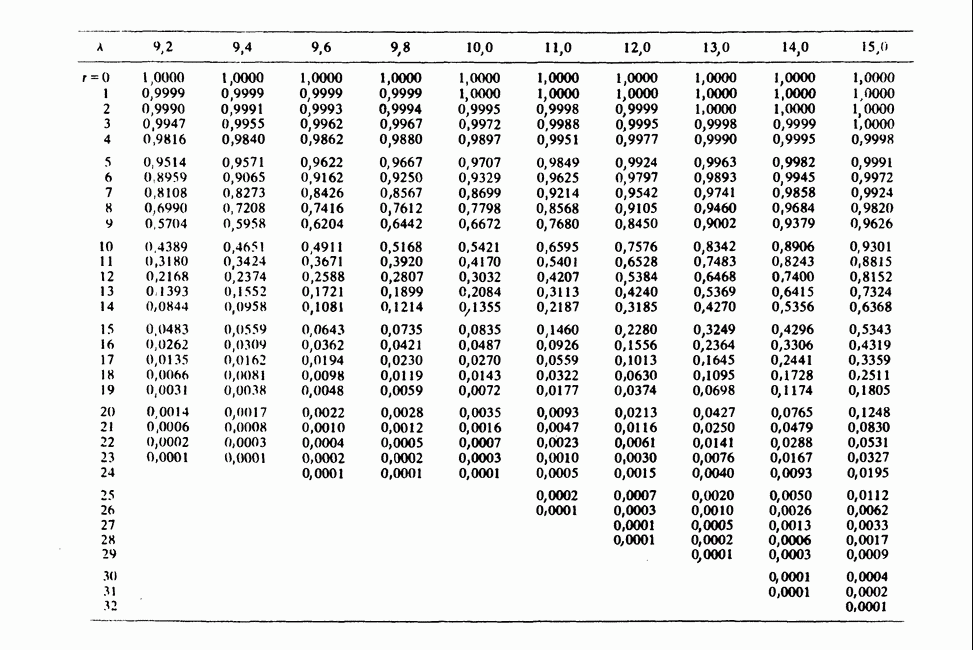
- Приложения. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
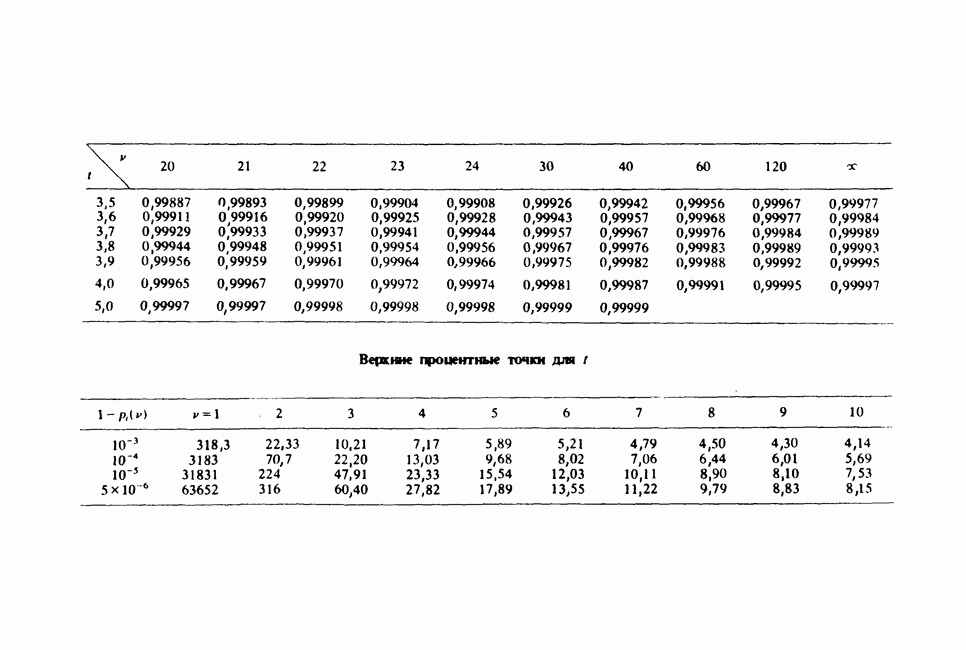
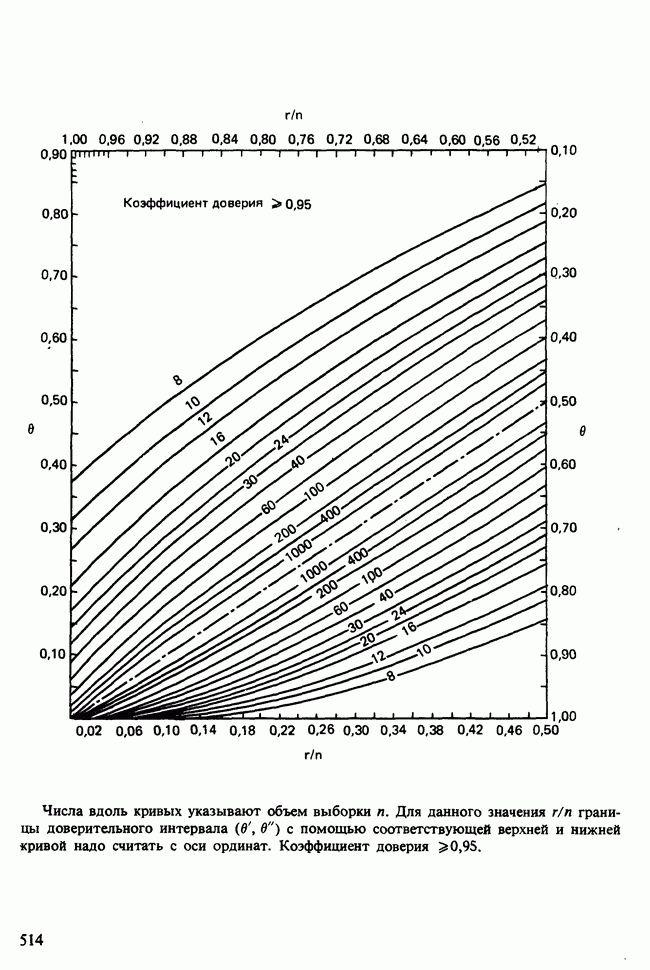
- ПРИЛОЖЕНИЕ 2
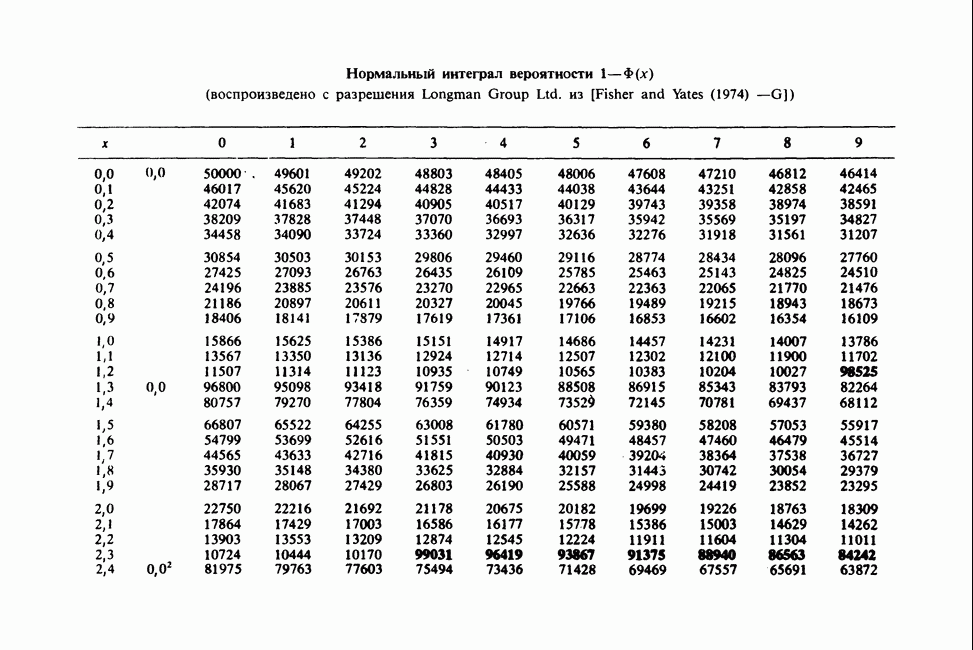
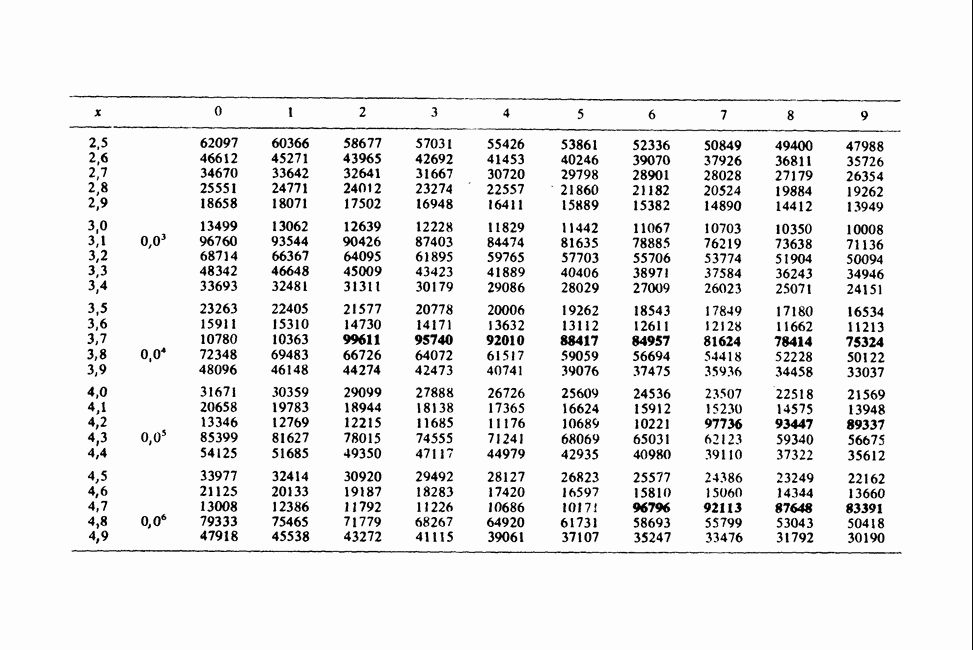
- ПРИЛОЖЕНИЕ 3
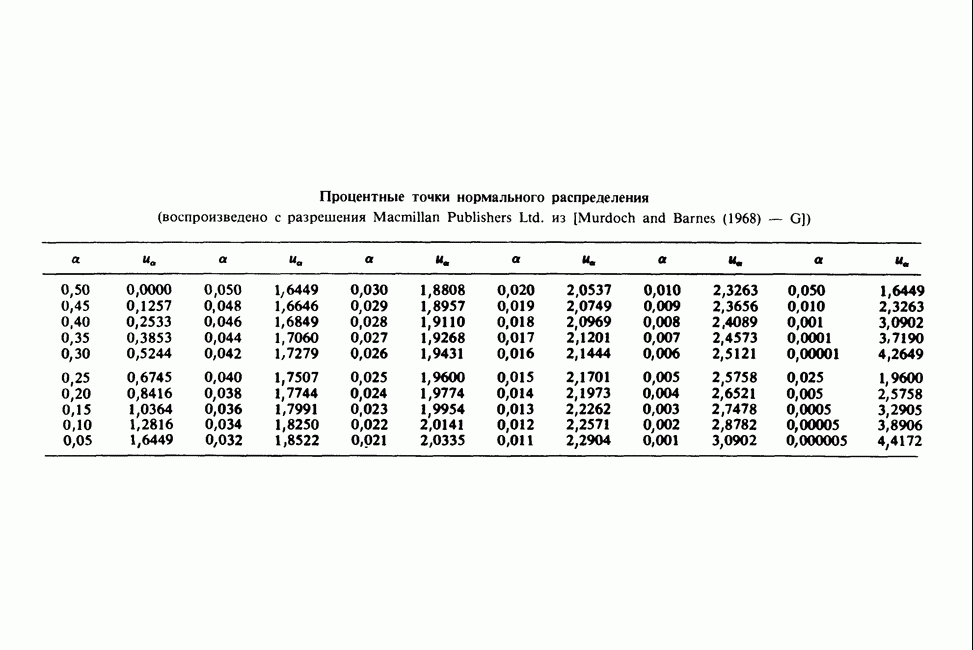
- ПРИЛОЖЕНИЕ 4
- ПРИЛОЖЕНИЕ 5
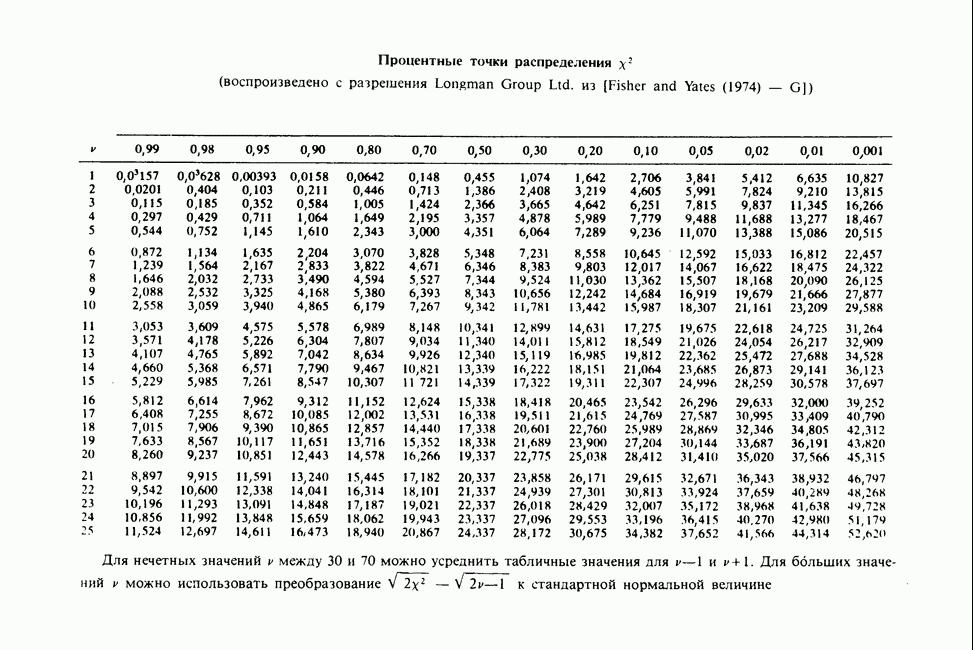
- ПРИЛОЖЕНИЕ 6
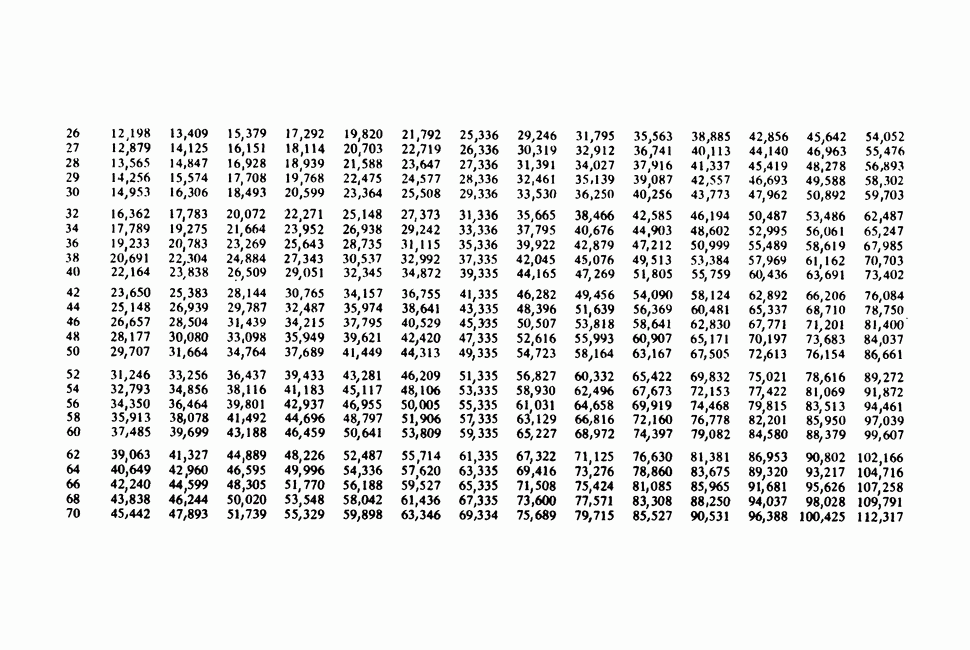
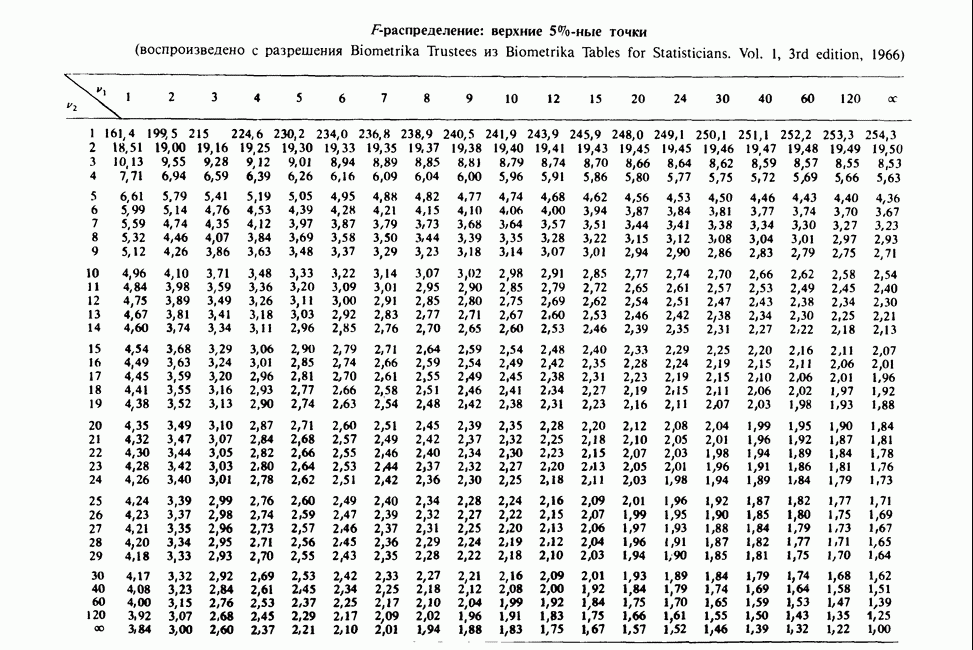
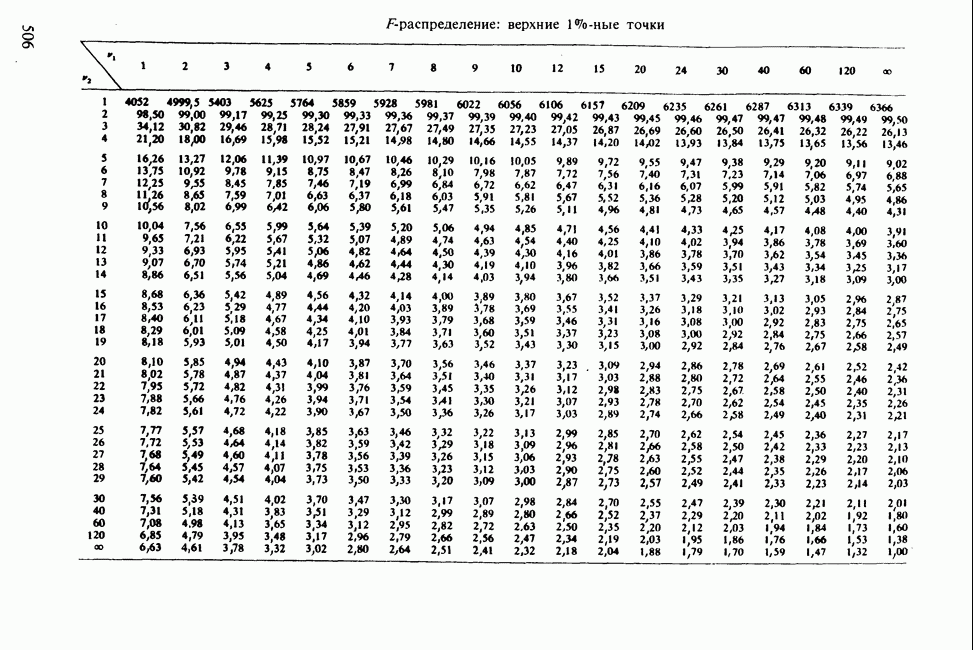
- ПРИЛОЖЕНИЕ 7
- ПРИЛОЖЕНИЕ 8
- ПРИЛОЖЕНИЕ 9
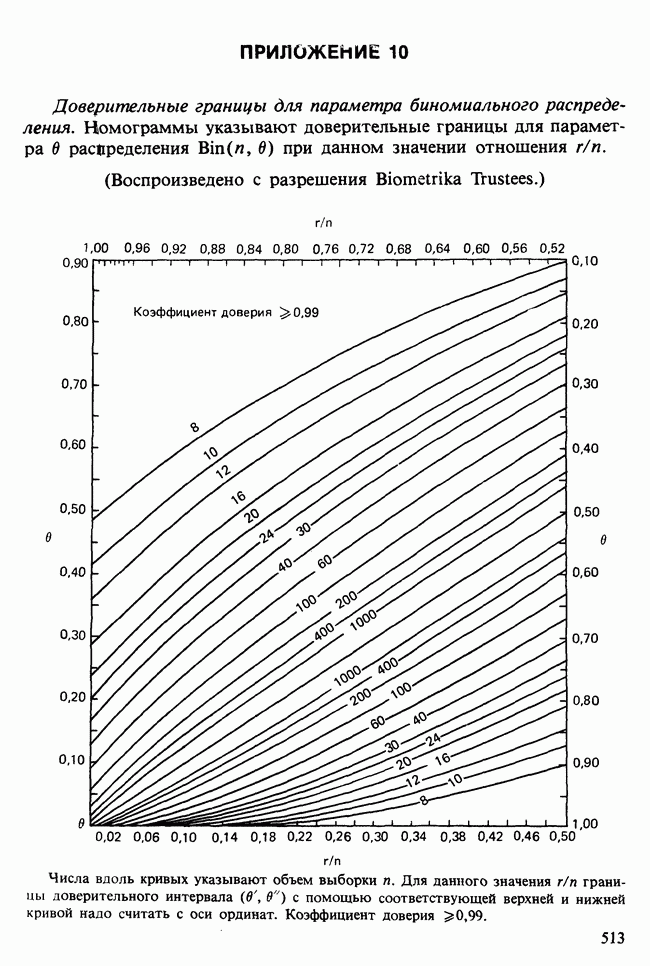
- ПРИЛОЖЕНИЕ 10
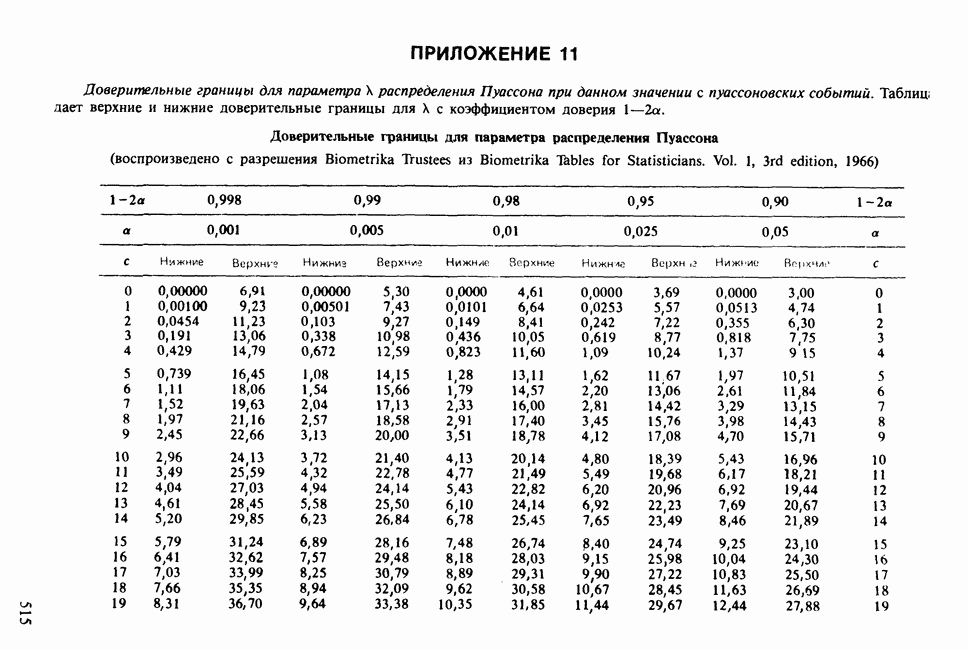
- ПРИЛОЖЕНИЕ 11