| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 197. Геометрия молекул
Накоплен обширный материал по значениям расстояний между центрами атомов в молекулах и кристаллах. Основная часть этого материала получена дифракционными методами. Если не претендовать на очень большую точность, то оказывается возможным изображение молекул моделями, дающими представление о форме и размерах молекулы.
Особенно простыми являются модели молекул типа  в которых атомы соединены ионной связью. Каждый ион можно представить сферой определенного радиуса. Представление о размерах ионов дает следующая табличка:
в которых атомы соединены ионной связью. Каждый ион можно представить сферой определенного радиуса. Представление о размерах ионов дает следующая табличка:
(см. скан)
При помощи такой таблички можно найти расстояние между центрами ионов в любой соли; например, расстояние в  равно
равно 
Однако, какой смысл вкладывается в утверждение: ион можно представить шаром? Чтобы увидеть законность такого представления, нужно выяснить, как близко к молекуле, скажем  может подойти еще один ион натрия (или хлора). Это можно узнать, так как, согласно опыту, и твердые, и расплавленные соли построены из ионов. Оказывается, что и второй, и третий ионы подходят к данному иону на те же расстояния, что и первый. Более того, одноименно заряженные ионы также могут приблизиться друг к другу на расстояние, равное сумме ионных радиусов. Действительно, ионы ведут себя как шары.
может подойти еще один ион натрия (или хлора). Это можно узнать, так как, согласно опыту, и твердые, и расплавленные соли построены из ионов. Оказывается, что и второй, и третий ионы подходят к данному иону на те же расстояния, что и первый. Более того, одноименно заряженные ионы также могут приблизиться друг к другу на расстояние, равное сумме ионных радиусов. Действительно, ионы ведут себя как шары.

Рис. 224.
Из этих геометрических фактов следует важный вывод, касающийся ионных молекул. Положим, что к одной молекуле подошла вплотную еще группа молекул. Создалось расположение ионов, показанное на рис. 224. При полном равенстве межатомных расстояний уже невозможно сказать, с каким из соседних атомов хлора образует молекулу данный ион натрия, и наоборот, какой ион натрия должен считать своей парой данный ион хлора. Понятие молекулы потеряло свой смысл.
Таким образом, геометрия расположения центров атомов приводит к заключению: в конденсированном состоянии (т. е. в жидком
и твердом), где атомы соединены ионной связью, молекул как выделенных образований не существует. Понятие молекулы оказывается неприменимым.
А как обстоит дело в газовой фазе? При испарении от жидкости легче всего отрывается пара разноименно заряженных ионов, не несущая в целом электрического заряда. Поэтому мы, прежде всего, находим в парах молекулы типа  Однако наряду с молекулами из жидкости испаряются и ионы разных типов.
Однако наряду с молекулами из жидкости испаряются и ионы разных типов.
Совсем не так обстоит дело в молекулах с гомеополярной (кова-лентной) связью. Анализируя встречающиеся в молекулах межатомные расстояния, мы приходим к выводу о возможности вычисления расстояний между центрами атомов при помощи так называемых атомных радиусов. Их значения (в ангстремах) для наиболее часто встречающихся атомов таковы:

Атомные радиусы уменьшаются с возрастанием кратности валентной связи. Из этой таблицы мы узнаем, что расстояние между двумя связанными атомами углерода  составляет 1,54 А, расстояние
составляет 1,54 А, расстояние  равно 1,07 А и т. д.
равно 1,07 А и т. д.
При создании модели молекулы мы обладаем также некоторыми простейшими сведениями о валентных углах. Можно говорить о нормальных валентных углах, происхождение которых понятно из соображений симметрии и находится в согласии с некоторыми качественными соображениями квантовой механики, о чем мы говорили в предыдущем параграфе. Так, нормальными углами атома углерода, связанного с четырьмя атомами, являются тетраэдрические углы  для ароматического атома углерода, а также для других атомов углерода, связанных с тремя атомами, нормальным валентным углом является угол 120°. Наконец, для атома углерода, связанного с двумя атомами, характерен валентный угол 180°. Нормальные валентные углы атомов кислорода, серы и азота, связанных с двумя, а для азота с тремя атомами, равны 90°. Атом азота нитрогруппы
для ароматического атома углерода, а также для других атомов углерода, связанных с тремя атомами, нормальным валентным углом является угол 120°. Наконец, для атома углерода, связанного с двумя атомами, характерен валентный угол 180°. Нормальные валентные углы атомов кислорода, серы и азота, связанных с двумя, а для азота с тремя атомами, равны 90°. Атом азота нитрогруппы  имеет нормальные валентные углы, равные 120°.
имеет нормальные валентные углы, равные 120°.
Валентные углы в ряде случаев значительно отклоняются от «нормы». В ряде циклических соединений типа циклобутана вместо  осуществляются углы, равные 90°. Весьма значительные отклонения от нормальных получают валентные углы из-за объемных препятствий. Однако, прежде чем разъяснить это последнее обстоятельство, необходимо остановиться на третьей геометрической характеристике молекулы — межмолекулярном радиусе.
осуществляются углы, равные 90°. Весьма значительные отклонения от нормальных получают валентные углы из-за объемных препятствий. Однако, прежде чем разъяснить это последнее обстоятельство, необходимо остановиться на третьей геометрической характеристике молекулы — межмолекулярном радиусе.
Исследования расположений молекул в кристаллах показали, что каждому атому можно приписать свой межмолекулярный радиус, такой, что в среднем и с достаточной точностью соседние молекулы будут соприкасаться. Так, например, межмолекулярный радиус водорода равен 1,17 А, кислорода 1,36 А, азота 
Это, однако, не значит, что расстояния между валентно не связанными атомами одной и той же молекулы будут определяться этими цифрами. Дело заключается в том, что размеры и форма молекулы определяются взаимодействием сил, устанавливающих равновесные расстояния между валентно не связанными атомами и нормальные валентные углы. При этом силы связи между атомами на порядок величины выше, поэтому межатомные расстояния не меняются и конфигурация молекулы определяется конкуренцией упругости валентного угла с сжимаемостью межмолекулярной сферы атома.

Рис. 225.
Приведем простой, но наглядный пример. Валентный угол в молекуле воды равен, как показывает оопыт, 105°. Расстояние между атомами водорода составляет 1,54 А. Следовательно, имеет место существенная спрессовка межмолекулярных сфер атомов водорода, равная  Эта спрессовка уравновешивается упругостью валентного угла, нормальное значение которого равно 90°. Таким образом, силы, спрессовывающие атомы водорода на 0,8 А, равны силам, изменяющим угол от 90° до 105°. Подтверждение этим простым соображениям находим, сравнивая структуру молекулы воды со структурой молекулы сероводорода. Так как длина связи водород — сера значительно больше длины связи водород — кислород, то атомам водорода в молекуле сероводорода значительно менее «тесно». Расстояние между атомами водорода оказывается равным 1,99 А, а валентный угол 92°. Спрессовка атомов водорода на 0,35 А уравновешивается изменением валентного угла всего лишь на 2°. Аналогичные картины могут быть продемонстрированы на огромном числе примеров органических молекул.
Эта спрессовка уравновешивается упругостью валентного угла, нормальное значение которого равно 90°. Таким образом, силы, спрессовывающие атомы водорода на 0,8 А, равны силам, изменяющим угол от 90° до 105°. Подтверждение этим простым соображениям находим, сравнивая структуру молекулы воды со структурой молекулы сероводорода. Так как длина связи водород — сера значительно больше длины связи водород — кислород, то атомам водорода в молекуле сероводорода значительно менее «тесно». Расстояние между атомами водорода оказывается равным 1,99 А, а валентный угол 92°. Спрессовка атомов водорода на 0,35 А уравновешивается изменением валентного угла всего лишь на 2°. Аналогичные картины могут быть продемонстрированы на огромном числе примеров органических молекул.
Рис. 225 показывает построение модели молекулы хлорбензола. Слева — атом углерода, в середине — начало построения, группа  справа — модель молекулы.
справа — модель молекулы.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. МЕХАНИЧЕСКОЕ И ТЕПЛОВОЕ ДВИЖЕНИЕ
- Уравнения движения материальной точки.
- Средняя скорость.
- Истинная скорость.
- Векторное ускорение.
- § 2. Силы
- Гравитационные силы.
- Электромагнитные силы.
- Ядерные силы.
- Силы «слабого» взаимодействия.
- Поле сил.
- § 3. Основной закон механики
- Законы Ньютона.
- Относительность движения.
- Законы механики в неинерциальной системе координат.
- § 4. Приложение основного закона механики к ускоренному прямолинейному движению
- Горизонтальное движение под действием постоянной силы.
- Вертикально движущийся лифт.
- Тяга свободно подвешенного груза.
- § 5. Приложение основного закона механики к движению по окружности
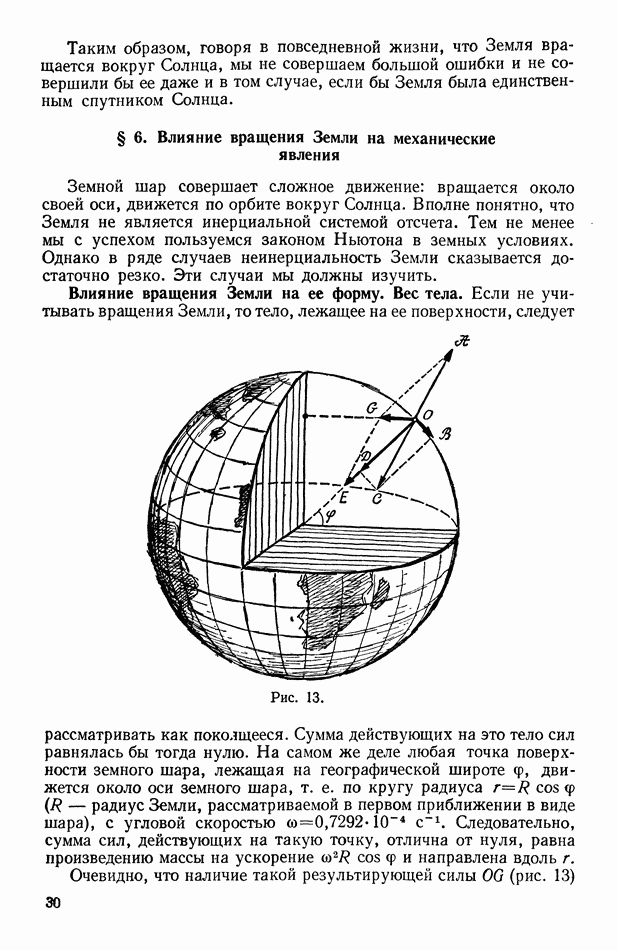
- § 6. Влияние вращения Земли на механические явления
- Влияние вращения Земли на ее форму. Вес тела.
- Влияние вращения Земли на движение тел по земной поверхности.
- § 7. Какие данные необходимы для решения механической задачи?
- § 8. Коэффициенты пропорциональности в формулах физики и размерности физических величин
- ГЛАВА 2. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
- § 9. Работа
- § 10. Кинетическая энергия
- § 11. Потенциальная энергия
- § 12. Закон сохранения механической энергии
- § 13. Потенциальные кривые. Равновесие
- ГЛАВА 3. ИМПУЛЬС
- § 14. Сохранение импульса
- § 15. Центр инерции
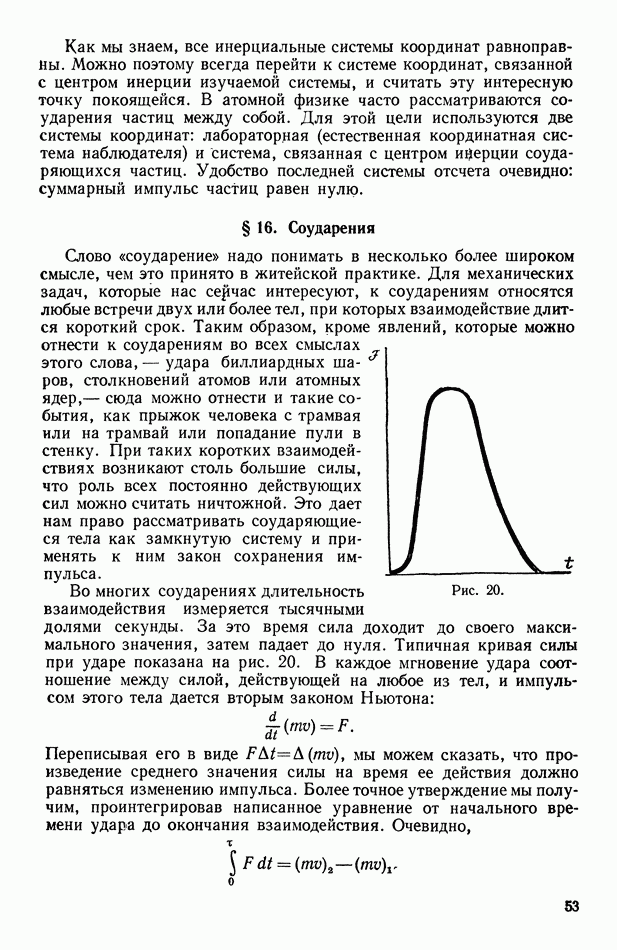
- § 16. Соударения
- § 17. Явления отдачи
- ГЛАВА 4. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 18. Кинетическая энергия вращения
- § 19. Момент инерции
- § 20. Работа вращения и основное уравнение вращения
- § 21. Момент импульса
- § 22. Свободные оси вращения
- § 23. Гироскопы
- ГЛАВА 5. КОЛЕБАНИЯ
- § 24. Малые отклонения от равновесия
- § 25. Частные случаи колебаний
- § 26. Превращения энергии. Затухающие колебания
- § 27. Вынужденные колебания
- § 28. Автоколебания
- § 29. Сложение колебаний одного направления
- § 30. Спектр колебания
- § 31. Сложение взаимно перпендикулярных колебаний
- ГЛАВА 6. БЕГУЩИЕ ВОЛНЫ
- § 32. Распространение деформации
- § 33. Возникновение волнового движения
- § 34. Волны давления и скорости колебания
- § 35. Поток энергии
- § 36. Затухание упругих волн
- § 37. Интерференция волн
- § 38. Принцип Гюйгенса — Френеля. Отражение и преломление волн
- § 39. Коэффициент отражения
- § 40. Явление Доплера
- ГЛАВА 7. СТОЯЧИЕ ВОЛНЫ
- § 41. Наложение двух волн, бегущих в противоположные стороны
- § 42. Собственные колебания стержней
- § 43. Собственные колебания двумерных и трехмерных систем
- § 44. Вынужденные колебания стержней и пластинок
- § 45. Колебания пьезоэлектриков
- ГЛАВА 8. ВОПРОСЫ АКУСТИКИ
- § 46. Объективная и субъективная характеристики звука
- § 47. Сила и громкость звука
- § 48. Архитектурная акустика
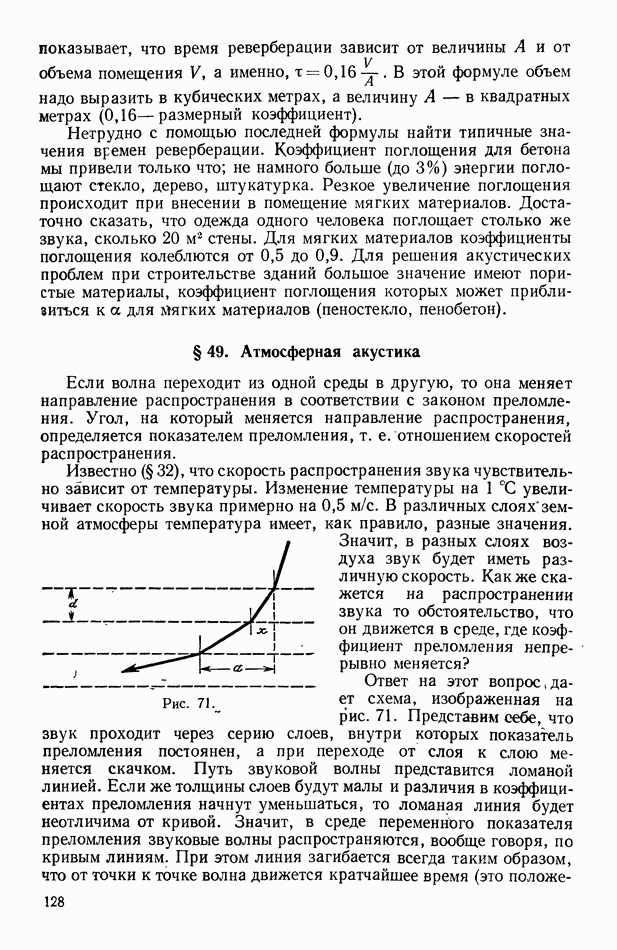
- § 49. Атмосферная акустика
- § 50. Действие ультразвука
- ГЛАВА 9. ТЕМПЕРАТУРА И ТЕПЛОТА
- § 51. Тепловое равновесие
- § 52. Внутренняя энергия
- § 53. Первое начало термодинамики
- § 54. Энергия микроскопических систем
- § 55. Уравнение состояния
- § 56. Уравнение газового состояния
- § 57. Уравнения состояния реальных газов
- ГЛАВА 10. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
- § 58. Графическое изображение процессов
- § 59. Работа. Циклы
- § 60. Процессы изменения состояния газов
- Изобарический процесс.
- Изотермический процесс.
- Адиабатический процесс.
- Измерение теплоемкостей газов.
- § 61. Процесс Джоуля — Томсона
- ГЛАВА 11. ЭНТРОПИЯ
- § 62. Принцип существования энтропии
- § 63. Принцип возрастания энтропии
- § 64. Принцип действия тепловой машины
- § 65. Цикл Карно. Максимальный к. п. д.
- § 66. Второе начало термодинамики
- ГЛАВА 12. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- § 68. Длина свободного пробега
- § 69. Давление газа. Средняя квадратичная скорость молекул
- § 70. Внутренняя энергия газа
- § 71. Статистическое распределение
- § 72. Закон Больцмана
- § 73. Распределение частиц по высоте в поле тяжести
- § 74. Распределение молекул по скоростям
- § 75. Измерение скоростей молекул газа
- § 76. Вероятность состояния
- § 77. Необратимые процессы с молекулярной точки зрения
- § 78. Флуктуации. Границы применения второго начала
- ГЛАВА 13. ПРОЦЕССЫ ПЕРЕХОДА К РАВНОВЕСИЮ
- § 79. Диффузия
- § 80. Теплопроводность и вязкость
- § 81. Быстрота выравнивания
- § 82. Стационарные процессы
- § 83. Движение в вязкой среде
- § 84. Коэффициенты диффузии, вязкости и теплопроводности для газов
- § 85. Ультраразреженные газы
- ЧАСТЬ II. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 86. Векторные характеристики электрического поля: напряженность и смещение
- § 87. Диэлектрическая проницаемость
- § 88. Законы электрического поля
- § 89. Вычисление полей простейших систем
- Система точечных зарядов.
- Универсальные формулы потенциала.
- Поле сферического конденсатора.
- Поле равномерно заряженной сферы.
- Поле с цилиндрической симметрией.
- Однородные поля.
- Поле на поверхности металла.
- Электрическое изображение.
- § 90. Электрическая энергия
- Энергия конденсатора.
- Энергия поля
- Энергия взаимодействия.
- § 91. Радиус электрона и границы классической электродинамики
- § 92. Электрические силы
- § 93. Дипольный момент системы зарядов
- § 94. Поляризация изотропного диэлектрика
- § 95. Поляризация кристаллических веществ
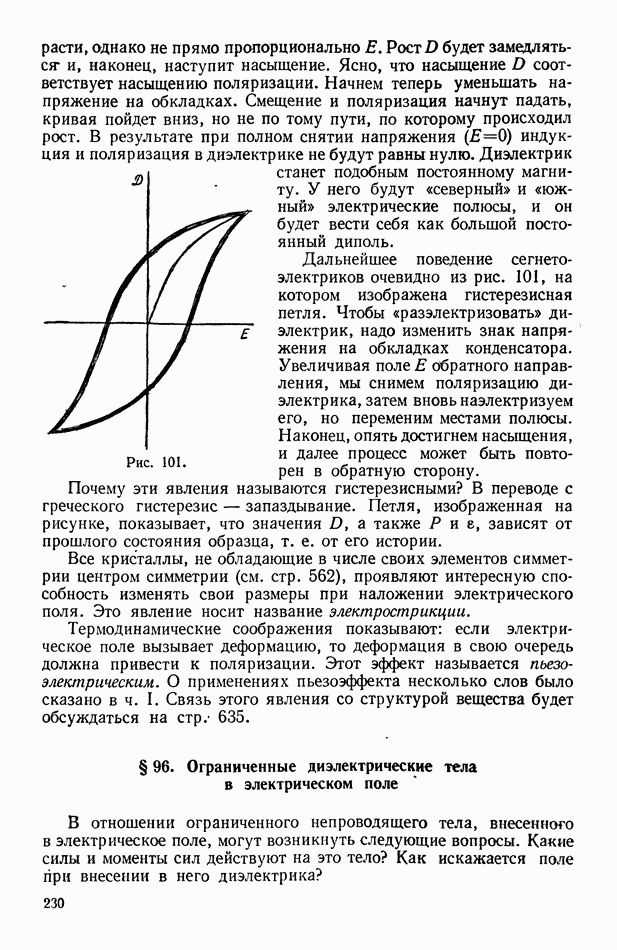
- § 96. Ограниченные диэлектрические тела в электрическом поле
- ГЛАВА 15. МАГНИТНОЕ ПОЛЕ
- § 97. Магнитный момент
- § 98. Сила Ампера
- § 99. Сила, действующая на движущийся заряд
- § 100. Магнитное поле, создаваемое постоянными магнитами
- § 101. Напряженность магнитного поля
- § 102. Взаимодействия токов и магнитов
- § 103. Эквивалентность токов и магнитов
- § 104. Вихревой характер магнитного поля
- § 105. Закон электромагнитной индукции и сила Лоренца
- § 106. Измерения магнитного поля методом индукционного толчка
- § 107. Ограниченные тела в магнитном поле
- § 108. Связь между магнитной проницаемостью и восприимчивостью
- § 109. Искажение магнитного поля при внесении в него магнетика
- § 110. Магнитный гистерезис
- ГЛАВА 16. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ. УРАВНЕНИЯ МАКСВЕЛЛА
- § 111. Обобщение закона электромагнитной индукции
- § 112. Ток смещения
- § 113. Картина электромагнитного поля
- ГЛАВА 17. ЭНЕРГЕТИЧЕСКИЕ ПРЕВРАЩЕНИЯ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
- § 114. Превращения в цепи постоянного тока
- § 115. Превращения в замкнутой цепи переменного тока
- § 116. Магнитная энергия поля
- § 117. Электрические колебания
- § 118. Электромагнитная энергия
- § 119. Импульс и давление электромагнитного поля
- ГЛАВА 18. ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- § 120. Элементарный диполь
- § 121. Антенна как электрический диполь
- § 122. Излучение диполя
- § 123. Электромагнитный спектр
- § 124. Квантовая природа излучения
- ГЛАВА 19. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- § 126. Поведение электромагнитной волны на границе двух сред
- § 127. Естественный и поляризованный свет. Поляризация при отражении
- § 128. Распространение световых волн в среде с градиентом показателя преломления
- § 129. Распространение радиоволн
- § 130. Радиолокация
- ГЛАВА 20. ИНТЕРФЕРЕНЦИОННЫЕ ЯВЛЕНИЯ
- § 131. Сложение волн от двух источников
- § 132. Когерентность
- § 133. Интерференция в пластинке
- § 134. Полосы равной толщины и полосы равного наклона
- § 135. Практические применения интерференции
- ГЛАВА 21. РАССЕЯНИЕ
- § 136. Вторичное излучение
- § 137. Дифракция волн на отверстиях
- § 138. Система беспорядочно расположенных рассеивателей
- § 139. Поведение сплошной однородной среды
- § 140. Рассеяние в неоднородной среде
- § 141. Дифракционная решетка
- § 142. Направленные излучатели радиоволн
- § 142а. Голография
- ГЛАВА 22. ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ НА КРИСТАЛЛЕ
- § 143. Кристалл как дифракционная решетка
- § 144. Определение параметров элементарной ячейки кристалла
- § 145. Интенсивность дифракционных лучей
- § 146. Методы рентгеновского анализа
- ГЛАВА 23. ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ
- § 147. Анизотропия поляризуемости
- § 148. Раснространение света в одноосных кристаллах
- § 149. Поляризаторы. Исследование поляризационного состояния света
- § 150. Кристаллическая пластинка между «скрещенными» николями
- § 151. Двойное лучепреломление, вызванное внешним воздействием
- § 152. Оптическая активность
- § 153. Принципы теории оптической активности
- ГЛАВА 24. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 155. Опытные подтверждения принципа постоянства скорости света
- § 156. Время в теории относительности
- § 157. Масса
- § 158. Энергия
- § 159. Дефект массы
- § 160. Принцип эквивалентности и понятие об общей теории относительности
- ГЛАВА 25. КВАНТОВАЯ ПРИРОДА ПОЛЯ
- § 161. Фотон
- § 162. Фотоэлектрический эффект
- § 163. Флуктуации светового потока
- § 164. Закон Кирхгофа
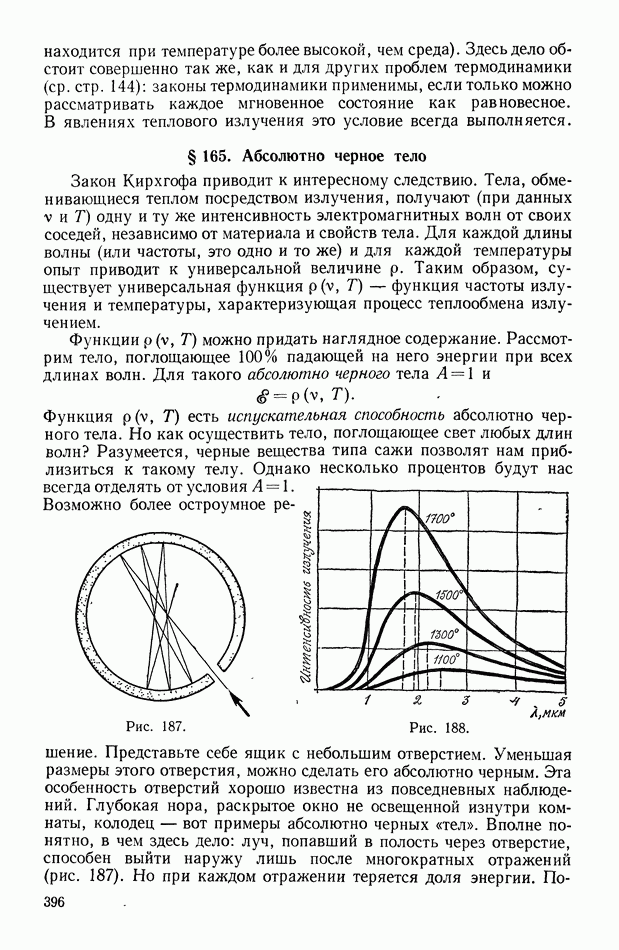
- § 165. Абсолютно черное тело
- § 166. Теория теплового излучения
- § 166а. Стимулированное излучение
- § 166б, Люминесценция
- ЧАСТЬ III. СТРОЕНИЕ И СВОЙСТВА ВЕЩЕСТВА
- § 167. Движение заряженной частицы в электрическом и магнитном полях
- § 168. Получение пучков заряженных частиц
- § 169. Электронные линзы
- § 170. Электронный микроскоп
- § 171. Электронные и ионные проекторы
- § 172. Электронно-лучевая трубка
- § 173. Масс-спектрограф
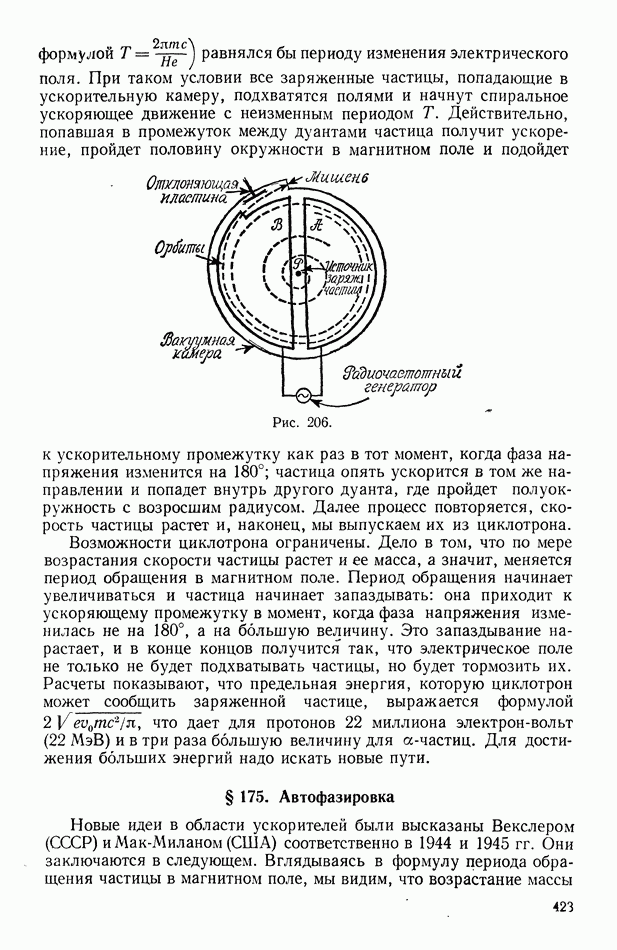
- § 174. Ускорители заряженных частиц
- § 175. Автофазировка
- § 176. Синхрофазотрон. Синхротрон
- § 177. Ионизованный газ
- § 178. Электрический разряд в газе
- § 178а. Плазма
- Вещество в состоянии плазмы.
- Плазма в магнитном поле.
- Проблемы устойчивости.
- ГЛАВА 27. ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ
- § 179. Дифракция электронов
- § 180. Основные идеи квантовой механики
- § 181. Принцип неопределенности
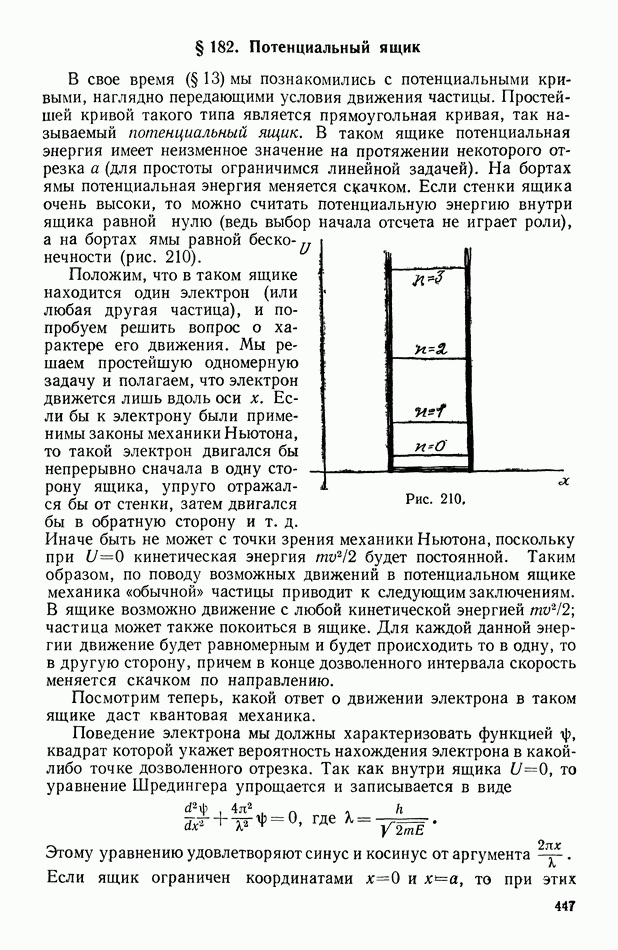
- § 182. Потенциальный ящик
- § 183. Что дает решение уравнения Шредингера
- § 184. Туннельный переход
- ГЛАВА 28. СТРОЕНИЕ АТОМА
- § 185. Энергетические уровни атома водорода
- § 186. Квантовые числа
- § 187. Электронное облако для s- и p-состояний
- § 188. Принцип Паули
- § 189. Отклонение атомного пучка в магнитном поле
- § 190. Спин электрона
- § 191. Магнитные моменты атомов
- § 192. Периодический закон Менделеева
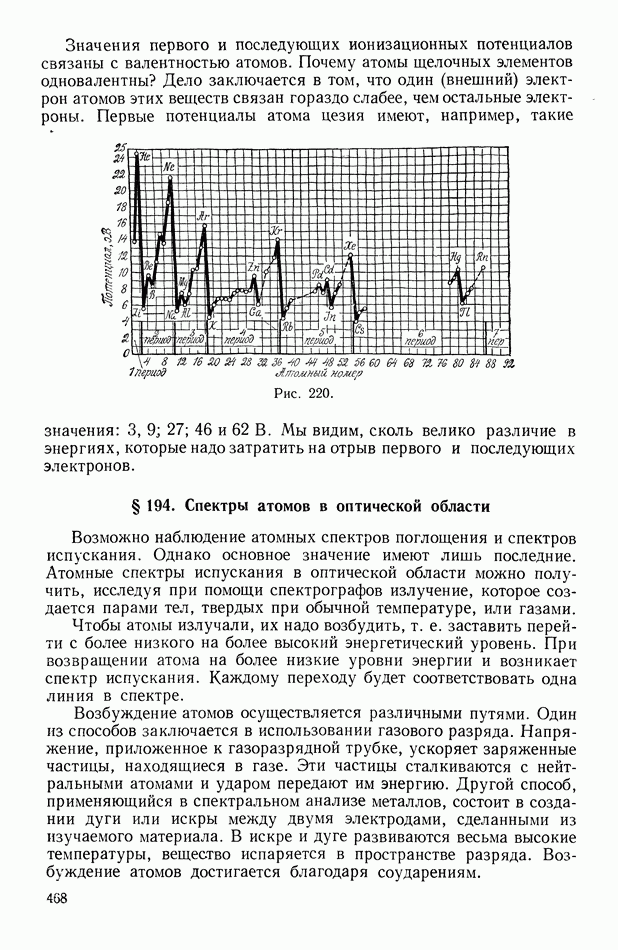
- § 193. Ионизационные потенциалы
- § 194. Спектры атомов в оптической области
- § 195. Атомные рентгеновские спектры
- ГЛАВА 29. МОЛЕКУЛА
- § 196. Химическая связь
- § 197. Геометрия молекул
- § 198. Электронная оболочка молекулы
- § 199. Энергетические уровни молекул
- § 200. Вращательный спектр молекул
- § 201. Инфракрасный колебательно-вращательный спектр
- Колебания многоатомной молекулы.
- § 202. Комбинационное рассеяние света
- § 203. Электронный спектр поглощения
- § 204. Магнитный резонанс
- § 205. Квадрупольный резонанс
- § 206. Газовые лазеры
- ГЛАВА 30. АТОМНОЕ ЯДРО
- § 207. Экспериментальные методы ядерной физики
- § 208. Частицы, входящие в состав ядра
- § 209. Масса и энергия атомного ядра
- § 210. Спин и магнитный момент ядра
- § 211. Силы взаимодействия нуклонов
- § 212. Нуклоны в ядре
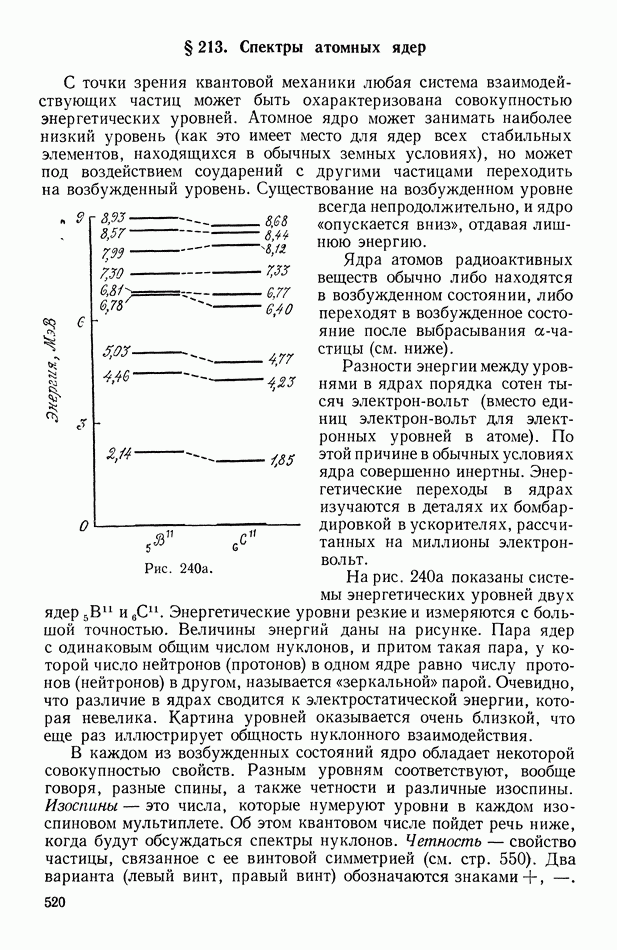
- § 213. Спектры атомных ядер
- § 214. Нейтрино бета-распада
- § 215. Общие закономерности химических и ядерных превращений
- § 216. Радиоактивность
- § 217. Ядерные реакции
- § 217а. Реакции деления тяжелых ядер
- § 217б. Цепная реакция
- § 217в. Принципы действия ядерного реактора
- § 217г. Искусственные радиоактивные продукты
- § 218. Термоядерные реакции
- ГЛАВА 31. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 219. Термин «элементарная» частица
- § 220. Взаимодействие быстродвижущихся электронов
- § 221. Мезонная теория взаимодействия нуклонов
- § 222. Мезоны
- § 223. Релятивистская теория электрона
- § 224. Рождение и аннигиляция пар частиц
- § 225. Частицы и античастицы
- § 226. Асимметрия элементарных частиц
- § 226а. Барионный спектр
- § 2266. Кварки
- ГЛАВА 32. АТОМНОЕ СТРОЕНИЕ ТЕЛ
- § 227. Поликристаллическое вещество и монокристаллы
- § 228. Пространственная решетка
- § 229. Выбор ячейки. Симметрия кристалла
- § 230. Упаковка частиц в кристалле
- § 231. Молекулярный кристалл
- § 232. Плотные упаковки шаров
- § 233. Примеры кристаллических структур
- § 234. Тепловые колебания в кристалле
- § 235. Тепловые волны
- § 236. Тепловое расширение
- § 237. Дефекты кристалла
- § 238. Ближний порядок. Жидкости
- § 239. Аморфные тела
- § 240. Дальний и ближний порядок расположения атомов в сплавах
- § 241. Жидкие кристаллы
- § 242. Полимерные вещества
- § 242а. Биологические макромолекулы
- ГЛАВА 33. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
- § 244. Фазовые превращения
- § 244а. Диаграмма состояния и свойства гелия
- § 245. Условия устойчивого состояния фазы
- § 246. Метастабильные состояния
- § 247. Превращения газ жидкость
- § 248. Сжижение газов
- § 249. Превращения газ кристалл
- § 250. Превращения жидкость кристалл
- § 251. Превращения кристалл-кристалл
- § 252. Диффузия в твердых телах
- ГЛАВА 34. ДЕФОРМАЦИЯ ТЕЛ
- § 254. Пластические свойства
- § 255. Предел прочности
- § 256. Механические свойства поликристаллического материала
- § 257. Влияние поверхностно-активных веществ на деформацию
- § 258. Разрушение материалов под действием потока частиц
- ГЛАВА 35. ДИЭЛЕКТРИКИ
- § 259. Связь между диэлектрической проницаемостью и поляризуемостью молекулы
- § 260. Поляризация полярных и неполярных молекул
- § 261. Аддитивность молекулярной рефракции
- § 262. Пиро- и пьезоэлектрики
- § 262а. Сегнетоэлектрики
- ГЛАВА 36. МАГНЕТИКИ
- § 263. Три класса магнетиков
- § 264. Диамагнетизм
- § 265. Парамагнетизм
- § 266. Ферромагнетизм
- ГЛАВА 37. ЭЛЕКТРОННОЕ СТРОЕНИЕ И СВОЙСТВА ТЕЛ
- § 267. Свободные электроны
- § 268. Энергетические уровни в твердом теле
- § 269. Электронный газ
- § 270. Проводимость
- § 271. Сверхпроводимость
- § 272. Полупроводники
- § 273. Эмиссия электронов
- § 274. Фотоэлектрический эффект
- § 275. Запирающие слои
- § 276. Контактная разность потенциалов
- § 276a. Электролюминесценция полупроводников
- § 277. Распределение зарядов в неравномерно нагретом теле
- § 278. Термоэлектродвижущая сила
- § 279. Выделение тепла в электрических цепях
- § 280. Применения термоэлектрического эффекта